Dark Matter Investigation Using Double Beta Decay Experiments †
Abstract
:1. Introduction
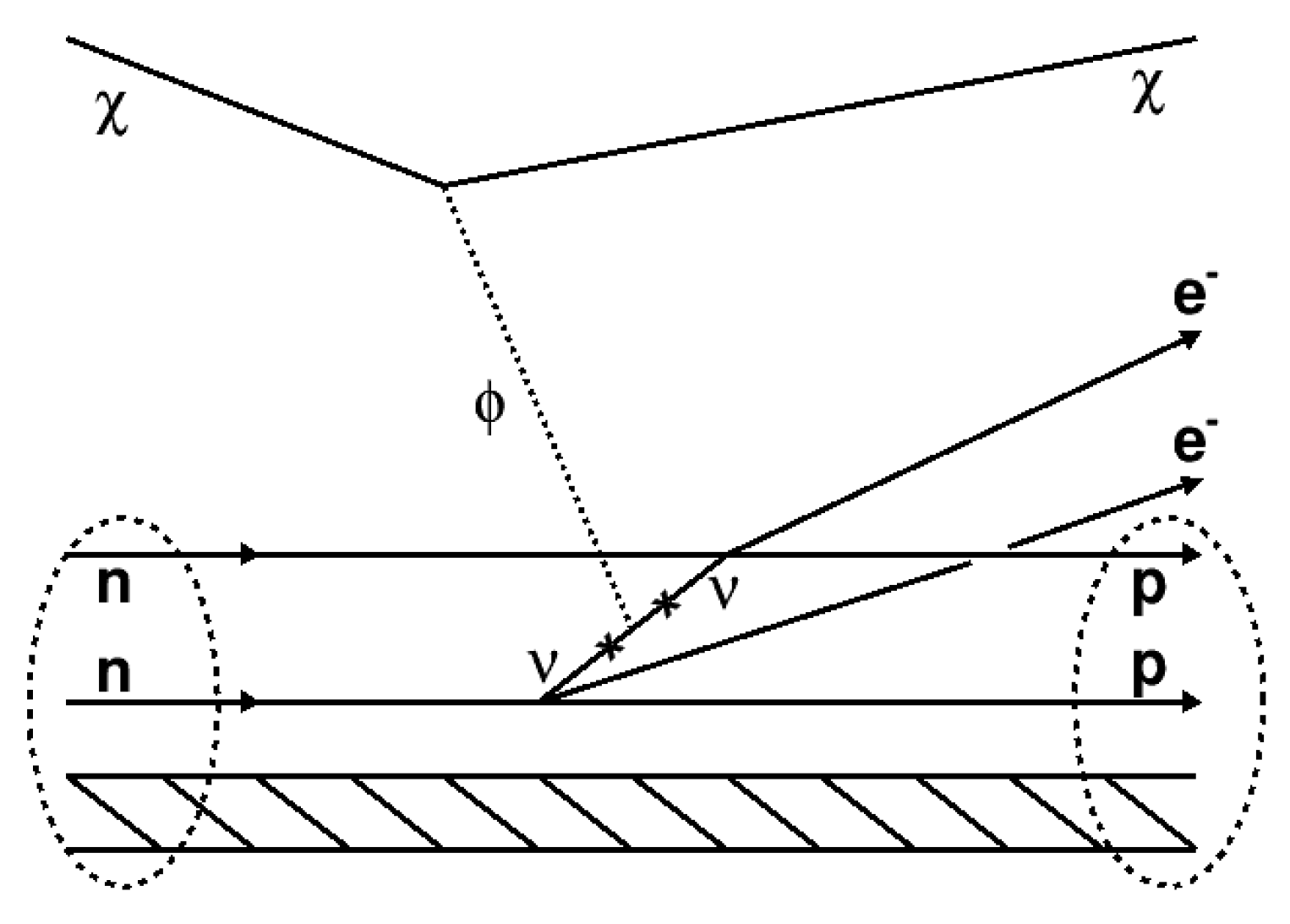
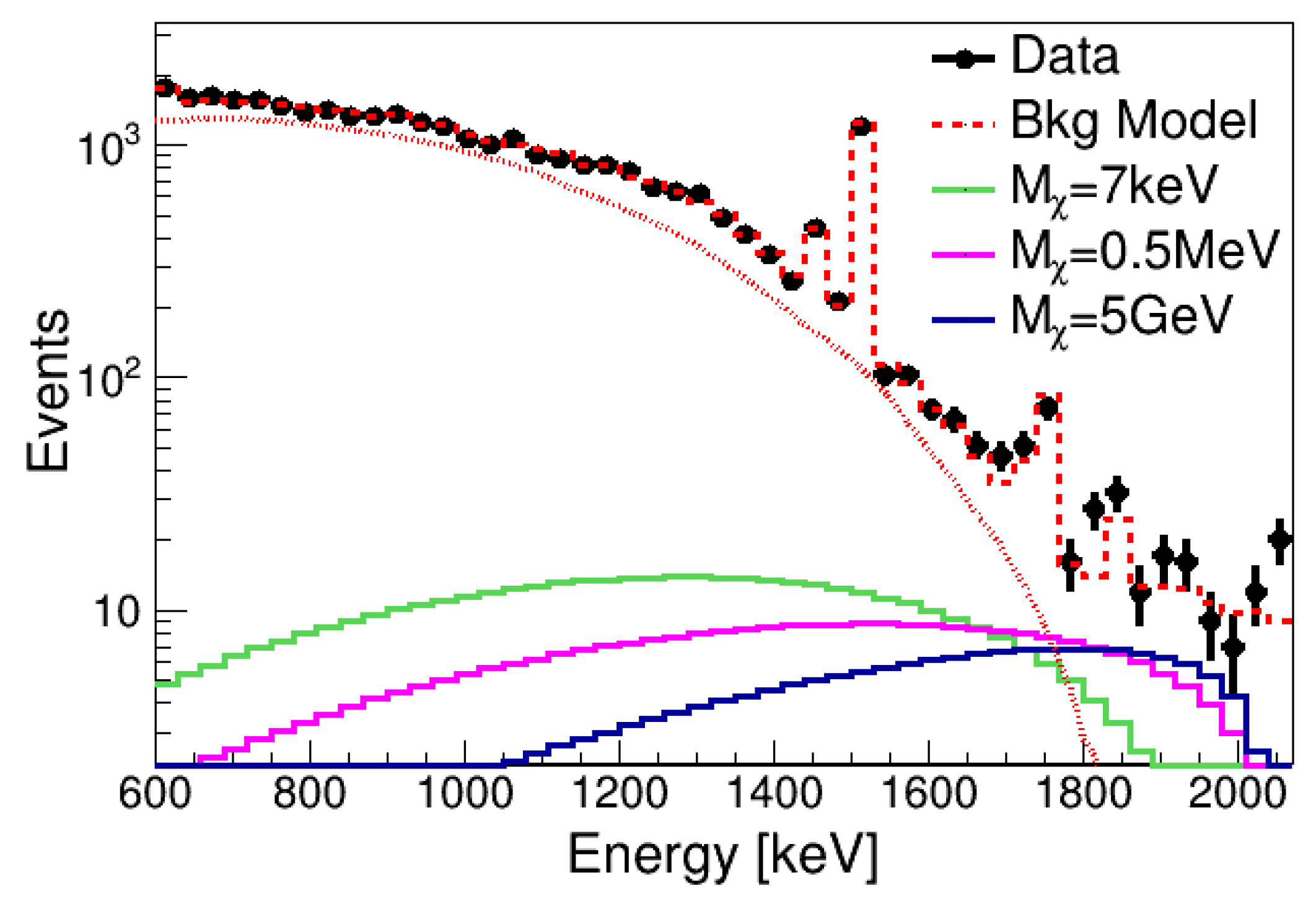
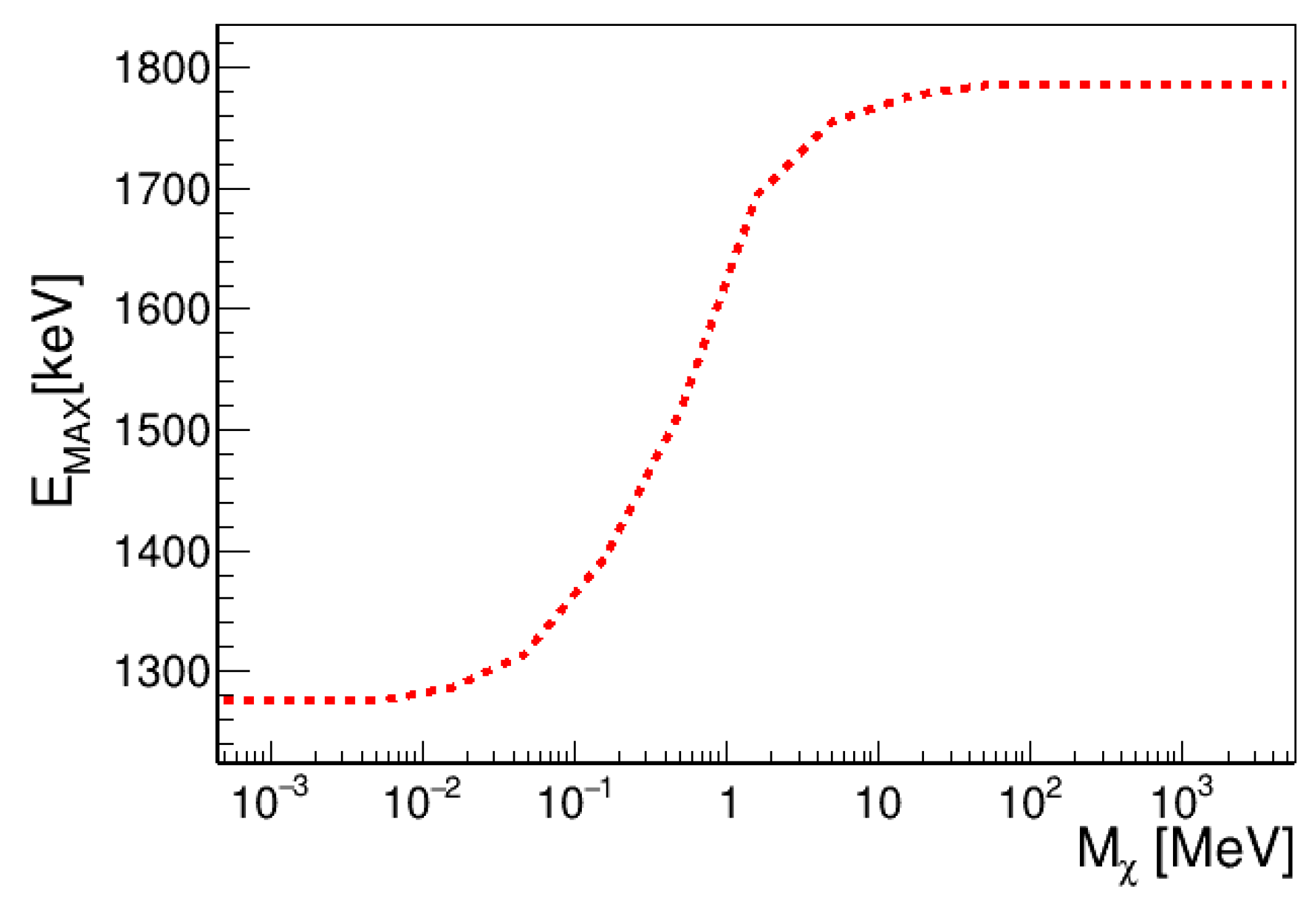
2. Expected Energy Distribution
3. Conclusions and Outlooks
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| DM | Dark Matter. |
| SM | Standard Model. |
References
- Zeldovich, Y.B.; Khlopov, M.Y. Possibilities of studying the nature of neutrino mass in double beta decay. Pisma Zh. Eksp. Teor. Fiz. 1981, 34, 148–152. (In Russian) [Google Scholar]
- Schechter, J.; Valle, J.W.F. Neutrinoless double-β decay in SU(2) X U(1) theories. Phys. Rev. D 1982, 25, 2951–2954. [Google Scholar] [CrossRef]
- Escudero, M.; Schwetz, T.; Terol-Calvo, J. A seesaw model for large neutrino masses in concordance with cosmology. arXiv 2022. [Google Scholar] [CrossRef]
- Fukugita, M.; Yanagida, T. Barygenesis without grand unification. Phys. Lett. B 1986, 174, 45–47. [Google Scholar] [CrossRef]
- Mandal, S.; Rojas, N.; Srivastava, R.; Valle, J.W. Dark matter as the origin of neutrino mass in the inverse seesaw mechanism. Phys. Lett. B 2021, 821, 136609. [Google Scholar] [CrossRef]
- Arcadi, G.; Profumo, S.; Queiroz, F.; Siqueira, C. Right-handed neutrino dark matter, neutrino masses, and non-standard cosmology in a 2HDM. J. Cosmol. Astropart. Phys. 2020, 2020, 30. [Google Scholar] [CrossRef]
- Dutta, M.; Bhattacharya, S.; Ghosh, P.; Sahu, N. Majorana Dark Matter and Neutrino Mass in a Singlet-Doublet Extension of the Standard Model. In Proceedings of the XXIV DAE-BRNS High Energy Physics Symposium, Jatni, India; Mohanty, B., Swain, S.K., Singh, R., Kashyap, V.K.S., Eds.; Springer Nature: Singapore, 2022; pp. 685–689. [Google Scholar]
- Heeck, J. Phenomenology of Majorons. arXiv 2017, arXiv:1709.07670. [Google Scholar] [CrossRef]
- Manna, S.K.; Sil, A. Majorons Revisited: Light Dark Matter as FIMP. arXiv 2022, arXiv:2212.08404. [Google Scholar] [CrossRef]
- Bernabei, R.; Belli, P.; Cappella, F.; Cerulli, R.; Dai, C.J.; He, H.L.; Incicchitti, A.; Kuang, H.H.; Ma, J.M.; Ma, X.H.; et al. Investigation on light dark matter. Mod. Phys. Lett. A 2008, 23, 2125–2140. [Google Scholar] [CrossRef]
- Dror, J.A.; Elor, G.; McGehee, R. Directly Detecting Signals from Absorption of Fermionic Dark Matter. Phys. Rev. Lett. 2020, 124, 181301. [Google Scholar] [CrossRef] [PubMed]
- Dror, J.A.; Elor, G.; McGehee, R. Absorption of fermionic dark matter by nuclear targets. J. High Energy Phys. 2020, 2020. [Google Scholar] [CrossRef]
- Dror, J.A.; Elor, G.; McGehee, R.; Yu, T.T. Absorption of sub-MeV fermionic dark matter by electron targets. Phys. Rev. D 2021, 103, 035001. [Google Scholar] [CrossRef]
- Kotila, J.; Barea, J.; Iachello, F. Phase-space factors and half-life predictions for Majoron-emitting β−β− decay. Phys. Rev. C 2015, 91, 064310. [Google Scholar] [CrossRef]
- Agostini, M.; Allardt, M.; Bakalyarov, A.M.; Balata, M. Results on ββ decay with emission of two neutrinos or Majorons in 76Ge from GERDA Phase I. Eur. Phys. J. C 2015, 75, 416. [Google Scholar] [CrossRef]
- Hofmann, F.; Wegg, C. 7.1 keV sterile neutrino dark matter constraints from a deep Chandra X-ray observation of the Galactic bulge Limiting Window. Astron. Astrophys. 2019, 625, L7. [Google Scholar] [CrossRef]
- Bernabei, R.; Belli, P.; Montecchia, F.; Nozzoli, F.; Cappella, F.; Incicchitti, A.; Prosperi, D.; Cerulli, R.; Dai, C.J.; He, H.L.; et al. On electromagnetic contributions in WIMP quests. Int. J. Mod. Phys. A 2007, 22, 3155–3168. [Google Scholar] [CrossRef]
- SuperCDMS, Collaboration; Al-Bakry, M.; Alkhatib, I.; Amaral, D.P.D.; Aralis, T.; Aramaki, T.; Arnquist, I.; Langroudy, I.A.; Azadbakht, E.; Banik, S.; et al. A Search for Low-mass Dark Matter via Bremsstrahlung Radiation and the Migdal Effect in SuperCDMS. arXiv 2022, arXiv:2203.02594. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nozzoli, F.; Cernetti, C. Dark Matter Investigation Using Double Beta Decay Experiments. Phys. Sci. Forum 2023, 7, 29. https://doi.org/10.3390/ECU2023-14056
Nozzoli F, Cernetti C. Dark Matter Investigation Using Double Beta Decay Experiments. Physical Sciences Forum. 2023; 7(1):29. https://doi.org/10.3390/ECU2023-14056
Chicago/Turabian StyleNozzoli, Francesco, and Cinzia Cernetti. 2023. "Dark Matter Investigation Using Double Beta Decay Experiments" Physical Sciences Forum 7, no. 1: 29. https://doi.org/10.3390/ECU2023-14056
APA StyleNozzoli, F., & Cernetti, C. (2023). Dark Matter Investigation Using Double Beta Decay Experiments. Physical Sciences Forum, 7(1), 29. https://doi.org/10.3390/ECU2023-14056






