Abstract
Machine improvisation is the ability of musical generative systems to interact with either another music agent or a human improviser. This is a challenging task, as it is not trivial to define a quantitative measure that evaluates the creativity of the musical agent. It is also not feasible to create huge paired corpora of agents interacting with each other to train a critic system. In this paper we consider the problem of controlling machine improvisation by switching between several pre-trained models by finding the best match to an external control signal. We introduce a measure SymTE that searches for the best transfer entropy between representations of the generated and control signals over multiple generative models.
1. Introduction
Learning generative models of complex temporal data is a formidable problem in Machine Learning. In domains such as music, speech or video, deep latent-variable models manage today to generate realistic outputs by sampling from predictive models over a structured latent semantic space. The problem is often further complicated by the need to sample from non-stationary data where the latent features and its statistics change over time. Such situations often occur in music and audio generation, since musical structure and the type or characteristics of musical sounds change during the musical piece. Moreover, in interactive systems the outputs need to be altered so as to fit user specifications, or to match another signal that comes from the environment, which provides the context or constraint for the type of desired outcome produced by the generative system at every instance. In such cases generation by conditional sampling might be impossible due to lack of labeled training data and the need to retrain the models for each case.
We call this problem Improvisation Modeling, since it is often encountered in musical interaction with artificial musical agents that need to balance their own artificial “creativity” with responsiveness to the overall musical context in order to create a meaningful interaction with other musicians. The ability of the artificial musical agent to make decisions and switch its responses by listening to a human improviser is important for establishing the conditions for man-machine co-creation. We consider this as a problem of controlling machine improvisation by switching between several pre-trained models by finding the best match to an external context signal. Since the match can be partially found in different generative domains, we search for best transfer entropy between reduced representations of the generated and context signals across multiple models. The added step of matching in the reduced latent space is one of the innovations of the proposed method, also motivated by theories of cognition that suggest mental representation as lossy data encoding.
In order to allow quantitative analysis of what is happening in the “musical mind”, we base our work on an information theoretic music analysis method of Music Information Dynamics (MID). MID performs structural analysis of music by considering the predictive aspects of music data, quantified by the amount of information passing from past to present in a sound recording or symbolic musical score. We extend the MID idea to include the relation between the generated and context signals and their latent representations, amounting to a total of five factors: the signal past X with its latent encoding Z, the signal present sample Y, a context signal C and its encoding into latent features T. Assuming Markov chain relations between Z-X-Y, we are looking for the smallest latent representation Z that predicts the present Y, while at the same time having maximal mutual information to the latent features T of the constraint signal. For each model we compute transfer entropy between the generated and context latent variables Z and T, respectively, and the present sample Y. It should be noted that our notion of Transfer Entropy is different from the standard definition of directed information between two random variables, since transfer entropy is estimated in the latent space of the generative model and the context signal.
We propose the use of a new metric called Symmetric Transfer Entropy (SymTE) to switch between multiple pre-trained generative models. This means that given any audio context signal, we can use SymTE to effectively switch between multiple outputs of generative models. In the paper we will present the theory and some experimental results of switching pre-trained models according to second musical improvisation input. An important aspect of our model is eliminating the need to re-train the temporal model at each compression rate of Z since estimation of I(Y,Z) is not needed for model selection. Our assumption is that we have several pre-trained generative models(or random generators), each providing one of multiple options for improvised generation. The best model is chosen according to criteria of highest latent transfer entropy by search for the optimal reduced rate for every model, balancing between the quality of signal prediction (predicting Y from full rate Z) and matching between the past latent representation of Z and the latent representation T of the context signal for that model.
1.1. Causal Information
The problem of inferring causal interactions from data was formalized in terms of linear autoregression by Granger [1]. The information-theoretic notion of transfer entropy was formulated by Schreiber [2] not in terms of prediction, like in the Granger case, but in terms of reduction of uncertainty, where transfer entropy from Y to X is the degree to which Y reduced the residual uncertaintly about the future of X after the past of X was already taken into consideration. It can be shown that Granger Causality and Transfer Entropy Are Equivalent for Gaussian Variables [3] Causal entropy measures the uncertainty present in the conditioned distribution of the Y variable sequence given the preceding partial X variable sequence [4].
It can be interpreted as the expected number of bits needed to encode the sequence given the sequentially revealed previous Y variables and side information, . Causal information (also known as the directed information) is a measure of the shared information between sequences of variables when the variables are revealed sequentially [5]. Transfer Entropy is closely related to Causal information, except for considering the influence on Y from past of X only, not including the present instance t. Moreover, in some instances the past of X is considered for shorter past, or even just a single previous sample.
Understanding causality is important for man-machine co-creativity, especially in improvisational settings, since creating a meaningful interaction also requires answering the question of how does the human mind go beyond the data to create an experience [6]. In a way, the current work goes beyond the predictive brain hypothesis [7] to address issues of average predictability and of reduced representation of sensations as “hidden causes” or “distal causes” that maximize the communication between human and a machine in improvisational setting.
1.2. Estimating Transfer Entropy
Several tools and methods have been proposed to estimate transfer entropy. Refs. [8,9] use entropy estimates based on k-nearest neighbours instead of conventional methods such as binnings to estimate mutual information. This can be extended to estimating transfer entropy, as transfer entropy can also be expressed as conditional mutual information. Similarly, methods based on Bayesian estimators [10] and Maximum Likelihood Estimation [11,12] proposed a method to estimate transfer entropy based on Copula Entropy.
Methods using neural networks have also been proposed to estimate mutual information. Mutual Information Neural Estimator (MINE) [13] estimate mutual information by performing gradient descent on neural networks. Intrinsic Transfer Entropy Neural Estimator (ITENE) [14] proposes a two-sample neural network classifiers to estimate transfer entropy. Their method is based on variational bound on KL-divergence and pathwise estimator of Monte Carlo gradients.
Several toolboxes and plugins such as Java Information Dynamics Toolkit (JIDT) [15] provide implementations of the above mentioned methods. However, most of them have not been tested on complex high-dimensional data such as music. To our best knowledge, we are the first to propose a transfer entropy estimation method on complex data such as music and demonstrate results on tasks such as music generation.
2. Methodology
The main objective of our work is to calculate a metric based on transfer entropy to switch between outputs of different generative processes ( say ), so that the output is semantically meaningful to a context signal (C). For a given , we denote the past by and similarly we denote the past of C as .
Transfer Entropy between two sequences is the amount of information passing from the past of one sequence to another, when the dependencies of the past of the other sequence (the sequence own dynamcis) have been already taken into account. In the case of C and model’s i data we have Similarly . Writing mutual information in terms of entropy
Adding and subtracting H(C):
Also:
We consider a sum of (1) and (2), let’s call it symmetrical transfer entropy(SymTE):
As shown in the Appendix A, one can derive the following equivalent expression
where we used a notation for past of the joint pair .
The measure of mutual information between the present and the past of a signal, known as information rate (IR), will be explained in the next section. IR is commonly used in analysis of Music Information Dynamics (MID) that captures the amount of average surprisal in music signals when the next sound event is anticipated from its past. If we assume that the generation of is independent of C given their joint past , then , resulting in
which is a sum of IR of the joint pair and the mutual information between C and regardless of time, minus IR of the separate stream. In other words, the Symmetrical TE is a measure of surprisal present in the joint stream minus the surprisal of each of its component, plus the mutual information (lack of independence) between the individual components. In a way this captures the difference between predictive surprisal when listening to a compound stream versus surprisal when listening separately, with added component of mutual information between the voices regardless of time.
This process is schematically represented in Figure 1 as a combination of Information Rate and Mutual Information estimates for two musical melodies

Figure 1.
Estimate of SymTE as a combination of Information Rate IR and Mutual Information I estimates from a generated X and control signal C.
2.1. Predictive Surprisal Using VMO
The essential step in estimating the predictive surprisal is building a model called Variable Markov Oracle (VMO). Based on Factor Oracle (FO) string matching algorithm VMO was decveloped to allow generative improvisation for real-valued scalar or vector data, such as sequences of audio feature vectors, or data vectors extracted from human poses during dance movements. VMO uses suffix data structure for query-guided audio content generation [16] and multimedia query-matching [17,18]. VMO operates on multivariate time serie data, VMO symbolizing a signal X sampled at time t, , into a sequence , having T states and observation frame labeled by . The labels are formed by following suffix links along the states in an oracle structure, whose value is one of the symbols in a finite sized alphabet .
Predictive surprisal is estimated by constructing an FO automata for different threshold when search for suffix links. At each threshold value, a different oracle graph is created, and for each such oracle, a compression method of Compror (Compression Oracle) [19] algorithm C is used as an approximation to predictive information . Here the entropy H is approximated by a compression algorithm C, and is taken as the number of encoding bits for individual symbols over alphabet S, and is the number of bits in a block-wise encoding that recursively points to repeated sub-sequences [17].
As mentioned in the introduction, one of the advantages of using VMO for mutual information estimation is that it allows instantaneous time-varying estimates of IR based on the local information gain of encoding a signal based on linking it to its similar past. This differs from other methods of mutual information estimation like MINE that averages over the whole signal.
2.2. Border Cases
If , and since , we get and , which is the conditional entropy of X given its past. So TE of a pair of identical streams is its entropy rate.
If C and X are independent, . This is based on the ideal case of IR estimator of the joint sequence being able to reveal the IR of the individual sequences, and additionally capture any new emerging structure resulting from their joint occurrence.
In theory, if C and X are independent, , and , so . Thus, a combination of two streams may add additional information, but in practice it could be that VMO will not be able to find sufficient motifs or additional temporal structure when a mix is done. In such a case it can be that estimate will become negative.
3. Representation Using VQ-VAE
Computing Information Rate and Mutual information for raw audio signals is an extremely challenging and computationally expensive task. We need some form of dimensionality reduction that preserves the semantic meaning of audio (style, musical rules, composer attributes etc) in the latent space. Then, we can estimate IR and MI in the lower dimensional space, quite easily. For our framework, we use a pre-trained Jukebox’s Vector Quantized-Variational Autoencoder (VQ-VAE) [20,21] to encode raw audio files to low-dimensional vectors. VQ-VAE is a type of variational autoencoder that encodes data into a discrete latent space. These discrete codes correspond to continuous vectors in a codebook. Using this, we transform our data into 8192 64-dimensional latent vectors.
4. Switching between Generative Models
In this section, we explain the overall workflow of our method Figure 2. The main objective of our method is to switch between N different generative models to match a given query C. Given training data points (musical sequences), , we compute latent representations/embeddings of each data point to get . For our method, we use the embeddings of a pretrained VQ-VAE encoder from Jukebox. We construct each generative model i as follows: (1) First we convert the query musical signal to the same latent space using Jukebox’s VQ-VAE. (2) We create a for datapoint i (in our case, we assume each datapoint represents a different composer). (3) Finally, we get the output of generative model i by querying with embeddings of C to get , algorithm provided in [16].
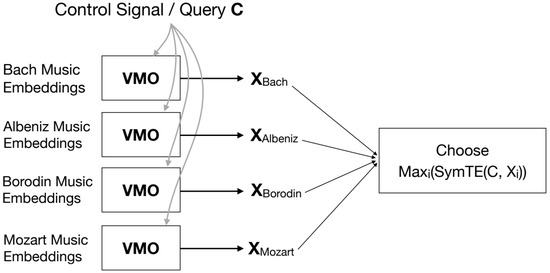
Figure 2.
Our Methodology. Given music embeddings, we construct a VMO for each composer. For a control signal C, we query each composer’s VMO to get . We switch to the output for a control singal C, if is maximum for i.
In order to choose the best output for a given query C, we calculate for all . To calculate , we need to calculate the individual terms of Equation 5, , , and . To calculate , , we use VMO algorithm to create an oracle based on and another oracle for C to retrieve the information rate. To calculate , we use MINE to calculate the mutual information between C and . To calculate , we propose two methods, we combine both and C to create a mixture, based on two methods concatenation and addition of the respective latent vectors. Then, we create an oracle for the combined to calculate the IR.
5. Experiments and Results
We show the advantage of our method compared to other baselines by running simulations on the Labrosa APT dataset [22]. We construct a dataset with audio wav files of 4 different composers (Bach, Albeniz, Borodin, Mozart). We convert each audio file to the corresponding embeddings from a pre-trained Jukebox VQVAE [20,21]. For , we create a VMO for each composer, that can synthesize a sequence of embeddings for a given query/context signal C. For our simulations, we construct C as a segment of music (not included in the VMO construction) from any of the composers. Ideally, our SymTE measure should be high for the (VMO) of the same composer C.
We evaluate the effectiveness of SymTE by measuring the accuracy and F1 score. We conducted 20 trials for all the experiments. Each trial consisted of 20 query/context signals, randomly sampled from either of the 4 composers. For our baselines, we choose a random baseline and another baseline based on the euclidean distance of the embeddings, i.e., choose the composer i’s output, for which the euclidean distance between the embeddings of C and embeddings of is the minimum. Table 1 shows the results of our methods and the baselines. We compare both averaging(avg) and concatenating (concat) the sequences in our experiments.We observe that our concat method achieves the best accuracy and F1-Score compared to all our baselines.

Table 1.
Comparison of Accuracy and F1-Score of our methods and baselines.
6. Discussion and Future Work
The methods presented in the paper use sequence of latent vectors coming from pre-trained neural models of audio. We use VQ-VAE’s embeddings and not the quantized codes, so there is only one quantization happening in this work, which is the VMO’s. The reason why we chose VQ-VAE over other models is that we need strong pre-trained models and the best one currently is considered to be jukebox’s VQ-VAE. Other neural models can be explored as well, as the representation is important for estimation of TE. Our query signals are 256 dimensional (≈0.71 s). Our method should work for longer queries, but the main bottleneck is the complexity of the generative model. We plan to extend this work with more elaborate results with a bigger data set and query size. We also plan to test the framework in terms of computational time, so as to enable real-time switching for music improvisation.
Author Contributions
Conceptualization, S.D., G.A. and V.G.; Software: S.D. and V.G.; Writing: S.D., V.G. and G.A.; Funding Acquisition: S.D. and G.A.; Project Administration: S.D. and G.A.; Supervision: S.D. All authors have read and agreed to the published version of the manuscript.
Funding
This research has received funding from the European Research Council (ERC REACH project) under the European Union’s Horizon 2020 research and innovation programme (Grant agreement #883313).
Institutional Review Board Statement
Not Applicable.
Informed Consent Statement
Not Applicable.
Data Availability Statement
Data available in a publicly accessible repository that does not issue DOIs Publicly available datasets were analyzed in this study. This data can be found here: http://labrosa.ee.columbia.edu/projects/piano/.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A
We provide a proof that Symmetric Transfer Entropy (SymTE), between two sequences X and C, defined as a sum of individual Transfer Entropies given by
equals to
where we used a notation for past of the joint pair
Using the relation
and similarily
We consider a sum of both, let’s call it symmetrical TE:
continuing the derivation
this gives general equality:
plugging back to SymTE:
References
- Granger, C.W. Investigating causal relations by econometric models and cross-spectral methods. Econometrica 1969, 37, 424–438. [Google Scholar] [CrossRef]
- Schreiber, T. Measuring information transfer. Phys. Rev. Lett. 2000, 85, 461. [Google Scholar] [PubMed]
- Barnett, L.; Barrett, A.B.; Seth, A.K. Granger causality and transfer entropy are equivalent for Gaussian variables. Phys. Rev. Lett. 2009, 103, 238701. [Google Scholar] [CrossRef] [PubMed]
- Permuter, H.H.; Kim, Y.H.; Weissman, T. On directed information and gambling. In Proceedings of the 2008 IEEE International Symposium on Information Theory, Toronto, ON, Canada, 6–11 July 2008; pp. 1403–1407. [Google Scholar]
- Massey, J. Causality, feedback and directed information. In Proceedings of the International Symposium on Information Theory and Its Applications (ISITA-90), Honolulu HI, USA, 27–30 November 1990; pp. 303–305. [Google Scholar]
- Griffiths, T.L.; Kemp, C.; Tenenbaum, J.B. Bayesian models of cognition. In The Cambridge Handbook of Computational Psychology; Cambridge University Press: Cambridge, UK, 2008. [Google Scholar]
- Clark, A. Whatever next? Predictive brains, situated agents, and the future of cognitive science. Behav. Brain Sci. 2013, 36, 181–204. [Google Scholar] [CrossRef] [PubMed]
- Runge, J. Conditional independence testing based on a nearest-neighbor estimator of conditional mutual information. In Proceedings of the International Conference on Artificial Intelligence and Statistics, Lanzarote, Spain, 9–11 April 2018; pp. 938–947. [Google Scholar]
- Frenzel, S.; Pompe, B. Partial mutual information for coupling analysis of multivariate time series. Phys. Rev. Lett. 2007, 99, 204101. [Google Scholar] [PubMed]
- Suzuki, T.; Sugiyama, M.; Sese, J.; Kanamori, T. Approximating mutual information by maximum likelihood density ratio estimation. In Proceedings of the New Challenges for Feature Selection in Data Mining and Knowledge Discovery, Antwerp, Belgium, 15 September 2008; pp. 5–20. [Google Scholar]
- Wolpert, D.H.; Wolf, D.R. Estimating functions of probability distributions from a finite set of samples. Phys. Rev. E 1995, 52, 6841. [Google Scholar]
- Ma, J. Estimating transfer entropy via copula entropy. arXiv 2019, arXiv:1910.04375. [Google Scholar]
- Belghazi, M.I.; Baratin, A.; Rajeswar, S.; Ozair, S.; Bengio, Y.; Courville, A.; Hjelm, R.D. Mine: Mutual information neural estimation. arXiv 2018, arXiv:1801.04062. [Google Scholar]
- Zhang, J.; Simeone, O.; Cvetkovic, Z.; Abela, E.; Richardson, M. Itene: Intrinsic transfer entropy neural estimator. arXiv 2019, arXiv:1912.07277. [Google Scholar]
- Lizier, J.T. JIDT: An information-theoretic toolkit for studying the dynamics of complex systems. Front. Robot. AI 2014, 1, 11. [Google Scholar] [CrossRef]
- Wang, C.i.; Dubnov, S. Guided music synthesis with variable markov oracle. In Proceedings of the Tenth Artificial Intelligence and Interactive Digital Entertainment Conference, Raleigh, NC, USA, 3–7 October 2014. [Google Scholar]
- Wang, C.i.; Hsu, J.; Dubnov, S. Music Pattern Discovery with Variable Markov Oracle: A Unified Approach to Symbolic and Audio Representations. In Proceedings of the International Society for Music Information Retrieval Conference, Málaga, Spain, 26–30 October 2015; pp. 176–182. [Google Scholar]
- Gokul, V.; Balakrishnan, G.P.; Dubnov, T.; Dubnov, S. Semantic Interaction with Human Motion Using Query-Based Recombinant Video Synthesis. In Proceedings of the 2019 IEEE Conference on Multimedia Information Processing and Retrieval (MIPR), San Jose, CA, USA, 28–30 March 2019; pp. 379–382. [Google Scholar]
- Lefebvre, A.; Lecroq, T. Compror: On-line lossless data compression with a factor oracle. Inf. Process. Lett. 2002, 83, 1–6. [Google Scholar]
- Dhariwal, P.; Jun, H.; Payne, C.; Kim, J.W.; Radford, A.; Sutskever, I. Jukebox: A generative model for music. arXiv 2020, arXiv:2005.00341. [Google Scholar]
- Van Den Oord, A.; Vinyals, O.; Kavukcuoglu, K. Neural discrete representation learning. In Proceedings of the Advances in Neural Information Processing Systems, Long Beach, CA, USA, 4–9 December 2017; Volume 30. [Google Scholar]
- Poliner, G.E.; Ellis, D.P. A discriminative model for polyphonic piano transcription. EURASIP J. Adv. Signal Process. 2006, 2007, 48317. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).