A Computational Model to Determine Membrane Ionic Conductance Using Electroencephalography in Epilepsy †
Abstract
1. Introduction
2. Materials and Methods
2.1. Dataset
2.2. Hodgkin–Huxley Membrane Model Implementation
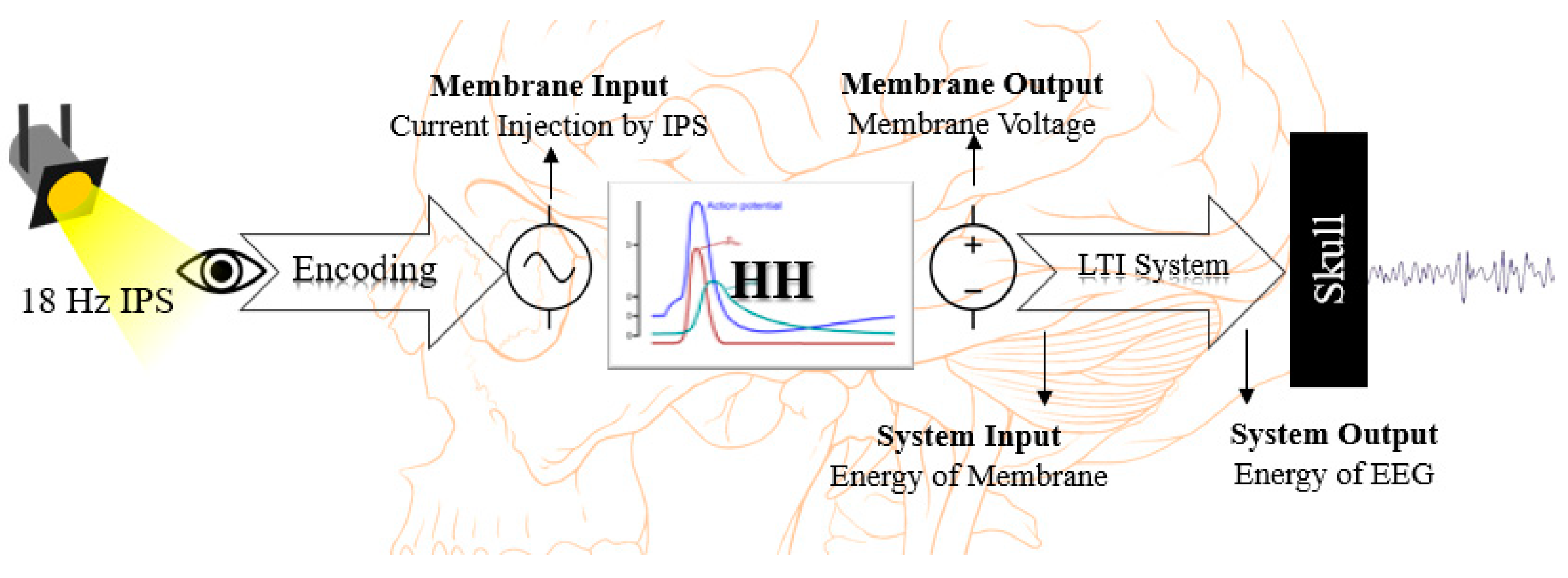
2.3. Encoding Process of Intermittent Photic Stimulation
2.4. Energy Calculation and Principle Linear Time Invariant System
2.5. Hodgkin–Huxley Model Parameter Modification
3. Results and Discussion
3.1. Intermittent Photic Stimulation Encoding
3.2. Energy
3.3. Principle Linear Time Invariant System
3.4. Rates of Ionic Conductance in Epilepsy
3.5. Simulation Signals and Filtering
3.6. Test and Validation
3.6.1. Feature Extraction and Feature Dimensionality Reduction
3.6.2. Classification Model Performance
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Renzel, R.; Tschaler, L.; Mothersill, I.; Imbach, L.L.; Poryazova, R. Sensitivity of long-term EEG monitoring as a second diagnostic step in the initial diagnosis of epilepsy. Epileptic Disord. 2021, 23, 572–578. [Google Scholar] [CrossRef]
- Olejniczak, P. Neurophysiologic basis of EEG. J. Clin. Neurophysiol. 2006, 23, 186–189. [Google Scholar] [CrossRef] [PubMed]
- Zhang, L.; Jiang, X.-Y.; Zhou, D.; Zhang, H.; Bao, S.-M.; Li, J.-M. Postoperative seizure outcome and timing interval to start antiepileptic drug withdrawal: A retrospective observational study of non-neoplastic drug resistant epilepsy. Sci. Rep. 2018, 8, 13782. [Google Scholar] [CrossRef] [PubMed]
- Biedermann, J.; Braunbeck, S.; Plested, A.J.R.; Sun, H. Nonselective cation permeation in an AMPA-type glutamate receptor. Proc. Natl. Acad. Sci. USA 2021, 118, e2012843118. [Google Scholar] [CrossRef] [PubMed]
- Worrell, G.A.; Lagerlund, T.D.; Sharbrough, F.W.; Brinkmann, B.H.; Busacker, N.E.; Cicora, K.M.; O’Brien, T.J. Localization of the epileptic focus by low-resolution electromagnetic tomography in patients with a lesion demonstrated by MRI. Brain Topogr. 2000, 12, 273–282. [Google Scholar] [CrossRef]
- Tadel, F.; Baillet, S.; Mosher, J.C.; Pantazis, D.; Leahy, R.M. Brainstorm: A User-Friendly Application for MEG/EEG Analysis. Comput. Intell. Neurosci. 2011, 2011, 879716. [Google Scholar] [CrossRef]
- Grech, R.; Cassar, T.; Muscat, J.; Camilleri, K.P.; Fabri, S.G.; Zervakis, M.; Xanthopoulos, P.; Sakkalis, V.; Vanrumste, B. Review on solving the inverse problem in EEG source analysis. J. Neuroeng. Rehabil. 2008, 5, 25. [Google Scholar] [CrossRef]
- Gao, F.; Song, X.; Zhu, D.; Wang, X.; Hao, A.; Nadler, J.V.; Zhan, R.Z. Dendritic morphology, synaptic transmission, and activity of mature granule cells born following pilocarpine-induced status epilepticus in the rat. Front. Cell. Neurosci. 2015, 9, 384. [Google Scholar] [CrossRef]
- Sun, H.; Takesian, A.E.; Wang, T.T.; Lippman-Bell, J.J.; Hensch, T.K.; Jensen, F.E. Early Seizures Prematurely Unsilence Auditory Synapses to Disrupt Thalamocortical Critical Period Plasticity. Cell Rep. 2018, 23, 2533–2540. [Google Scholar] [CrossRef]
- Faber, D.S.; Pereda, A.E. Two Forms of Electrical Transmission Between Neurons. Front. Mol. Neurosci. 2018, 11, 427. [Google Scholar] [CrossRef]
- Aminoff, M.J. Aminoff’s Electrodiagnosis in Clinical Neurology, 6th ed.; Elsevier Inc.: Amsterdam, The Netherlands, 2012; ISBN 978-1-4557-0308-1. [Google Scholar]
- Rose, C.R.; Felix, L.; Zeug, A.; Dietrich, D.; Reiner, A.; Henneberger, C. Astroglial Glutamate Signaling and Uptake in the Hippocampus. Front. Mol. Neurosci. 2018, 10, 451. [Google Scholar] [CrossRef] [PubMed]
- Miyachi, E.-I.; Kawai, F. Voltage-Gated Ion Channels in Human Photoreceptors: Na+ and Hyperpolarization-Activated Cation Channels. In The Neural Basis of Early Vision; Kaneko, A., Ed.; Springer: Tokyo, Japan, 2003; ISBN 978-4-431-68449-7. [Google Scholar]
- Kerr, C.C.; Rennie, C.J.; Robinson, P.A. Physiology-based modeling of cortical auditory evoked potentials. Biol. Cybern. 2008, 98, 171–184. [Google Scholar] [CrossRef] [PubMed]
- Robinson, P.A.; Rennie, C.J.; Rowe, D.L.; O’Connor, S.C.; Gordon, E. Multiscale brain modelling. Philos. Trans. R. Soc. B Biol. Sci. 2005, 360, 1043–1050. [Google Scholar] [CrossRef]
- Najafi, T.; Jaafar, R.; Remli, R.; Zaidi Wan, A.W.; Chellappan, K. Brain Dynamics in Response to Intermittent Photic Stimulation in Epilepsy. Int. J. Online Biomed. Eng. 2022, 18, 80–95. [Google Scholar] [CrossRef]
- Hodgkin, A.L.; Huxley, A.F. A quantitative description of membrane current and its application to conduction and excitation in nerve. J. Physiol. 1952, 117, 500–544. [Google Scholar] [CrossRef]
- Tuckwell, H.C. Introduction to Theoretical Neurobiology; Cambridge Studies in Mathematical Biology; Cambridge University Press: Cambridge, UK, 1988; Volume 2. [Google Scholar] [CrossRef]
- Goldwyn, J.H.; Shea-Brown, E. The what and where of adding channel noise to the Hodgkin-Huxley equations. PLoS Comput. Biol. 2011, 7, e1002247. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, K.; Yuan, Y.; Sui, D.; Zhang, H. Effects of Maximal Sodium and Potassium Conductance on the Stability of Hodgkin-Huxley Model. Comput. Math. Methods Med. 2014, 2014, 761907. [Google Scholar] [CrossRef] [PubMed]
- Bhattacharya, B.S.; Patterson, C.; Galluppi, F.; Durrant, S.J.; Furber, S. Engineering a thalamo-cortico-thalamic circuit on spinnaker: A preliminary study toward modeling sleep and wakefulness. Front. Neural Circuits 2014, 8, 46. [Google Scholar] [CrossRef]
- Skinner, F.K. Moving beyond Type I and Type II neuron types. F1000Research 2013, 2, 19. [Google Scholar] [CrossRef] [PubMed]
- Brunel, N.; Chance, F.S.; Fourcaud, N.; Abbott, L.F. Effects of synaptic noise and filtering on the frequency response of spiking neurons. Phys. Rev. Lett. 2001, 86, 2186–2189. [Google Scholar] [CrossRef] [PubMed]
- Rowat, P. Interspike interval statistics in the stochastic Hodgkin-Huxley model: Coexistence of gamma frequency bursts and highly irregular firing. Neural Comput. 2007, 19, 1215–1250. [Google Scholar] [CrossRef] [PubMed]
- Xu, L.; Qi, G.; Ma, J. Modeling of memristor-based Hindmarsh-Rose neuron and its dynamical analyses using energy method. Appl. Math. Model. 2022, 101, 503–516. [Google Scholar] [CrossRef]
- Usha, K.; Sreepriya, M.K.; Subha, P.A. Energy consumption in Hodgkin–Huxley type fast spiking neuron model exposed to an external electric field. Perspect. Sci. 2016, 8, 132–134. [Google Scholar] [CrossRef]
- Grider, M.H.; Jessu, R.; Kabir, R. Physiology, Action Potential; Springer Nature: Treasure Island, FL, USA, 2022. [Google Scholar]
- Graaf, D.; De Graaf, T.A.; Gross, J.; Paterson, G.; Rusch, T.; Sack, A.T.; Thut, G. Alpha-Band Rhythms in Visual Task Performance: Phase- Locking by Rhythmic Sensory Stimulation. PLoS ONE 2013, 8, e60035. [Google Scholar] [CrossRef] [PubMed]
- Mathewson, K.E.; Basak, C.; Maclin, E.L.; Low, K.A.; Boot, W.R.; Kramer, A.F.; Fabiani, M.; Gratton, G. Different slopes for different folks: Alpha and delta EEG power predict subsequent video game learning rate and improvements in cognitive control tasks. Psychophysiology 2012, 49, 1558–1570. [Google Scholar] [CrossRef] [PubMed]
- Thut, G.; Schyns, P.G.; Gross, J.; Rosenblum, M. Entrainment of perceptually relevant brain oscillations by non-invasive rhythmic stimulation of the human brain. Front. Psychol. 2011, 2, 170. [Google Scholar] [CrossRef]
- Rosa, M.J.; Kilner, J.; Blankenburg, F.; Josephs, O.; Penny, W. Estimating the transfer function from neuronal activity to BOLD using simultaneous EEG-fMRI. Neuroimage 2010, 49, 1496–1509. [Google Scholar] [CrossRef]
- Fabri, G.S.; Camilleri, K.P.; Cassar, T. Parametric Modelling of EEG Data for the Identification of Mental Tasks. In Biomedical Engineering, Trends in Electronics, Communications and Software; IntechOpen: London, UK, 2011. [Google Scholar]
- Narasimhan, S.V. Pole-zero spectral modeling of EEG. Signal Process. 1989, 18, 17–32. [Google Scholar] [CrossRef]
- Groppa, S.; Siebner, H.R.; Kurth, C.; Stephani, U.; Siniatchkin, M. Abnormal response of motor cortex to photic stimulation in idiopathic generalized epilepsy. Epilepsia 2008, 49, 2022–2029. [Google Scholar] [CrossRef]
- Barker-Haliski, M.; Steve White, H. Glutamatergic mechanisms associated with seizures and epilepsy. Cold Spring Harb. Perspect. Med. 2015, 5, a022863. [Google Scholar] [CrossRef]
- Czapiński, P.; Blaszczyk, B.; Czuczwar, S.J. Mechanisms of action of antiepileptic drugs. Curr. Top. Med. Chem. 2005, 5, 3–14. [Google Scholar] [CrossRef] [PubMed]
- Demarque, M.; Villeneuve, N.; Manent, J.-B.; Becq, H.; Represa, A.; Ben-Ari, Y.; Aniksztejn, L. Glutamate transporters prevent the generation of seizures in the developing rat neocortex. J. Neurosci. 2004, 24, 3289–3294. [Google Scholar] [CrossRef] [PubMed]
- Raimondo, J.V.; Burman, R.J.; Katz, A.A.; Akerman, C.J. Ion dynamics during seizures. Front. Cell. Neurosci. 2015, 9, 419. [Google Scholar] [CrossRef] [PubMed]
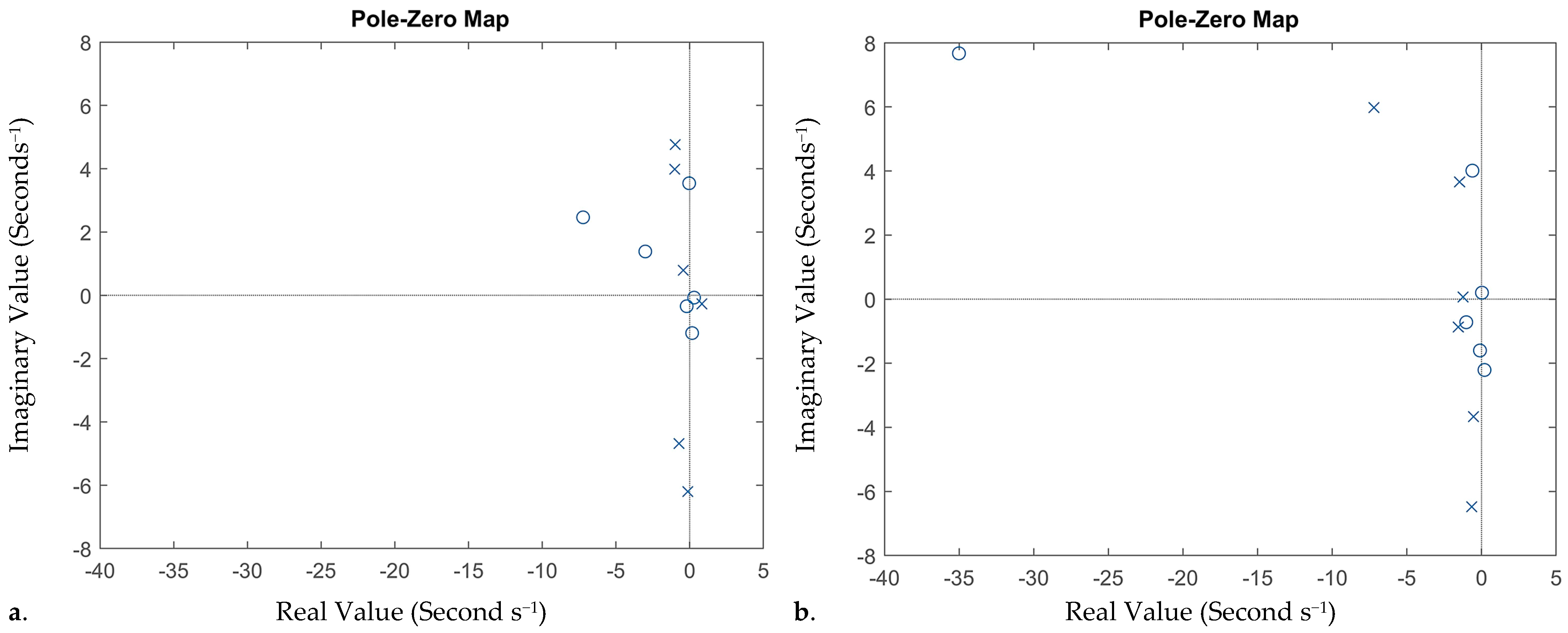


| Gain | Normal | −0.8401 | |||||
| Epilepsy | −0.06001 | ||||||
| First | Second | Third | Fourth | Fifth | Sixth | ||
| Zero | Normal | −7.23 + 2.464i | −3.01 + 1.385i | −0.033 + 3.54i | 0.3002 − 0.072i | 0.1672 − 1.193i | −0.201 − 0.345i |
| Epilepsy | −35.01 + 7.67i | −0.61 + 4.01i | −0.102 − 1.602i | 0.031 + 0.2012i | 0.201 − 2.21i | −1.021 − 0.72i | |
| Pole | Normal | −0.98 + 4.76i | −1.01 + 3.983i | −0.12 − 6.204i | −0.72 − 4.68i | −0.43 + 0.79i | 0.83 − 0.27i |
| Epilepsy | −7.206 + 5.98i | −0.65 − 6.478i | −1.47 + 3.659i | −0.543 − 3.67i | −1.23 + 0.067i | −1.56 − 0.87i |
| Training | Testing | Rates of Ionic Conductance | ||||||||
| Features | Classifier | Acc | Sen | Spc | 1 | 0.5 | 0.6 | 0.7 | ||
| Kurt, P2P | Opt SVM | 80.6% | 78.5% | 81.04% | ✓ | ✗ | ✓ | ✓ | ||
| Kurt, P2P, Alpha | Opt SVM | 82.1% | 89.2% | 78.3% | ✓ | ✗ | ✓ | ✗ | ||
| Skew, RSS | Opt SVM | 81.3% | 71.08% | 69.84% | ✓ | ✗ | ✓ | ✗ | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Najafi, T.; Jaafar, R.; Remli, R.; Zaidi, W.A.W.; Chellappan, K. A Computational Model to Determine Membrane Ionic Conductance Using Electroencephalography in Epilepsy. Phys. Sci. Forum 2022, 5, 45. https://doi.org/10.3390/psf2022005045
Najafi T, Jaafar R, Remli R, Zaidi WAW, Chellappan K. A Computational Model to Determine Membrane Ionic Conductance Using Electroencephalography in Epilepsy. Physical Sciences Forum. 2022; 5(1):45. https://doi.org/10.3390/psf2022005045
Chicago/Turabian StyleNajafi, Tahereh, Rosmina Jaafar, Rabani Remli, Wan Asyraf Wan Zaidi, and Kalaivani Chellappan. 2022. "A Computational Model to Determine Membrane Ionic Conductance Using Electroencephalography in Epilepsy" Physical Sciences Forum 5, no. 1: 45. https://doi.org/10.3390/psf2022005045
APA StyleNajafi, T., Jaafar, R., Remli, R., Zaidi, W. A. W., & Chellappan, K. (2022). A Computational Model to Determine Membrane Ionic Conductance Using Electroencephalography in Epilepsy. Physical Sciences Forum, 5(1), 45. https://doi.org/10.3390/psf2022005045






