What Is Randomness? The Interplay between Alpha Entropies, Total Variation and Guessing ^†

Abstract

In many areas of computer science, it is of primary importance to assess the randomness of a certain variable X. Many different criteria can be used to evaluate randomness, possibly after observing some disclosed data. A “sufficiently random” X is often described as “entropic”. Indeed, Shannon’s entropy is known to provide a resistance criterion against modeling attacks. More generally one may consider the Rényi $\alpha$-entropy where Shannon’s entropy, collision entropy and min-entropy are recovered as particular cases $\alpha =1$, 2 and $+\infty$, respectively. Guess work or guessing entropy is also of great interest in relation to $\alpha$-entropy. On the other hand, many applications rely instead on the “statistical distance”, also known as “total variation" distance, to the uniform distribution. This criterion is particularly important because a very small distance ensures that no statistical test can effectively distinguish between the actual distribution and the uniform distribution. In this paper, we establish optimal lower and upper bounds between $\alpha$-entropy, guessing entropy on one hand, and error probability and total variation distance to the uniform on the other hand. In this context, it turns out that the best known “Pinsker inequality” and recent “reverse Pinsker inequalities” are not necessarily optimal. We recover or improve previous Fano-type and Pinsker-type inequalities used for several applications.

1. Some Well-Known “Randomness” Measures

It is of primary importance to assess the “randomness” of a certain random variable X, which represents some identifier, cryptographic key, signature or any type of intended secret. Applications include pseudo-random bit generators [1], general cipher security [2], randomness extractors [3] and hash functions ([4], Chapter 8), physically unclonable functions [5], true random number generators [6], to list but a few. In all of these examples, X takes finitely many values $x\in \{x_1,x_2,\dots ,x_M\}$ with probabilities $p_X\left(x\right)=\mathbb{P}(X=x)$. In this paper, it will be convenient to denote

$$p_{\left(1\right)}\ge p_{\left(2\right)}\ge \cdots \ge p_{\left(M\right)}$$

(1)

any rearrangement of the probabilities $p\left(x\right)$ in descending order (where ties can be resolved arbitrarily), $p_{\left(1\right)}={max}_x{p}_X\left(x\right)$ is the maximum probability, $p_{\left(2\right)}$ the second maximum, etc. In addition, we need to define the cumulative sums

$$P_{\left(k\right)}\triangleq p_{\left(1\right)}+\dots +p_{\left(k\right)}(k=1,2,\dots ,M)$$

(2)

where, in particular, $P_{\left(M\right)}=1$.

Many different criteria can be used to evaluate the randomness of X or its distribution $p_X$, depending on the type of attack that can be carried out to recover the whole or part of the secret, possibly after observing disclosed data Y. The observed random variable Y can be any random variable and is not necessarily discrete. The conditional probability distribution of X having observed $Y=y$ is denoted by $p_{X|y}$ to distinguish it from from the unconditional distribution $p_X$. To simplify the notation, we write

$$\begin{array}{cc}\hfill p\left(x\right)& \triangleq p_X\left(x\right)=\mathbb{P}(X=x)\hfill \end{array}$$

(3)

$$\begin{array}{cc}\hfill p\left(x\right|y)& \triangleq p_{X|y}\left(x\right)=\mathbb{P}(X=x|Y=y).\hfill \end{array}$$

(4)

A “sufficiently random” secret is often described as “entropic” in the literature. Indeed, Shannon’s entropy

$$H\left(X\right)=H\left(p\right)\triangleq \sum _{x}p\left(x\right)log\frac{1}{p\left(x\right)}=\mathbb{E}log\frac{1}{p\left(X\right)}$$

(5)

(with the convention $0log\frac{1}{0}=0$) is known to provide a resistance criterion against modeling attacks. It was introduced by Shannon as a measure of uncertainty of X. The average entropy after having observed Y is the usual conditional entropy

$$H\left(X\right|Y)\triangleq {\mathbb{E}}_{y}H\left(p_{X|y}\right)=\mathbb{E}log\frac{1}{p\left(X\right|Y)}.$$

(6)

A well-known generalization of Shannon’s entropy is the Rényi entropy of order $\alpha >0$ or $\alpha$-entropy

$$H_{\alpha }\left(X\right)=H_{\alpha }\left(p\right)\triangleq \frac{1}{1-\alpha }log\sum _{x}p{\left(x\right)}^{\alpha }=\frac{\alpha }{1-\alpha }log{\parallel p_X\parallel }_{\alpha }$$

(7)

where, by continuity as $\alpha \to 1$, the 1-entropy $H_1\left(X\right)=H\left(X\right)$ is Shannon’s entropy. One may consider many different definitions of conditional $\alpha$-entropy [7], but for many applications the preferred choice is Arimoto’s definition [8,9,10]

$$H_{\alpha }\left(X\right|Y)\triangleq \frac{\alpha }{1-\alpha }log{\mathbb{E}}_y{\parallel p_{X|y}\parallel }_{\alpha }$$

(8)

where the expectation over Y is taken over the “$\alpha$-norm” inside the logarithm. (Strictly speaking, ${\parallel ·\parallel }_{\alpha }$ is not a norm when $\alpha <1$.)

For $\alpha =2$, the collision entropy

$$H_2\left(X\right)=H_2\left(p\right)=log\frac{1}{\mathbb{P}(X=X^{\prime })},$$

(9)

where $X^{\prime }$ is an independent copy of X, is often used to ensure security against collision attacks. Perhaps one of the most popular criteria is the min-entropy defined when $\alpha \to +\infty$ as

$$H_{\infty }\left(X\right)=H_{\infty }\left(p\right)=log\frac{1}{p_{\left(1\right)}}=log\frac{1}{1-{\mathbb{P}}_e\left(X\right)},$$

(10)

whose maximization is equivalent to a probability criterion to ensure a worst-case security level. Arimoto’s conditional ∞-entropy takes the form

$$H_{\infty }\left(X\right|Y)=log\frac{1}{1-{\mathbb{P}}_e\left(X\right|Y)}$$

(11)

where we have noted

$$\begin{array}{cc}\hfill {\mathbb{P}}_e\left(X\right)={\mathbb{P}}_e\left(p\right)& \triangleq 1-p_{\left(1\right)}=1-P_{\left(1\right)}\hfill \end{array}$$

(12)

$$\begin{array}{cc}\hfill {\mathbb{P}}_e\left(X\right|Y)& \triangleq {\mathbb{E}}_y{\mathbb{P}}_e\left(X\right|y).\hfill \end{array}$$

(13)

The latter quantities correspond to the minimum probability of decision error using a MAP (maximum a posteriori probability) rule (see, e.g., [11]).

Guess work or guessing entropy [2,12]

$$G\left(X\right)=G\left(p_X\right)\triangleq \sum _{i=1}^{M}i·p_{\left(i\right)}$$

(14)

and more generally guessing moments of order $\rho >0$ or $\rho$-guessing entropy

$$G_{\rho }\left(X\right)=G_{\rho }\left(p_X\right)\triangleq \sum _{i=1}^M{i}^{\rho }·p_{\left(i\right)}$$

(15)

are also of great interest in relation to $\alpha$-entropy [10,13,14]. The conditional versions given observation Y are the expectations

$$G_{\rho }\left(X\right|Y)\triangleq {\mathbb{E}}_y{G}_{\rho }\left(X\right|y).$$

(16)

When $\rho =1$, this represents the average number of guesses that an attacker has to make to guess the secret X correctly after having observed Y [13].

2. Statistical (Total Variation) Distance to the Uniform Distribution

As shown in the sequel, all quantities introduced in the preceding section (H, $H_{\alpha }$, ${\mathbb{P}}_e$, G, $G_{\rho }$) have many properties in common. In particular, each of these quantities attains

• its minimum value for a delta (Dirac) distribution $p=\delta$, that is, a deterministic random variable X with $p_{\left(1\right)}=1$ and all other probabilities $=0$;
• its maximum value for the uniform distribution $p=u$, that is, a uniformly distributed random variable X with $p\left(x\right)=\frac{1}{M}$ for all x.

Indeed, it can be easily checked that

$$\begin{array}{cc}\hfill 0& \le H_{\alpha }\left(X\right)\le logM\hfill \end{array}$$

(17)

$$\begin{array}{cc}\hfill 1& \le G\left(X\right)\le \frac{M+1}{2}\hfill \end{array}$$

(18)

$$\begin{array}{cc}\hfill 0& \le {\mathbb{P}}_e\left(X\right)\le 1-\frac{1}{M}\hfill \end{array}$$

(19)

where the lower (resp. upper) bounds are attained for a delta (resp. uniform) distribution, the uniform distribution is the “most entropic” ($H_{\alpha }$), “hardest to guess” (G), and “hardest to detect” (${\mathbb{P}}_e$).

The maximum entropy property is related to the minimization of divergence [15]

$$D(p\parallel u)=logM-H\left(p\right)$$

(20)

where $D(p\parallel q)=\sum p\left(x\right)log\frac{p\left(x\right)}{q\left(x\right)}\ge 0$ denotes the Kullback-Leibler divergence which vanishes if and only if $p=q$. Therefore, entropy appears as the complementary value of the divergence to the uniform distribution. Similarly, for $\alpha$-entropy,

$$D_{\alpha }(p\parallel u)=logM-H_{\alpha }\left(p\right)$$

(21)

where $D_{\alpha }(p\parallel q)=\frac{1}{\alpha -1}log{\sum }_{x}p{\left(x\right)}^{\alpha }q{\left(x\right)}^{1-\alpha }$ denotes the Rényi $\alpha$-divergence [16] (Bhattacharyya distance for $\alpha =\frac{1}{2}$).

Instead of the divergence to the uniform distribution, it is often desirable to rely instead on the statistical distance, also known as total variation distance to the uniform distribution. The general expression of the total variation distance is

$$\Delta (p,q)=\frac{1}{2}\sum _x|p\left(x\right)-q\left(x\right)|$$

(22)

where the $1/2$ factor is there to ensure that $0\le \Delta (p,q)\le 1$. Equivalently,

$$\Delta (p,q)=\underset{T}{max}|\mathbb{P}\left(T\right)-\mathbb{Q}\left(T\right)|$$

(23)

where the maximum is over any event T and $\mathbb{P}$, $\mathbb{Q}$ denote the respective probabilities w.r.t. p and q. As is well known, the maximum

$$\Delta (p,q)=\mathbb{P}\left(T_{+}\right)-\mathbb{Q}\left(T_{+}\right)$$

(24)

is attained when $T=T_{+}=\{x\mid p\left(x\right)\ge q\left(x\right)\}$.

The total variation criterion is particularly important because a very small distance $\Delta (p,q)$ ensures that no statistical test can effectively distinguish between p and q. In fact, given some observation X following either p (null hypothesis $H_0$) or q (alternate hypothesis $H_1$), such a statistical test takes the form “is $X\in T$?” (then accept $H_0$, otherwise reject $H_0$). If $\left|\mathbb{P}\right(X\in T)-\mathbb{Q}(X\in T\left)\right|\le \Delta (p,q)$ is small enough, the type-I or type-II errors have total probability $\mathbb{P}(X\notin T)+\mathbb{Q}(X\in T)\approx 1$. Thus, in this sense the two hypotheses p and q are undistinguishable (statistically equivalent).

By analogy with (20) and (21) we can then define “statistical randomness” $R\left(X\right)=R\left(p\right)\ge 0$ as the complementary value of the statistical distance to the uniform distribution, i.e., such that

$$\Delta (p,u)=1-R\left(p\right)$$

(25)

holds. With this definition,

$$R\left(X\right)=R\left(p\right)\triangleq 1-\frac{1}{2}\sum _x|p\left(x\right)-\frac{1}{M}|$$

(26)

is maximum $=1$ when $\Delta (p,u)=0$, i.e., $p=u$. Thus the uniform distribution u is the “most random”. What is fundamental is that $R\left(X\right)\approx 1$ ensures that no statistical test can effectively distinguish the actual distribution from the uniform distribution.

Again the “least random” distribution corresponds to the deterministic case. In fact, from (24) we have

$$\Delta (p,u)=\mathbb{P}\left(T_{+}\right)-\frac{K}{M}=P_{\left(K\right)}-\frac{K}{M}$$

(27)

where $T_{+}=\{x\mid p\left(x\right)\ge \frac{1}{M}\}$ of cardinality $K=|T_{+}|$, and $\mathbb{P}\left(T_{+}\right)=P_{\left(K\right)}$ by definition (2). It is easily seen that $\Delta (p,u)$ attains its maximum value $=1-\frac{1}{M}$ if and only if $p=\delta$ is a delta distribution. In summary

$$\frac{1}{M}\le R\left(X\right)\le 1$$

(28)

where the lower (resp. upper) bound is attained for a delta (resp. uniform) distribution. The conditional version is again taken by averaging over the observation:

$$R\left(X\right|Y)\triangleq {\mathbb{E}}_{y}R\left(X\right|y).$$

(29)

3. F-Concavity: Knowledge Reduces Randomness and Data Processing

Knowledge of the observed data Y (on average) reduces uncertainty, improves detection or guessing, and reduces randomness in the sense that:

$$\begin{array}{cc}\hfill H_{\alpha }\left(X\right|Y)& \le H_{\alpha }\left(X\right)\hfill \end{array}$$

(30)

$$\begin{array}{cc}\hfill G\left(X\right|Y)& \le G\left(X\right)\hfill \end{array}$$

(31)

$$\begin{array}{cc}\hfill {\mathbb{P}}_e\left(X\right|Y)& \le {\mathbb{P}}_e\left(X\right)\hfill \end{array}$$

(32)

$$\begin{array}{cc}\hfill R\left(X\right|Y)& \le R\left(X\right).\hfill \end{array}$$

(33)

When $\alpha =1$, the property $H\left(X\right|Y)\le H(X)$ is well-known (“conditioning reduces entropy” [15]): the difference $H\left(X\right)-H\left(X\right|Y)=I(X;Y)$ is the mutual information, which is nonnegative. Property (30) for $\alpha \ne 1$ is also well known, see [7,8]. In view of (10) and (11), the case $\alpha =+\infty$ in (30) is equivalent to (32) which is obvious in the sense that any observation can only improve MAP detection. This, as well as (31), is also easily proved directly (see, e.g., [17]).

For all quantities H, ${\mathbb{P}}_e$, G, R, the conditional quantity is obtained by averaging over the observation as in (6), (13), (16) and (29). Since $p\left(x\right)={\mathbb{E}}_{y}p\left(x\right|y)$, the fact that knowledge of Y reduces H, ${\mathbb{P}}_e$, G or R amounts to saying that these are concave functions of the distribution p of X. Note that concavity of $R\left(X\right)=R\left(p\right)$ in p is clear from the definition (26), which shows (33).

For entropy H, this also has been given some physical interpretation: “mixing” distributions (taking convex combinations of probability distributions) can only increase the entropy on average. For example, given any two distributions p and q, $H(\lambda p+\overline{\lambda }q)\ge \lambda H\left(p\right)+\overline{\lambda }H\left(q\right)$ where $0\le \lambda =1-\overline{\lambda }\le 1$. Similarly, such mixing of distributions increases the average probability of error ${\mathbb{P}}_e$, guessing entropy G, and statistical randomness R.

For conditional $\alpha$-entropy $H_{\alpha }\left(X\right|Y)$ where $\alpha \ne 1$, averaging over Y in the definition (8) is made on the $\alpha$-norm of the distribution $p_{X|y}$, which is known to be convex for $\alpha >1$ (by Minkowski’s inequality) and concave for $0<\alpha <1$ (by the reverse Minkowski inequality), the fact that knowledge reduces $\alpha$-entropy (inequality (30)) is equivalent to the fact that $H_{\alpha }\left(p\right)$ in (6) is an F-concave function, that is, an increasing function F of a concave function in p, where $F\left(x\right)=\frac{\alpha }{1-\alpha }log\left(\mathrm{sgn}(1-\alpha )x\right)$. The average over Y in $H_{\alpha }\left(X\right|Y)$ is made on the quantity $F^{-1}\left(H_{\alpha }\right)$ instead of $H_{\alpha }$. Thus, for example, $H_{1/2}\left(p\right)$ is a log-concave function of p.

A straightforward generalization of (30)–(33) is the data processing inequality: for any Markov chain $X-Y-Z$, i.e., such that $p\left(x\right|y,z)=p(x\left|y\right)$,

$$\begin{array}{cc}\hfill H_{\alpha }\left(X\right|Y)& \le H_{\alpha }\left(X\right|Z)\hfill \end{array}$$

(34)

$$\begin{array}{cc}\hfill G\left(X\right|Y)& \le G\left(X\right|Z)\hfill \end{array}$$

(35)

$$\begin{array}{cc}\hfill {\mathbb{P}}_e\left(X\right|Y)& \le {\mathbb{P}}_e\left(X\right|Z)\hfill \end{array}$$

(36)

$$\begin{array}{cc}\hfill R\left(X\right|Y)& \le R\left(X\right|Z)\hfill \end{array}$$

(37)

When $\alpha =1$, the property $H\left(X\right|Y)\le H(X\left|Z\right)$ amounts to $I(X;Z)\le I(X;Y)$, i.e., (post)-processing can never increase information. Inequalities (34)–(37) can be deduced from (30)–(33) by considering a fixed $Z=z$, averaging over Z to show that $H\left(X\right|Y,Z)\le H(X\left|Z\right)$, etc. (additional knowledge reduces randomness) and then noting that $p\left(x\right|y,z)=p(x\left|y\right)$ by the Markov property—see, e.g., [7,18] for $H_{\alpha }$ and [17] for G. Conversely, (30)–(33) can be re-obtained from (34)–(37) as the particular case $Z=0$ (any deterministic variable representing zero information).

4. S-Concavity: Mixing Increases Randomness and Data Processing

Another type of mixing (different from the one described in the preceding section) is also useful in certain physical science considerations. It can be described as a sequence of elementary mixing operations as follows. Suppose that one only modifies two probability values $p_i=p\left(x_i\right)$ and $p_j=p\left(x_j\right)$ for $i\ne j$. Since the result should be again a probability distribution, the sum $p_i+p_j$ should be kept constant. Then there are two possibilities:

• $|p_i-p_j|$ decreases; the resulting distribution is “smoother”, “more spread out”, “more disordered”; the resulting operation can be written as $(p_i,p_j)\mapsto (\lambda p_i+\overline{\lambda }{p}_j,\lambda p_j+\overline{\lambda }{p}_i)$ where $0\le \lambda =1-\overline{\lambda }\le 1$, also known as “transfer” operation. We call it elementary mixing operation or M-transformation in short.
• $|p_i-p_j|$ increases; this is the reverse operation, an elementary unmixing operation or U-transformation in short.

We say that a quantity is s-concave if it increases by any M-transformation (equivalently, decreases by any U-transformation). Note that any increasing function F of an s-concave function is again s-concave.

This notion coincides with that of Schur-concavity from majorization theory [19]. In fact, we can say that p is majorized by q, and we write $p\prec q$, if p is obtained from q by a (finite) sequence of elementary M-transformations, or, what amounts the same, that q majorizes p, that is, q is obtained from p by a (finite) sequence of elementary U-transformations. A well-known result ([19], p. 34) states that $p\prec q$ if and only if

$$P_{\left(k\right)}\le Q_{\left(k\right)}(0<k<M)$$

(38)

(see definition (2)) where always $P_{\left(M\right)}=Q_{\left(M\right)}=1$.

From the above definitions it is immediate to see that all previously considered quantities H, $H_{\alpha }$, G, $G_{\rho }$, ${\mathbb{P}}_e$, R are s-concave, mixing increases uncertainty, guessing, error, and randomness, that is, $p\prec q$ implies

$$\begin{array}{cc}\hfill H_{\alpha }\left(p\right)& \ge H_{\alpha }\left(q\right)\hfill \end{array}$$

(39)

$$\begin{array}{cc}\hfill G_{\rho }\left(p\right)& \ge G_{\rho }\left(q\right)\hfill \end{array}$$

(40)

$$\begin{array}{cc}\hfill {\mathbb{P}}_e\left(p\right)& \ge {\mathbb{P}}_e\left(q\right)\hfill \end{array}$$

(41)

$$\begin{array}{cc}\hfill R\left(p\right)& \ge R\left(q\right).\hfill \end{array}$$

(42)

For $H_{\alpha }$ and R this can be easily seen from the fact that these quantities can be written as (an increasing function of) a quantity of the form ${\sum }_x\varphi \left(p\left(x\right)\right)$ where $\varphi$ is concave. Then the effet of an M-transformation $(p_i,p_j)\mapsto (\lambda p_i+\overline{\lambda }{p}_j,\lambda p_j+\overline{\lambda }{p}_i)$ gives $\varphi (\lambda p_i+\overline{\lambda }{p}_j)+\varphi (\lambda p_j+\overline{\lambda }{p}_i)\ge \lambda \varphi \left(p_i\right)+\overline{\lambda }\varphi \left(p_j\right)+\lambda \varphi \left(p_j\right)+\overline{\lambda }\varphi \left(p_i\right)=\varphi \left(p_i\right)+\varphi \left(p_j\right)$. For ${\mathbb{P}}_e$ it is obvious, and for G and $G_{\rho }$ it is also easily proved using characterization (38) and summation by parts [17].

Another kind of (functional or deterministic) data processing inequality can be obtained from (39)–(42) as a particular case. For any deterministic function f,

$$\begin{array}{cc}\hfill H_{\alpha }\left(f\left(X\right)\right)& \le H_{\alpha }\left(X\right)\hfill \end{array}$$

(43)

$$\begin{array}{cc}\hfill G\left(f\right(X\left)\right)& \le G\left(X\right)\hfill \end{array}$$

(44)

$$\begin{array}{cc}\hfill {\mathbb{P}}_e\left(f\left(X\right)\right)& \le {\mathbb{P}}_e\left(X\right)\hfill \end{array}$$

(45)

$$\begin{array}{cc}\hfill R\left(f\right(X\left)\right)& \le R\left(X\right)\hfill \end{array}$$

(46)

Thus deterministic processing (by f) decreases (cannot increase) uncertainty, can only make guessing or detection easier, and decreases randomness. For $\alpha =1$ the inequality $H\left(f\right(X\left)\right)\le H\left(X\right)$ can also be seen from the data processing inequality of the preceding section by noting that $H\left(f\right(X\left)\right)=I\left(f\right(X);f(X\left)\right)\le I(X;f(X\left)\right)\le H\left(X\right)$ (since $X-f\left(X\right)-f\left(X\right)$ is trivially a Markov chain).

To prove (43)–(46) in general, consider preimages by f of values of $y=f\left(x\right)$; it is enough to show that each of the quantities $H_{\alpha }$, ${\mathbb{P}}_e$, G, or R decreases by the elementary operation consisting in putting together two distincts values $x_i,x_j$ of x in the same preimage of y. However, for probability distributions, this operation amounts the U-transformation $(p_i,p_j)\mapsto (p_i+p_j,0)$ and the result follows by s-concavity.

An equivalent property of (43)–(46) is the fact that any additional random variable Y increases uncertainty, probability of error, guessing, and randomness in the sense that

$$\begin{array}{cc}\hfill H_{\alpha }\left(X\right)& \le H_{\alpha }(X,Y)\hfill \end{array}$$

(47)

$$\begin{array}{cc}\hfill G\left(X\right)& \le G(X,Y)\hfill \end{array}$$

(48)

$$\begin{array}{cc}\hfill {\mathbb{P}}_e\left(X\right)& \le {\mathbb{P}}_e(X,Y)\hfill \end{array}$$

(49)

$$\begin{array}{cc}\hfill R\left(X\right)& \le R(X,Y)\hfill \end{array}$$

(50)

This is a particular case of (43)–(46) applied to the joint $(X,Y)$ and the first projection $f(x,y)=x$. Conversely, (43)–(46) follows from (47)–(50) by applying it to $\left(f\right(X),X)$ in place of $(X,Y)$ and noting that the distribution of $\left(f\right(X),X)$ is essentially that of X.

5. Optimal Fano-Type and Pinsker-Type Bounds

We have seen that informational quantities such as entropies H, $H_{\alpha }$, guessing entropies G, $G_{\rho }$ on one hand, and statistical quantities such as probability of error for MAP detection ${\mathbb{P}}_e$ and statistical randomness R on the other hand, satisfy many common properties: decrease by knowledge, data processing, increase by mixing, etc. For this reason, it is desirable to establish the best possible bounds between one informational quantity (such as $H_{\alpha }$ or $G_{\rho }$) and one statistical quantity (${\mathbb{P}}_e$ or $R=1-\Delta (p,u)$).

To achieve this, we remark that for any distribution p, we have the following majorizations. For fixed ${\mathbb{P}}_e=1-{\mathbb{P}}_s$:

$$({\mathbb{P}}_s,\frac{{\mathbb{P}}_e}{M-1},\dots ,\frac{{\mathbb{P}}_e}{M-1})\prec p\prec ({\mathbb{P}}_s,\dots ,{\mathbb{P}}_s,1-K{\mathbb{P}}_s,0,\dots ,0)$$

(51)

where (necessarily) $K=\lfloor \frac{1}{{\mathbb{P}}_s}\rfloor$, and for fixed $R=1-\Delta$:

$$(\underset{K\mathrm{times}}{\underbrace{\frac{1}{M}+\frac{\Delta }{K},\dots ,\frac{1}{M}+\frac{\Delta }{K}}},\underset{M-K\mathrm{times}}{\underbrace{\frac{1}{M}-\frac{\Delta }{M-K},\dots ,\frac{1}{M}-\frac{\Delta }{M-K}}})\prec p\prec (\Delta +\frac{1}{M},\underset{L-1\mathrm{times}}{\underbrace{\frac{1}{M},\dots ,\frac{1}{M}}},R-\frac{L}{M},0,\dots ,0)$$

(52)

where $K=\left|\right\{p\ge \frac{1}{M}\left\}\right|$ as in (27) and (necessarily) $L=\lfloor MR\rfloor$ (K can possibly be any integer between 1 and L). These majorizations are easily established using characterizations (12), (27) and (38).

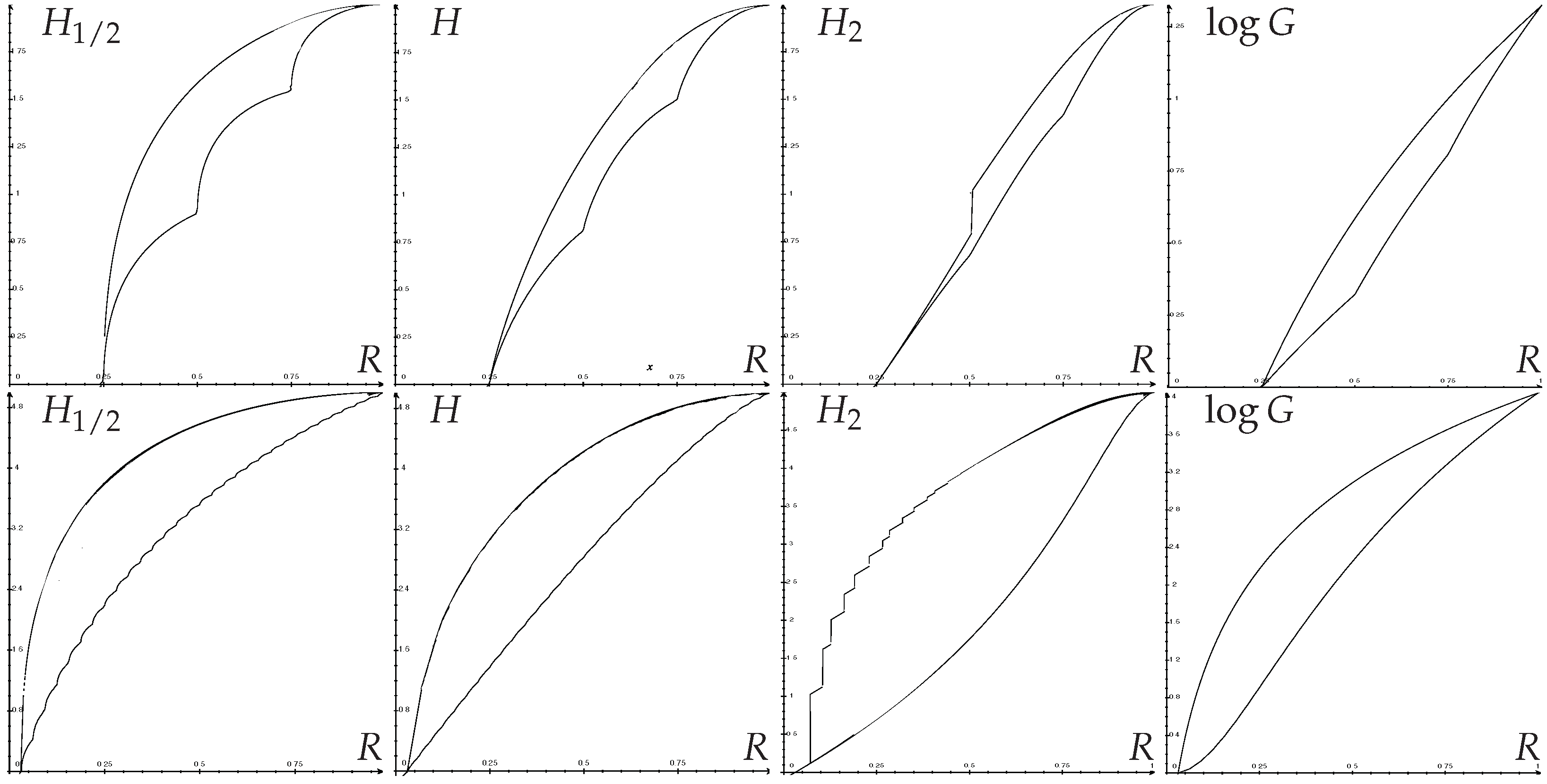
Applying s-concavity of entropies $H_{\alpha }$ or $G_{\rho }$ to (51) gives closed-form upper bounds of entropies as a function of ${\mathbb{P}}_e$, known as Fano inequalities; and closed-form lower bounds, known as reverse Fano inequalities. Figure 1 shows some optimal regions.

The original Fano inequality was an upper bound on conditional entropy $H\left(X\right|Y)$ as a function of ${\mathbb{P}}_e\left(X\right|Y)$. It can be shown that upper bounds in the conditional case are unchanged. Lower bounds of conditional entropies or $\alpha$-entropies, however, have to be slightly changed due to the average operation inside the function F (see Section 3 above) by taking the convex enveloppe (piecewise linear) of the lower curve on $F^{-1}\left(H_{\alpha }\right)$. In this way, one recovers easily the results of [20] for H,11] for $H_{\alpha }$, and [14,17] for G and $G_{\rho }$.

Likewise, applying s-concavity of entropies $H_{\alpha }$ or $G_{\rho }$ to (52) gives closed-form upper bounds of entropies as a function of R, similar to Pinsker inequalities; and closed-form lower bounds, similar to reverse Pinsker inequalities. Figure 2 shows some optimal regions.

The various Pinsker and reverse Pinsker inequalities that can be found in the literature give bounds between $\Delta (p,q)$ and $D(p\parallel q)$ for general q. Such inequalities find application in Quantum physics [21] and to derive lower bounds on the minimax risk in nonparametric estimation [22]. As they are of more general applicability, they turn out not to be optimal here since we have optimized the bounds in the particular case $q=u$. Using our method, one again recovers easily previous results of [23] (and [24], Theorem 26) for H, and improves previous inequalities used for several applications [3,4,6].

6. Conclusions

Using a simple method based on “mixing” or majorization, we have established optimal (Fano-type and Pinsker-type) bounds between entropic quantities ($H_{\alpha }$, $G_{\rho }$) and statistical quantities (${\mathbb{P}}_e$, R) in an interplay between information theory and statistics. As a perspective, similar methodology could be developed for statistical distance to an arbitrary (not necessarily uniform) distribution.