Adaptive Importance Sampling for Equivariant Group-Convolution Computation ^†

Abstract

This paper introduces an adaptive importance sampling scheme for the computation of group-based convolutions, a key step in the implementation of equivariant neural networks. By leveraging information geometry to define the parameters update rule for inferring the optimal sampling distribution, we show promising results for our approach by working with the two-dimensional rotation group $SO\left(2\right)$ and von Mises distributions. Finally, we position our AIS scheme with respect to quantum algorithms for computing Monte Carlo estimations.

1. Introduction and Motivations

Geometric deep learning [1] is an emerging field receiving more and more traction because of its successful application to a wide range of domains [2,3,4]. In this context, equivariant neural networks (ENN) [5] have been shown to be superior to conventional deep learning approaches from both accuracy and robustness standpoints and appear as a natural alternative to data augmentation techniques [6,7] to achieve geometrical robustness.

One key bottleneck for scaling ENN to industrial applications lies with the numerical computation of the associated equivariant operators. More precisely, two main approaches have been used in the literature, namely a Monte Carlo sampling method [2] (which can be made exhaustive for small finite groups) and a generalized Fourier-based method [4,8,9]. However, these approaches suffer from scalability issues as the complexity of the underlying group increases (e.g., handling non-compact groups such as SU(1,1) or large finite groups such as the symmetric group $S_n$ is challenging). Even for groups such as SO(2) for which previous works on the use of spherical harmonics can be leveraged on, the efficient computation of a reliable estimate of the convolution remains a challenge (convergence).

In this context, the authors of [10] have proposed an efficient method for building adequate kernel functions to be used within steerable neural networks [11] by leveraging on the knowledge of infinitesimal generators of the considered Lie group and on a Krylov approach for solving the linear constraints. We propose in this paper to cover the specific case of group-convolutional neural networks (G-CNN) [2,12], which in particular, rely on the computation of group-based convolution operators. By leveraging on information geometry as proposed in [13] for quantile estimation, we introduce here an adaptive importance sampling (AIS) variance reduction method based on information geometric optimization [14] to improve the convergence of Monte Carlo estimators for the numerical computation of group-based convolution feature maps, as used in several recent works [2,9,15]. We illustrate our approach on the two-dimensional rotation group SO(2) by regularizing with von Mises distributions [16], a set-up for which the Fisher information metric [17] can be computed using closed form formulas.

Finally, we shed some light on the benefits of working toward a quantum version of our proposed AIS scheme in order to reach a quadratic speed-up [18]. Improving quantum Monte Carlo integration schemes is indeed a very active topic of research [19], mainly driven by applications within the financial industry [20]. Benchmarking with group-Fourier transform-based approaches, such as [21], which are more theoretically involved but with a promise of an exponential speed-up, will be of particular interest in this context.

2. Group Convolution and Expectation

We consider in the following a compact group G with corresponding Haar measure ${\mu }^G$. As ${\mu }^G\left(G\right)<\infty$, we can choose ${\mu }^G$ so that ${\int }_{G}d{\mu }^G=1$ by using an adequate normalization.

We are interested in evaluating the group-based convolution operator ${\psi }^G$ defined below for functionals $f,k:G\to \mathbb{R}$ and $g\in G$:

$${\psi }^G\left(g\right)={\int }_{G}k\left(h^{-1}g\right)f\left(h\right)d{\mu }^G\left(h\right)$$

(1)

Using a probabilistic interpretation of (1), we can write

$${\psi }^G\left(g\right)={\mathbb{E}}^{{\mu }^G}\left[k\left(H^{-1}g\right)f\left(H\right)\right]$$

(2)

where H is a $G—$valued random variable distributed according to ${\mu }^G$. The convolution can therefore be estimated with a Monte Carlo method by using the following estimator

$${\tilde{\psi }}_n^G\left(g\right)=\frac{1}{n}\sum _{i=1}^{n}k\left(h_i^{-1}g\right)f\left(h_i\right)$$

(3)

where $h_i\sim {\mu }^G$ and for which the efficiency could be improved through variance reduction techniques [22]. By anchoring in [13], we describe in the following an adaptive importance sampling approach for the computation of (1). Similar ideas were also used in [23] for financial applications.

3. Adaptive Importance Sampling

We consider in the following a set ${\Phi }_{\Theta }$ of parametric probability density functions on G, where $\Theta$ represents the parameters space. Each density ${\varphi }_{\theta }\in {\Phi }_{\Theta }$ is assumed to be absolutely continuous with respect to the Haar measure ${\mu }^G$ of the group G, so that the corresponding probability measure can be written as $d{\mu }_{\theta }={\varphi }_{\theta }d{\mu }^G$ and the Radon–Nikodym derivative ${\omega }_{\theta }=\frac{d{\mu }^G}{d{\mu }_{\theta }}$ can be considered.

Using the conventional importance sampling approach, we can then write:

$$\begin{array}{cc}\hfill {\psi }^G\left(g\right)& ={\int }_{G}k\left(h^{-1}g\right)f\left(h\right)\left(\frac{d{\mu }^G}{d{\mu }_{\theta }}\right)\left(h\right)d{\mu }_{\theta }\left(h\right)\hfill \end{array}$$

(4)

$$\begin{array}{cc}\hfill & ={\mathbb{E}}^{{\mu }_{\theta }}\left[{\omega }_{\theta }\left(H\right)k\left(H^{-1}g\right)f\left(H\right)\right]\hfill \end{array}$$

(5)

The idea is then to choose a measure ${\mu }_{{\theta }^{*}}$ for which ${\theta }^{*}$ minimizes the variance $v^{k,f,g}$ of the random variable $k\left(H^{-1}g\right){\omega }_{\theta }\left(H\right)f\left(H\right),$ which can be written as

$$\begin{array}{cc}\hfill v^{k,f,g}\left(\theta \right)& ={\mathbb{E}}^{{\mu }_{\theta }}\left[{\left({\omega }_{\theta }\left(H\right)k\left(H^{-1}g\right)f\left(H\right)\right)}^2\right]-{\psi }^G{\left(g\right)}^2\hfill \end{array}$$

(6)

$$\begin{array}{cc}\hfill & =m_2^{k,f,g}\left(\theta \right)-{\psi }^G{\left(g\right)}^2\hfill \end{array}$$

(7)

where

$$\begin{array}{cc}\hfill m_2^{k,f,g}\left(\theta \right)& ={\mathbb{E}}^{{\mu }_{\theta }}\left[{\left(k\left(H^{-1}g\right){\omega }_{\theta }\left(H\right)f\left(H\right)\right)}^2\right]\hfill \end{array}$$

(8)

$$\begin{array}{cc}\hfill & ={\mathbb{E}}^{{\mu }^G}\left[{\omega }_{\theta }\left(H\right){\left(k\left(H^{-1}g\right)f\left(H\right)\right)}^2\right]\hfill \end{array}$$

(9)

3.1. Monte Carlo Estimator and Convergence

We assume that we can construct a sequence of parameters ${\left({\theta }_i\right)}_{i=0}^{n-1}$, together with realizations ${\left(h_i\right)}_{i=1}^n$ of the random variables ${\left(H_i\right)}_{i=1}^n$ such that $H_i\sim {\mu }_{{\theta }_{i-1}}$ and that ${\theta }_n\to {\theta }^{*}\in \Theta$ as $n\to \infty$. We can then consider the following Monte Carlo estimator:

$${\widehat{\psi }}_n^G\left(g\right)=\frac{1}{n}\sum _{i=1}^n{\omega }_{{\theta }_{i-1}}\left(h_i\right)k\left(h_i^{-1}g\right)f\left(h_i\right)$$

(10)

Under usual integrability conditions, Theorem 3.1 of [13] states that ${\widehat{\psi }}_n^G\left(g\right)\to {\psi }^G\left(g\right)$ almost surely as $n\to \infty$. Furthermore, we have the following distributional convergence result,

$$\sqrt{n}\left({\widehat{\psi }}_n^G\left(g\right)-{\psi }^G\left(g\right)\right)\to \mathcal{N}\left(0,v^{k,f,g}\left({\theta }^{*}\right)\right)$$

(11)

where $\mathcal{N}\left(0,{\sigma }^2\right)$ refers to the Gaussian distribution with 0 mean and variance ${\sigma }^2$.

3.2. Natural Gradient Descent

We now discuss how to build the sequence of parameters ${\left({\theta }_i\right)}_{i=0}^{n-1}$ and corresponding realizations ${\left(h_i\right)}_{i=1}^n$ as introduced in Section 3.1, reminding ourselves that we have

$${\theta }^{*}=arg\underset{\theta \in \Theta }{min}{v}^{k,f,g}\left(\theta \right)=arg\underset{\theta \in \Theta }{min}{m}_2^{k,f,g}\left(\theta \right)$$

(12)

Assuming that the parameter space $\Theta \subseteq {\mathbb{R}}^m$ is a smooth manifold, we can consider the Fisher information metric g on the density space ${\Phi }_{\Theta }$, which is defined as it follows [17]:

$$g_{ij}={\mathbb{E}}^{{\mu }_{\theta }}\left[\frac{\partial log{\varphi }_{\theta }}{\partial {\theta }_i}\frac{\partial log{\varphi }_{\theta }}{\partial {\theta }_j}\right]$$

(13)

We then propose using a natural gradient descent strategy to minimize the quantity $m_2^{k,f,g}$, namely

$${\theta }_{k+1}={\theta }_k-{\alpha }_k{F}_k^{-1}\nabla \left(m_2^{k,f,g}\left({\theta }_k\right)\right)$$

(14)

where $F_k$ is the Fisher information matrix, i.e., the representation of the Fisher metric as a $m\times m$ matrix and ${\alpha }_k\in {\mathbb{R}}_{+}^{*}$. Assuming that the considered functions are smooth enough, it is possible to write:

$$\begin{array}{cc}\hfill \nabla \left(m_2^{k,f,g}\left(\theta \right)\right)& ={\mathbb{E}}^{{\mu }^G}\left[\nabla {\omega }_{\theta }\left(H\right){\left(k\left(H^{-1}g\right)f\left(H\right)\right)}^2\right]\hfill \end{array}$$

(15)

$$\begin{array}{cc}\hfill & =-{\mathbb{E}}^{{\mu }^G}\left[{\omega }_{\theta }\left(H\right)\nabla log{\varphi }_{\theta }\left(H\right){\left(k\left(H^{-1}g\right)f\left(H\right)\right)}^2\right]\hfill \end{array}$$

(16)

$$\begin{array}{cc}\hfill & =-{\mathbb{E}}^{{\mu }_{\theta }}\left[\nabla log{\varphi }_{\theta }\left(H\right){\left({\omega }_{\theta }\left(H\right)k\left(H^{-1}g\right)f\left(H\right)\right)}^2\right]\hfill \end{array}$$

(17)

Using a stochastic approximation scheme such as the Robbins–Monro algorithm [24] then leads to consider the following update rule,

$${\theta }_{k+1}={\theta }_k+{\alpha }_k{F}_k^{-1}\mathsf{\Lambda }\left(H_{k+1},{\theta }_k\right)$$

(18)

where $\mathsf{\Lambda }\left(H,\theta \right)=\nabla log{\varphi }_{\theta }\left(H\right){\left({\omega }_{\theta }\left(H\right)k\left(H^{-1}g\right)f\left(H\right)\right)}^2$, $H_k\sim {\mu }_{{\theta }_{k-1}}$ and the sequence of numbers ${\alpha }_k$ is such that ${\sum }_k$${\alpha }_k=\infty$ and ${\sum }_k$${\alpha }_k^2<\infty$.

3.3. About IGO Algorithms

Information geometric optimization (IGO) algorithms are introduced in [14] as a unified framework to solve black-box optimization problems. IGO algorithms can be seen as performing an estimation of a distribution over the considered search space $\mathcal{X}$ leading to small values of the target function Q when sampling according to it. More precisely, the idea is to maintain at each iteration t a parametric probability distribution $P_{{\lambda }_t}$ on the search space $\mathcal{X}$, for ${\lambda }_t\in \mathsf{\Lambda }\subseteq {\mathbb{R}}^p$ and to have the value ${\lambda }_t$ evolve over time as to shift $P_{{\lambda }_t}$ toward giving more weight to points $x\in \mathcal{X}$ associated with a lower value of Q.

The IGO algorithms described [14] first transfer the function Q from $\mathcal{X}$ to $\mathsf{\Lambda }$ by using an adaptive quantile-based approach and then applying a natural gradient descent by leveraging on the Fisher information metric of the considered statistical model. The scheme described in the Definition 5 of [14] defines the following the update rule for the parameter ${\lambda }_t$:

$${\lambda }_{t+dt}={\lambda }_t+dt\times I^{-1}\left({\lambda }_t\right)\sum _{i=1}^N{\omega }_i{\left.\frac{\partial ln{P}_{\lambda }\left(x_{i:N}\right)}{\partial \lambda }\right|}_{\lambda ={\lambda }_t}$$

(19)

where I is the fisher matrix of the model, $x_1,...,x_N$ are N samples drawn according to $P_{{\lambda }_t}$ at step t, $x_{i:N}$ denotes the sample point ranked $i^{th}$ according to Q (i.e., $Q\left(x_{1:N}\right)<\dots <Q\left(x_{N:N}\right)$ ) and ${\omega }_i=\frac{1}{N}\omega \left(\frac{i-1}{2}\right),$ with $\omega \left(q\right)=1_{q<q_0}$ a quantile-based selection function of threshold $q_0$.

IGO algorithms could therefore be used in our context by setting $Q=m_2^{k,f,g}\left(\theta \right)$ and $\mathcal{X}=\Theta$ to infer the optimal value ${\theta }^{*}\in \Theta$. Implementing the update rule (19) requires a priori a large number of evaluations of the term $Q=m_2^{k,f,g}\left(\theta \right)$ to derive the sorted samples $x_{i:N}$, making this approach generally not well suited to our context.

4. Application to $SO\left(2\right)$-Convolutions

We give here an application of our AIS approach for the computation of $SO\left(2\right)$-convolutions by using von Mises densities [16] for the weighting. This type of computation is in particular relevant when working with $SE\left(2\right)$-ENN by exploiting the semi-direct product structure $SE\left(2\right)={\mathbb{R}}^2⋉SO\left(2\right)$, as performed in [3].

4.1. Fisher Information Metric

The Haar measure on $SO\left(2\right)$ is simply the Lebesgue measure on the unit circle $[0,2\pi ]$ and will be denoted $d\alpha$ before normalization. The convolution operator (1) is therefore applied to functionals defined on $[0,2\pi ]$, so that we are interested in evaluating the following quantity for ${\alpha }_0\in [0,2\pi ]$:

$${\psi }^{SO\left(2\right)}\left({\alpha }_0\right)=\frac{1}{2\pi }{\int }_0^{2\pi }k\left({\alpha }_0-\alpha \right)f\left(\alpha \right)d\alpha$$

(20)

We consider in the following a family of von Mises densities ${\varphi }_{\theta }$ on $[0,2\pi ]$, for $\theta =\left(\mu ,\kappa \right)$, and for which $\forall \alpha \in [0,2\pi ]$,

$${\varphi }_{\theta }\left(\alpha \right)=\frac{e^{\kappa cos\left(\alpha -\mu \right)}}{2\pi I_0\left(\kappa \right)}$$

(21)

where for $n\in \mathbb{N}$, $I_n\left(\kappa \right)=\frac{1}{\pi }{\int }_0^{\pi }{e}^{\kappa cos\left(\theta \right)}cos\left(n\theta \right)d\theta$ refers to modified Bessel functions. Denoting in the following ${\ell }_{\mu ,\kappa }=log{\varphi }_{\theta }$, we have ${\partial }_{\mu }{\ell }_{\mu ,\kappa }\left(\alpha \right)=\kappa sin\left(\alpha -\mu \right)$ and ${\partial }_{\kappa }{\ell }_{\mu ,\kappa }\left(\alpha \right)=cos\left(\alpha -\mu \right)-\frac{I_0^{{}^{\prime }}\left(\kappa \right)}{I_0\left(\kappa \right)}$ and it is now possible to evaluate the metric tensor $g.$ More precisely, we easily obtain:

$$\begin{array}{cc}\hfill g_{\mu ,\mu }& ={\mathbb{E}}^{{\mu }_{\theta }}\left[{\left({\partial }_{\mu }{\ell }_{\mu ,\kappa }\left(\alpha \right)\right)}^2\right]\hfill \end{array}$$

(22)

$$\begin{array}{cc}\hfill & ={\int }_0^{2\pi }{\kappa }^2{sin}^2\left(\alpha -\mu \right){\varphi }_{\theta }\left(\alpha \right)d\alpha \hfill \end{array}$$

(23)

$$\begin{array}{cc}\hfill & =\kappa \frac{I_1\left(\kappa \right)}{I_0\left(\kappa \right)}\hfill \end{array}$$

(24)

$$\begin{array}{cc}\hfill g_{\kappa ,\kappa }& ={\mathbb{E}}^{{\mu }_{\theta }}\left[{\left({\partial }_{\kappa }{\ell }_{\mu ,\kappa }\left(\alpha \right)\right)}^2\right]\hfill \end{array}$$

(25)

$$\begin{array}{cc}\hfill & ={\int }_0^{2\pi }{\left(cos\left(\alpha -\mu \right)-\frac{I_0^{{}^{\prime }}\left(\kappa \right)}{I_0\left(\kappa \right)}\right)}^2{\varphi }_{\theta }\left(\alpha \right)d\alpha \hfill \end{array}$$

(26)

$$\begin{array}{cc}\hfill & =1-\frac{1}{\kappa }\frac{I_1\left(\kappa \right)}{I_0\left(\kappa \right)}-2\frac{I_0^{{}^{\prime }}\left(\kappa \right)I_1\left(\kappa \right)}{I_0{\left(\kappa \right)}^2}+\frac{I_0^{{}^{\prime }}{\left(\kappa \right)}^2}{I_0{\left(\kappa \right)}^2}\hfill \end{array}$$

(27)

$$\begin{array}{cc}\hfill g_{\mu ,\kappa }& ={\mathbb{E}}^{{\mu }_{\theta }}\left[{\partial }_{\mu }{\ell }_{\mu ,\kappa }\left(\alpha \right){\partial }_{\kappa }{\ell }_{\mu ,\kappa }\left(\alpha \right)\right]\hfill \end{array}$$

(28)

$$\begin{array}{cc}\hfill & ={\int }_0^{2\pi }\kappa sin\left(\alpha -\mu \right)\left(cos\left(\alpha -\mu \right)-\frac{I_0^{{}^{\prime }}\left(\kappa \right)}{I_0\left(\kappa \right)}\right){\varphi }_{\theta }\left(\alpha \right)d\alpha \hfill \end{array}$$

(29)

$$\begin{array}{cc}\hfill & =0\hfill \end{array}$$

(30)

The inverse of the Fisher information matrix in the scheme (18) can therefore be computed with closed-form formulas, making its evaluation very efficient for the considered case.

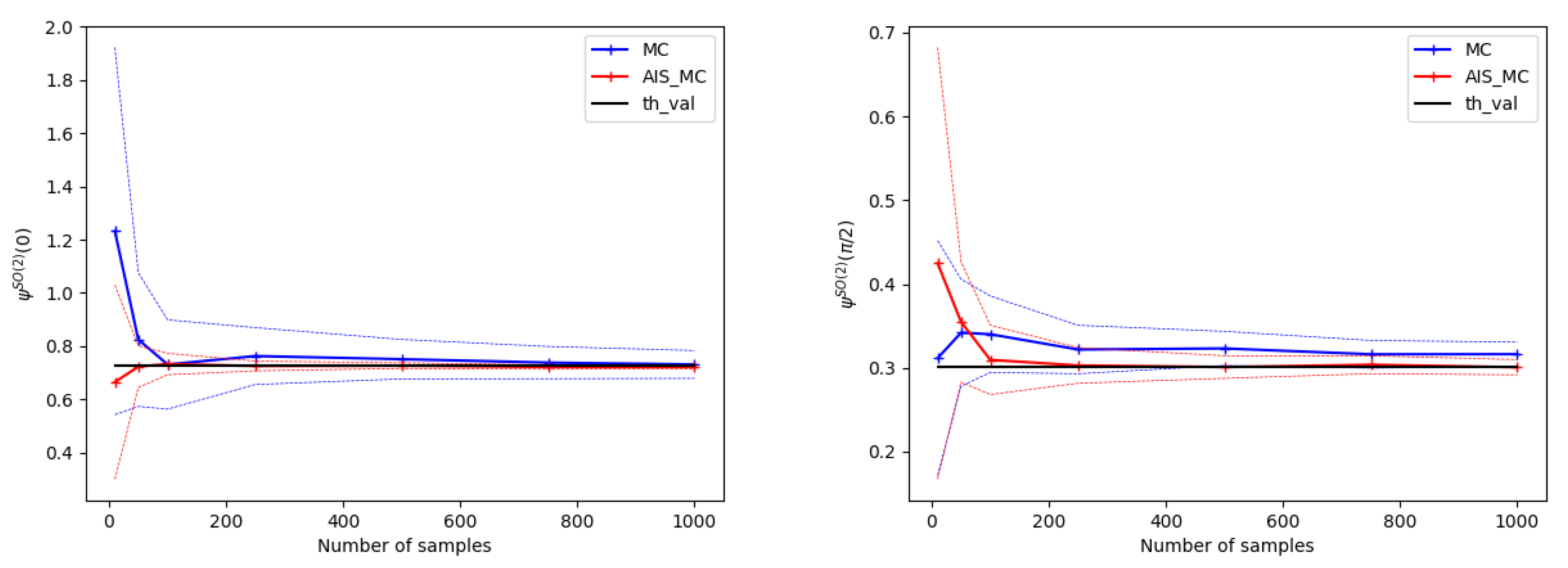
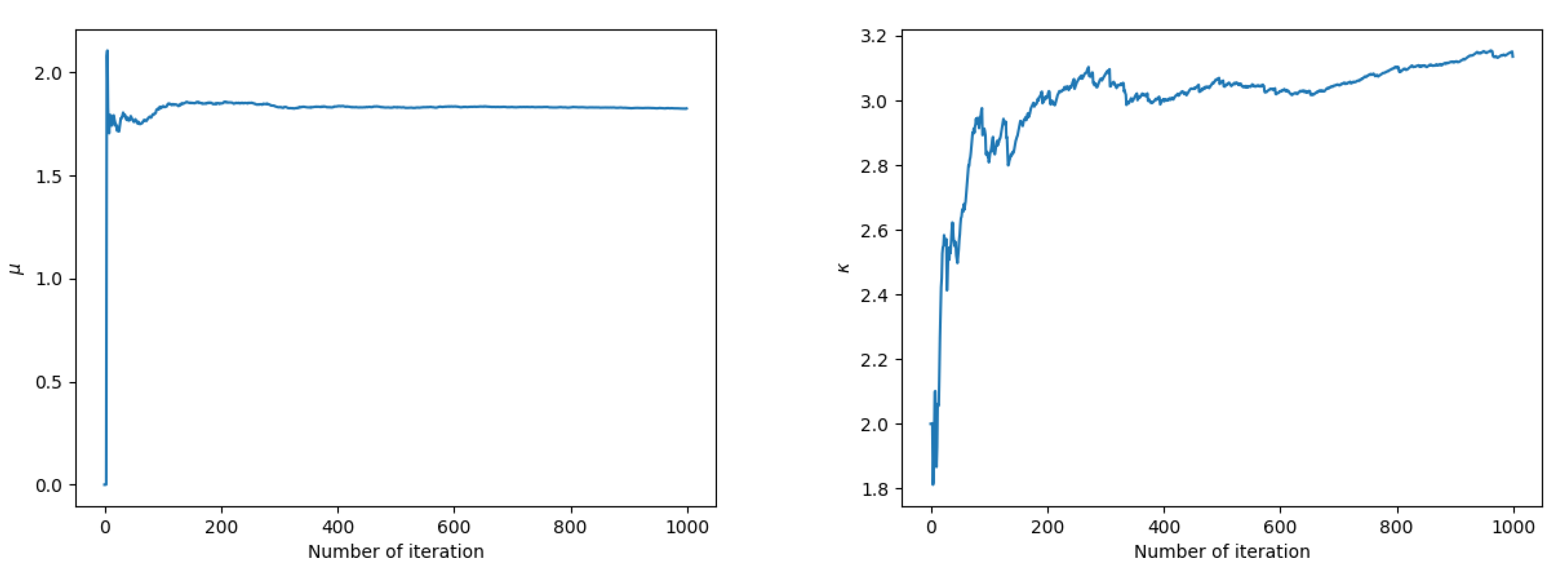
4.2. Numerical Experiments

To numerically validate our approach, we have considered von Mises type feature functions $f_{{\kappa }_0,{\alpha }_0}:\alpha \to e^{{\kappa }_{0}cos\left({\alpha }_0-\mu \right)}$ and kernel functions $k:[0,2\pi ]\to \mathbb{R}$ modeled as small fully connected neural networks with one hidden layer of 128 neurons with ReLu activation and uniform random weights initialization. To run our testing, we have used ${\kappa }_0=3$ and ${\mu }_0=\frac{\pi }{2}$.

Figure 1 shows the comparison between the results obtained with the estimator (10) using the adaptive importance sampling scheme and those obtained with the conventional estimator (3). We can in particular see that the adaptive importance sampling scheme converges faster to the theoretical value (here computed by using (3) with $n=50,000$ and displayed in black in Figure 1), while providing much narrower confidence intervals (because of lower variance) than the conventional Monte Carlo estimator. Figure 2 shows the evolution of the parameter $\theta =\left(\mu ,\kappa \right)$ as we iterate through the update rule (18), from which we can also observe a fast convergence.

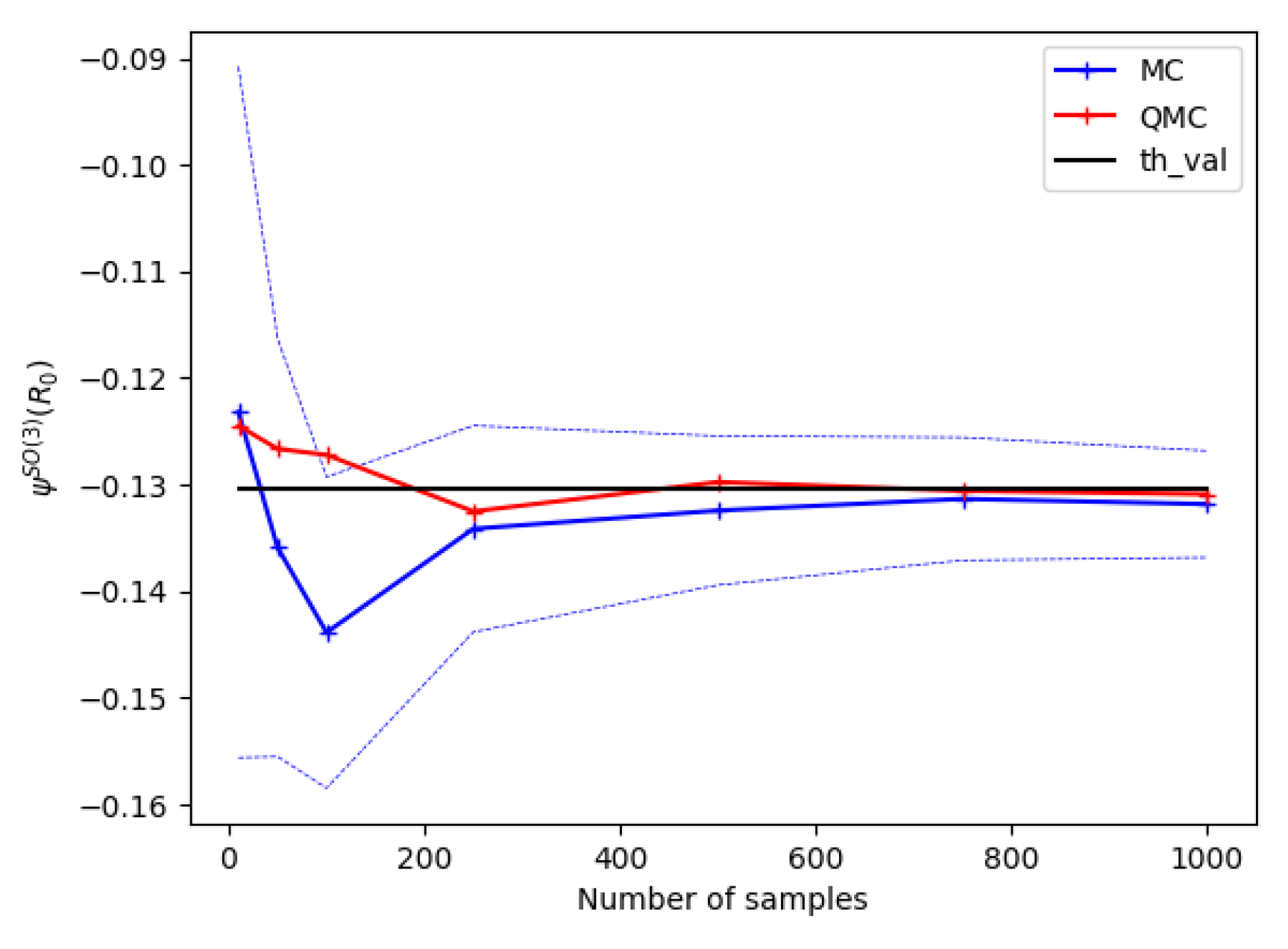
4.3. Extension to $SO\left(3\right)$-Convolutions

Generalizing the above results to cover $SO\left(3\right)$-convolutions is of particular interest when using ENN for processing spherical data such as fish-eye images [4,25]. The Fisher–Bingham distribution [26], also known as the Kent distribution, can be leveraged in this context. More precisely, we have in this case, for $x\in {\mathbb{S}}_2$ (the 2D-sphere in ${\mathbb{R}}^3$):

$${\varphi }_{\theta }\left(x\right)=c{\left(\kappa ,\beta \right)}^{-1}exp\left(\kappa {\gamma }_1.x+\beta \left[{\left({\gamma }_2.x\right)}^2-{\left({\gamma }_3.x\right)}^2\right]\right)$$

(31)

where ${\gamma }_i$ for $i=1,2,3$ are vectors of ${\mathbb{R}}^3$ so that the $3\times 3$ matrix $\Gamma =\left[{\gamma }_1,{\gamma }_2,{\gamma }_3\right]$ is orthogonal and $c\left(\kappa ,\beta \right)$ is a normalizing constant.

Although we defer to further work the details of the derivation of the corresponding AIS estimator (10), we illustrate on Figure 3 that $SO\left(3\right)$-convolutions could also benefit from variance reduction methods by using a simple quasi-Monte Carlo scheme [27] with a three-dimensional Sobol sequence [28].

5. Monte Carlo Methods in the Quantum Set-Up

Monte Carlo computations can generally benefit from a quadratic speed-up in a quantum computing set-up [18] and improving quantum Monte Carlo integration schemes is a very active topic of research [19], mainly driven by applications within the financial industry [20,29].

A similar speed-up can therefore be expected in our context by estimating (1) by leveraging on the quantum amplitude estimation (QAE) algorithm [30]. For $g\in G$, we denote ${\varphi }_g^{f,k}:G\to \mathbb{R}$ the function such that $\forall h\in G$, ${\varphi }_g^{f,k}\left(h\right)=k\left(h^{-1}g\right)f\left(h\right)$.

We first construct the operator ${\mathcal{U}}_{{\mu }^G}$ to load a discretized version of ${\mu }^G$ so that ${\mathcal{U}}_{{\mu }^G}\left|0\right.〉={\sum }_{h\in G_{ϵ}}\sqrt{p\left(h\right)}\left|h\right.〉$, with $p\left(h\right)={\int }_{g\in \mathcal{B}\left(h,r_{ϵ}\right)}{\mu }^G\left(g\right)$, $\mathcal{B}\left(x,r\right)$ the ball of radius $r>0$ centered in $x\in G$ and $G_{ϵ}$ a discrete subset of G. We scale ${\varphi }_g^{f,k}$ to ${\tilde{\varphi }}_g^{f,k}:G\to \left[0,1\right]$ and build another unitary operator ${\mathcal{U}}_{\varphi }$ to compute and load the values of ${\varphi }_g^{f,k}$ taken on $G_{ϵ}$, that we defined by ${\mathcal{U}}_{\varphi }\left|h\right.〉=\sqrt{1-{\tilde{\varphi }}_g^{f,k}\left(h\right)}\left|h\right.〉\left|0\right.〉+\sqrt{{\tilde{\varphi }}_g^{f,k}\left(h\right)}\left|h\right.〉\left|1\right.〉$. Using the QAE algorithm on ${\mathcal{U}}_{\varphi }{\mathcal{U}}_{{\mu }^G}$ gives us access to an estimate of (1) after proper rescaling, with a precision of $\delta$ in $\mathcal{O}\left(\frac{\sqrt{V^{k,f,g}}}{\delta }\right)$ queries, with $V^{k,f,g}={\mathbb{V}}^{{\mu }^G}\left({\varphi }_g^{f,k}\left(H\right)\right)$.

As described in Section 3.1, the AIS estimator (10) leads to a precision of $\delta$ for $n=O\left(\frac{v^{k,f,g}\left({\theta }^{*}\right)}{{\delta }^2}\right)$ samples, which is asymptotically less efficient than the above quantum estimator. However, no quantum advantage has been evidenced on current hardware for general Monte Carlo estimations and further challenges with respect to the precision of the evaluation of the integrand ${\varphi }_g^{f,k}$ are expected in our specific context. Keeping working on the optimization of the estimators in the classical set-up while keeping track of the progress made on the development of quantum hardware therefore appears a reasonable path to follow.

6. Conclusions and Further Work

By leveraging on the approach proposed in [13] for quantile estimation, we have introduced in this paper an AIS variance reduction method for the computation of group-based convolution operators, a key component of equivariant neural networks. We have in particular used information geometry concepts to define an efficient update rule to infer the optimal sampling parametric distribution and have also shown promising results when working with the two-dimensional rotation group $SO\left(2\right)$ and von Mises distributions.

Further work will include the study of non-compact groups such as $SU(1,1)$ as to improve the efficiency of the computations underlying to the ENN introduced in [9]. As shown in [31], Souriau Thermodynamics can be used to build Gaussian distributions over $SU(1,1)$, which appear as natural candidates for applying the AIS scheme presented in this paper.

We have also seen that Monte Carlo computations can generally benefit from a quadratic speed-up in a quantum computing set-up. Further work will include the study of using AIS in this context as to provide a generic and efficient quantum algorithm for group-convolution computation. Benchmarking with group-Fourier transform-based approaches such as [21], which are more theoretically involved but with a promise of exponential speed-up, will also be of high interest, as it will be the case for results coming from the emerging field of quantum geometric deep learning [32,33].