Abstract
Earth’s gravitational field provides invaluable insights into the changing nature of our planet. It reflects mass change caused by geophysical processes like continental hydrology, changes in the cryosphere or mass flux in the ocean. Satellite missions such as the NASA/DLR operated Gravity Recovery and Climate Experiment (GRACE), and its successor GRACE Follow-On (GRACE-FO) continuously monitor these temporal variations of the gravitational attraction. In contrast to other satellite remote sensing datasets, gravity field recovery is based on geophysical inversion which requires a global, homogeneous data coverage. GRACE and GRACE-FO typically reach this global coverage after about 30 days, so short-lived events such as floods, which occur on time frames from hours to weeks, require additional information to be properly resolved. In this contribution we treat Earth’s gravitational field as a stationary random process and model its spatio-temporal correlations in the form of a vector autoregressive (VAR) model. The satellite measurements are combined with this prior information in a Kalman smoother framework to regularize the inversion process, which allows us to estimate daily, global gravity field snapshots. To derive the prior, we analyze geophysical model output which reflects the expected signal content and temporal evolution of the estimated gravity field solutions. The main challenges here are the high dimensionality of the process, with a state vector size in the order of to , and the limited amount of model output from which to estimate such a high-dimensional VAR model. We introduce geophysically motivated constraints in the VAR model estimation process to ensure a positive-definite covariance function.
1. Introduction
Earth’s gravitational field is key quantity for observing the state and change of our planet. Its variations in time can be related to surface mass changes [1] and thus it provides insight into geophysical and climate relevant processes, for example, sea level rise [2], ice mass loss [3], or the terrestrial water cycle [4]. Since 2002, the dedicated satellite mission Gravity Recovery And Climate Experiment (GRACE) [5,6] and its successor GRACE Follow-On (GRACE-FO) [7] have monitored temporal variations of Earth’s gravitational field and have provided an invaluable data record for climate and Earth system sciences. The standard data products of both missions are unconstrained and constrained monthly snapshots of potential or surface mass changes. The time period of one month is not chosen arbitrarily but is a consequence of the orbit geometry of the satellites. As the satellites do not directly observe the changes in gravitational attraction but rather provide very precise measurements of their absolute and relative motion, the underlying potential field must be determined by an inversion process. This inversion process requires a global, homogeneous data coverage which for GRACE and GRACE-FO is reached after about 30 days.
However, in recent years different approaches to derive sub-monthly gravity field variations which combine satellite measurements with prior information have been developed. Notable examples are the Kalman smoother approach by [8], a moving window approach by [9], constrained surface mass estimates from the Center of Space Research (CSR) [10] and a Kalman filter approach for regional applications [11]. Data sets dervied with these approaches have seen various applications in Earth system sciences, for example, analysis of large scale flood events [12], evaluation of geophysical models [13,14] or near real-time flood monitoring [15].
In this contribution we show how maximum entropy spectral estimation can be used to derive prior information for regularizing the inversion process for daily gravity field variations. To that end, we estimate a vector autoregressive (VAR) model from a time series of geophysical model output which approximates the expected signal. Following [15], we show how this spatio-temporal covariance information can be introduced into the inversion process and present a time series of daily gravity field variations derived from approximately thee years of GRACE-FO data.
2. Materials and Methods
A widely used method to recover Earth’s gravitational field from a set of measurements is to solve an overdetermined system of equations in a least-squares adjustment [16]. Here, the measurements or observations are related to unknown gravity field parameters through a (possibly non-linear) functional model with:
We added the residual vector because (1) equation is generally not consistent due to the stochastic nature of . To solve for , we expand into a Taylor series around and truncate it after the linear term. This yields the reduced observations equations:
where the matrix consists of the partial derivatives of with respect to the parameter vector . In (2), the residual vector is assumed to be centered and normally distributed with the covariance matrix . This system of linear equations can be solved for the parameter corrections by forming the system of normal equations:
or more concise, . For this study, we express the changes Earth’s gravitational field as spherical harmonic series expansion:
where the fully normalized surface spherical harmonics are given by:
with being the fully normalized associated Legendre functions [17]. In practice, the series is truncated at a maximum degree , which depends on the application and is chosen here with . Furthermore, we set degrees to zero because we assume that Earth’s mass does not vary and we fix the coordinate reference frame in Earth’s center of mass. The unknown parameter corrections therefore consist of the spherical harmonic coefficients with .
Since we want to determine daily temporal changes in Earth’s gravitational field we set up this least-squares adjustment for a time series , where is 1 day. We denote the resulting observation equations for time step i with a corresponding subscript: . All epochs can be combined in a single least squares adjustment with the block-diagonal normal equation coefficient matrix and the right hand side . Given the block-diagonal structure of we can solve for each time step individually resulting in the estimated parameter corrections and their corresponding variance-covariance matrix . Next to the input data quality, the uncertainty of primarily depends on the spatial data coverage within the observation interval. To recover the full spherical harmonic spectrum, a global homogeneous data coverage is required. For the application here, where the observation time span is a single day, the satellites perform approximately 15 revolutions and thus we can only infer spherical harmonic coefficients up to order [18]. The effect this sparse data coverage has on the estimated gravity field solution can be seen in Figure 1, where we propagated the uncertainty of an unconstrained daily GRACE-FO solution to equivalent water height (EWH) in space domain.
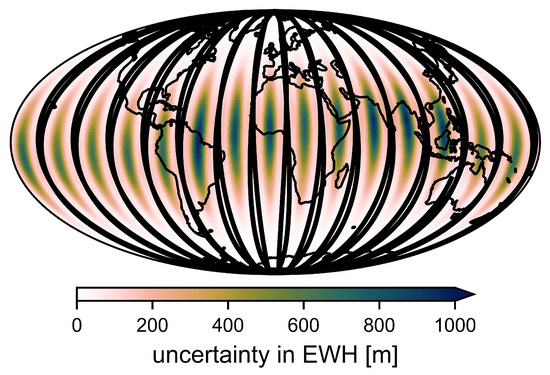
Figure 1.
Uncertainty of an unconstrained daily gravity field estimated from one day of GRACE-FO data propagated to equivalent water height (EWH) in space domain. The solid black lines show the satellite ground tracks for this given day.
The uncertainty between the satellite ground tracks is magnitudes higher than the expected signal, which is in the order of ±25 cm. Consequently, to recovery global, sub-monthly gravity field variations, additional external information is required.
We introduce prior information on the parameter corrections in the form of a positive definite covariance matrix . We further assume that is a Gaussian, temporally stationary random process with an expected value of zero. This implies that their temporal covariance function only depends on the lag h between the epoch i and j [19]. The prior distribution is then given by:
If we sort all epochs in temporally ascending order, the variance-covariance matrix of the resulting vector is block-Toeplitz with the individual blocks given by
This prior information is then incorporated into the least squares adjustment as pseudo-observations of the form:
with . The constrained system of normal equations for the whole time series is subsequently given by:
The solution to this augmented least-squares problem is numerically equivalent to the Bayes estimate under the assumption of the given prior information.
Both GRACE and GRACE-FO exhibit an approximate repeat cycle of 4–5 days at the equator. As the observation information is closely tied to the ground track coverage es presented in Figure 1, this means that points at the equator are also updated at this repeat frequency. Between these updates, the solutions are supported by the introduced temporal constraint and slowly tend towards the Taylor series expansion point . We chose as a long-term estimate of the secular and seasonal gravity field variations, which captures a large part of the total signal. In higher latitudes, where the ground tracks converge, observation updates occur more frequently. This means that as we move closer to the poles, the gravity field solutions become less reliant on the prior information.
Note that the covariance function is still unknown at this point. To estimate the stochastic properties we perform maximum entropy spectral estimation by fitting a vector autoregressive model (VAR) with:
to a time series of geophysical model output , which approximates the true spatio-temporal covariance structure of Earth’s time-variable gravity field. We make use of the Earth System Model of the European Space Agency (ESA ESM, [20]) to generate daily spherical harmonics coefficients vectors. To estimate the VAR model, we use Yule–Walker equations [19] to estimate the empirical covariance matrices for lags using the unbiased estimator:
After estimating the empirical covariance function and before solving the Yule–Walker equations, we apply geophysically motivated constraints onto the obtained covariance matrices. Specifically, we want set correlations between land and ocean to zero and reduce the overall correlation length. These constraints are very easy to introduce in space domain so we first propagate from the spherical harmonics domain to an EWH grid in space domain. Now the matrices can be decomposed into , where represents the correlation between two grid points at lag h and is the standard deviation of the corresponding grid points. The constraints are then realized by setting if the points i and j are on different domains and applying a decay function . The amount at which the correlation between points in dependence of their spherical distance is reduced is governed by the the parameter which we chose as 1100 km. After propagating the modified empirical covariance matrices back to spherical harmonics domain, we can now solve the Yule–Walker equations to obtain the VAR model coefficients and compute the white noise covariance matrix . Now we could compute the covariance function for all lags h, however, given the high dimensionality of the problem, assembling the full block variance-covariance matrix is not feasible. Instead we use the VAR model to transform the pseudo-observation equations (8). For each time step i, we apply , which can also be written as a lower triangular block matrix applied to the full time series as in:
where is a block diagonal matrix with on the main diagonal. This has the great advantage that the resulting normal equation coefficient matrix is block-banded with a bandwith of and thus greatly reduces the memory demands. The transformed system of normal equations which we use to estimate the full time series of gravity field variations is then given by:
Note that for a VAR model of order 1, (13) yields the same results as the Kalman smoother approach presented in [8].
3. Results
To showcase how the VAR regularization affects the gravity field estimates, we computed systems of normal equations from close to three years of GRACE-FO sensor data [21]. Figure 2 shows the autocovariance matrix computed from the VAR model and the temporal variability of the computed time series propagated to space domain.
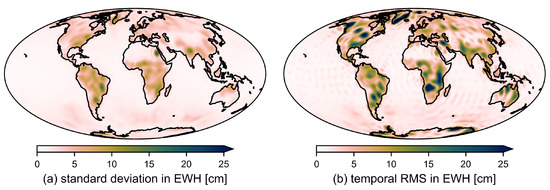
Figure 2.
Comparison of (a) the autocovariance matrix derived from the estimated VAR model expressed as standard deviation per grid point and (b) the temporal RMS of the computed gravity field solutions.
As can be seen, the estimated gravity field time series shows a lot more signatures than the expected signal covariance. This means that the GRACE-FO observations provide significant information and are not overly constrained by the derived VAR model. It should be noted that the VAR model and subsequently the spatio-temporal constraints depend on the geophysical models used in their derivation. However, the influence of different hydrological models is very small as shown in [12]. This suggests that the daily gravity field solutions are primarily data driven.
To gauge how the daily gravity field variations compare with standard GRACE/GRACE-FO products, we compute area mean time series for selected hydrological basins. As monthly data set we use the unconstrained monthly solutions of ITSG-Grace_operational [22,23] computed at Graz University of Technology, filtered with DDK4 spatial filter [24].
Figure 3 shows the area mean time series of 4 regions where we see larger water storage variations. We can see that the daily gravity field solutions clearly pick up sub-monthly signal and thus provide additional information compared to the standard GRACE/GRACE-FO products.
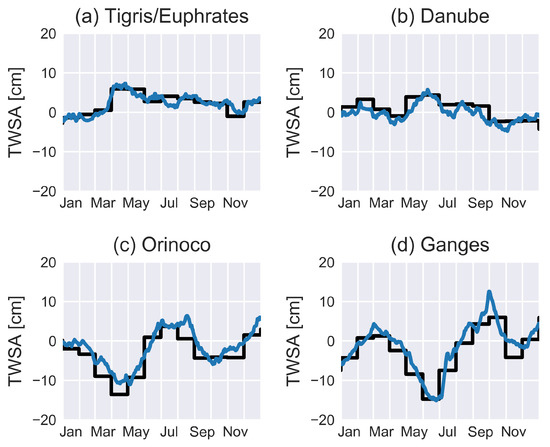
Figure 3.
Total water storage anomaly (TWSA) in equivalent water height for (a) Tigris/Euhprates, (b) Danube, (c) Orinoco, and (d) Ganges basin for the year 2019 (trend and annual signal are removed). The estimated daily solutions are compared with DDK4-filtered monthly solutions from ITSG-Grace_operational shown as step function.
4. Discussion
We have shown that VAR models provide an efficient way of introducing spatio-temporal prior information into the gravity field inversion process. This approach is equivalent to constraining the gravity field estimates with the full block-Toeplitz variance-covariance matrix, however requires only a fraction of the memory. Constraining the inversion of daily gravity field variations with a VAR model of arbitrary order p constitutes the generalization of the Kalman smoother approach of [8], which is the special case for . If the VAR model is derived as a maximum entropy spectral estimate from a time series of geophysical model output, a few challenges arise. The high-dimensionality of the problem with a state vector size in the order of to , combined with the limited availability of model output results in a very low redundancy in the VAR model estimation. We counteract this by introducing geophysically motivated constraints on the empirical covariance matrix estimates. First, we decouple the land and ocean domain and then we reduce the remaining correlation between far away point by introducing an exponential decay function dependent on the spherical distance. This drastically improves the condition of the VAR estimation problem. Finally, we show that the derived prior information in combination with GRACE-FO measurement data yields reasonable results by computing a time series of daily gravity field variations from June 2018 to March 2021. Here, we can clearly see sub-monthly signals which underlines the proficiency of the approach.
Author Contributions
A.K. worked on the theoretical background, performed the gravity field recovery and wrote the manuscript; T.M.-G. worked on the theoretical background. All authors have read and agreed to the published version of the manuscript.
Data Availability Statement
The full time series of gravity field variations and the estimated autoregressive model are available on ftp://ftp.tugraz.at/outgoing/ITSG/GRACE/ITSG-Grace_operational/daily_kalman (accessed on 21 March 2021).
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
The following abbreviations are used in this manuscript:
| GRACE | Gravity Recovery And Climate Experiment |
| GRACE-FO | GRACE Follow-On |
| CSR | Center for Space Research |
| VAR | vector autoregressive |
| EWH | equivalent water height |
| RMS | root mean square |
References
- Wahr, J.; Molenaar, M.; Bryan, F. Time variability of the Earth’s gravity field: Hydrological and oceanic effects and their possible detection using GRACE. J. Geophys. Res. Solid Earth 1998, 103, 30205–30229. [Google Scholar] [CrossRef]
- Dobslaw, H.; Dill, R.; Bagge, M.; Klemann, V.; Boergens, E.; Thomas, M.; Dahle, C.; Flechtner, F. Gravitationally Consistent Mean Barystatic Sea Level Rise From Leakage-Corrected Monthly GRACE Data. J. Geophys. Res. Solid Earth 2020, 125, e2020JB020923. [Google Scholar] [CrossRef]
- Groh, A.; Horwath, M.; Horvath, A.; Meister, R.; Sørensen, L.S.; Barletta, V.R.; Forsberg, R.; Wouters, B.; Ditmar, P.; Ran, J.; et al. Evaluating GRACE Mass Change Time Series for the Antarctic and Greenland Ice Sheet—Methods and Results. Geosciences 2019, 9, 415. [Google Scholar] [CrossRef] [Green Version]
- Eicker, A.; Forootan, E.; Springer, A.; Longuevergne, L.; Kusche, J. Does GRACE see the terrestrial water cycle “intensifying”? J. Geophys. Res. Atmos. 2016, 121, 733–745. [Google Scholar] [CrossRef] [Green Version]
- Tapley, B.D.; Bettadpur, S.; Watkins, M.; Reigber, C. The gravity recovery and climate experiment: Mission overview and early results. Geophys. Res. Lett. 2004, 31. [Google Scholar] [CrossRef] [Green Version]
- Tapley, B.D.; Watkins, M.M.; Flechtner, F.; Reigber, C.; Bettadpur, S.; Rodell, M.; Sasgen, I.; Famiglietti, J.S.; Landerer, F.W.; Chambers, D.P.; et al. Contributions of GRACE to understanding climate change. Nat. Clim. Chang. 2019, 9, 358–369. [Google Scholar] [CrossRef] [PubMed]
- Landerer, F.W.; Flechtner, F.M.; Save, H.; Webb, F.H.; Bandikova, T.; Bertiger, W.I.; Bettadpur, S.V.; Byun, S.H.; Dahle, C.; Dobslaw, H.; et al. Extending the Global Mass Change Data Record: GRACE Follow-On Instrument and Science Data Performance. Geophys. Res. Lett. 2020, 47, e2020GL088306. [Google Scholar] [CrossRef]
- Kurtenbach, E.; Eicker, A.; Mayer-Gürr, T.; Holschneider, M.; Hayn, M.; Fuhrmann, M.; Kusche, J. Improved daily GRACE gravity field solutions using a Kalman smoother. J. Geodyn. 2012, 59–60, 39–48. [Google Scholar] [CrossRef]
- Sakumura, C.; Bettadpur, S.; Save, H.; McCullough, C. High-frequency terrestrial water storage signal capture via a regularized sliding window mascon product from GRACE. J. Geophys. Res. Solid Earth 2016, 121, 4014–4030. [Google Scholar] [CrossRef] [Green Version]
- Save, H. CSR RL05 GRACE Daily Swath Mass Anomaly Estimates over the Ocean; Center for Space Research, The University of Texas at Austin: Austin, TX, USA, 2019. [Google Scholar] [CrossRef]
- Ramillien, G.; Seoane, L.; Schumacher, M.; Forootan, E.; Frappart, F.; Darrozes, J. Recovery of Rapid Water Mass Changes (RWMC) by Kalman Filtering of GRACE Observations. Remote Sens. 2020, 12, 1299. [Google Scholar] [CrossRef] [Green Version]
- Gouweleeuw, B.; Kvas, A.; Gruber, C.; Gain, A.; Mayer-Gürr, T.; Flechtner, F.; Güntner, A. Daily GRACE gravity field solutions track major flood events in the Ganges-Brahmaputra Delta. Hydrol. Earth Syst. Sci. 2018, 22, 2867–2880. [Google Scholar] [CrossRef] [Green Version]
- Eicker, A.; Jensen, L.; Wöhnke, V.; Dobslaw, H.; Kvas, A.; Mayer-Gürr, T.; Dill, R. Daily GRACE satellite data evaluate short-term hydro-meteorological fluxes from global atmospheric reanalyses. Sci. Rep. 2020, 10, 4504. [Google Scholar] [CrossRef] [PubMed]
- Schindelegger, M.; Harker, A.A.; Ponte, R.M.; Dobslaw, H.; Salstein, D.A. Convergence of Daily GRACE Solutions and Models of Submonthly Ocean Bottom Pressure Variability. J. Geophys. Res. Oceans 2021, 126, e2020JC017031. [Google Scholar] [CrossRef]
- Kvas, A. Estimation of High-Frequency Mass Variations from Satellite Data in near Real-Time: Implementation of a Technology Demonstrator for near Real-Time GRACE/GRACE-FO Gravity Field Solutions. Ph.D. Thesis, Graz University of Technology, Graz, Austria, 2020. [Google Scholar] [CrossRef]
- Koch, K.R. Least squares adjustment and collocation. Bulletin Géodésique 1977, 51, 127–135. [Google Scholar] [CrossRef]
- Heiskanen, W.A.; Moritz, H. Physical geodesy. Bulletin Géodésique (1946–1975) 1967, 86, 491–492. [Google Scholar] [CrossRef]
- Weigelt, M.; Sneeuw, N.; Schrama, E.J.; Visser, P.N. An improved sampling rule for mapping geopotential functions of a planet from a near polar orbit. J. Geod. 2013, 87, 127–142. [Google Scholar] [CrossRef] [Green Version]
- Lütkepohl, H. New Introduction to Multiple Time Series Analysis; Springer: Berlin/Heidelberg, Germany, 2005; Volume 1, pp. 1–764. [Google Scholar] [CrossRef]
- Dobslaw, H.; Bergmann-Wolf, I.; Dill, R.; Forootan, E.; Klemann, V.; Kusche, J.; Sasgen, I. The updated ESA Earth System Model for future gravity mission simulation studies. J. Geod. 2015, 89, 505–513. [Google Scholar] [CrossRef]
- NASA Jet Propulsion Laboratory. GRACE-FO Level-1B Release Version 4.0 from JPL in ASCII. 2019. Available online: https://podaac-tools.jpl.nasa.gov/drive/files/allData/gracefo/L1B/JPL/RL04/ASCII (accessed on 21 March 2021). [CrossRef]
- Kvas, A.; Behzadpour, S.; Ellmer, M.; Klinger, B.; Strasser, S.; Zehentner, N.; Mayer-Gürr, T. ITSG-Grace2018: Overview and Evaluation of a New GRACE-Only Gravity Field Time Series. J. Geophys. Res. Solid Earth 2019, 124, 9332–9344. [Google Scholar] [CrossRef] [Green Version]
- Mayer-Gürr, T.; Behzadpur, S.; Ellmer, M.; Kvas, A.; Klinger, B.; Strasser, S.; Zehentner, N. ITSG-Grace2018—Monthly, Daily and Static Gravity Field Solutions from GRACE; GFZ Data Services: Potsdam, Germany, 2018. [Google Scholar] [CrossRef]
- Kusche, J.; Schmidt, R.; Petrovic, S.; Rietbroek, R. Decorrelated GRACE time-variable gravity solutions by GFZ, and their validation using a hydrological model. J. Geod. 2009, 83, 903–913. [Google Scholar] [CrossRef] [Green Version]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).