Abstract
According to the Cosmological Principle, the Universe should appear isotropic, without any preferred directions, to a comoving observer. However, a peculiar motion of the observer, or equivalently of the solar system, might introduce a dipole anisotropy in some of the observed properties of the Cosmos. The peculiar motion of the solar system, determined from the dipole anisotropy in the Cosmic Microwave Background Radiation (CMBR), gave a velocity 370 km/s along l = 264°, b = 48°. However, dipoles from number counts, sky brightness or redshift distributions in large samples of distant active galactic Nuclei (AGNs) have yielded values of the peculiar velocity many times larger than that from the CMBR, though in all cases the directions agreed with the CMBR dipole. Here we determine our peculiar motion from a sample of ~0.28 million AGNs, selected from the Mid Infra Red Active Galactic Nuclei (MIRAGN) sample comprising more than a million sources. We find a peculiar velocity more than four times the CMBR value, although the direction seems to be within ~2σ of the CMBR dipole. Since a real solar peculiar velocity should be the same whatever the data or the technique of observations may be, such discordant dipoles could imply that the explanation for the genesis of these dipoles, including that of the CMBR, might lie elsewhere. At the same time, a common direction for all these dipoles, determined from completely independent surveys by different groups, does indicate that these dipoles are not merely due to some systematics, and it might instead suggest a preferred direction in the Universe implying a genuine anisotropy, which would violate the Cosmological Principle, the core of modern cosmology.
1. Introduction
According to the Cosmological Principle, the Universe, when seen on a sufficiently large scale (beyond a few hundred Mpc), should appear isotropic, without any preferred directions, to a co-moving observer in the expanding Universe. Such an observer is at rest with respect to the Universe at large and the angular distribution of sources in sky should appear to be the same in all directions. However, if relative to the co-moving coordinates the observer has a motion, called a peculiar motion, then because of the Doppler boosting as well as aberration, the observer will find the number counts to manifest a dipole anisotropy, proportional to the peculiar velocity of the observer. The Cosmic Microwave Background Radiation (CMBR), shows such a dipole anisotropy, which, when ascribed to the peculiar motion of the Solar system, yields a peculiar velocity 370 km/s along l = 264°, b = 48° [1,2,3].
On the other hand, our peculiar velocity has also been determined from the anisotropy observed in the sky distribution of large samples of discrete radio sources. The NRAO VLA Sky Survey (NVSS), comprising 1.8 million radio sources [4], showed a dipole asymmetry corresponding to a velocity ~4 times the CMBR value [5], at that time a totally unexpected result, but confirmed subsequently by many independent groups [6,7,8,9]. Further, in the TIFR GMRT Sky Survey (TGSS) [10], comprising 0.62 million sources [11], a very significant (>10σ) dipole anisotropy, amounting to a velocity ~10 times the CMBR value, is detected [9,12]. However, the direction of motion in both cases has turned out to be along the CMBR dipole. Recently, a homogeneously selected DR12Q sample of 103,245 distant quasars has shown a redshift dipole along the CMBR dipole direction, implying a velocity ~6.5 times though in a direction directly opposite to the CMBR dipole [13]. A more recent determination of the peculiar motion from a sample of quasars derived from the Wide-field Infrared Survey Explorer (WISE) has shown an amplitude over twice as large the CMBR value [14]. Now a genuine solar peculiar velocity cannot vary from one set of measurements to another and such discordant dipoles could imply that the explanation for the genesis of these dipoles, including that of the CMBR, might lie elsewhere. At the same time, a common direction for all these dipoles, determined from completely independent surveys by different groups, using independent computational routines, does indicate that the differences in the dipoles are not merely random fluctuations or due to some systematics in data or procedures, otherwise their directions too should be different. Instead, it might suggest a preferred direction in the Universe implying a genuine anisotropy, which would violate the Cosmological Principle, the core of modern cosmology. Because of the huge impact on the cosmological models any genuine variations in the dipole magnitudes may impart, further independent determinations of the dipole vectors are warranted. Here we determine our peculiar motion from a sample of ~0.28 million AGNs, selected from the Mid Infra Red Active Galactic Nuclei (MIRAGN) sample comprising more than a million sources [15].
2. Dipole Vector Due to the Observer’s Motion
An observer moving with a velocity v will find a source along an angle θ with respect to the direction of motion, to appear brighter due to Doppler boosting by a factor , where δ = 1 + (v/c) is the Doppler factor and α is the spectral index defined by [16]. Here we have used the non-relativistic formula for the Doppler factor as all previous observations indicate that v c. As the integral source counts of the extragalactic source population usually follow a power law, N(>S) , the number of sources observed by a telescope of a given sensitivity will be higher by a factor, , due to the Doppler boosting [16]. Additionally, due to the aberration of light, the apparent position of a source will shift by a small value, (v/c) , thereby changing the number density by another factor . Thus, as a combined effect of Doppler boosting and aberration, the observed number counts will vary with direction as , which, for v c, can be expressed as a dipole anisotropy, 1 + of amplitude D = [2 + x(1 + α)](v/c) [5,16,17].
Let ri be the position vector of ith source, then a stationary observer, due to the assumed isotropy of the Universe, à la Cosmological Principle, should get Σri = 0. However, for a moving observer, Σri will yield a net vector along the direction of motion [17], and from θi computed with respect to that vector, the sum Σcosθi/Σ|cosθi| = 2D/3 [5,12], would then give the peculiar speed v of the observer.
Thus, using the angular positions of extragalactic sources in a large survey that covers the whole sky and is complete in the sense that it comprises all sources above a certain flux-density limit, we can determine our peculiar motion. It should be noted that exclusions of strips like the galactic plane, |b| < 15° (Figure 1), which affect the forward and backward measurements identically, do not have systematic effects on the results [5,16].
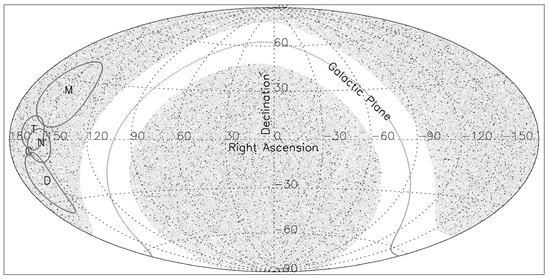
Figure 1.
The sky distribution of ~0.28 million AGNs of our MIRAGN sample, plotted in equatorial coordinates. The sky position of the pole determined from our MIRAGN sample is indicated by M, along with the error ellipse, while other pole positions for various dipoles shown on the map are: N(NVSS), T(TGSS) and D(DR12Q). The CMBR pole at C has negligible errors.
3. Our Sample of MIRAGNs
The sample of AGNs used in this study is selected from a publicly available larger all-sky sample of 1.4 million active galactic nuclei (AGNs) [15], in turn derived from the Wide-field Infrared Survey Explorer final catalog release (AllWISE), that incorporates data from the WISE Full Cryogenic, 3-Band Cryo, and NEOWISE Post-Cryo survey [18,19]. The WISE survey is an all-sky mid-IR survey at 3.4, 4.6, 12, and 22 μm (W1, W2, W3, and W4) with angular resolutions 6.1, 6. 4, 6.5 and 12 arcsec, respectively. AllWISE comprises data for almost 748 million objects, out of these about 1.4 million objects met a two-color infrared photometric selection criteria for AGNs, that formed the original MIRAGN sample [15].
For our purpose, we have restricted the MIRAGN sample to an upper limit of magnitude, W1 < 15.0, mainly because of a differential increase in the number density for weaker sources in various regions of the sky, especially near the ecliptic poles, due to deeper WISE coverage. However, due to the completeness of the basic survey at strong source levels, the number density distribution in the sky at low infrared magnitudes remains unaffected as a deeper coverage adds only fainter sources, which are at higher infrared magnitudes. From a detailed examination of the original MIRAGN sample data in small-range magnitude slices at different W1 levels, we find that from W1 ≈ 15.5 onward, there is a non-uniform distribution in sky that increases rapidly at higher magnitudes, i.e., for weaker sources. Accordingly, we have chosen W1 = 15.0 to be our upper magnitude limit. On the lower side, we have restricted our sample to W1 > 12.0. This is only to minimize the effects of the local bulk flows, which will affect sources at low redshifts, z < 0.05, corresponding to W1 < 12. In any case, the number of sources for W1 < 12 is relatively very small and their inclusion or exclusion hardly affects the results. Further, we have also excluded all sources in the galactic plane with |b| < 15o to avoid contamination by galactic sources [15]. Our final sample then comprises 279,139 AGNs.
4. Results and Discussion
Figure 1 shows the sky distribution of all ~0.28 million MIRAGN AGNs in our sample, in the Hammer-Aitoff equal-area projection map, plotted in equatorial coordinates. The source distribution looks quite uniform over the sky, except for the gap in the galactic plane band, where we have removed a ±15° band about the galactic plane. As mentioned earlier, such exclusions, which affect the forward and backward measurements identically, do not have systematic effects on the results.
Before proceeding with the actual source sample, we made Monte–Carlo simulations with source distributions similar to that in our sample. In each simulation, for the magnitude (W1) distributions we took the actual values as in our sample, however, the sky position was allotted randomly for each one of the 0.28 million sources. On this were superimposed Doppler boosting and aberration effects of an assumed peculiar motion of the observer, choosing a different velocity vector for each simulation. The resultant artificial sky was then used to recover the velocity vector and compared with the value actually used in that particular simulation. This not only verified our procedure and the computation routine, but also allowed us to make an estimate of errors in the dipole direction from the spread observed in 500 independent simulations.
In Table 1, we give the results for the dipole, determined from the anisotropy in number counts in our sample of about 0.28 million MIRAGNs in the 12 < W1 < 15 range. We find a peculiar speed 1700 ± 200 km/s, which is more than four times the peculiar speed estimated from the CMBR dipole. In order to ensure that this excess in speed is not due to a skew distribution of sources belonging to a particular magnitude, we divided our sample into three magnitude bins, with approximately 0.1 million sources in each bin. The results for the three bins are also presented in Table 1. Here, N is the total number of sources in the corresponding W1 bin, RA and Dec give the dipole direction in the sky, D is the dipole value computed from D = 3Σcosθi/2Σ|cosθi|, with error ΔD = √(3/N) [5,12,17]. Then the peculiar speed of the observer, or rather of the Solar system, is computed from D = [2 + x(1 + α)](v/c). In order to determine x we have made a plot of the integrated source counts N(<W1) against W1, for our MIRAGN sample, in Figure 2, which shows a power law behaviour of the integrated source counts, with a slope that varies between 0.71 and 0.65, with a mean value of 0.68. From this we estimate the index of integral source counts in our sample to be x = 2.5 0.68 = 1.7, consistent with the value quoted in the literature [14]. For the spectral index, we have taken α ≈ 1, a value quoted in the literature [14], for the extragalactic population of AGNs. The peculiar speed, accordingly, is given by, v = c D/5.4 ≈ 5.55 × 104 D km/s.

Table 1.
Peculiar velocity estimated from the dipole asymmetry in number counts.
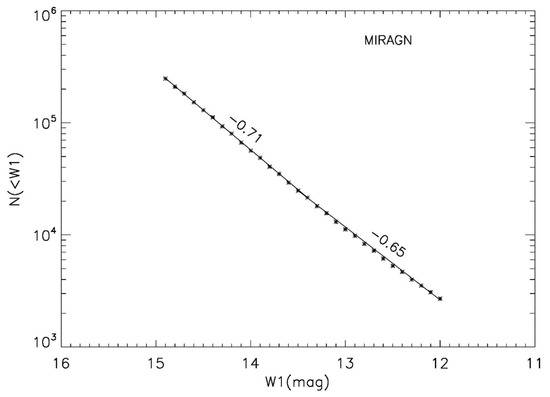
Figure 2.
A plot of the integrated source counts N(<W1) against W1, for our MIRAGN sample, showing the power law behaviour of the source counts.
In Table 1, we have also listed the direction of the dipole, along with the estimated errors, as determined in each case. The direction of the velocity vector (with our best estimate from Table 1), is given by the pole at RA = 148° ± 19°, Dec = 23° ± 17°, within about 2σ of the CMBR pole at RA = 168°, Dec = −7° (in galactic co-ordinates, the MIRAGN pole lies at l = 209°, b = 49° while the CMBR pole is at l = 264°, b = 48°). However the estimates of v (1.7 ± 0.2103 km/s) appear much higher than the CMBR value (370 km/s) by a factor >4 at a statistically significant (~6σ) level. In Figure 1, the sky position of our MIRAGN pole is shown by M, while the CMBR pole position is indicated by C. Also plotted are the various other determined pole positions, N for the NVSS dipole, T for the TGSS dipole and D for the DR12Q dipole, along with their 1σ error ellipses. From Figure 1, it does seem that various AGN dipoles are pointing along the same direction as the CMBR dipole.
Although we have restricted our sample to W1 > 12.0 to minimize the effect of local bulk flows, still, in order to estimate the influence on our results of any local clustering, like the virgo super-cluster, we determined dipole vectors by excluding sources at low super-galactic latitudes, progressively in steps of five degrees, and from a comparison of these cases (|SGB| > 0°, 5°, 10°, 15°, 20°; Table 2), no unusually large variations, beyond the statistical uncertainties were seen in the computed dipole vectors.

Table 2.
Dipole estimates for various |SGB| limits.
A genuine peculiar velocity of the Solar system should not be dependent upon the specific data or the technique used to determine it. The discordant values of the inferred peculiar motion from observed dipoles for the AGNs, may imply that we should instead look for some other possible cause for the genesis of these dipoles, including that of the CMBR. One could not say that the CMBR provides a reference frame which is to be considered as more fundamental than the other ones for establishing the peculiar motion of the solar system. While the CMBR refers to the radiation era, AGNs represent the much later matter era. A common direction for all these dipoles (Figure 1), determined from completely independent surveys by different groups, does indicate that these dipole amplitudes differ not because of random statistical fluctuations, or due to some systematics in the observations or in the data analysis, otherwise even their directions should have been different. A not-too-far-fetched inference drawn could be that a common direction for the dipoles, including of the CMBR, is a pointer toward the presence of an inherently preferred cosmic direction (axis!), implying perhaps an anisotropic Universe, in conflict with the Cosmological Principle, a cornerstone of the modern cosmology.
5. Conclusions
From the angular positions in the sky of a sample of ~0.28 million Mid Infra Red AGNs, we found an anisotropy in their number densities in different directions. Ascribing this anisotropy to the peculiar motion of the observer, we determined the peculiar velocity of the Solar system that turned out to be, like other earlier AGN dipoles, at least a factor of four larger than that inferred from the CMBR dipole, but along the same direction. Since the peculiar velocity of the Solar system should not depend upon the specific data or the technique used to determine it, the question arises about the nature of these dipoles seen in the sky and whether the genesis of some or all of these dipoles indeed is due to the peculiar motion of the Solar system. A common direction for all these dipoles, including the CMBR one, determined from completely independent surveys by different groups, does indicate that the differences in the dipole amplitudes are genuine and not because of random statistical fluctuations, or due to some systematics in the observations or in the data analysis, otherwise even the dipole directions would be different. An inference that could possibly be drawn from a common direction for all the dipoles is that it might be a pointer toward the presence of an inherently preferred cosmic direction (axis!), implying perhaps an anisotropic Universe, in discordance with the Cosmological Principle, a cornerstone of the modern cosmology. See supplementary materials with more relevant information.
Supplementary Materials
The following are available online at https://www.mdpi.com/article/10.3390/ECU2021-09270/s1.
Data Availability Statement
The data underlying this article can be downloaded from VizieR Astronomical Server in the public domain at http://vizier.u-strasbg.fr/viz-bin/VizieR by selecting catalog: J/ApJS/221/12/table1.
Conflicts of Interest
The author has no conflicts of interest to declare that are relevant to the content of this paper. No funds, grants, or other support of any kind was received from anywhere for this research.
References
- Lineweaver, C.H.; Tenorio, L.; Smoot, G.F.; Keegstra, P.; Banday, A.J.; Lubin, P. The dipole observed in the COBE DMR 4 year data. Astrophys. J. 1996, 470, 38–42. [Google Scholar] [CrossRef] [Green Version]
- Hinshaw, G.; Weiland, J.L.; Hill, R.S.; Odegard, N.; Larson, D.R.; Bennett, C.; Dunkley, J.; Gold, B.; Greason, M.R.; Jarosik, N.; et al. Five-year Wilkinson microwave anisotropy probe observations: Data processing, sky maps, and basic results. Astrophys. J. Suppl. Ser. 2009, 180, 225–245. [Google Scholar] [CrossRef] [Green Version]
- Aghanim, N.; Akrami, Y.; Arroja, F.; Ashdown, M.; Aumont, J.; Baccigalupi, C.; Ballardini, M.; Banday, A.J.; Barreiro, R.B.; Bartolo, N.; et al. Planck 2018 results I. Overview and the cosmological legacy of Planck. Astron. Astrophys. 2020, 641, A1. [Google Scholar]
- Condon, J.J.; Cotton, W.D.; Greisen, E.W.; Yin, Q.F.; Perley, R.A.; Taylor, G.B.; Broderick, J.J. The NRAO VLA sky survey. Astron. J. 1998, 115, 1693–1716. [Google Scholar] [CrossRef]
- Singal, A.K. Large peculiar motion of the solar system from the dipole anisotropy in sky brightness due to distant radio sources. Astrophys. J. 2011, 742, L23–L26. [Google Scholar] [CrossRef]
- Rubart, M.; Schwarz, D.J. Cosmic radio dipole from NVSS and WENSS. Astron. Astrophys. 2013, 555, A117. [Google Scholar] [CrossRef] [Green Version]
- Tiwari, P.; Kothari, R.; Naskar, A.; Nadkarni-Ghosh, S.; Jain, P. Dipole anisotropy in sky brightness and source count distribution in radio NVSS data. Astropart. Phys. 2015, 61, 1–11. [Google Scholar] [CrossRef] [Green Version]
- Colin, J.; Mohayaee, R.; Rameez, M.; Sarkar, S. High-redshift radio galaxies and divergence from the CMB dipole. Mon. Not. R. Astron. Soc. 2017, 471, 1045–1055. [Google Scholar] [CrossRef]
- Bengaly, C.A.P.; Maartens, R.; Santos, M.G. Probing the cosmological principle in the counts of radio galaxies at different frequencies. J. Cosmol. Astropart. Phys. 2018, 4, 31. [Google Scholar] [CrossRef] [Green Version]
- Swarup, G.; Ananthakrishnan, S.; Kapahi, V.K.; Rao, A.P.; Subrahmanya, C.R.; Kulkarni, V.K. The giant metre-wave radio telescope. Curr. Sci. 1991, 60, 95–105. [Google Scholar]
- Intema, H.T.; Jagannathan, P.; Mooley, K.P.; Frail, D.A. The GMRT 150 MHz all-sky radio survey. First alternative data release TGSS ADR1. Astron. Astrophys. 2017, 598, A78. [Google Scholar] [CrossRef] [Green Version]
- Singal, A.K. Large disparity in cosmic reference frames determined from the sky distributions of radio sources and the microwave background radiation. Phys. Rev. D 2019, 100, 063501. [Google Scholar] [CrossRef] [Green Version]
- Singal, A.K. Peculiar motion of the solar system derived from a dipole anisotropy in the redshift distribution of distant quasars. Mon. Not. R. Astron. Soc. 2019, 488, L104–L108. [Google Scholar] [CrossRef]
- Secrest, N.J.; Hausegger, S.v.; Rameez, M.; Mohayaee, R.; Sarkar, S.; Colin, J. A test of the cosmological principle with quasars. Astrophys. J. 2021, 908, L51. [Google Scholar] [CrossRef]
- Secrest, N.J.; Dudik, R.P.; Dorland, B.N.; Zacharias, N.; Makarov, V.; Fey, A.; Frouard, J.; Finch, C. Identification of 1.4 million active galactic nuclei in the mid-Infrared using WISE Data. Astrophys. J. Suppl. Ser. 2015, 221, 12. [Google Scholar] [CrossRef] [Green Version]
- Ellis, G.F.R.; Baldwin, J.E. On the expected anisotropy of radio source counts. Mon. Not. R. Astron. Soc. 1984, 206, 377–381. [Google Scholar] [CrossRef] [Green Version]
- Crawford, F. Detecting the cosmic dipole anisotropy in large-scale radio surveys. Astrophys. J. 2009, 692, 887–893. [Google Scholar] [CrossRef] [Green Version]
- Wright, E.L.; Eisenhardt, P.R.; Mainzer, A.K.; Ressler, M.E.; Cutri, R.M.; Jarrett, T.; Kirkpatrick, J.D.; Padgett, D.; McMillan, R.S.; Skrutskie, M.; et al. The wide-field infrared survey explorer (WISE): Mission description and initial on-orbit performance. Astron. J. 2010, 140, 1868–1881. [Google Scholar] [CrossRef]
- Mainzer, A.; Bauer, J.; Cutri, R.M.; Grav, T.; Masiero, J.; Beck, R.; Clarkson, P.; Conrow, T.; Dailey, J.; Eisenhardt, P.; et al. Initial performance of the NEOWISE reactivation mission. Astrophys. J. 2014, 792, 30. [Google Scholar] [CrossRef] [Green Version]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).