Dark Atom Solution for the Puzzles of Direct Dark Matter Search †
Abstract
:1. Introduction
2. Results
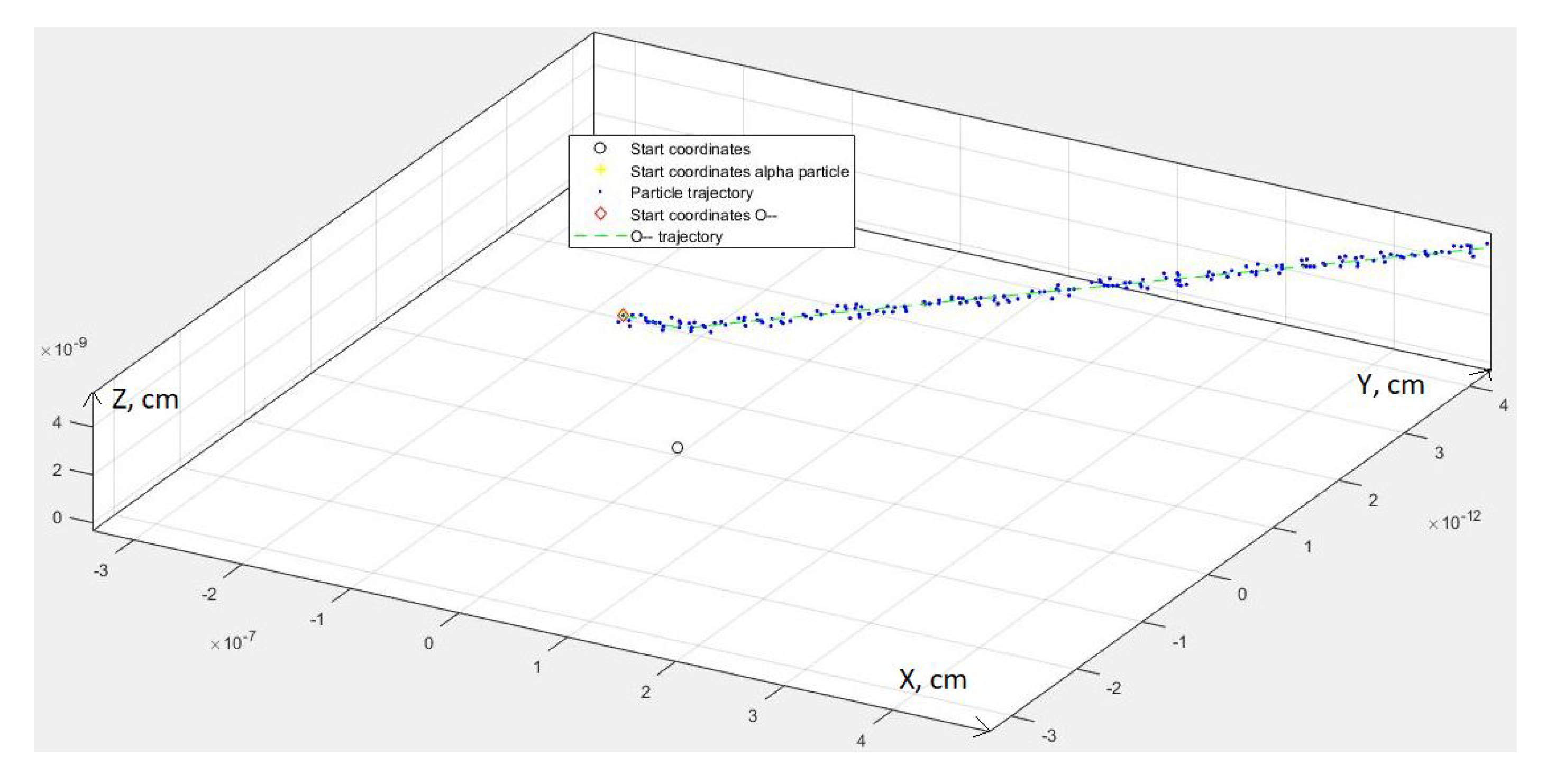
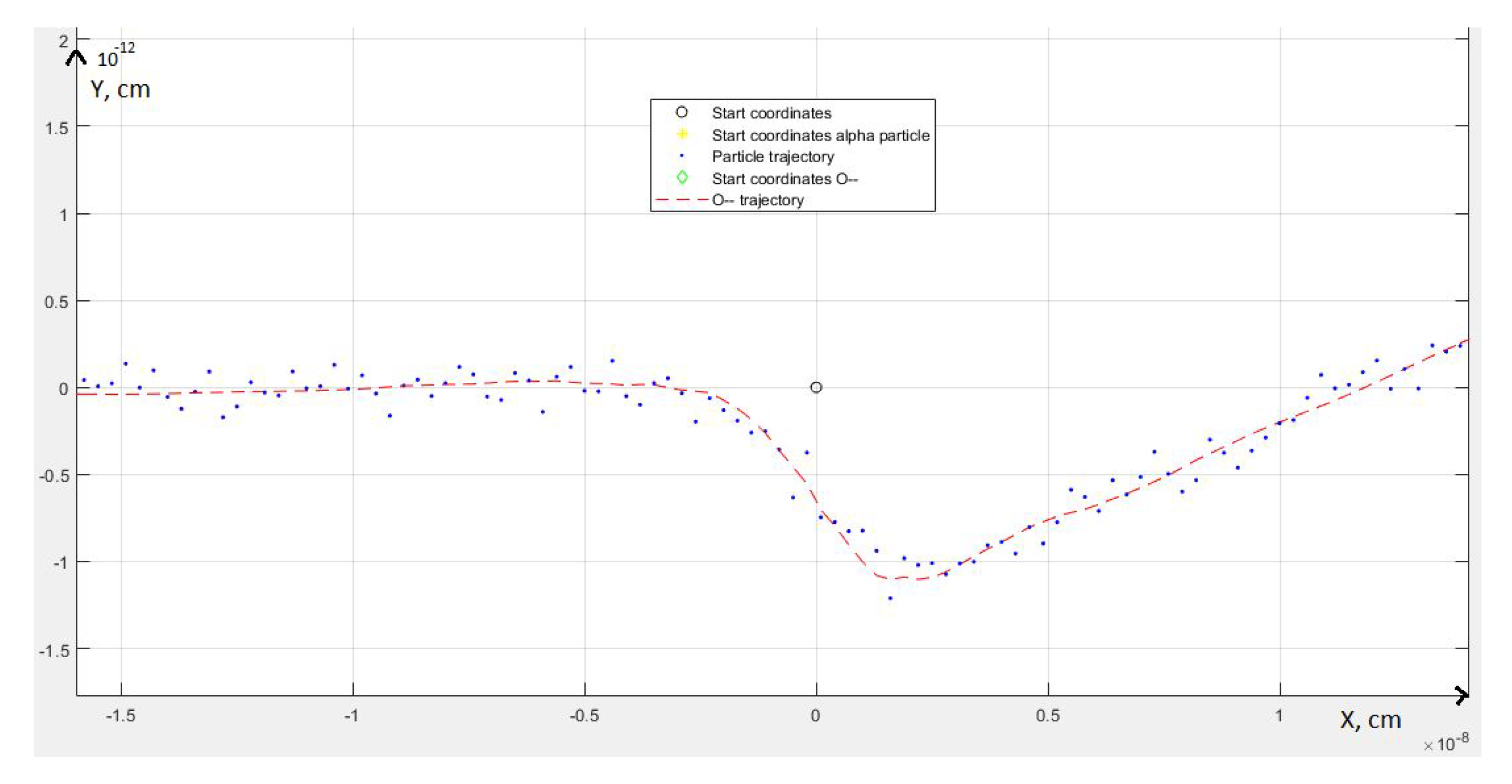
2.1. Numerical Simulation of the Interaction of OHe with the Nucleus
2.1.1. Simulation of OHe
2.1.2. Coulomb Interaction in the OHe—Nucleus System
2.1.3. Nuclear Interaction in the OHe—Nucleus System
3. Discussion
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Khlopov, M.Y. Fundamental particle structure in the cosmological dark matter. Int. J. Mod. Phys. A 2013, 28, 1330042. [Google Scholar] [CrossRef] [Green Version]
- Khlopov, M.Y. Dark matter reflection of particle symmetry. Mod. Phys. Lett. A. 2017, 32, 1740001. [Google Scholar] [CrossRef] [Green Version]
- Bulekov, O.V.; Khlopov, M.Y.; Romaniouk, A.S.; Smirnov, Y.S. Search for Double Charged Particles as Direct Test for Dark Atom Constituents. Bled Work. Phys. 2017, 18, 11–24. [Google Scholar]
- Khlopov, M.Y. Removing the conspiracy of BSM physics and BSM cosmology. Int. J. Mod. Phys. D 2019, 28, 1941012. [Google Scholar] [CrossRef]
- Khlopov, M.Y.; Stephan, C.A.; Fargion, D. Dark matter with invisible light from heavy double charged leptons of almost-commutative geometry? Class. Quantum Gravity 2006, 23, 7305–7354. [Google Scholar] [CrossRef]
- Khlopov, M.Y.; Kouvaris, C. Strong interactive massive particles from a strong coupled theory. Phys. Rev. D 2008, 77, 065002. [Google Scholar] [CrossRef] [Green Version]
- Khlopov, M.Y.; Mayorov, A.G.; Soldatov, E.Y. The dark atoms of dark matter. Prespace. J. 2010, 1, 1403–1417. [Google Scholar]
- Khlopov, M.Y. Composite dark matter from 4th generation. JETP Lett. 2006, 83, 1–4. [Google Scholar] [CrossRef]
- Beylin, V.; Khlopov, M.; Kuksa, V.; Volchanskiy, N. New physics of strong interaction and Dark Universe. Universe 2020, 6, 196. [Google Scholar] [CrossRef]
- Bernabei, R. Dark matter investigation by dama at gran sasso. Int. J. Mod. Phys. A 2013, 28, 1330022. [Google Scholar] [CrossRef] [Green Version]
- Cudell, J.R.; Khlopov, M.Y.; Wallemacq, Q. The nuclear physics of OHe. Bled Work. Phys. 2012, 13, 10–27. [Google Scholar]
- Bikbaev, T.E.; Khlopov, M.Y.; Mayorov, A.G. Numerical simulation of dark atom interaction with nuclei. Bled Work. Phys. 2020, 21, 105–117. [Google Scholar]


Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bikbaev, T.; Khlopov, M.; Mayorov, A. Dark Atom Solution for the Puzzles of Direct Dark Matter Search. Phys. Sci. Forum 2021, 2, 3. https://doi.org/10.3390/ECU2021-09263
Bikbaev T, Khlopov M, Mayorov A. Dark Atom Solution for the Puzzles of Direct Dark Matter Search. Physical Sciences Forum. 2021; 2(1):3. https://doi.org/10.3390/ECU2021-09263
Chicago/Turabian StyleBikbaev, Timur, Maxim Khlopov, and Andrey Mayorov. 2021. "Dark Atom Solution for the Puzzles of Direct Dark Matter Search" Physical Sciences Forum 2, no. 1: 3. https://doi.org/10.3390/ECU2021-09263
APA StyleBikbaev, T., Khlopov, M., & Mayorov, A. (2021). Dark Atom Solution for the Puzzles of Direct Dark Matter Search. Physical Sciences Forum, 2(1), 3. https://doi.org/10.3390/ECU2021-09263






