1. Introduction
Observation evidence of astrophysical black holes, such as supermassive black holes (SMBHs) and stellar black holes, provides new motivation to investigate charged particle dynamics in the presence of the external electromagnetic field around black holes. It is generally accepted that a magnetic field is considered one of main sources of the most energetic processes around supermassive black holes at the center of galaxies, playing the role of “feeder" of the supermassive black hole by trapping dust near the galaxy’s center [
1].
Synchrotron radiation is, a relativistic case of cyclotron radiation, characterized by emitting photons due to the acceleration of charged particles in the external magnetic field. In a flat space, radiation from a rapidly moving charge and synchrotron radiation (magnetic bremsstrahlung) from a charged particle moving along a circular trajectory, with an arbitrary relativistic velocity in a uniform magnetic field, has been investigated in [
2]. These facts provide new motivations for the investigation of radiation from charged particles in the framework of general relativity (GR).
It is worth noting that, according to the “no-hair theorem”, the black hole cannot possess a magnetic field. However, the external magnetic field around the black hole can be generated by its accretion disc, or a surrounded rotating matter, or a companion in binary systems containing a neutron star (NS) or magnetar with a strong magnetic field. One of simple model of magnetized black hole has performed by Wald [
3], and similar physical scenarios on magnetized black hole have been considered later, e.g., in [
4,
5,
6,
7,
8,
9,
10,
11,
12,
13,
14,
15,
16]. According to this model, the black hole immersed in an asymptotically uniform external magnetic field that is small enough to change its space-time geometry. In Reference [
15], it is shown that the external magnetic field
B is negligibly small than the critical magnetic field
that can influence the space-time of the black hole and satisfies the following condition:
According to Reference [
17] the magnetic field strength around supermassive black hole (SMBH) is order of
, while in the vicinity of the stellar black hole (SBH), it is about
. The energy of the emitted photon through the cyclotron frequency around SMBH then estimated as
while around SBH, it has
A complete detailed analysis of interaction between black hole and magnetic field generated by the accretion disc or companion object (it can be neutron star or magnetar with a strong magnetic field) is complicated problem which requires numerical magnetohydrodynamic (MHD) simulations [
18]. However, approximative methods are also very useful to draw a picture of this phenomenon, by considering stationary magnetized black hole solutions in general relativity as was done by Wald [
3] and Ernst [
19].
The discussion of an interaction between charged particle and electromagnetic fields is a very interesting topic from a theoretical and observational point of view. A comprehensive study of the physical aspects of black holes in an external electromagnetic field are reviewed in [
20,
21,
22,
23]. In the papers [
24,
25] propagation of a scalar field in the background of a strongly magnetized black hole (or Ernst space-time) has been studied and, later, it is considered for the massive scalar field in [
26]. It is shown that, in the presence of the strong magnetic field, the quasinormal modes are longer lived and have larger oscillation frequencies in both massless and massive scalar fields [
27,
28]. The effect of the magnetic field in optical properties of black hole has been discussed in References [
29,
30].
The paper is organized as follows. In
Section 2, we provide basic necessary equations related to charged test particle motion around the Schwarzschild black hole in the presence of the electromagnetic field. In
Section 3, we investigate a general description to derive the fundamental frequencies for charged particle orbiting around static black hole, described by arbitrary space-time with given stationary, spherical–symmetric metric coefficients and electromagnetic fields. Later on, we derived the fundamental frequencies, such as, Keplerian, Larmor, and epicyclic frequencies of charge particle around magnetized Schwarzschild black hole. In the next
Section 4, we discuss synchrotron radiation from a relativistic charged particle orbiting around the magnetized black hole. Finally, in
Section 5, we summarize the found results and give a future outlook related to this work. Throughout the paper we use the geometric system of units
and spacelike signature (
). However, we restore constants when we compare the obtained results with observational data.
2. Charged Particle Dynamics
In this section, we provide equations of motion for charged particle around the black hole immersed in the uniform magnetic field. In Boyer-Lindquist coordinates
, the Schwarzschild metric is given by
where
M is total mass of the black hole.
The configuration of the electromagnetic field near the black hole has explicitly shown in [
3], the non-zero component of the vector potential is given by
where
B is the magnetic field strength.
The dynamical motion of charged particle of the mass
m and charge
q is governed by the following non-geodesic equation
where
is the four-velocity of the test particle,
is an affine parameter,
are the Christoffel symbols and
is the electromagnetic field tensor. The conserved quantities, namely, the specific energy
, and specific angular momentum
of charged particle measured at the infinity, can be easily found as
Using the normalization of four-velocity of the test particle, one can have the following expression:
and, hereafter, introducing the spatial components of the velocity of particle measured by a local observer
with the total velocity
, the expression for the specific energy of charged particle can be expressed as
Note that the energy Expression (
10) is obviously independent of the external magnetic field, however, the radius
r and velocity
v of charged particle depend on the external magnetic field. One can easily see from the Expression (
10) that absence the black hole’s mass, i.e.,
, the classical expression for the energy of relativistic particle can be obtained as follows,
.
3. Fundamental Frequency of Charged Particle
Hereafter using normalization of the four-velocity of the test particle, i.e.,
, taking into account the Expression (
7), one can obtain
where
As one can see from the expression for the Potential (
12), for a charged particle one needs the explicit form of the vector potential, while a magnetized particle depends on the components of the magnetic field, which means that if we wish to consider both the charged and magnetized particle in the presence of external magnetic field then we need the expressions for the vector potential and components of the magnetic field.
It is interesting to consider the periodic motion of the charged particle orbiting around the black hole which allows the determining of the fundamental frequencies, such as Keplerian and Larmor frequencies. The simple way of deriving the expressions for thus frequencies is to consider motion in the stable circular orbit with,
, which allows writing
where
is the angular velocity of the orbital motion measured by a distant observer.
It is important to determine the radius of the innermost stable circular orbit (ISCO) for charged particle. The ISCO radius can be easily determined from the following conditions:
Considering charged particle motion in the vicinity of the Schwarzschild black hole in the presence of the uniform magnetic field, we found that the ICSO radii for both positively and negatively charged particles decrease due to the external uniform magnetic field. Similarly, careful numerical analyses show that the radius of the marginally bound orbit, where the energy of the particle in circular orbit will be the same as its rest energy, or
, for charged particle also decreases due to the effect of the external magnetic field.
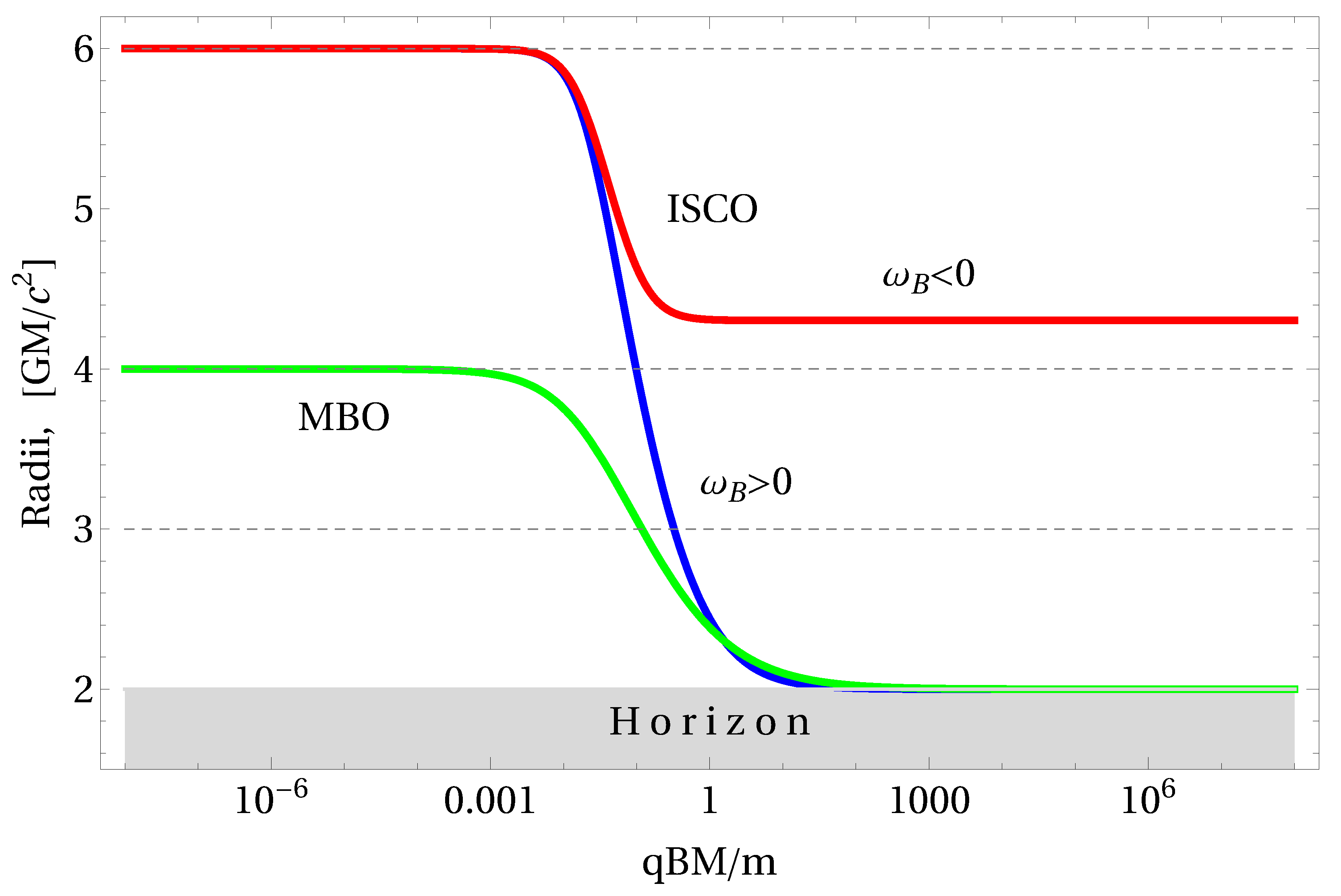
Figure 1 shows the dependence of the ISCO and MBO radii from the magnetic coupling parameter
.
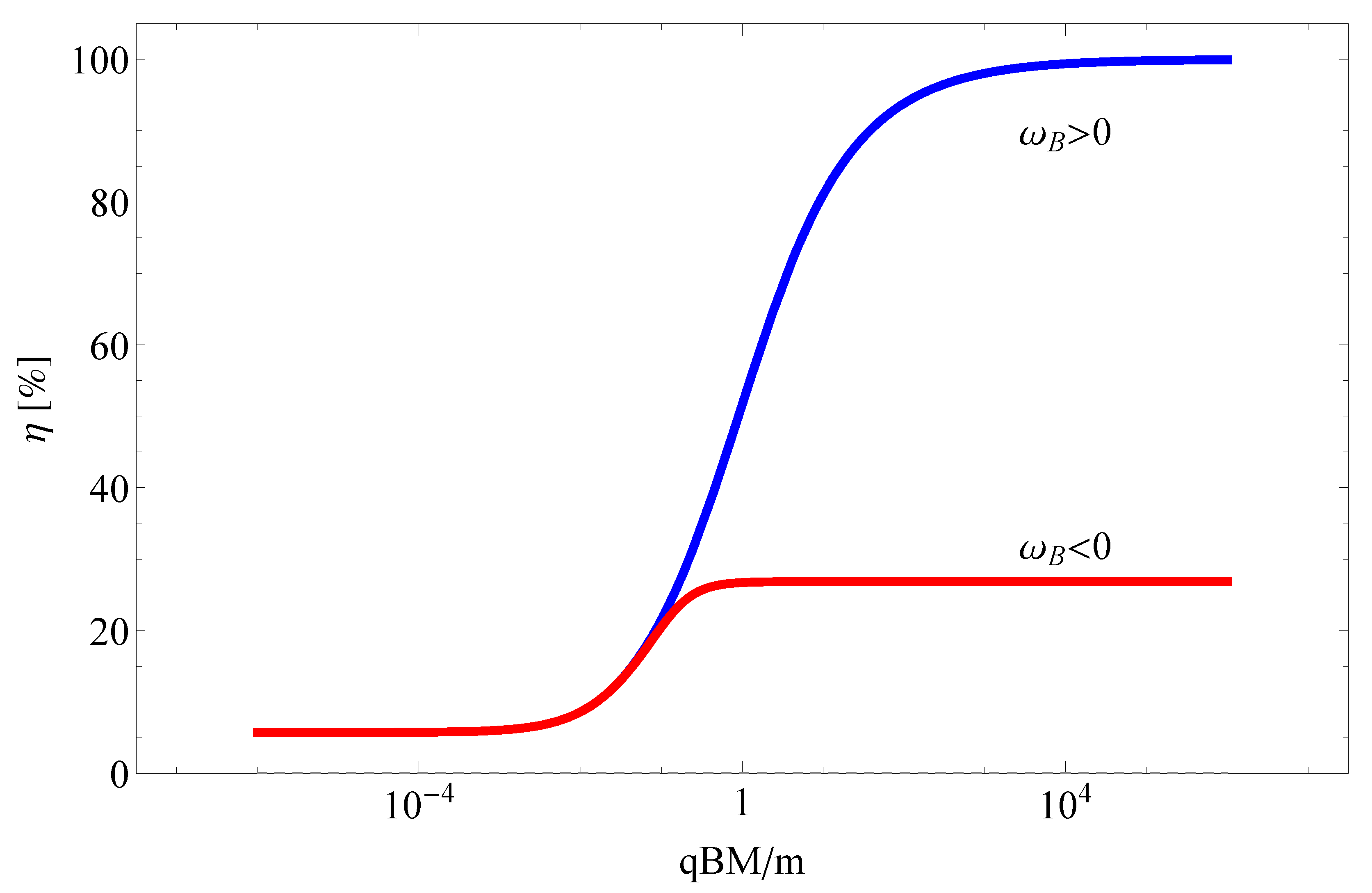
Another important quantity in particle dynamics is the energy efficiency (or, sometimes, it is called gravitational defect mass), calculation of the energy efficiency is rather simple, i.e.,
. Our numerical calculations show that the energy efficiency for positively charged particle reaches up to
(but, never reaches
), while for negatively charged particles it reaches up to
.
Figure 2 illustrates dependence of the energy efficiency from the magnetic coupling parameter
.
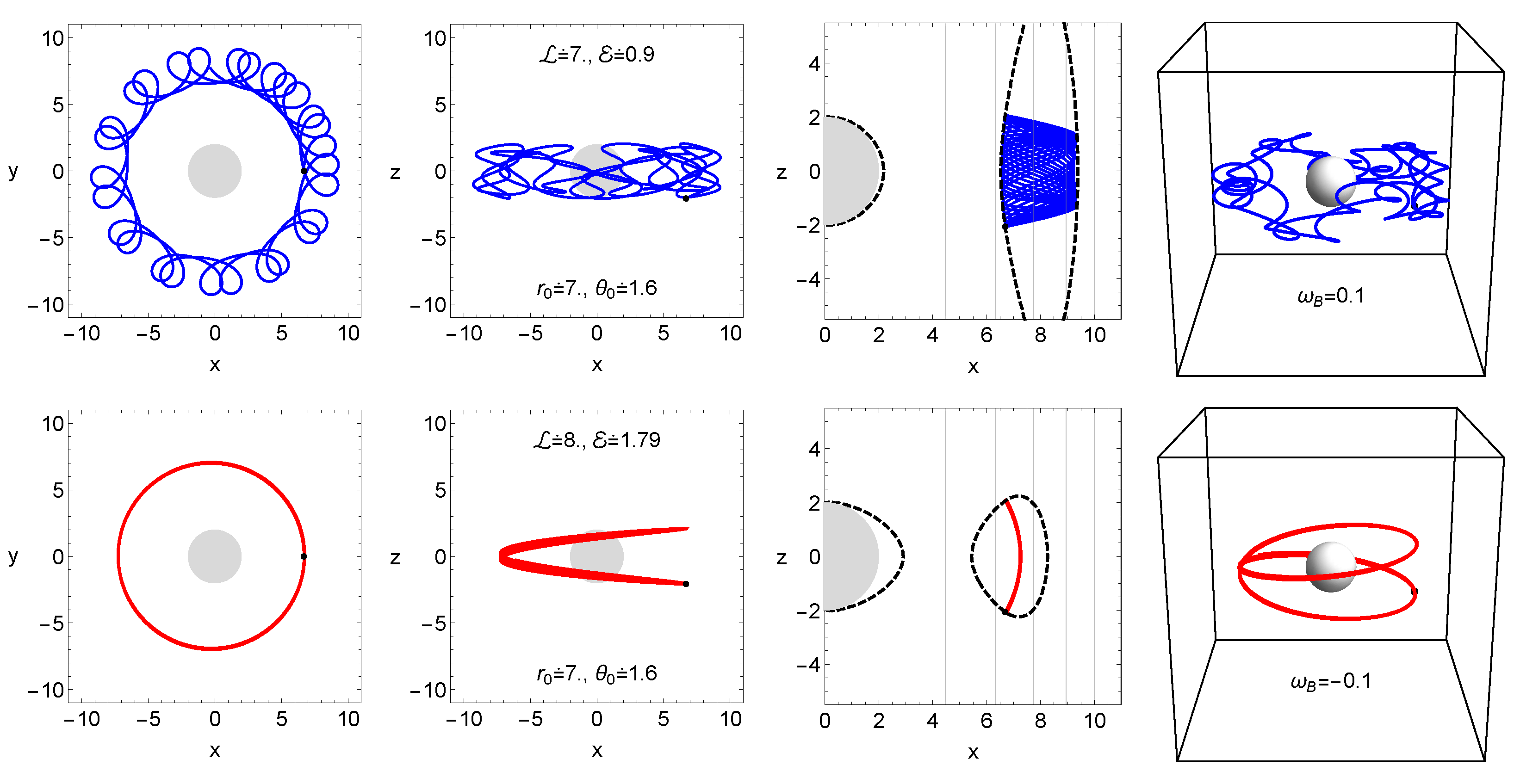
It is also interesting to produce the trajectories of the charged particle orbiting around the magnetized black hole. As we mentioned before that charged particle moves in the gravitational and magnetic field and motion is governed by the four second order equations as shown in (
6). In order to construct particle trajectory one needs eight initial conditions, two of them can be eliminated using the conserved quantities, due to symmetry other two conditions can be written as
, while normalization of the four-velocity eliminates one of conditions. Then, we only need to give initial position of particle with random velocity.
Figure 3 illustrates the trajectories of charged particle orbiting around weakly magnetized black hole.
3.1. Keplerian and Larmor Frequency
Now we focus on the derivation of the expression for the orbital angular frequencies, such as Keplerian, and Larmor frequencies, of the charged particle orbiting around the black hole. To do this, let us again consider motion in a circular orbit, with
. In the case from (
6), equations for radial and vertical motion can be written
Note that the physical meaning of the quantity
above equations are different and this difference can be easily shown by considering neutral particle motion, i.e.,
. In this case, the solution of the first equation in (
17) becomes
, which represents Keplerian frequency for the neutral particle. On the other hand, the solution of the second equation of (
17) vanishes
for the neutral particle, so that the non-trivial solution can be found only for charged particle in the presence of the external electromagnetic field. In order to find the explicit expressions for Keplerian and Larmor frequencies, one has to eliminate
by inserting the Expression (
13) into (
17), and after performing simple algebraic manipulations one can obtain
3.2. The Epicyclic Frequencies
It is also interesting to determine the epicyclic frequencies (
) produced by oscillatory motion of charged particle along radial and vertical direction at stable circular orbit around black hole in the presence of an external magnetic field. Here we study quasi-periodic oscillation of the charged particle around a given stable, circular orbit. Before we move on further, it is necessary to expand the function
in the form
where
are the stationary points. Here we have used the conditions (
16). Now inserting the Expression (
12) into (
11), using the Expression (
20) one can obtain the equation of harmonic oscillatory motion for the charged particle, around the stationary orbit (
), for the displacement
,
in the form:
where the epicyclic frequencies in (
21) can be calculated by
Finally, using the Equations (
12)–(15) the explicit form of the epicyclic frequencies (
) of charged particle orbiting around black hole can be expressed as:
From Equation (
23) one can see that the radial and vertical frequencies (
) depend on the the background geometry, the external magnetic field and also parameters of the test particle. Once background space-time geometry and external magnetic field are obtained, then one can immediately determine
and
, however it is important to recognize that they still depend upon Keplerian frequency, which is most important in the calculation of the fundamental frequencies.
Using the general Expressions (
18), (19), and (
23) for the fundamental frequencies such as Keplerian, epicyclic, and Larmor frequencies of charged particle orbiting around a Schwarzschild black hole immersed in a uniform magnetic field can be expressed as:
where
is the cyclotron frequency for the charged particle and
is Keplerian frequency for the neutral particle in Schwarzschild space. Absence of the external uniform magnetic field, i.e.,
or
, the expressions for the fundamental frequencies take the form:
It is worth noting that these frequencies can be observed at distance greater that the ISCO position of test particle around the black hole.
Figure 4 draws radial dependence of the fundamental frequencies for positive, negative and zero values of the interaction parameter. As one can see from
Figure 4 that near the ISCO position the values of the fundamental frequencies of charged particle are almost same as for neutral particle. While for a large distance they are dramatically changed due to the external magnetic field, in particular, the radial frequency increases at the distance far from the central object.
4. Synchrotron Radiation by Magnetized Black Hole
Now we focus on investigating of synchrotron radiation from relativistic charged particle in the vicinity of magnetized Schwarzschild black hole. According to Reference [
2], the expression for the four-momentum loss of the accelerated test particle can be written as
It is well-known that the accelerated relativistic charged particle emits radiation. Now we concentrate on the radiation of the accelerated charged particle orbiting around the black hole. The radiation spectrum of the relativistic charged particle in curved space-time can be expressed as [
2]
where
is the four-acceleration of particle in a curved space defined as
, on the other hand taking account non-geodesic equation (
6), one can write:
For simplicity, we consider the motion of charged particle in the stable circular orbit with
and to see the behavior of the radiation spectrum. Since the velocity and acceleration of particle are orthogonal to each other, i.e.,
, we can immediately express the four-acceleration of particle in the form,
, where the components of the acceleration can be defined as:
Finally, the expressions for the intensity (
30) of the radiating accelerated charged particle orbiting around magnetized black hole are:
Similarly, one can also consider the more realistic situation that the charged particle falling into black hole with the four-velocity,
, where
is radial velocity and
is angular velocity of particle. In this case, from the condition
, one can argue that the radial acceleration of charged particle vanishes
, however, vertical acceleration should still exist, i.e.,
. Finally, the intensity of charged particle can be expressed as
which concludes that the accreting accelerated charged particle moving onto the magnetized black hole emits the electromagnetic radiation.
5. Summary and Discussions
The study of black holes, analyzing the observed data on the accretion disc, may be helpful to investigate the electromagnetic radiation in the vicinity of compact objects. In the present research work, we have investigated the motion of charged particle and the energetic process, namely, the fundamental frequencies and synchrotron radiation by the magnetized Schwarzschild black hole. The main results of the paper can be summarized as follows:
In this paper, we have done analyses for the effects of the charge coupling parameter, on the ISCO parameters representing the specific energy, specific angular momentum, the critical angle, and the innermost radius, respectively. To that end, we have written the equations of motion for a charged particle in the vicinity of the magnetized Schwarzschild black hole and then have numerically calculated the ISCO parameters according to the standard way of derivation for the charged particles. Numerical results show that the ISCO radius for charged particle may change non-monotonously with its charge parameter . As a result, we can see that particles owning identical charges but different mass may degenerate into one ISCO depending on the external magnetic field.
Investigations into particle motion in the vicinity of the black hole can provide valuable references for the study of astrophysical events, for example, quasiperiodic oscillations and high energy events relating to the fundamental frequencies of a test particle orbiting around an astrophysical black hole. Our results about the degeneration of the particle orbits may provide a useful theoretical prediction for the observation of the electromagnetic waves. Thinking of the magnetized black hole space-time, one can envisage that two particles endowed with identical mass but opposite electrical charge move at the same ISCO in the same directions and have an elastic collision with each other, resulting in other two particles with the same spin but less charge, then both of these two particles will have a smaller ISCO orbit after the instantaneous event. We suspect that there must be an astrophysically observable phenomenon corresponding to this interesting collisional event.
Finally, we investigate synchrotron radiation from the acceleration of charged particle in the vicinity of the magnetized Schwarzschild black hole. The explicit expressions for the intensity of radiating charged relativistic particles around the magnetized black hole due to acceleration by electromagnetic (Coulomb and Lorentz) forces have been derived. Numerical calculations show that the radiation intensity of accelerated charged particle around the magnetized black hole is in order of . Another important result shows that radially falling charged particle onto the black hole possess vertical acceleration which means in that case it can emit electromagnetic radiation.
It is also interesting to study charged particle acceleration around rotating magnetized black hole (magnetized Kerr black hole). The effects from the rotation of the black hole and the external magnetic field in synchrotron radiation by an accelerated charged particle. The following investigations are underway.