Combining Knowledge About Metabolic Networks and Single-Cell Data with Maximum Entropy †
Abstract
1. Introduction
2. Materials and Methods
2.1. Microfluidic Live-Cell Experiments
2.2. Genome-Scale Metabolic Model
2.3. Constraint-Based Modeling
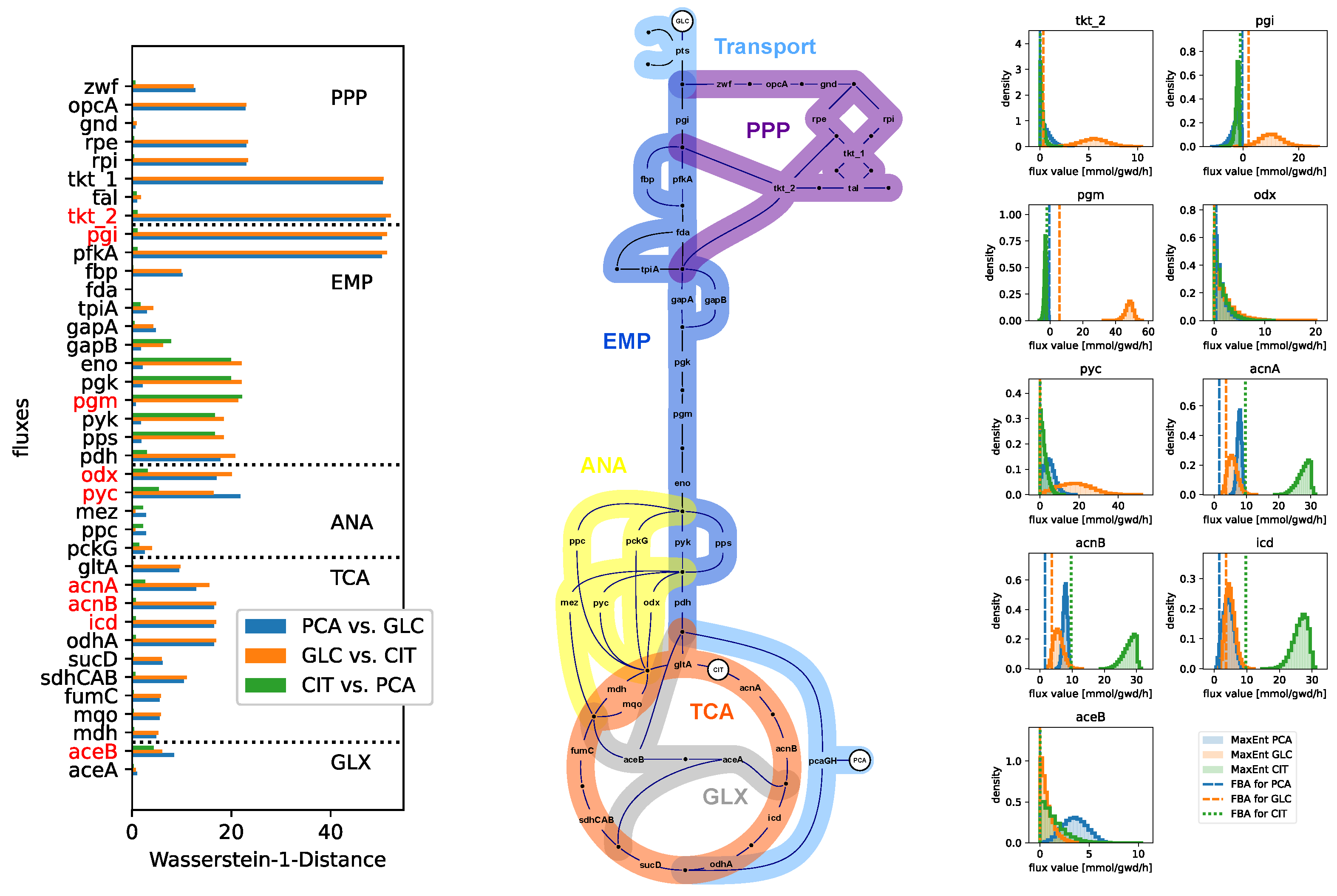
Wasserstein Distance
3. Results
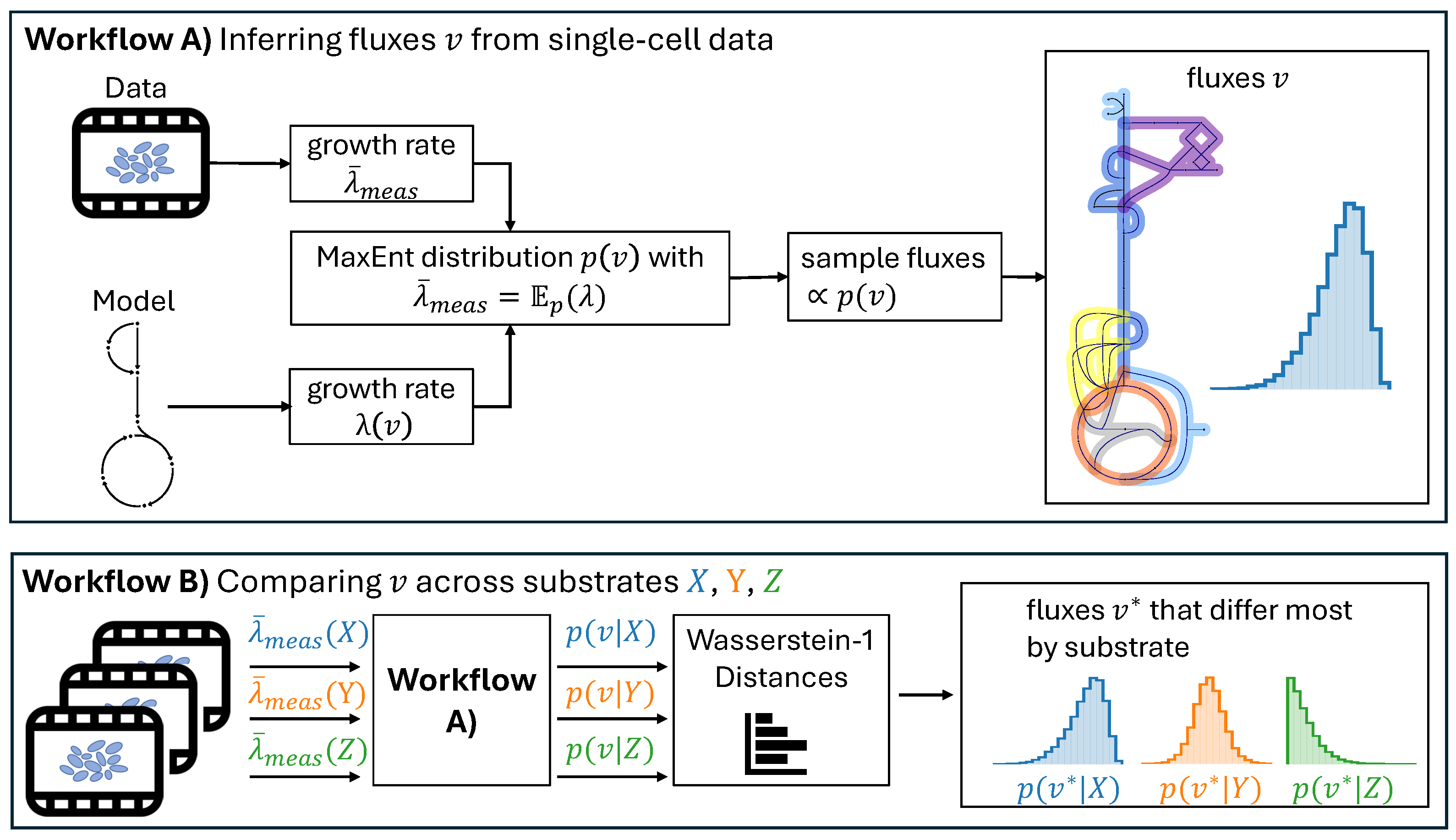
3.1. Maximum Entropy-Based Metabolic Flux Analysis
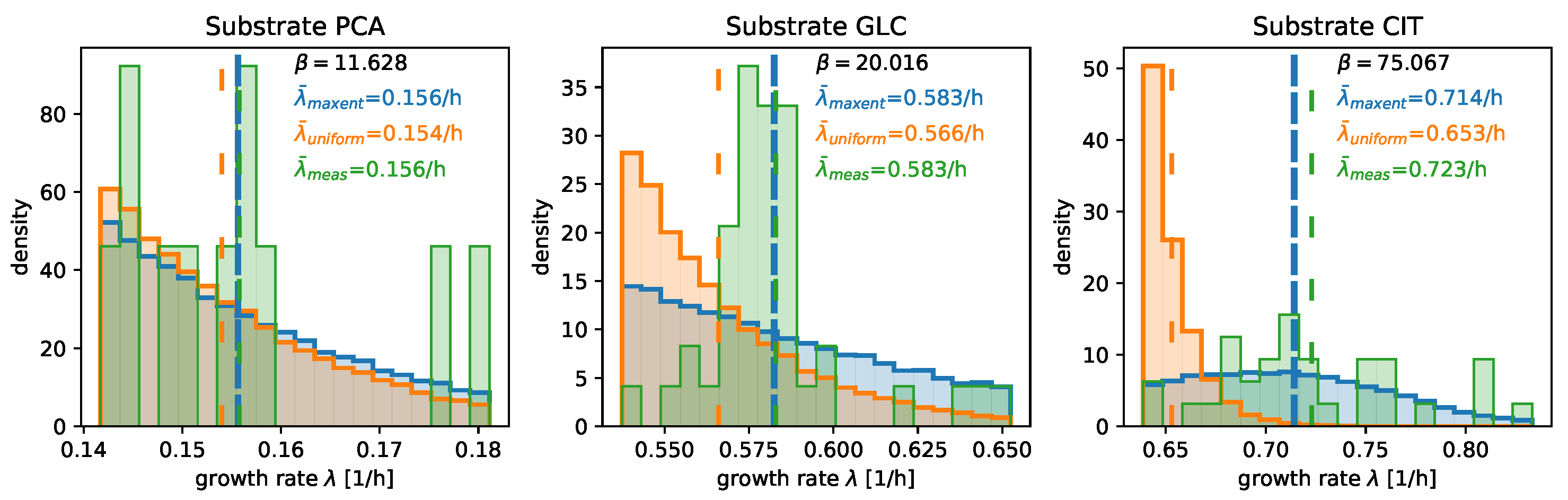
3.2. Numerical Results
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| FBA | Flux Balance Analysis |
| MaxEnt | Maximum Entropy |
References
- Gurdo, N.; Volke, D.C.; McCloskey, D.; Nikel, P.I. Automating the design-build-test-learn cycle towards next-generation bacterial cell factories. New Biotechnol. 2023, 74, 1–15. [Google Scholar] [CrossRef]
- de Witt, J.; Luthe, T.; Wiechert, J.; Jensen, K.; Polen, T.; Wirtz, A.; Thies, S.; Frunzke, J.; Wynands, B.; Wierckx, N. Upcycling of polyamides through chemical hydrolysis and engineered Pseudomonas putida. Nat. Microbiol. 2025, 10, 667–680. [Google Scholar] [CrossRef] [PubMed]
- Takors, R. Scale-up of microbial processes: Impacts, tools and open questions. J. Biotechnol. 2012, 160, 3–9. [Google Scholar] [CrossRef] [PubMed]
- Delvigne, F.; Zune, Q.; Lara, A.R.; Al-Soud, W.; Sørensen, S.J. Metabolic variability in bioprocessing: Implications of microbial phenotypic heterogeneity. Trends Biotechnol. 2014, 32, 608–616. [Google Scholar] [CrossRef]
- Mustafi, N.; Grünberger, A.; Mahr, R.; Helfrich, S.; Nöh, K.; Blombach, B.; Kohlheyer, D.; Frunzke, J. Application of a genetically encoded biosensor for live cell imaging of L-valine production in pyruvate dehydrogenase complex-deficient Corynebacterium glutamicum strains. PLoS ONE 2014, 9, e85731. [Google Scholar] [CrossRef]
- Elowitz, M.B.; Levine, A.J.; Siggia, E.D.; Swain, P.S. Stochastic gene expression in a single cell. Science 2002, 297, 1183–1186. [Google Scholar] [CrossRef]
- Kiviet, D.J.; Nghe, P.; Walker, N.; Boulineau, S.; Sunderlikova, V.; Tans, S.J. Stochasticity of metabolism and growth at the single-cell level. Nature 2014, 514, 376–379. [Google Scholar] [CrossRef] [PubMed]
- Schirmer, M.; Dusny, C. Microbial single-cell mass spectrometry: Status, challenges, and prospects. Curr. Opin. Biotechnol. 2023, 83, 102977. [Google Scholar] [CrossRef]
- Thomas, P.; Terradot, G.; Danos, V.; Weiße, A.Y. Sources, propagation and consequences of stochasticity in cellular growth. Nat. Commun. 2018, 9, 4528. [Google Scholar] [CrossRef]
- Tonn, M.K.; Thomas, P.; Barahona, M.; Oyarzún, D.A. Stochastic modelling reveals mechanisms of metabolic heterogeneity. Commun. Biol. 2019, 2, 108. [Google Scholar] [CrossRef]
- Bijman, E.Y.; Kaltenbach, H.M.; Stelling, J. Experimental analysis and modeling of single-cell time-course data. Curr. Opin. Syst. Biol. 2021, 28, 100359. [Google Scholar] [CrossRef]
- Tourigny, D.S.; Goldberg, A.P.; Karr, J.R. Simulating single-cell metabolism using a stochastic flux-balance analysis algorithm. Biophys. J. 2021, 120, 5231–5242. [Google Scholar] [CrossRef] [PubMed]
- Pleyer, J.; Fleck, C. Agent-based models in cellular systems. Front. Phys. 2023, 10, 968409. [Google Scholar] [CrossRef]
- Narayanankutty, K.; Pereiro-Morejon, J.A.; Ferrero, A.; Onesto, V.; Forciniti, S.; del Mercato, L.L.; Mulet, R.; De Martino, A.; Tourigny, D.S.; De Martino, D. Metabolic coordination and phase transitions in spatially distributed multi-cellular systems. Commun. Phys. 2025, 8, 205. [Google Scholar] [CrossRef]
- De Martino, A.; De Martino, D. An introduction to the maximum entropy approach and its application to inference problems in biology. Heliyon 2018, 4, e00596. [Google Scholar] [CrossRef]
- Orth, J.D.; Thiele, I.; Palsson, B.Ø. What is flux balance analysis? Nat. Biotechnol. 2010, 28, 245–248. [Google Scholar] [CrossRef]
- Grünberger, A.; Paczia, N.; Probst, C.; Schendzielorz, G.; Eggeling, L.; Noack, S.; Wiechert, W.; Kohlheyer, D. A disposable picolitre bioreactor for cultivation and investigation of industrially relevant bacteria on the single cell level. Lab Chip 2012, 12, 2060–2068. [Google Scholar] [CrossRef]
- Grünberger, A.; Probst, C.; Helfrich, S.; Nanda, A.; Stute, B.; Wiechert, W.; von Lieres, E.; Nöh, K.; Frunzke, J.; Kohlheyer, D. Spatiotemporal microbial single-cell analysis using a high-throughput microfluidics cultivation platform. Cytom. Part A 2015, 87, 1101–1115. [Google Scholar] [CrossRef]
- Seiffarth, J.; Scherr, T.; Wollenhaupt, B.; Neumann, O.; Scharr, H.; Kohlheyer, D.; Mikut, R.; Nöh, K. ObiWan-Microbi: OMERO-based integrated workflow for annotating microbes in the cloud. SoftwareX 2024, 26, 101638. [Google Scholar] [CrossRef]
- Cutler, K.J.; Stringer, C.; Lo, T.W.; Rappez, L.; Stroustrup, N.; Brook Peterson, S.; Wiggins, P.A.; Mougous, J.D. Omnipose: A high-precision morphology-independent solution for bacterial cell segmentation. Nat. Methods 2022, 19, 1438–1448. [Google Scholar] [CrossRef] [PubMed]
- Zelle, E.; Nöh, K.; Wiechert, W. Growth and production capabilities of Corynebacterium glutamicum: Interrogating a genome-scale metabolic network model. In Corynebacterium glutamicum: From Systems Biology to Biotechnological Applications; Burkovski, A., Ed.; Caister Academic Press: Poole, UK, 2015; Chapter 4; p. 190. [Google Scholar] [CrossRef]
- Zelle, E.; Pfelzer, N.; Oldiges, M.; Koch-Koerfges, A.; Bott, M.; Nöh, K.; Wiechert, W. An energetic profile of Corynebacterium glutamicum underpinned by measured biomass yield on ATP. Metab. Eng. 2021, 65, 66–78. [Google Scholar] [CrossRef]
- Maarleveld, T.R.; Khandelwal, R.A.; Olivier, B.G.; Teusink, B.; Bruggeman, F.J. Basic concepts and principles of stoichiometric modeling of metabolic networks. Biotechnol. J. 2013, 8, 997–1008. [Google Scholar] [CrossRef]
- Jadebeck, J.; Wiechert, W.; Nöh, K. Practical sampling of constraint-based models: Optimized thinning boosts CHRR performance. PLoS Comput. Biol. 2023, 19, e1011378. [Google Scholar] [CrossRef]
- Ebrahim, A.; Lerman, J.; Palsson, B.Ø.; Hyduke, D. COBRApy: COnstraints-Based Reconstruction and Analysis for Python. BMC Syst. Biol. 2013, 7, 74. [Google Scholar] [CrossRef]
- Villani, C. Optimal Transport: Old and New; Springer: Berlin/Heidelberg, Germany, 2009; Volume 338. [Google Scholar]
- Jaynes, E.T. Information Theory and Statistical Mechanics. Phys. Rev. 1957, 106, 620–630. [Google Scholar] [CrossRef]
- Paul, R.; Jadebeck, J.; Stratmann, A.; Wiechert, W.; Nöh, K. hopsy—A methods marketplace for convex polytope sampling in Python. Bioinformatics 2024, 40, btae430. [Google Scholar] [CrossRef] [PubMed]
- Virtanen, P.; Gommers, R.; Oliphant, T.E.; Haberland, M.; Reddy, T.; Cournapeau, D.; Burovski, E.; Peterson, P.; Weckesser, W.; Bright, J.; et al. SciPy 1.0: Fundamental Algorithms for scientific computing in Python. Nat. Methods 2020, 17, 261–272. [Google Scholar] [CrossRef] [PubMed]
- De Martino, D.; Mc Andersson, A.; Bergmiller, T.; Guet, C.C.; Tkačik, G. Statistical mechanics for metabolic networks during steady state growth. Nat. Commun. 2018, 9, 2988. [Google Scholar] [CrossRef]
- Vehtari, A.; Gelman, A.; Simpson, D.; Carpenter, B.; Bürkner, P.C. Rank-Normalization, folding, and localization: An improved for assessing convergence of MCMC. Bayesian Anal. 2021, 16, 667–718. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Heinzel, C.S.; Jadebeck, J.F.; Zelle, E.; Seiffarth, J.; Nöh, K. Combining Knowledge About Metabolic Networks and Single-Cell Data with Maximum Entropy. Phys. Sci. Forum 2025, 12, 3. https://doi.org/10.3390/psf2025012003
Heinzel CS, Jadebeck JF, Zelle E, Seiffarth J, Nöh K. Combining Knowledge About Metabolic Networks and Single-Cell Data with Maximum Entropy. Physical Sciences Forum. 2025; 12(1):3. https://doi.org/10.3390/psf2025012003
Chicago/Turabian StyleHeinzel, Carola S., Johann F. Jadebeck, Elisabeth Zelle, Johannes Seiffarth, and Katharina Nöh. 2025. "Combining Knowledge About Metabolic Networks and Single-Cell Data with Maximum Entropy" Physical Sciences Forum 12, no. 1: 3. https://doi.org/10.3390/psf2025012003
APA StyleHeinzel, C. S., Jadebeck, J. F., Zelle, E., Seiffarth, J., & Nöh, K. (2025). Combining Knowledge About Metabolic Networks and Single-Cell Data with Maximum Entropy. Physical Sciences Forum, 12(1), 3. https://doi.org/10.3390/psf2025012003




