Model-Based and Physics-Informed Deep Learning Neural Network Structures †
Abstract
1. Introduction
- Training step: For this, we need to access the training data in a data base. Then, we have to choose an appropriate criterion based on the category of the problem to be solved: Classification, Clustering, Regression, etc. The next step is to choose an appropriate optimization algorithm, some parameters, such as the learning rate, and finally, train the model. This means that the parameters of the model are obtained at the end of the convergence of the optimization algorithm.
- Model validation and hyperparameter tuning: As there are many hyperparameters (related to the optimization criteria and optimization algorithms), a validation step is necessary before the final use of the model. In this step, in general, we may use a subset of the training data or some other good-quality training data in which we can be confident, to tune the hyperparameters of the model and validate it.
- The last step before using the model is testing it and evaluating its performance on a testing data set. There are also a great number of testing and evaluation metrics, which have to be selected appropriately depending on the objectives of the considered problem.
- The final step is uploading the implemented model and using it. The amount of memory needed for this step has to be considered.
- Methods based on explicit analytical solutions;
- Methods based on transform domain processing;
- Methods based on the operator decomposition structure;
- Methods based on the unfolding of iterative optimization algorithms;
- Methods known as physics-informed NNs (PINNs).
2. Inverse Problems Considered
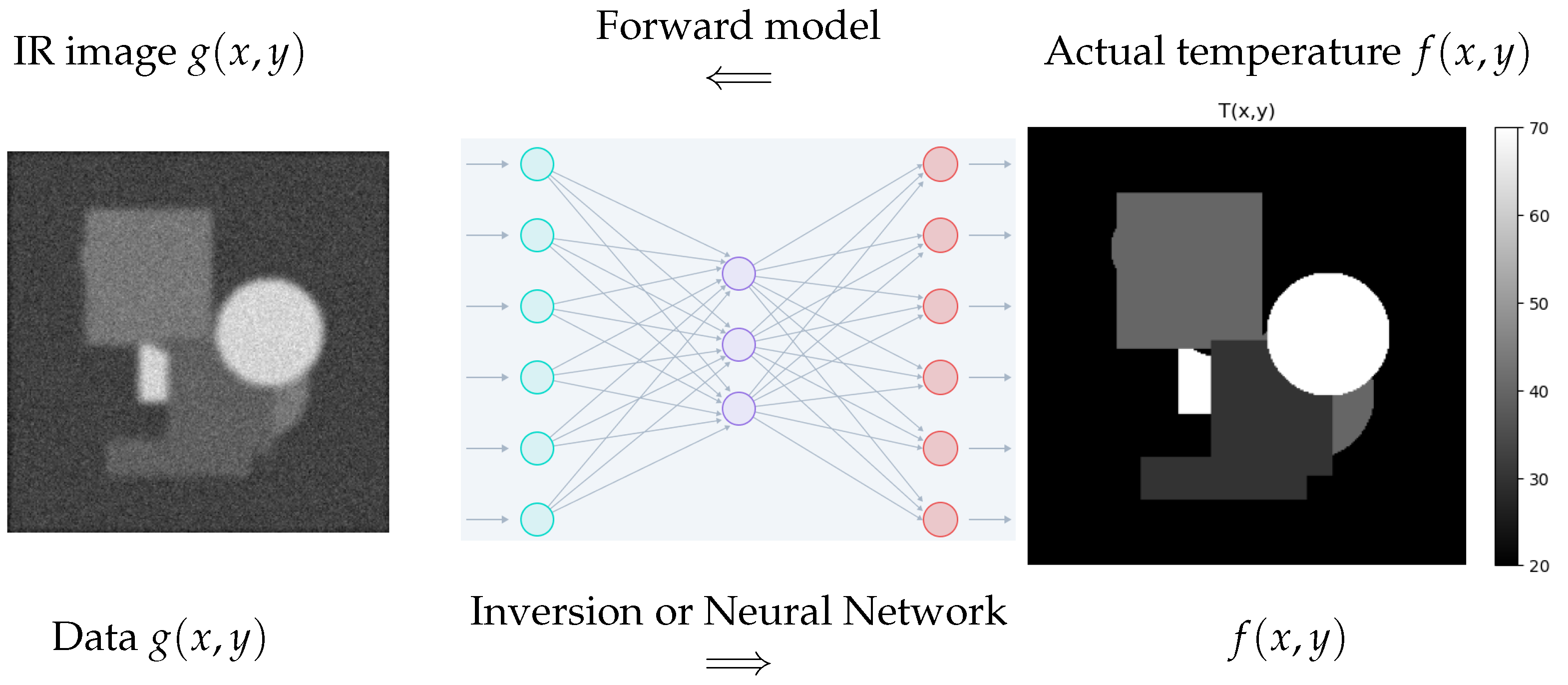
2.1. Infrared Imaging
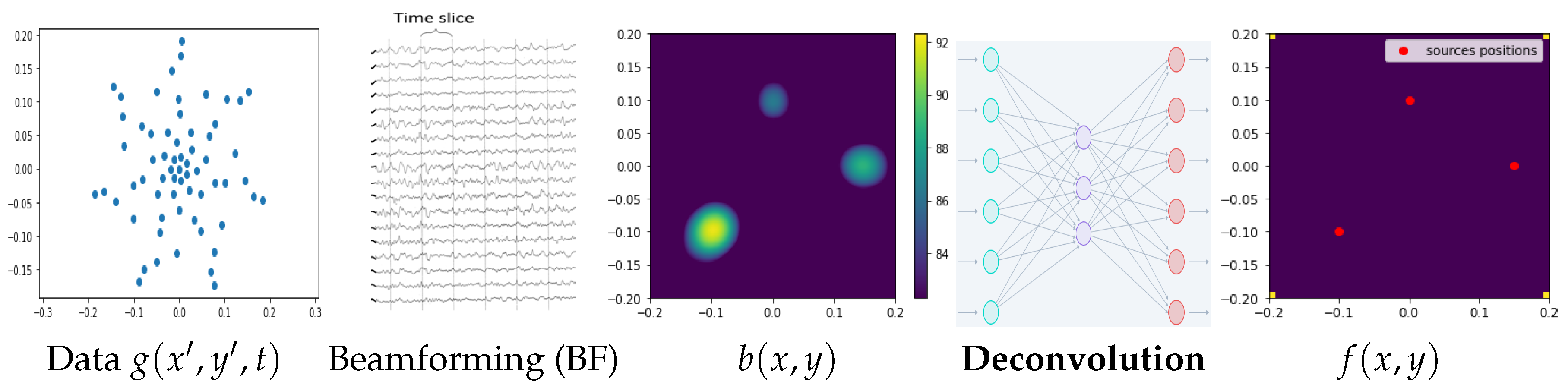
2.2. Acoustical Imaging
3. Bayesian Inference for Inverse Problems
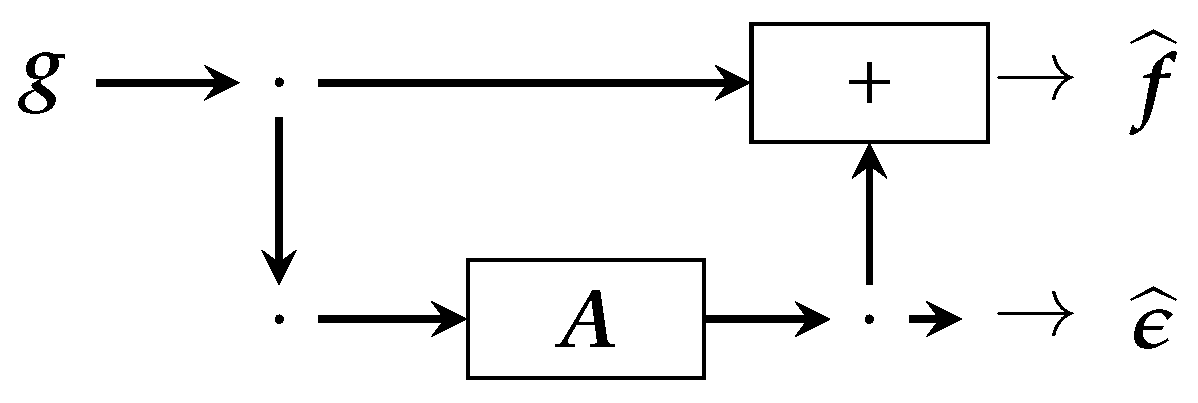
4. NN Structures Based on Analytical Solutions
4.1. Linear Analytical Solutions
- can be implemented directly or by a Neural Network (NN)
- When H is a convolution operator, is also a convolution operator and can be implemented by a Convolutional Neural Network (CNN).
- and are, in general, dense NNs.
- When H is a convolution operator, B and C can also be approximated by convolution operators, and so by CNNs.
4.2. Feed-Forward and Residual NN Structure
5. NN Structures Based on Transformation and Decomposition
5.1. Fourier Transform-Based Networks
5.2. Wavelet Transform-Based Networks
5.3. NN Structures Based on Operator Decomposition and Encoder–Decoder Structure
| : N-Layer Network: , , , , ⋮, | : N-Layer Network: , ⋮, , , , |
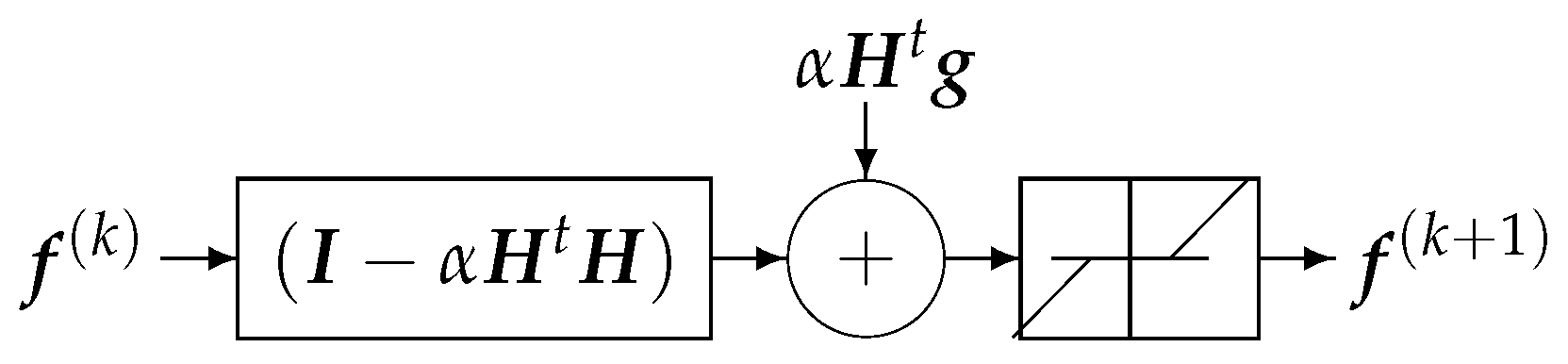
6. DNN Structures Obtained by Unfolding Optimization Algorithms
7. Physics-Informed Neural Networks (PINNs)
- NNs are universal function approximators. Therefore an NN, provided that it is deep enough, can approximate any function, and also the solution for the differential equations.
- Computing the derivatives of an NN’s output with respect to any of its inputs (and the model parameters during backpropagation), using Automatic Differentiation (AD), is easy and cheap. This is actually what makes NNs so efficient and successful.
- Usually NNs are trained to fit the data, but do not care where those data come from. This is where physics-informed NNs come into play.
- Physics-based or physics-informed NNs: If, in addition to fitting the data, the NNs also fits the equations that govern that system and produce those data, their predictions will be much more precise and will generalize much better.
7.1. PINN When an Explicit Forward Model Is Available
7.2. A PINN When the Forward Model Is Described by an ODE or a PDE
- Unknown parameters model: As a simple dynamical system, considerwhere the problem becomes estimating the parameters .
- Unknown right side function:
- Unknown parameters as well as the unknown function :
- Classical NN: The criterion to optimize is just a function of the output error, shown in Figure 17.
- PINN: The criterion to optimize is a function of the output error and the forward error, shown in Figure 18.
- Parametric PINN: When a parameter of the PDE is also unknown, we may also estimate it at the same time as the parameter w of the NN, as shown in Figure 19.
- Nonparametric PINN inverse problem: When the right-hand side of the ODE is an unknown function to be estimated too, we may consider a separate NN for it, as shown in Figure 20.
- PINN for forward models described by PDE: For a more complex dynamical system with a PDE model, such as , the criterion must also account for the initial conditions (ICs), , as well as the boundary conditions (BCs), :
8. Applications
- Vibration analysis using Fourier and Wavelet analysis;
- Acoustics: Sound source localization and estimation using acoustical imaging;
- Infrared imaging to monitor the temperature distribution;
- Visible images to monitor the system and its environment.
An Example of Infrared Image Processing
9. Conclusions
- Deep Neural Networks (DNNs) have been extensively used in Computer Vision and many other areas. There are, nowadays, a great number of NN structures, both “on the shelf” and user-selected, to try and use. If they work, they can be kept; if not, another can be selected, and so on!
- In particular, in inverse problems of Computer Vision, there is a need to guide the selection of an explainable structure, and so, explainable ML and AI are chosen.
- In this work, a few directions have been proposed. These methods are classified as model-based, physics-based, and physics-informed NNs (PINNs). Model-based and physics-based NNs have become a necessity for developing robust methods across all Computer Vision and imaging systems.
- PINNs were originally developed for inverse problems described by Ordinary or Partial Differential Equations (ODEs/PDEs). The main idea in all these problems is to appropriately choose NNs and use them as “Explainable” AI in industrial applications.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Udayakumar, R.; Paulraj, C.; Kumar, S. Infrared thermography for condition monitoring–A review. Infrared Phys. Technol. 2013, 60, 35–55. [Google Scholar]
- Bhowmik, S.; Jha, M. Advances in infrared thermography for detection and characterization of defects in materials. Infrared Phys. Technol. 2012, 55, 363–371. [Google Scholar]
- Klein, T.; Maldague, X. Advanced thermography techniques for material inspection and characterization. J. Appl. Remote Sens. 2016, 10, 033508. [Google Scholar]
- Wang, L.; Zhao, P.; Ning, C.; Yu, L.; Mohammad-Djafari, A. A hierarchical Bayesian fusion method of infrared and visible images for temperature monitoring of high-speed direct-drive blower. IEEE Sens. J. 2022, 22, 18815–18830. [Google Scholar] [CrossRef]
- Chu, N.; Zhao, H.; Yu, L.; Huang, Q.; Ning, Y. Fast and High-Resolution Acoustic Beamforming: A Convolution Accelerated Deconvolution Implementation. IEEE Trans. Instrum. Meas. 2020, 70, 6502415. [Google Scholar] [CrossRef]
- Chen, F.; Xiao, Y.; Yu, L.; Chen, L.; Zhang, C. Extending FISTA to FISTA-Net: Adaptive reflection parameters fitting for the deconvolution-based sound source localization in the reverberation environment. Mech. Syst. Signal Process. 2024, 210, 111130. [Google Scholar] [CrossRef]
- Luo, X.; Yu, L.; Li, M.; Wang, R.; Yu, H. Complex approximate message passing equivalent source method for sparse acoustic source reconstruction. Mech. Syst. Signal Process. 2024, 217, 111476. [Google Scholar] [CrossRef]
- Nelson, C. Machine learning in acoustic imaging for industrial applications. J. Acoust. Mach. Learn. 2021, 5, 120–140. [Google Scholar]
- Raissi, M.; Perdikaris, P.; Karniadakis, G.E. Physics-informed neural networks: A deep learning framework for solving forward and inverse problems involving nonlinear partial differential equations. J. Comput. Phys. 2019, 378, 686–707. [Google Scholar] [CrossRef]
- Lu, L.; Meng, X.; Mao, Z.; Karniadakis, G.E. DeepXDE: A deep learning library for solving differential equations. SIAM Rev. 2021, 63, 208–228. [Google Scholar] [CrossRef]
- Karniadakis, G.E.; Kevrekidis, I.G.; Lu, L.; Perdikaris, P.; Wang, S.; Yang, L. Physics-informed machine learning. Nat. Rev. Phys. 2021, 3, 422–440. [Google Scholar] [CrossRef]
- Chen, W.; Cheng, X.; Habib, E.; Hu, Y.; Ren, G. Physics-informed neural networks for inverse problems in nano-optics and metamaterials. Opt. Express 2020, 28, 39705–39724. [Google Scholar] [CrossRef] [PubMed]
- Yang, L.; Meng, X.; Karniadakis, G.E. B-PINNs: Bayesian physics-informed neural networks for forward and inverse PDE problems with noisy data. J. Comput. Phys. 2021, 425, 109913. [Google Scholar] [CrossRef]
- Zhu, Y.; Zabaras, N.; Koutsourelakis, P.S.; Perdikaris, P. Physics-constrained deep learning for high-dimensional surrogate modeling and uncertainty quantification without labeled data. J. Comput. Phys. 2019, 394, 56–81. [Google Scholar] [CrossRef]
- Yang, Y.; Perdikaris, P. Adversarial uncertainty quantification in physics-informed neural networks. J. Comput. Phys. 2019, 394, 136–152. [Google Scholar] [CrossRef]
- Geneva, N.; Zabaras, N. Modeling the dynamics of PDE systems with physics-constrained deep auto-regressive networks. J. Comput. Phys. 2020, 403, 109056. [Google Scholar] [CrossRef]
- Gao, H.; Sun, L.; Wang, J.X. PhyGeoNet: Physics-informed geometry-adaptive convolutional neural networks for solving parameterized steady-state PDEs on irregular domain. J. Comput. Phys. 2021, 428, 110079. [Google Scholar] [CrossRef]
- Cai, S.; Wang, Z.; Wang, S.; Perdikaris, P.; Karniadakis, G.E. Physics-informed neural networks for heat transfer problems. J. Heat Transf. 2021, 143, 060801. [Google Scholar] [CrossRef]



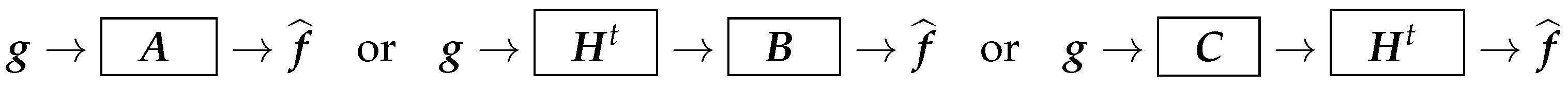

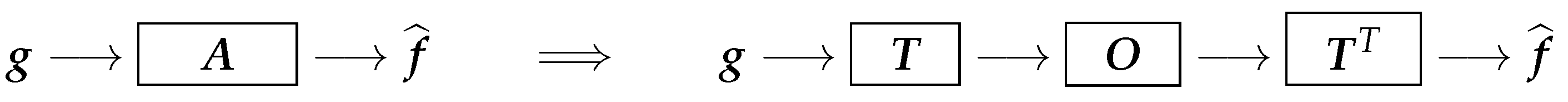
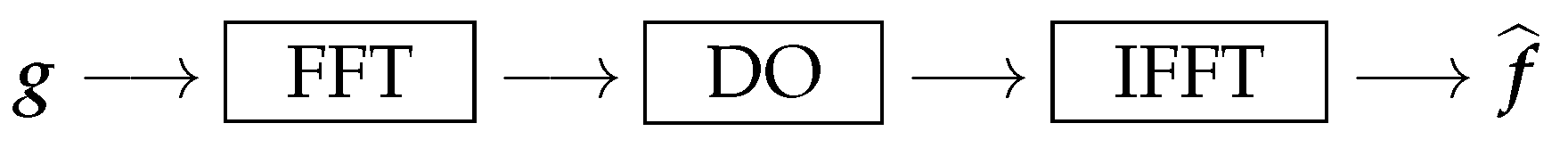



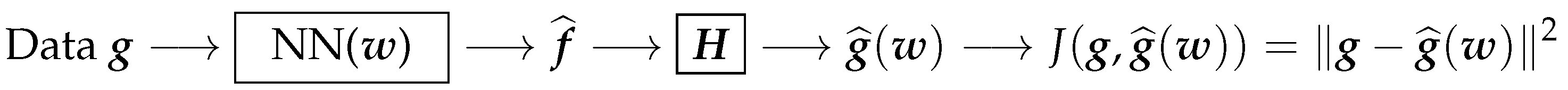


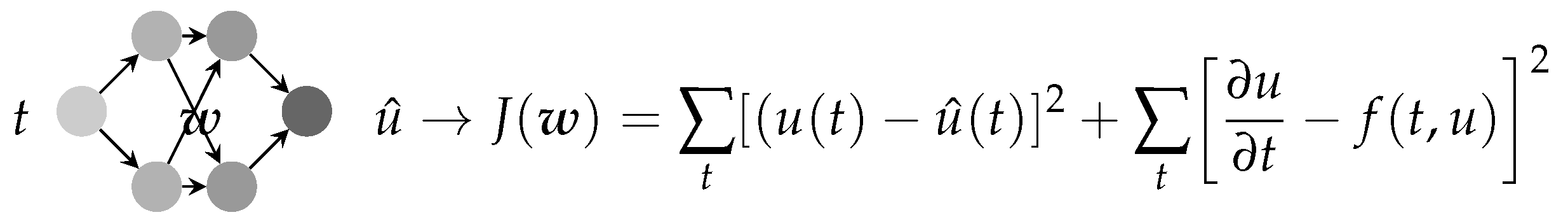

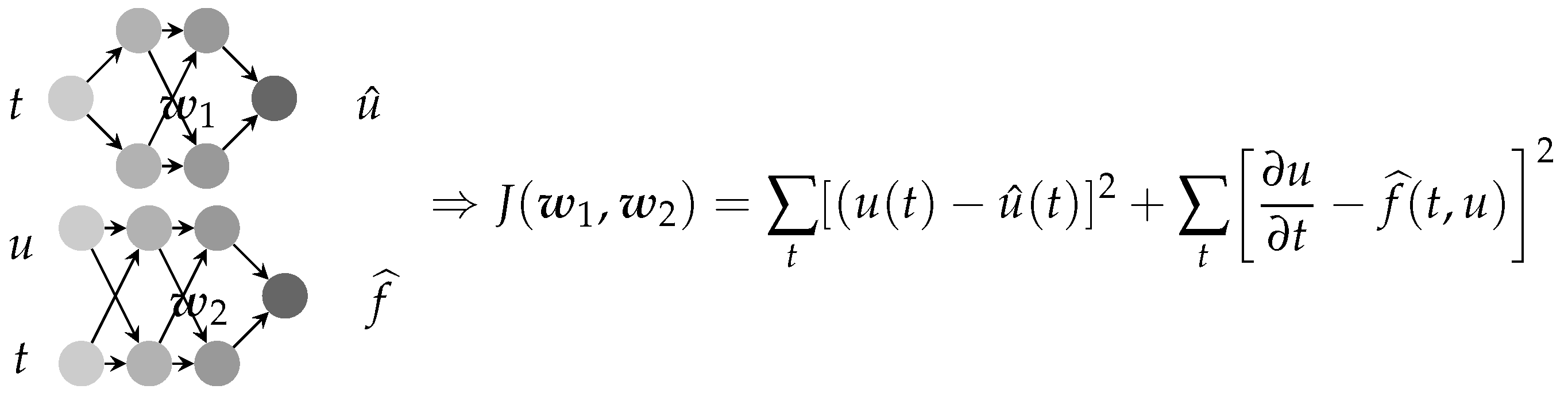


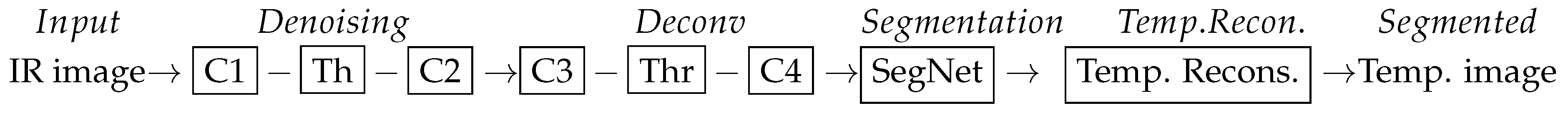

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mohammad-Djafari, A.; Chu, N.; Wang, L.; Cai, C.; Yu, L. Model-Based and Physics-Informed Deep Learning Neural Network Structures. Phys. Sci. Forum 2025, 12, 10. https://doi.org/10.3390/psf2025012010
Mohammad-Djafari A, Chu N, Wang L, Cai C, Yu L. Model-Based and Physics-Informed Deep Learning Neural Network Structures. Physical Sciences Forum. 2025; 12(1):10. https://doi.org/10.3390/psf2025012010
Chicago/Turabian StyleMohammad-Djafari, Ali, Ning Chu, Li Wang, Caifang Cai, and Liang Yu. 2025. "Model-Based and Physics-Informed Deep Learning Neural Network Structures" Physical Sciences Forum 12, no. 1: 10. https://doi.org/10.3390/psf2025012010
APA StyleMohammad-Djafari, A., Chu, N., Wang, L., Cai, C., & Yu, L. (2025). Model-Based and Physics-Informed Deep Learning Neural Network Structures. Physical Sciences Forum, 12(1), 10. https://doi.org/10.3390/psf2025012010




