A Diseased Three-Species Harvesting Food Web Model with Various Response Functions †
Abstract
1. Introduction
2. Formation and Flowchart of the Equation
3. Positivity and Boundedness
4. Presence of Boundary Equilibrium Points
- is the equilibria of a trivial point. Here, (0, 0, 0) exists.
- is no infection and predator-free equilibria; exists for <
- is the equilibria of without a predator; where = and= . exists for and .
- is the no diseases of the equilibria; where = and= . exists for and .
- is the equilibria of the coexistent state; . It exists for , , , , where=, =, and=.
5. Stability Analysis
5.1. Local Analysis
- 1.
- The trivial point of equilibria is LAS if .
- 2.
- The infectious and predator-free points are LAS if , , and .
- 3.
- The equilibria with no predator is LAS if , , and .
- The trivial point of equilibria of the eigen values are , , and −δ. Hence, it is LAS when ; if not, it is unstable.
- The eigen values of are , , and . Hence, it is LAS if , , and ; if not, it is unstable.
- The matrix in its Jacobian form is
5.2. Global Analysis
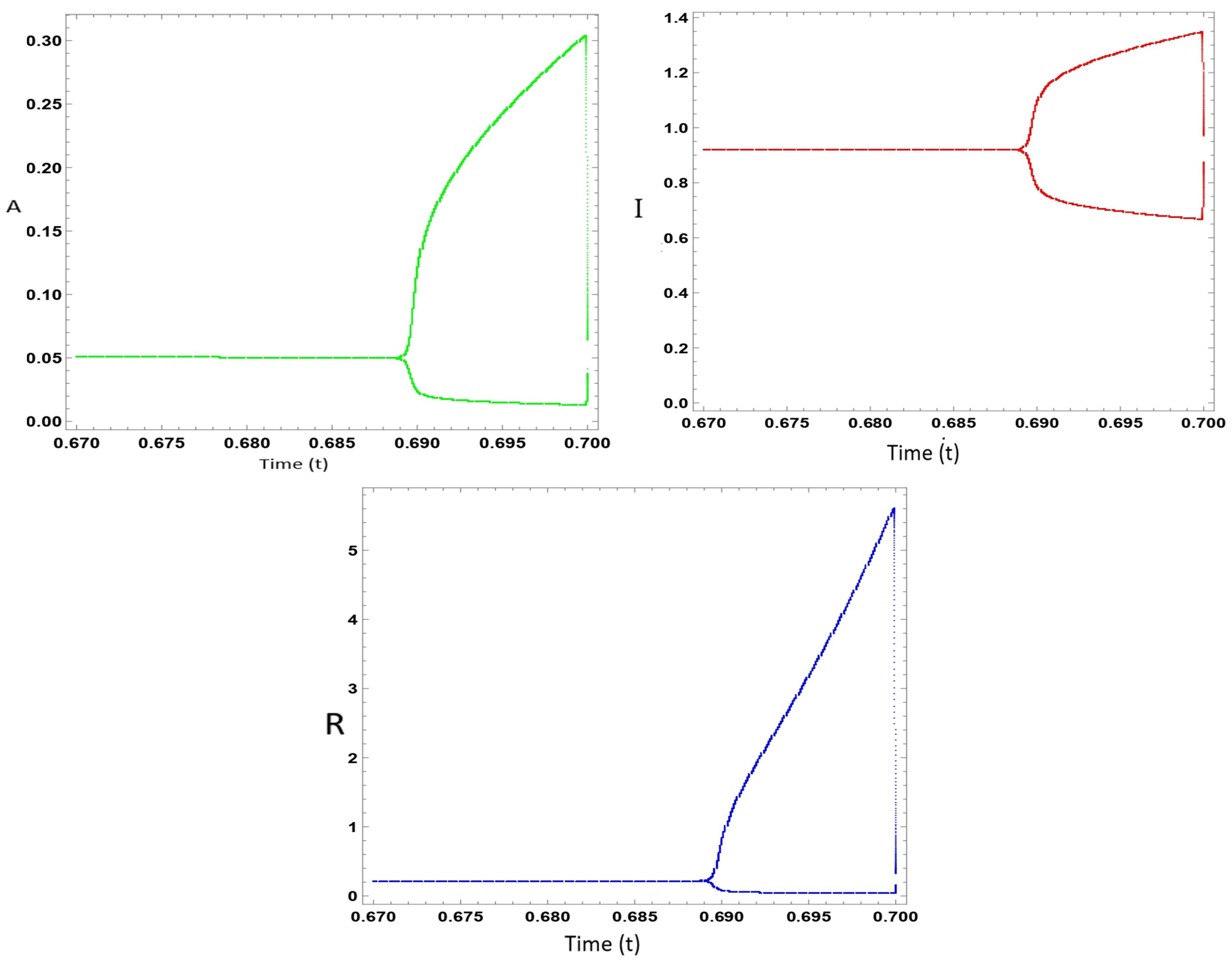
6. Analysis of the Hopf Bifurcation
- 1.
- 2.
- where γ represents the positive value of the equilibrium point and is the zero of the characteristic equation.
7. Numerical Calculations of the Model
8. Conclusions and Discussion
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| LAS | Locally Asymptotically Stable |
| GAS | Globally Asymptotically Stable |
| LAU | Locally Asymptotically Unstable |
References
- May, R.M. Stability and Complexity in Model Ecosystems; Princeton University Press: Princeton, NJ, USA, 2019; Volume 1. [Google Scholar]
- Kant, S.; Kumar, V. Dynamics of a Prey-Predator System with Infection in Prey; Department of Mathematics, Texas State University: San Marcos, TX, USA, 2017. [Google Scholar]
- Pradeep, M.S.; Gopal, T.N.; Magudeeswaran, S.; Deepak, N.; Muthukumar, S. Stability analysis of diseased preadator–prey model with holling type II functional response. AIP Conf. Proc. 2023, 2901, 030017. [Google Scholar]
- Thangavel, M.; Thangaraj, N.G.; Manickasundaram, S.P.; Arunachalam, Y. An Eco–Epidemiological Model Involving Prey Refuge and Prey Harvesting with Beddington–DeAngelis, Crowley–Martin and Holling Type II Functional Responses. Eng. Proc. 2023, 56, 325. [Google Scholar] [CrossRef]
- Abdulghafour, A.S.; Naji, R.K. The impact of refuge and harvesting on the dynamics of prey-predator system. Sci. Int. 2018, 30, 315–323. [Google Scholar]
- Agnihotri, K.B.; Gakkhar, S. The dynamics of disease transmission in a prey predator system with harvesting of prey. Int. J. Adv. Res. Comput. Eng. Technol. 2012, 1, 1–17. [Google Scholar]
- Magudeeswaran, S.; Vinoth, S.; Sathiyanathan, K.; Sivabalan, M. Impact of fear on delayed three species food-web model with Holling type-II functional response. Int. J. Biomath. 2022, 15, 2250014. [Google Scholar] [CrossRef]
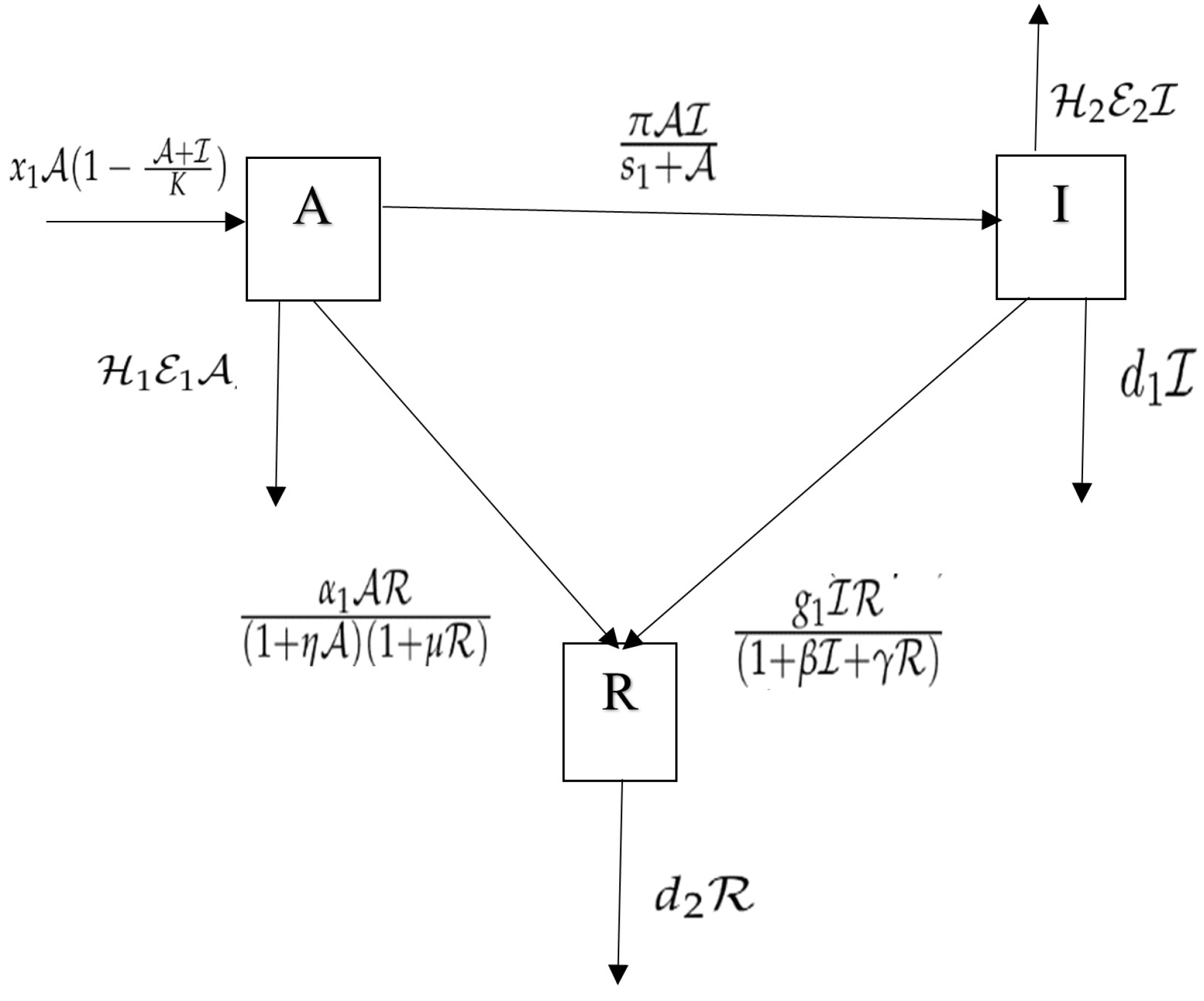
| Parameters | Ecological Description |
|---|---|
| predator species, susceptible prey, infected prey | |
| , x | infectious and growth rate of prey |
| K, , | carrying capacity, handling time of predators, harvesting effort |
| and | infected prey and predators half-saturation constant |
| conversion of prey to predators, of susceptible prey’s predation rate | |
| magnitude of interference by predators of Beddington and Crowley | |
| consuming rate of susceptible prey by predator | |
| and | mortality rate infectious prey and predators |
| , | susceptible and infected prey’s catchability coefficient |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Megala, T.; Nandha Gopal, T.; Siva Pradeep, M.; Yasotha, A. A Diseased Three-Species Harvesting Food Web Model with Various Response Functions. Biol. Life Sci. Forum 2024, 30, 17. https://doi.org/10.3390/IOCAG2023-16876
Megala T, Nandha Gopal T, Siva Pradeep M, Yasotha A. A Diseased Three-Species Harvesting Food Web Model with Various Response Functions. Biology and Life Sciences Forum. 2024; 30(1):17. https://doi.org/10.3390/IOCAG2023-16876
Chicago/Turabian StyleMegala, Thangavel, Thangaraj Nandha Gopal, Manickasundaram Siva Pradeep, and Arunachalam Yasotha. 2024. "A Diseased Three-Species Harvesting Food Web Model with Various Response Functions" Biology and Life Sciences Forum 30, no. 1: 17. https://doi.org/10.3390/IOCAG2023-16876
APA StyleMegala, T., Nandha Gopal, T., Siva Pradeep, M., & Yasotha, A. (2024). A Diseased Three-Species Harvesting Food Web Model with Various Response Functions. Biology and Life Sciences Forum, 30(1), 17. https://doi.org/10.3390/IOCAG2023-16876







