Abstract
The Solitonic Windkessel model, which is successful for explaining the intracranial aneurysmal rupture based on the Windkessel-type hemodynamic circulation modelling, is employed for explaining unexpected and sudden intracranial aneurysmal rupture. In this paper, by focusing on the appearance of resonance, some aneurysmal ruptures are shown to possibly arise unexpectedly and suddenly as a resonance phenomenon.
1. Introduction
The Windkessel model is known as a nonlinear model for explaining hemodynamic circulation. While turbulence and vortex formation in the blood vessel are not considered in Windkessel models, steady fluid mechanics are taken into account to a sufficient extent. In the preceding work [1], a five-element type solitonic Windkessel model was introduced for modelling the two-story aneurysm, and the rupture condition of the intracranial aneurysm was identified. Ujiie-Iwata [1] was the first attempt to utilize the Windkessel model to evaluate aneurysmal flow and local pressure. In particular, that attempt was successful in identifying some resonating beats and the soliton wave propagation as key factors for aneurysmal rupture. In fact, significant increase of local blood pressure is naturally understood by the existence of resonating beats and soliton propagation.
Although there have been a lot of studies related to risk factors to cause aneurysmal rupture [2,3,4] it is still impossible to accurately predict when an intracranial aneurysm will rupture. Our study is showing one of the answers to this question. Flow-mediated resonance within a daughter aneurysm gives sudden rise to the forced vibration and then destroys the aneurysm. Therefore, we have to clarify the specific condition to realize the flow-mediated resonance.
In this paper, following the preceding work [1], we employ a solitonic Windkessel model for understanding unexpected and sudden rupture of intracranial aneurysm. It will clarify a substantial role of so-called “resonance” in the aneurysmal rupture. Here, we focus on the resonance between the heartbeat and the oscillatory frequency inherent to the mother and daughter aneurysms.
2. Solitonic Windkessel Model
2.1. Five-Element Formalism
The two-story aneurysm consisting of the mother and daughter aneurysm on the parent artery is shown in Figure 1. The five-element solitonic Windkessel model is exactly the same as the model studied in Ref. [1]. In the solitonic Windkessel model, blood flow inside the two-story aneurysm is analogously modelled by the electric flow inside electric circuit shown in Figure 2. Let C1 and C2 represent the compliance of the mother and daughter aneurysm, L1 and L2 stand for the inductance of the mother and daughter aneurysm, and F1, and F2 be the blood flow in the mother aneurysm and that in the daughter aneurysm, respectively. According to analogy between electric circuits and blood system, the following three equations are logically introduced (Figure 2). Let t be the time variable. The solitonic Windkessel model, which corresponds to the five-element Windkessel model, reads:
where F(t) and P(t) mean the blood flow and the blood pressure of the parent artery, respectively. The quantity Q1(t) and Q2(t) denote the amount of blood inside the mother and daughter aneurysms, respectively. The quantity R is the resistance associated with the neck size, which is taken to be low for most of the blood flows going through the parent vessel. As the oscillation of flows possibly appear inside aneurysms, the flows F1(t) and F2(t) can be either positive, zero, or negative (for the default direction of the flows inside the aneurysms, see Figure 2).
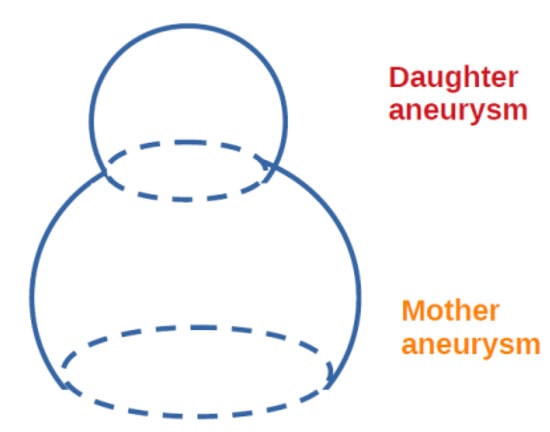
Figure 1.
Two-story intracranial aneurysm (so-called dumbbell-shaped aneurysm).
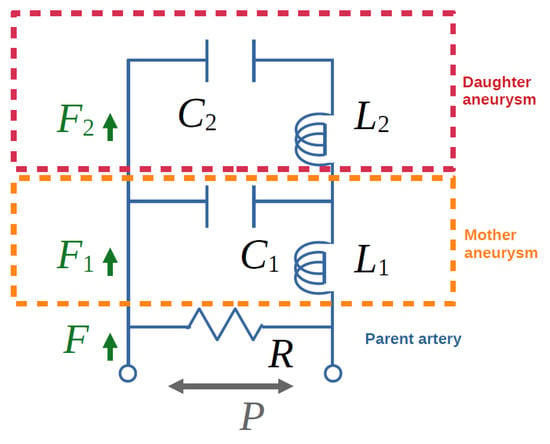
Figure 2.
Solitonic Windkessel model for the two-story intracranial aneurysm. The corresponding electric circuit is shown, where C1 and C2 correspond to the size/dimension of mother and daughter aneurysms, respectively. R determines the branching ratio F1/F of the blood flow. The constants L1 and L2 are related to the elasticity of blood vessel wall. P0, P1, and P2 denote the local pressures, and F, F1, and F2 are blood flows.
2.2. Reduced Single Equation
Following Ref. [1], the solitonic Windkessel model (1) consisting of three equations is reduced to the single equation. Let local pressures P1 and P2 correspond to the pressures on the capacitor C1 and C2, respectively. Much attention is paid to the effect due to the existence of the daughter aneurysm. Here, blood pressure P(t) and the blood flow F(t) in the parent artery are assumed to be given. In this situation, the blood flows F1(t) and F2(t) inside the aneurysms are the unknowns, as well as the local pressures P1(t) and P2(t) inside the aneurysms. By substituting first and second equality of (1) to the third equality, the model equation is reduced to a single equation
It is the second-order ordinary differential equation. For this equation, external conditions arising from the heartbeat are given as:
where f = 70/60 [1/sec], F(0) = 50 [mL/min], and P(0) = 100 [mmHg] are the frequency of the heartbeat, initial blood flow, and initial blood pressure, respectively. The values follow from the typical blood flow and heart rate (the same setting as Ref. [1]). Indeed, for the human being, the typical blood flow of the middle cerebral artery is around 50 mL/min, the typical blood velocity is 60 cm/sec, the blood pressure is between 80 to 120 mmHg, and the heart rate is from 40 to 120 beat per minutes with mean value 70. In the natural situation, the blood flow in the parent artery (F + F1) is not so different before and after aneurysmal formation. To realize this feature, the amount of artery blood flow is adjusted by choosing the value of R, and the resistance parameter R is fixed to R = 2.2 [mmHg min/mL] for all of the systematic calculations. Consequently, the initial condition is given by
which means that no blood flow and no blood velocity are assumed to exist inside the daughter aneurysm at the beginning. Note that the constants L1, L2, C1, and C2 are assumed to be positive.
F(t) = 10 sin(2πft) + F(0),
P(t) = 20 sin(2πft) + P(0),
F2(0) = 0
Since F(t) and P(t) are given by the heartbeat in this specific modelling, the right-hand side of Equation (2) is a given function, and unknown function is only F2(t). If F2(t) is obtained, Q2(t) is automatically obtained by dQ2(t)/dt = F2(t), and then Q1(t) follows from the third equality of Equation (1). P2(t) is obtained by Q2(t) = C2(t) P2(t). Next, F1(t) is obtained by the second equality of Equation (1). Q1(t) and P1(t) are obtained similarly to Q2(t) and P2(t). Consequently, all the unknowns are obtained by solving single Equation (2). For the details of solitonic Windkessel model, see Ref. [1].
3. Result
3.1. Analytic Solution
Although a systematic numerical research has been carried out in Ref. [1], here we present an analytical solution of solitonic Windkessel model in the given setting. The inhomogeneous term (the right-hand side of Equation (2)) is calculated as
where the initial phase angle is determined only by R and L1; i.e., the specific feature of mother aneurysm.
In this case, as seen in the second term of the left-hand side of Equation (2), decisive factor of oscillation described by (2) is whether
is positive or not (here it is always assumed to be positive). Oscillation appears for > 0.
Another factor is
which means the amplitude of a particular solution of Equation (2). That is, the resonance appears if the denominator
is equal to zero. It corresponds to the violent rupture whose oscillation amplitude diverges rapidly. It is actually a tragic situation in which aneurysm rupture takes place even when no significant increase of local blood pressure is noticed. Consequently, the general solution of (2) is given by
where A and B are constants being determined by the initial condition:
We have the same denominator for the three terms consisting of the right-hand side of Equation (3).
3.2. Condition for the Resonance
The condition for the appearance of resonance is represented by
in the present settings (Figure 3). It arises from equality for the denominator seen in Equation (3): . A constant 3/7 in the right-hand side of Equation (4) arises from the heartbeat, and the left-hand side arises from the specific feature of daughter aneurysm. It is worth reminding here the physical meaning of and at this point. is the compliance of daughter aneurysm, and is the inductance of daughter aneurysm. More concretely, is the volume of daughter aneurysm, and is the thinness of the blood wall of daughter aneurysm. Most importantly, it is readily seen from the condition (4) that the appearance of resonance is dependent only on the property of daughter aneurysm. In other words, formation of the daughter aneurysm (i.e., two-story aneurysm) possibly brings about unexpected and sudden aneurysmal rupture.
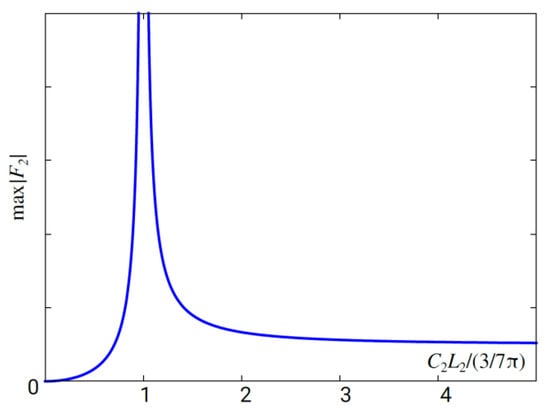
Figure 3.
Maximum amplitude of F2 as a function of . Resonance appears if is satisfied.
According to Figure 4 of Ref. [1], values of range from 30 to 100 [mmHg min2/mL]. The condition tells us the value of at the resonance ranges from 0.002 to 0.004 [mL/mmHg]. Since the standard value of (=standard size of mother aneurysm) is taken equal to 0.10 [mL/mmHg] in Ref. [1], in terms of adjusting the possible increase of local pressure inside aneurysms, daughter aneurysms with their volumes 2% or 3% of mother aneurysm, are exposed to the resonance. The size of the daughter aneurysm is not so large in this situation, and therefore the rupture takes place unexpectedly.
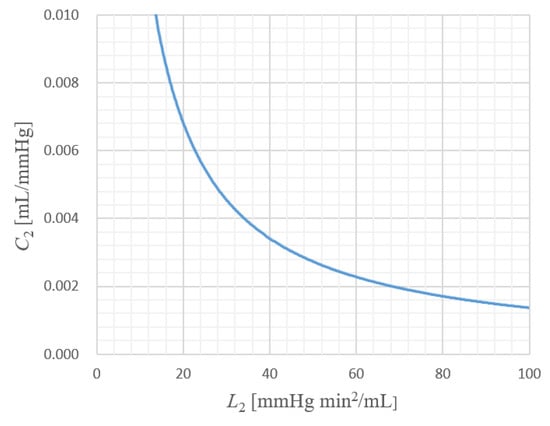
Figure 4.
Resonance condition is depicted. If this condition is satisfied, violent rupture appears due to the increase of max|F2(t)|.
4. Conclusions
Based on the solitonic Windkessel model, the condition for unexpected and sudden aneurysmal rupture is obtained by Equation (4). It arises from the flow-mediated resonance. There are several discoveries to be noted for interpreting this type of rupture:
- the sudden rupture appears only when the two-story intracranial aneurysm (so called, dumbbell-shaped aneurysm) is formed;
- the sudden rupture appears even when the daughter aneurysm is not so growing up well, where rupture condition reported in the preceding work [1] claims that rupture appears if the size of daughter aneurysm is comparable to that of mother aneurysm;
- the sudden rupture does not arise from the increase of local/global blood pressure, but rather from the sudden increase of the local blood flow inside daughter aneurysm, where rupture condition reported in the preceding work [1] takes into account ruptures only caused from the increase of local pressure.
According to the second point of the above, the mechanisms in the preceding work, such as the soliton propagation and resonating beat effect, are less useful to explain unexpected aneurysmal ruptures. On the other hand, most of the aneurysmal ruptures appear unexpectedly even without a significant increase of blood pressure. The rupture of resonance type will play a role in explaining such unexpected ruptures.
Author Contributions
The first author (Y.I.) wrote the manuscript, and responsible for the mathematical modelling and calculations. The second author (H.U.) designed the research. All authors have read and agreed to the published version of the manuscript.
Funding
This work was supported by Ujiie funds for scientific research.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Ujiie, H.; Iwata, Y. Solitonic Windkessel Model for Intracranial Aneurysm. Brain Sci. 2022, 12, 1016. [Google Scholar] [CrossRef] [PubMed]
- Ujiie, H.; Tachibana, H.; Hiramatsu, O.; Hazel, A.L.; Mtsumoto, T.; Ogasawara, Y.; Nakajima, H.; Hori, T.; Takakura, K.; Kajiya, F. Efffect of size and shape (aspect ratio) on the hemodynamics of saccular aneurysms: A possible index for surgical treatment of intracranial aneurysms. Neurosurgery 1999, 45, 119–130. [Google Scholar] [PubMed]
- Shojima, M.; Oshima, M.; Takagi, K.; Torii, R.; Nagata, K.; Shirouzu, I.; Morita, A.; Kirino, T. Role of bloodstream impacting force and the local pressure elevation in the rupture of cerebral aneurysms. Stroke 2005, 36, 1933–1938. [Google Scholar] [CrossRef] [PubMed]
- Tulamo, R.; Froesen, J.; Hernesniemi, J.; Niemela, M. Inflammatory changes in the aneurysm wall: A review. J. Neurointerv. Surg. 2010, 2, 120–130. [Google Scholar] [CrossRef] [PubMed]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).