Presenting a Model to Predict Changing Snow Albedo for Improving Photovoltaic Performance Simulation
Abstract
1. Introduction
- A detailed description of our team’s multi-year analysis of time-series albedo data;
- A method to model the albedo of snow as a function of temperature and time since the last snowfall;
- A comparison of the performance of the developed model against existing common models for estimating ground albedo and remote sensing albedo measurements;
- Evidence showing that improved snow albedo modeling can improve the accuracy of PV performance models.
Historical Approaches to Modeling the Changing Albedo of Snow
2. The Melt-Hour Albedo Model
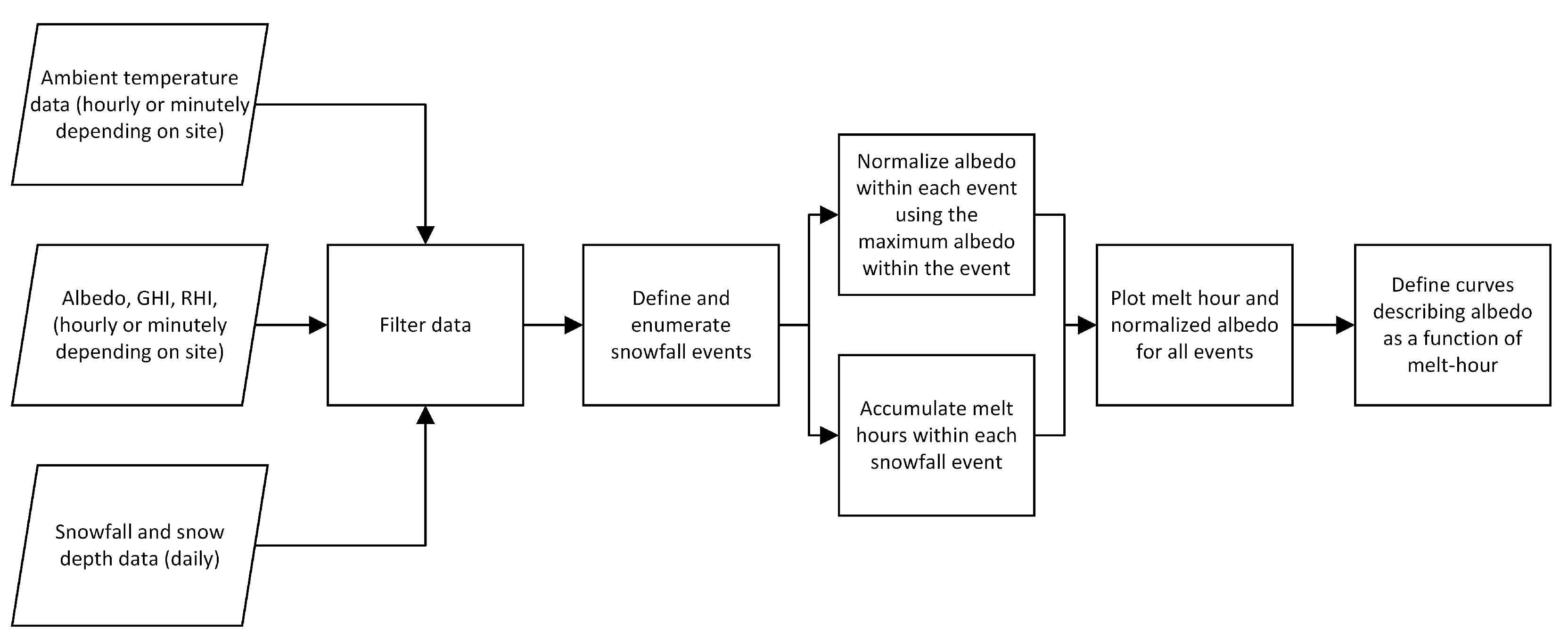
3. Data Acquisition and Preparation
- Global horizontal irradiance (GHI) > 1200 W/m2;
- Reflected horizontal irradiance (RHI (reflected GHI that is measured with a downward-facing horizontal pyranometer [28])) > 1100 W/m2;
- -
- The maximum GHI and RHI figures were derived from testing performed at Sandia National Lab in Albuquerque, New Mexico [29] (See the Supplementary Materials).
- -
- Past research suggests that albedo values outside these bounds are exceedingly rare and represent errors in the data.
- Albedo values measured when solar elevation was less than 5 degrees;
- -
- Quality control data filtering of irradiance data often flags data collected when the zenith angle > 80 degrees (10 degree solar elevation) in order to manage the effect of air mass [32]. This research chose to filter out data collected when the solar elevation < 5 degrees in order to minimize winter-time data losses at high latitudes.
- Albedo values measured more than one hour outside of solar noon;
- -
- Collecting albedo data around solar noon ensures consistency and minimizes the diurnal variation of albedo during low sun elevation angles [33].
- Other known shading or non-standard events.
4. Model Development
- the albedo of the snow-free ground (default = 0.2);
- the snow depth before the first time step of the dataset (default = 0 cm);
- the minimum albedo present when snow is present (default = 0.4);
- the albedo of fresh snow for the site (default = 0.8);
- the minimum snow depth threshold used to indicate whether the modeled snow albedo or the ground albedo shall be used (default = 2.5 cm);
- the change in daily snow depth needed to trigger a snow event that resets the melt-hour count (default = 0 cm).
- Actual albedo is calculated as the product of the normalized albedo and the specified maximum albedo for the site as in Equation (3).
- If the calculated actual albedo values fall below the specified minimum albedo for the site, it is set to the minimum site albedo.
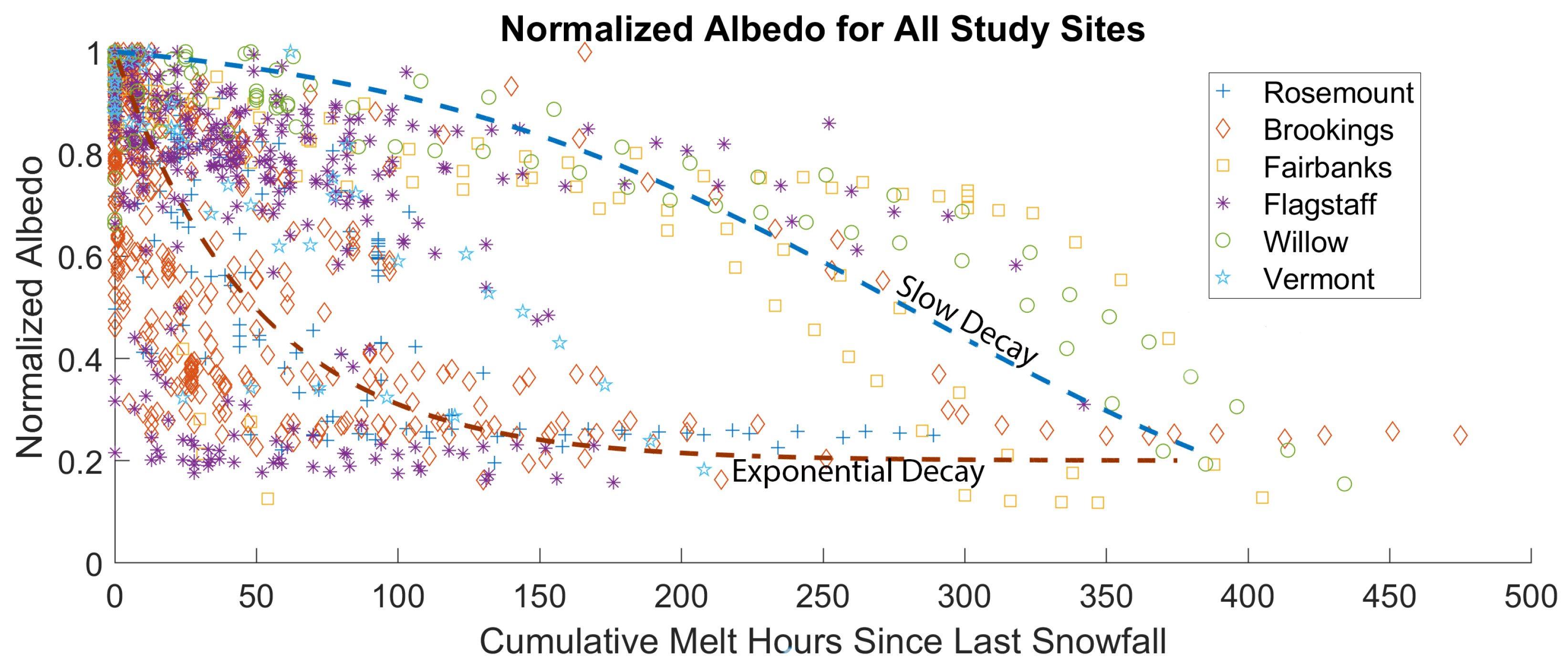
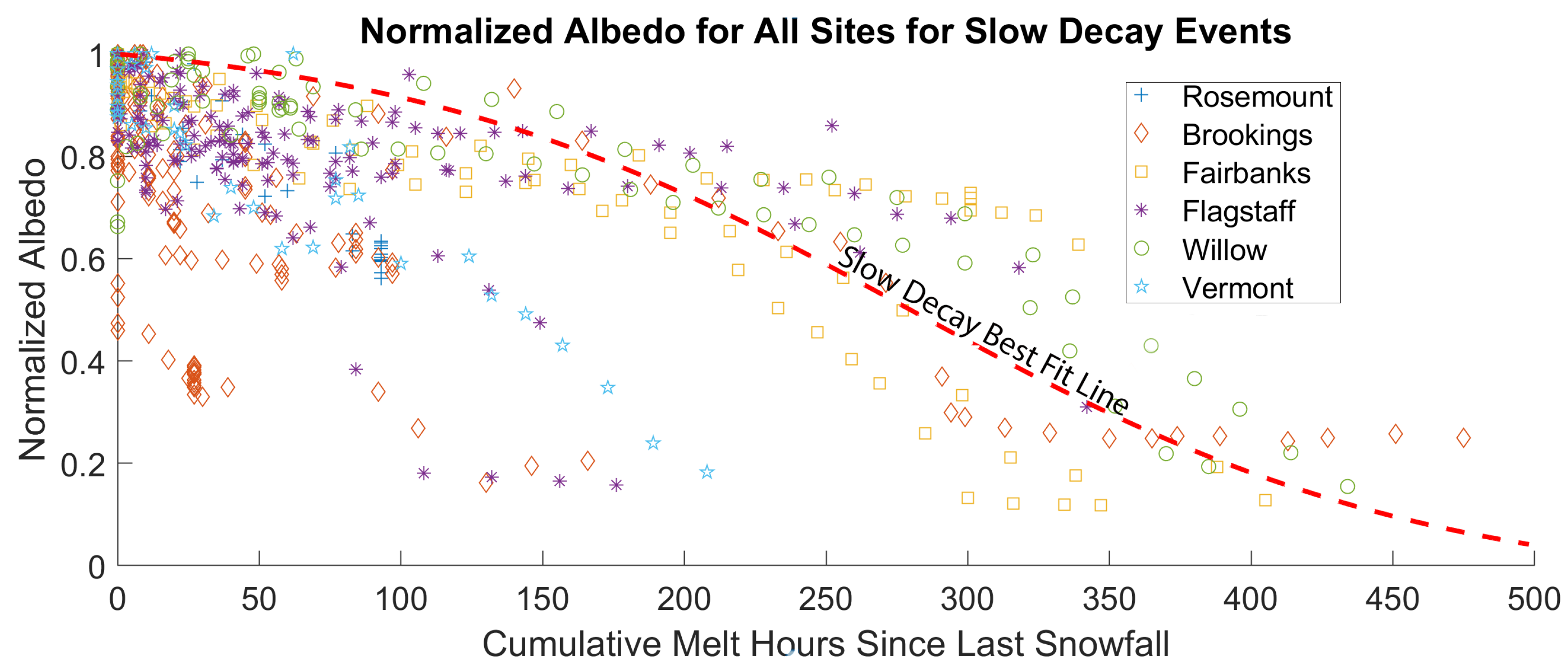
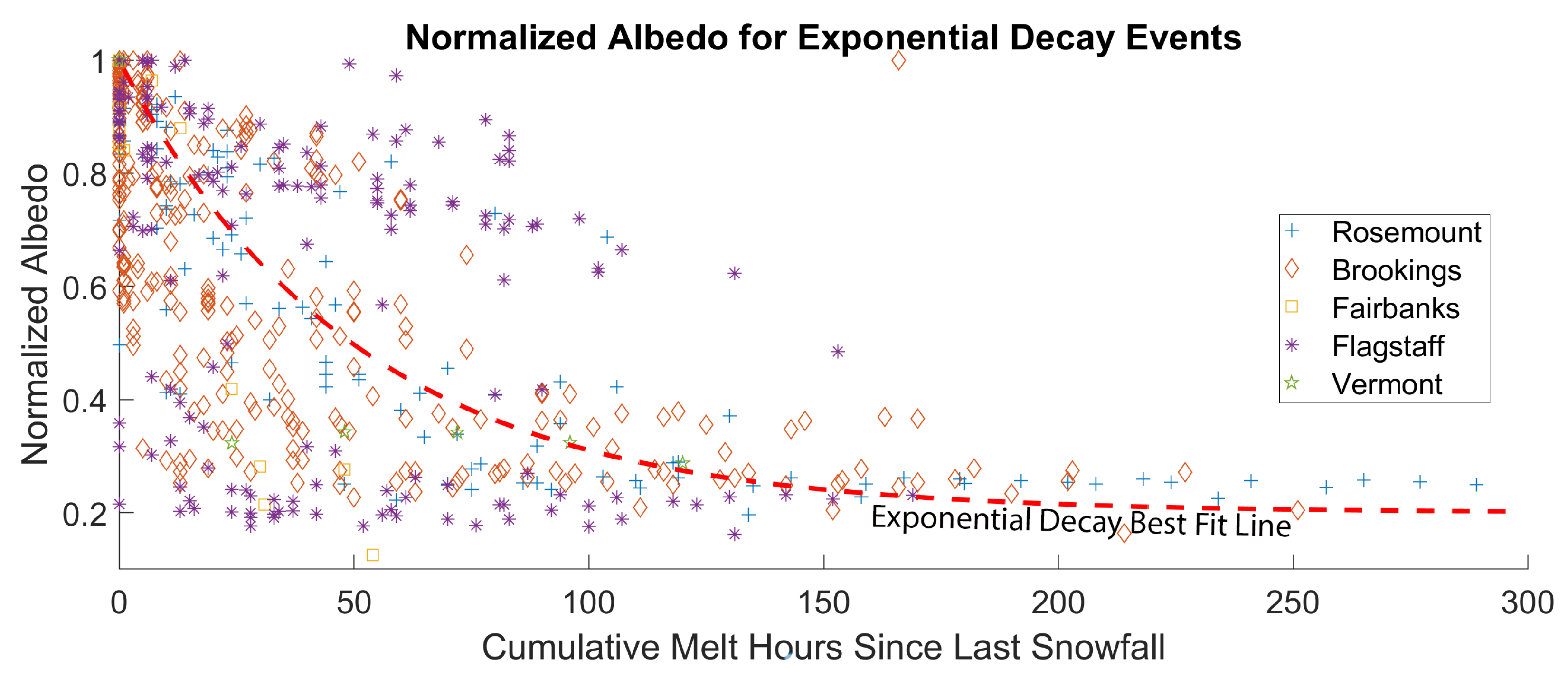
5. Results and Discussion
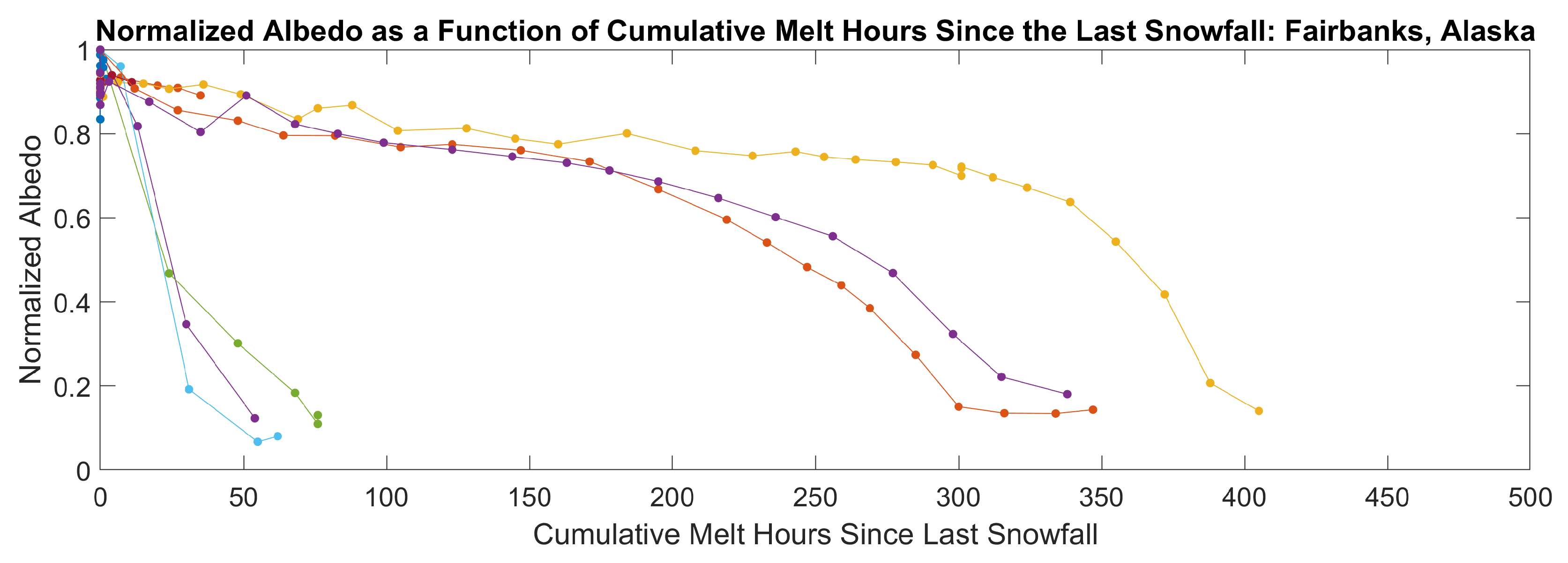
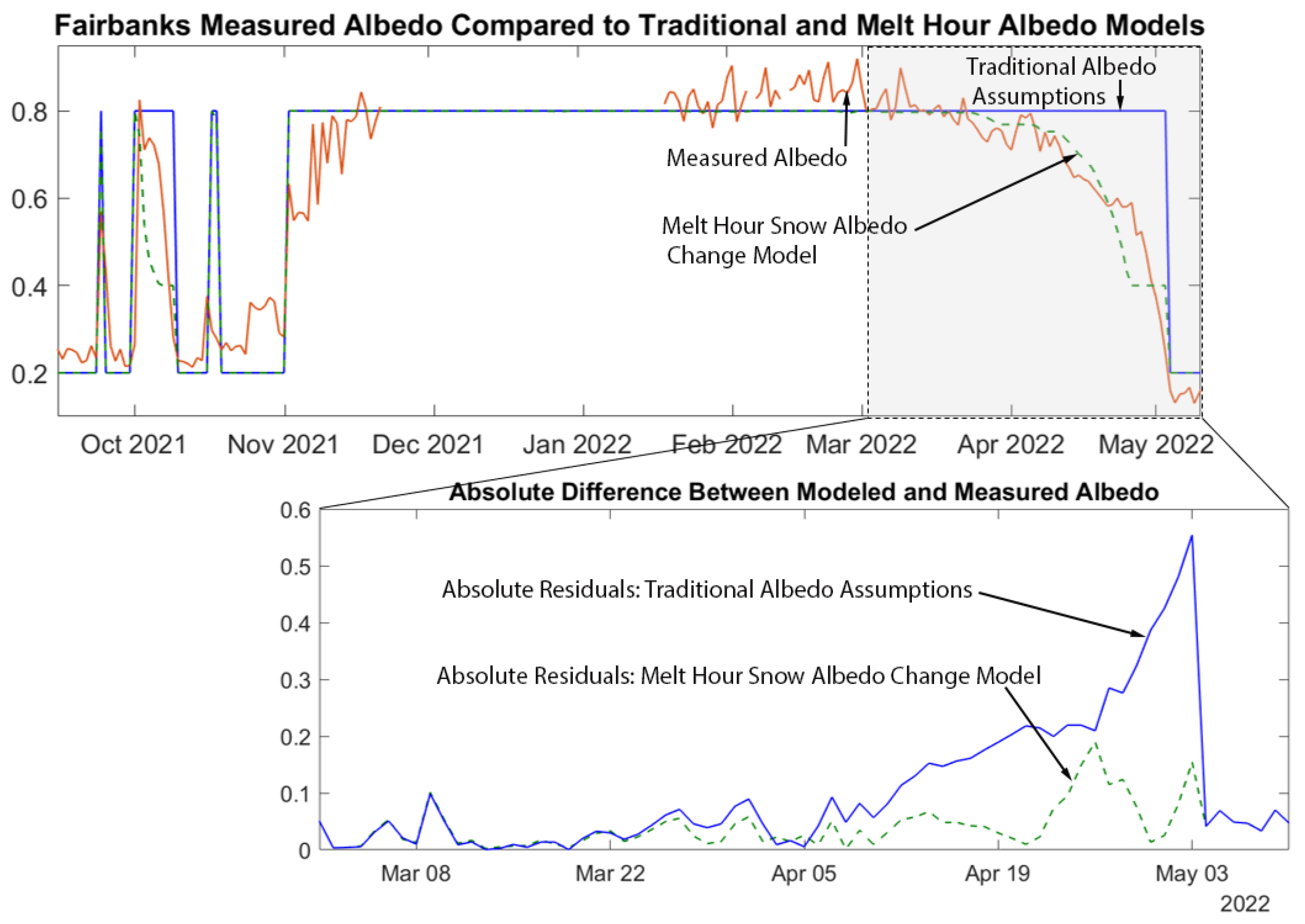
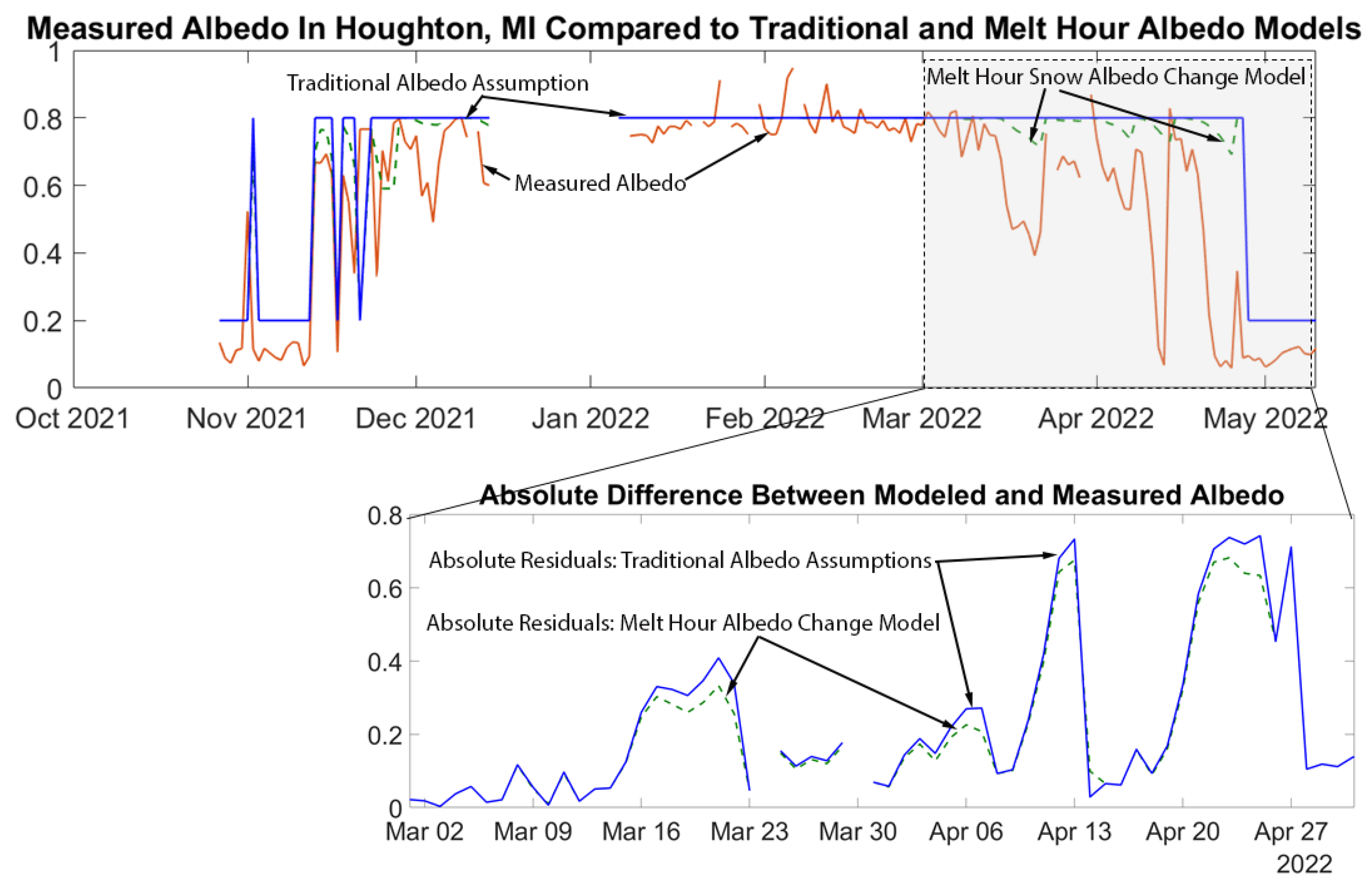
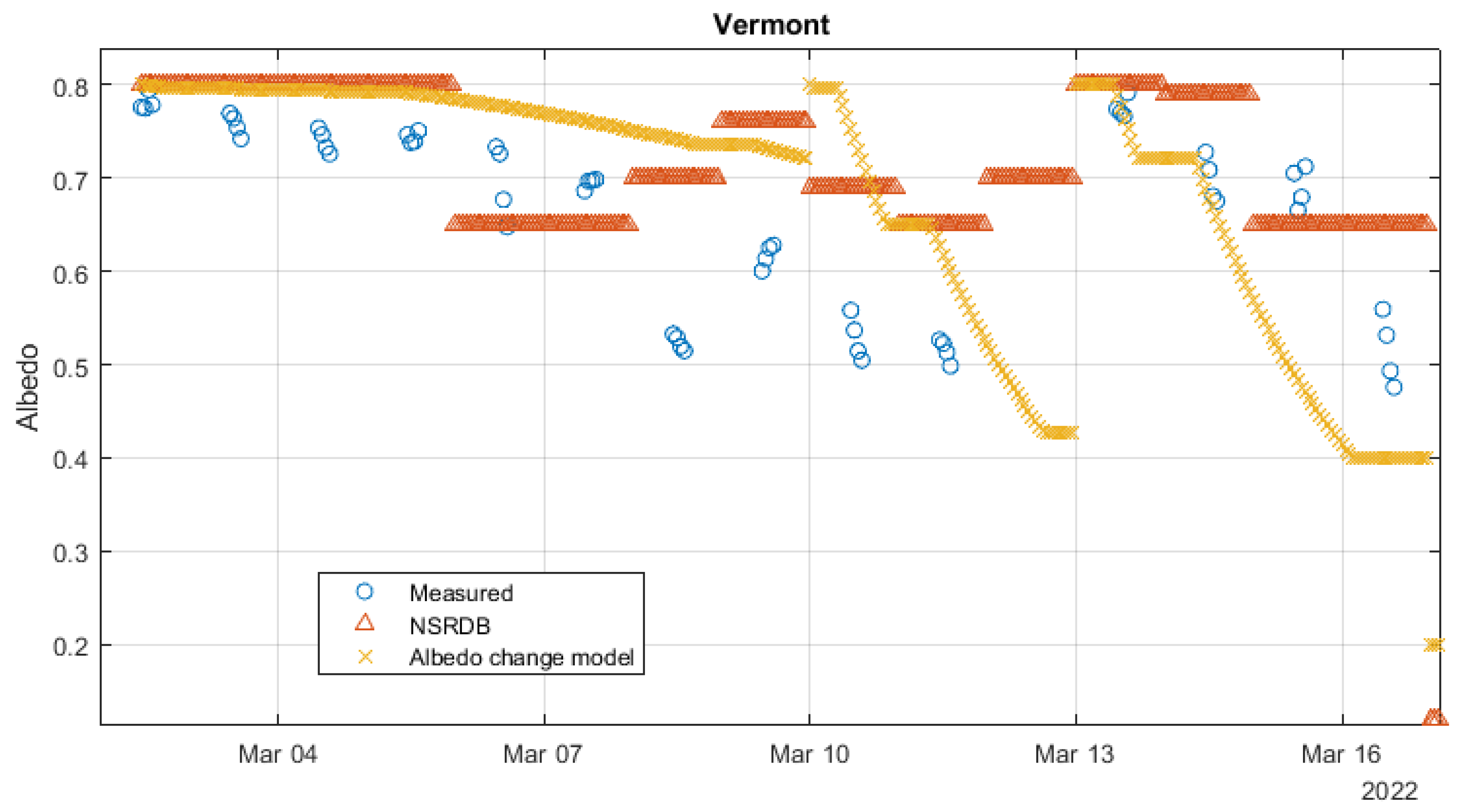
5.1. Validation against Measured Albedo
- Fairbanks, Alaska;
- Haines, Alaska;
- Calumet, Michigan;
- Fairlee, Vermont.
5.2. Validation against Satellite-Derived Albedo
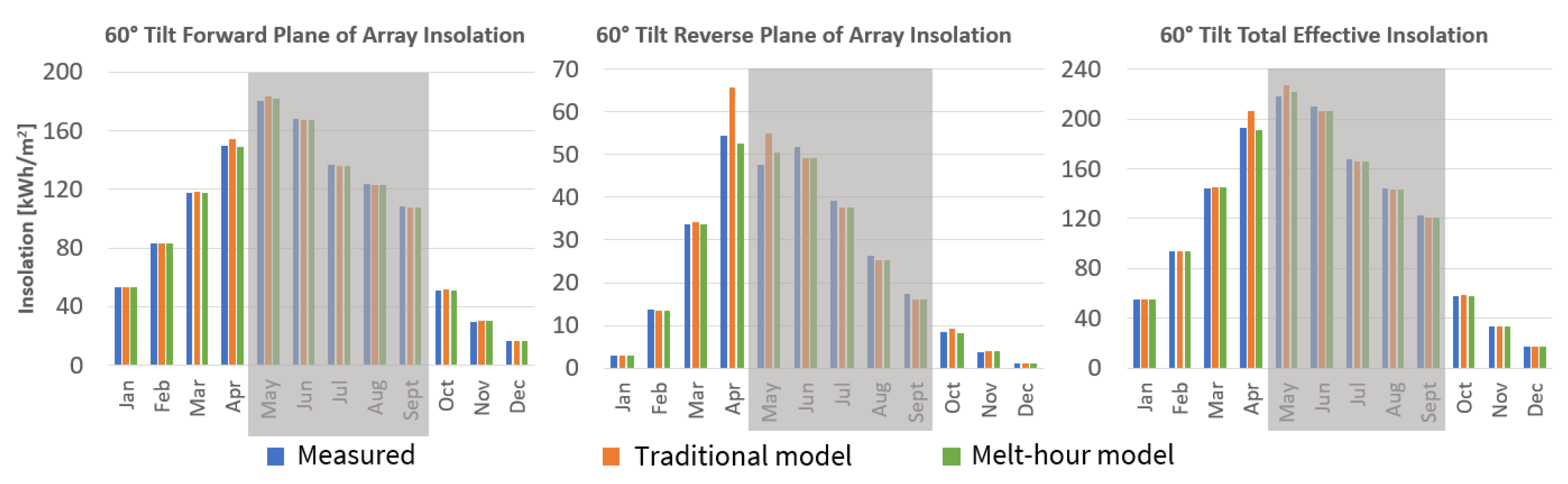
5.3. Model Impact
6. Conclusions
- It uses commonly available ambient temperature and snow depth data;
- It allows users the ability to incorporate site-specific measured data to replace default values and improve model accuracy;
- It is available in pvlib model repositories [38];
- It allows for real-time estimation of snow surface albedo.
- Situations where snow depth may change independently of snowfall or temperature-driven melting, such as due to wind-blown snow or a rainfall event;
- Snow albedo changes that are not caused by time and temperature, such as soiling of the snow by particulates, including ash, dust, debris, etc.
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| GHI | global horizontal irradiance |
| DHI | diffuse horizontal irradiance |
| DNI | direct normal irradiance |
| RHI | reflected horizontal irradiance |
| SAM | System Advisor Model |
| NSRDB | National Solar Radiation Database |
| RMSE | root-mean-square error |
| MAPE | mean absolute percentage error |
| NREL | National Renewable Energy Laboratory |
| PV | photovoltaic(s) |
| ITRPV | International Technology Roadmap for Photovoltaic |
| LCOE | levelized cost of energy |
| POA | plane-of-array |
| NOAA | National Oceanic and Atmospheric Administration |
| MISR | Multi-Angle Imaging Spectroradiometer |
| AVHRR | Advanced Very High Resolution Radiometer |
| MODIS | Moderate Resolution Imaging Spectroradiometer |
References
- Burnham, L. PV Performance and Reliability in Snowy Climates: Opportunities and Challenges; Technical Report; Sandia National Lab. (SNL-NM): Albuquerque, NM, USA, 2019. [Google Scholar]
- Burnham, L.; Riley, D.; Walker, B.; Pearce, J.M. Performance of bifacial photovoltaic modules on a dual-axis tracker in a high-latitude, high-albedo environment. In Proceedings of the 2019 IEEE 46th Photovoltaic Specialists Conference (PVSC), Chicago, IL, USA, 16–21 June 2019; pp. 1320–1327. [Google Scholar]
- Rodríguez-Gallegos, C.D.; Liu, H.; Gandhi, O.; Singh, J.P.; Krishnamurthy, V.; Kumar, A.; Stein, J.S.; Wang, S.; Li, L.; Reindl, T.; et al. Global techno-economic performance of bifacial and tracking photovoltaic systems. Joule 2020, 4, 1514–1541. [Google Scholar] [CrossRef]
- Deline, C.; Ayala Pelaez, S.; MacAlpine, S.; Olalla, C. Estimating and parameterizing mismatch power loss in bifacial photovoltaic systems. Prog. Photovoltaics Res. Appl. 2020, 28, 691–703. [Google Scholar] [CrossRef]
- Stein, J.; Reise, C.; Castro, J.B.; Friesen, G.; Maugeri, G.; Urrejola, E.; Ranta, S. Bifacial Photovoltaic Modules and Systems: Experience and Results from International Research and Pilot Applications; Technical Report; Sandia National Lab. (SNL-NM): Albuquerque, NM, USA; Fraunhofer ISE: Freiburg, Germany, 2021. [Google Scholar]
- Pike, C.; Whitney, E.; Wilber, M.; Stein, J.S. Field performance of south-facing and east-west facing bifacial modules in the arctic. Energies 2021, 14, 1210. [Google Scholar] [CrossRef]
- DeMarban, A. Developers Set to Flip Switch at Alaska’s Largest Solar Farm. Anchorage Daily News, 31 August 2023; pp. A1, A15. [Google Scholar]
- Baliozian, P.; Tepner, S.; Fischer, M.; Trube, J.; Herritsch, S.; Gensowski, K.; Clement, F.; Nold, S.; Preu, R. The international technology roadmap for photovoltaics and the significance of its decade-long projections. In Proceedings of the 37th European PV Solar Energy Conference and Exhibition, Online, 7–11 September 2020; Volume 7, p. 11. [Google Scholar]
- Marion, B. Measured and satellite-derived albedo data for estimating bifacial photovoltaic system performance. Sol. Energy 2021, 215, 321–327. [Google Scholar] [CrossRef]
- Chiodetti, M.; Kang, J.; Reise, C.; Lindsay, A. Predicting yields of bifacial PV power plants—What accuracy is possible? System 2018, 2, 1–7. [Google Scholar]
- Kotak, Y.; Gul, M.; Muneer, T.; Ivanova, S. Investigating the impact of ground albedo on the performance of PV systems. In Proceedings of the CIBSE Technical Symposium, London, UK, 16–17 April 2015. [Google Scholar]
- PVsyst. Albedo Coefficient, PVsyst 7 Help Documentation. Available online: https://www.pvsyst.com/help/albedo.htm (accessed on 20 June 2024).
- Sandia National Laboratory; PV Performance Modeling Collaborative. Albedo. Available online: https://pvpmc.sandia.gov/modeling-guide/1-weather-design-inputs/plane-of-array-poa-irradiance/calculating-poa-irradiance/poa-ground-reflected/albedo/ (accessed on 20 June 2024).
- Kane, D.L.; Gieck, R.E.; Hinzman, L.D. Snowmelt modeling at small Alaskan Arctic watershed. J. Hydrol. Eng. 1997, 2, 204–210. [Google Scholar] [CrossRef]
- Mueller-Stoffels, M.; Wackerbauer, R. Regular network model for the sea ice-albedo feedback in the Arctic. Chaos Interdiscip. J. Nonlinear Sci. 2011, 21, 013111. [Google Scholar] [CrossRef]
- Calleja, J.F.; Muñiz, R.; Fernández, S.; Corbea-Pérez, A.; Peón, J.; Otero, J.; Navarro, F. Snow albedo seasonal decay and its relation with shortwave radiation, surface temperature and topography over an Antarctic ice cap. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2021, 14, 2162–2172. [Google Scholar] [CrossRef]
- Rango, A.; Martinec, J. Revisiting the degree-day method for snowmelt computations 1. JAWRA J. Am. Water Resour. Assoc. 1995, 31, 657–669. [Google Scholar] [CrossRef]
- Dirmhirn, I.; Eaton, F.D. Some characteristics of the albedo of snow. J. Appl. Meteorol. Climatol. 1975, 14, 375–379. [Google Scholar] [CrossRef]
- Anderson, E. Techniques for predicting snow cover runoff. In Role of Snow and Ice in Hydrology: Proceedings of the Banff Symposia; Unesco-WMO-IAHS: Geneva, Switzerland, 1972. [Google Scholar]
- Jin, Z.; Simpson, J.J. Anisotropic reflectance of snow observed from space over the Arctic and its effect on solar energy balance. Remote Sens. Environ. 2001, 75, 63–75. [Google Scholar] [CrossRef]
- Stroeve, J.C.; Nolin, A.W. New methods to infer snow albedo from the MISR instrument with applications to the Greenland ice sheet. IEEE Trans. Geosci. Remote Sens. 2002, 40, 1616–1625. [Google Scholar] [CrossRef]
- Amaral, T.; Wake, C.P.; Dibb, J.E.; Burakowski, E.A.; Stampone, M. A simple model of snow albedo decay using observations from the Community Collaborative Rain, Hail, and Snow-Albedo (CoCoRaHS-Albedo) Network. J. Glaciol. 2017, 63, 877–887. [Google Scholar] [CrossRef]
- Ameriflux. Ameriflux: Measuring Carbon, Water, and Energy Flux across the Americas. Available online: https://ameriflux.lbl.gov/ (accessed on 31 July 2024).
- Dore, S.; Kolb, T. AmeriFlux AmeriFlux US-Fwf Flagstaff-Wildfire; Lawrence Berkeley National Laboratory (LBNL): Berkeley, CA, USA; Northern Arizona University: Flagstaff, AZ, USA, 2016. [Google Scholar]
- Meyers, T. AmeriFlux AmeriFlux US-Bkg Brookings; Lawrence Berkeley National Laboratory (LBNL): Berkeley, CA, USA, 2016. [Google Scholar]
- Baker, J.; Griffis, T. AmeriFlux FLUXNET-1F US-Ro4 Rosemount Prairie; Lawrence Berkeley National Lab. (LBNL): Berkeley, CA, USA; University of Minnesota: Minneapolis, MN, USA; US Department of Agriculture (USDA): Washington, DC, USA, 2022. [Google Scholar]
- National Centers for Environmental Information (NCEI). Climate Data Online. Available online: https://www.ncdc.noaa.gov/cdo-web/ (accessed on 22 June 2021).
- Sengupta, M.; Habte, A.; Wilbert, S.; Gueymard, C.; Remund, J. Best Practices Handbook for the Collection and Use of Solar Resource Data for Solar Energy Applications, 3rd ed.; National Renewable Energy Laboratory: Golden, CO, USA, 2021. [Google Scholar] [CrossRef]
- Riley, D. High Irradiance Conditions; Sandia National Lab: Albuquerque, NM, USA, Upublished Report.
- de Vrese, P.; Stacke, T.; Caves Rugenstein, J.; Goodman, J.; Brovkin, V. Snowfall-albedo feedbacks could have led to deglaciation of snowball Earth starting from mid-latitudes. Commun. Earth Environ. 2021, 2, 91. [Google Scholar] [CrossRef]
- Markvart, T.; Castañer, L. Practical Handbook of Photovoltaics: Fundamentals and Applications; Elsevier: Amsterdam, The Netherlands, 2003. [Google Scholar]
- Maxwell, E.; Wilcox, S.; Rymes, M. Users Manual for SERI QC Software, Assessing the Quality of Solar Radiation Data; Solar Energy Research Institute: Golden, CO, USA, 1993. [Google Scholar]
- Song, J. Diurnal asymmetry in surface albedo. Agric. For. Meteorol. 1998, 92, 181–189. [Google Scholar] [CrossRef]
- National Renewable Energy Laboratory. NSRDB: National Solar Radiation Database. Available online: https://nsrdb.nrel.gov (accessed on 20 June 2024).
- Sengupta, M.; Xie, Y.; Lopez, A.; Habte, A.; Maclaurin, G.; Shelby, J. The national solar radiation data base (NSRDB). Renew. Sustain. Energy Rev. 2018, 89, 51–60. [Google Scholar] [CrossRef]
- U.S. National Ice Center. IMS Snow and Ice Products. Available online: https://usicecenter.gov/Products/ImsHome (accessed on 20 June 2024).
- Ross, B.; Walsh, J.E. A comparison of simulated and observed fluctuations in summertime Arctic surface albedo. J. Geophys. Res. Oceans 1987, 92, 13115–13125. [Google Scholar] [CrossRef]
- Holmgren, W.F.; Hansen, C.W.; Mikofski, M.A. pvlib python: A python package for modeling solar energy systems. J. Open Source Softw. 2018, 3, 884. [Google Scholar] [CrossRef]
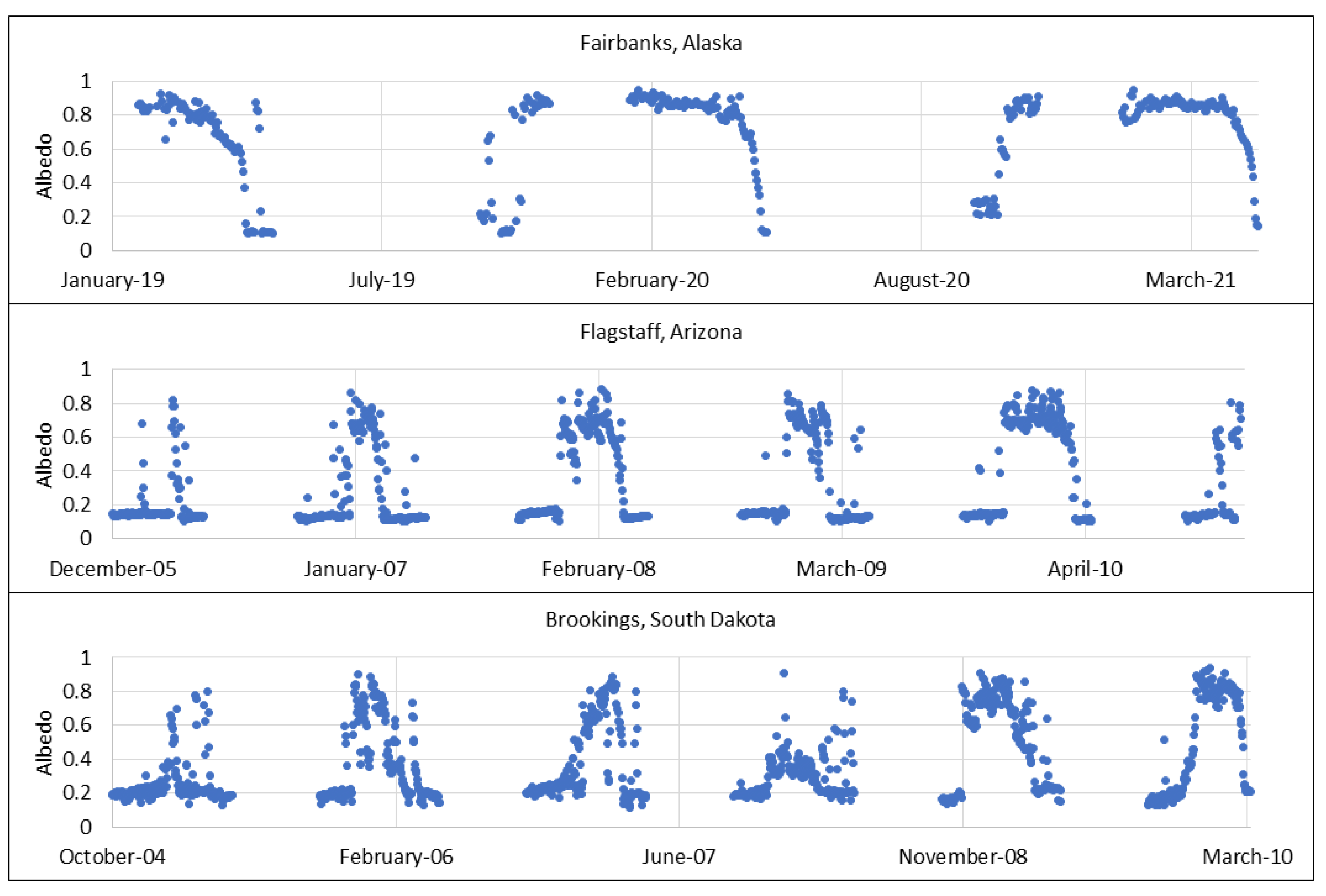
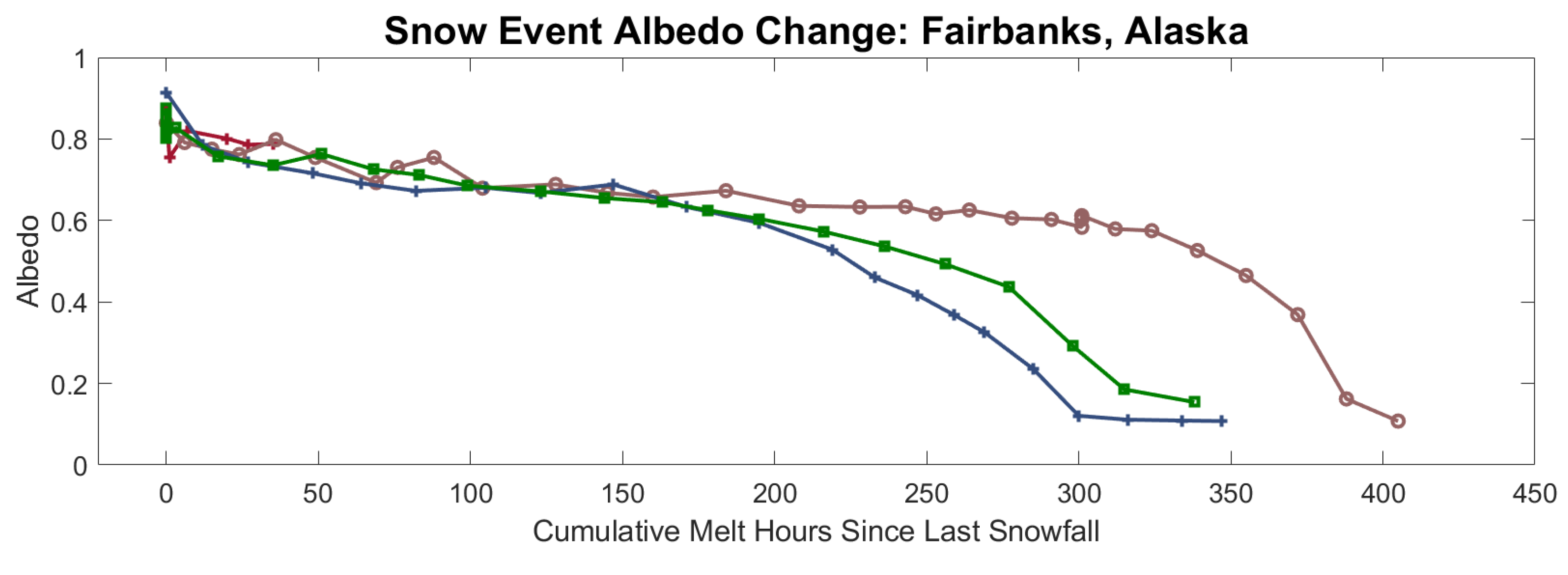
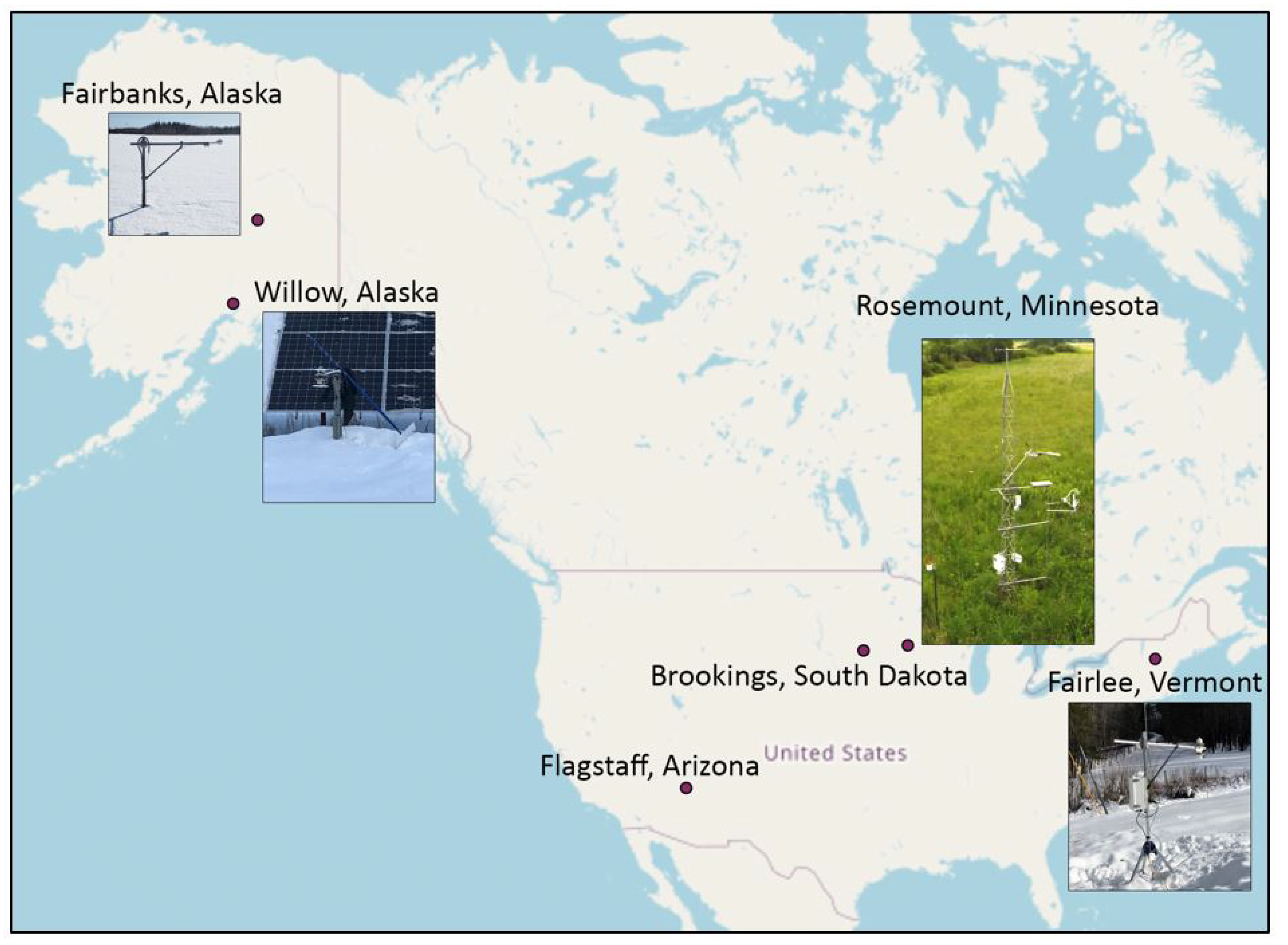


| Location | Albedometer Coordinates | Time Span | Data Time Resolution | Snow Observation Locations * | Distance between Locations (km) |
|---|---|---|---|---|---|
| Fairbanks, Alaska | 64.853, −147.8603 | 1/2019–5/2021 | 1 min | 64.8039, −147.876 | 6 |
| Willow, Alaska | 61.688, −149.968 | 3/2020–5/2021 | 1 min | Camera at albedometer | Same location |
| Fairlee, Vermont | 43.86, −72.22 | 2/2021–4/2021 | 1 min | 43.7917, −72.2578 | 8 |
| Brookings, South Dakota [25] ** | 44.3453, −96.8362 | 4/2004–3/2010 | 1 h | 44.32503, −96.7686 | 6 |
| Flagstaff, Arizona [24] ** | 35.4454, −111.772 | 12/2005–1/2011 | 1 h | 35.19037, −111.674 | 30 |
| Rosemount, Minnesota [26] ** | 44.6781, −93.0723 | 11/2015–12/2018 | 1 h | 44.8831, −93.2289 | 26 |
| Location | RMSE Melt-Hour Model | RMSE Traditional Model | MAPE Melt-Hour Model (%) | MAPE Traditional Model (%) |
|---|---|---|---|---|
| Fairbanks 2019–2021 | 0.0857 | 0.0969 | 18.3954 | 19.7871 |
| Flagstaff | 0.1137 | 0.1241 | 48.2178 | 49.8154 |
| Rosemount | 0.1431 | 0.1584 | 27.8605 | 30.2037 |
| Brookings | 0.1392 | 0.1463 | 23.2169 | 24.042 |
| Fairlee, Vermont 2020–2021 | 0.0893 | 0.2001 | 18.8632 | 39.4351 |
| Location | RMSE Melt-Hour Model | RMSE Traditional Model | MAPE Melt-Hour Model (%) | MAPE Traditional Model (%) |
|---|---|---|---|---|
| Fairbanks 2021–2022 | 0.0835 | 0.1118 | 12.1099 | 15.6022 |
| Haines | 0.1806 | 0.2158 | 57.1033 | 64.2638 |
| Calumet | 0.1604 | 0.1729 | 75.4356 | 78.3075 |
| Vermont 2021–2022 | 0.0812 | 0.0863 | 12.9847 | 13.7809 |
| Location | RMSE Melt-Hour Model | RMSE NSRDB | MAPE Melt-Hour Model (%) | MAPE NSRDB (%) |
|---|---|---|---|---|
| Calumet, MI 2021–2022 | 0.168 | 0.134 | 31.4 | 25.3 |
| Fairlee, VT 2021–2022 | 0.136 | 0.106 | 12.5 | 10.5 |
| Rear Plane of Array | ||||
|---|---|---|---|---|
| Traditional Model | Melt-Hour Model | |||
| Month | % Error | Abs. Error [kWh/m2] | % Error | Abs. Error [kWh/m2] |
| October | −10.26 | −0.86 | 4.24 | 0.36 |
| November | −4.88 | −0.19 | −6.09 | −0.23 |
| December | 0.75 | 0.01 | 0.72 | 0.01 |
| January | 1.74 | 0.05 | 1.75 | 0.05 |
| February | 2.19 | 0.30 | 2.23 | 0.30 |
| March | −1.57 | −0.53 | −0.65 | −0.22 |
| April | −20.81 | −11.34 | 3.43 | 1.87 |
| Total | N/A | −13.22 | N/A | 5.88 |
| Plane of Array | ||||
| Traditional Model | Melt-Hour Model | |||
| Month | % Error | Abs. Error [kWh/m2] | % Error | Abs. Error [kWh/m2] |
| October | −0.64 | −0.33 | 0.25 | 0.13 |
| November | −0.22 | −0.07 | −0.27 | −0.08 |
| December | 0.00 | 0.00 | 0.00 | 0.00 |
| January | 0.03 | 0.01 | 0.03 | 0.01 |
| February | 0.13 | 0.11 | 0.13 | 0.11 |
| March | −0.22 | −0.07 | −0.10 | −0.12 |
| April | −3.08 | −4.61 | 0.51 | 0.76 |
| Total | N/A | −5.30 | N/A | 2.45 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pike, C.; Riley, D.; Toal, H.; Burnham, L. Presenting a Model to Predict Changing Snow Albedo for Improving Photovoltaic Performance Simulation. Solar 2024, 4, 422-439. https://doi.org/10.3390/solar4030019
Pike C, Riley D, Toal H, Burnham L. Presenting a Model to Predict Changing Snow Albedo for Improving Photovoltaic Performance Simulation. Solar. 2024; 4(3):422-439. https://doi.org/10.3390/solar4030019
Chicago/Turabian StylePike, Christopher, Daniel Riley, Henry Toal, and Laurie Burnham. 2024. "Presenting a Model to Predict Changing Snow Albedo for Improving Photovoltaic Performance Simulation" Solar 4, no. 3: 422-439. https://doi.org/10.3390/solar4030019
APA StylePike, C., Riley, D., Toal, H., & Burnham, L. (2024). Presenting a Model to Predict Changing Snow Albedo for Improving Photovoltaic Performance Simulation. Solar, 4(3), 422-439. https://doi.org/10.3390/solar4030019






