Generated Value of Electricity Versus Incurred Cost for Solar Arrays under Conditions of High Solar Penetration
Abstract
:1. Introduction
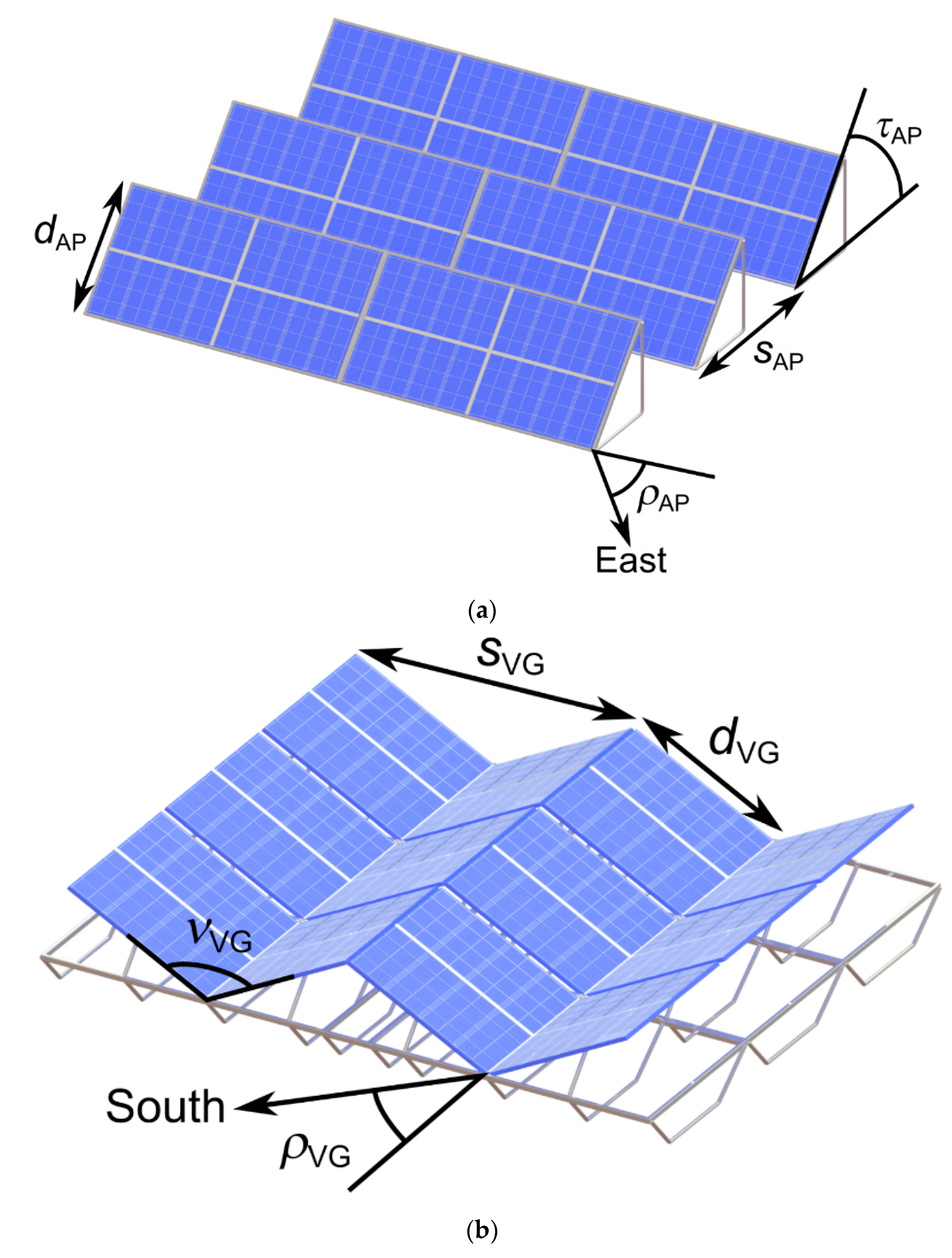
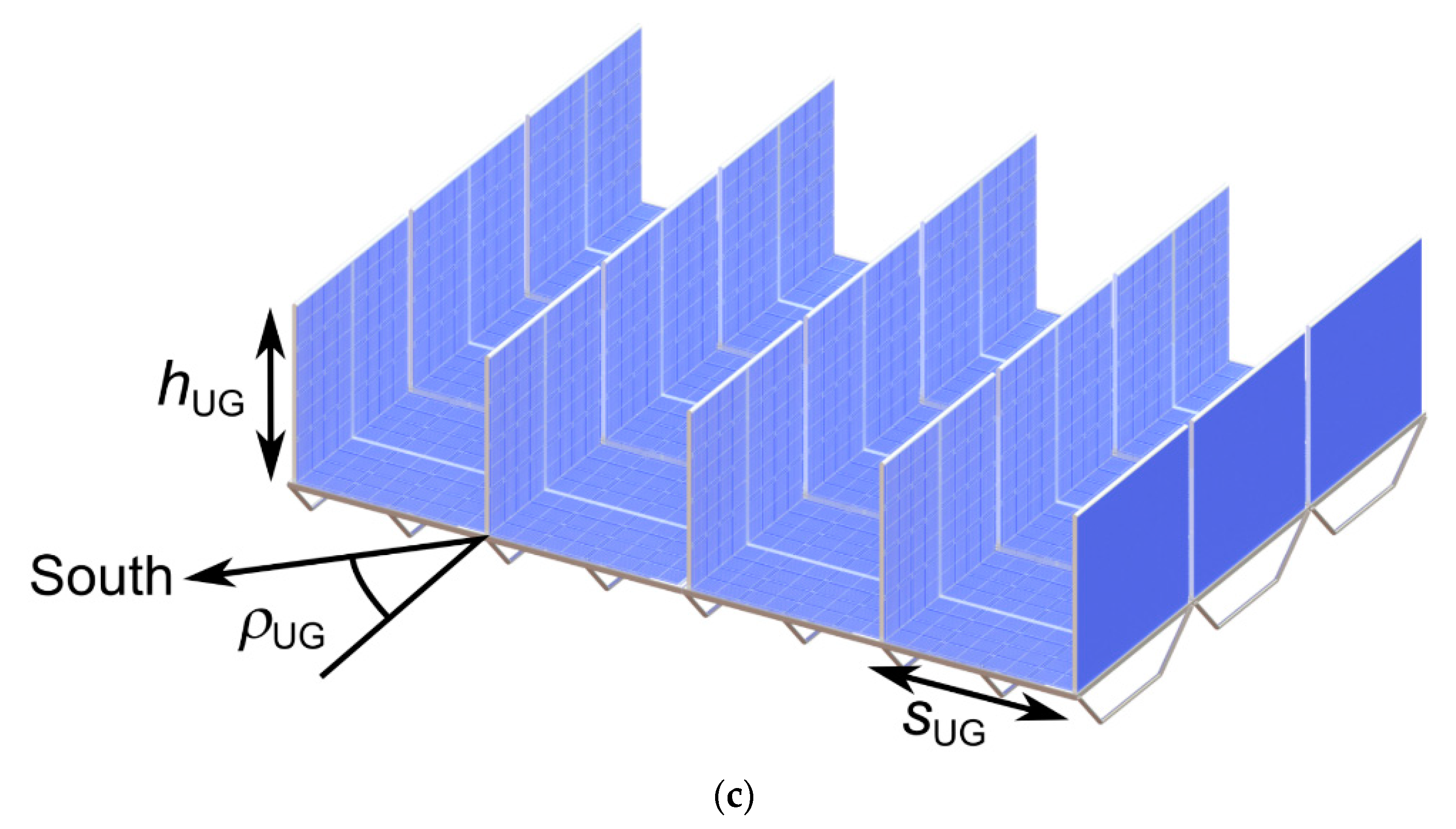
2. Solar Array Geometries
3. Analyses
3.1. Experimental Analyses (of the Constituent Solar Cells)
3.2. Theoretical Analyses (of the Assembled Solar Arrays)
3.2.1. Angled-Panel Array
3.2.2. V-Groove Array
3.2.3. U-Groove Array
3.3. Economic Analyses (of Generated Value versus Incurred Cost)
- Specular and diffuse solar irradiance is computed via Equations (3) and (4), respectively;
- The captured optical power density is then computed for each of the flat-panel, angled-panel, V-groove, and U-groove arrays via Equations (7), (18), (29) and (51), respectively;
- The generated electrical power is then computed for each array using its captured optical power density, the NOAA temperature data from [53], and the I–V characteristics of Equation (1), assuming that each array has one maximum power point tracking (MPPT) system;
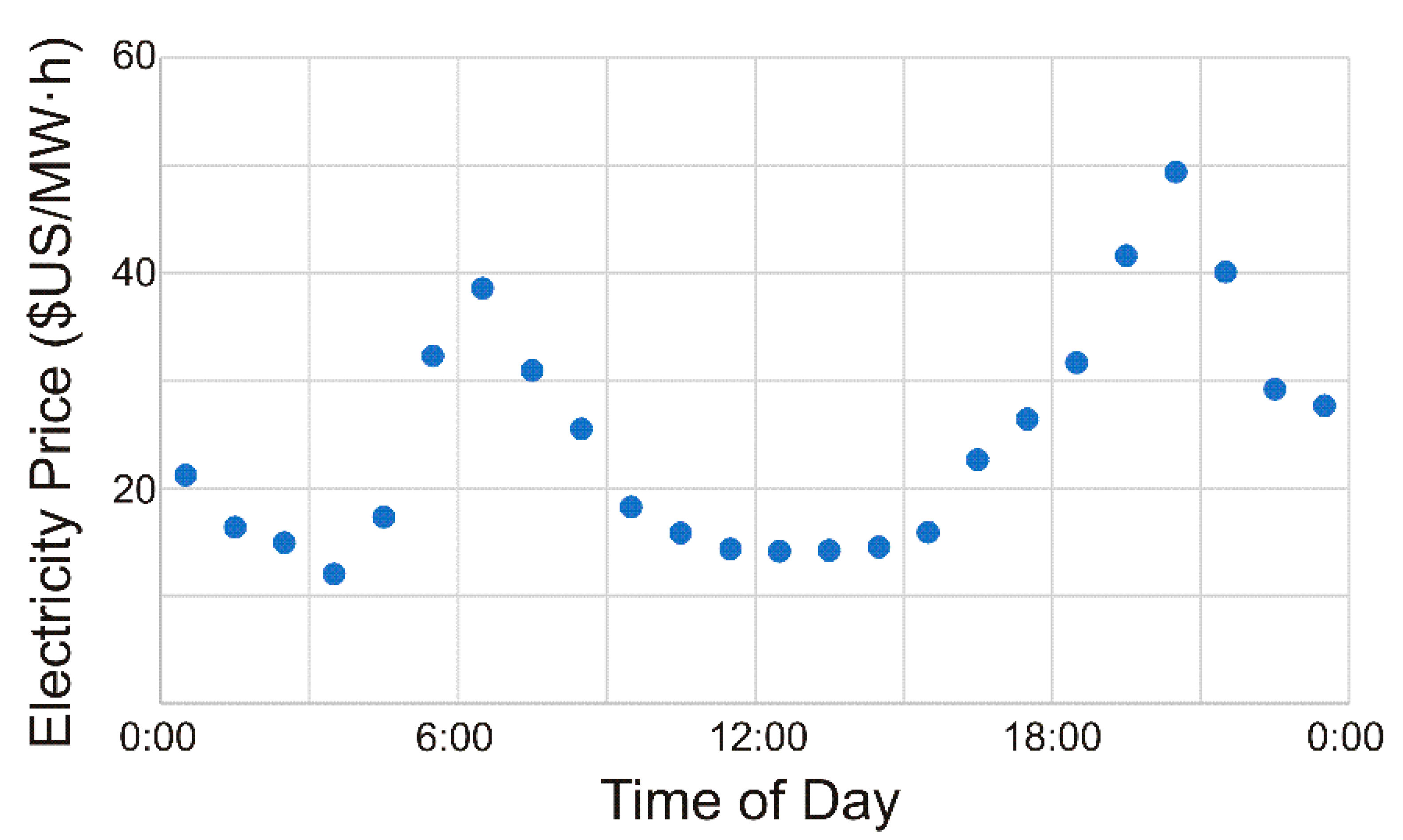
- The generated value of electricity is then computed for each array as an accumulating product of generated electrical power and CAISO OASIS electricity pricing data from [3].
4. Results and Discussions
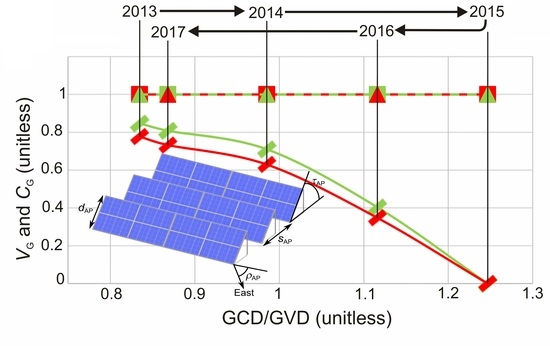
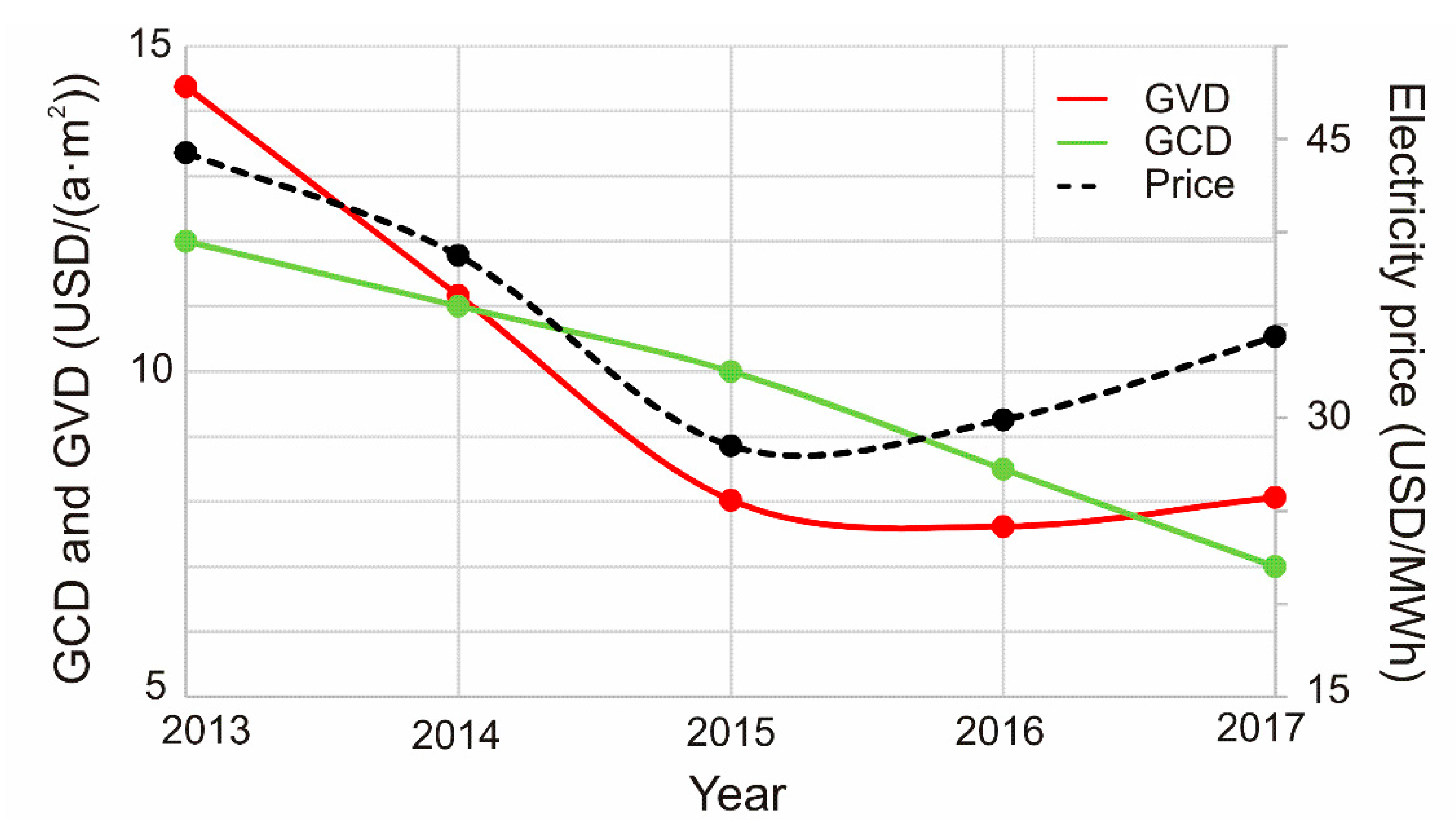
4.1. Historical Trends
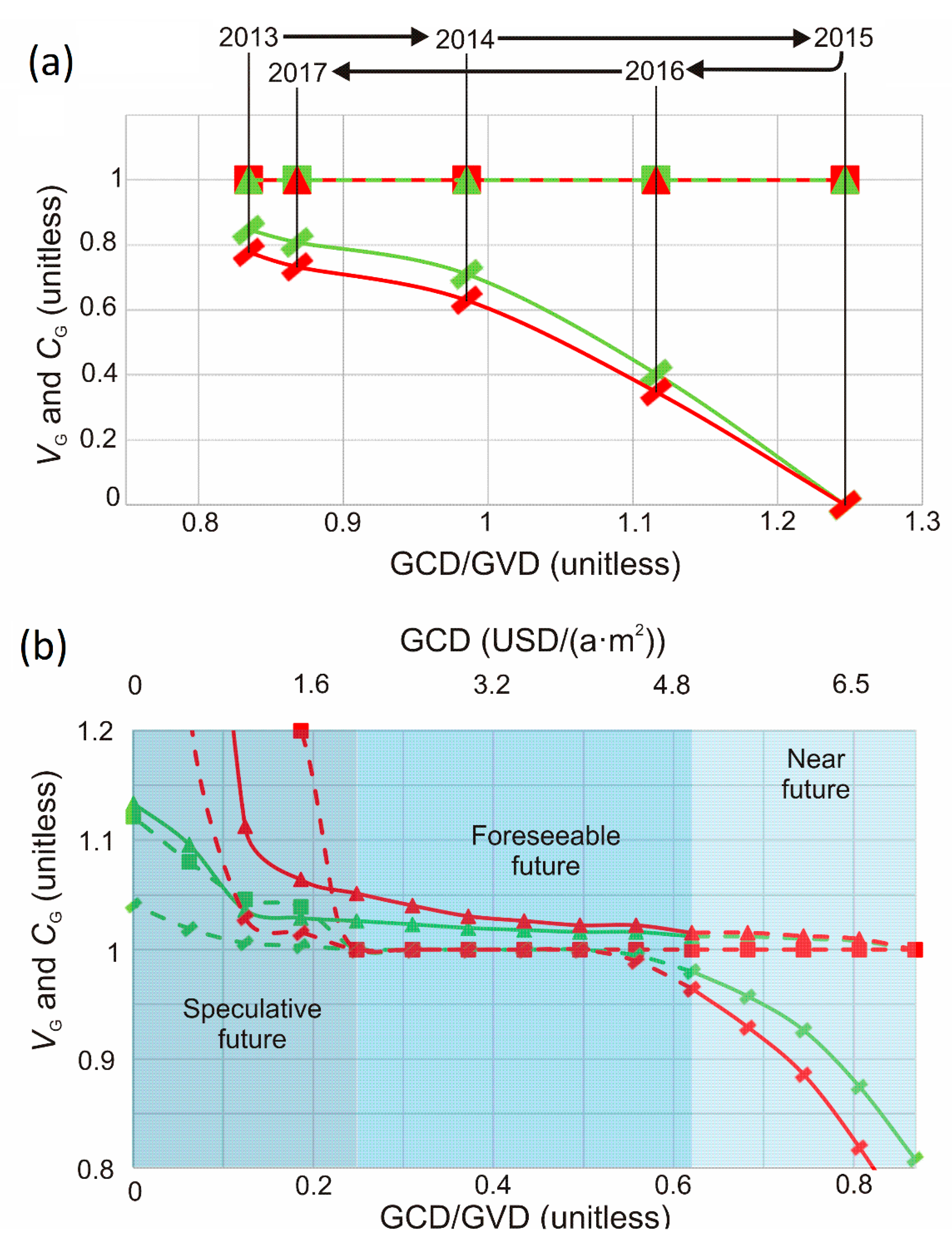
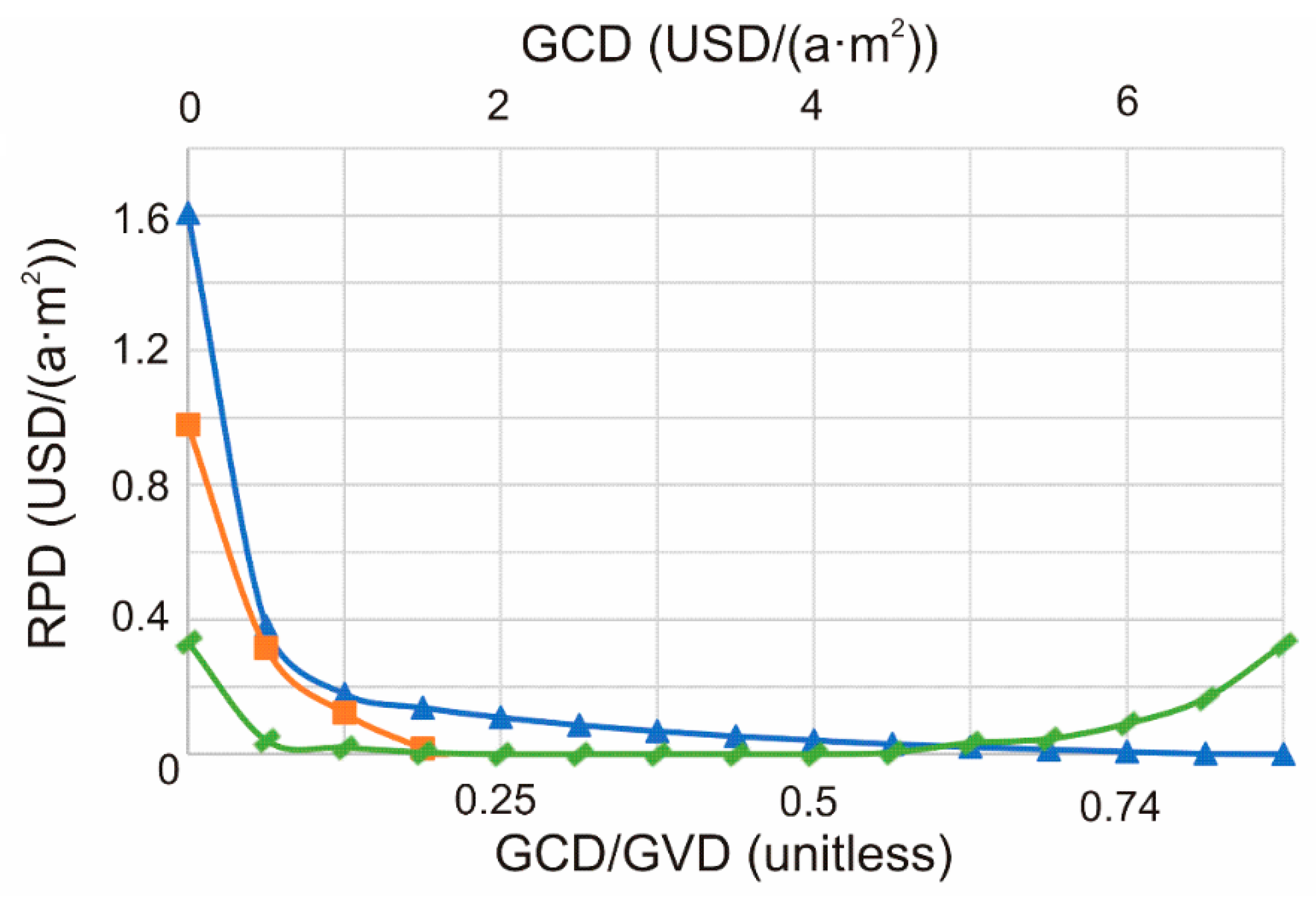
4.2. Future Trends
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- International Energy Agency (IEA). Photovoltaic Power System Programme (PVPS). In 2016 Snapshot of Global Photovoltaic Markets; IEA: Paris, France, 2016. [Google Scholar]
- California Independent System Operator (CAISO). Demand Response and Energy Efficiency Roadmap: Maximizing Preferred Resources; CAISO: Folsom, California, 2013. [Google Scholar]
- California Independent Systems Operator (CAISO) Open-Access Same-Time Information System (OASIS) website. Available online: https://oasis.caiso.com (accessed on 15 September 2018).
- Li, M.; Pan, J.; Su, Q.; Niu, Y. Analyzing sensitivity of power system wind penetration to thermal generation flexibility. In Proceedings of the 2017 13th IEEE Conference on Automation Science and Engineering (CASE), Xi’an, China, 20–23 August 2017; pp. 1628–1632. [Google Scholar]
- Obi, M.; Bass, R. Trends and challenges of grid-connected photovoltaic systems–A review. Renew. Sustain. Energy Rev. 2016, 58, 1082–1094. [Google Scholar] [CrossRef]
- Janko, S.A.; Arnold, M.R.; Johnson, N.G. Implications of high-penetration renewables for ratepayers and utilities in the residential solar photovoltaic (PV) market. Appl. Energy 2016, 180, 37–51. [Google Scholar] [CrossRef]
- Hassan, A.S.; Cipcigan, L.; Jenkins, N. Optimal battery storage operation for PV systems with tariff incentives. Appl. Energy 2017, 203, 422–441. [Google Scholar] [CrossRef]
- Schoenung, S.M.; Keller, J.O. Commercial potential for renewable hydrogen in California. Int. J. Hydrog. Energy 2017, 42, 13321–13328. [Google Scholar] [CrossRef]
- Zhang, N.; Lu, X.; McElroy, M.B.; Nielsen, C.P.; Chen, X.; Deng, Y.; Kang, C. Reducing curtailment of wind electricity in China by employing electric boilers for heat and pumped hydro for energy storage. Appl. Energy 2016, 184, 987–994. [Google Scholar] [CrossRef] [Green Version]
- Gür, T.M. Review of electrical energy storage technologies, materials and systems: Challenges and prospects for large-scale grid storage. Energy Environ. Sci. 2018, 11, 2696–2767. [Google Scholar] [CrossRef]
- Chaudhary, P.; Rizwan, M. Energy management supporting high penetration of solar photovoltaic generation for smart grid using solar forecasts and pumped hydro storage system. Renew. Energy 2018, 118, 928–946. [Google Scholar] [CrossRef]
- Le Floch, C.; Belletti, F.; Moura, S. Optimal Charging of Electric Vehicles for Load Shaping: A Dual-Splitting Framework With Explicit Convergence Bounds. IEEE Trans. Transp. Electrif. 2016, 2, 190–199. [Google Scholar] [CrossRef]
- Sanandaji, B.M.; Vincent, T.L.; Poolla, K. Ramping Rate Flexibility of Residential HVAC Loads. IEEE Trans. Sustain. Energy 2015, 7, 865–874. [Google Scholar] [CrossRef]
- Perez, M.; Perez, R.; Rábago, K.R.; Putnam, M. Overbuilding & curtailment: The cost-effective enablers of firm PV generation. Sol. Energy 2019, 180, 412–422. [Google Scholar] [CrossRef]
- Perez, R.; Perez, M.; Schlemmer, J.; Dise, J.; Hoff, T.E.; Swierc, A.; Keelin, P.; Pierro, M.; Cornaro, C. From Firm Solar Power Forecasts to Firm Solar Power Generation an Effective Path to Ultra-High Renewable Penetration a New York Case Study. Energies 2020, 13, 4489. [Google Scholar] [CrossRef]
- Perez, R.; Rábago, K.R.; Trahan, M.; Rawlings, L.; Norris, B.; Hoff, T.; Putnam, M.; Perez, M. Achieving very high PV penetration–The need for an effective electricity remuneration framework and a central role for grid operators. Energy Policy 2016, 96, 27–35. [Google Scholar] [CrossRef] [Green Version]
- Borenstein, S. The Market Value and Cost of Solar Photovoltaic Energy Production; Center for the Study of Energy Markets: Berkeley, CA, USA, 2008. [Google Scholar]
- Hartner, M.; Ortner, A.; Hiesl, A.; Haas, R. East to west–The optimal tilt angle and orientation of photovoltaic panels from an electricity system perspective. Appl. Energy 2015, 160, 94–107. [Google Scholar] [CrossRef]
- Rowlands, I.H.; Kemery, B.P.; Beausoleil-Morrison, I. Optimal solar-PV tilt angle and azimuth: An Ontario (Canada) case-study. Energy Policy 2011, 39, 1397–1409. [Google Scholar] [CrossRef]
- Masrur, H.; Konneh, K.; Ahmadi, M.; Khan, K.; Othman, M.; Senjyu, T. Assessing the Techno-Economic Impact of Derating Factors on Optimally Tilted Grid-Tied Photovoltaic Systems. Energies 2021, 14, 1044. [Google Scholar] [CrossRef]
- Maleki, S.A.M.; Hizam, H.; Gomes, C. Estimation of Hourly, Daily and Monthly Global Solar Radiation on Inclined Surfaces: Models Re-Visited. Energies 2017, 10, 134. [Google Scholar] [CrossRef] [Green Version]
- Al-Rousan, N.; Isa, N.A.M.; Desa, M.K.M. Advances in solar photovoltaic tracking systems: A review. Renew. Sustain. Energy Rev. 2018, 82, 2548–2569. [Google Scholar] [CrossRef]
- Vasantha, P.N.; Dehankar, S.; Raman, M.; Karnataki, K.; Shankar, G. Space optimization and backtracking for dual axis so-lar photovoltaic tracker. In Proceedings of the IEEE International WIE Conference on Electrical and Computer Engineering, Dhaka, Bangladesh, 19–20 December 2015; pp. 451–454. [Google Scholar]
- Brecl, K.; Topic, M. Self-shading losses of fixed free-standing PV arrays. Renew. Energy 2011, 36, 3211–3216. [Google Scholar] [CrossRef]
- Gordon, J.; Wenger, H.J. Central-station solar photovoltaic systems: Field layout, tracker, and array geometry sensitivity studies. Sol. Energy 1991, 46, 211–217. [Google Scholar] [CrossRef]
- Vaillon, R.; Dupré, O.; Cal, R.B.; Calaf, M. Pathways for mitigating thermal losses in solar photovoltaics. Sci. Rep. 2018, 8, 13163. [Google Scholar] [CrossRef]
- Stanislawski, B.; Margairaz, F.; Cal, R.; Calaf, M. Potential of module arrangements to enhance convective cooling in solar photovoltaic arrays. Renew. Energy 2020, 157, 851–858. [Google Scholar] [CrossRef]
- Glick, A.; Smith, S.E.; Ali, N.; Bossuyt, J.; Recktenwald, G.; Calaf, M.; Cal, R.B. Influence of flow direction and turbulence intensity on heat transfer of utility-scale photovoltaic solar farms. Sol. Energy 2020, 207, 173–182. [Google Scholar] [CrossRef]
- Glick, A.; Ali, N.; Bossuyt, J.; Calaf, M.; Cal, R.B. Utility-scale solar PV performance enhancements through system-level modifications. Sci. Rep. 2020, 10, 1–9. [Google Scholar] [CrossRef] [PubMed]
- Glick, A.; Ali, N.; Bossuyt, J.; Recktenwald, G.; Calaf, M.; Cal, R.B. Infinite photovoltaic solar arrays: Considering flux of momentum and heat transfer. Renew. Energy 2020, 156, 791–803. [Google Scholar] [CrossRef]
- Sista, S.; Hong, Z.; Chen, L.-M.; Yang, Y. Tandem polymer photovoltaic cells—current status, challenges and future outlook. Energy Environ. Sci. 2011, 4, 1606–1620. [Google Scholar] [CrossRef]
- Andersson, B.V.; Würfel, U.; Inganäs, O. Full day modelling of V-shaped organic solar cell. Sol. Energy 2011, 85, 1257–1263. [Google Scholar] [CrossRef]
- Ding, K.; Zhang, J.; Bian, X.; Xu, J. A simplified model for photovoltaic modules based on improved translation equations. Sol. Energy 2014, 101, 40–52. [Google Scholar] [CrossRef]
- Humada, A.M.; Hojabri, M.; Mekhilef, S.; Hamada, H.M. Solar cell parameters extraction based on single and double-diode models: A review. Renew. Sustain. Energy Rev. 2016, 56, 494–509. [Google Scholar] [CrossRef] [Green Version]
- Aberle, A.G.; Zhang, W.; Hoex, B. Advanced loss analysis method for silicon wafer solar cells. Energy Procedia 2011, 8, 244–249. [Google Scholar] [CrossRef] [Green Version]
- Du, Y.; Tao, W.; Liu, Y.; Le, Z.; Zhang, M. Cell-to-Module Variation of Optical and Photovoltaic Properties for Monocrystalline Silicon Solar Cells with Different Texturing Approaches. ECS J. Solid State Sci. Technol. 2017, 6, P332–P338. [Google Scholar] [CrossRef]
- Saynova, D.; Mihailetchi, V.; Geerligs, L.; Weeber, A. Comparison of high efficiency solar cells on large area n-type and p-type silicon wafers with screen-printed Aluminum-alloyed rear junction. In Proceedings of the 2008 33rd IEEE Photovolatic Specialists Conference, San Diego, CA, USA, 11–16 May 2008; pp. 1–5. [Google Scholar]
- Solanki, C.S.; Singh, H.K. Anti-Reflection and Light Trapping in c-Si Solar Cells; Springer Nature: Singapore, 2017. [Google Scholar]
- Riordan, C.; Hulstron, R. What is an air mass 1.5 spectrum? (solar cell performance calculations). In Proceedings of the IEEE Conference on Photovoltaic Specialists, Kissimmee, FL, USA, 21–25 May 1990; pp. 1085–1088. [Google Scholar]
- Breitenstein, O. Understanding the current-voltage characteristics of industrial crystalline silicon solar cells by considering inhomogeneous current distributions. Opto-Electron. Rev. 2013, 21, 259–282. [Google Scholar] [CrossRef]
- Koehl, M.; Heck, M.; Wiesmeier, S.; Wirth, J. Modeling of the nominal operating cell temperature based on outdoor weathering. Sol. Energy Mater. Sol. Cells 2011, 95, 1638–1646. [Google Scholar] [CrossRef]
- Singh, P.; Ravindra, N. Temperature dependence of solar cell performance—an analysis. Sol. Energy Mater. Sol. Cells 2012, 101, 36–45. [Google Scholar] [CrossRef]
- Wolf, M.; Noel, G.T.; Stirn, R.J. Investigation of the double exponential in the current-voltage characteristics of silicon solar cells. IEEE T. Electron. Dev. 1977, 24, 419–428. [Google Scholar] [CrossRef]
- Boivin, A.B.; Westgate, T.M.; Holzman, J.F. Design and performance analyses of solar arrays towards a metric of energy value. Sustain. Energy Fuels 2018, 2, 2090–2099. [Google Scholar] [CrossRef]
- Boivin, A.B. Performance and value of geometric solar arrays subject to cyclical electricity prices and high solar penetration. Master’s Thesis, The University of British Columbia, Kelowna, BC, Canada, 2019. [Google Scholar]
- Young, A. Air mass and refraction. Appl. Opt. 1994, 33, 1108–1110. [Google Scholar] [CrossRef]
- American Society for Testing and Materials (ASTM). G173-03 (2012) Standard Tables for Reference Solar Spectral Irradiances: Direct Normal and Hemispherical on 37° Tilted Surface; American Society for Testing and Materials: West Conshohocken, PA, USA, 2012. [Google Scholar] [CrossRef]
- American Society for Testing and Materials (ASTM). E490-00a (2014) Standard Solar Constant and Zero Air Mass Solar Spectral Irradiance Tables; American Society for Testing and Materials: West Conshohocken, PA, USA, 2014. [Google Scholar] [CrossRef]
- Becker, S. Calculation of direct solar and diffuse radiation in Israel. Int. J. Clim. 2001, 21, 1561–1576. [Google Scholar] [CrossRef]
- Koomen, M.J.; Lock, C.; Packer, D.M.; Scolnik, R.; Tousey, R.; Hulburt, E.O. Measurements of the Brightness of the Twilight Sky. J. Opt. Soc. Am. 1952, 42, 353. [Google Scholar] [CrossRef]
- Coblentz, W. The diffuse reflecting power of various substances. J. Wash. Acad. Sci. 1912, 2, 447–451. [Google Scholar] [CrossRef]
- Liu, X.; Wu, Y.; Hou, X.; Liu, H. Investigation of the optical performance of a novel planar static PV concentrator with Lambertian rear reflectors. Buildings 2017, 7, 88. [Google Scholar] [CrossRef] [Green Version]
- National Oceanic and Atmospheric Administration (NOAA) Online Weather Data website. Available online: https://w2.weather.gov/climate (accessed on 15 May 2019).
- Darling, S.B.; You, F.; Veselka, T.; Velosa, A. Assumptions and the levelized cost of energy for photovoltaics. Energy Environ. Sci. 2011, 4, 3133–3139. [Google Scholar] [CrossRef]
- Awad, H.; Gül, M.; Ritter, C.; Verma, P.; Chen, Y.; Salim, K.M.E.; Al-Hussein, M.; Yu, H.; Kasawski, K. Solar photovoltaic optimization for commercial flat rooftops in cold regions. In Proceedings of the IEEE Conference on Technologies for Sustainability, Phoenix, AZ, USA, 9–11 October 2016; pp. 39–46. [Google Scholar]
- Fu, R.; Margolis, R.; Feldman, D. US Solar Photovoltaic System Cost Benchmark: Q1 2018; National Renewable Energy Laboratory: Golden, CO, USA, 2018. [Google Scholar]
- Barbose, G.; Darghouth, N.; Millstein, D.; Cates, S.; DiSanti, N.; Widiss, R. Tracking the Sun IX: The Installed Price of Residential and Non-Residential Photovoltaic Systems in the United States; Lawrence Berkeley National Laboratory: Berkeley, CA, USA, 2016. [Google Scholar]
- Lave, M.; Kleissl, J. Optimum fixed orientations and benefits of tracking for capturing solar radiation in the continental United States. Renew. Energy 2011, 36, 1145–1152. [Google Scholar] [CrossRef] [Green Version]
- Mundada, A.S.; Prehoda, E.W.; Pearce, J.M. U.S. market for solar photovoltaic plug-and-play systems. Renew. Energy 2017, 103, 255–264. [Google Scholar] [CrossRef] [Green Version]
- Timilsina, G.R.; Kurdgelashvili, L.; Narbel, P.A. Solar energy: Markets, economics and policies. Renew. Sustain. Energy Rev. 2012, 16, 449–465. [Google Scholar] [CrossRef]
- Bouchakour, S.; Valencia-Caballero, D.; Luna, A.; Roman, E.; Boudjelthia, E.; Rodríguez, P. Modelling and Simulation of Bifacial PV Production Using Monofacial Electrical Models. Energies 2021, 14, 4224. [Google Scholar] [CrossRef]
| Year | sAP (mm) | τAP (°) | ρAP (°) |
|---|---|---|---|
| 2013–2014 | 98 | 18 | −5 |
| 2014–2015 | 121 | 27 | −10 |
| 2015–2016 | ∞ | 41 | −20 |
| 2016–2017 | 219 | 37 | −20 |
| 2017–2018 | 104 | 21 | −15 |
| GCD (USD/(a·m2)) | GCD/GVD | sAP (mm) | τAP (°) | νVG (°) | sUG (mm) |
|---|---|---|---|---|---|
| 0 | 0 | 30 | 34 | 31 | 76.2 |
| 0.5 | 0.062 | 62 | 9 | 68 | 228.6 |
| 1 | 0.124 | 74 | 1 | 128 | 609.6 |
| 1.5 | 0.186 | 75 | 1 | 140 | ≥762 |
| 2 | 0.248 | 76.2 | 0 | 144 | >7620 |
| 2.5 | 0.31 | 76.2 | 0 | 148 | >7620 |
| 3 | 0.372 | 76.2 | 0 | 152 | >7620 |
| 3.5 | 0.434 | 76.2 | 0 | 154 | >7620 |
| 4 | 0.496 | 76.2 | 0 | 156 | >7620 |
| 4.5 | 0.558 | 77 | 2 | 156 | >7620 |
| 5 | 0.62 | 79 | 5 | 160 | >7620 |
| 5.5 | 0.682 | 82 | 8 | 160 | >7620 |
| 6 | 0.744 | 86 | 11 | 162 | >7620 |
| 6.5 | 0.806 | 93 | 15 | 164 | >7620 |
| 7 | 0.868 | 103 | 19 | 180 | >7620 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Boivin, A.B.; Holzman, J.F. Generated Value of Electricity Versus Incurred Cost for Solar Arrays under Conditions of High Solar Penetration. Solar 2021, 1, 4-29. https://doi.org/10.3390/solar1010003
Boivin AB, Holzman JF. Generated Value of Electricity Versus Incurred Cost for Solar Arrays under Conditions of High Solar Penetration. Solar. 2021; 1(1):4-29. https://doi.org/10.3390/solar1010003
Chicago/Turabian StyleBoivin, Adrian B., and Jonathan F. Holzman. 2021. "Generated Value of Electricity Versus Incurred Cost for Solar Arrays under Conditions of High Solar Penetration" Solar 1, no. 1: 4-29. https://doi.org/10.3390/solar1010003
APA StyleBoivin, A. B., & Holzman, J. F. (2021). Generated Value of Electricity Versus Incurred Cost for Solar Arrays under Conditions of High Solar Penetration. Solar, 1(1), 4-29. https://doi.org/10.3390/solar1010003