Foundations and Clinical Applications of Fractal Dimension in Neuroscience: Concepts and Perspectives

Abstract

Fractal geometry offers a mathematical framework to quantify the complexity of brain structure and function. The fractal dimension (FD) captures self-similarity and irregularity across spatial and temporal scales, surpassing the limits of traditional Euclidean metrics. In neuroscience, FD serves as a key descriptor of the brain’s hierarchical organization—from dendritic arborization and cortical folding to neural dynamics measured by diverse neuroimaging techniques. This review summarizes theoretical foundations and methodological advances in FD estimation, including the box-counting approach for imaging, and Higuchi’s and Katz’s algorithms for electrophysiological data, addressing reliability and reproducibility issues. In addition, we illustrate how fractal analysis characterizes brain complexity in health and disease. Clinical applications include detecting white matter alterations in multiple sclerosis, atypical maturation in intrauterine growth restriction, reduced cortical complexity in Alzheimer’s disease, and altered neuroimaging patterns in schizophrenia. Emerging evidence highlights FD’s potential for distinguishing consciousness states and quantifying neural integration and differentiation. Bridging mathematics, physics, and neuroscience, fractal analysis provides a quantitative lens on the brain’s multiscale organization and pathological deviations. FD thus stands as both a theoretical descriptor and a translational biomarker whose standardization could advance precision diagnostics and understanding of neural dynamics.

1. Introduction

Fractal geometry, introduced by Benoit Mandelbrot in the 1970s and 1980s, provides a mathematical framework for characterizing irregular and self-similar patterns in natural objects [1,2]. This approach represents a fundamental departure from classical Euclidean geometry, which describes natural forms using smooth, whole-integer dimensions. In contrast, fractal dimension (FD) is not limited to integers and serves as a measure of morphometric complexity that captures how structural features change across spatial scales [3]. The FD quantifies the degree to which a complex pattern fills the space it occupies, with higher FD values indicating greater structural complexity and irregularity. This mathematical framework has proven particularly insightful for analyzing biological systems that exhibit statistical self-similarity and scaling properties, leading to the emergence of fractal analysis as a universal tool across biomedical sciences [4,5].

The human brain exemplifies a complex system characterized by hierarchical organization and topological complexity across multiple scales, from neurons and microcircuits to macronetworks [6]. This multi-scale organization gives rise to the brain’s remarkable functional and structural complexity, which traditional Euclidean measures often fail to adequately capture. Fractal analysis has emerged as a powerful tool for quantifying this complexity in both structural neuroanatomy and functional neurophysiology, enabling researchers to measure scaling properties inherent to neurological systems across micro-, meso-, and macroscales [6]. Applications of FD in neuroscience span diverse domains, including the analysis of cortical folding patterns, white matter microarchitecture, dendritic arborization, and neurophysiological time series. It has been demonstrated that fractal geometry can quantify shape complexity changes associated with aging and various neurodegenerative diseases including multiple sclerosis (MS), Alzheimer’s disease, Parkinson’s disease, and Huntington’s disease, among others [6].

Despite the growing adoption of FD in neuroscience, its use remains methodologically heterogeneous and conceptually fragmented across structural neuroimaging, neurophysiology, and theoretical modeling [7]. Differences in FD estimation methods, preprocessing pipelines, scale selection, and validation strategies have limited cross-study comparability and hindered the consolidation of FD as a robust and interpretable biomarker [8,9]. In parallel, biological interpretations of FD alterations often remain modality-specific, with limited integration across cellular, structural, and dynamical levels of brain organization [10]. As a result, the translational potential of FD measures—particularly for diagnosis, prognosis, and monitoring across neurological and psychiatric conditions—has yet to be fully realized.

This review synthesizes current knowledge on FD estimation methods, their validation and reliability across different imaging modalities and signal types, and clinical applications spanning consciousness research, cognitive dynamics, neurodevelopment, and neurodegenerative diseases. We examine how FD serves as a bridge connecting mathematical theory, physical principles, and neuroscientific inquiry, offering a quantitative framework for characterizing brain complexity that transcends traditional morphometric approaches. By integrating methodological advances with clinical findings, we aim to evaluate the potential of FD as a robust biomarker of brain complexity and outline future directions for translating fractal analysis into clinical practice and neuroscientific discovery.

Accordingly, this review is guided by the following research questions:

(1)

How do different FD estimation methods and methodological choices influence the interpretation and comparability of FD across neuroimaging and neurophysiological modalities?

(2)

What consistent patterns of FD alteration emerge across neurodevelopmental, neurodegenerative, and consciousness-related conditions, and how do these relate to underlying biological mechanisms?

(3)

To what extent can FD serve as a unifying multiscale biomarker bridging empirical measurements with theoretical models of brain dynamics and information integration?

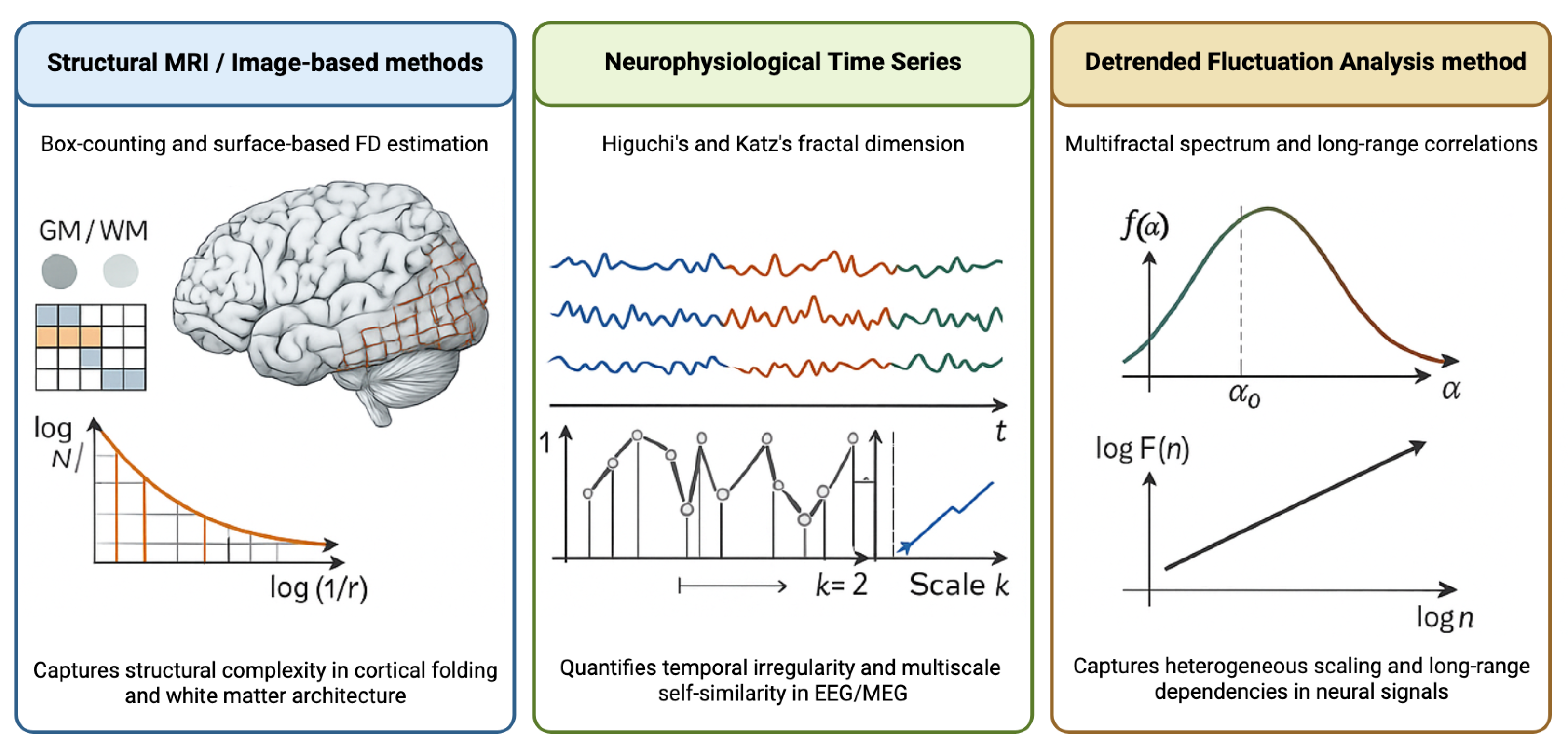
2. Methodological Foundations

Fractal analysis has emerged as a valuable approach for characterizing cortical complexity by quantifying the geometric properties of gray matter and white matter structures in magnetic resonance imaging (MRI) data [4]. The FD captures aspects of cortical architecture including folding patterns, gyrification, and thickness that conventional volumetric measures may not fully represent, providing complementary information about brain morphology [4,6]. For clarity and practical guidance,

Table 1. Comparison of Major FD Estimation Methods.

Method	Computational Approach	Advantages	Disadvantages	Typical Applications
Box-counting	Progressive grid refinement with nonempty box counting; slope from log N vs. log(1/r) plot	Intuitive implementation; applicable to 2D and 3D data; widely validated	Sensitive to image resolution and thresholding; requires careful scale range selection	Structural MRI analysis; cortical folding; white matter complexity
Higuchi’s FD	Time-domain curve length calculation at multiple temporal scales	No frequency transformation required; handles nonstationary signals; computationally efficient	Parameter selection affects estimates; sensitive to signal-to-noise ratio	EEG/MEG time series; neurophysiological dynamics; cognitive task analysis
Katz’s FD	Ratio of signal length to diameter using Euclidean distance	Fast computation; single-scale estimate; minimal parameters	Less sensitive to subtle complexity changes; limited scale information	Rapid clinical screening; real-time EEG monitoring; preliminary complexity assessment

EEG: electroencephalography; FD: fractal dimension; MEG: magnetoencephalography; MRI: magnetic resonance imaging.

provides a concise comparative overview of the main FD estimation methods, summarizing their computational principles, strengths, limitations, and typical neuroscience applications, thereby facilitating method selection depending on data modality and research goals.

The box-counting method represents the most widely used approach for FD estimation in brain imaging, providing a systematic framework for quantifying morphological complexity [6,11]. This technique divides the Euclidean space containing the image into a grid of boxes of size r, which is progressively reduced while counting the number of nonempty boxes (N) that cover the object at each scale (see figures at [11]). The FD is derived from the slope of the log-log plot of ln N versus ln (1/r), with steeper slopes indicating greater structural complexity. In practical neuroimaging applications, images undergo preprocessing including binary conversion through full-range thresholding to exclude background pixels (typically intensity selection from 1 to 255), and optionally skeletonization algorithms that reduce structures to their topological core while preserving connectivity patterns [11].

Three-dimensional FD computation from volumetric MRI data has advanced significantly through specialized software implementations that perform box-counting on entire brain volumes rather than individual slices [12]. Modern algorithms incorporate automated procedures for optimal scale range selection, addressing a critical challenge in FD estimation where inappropriate box size ranges can introduce systematic bias. As has been previously demonstrated [8], validation using mathematical solids with analytically known FD values confirms the accuracy of these implementations, while empirical assessments reveal that FD estimates are sensitive to image acquisition parameters and preprocessing choices. Importantly, scale optimization procedures can substantially improve estimation accuracy, and studies demonstrate that FD differences between scans do not simply track structural differences per se, suggesting that structural complexity and structural similarity represent distinct aspects of brain morphometry [8].

For neurophysiological time series, Higuchi’s FD (HFD) provides a nonlinear measure that quantifies complexity directly in the temporal domain without requiring transformation into the frequency domain [13]. This method evaluates self-similarity and irregularity of signals over multiple temporal scales, making it particularly well-suited for nonstationary data such as electroencephalography (EEG) recordings as we applied elsewhere [14]; the technique calculates average curve lengths at different time intervals to determine the scaling relationship that characterizes the signal’s fractal properties.

Beyond traditional fractal metrics, advanced scaling analyses have gained attention as complementary frameworks for characterizing the heterogeneous scale-free behavior of brain signals and structures. Unlike conventional FD estimates, which assume uniform self-similarity across scales, these approaches quantify a spectrum of scaling exponents, thereby capturing local variations in complexity that may reflect region-specific or state-dependent neural dynamics. In neurophysiology, detrended fluctuation analysis (DFA) provides a robust method for assessing long-range temporal correlations in EEG and functional magnetic resonance imaging (fMRI) time series, identifying power-law relationships that are conceptually linked to fractal organization. Studies applying DFA to neuronal activity have revealed that healthy brain dynamics operate near a critical regime where fluctuations exhibit scale invariance, whereas neurological and psychiatric disorders frequently show a loss of this property [15].

Incorporating this framework thus enriches the fractal characterization of neural signals, extending beyond global FD estimates to capture the dynamic variability of complexity across scales and brain regions. An overview of the main FD estimation methods in neuroscience is shown in Figure 1.

Rigorous methodological evaluation has established that FD demonstrates superior psychometric properties compared to conventional structural neuroimaging measures (see below), with formal assessments documenting higher test–retest reliability and enhanced robustness to head motion-related artifacts (as reviewed in [16]). These characteristics position FD as particularly valuable for longitudinal investigations tracking structural changes over time and for clinical research involving populations where excessive head motion represents a significant confound, including pediatric samples, elderly individuals, and patients with movement disorders or cognitive impairment. The enhanced stability of FD measures across repeated acquisitions suggests that this metric captures fundamental aspects of brain architecture that remain consistent despite technical variability, potentially reflecting intrinsic organizational principles less susceptible to measurement noise than volumetric or thickness-based indices.

Despite these favorable properties, substantial evidence indicates that image acquisition protocols and processing pipelines exert significant influence on FD estimates, creating potential heterogeneity across studies that may limit direct comparisons [17,18,19]. Critical methodological factors affecting FD computation include segmentation algorithms, spatial resolution, tissue compartment selection, and registration approaches [17,20]. Empirical investigations reveal that differences in FD between scans do not simply track structural differences per se, indicating that structural complexity and structural similarity represent distinct aspects of brain morphometry [8]. Scale optimization is therefore crucial, as automated procedures for box-size selection substantially improve estimation accuracy [8]. Validation studies using mathematical phantoms with known FD values confirm that adaptive scale selection yields more accurate and robust measurements [8].

Computational efficiency considerations have driven the development of advanced implementation strategies for three-dimensional FD calculation from volumetric neuroimaging data. GPU-accelerated algorithms leveraging CUDA parallel processing architectures dramatically reduce computation time for large datasets, enabling practical application to high-resolution whole-brain volumes and facilitating analysis of extensive cohorts [21]. Web-based platforms further extend accessibility by providing cloud-based calculation and interactive visualization capabilities, allowing researchers without specialized computational infrastructure to perform fractal analyses [21]. These technological advances democratize FD analysis while maintaining the computational rigor necessary for clinical translation. A summary of best practices for FD estimation in neuroimaging is presented in Appendix A.

3. Structural Neuroimaging Applications

During normal brain development and aging, FD exhibits systematic trajectories that reflect underlying structural complexity alterations across the lifespan (as reviewed in [16]). Recent large-scale investigations have documented a monotonic reduction in cortical structural complexity with advancing age, observable from early development through late adulthood (see also [16]). Machine learning models incorporating FD as a predictive feature achieve accurate individual age estimation in large cohorts, with performance critically dependent on optimal selection of spatial scale intervals for FD computation. These findings underscore the importance of methodological refinement in fractal analysis and demonstrate that white matter complexity measured by FD shows reliable alterations during healthy aging, positioning FD as a valuable biomarker for identifying structural changes in brain tissue. Regional analyses further reveal heterogeneous aging patterns across cortical territories, with accelerated FD reduction evident in orbitofrontal cortex regions during the transition from young to middle age and in occipital lobe areas progressing from middle to old age [16].

Sex differences in age-related FD trajectories have been documented, with males exhibiting faster and more significant reductions in cortical complexity compared to females [reviewed in 16]. Large-scale population studies, including analyses based on data from the UK Biobank, further confirm differential patterns of age-related changes in cortical FD according to sex, with relatively more cortical regions affected by aging in males [22]. Extending these observations across the lifespan, it has been demonstrated that cortical FD follows regionally heterogeneous, nonlinear age trajectories that also differ between sexes, underscoring that male and female brains follow distinct nonlinear patterns of complexity changes across development and aging [23,24]. These findings indicate differential vulnerability patterns in brain structural complexity across the lifespan and suggest that sex-specific normative trajectories may be necessary for accurate interpretation of FD as a clinical biomarker [16]. Longitudinal studies corroborate cross-sectional observations, consistently revealing negative relationships between FD and age, further validating the utility of fractal analysis for tracking brain structural changes over time [17,25].

FD analysis has also emerged as a sensitive tool for detecting cerebral changes in preterm infants, particularly those affected by intrauterine growth restriction (IUGR). Applying three-dimensional FD computation to segmented gray matter and white matter structures [26] reveals that IUGR infants exhibit significantly reduced morphological complexity compared to term controls when assessed at 12 months corrected age. Quantitative measurements demonstrate lower FD values in both non-skeletonized and skeletonized tissue compartments, with particularly pronounced reductions observed in skeletonized white matter structures [26]. Importantly, these complexity differences persist even after statistical adjustment for total brain volume, indicating that FD captures distinct architectural features of brain organization that extend beyond simple volumetric measurements [26]. This finding underscores the value of fractal analysis as a complementary morphometric approach that may reveal subtle neurodevelopmental alterations not detectable through conventional volumetric methods alone.

The clinical significance of reduced structural complexity in IUGR populations is supported by correlations between FD measures and neurodevelopmental outcomes assessed using standardized batteries. Multiple regression analyses incorporating gray matter FD values identify significant associations with language function, receptive communication abilities, and motor performance domains [26]. These predictive relationships suggest that fractal measures obtained during infancy may serve as early biomarkers for subsequent neurodevelopmental trajectories and cognitive outcomes. The observed pattern of decreased cortical complexity in IUGR infants is hypothesized to reflect underlying pathophysiological processes including impaired cortical convolution and regionally specific volume deficits, with particular vulnerability evident in frontal lobe territories critical for attention control and executive functions [26]. This neuroanatomical substrate aligns with longitudinal observations documenting attention deficits, executive dysfunction, and behavioral challenges in IUGR children during later developmental stages, providing a mechanistic framework linking early structural alterations to long-term functional outcomes. The application of fractal analysis to neurodevelopmental populations thus offers promise for early risk stratification and targeted intervention strategies in vulnerable infant populations [27].

Beyond conventional MRI-based FD applications, emerging work has explored the utility of fractal analysis in diffusion MRI, particularly in tractography and diffusion tensor imaging (DTI) [28,29]. In these studies, FD has been applied to characterize the complexity of white matter fiber tracts, with the aim of quantifying the organization and integrity of neural pathways. Furthermore, advanced microstructural diffusion metrics, such as fractional anisotropy (FA) and mean diffusivity (MD), have been combined with FD to explore the relationship between structural connectivity and neural function [30]. This area of research is still evolving, but it holds promise for enhancing the precision of diffusion MRI in studying white matter diseases and developmental disorders.

From a translational perspective, FD measures provide complementary diagnostic and prognostic information beyond conventional volumetric indices. In neurodevelopmental contexts, reduced FD captures altered cortical and white matter organization that correlates with later cognitive and motor outcomes, supporting its potential use for early risk stratification. Across aging, FD trajectories enable individualized characterization of structural decline and may serve as sensitive markers for distinguishing normative aging from pathological processes.

4. Neurodegenerative Disorders

Neurodegenerative disorders have been repeatedly associated with changes in fractal dimensionality [18] (

Table 2. Fractal dimension (FD) alterations across neurodegenerative diseases.

Disease	Affected Tissue	Direction of FD Change	Brain Regions	Clinical Correlations	Study Characteristics
Multiple sclerosis	White matter border	Decreased	Whole brain, NAWM	Lesion volume; early disease detection	Early to intermediate stages; detects diffuse damage
	Gray matter	Increased	Whole brain, GM	T1/T2 lesion load; disease subtype	RRMS and CIS patients; correlates with pathology extent
Alzheimer’s disease	Cortical GM	Decreased	Hippocampus, temporal cortex	Cognitive decline; disease severity	Correlates with neuropsychological performance
Parkinson’s disease	Subcortical structures	Decreased	Basal ganglia, substantia nigra	Motor symptom severity; disease duration	Reflects neuronal loss and structural degeneration
Amyotrophic Lateral Sclerosis	Motor cortex	Decreased	Precentral gyrus, corticospinal tract	Functional impairment; progression rate	Tracks upper motor neuron degeneration
Huntington’s disease	Striatal structures	Decreased	Caudate, putamen	CAG repeat length; functional capacity	Detectable in pre-manifest carriers

CIS: Clinically Isolated Syndrome; GM: gray matter; NAWM: Normal-appearing white matter; RRMS: Relapsing-Remitting Multiple Sclerosis.

). Among these, multiple sclerosis represents a paradigmatic application of fractal analysis in neurodegeneration, as the disease is characterized by diffuse white matter damage extending beyond visible demyelinating plaques into normal-appearing white matter (NAWM) [11]. FD analysis has emerged as a sensitive tool for detecting these subtle structural alterations that conventional volumetric approaches may miss, providing a quantitative assessment of morphological complexity changes in brain tissue [11]. Investigations applying box-counting methods to MRI data reveal that patients with MS exhibit significantly decreased white matter border complexity compared to healthy controls, with measurable differences detected even in early disease stages [11]. Critically, FD reductions occur not only in image sections with visible lesions but also in single slices containing only NAWM [11], suggesting that fractal measures capture microscopic pathological changes including inflammatory cell infiltration, microglial activation, blood vessel sclerosis, and axonal disruption that precede macroscopic tissue damage detectable by standard imaging protocols. This capacity to quantify diffuse central nervous system damage positions FD as a potentially valuable marker for disease monitoring and therapeutic response assessment.

In contrast to white matter findings, gray matter FD demonstrates opposite directional changes in MS pathology, with patients showing increased gray matter complexity compared to controls [31]. Three-dimensional computational analyses reveal that these gray matter alterations correlate significantly with lesion volume on both T1 and T2 imaging sequences [31], indicating that FD reflects the spectrum of tissue damage across different disease subtypes and imaging modalities. Both relapsing-remitting MS and clinically isolated syndrome patients exhibit significant FD differences from healthy controls during early to intermediate disease stages [31], demonstrating the method’s sensitivity to pathological changes early in the disease trajectory when therapeutic interventions may be most effective.

The bidirectional nature of FD changes across tissue compartments suggests that fractal analysis captures distinct pathophysiological processes in gray and white matter, potentially reflecting differences in cellular architecture, inflammatory responses, and compensatory mechanisms that characterize MS progression and may predict long-term disability outcomes.

Alzheimer’s disease represents a prototypical application domain for fractal analysis in neurodegeneration, with consistent evidence documenting decreased FD reflecting reduced structural brain complexity associated with progressive neurodegenerative processes [16]. These FD reductions are detectable across multiple cortical features including hippocampal morphology and temporal cortex architecture, with the magnitude of complexity loss correlating significantly with disease severity and cognitive impairment [32,33]. Regional analyses reveal that FD decreases are not uniformly distributed but rather follow patterns consistent with the known spatial progression of Alzheimer’s pathology [18], suggesting that fractal measures capture meaningful aspects of disease-specific neuroanatomical changes.

Beyond structural applications, the concept of “fractal dimension of cognition” has emerged as a theoretical framework proposing that scale-invariant brain dynamics underlie fundamental mental processes (as reviewed in [6]). This perspective suggests that cognitive functions themselves exhibit fractal properties characterized by power-law scaling and self-similarity across temporal scales, with alterations in these fractal signatures potentially reflecting disruptions to the hierarchical organization of neural information processing in dementia.

Comparative methodological investigations demonstrate that FD analysis achieves superior sensitivity relative to conventional volumetric voxel-based morphometry for detecting subtle brain tissue changes characteristic of early Alzheimer’s disease [4]. This enhanced detection capability extends beyond simple group-level discrimination to enable identification of distinct clinical phenotypes within the Alzheimer’s spectrum and more precise tracking of longitudinal disease progression trajectories. The mechanistic basis for this increased sensitivity likely relates to FD’s capacity to quantify microstructural complexity alterations—including dendritic pruning, synaptic loss, and disrupted cytoarchitectural organization—that precede macroscopic volumetric changes detectable by traditional morphometric approaches.

Complementing brain imaging advances, retinal vascular fractal analysis has emerged as a promising noninvasive biomarker strategy for neurodegenerative disease assessment [16]. Systematic reviews synthesizing evidence across multiple studies indicate that reduced retinal vascular network complexity, quantified through decreased FD, associates with cerebral pathology and predicts long-term stroke mortality risk [34]. The retinal vasculature shares embryological origins and physiological characteristics with cerebral circulation, and microvascular complexity changes visible in the retina may reflect parallel pathological processes affecting cerebral perfusion and neuronal health [35]. This approach offers particular translational promise as a cost-effective screening tool accessible through standard ophthalmological examination protocols, potentially enabling earlier detection and monitoring of neurodegenerative processes before advanced cognitive decline manifests [36].

Beyond macroscopic neuroimaging measures, fractal analysis has been extensively applied to the quantitative characterization of microglial morphology [37]. Microglial cells and neurons are structurally and functionally intertwined within a dynamic cellular network, in which microglia exhibit rapid morphological plasticity on timescales much shorter than those of neurons. In their surveillant state, microglia display highly ramified, scale-invariant branching patterns that contribute, together with neuronal dendritic architectures, to the fractal topology underlying brain organization and computation. Upon activation, microglial processes progressively retract, giving rise to simplified or amoeboid morphologies associated with inflammatory responses. FD provides a robust quantitative descriptor of these transitions, with reduced FD generally reflecting loss of process complexity and increased pathological activation, while also capturing more subtle phenotypes such as hyper-ramification. In this context, fractal analysis complements traditional morphometric measures by offering a unified framework to characterize neuron–microglia structural dynamics in health and disease [37].

Clinically, FD alterations have demonstrated diagnostic utility for detecting early and diffuse neurodegenerative changes that precede overt volumetric loss, as well as prognostic relevance through correlations with lesion burden, cognitive impairment, and disease severity. These properties position FD as a promising tool for disease staging and longitudinal monitoring of progression or therapeutic response, complementing conventional MRI metrics.

5. Neurophysiology and Consciousness

Building on the methodological foundations outlined in Section 2, FD naturally extends beyond a descriptive metric to a theoretical construct that links empirical neuroimaging and neurophysiological data with models of brain dynamics. The same scaling principles captured by box-counting approaches in structural MRI and by Higuchi’s FD in electrophysiological time series provide a common mathematical language for characterizing attractor dynamics, network organization, and information integration in theoretical neuroscience.

FD analysis of neurophysiological signals has emerged as a powerful approach for quantifying the complexity of brain dynamics associated with different states of consciousness. Recent investigations, employing combined transcranial magnetic stimulation and high-density electroencephalography (TMS-EEG), demonstrate that FD-based metrics can reliably discriminate between conscious and unconscious states in healthy individuals [14]. The FD Index (FDI) represents a particularly promising composite measure that integrates spatiotemporal complexity through 4D-FD calculation with temporal variability quantified by Higuchi’s FD [14]. This dual-component approach captures both the spatial integration of thalamocortical networks activated by magnetic perturbation and the differentiation of evoked responses as they evolve over time. Empirical validation across 69 TMS-EEG measurements in 18 healthy subjects transitioning from wakefulness to non-rapid eye movement sleep and pharmacologically induced unconsciousness reveals that FDI achieves a receiver operating characteristic curve area of 0.966, positioning it as a highly accurate classifier [14]. The optimal cutoff value for discriminating consciousness from unconsciousness was established at 3.73, with systematic reductions in both structural complexity and temporal evolution patterns observed during loss of consciousness [14]. These findings align with theoretical frameworks proposing that conscious experience depends on the brain’s capacity to generate integrated yet differentiated patterns of neural activity, with FDI providing a quantitative proxy for this integrated information [14].

Recent theoretical work has expanded the link between fractal complexity and consciousness, proposing that the fractal organization of neural dynamics reflects the brain’s proximity to criticality, a regime that optimally balances integration and differentiation of information. In this framework, loss of fractal complexity corresponds to states of reduced consciousness (such as deep sleep, anesthesia, or coma), whereas increased or dysregulated complexity may accompany psychedelic or psychotic states. Varley and colleagues [38] provided an updated synthesis of this idea, suggesting that fractal patterns in brain activity constitute empirical markers of the brain’s dynamical landscape, bridging empirical findings with theories such as the Entropic Brain Hypothesis and Integrated Information Theory. Their work supports the view that fractality is not merely a mathematical descriptor, but a potential signature of consciousness and self-organization within neural systems.

Applications of fractal complexity analysis extend beyond healthy consciousness to reveal pathological alterations in psychiatric populations characterized by cognitive impairment. A study, examining EEG complexity during cognitive tasks in schizophrenia patients, documents abnormal dynamic modulation patterns that distinguish these individuals from healthy controls [39]. Specifically, patients exhibit less differentiated complexity profiles across distinct cognitive demands, showing similar overall complexity patterns during external attention tasks and memory-based processing that healthy individuals clearly distinguish. Temporal evolution analyses provide additional mechanistic insights, revealing that control participants demonstrate consistent regional patterns with higher complexity during attentional versus memory tasks, particularly evident in central, frontal, and parietal topographies. In contrast, schizophrenia patients display irregular and variable temporal dynamics lacking clear task-dependent modulation. These findings suggest fundamental impairments in the dynamic reconfiguration of neural complexity that normally supports flexible cognitive control, with disrupted sensory integration and attentional mechanisms underlying the reduced differentiation observed across mental states [39].

Beyond electrophysiological recordings, fractal and multifractal approaches have also been increasingly applied to functional MRI data to characterize the temporal complexity of large-scale brain dynamics.

Recent advances in fractal and scaling analyses of brain activity have increasingly emphasized the scale-free temporal organization of ongoing neural dynamics, characterized by long-range temporal correlations across multiple time scales. In this context, the above commented DFA and its multifractal extensions have proven particularly valuable for quantifying the temporal complexity of resting-state fMRI signals and electrophysiological oscillations [15]. These approaches extend traditional FD analyses by capturing scale-invariant amplitude modulation dynamics that are largely independent of time-averaged signal power, thereby providing complementary information about the functional organization of neuronal systems. By revealing scale-free dynamics and critical-like properties of brain activity, DFA-based and multifractal approaches may offer a more nuanced characterization of functional connectivity, network dynamics, and information integration than conventional spectral or correlation-based measures, in both healthy and diseased brains.

Additionally, alterations in temporal fractal dynamics of resting-state fMRI have been increasingly linked to changes in states of consciousness, highlighting the utility of fractal and complexity-based measures for probing dynamic neural systems under pharmacological and anesthetic modulation [40]. In particular, emerging experimental and clinical frameworks combining psychedelics and anesthesia suggest that changes in fractal complexity, entropy, and network dynamics may differentiate conscious from unconscious brain states and relate to therapeutic outcomes [40]. These approaches offer a promising avenue for disentangling neurobiological effects that are contingent on subjective experience from those that arise independently of conscious awareness, thereby providing a quantitative bridge between brain dynamics, consciousness, and clinical response.

In neurophysiology, FD-based measures offer translational value for objective assessment of consciousness states, prognosis in disorders of consciousness, and monitoring of state transitions under anesthesia or neuromodulation. Compared with traditional spectral measures, FD captures integrated spatiotemporal complexity, providing added value for individualized clinical decision-making.

6. Integration with Computational Neuroscience and Network Analysis

The integration of fractal analysis with computational neuroscience and network theory has revealed deep connections between brain complexity and the mathematical structures underlying neural dynamics. From a theoretical perspective, dynamical systems operating on complex neural networks can be characterized through their global attractors, which capture the asymptotic behavior of the system and appear to underlie fundamental brain functionality [41]. These attractors are commonly described as fractal sets, with their FD serving as an index of complexity typically associated with chaotic dynamics [14]. This mathematical framework provides a bridge between phenomenological measures of fractality derived from empirical data and the theoretical concept of “informational structures” proposed within integrated information theory, suggesting that fractal signatures in brain signals may reflect the complexity of information integration processes fundamental to consciousness and cognition. The characterization of attractors as fractal objects offers a continuous and dynamical approach to quantifying integrated information, positioning fractal analysis as a computational tool for testing predictions from theoretical neuroscience frameworks [14].

Connectomics research has particularly benefited from fractal-based computational approaches that extend beyond traditional network metrics to characterize the hierarchical organization of brain connectivity in disorders of consciousness as described above [38]. In addition, previous studies have stated that fractal analysis has proven more accurate than conventional volumetric methods for detecting white matter changes across diverse neurological conditions and for identifying distinct clinical phenotypes in diseases including amyotrophic lateral sclerosis, Alzheimer’s disease, multiple sclerosis, and epilepsy [4]. These developments have expanded the analytical toolkit available for investigating brain development, age-related changes, and pathological alterations in white matter architecture across the lifespan.

7. Limitations and Future Directions

Despite major advances, current applications of FD analysis in neuroscience remain limited by methodological and interpretative challenges. Existing FD metrics provide global indices of morphological or signal complexity but do not identify the specific cellular or molecular mechanisms—such as synaptic loss, dendritic pruning, or myelination changes—that underlie observed alterations [14]. Linking FD to defined biological processes through histological validation, multimodal imaging, or computational modeling would substantially enhance its mechanistic interpretability [16].

Another critical gap is the scarcity of longitudinal studies capable of tracing individual trajectories of brain complexity across development, aging, or disease, which constrains evaluation of FD’s prognostic and therapeutic potential [16]. Standardization of acquisition, segmentation, and scale-selection protocols is also urgently needed to improve reproducibility and enable meta-analytic synthesis across studies. Future research should assess FD as a biomarker of treatment response and integrate it with genetic, molecular, and connectivity data through advanced machine-learning models to enhance predictive power.

Finally, web-based analytical platforms for automated computation and quality control [21] will be essential for democratizing access to fractal analysis and achieving methodological consistency across the neuroscience community. Appendix B compiles current key open questions and promising research directions.

8. Conclusions

FD provides a unified and mathematically elegant framework for quantifying brain complexity across spatial and temporal scales, bridging microscopic cellular organization with macroscopic network dynamics. By capturing self-similar principles that recur across measurement levels, fractal analysis offers a common language linking dendritic and glial morphology, neuroimaging architecture, and neurophysiological activity within a coherent systems perspective.

Clinically, FD has demonstrated high sensitivity to pathological alterations across neurodevelopmental, neurodegenerative, and consciousness disorders, enabling early detection of subtle changes that precede volumetric or symptomatic manifestations and supporting longitudinal monitoring of disease trajectories and treatment responses. Consistent findings of reduced cortical and white matter complexity in conditions such as Alzheimer’s disease and multiple sclerosis underscore its translational value as a biomarker of neural integrity. Recent advances in automated computation, GPU acceleration, and cloud-based analytics are democratizing access to fractal tools while enhancing standardization and reproducibility.

Ultimately, the mathematical elegance of fractal geometry, combined with its growing empirical robustness, positions FD as a key quantitative bridge between theoretical and clinical neuroscience, deepening our understanding of the complex dynamics that underlie brain function in health and disease.