Analysis of an SVEIR with Reinfection Model of Tuberculosis Disease Spread with Saturated Infected Rate and Imperfect Vaccination
Abstract
1. Introduction
2. Model and Methods
3. Mathematical Model Analysis
3.1. Positivity of Solutions
3.2. Invariant Region
3.3. Disease-Free Equilibrium (DFE)
3.4. Effective Reproduction Number
3.5. Local Stability of DFE
3.6. Global Stability of DFE
3.7. Endemic Equilibrium
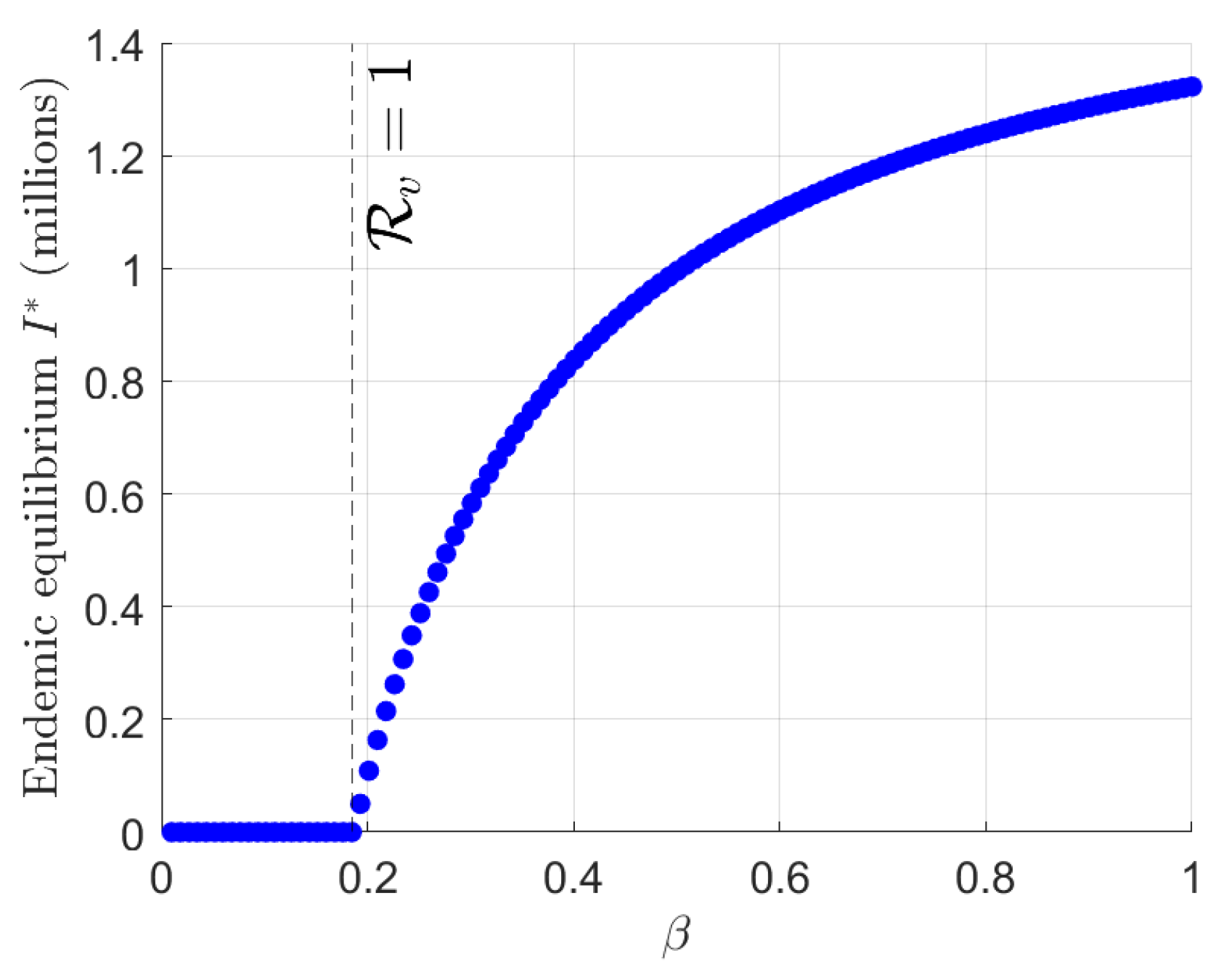
3.8. Bifurcation Analysis
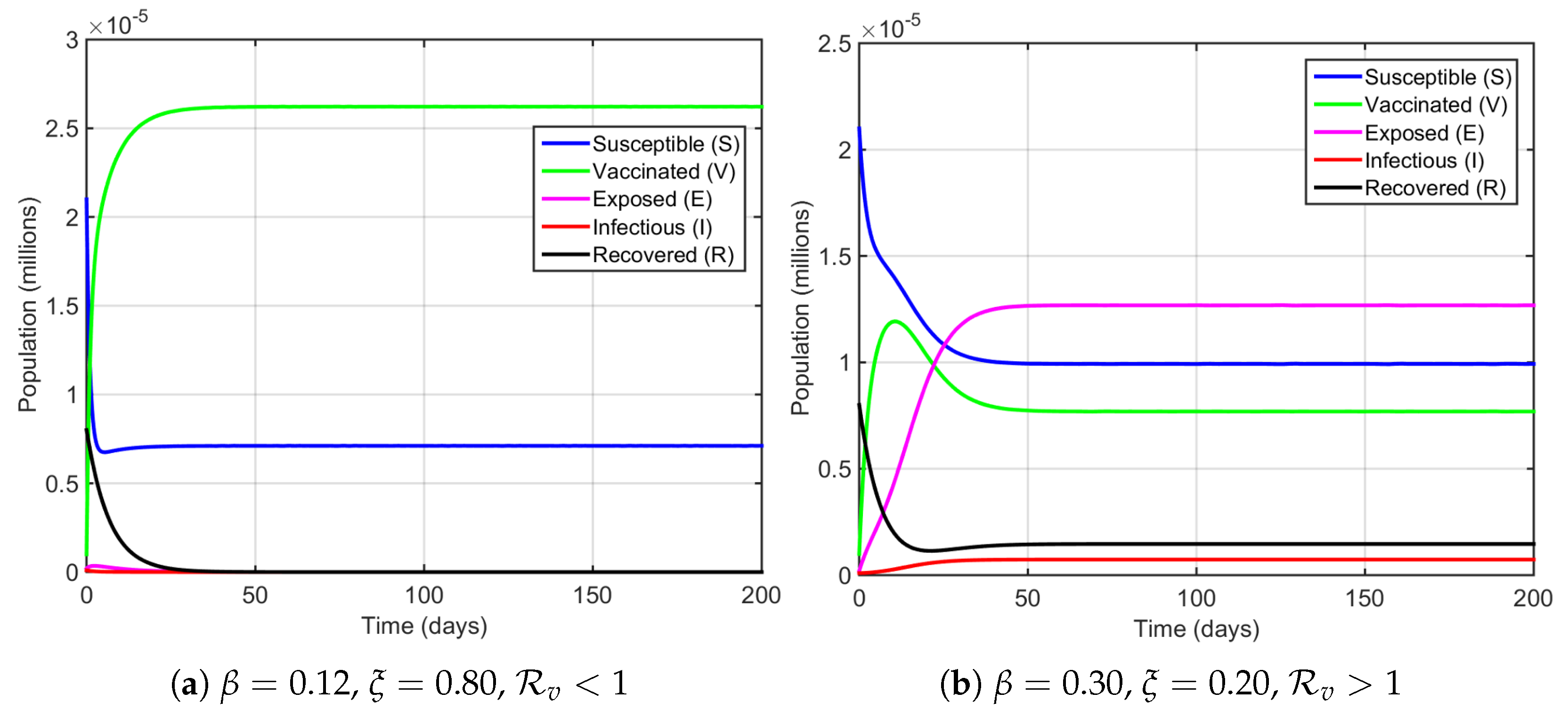
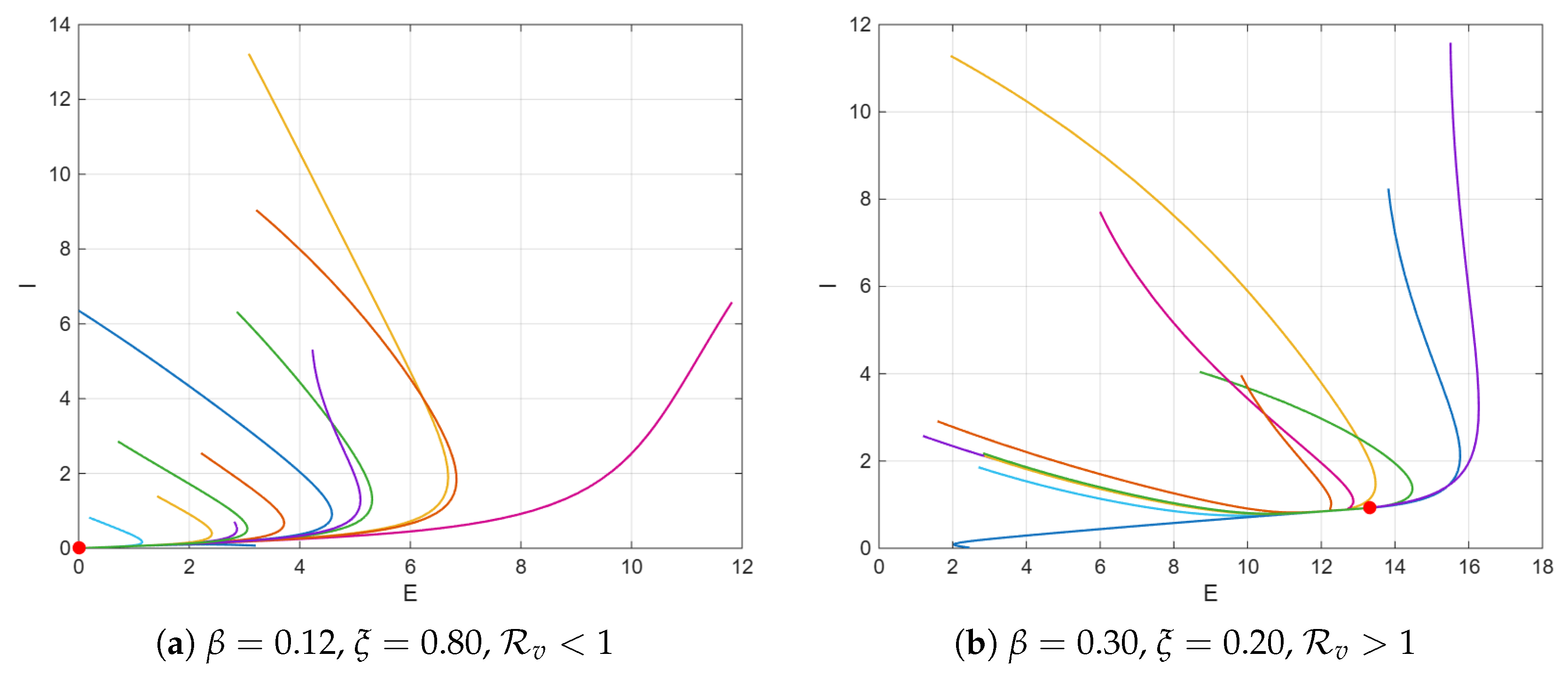
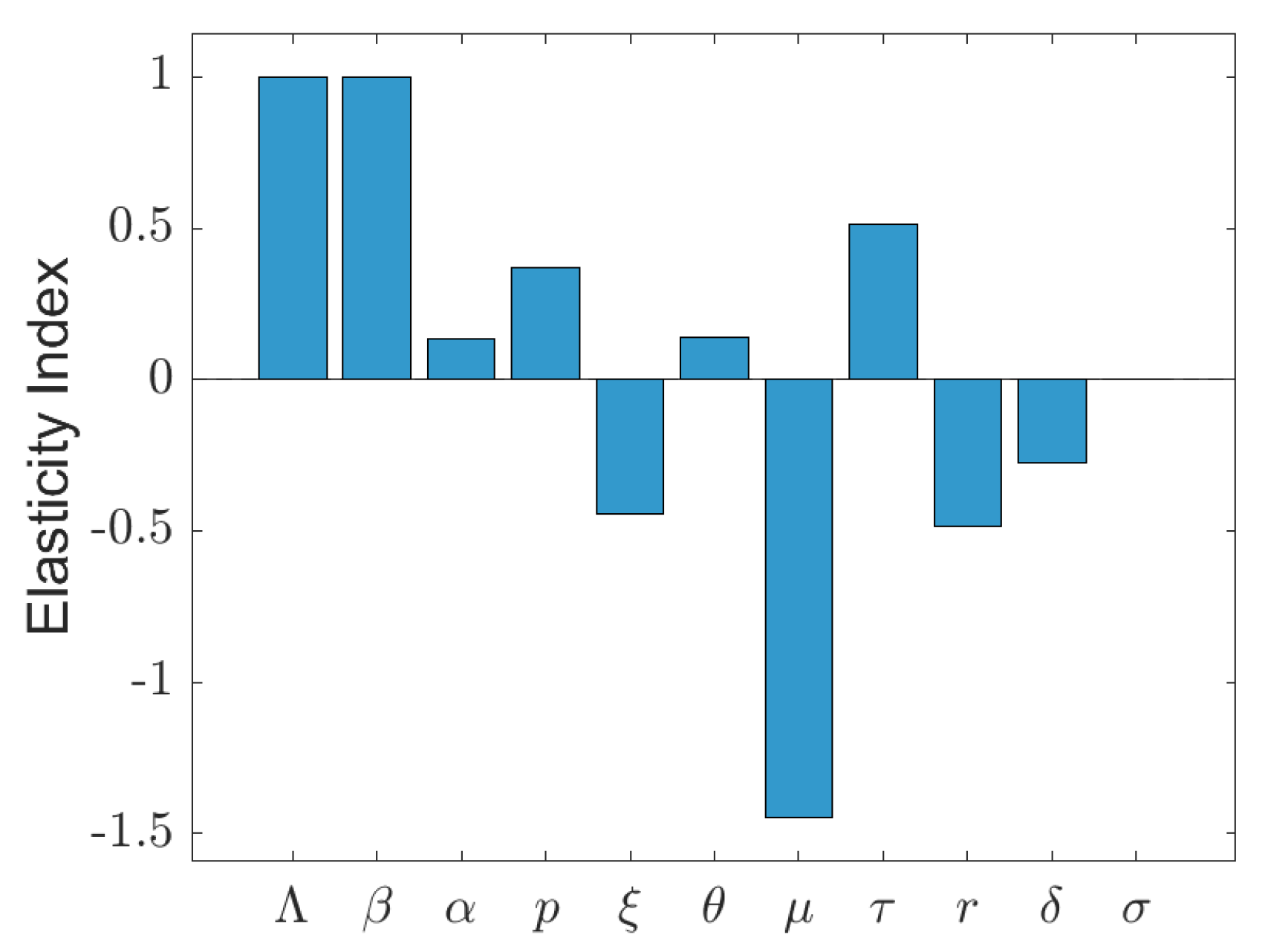
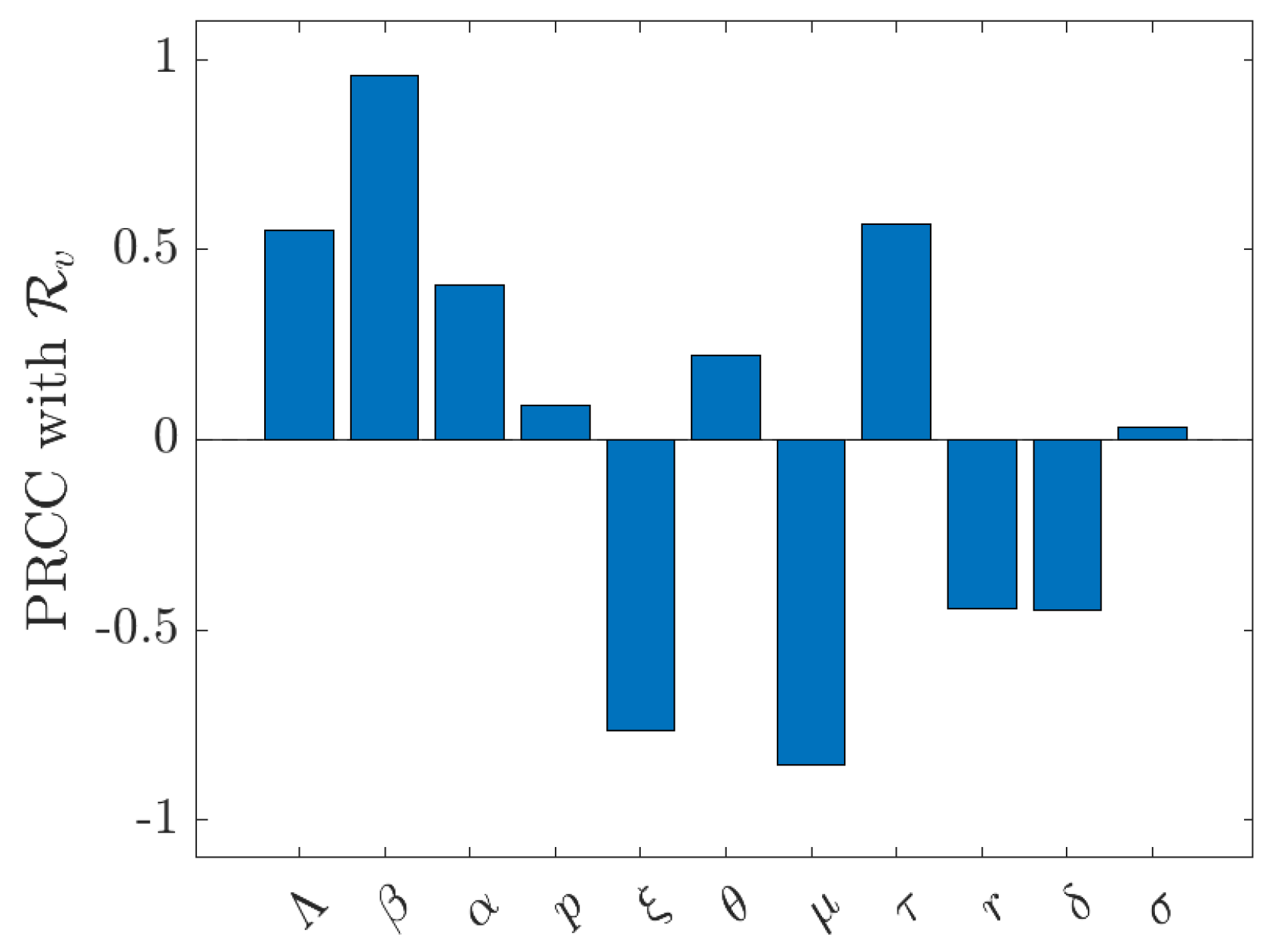
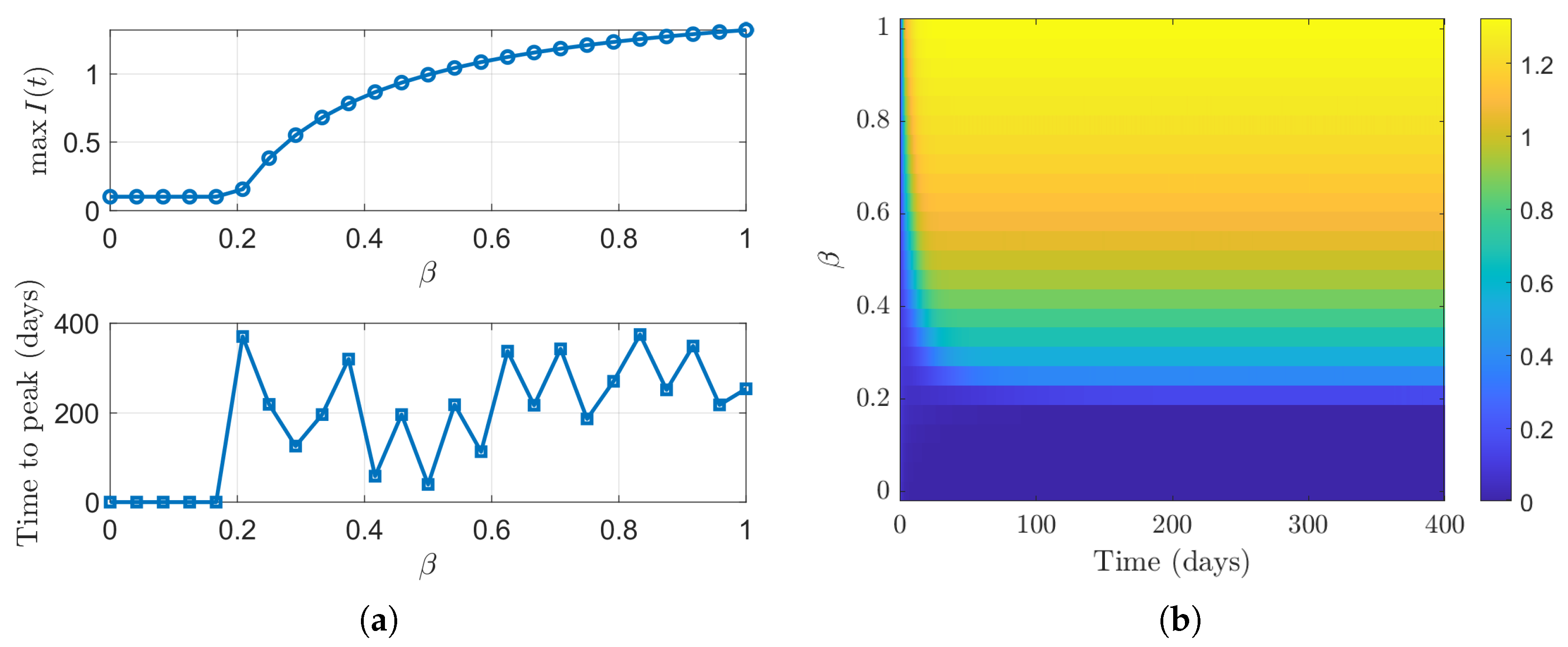
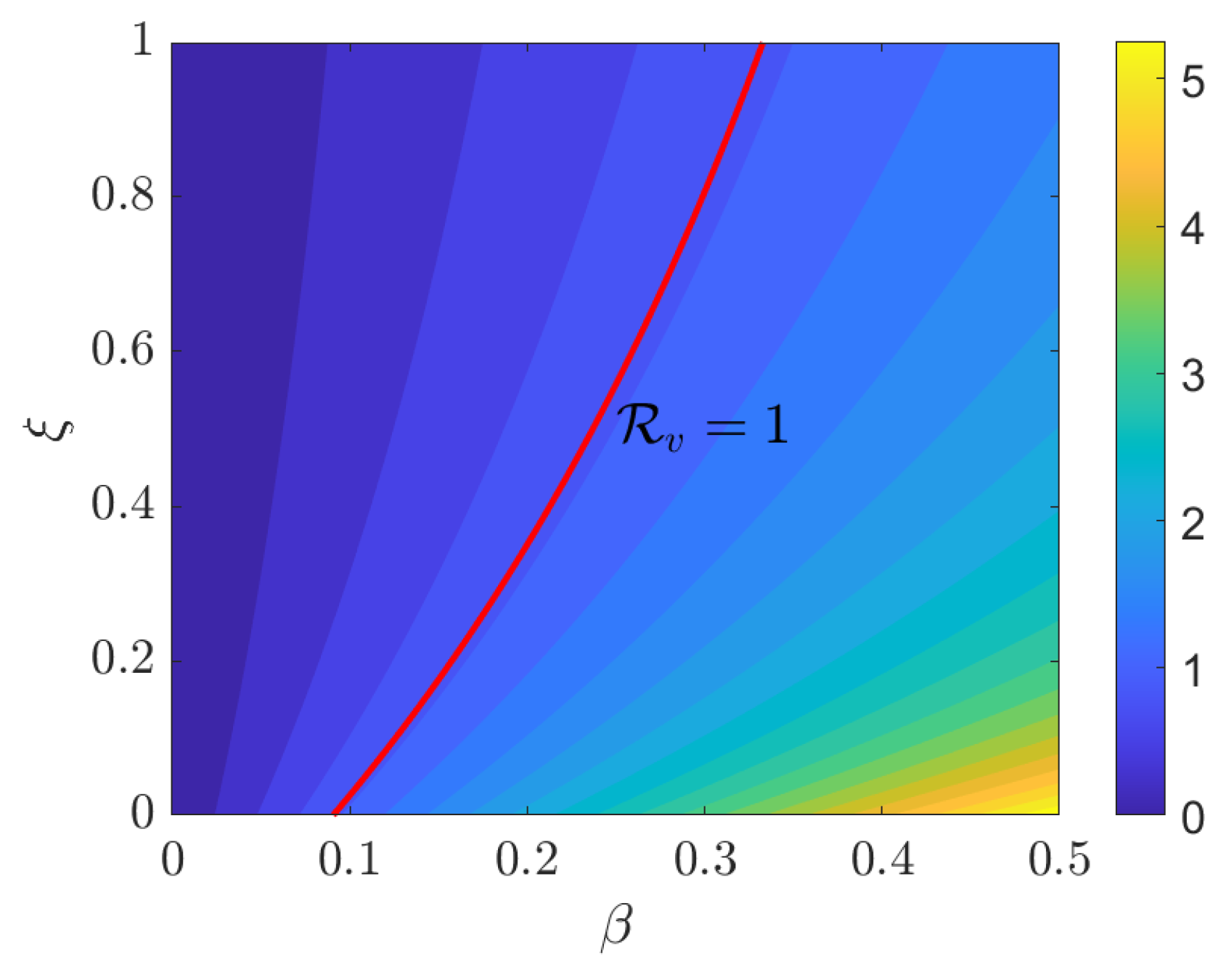
4. Numerical Simulations
5. Discussion
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| SVEIR | Susceptible–Vaccinated–Exposed–Infected–Recovered |
| SVEIL | Susceptible–Vaccinated–Exposed–Infected–Low-risk latent |
| TB | Tuberculosis |
| WHO | World Health Organization |
| BCG | Bacillus Bacillus Calmette–Guérin |
| EPI | Expanded Program on Immunization |
| ODE | Ordinary Differential Equation |
| DFE | Disease-Free Equilibrium |
| EE | Endemic Equilibrium |
| NGM | Next-Generation Matrix |
| PRCC | Partial Rank Correlation Coefficient |
Appendix A. Detailed Algebraic Derivations
Appendix A.1. The Calculation of Effective Reproduction Number ()
Appendix A.2. Proof of Local Stability of DFE in Theorem 3
- ,
- ,
- .
Appendix A.3. Proof of Global Stability of DFE in Theorem 4
Appendix A.4. Proof of Forward Bifurcation in Theorem 6
References
- Whang, S.; Choi, S.; Jung, E. A dynamic model for tuberculosis transmission and optimal treatment strategies in South Korea. J. Theor. Biol. 2011, 279, 120–131. [Google Scholar] [CrossRef]
- Peter, O.J.; Aldila, D.; Ayoola, T.A.; Balogun, G.B.; Oguntolu, F.A. Modeling tuberculosis dynamics with vaccination and treatment strategies. Sci. Afr. 2025, 28, e02647. [Google Scholar] [CrossRef]
- World Health Organization. Global Tuberculosis Report 2018; World Health Organization: Geneva, Switzerland, 2018; Available online: https://www.who.int/publications-detail-redirect/9789241565646 (accessed on 29 August 2025).
- Sulayman, F.; Abdullah, F.A.; Mohd, M.H. An SVEIRE model of tuberculosis to assess the effect of an imperfect vaccine and other exogenous factors. Mathematics 2021, 9, 327. [Google Scholar] [CrossRef]
- Harris, R.C.; Sumner, T.; Knight, G.M.; White, R.G. Systematic review of mathematical models exploring the epidemiological impact of future TB vaccines. Hum. Vaccin. Immunother. 2016, 12, 2813–2832. [Google Scholar] [CrossRef]
- Brennan, M.J.; Stone, M.R.; Evans, T. A rational vaccine pipeline for tuberculosis. Int. J. Tuberc. Lung Dis. 2012, 16, 1566–1573. [Google Scholar] [CrossRef] [PubMed]
- Fuller, N.M.; McQuaid, C.F.; Harker, M.J.; Weerasuriya, C.K.; McHugh, T.D.; Knight, G.M. Mathematical models of drug-resistant tuberculosis lack bacterial heterogeneity: A systematic review. PLoS Pathog. 2024, 20, e1011574. [Google Scholar] [CrossRef]
- Wu, Y.; Huang, M.; Wang, X.; Li, Y.; Jiang, L.; Yuan, Y. The prevention and control of tuberculosis: An analysis based on a tuberculosis dynamic model derived from the cases of Americans. BMC Public Health 2020, 20, 1173. [Google Scholar] [CrossRef] [PubMed]
- Ahmad, Y.U.; Andrawus, J.; Ado, A.; Maigoro, Y.A.; Yusuf, A.; Althobaiti, S.; Mustapha, U.T. Mathematical modeling and analysis of human-to-human monkeypox virus transmission with post-exposure vaccination. Model. Earth Syst. Environ. 2024, 10, 2711–2731. [Google Scholar] [CrossRef]
- Rajan, P.K.; Kuppusamy, M.; Yusuf, A. A fractional-order modeling of human papillomavirus transmission and cervical cancer. Model. Earth Syst. Environ. 2024, 10, 1337–1357. [Google Scholar] [CrossRef]
- Öztürk, B.A.; Yusuf, A.; Inc, M. Fractional HIV infection model described by the Caputo derivative with real data. Bol. Soc. Mat. Mex. 2024, 30, 1–23. [Google Scholar] [CrossRef]
- Al-Shomrani, M.M.; Musa, S.S.; Yusuf, A. Unfolding the transmission dynamics of monkeypox virus: An epidemiological modeling analysis. Mathematics 2023, 11, 1121. [Google Scholar] [CrossRef]
- Lee, S.; Park, H.-Y.; Ryu, H.; Kwon, J.-W. Age-specific mathematical model for tuberculosis transmission dynamics in South Korea. Mathematics 2021, 9, 804. [Google Scholar] [CrossRef]
- Saber, S.; Dridi, B.; Alahmari, A.; Messaoudi, M. Hyers–Ulam stability and control of fractional glucose–insulin systems. Eur. J. Pure Appl. Math. 2025, 18, 6152. [Google Scholar] [CrossRef]
- Alhazmi, M.; Saber, S. Application of a fractal–fractional derivative with a power-law kernel to the glucose–insulin interaction system based on Newton’s interpolation polynomials. Fractals 2025. [Google Scholar] [CrossRef]
- Trauer, J.M.; Denholm, J.T.; McBryde, E.S. Construction of a mathematical model for tuberculosis transmission in highly endemic regions of the Asia-Pacific. J. Theor. Biol. 2014, 358, 74–84. [Google Scholar] [CrossRef]
- Qiu, Z.; Feng, Z. Transmission dynamics of an influenza model with vaccination and antiviral treatment. Bull. Math. Biol. 2010, 72, 1–33. [Google Scholar] [CrossRef]
- Ahmad, S.; Pak, S.; Rahman, M.U.; Al-Bossly, A. On the analysis of a fractional tuberculosis model with the effect of an imperfect vaccine and exogenous factors under the Mittag–Leffler kernel. Fractal Fract. 2023, 7, 526. [Google Scholar] [CrossRef]
- Nandi, T.R.; Saha, A.K.; Roy, S. Analysis of a fractional order epidemiological model for tuberculosis transmission with vaccination and reinfection. Sci. Rep. 2024, 14, 28290. [Google Scholar] [CrossRef] [PubMed]
- Saputra, H.L.; Darti, I.; Suryanto, A. Analysis of SVEIL model of tuberculosis disease spread with imperfect vaccination. J. Teor. Apl. Mat. 2023, 7, 125–135. [Google Scholar] [CrossRef]
- Zhang, J.; Jia, J.; Song, X. Analysis of an SEIR epidemic model with saturated incidence and saturated treatment function. Sci. World J. 2014, 2014, 910421. [Google Scholar] [CrossRef] [PubMed]
- Baba, I.A.; Abdulkadir, R.A.; Esmaili, P. Analysis of tuberculosis model with saturated incidence rate and optimal control. Phys. A Stat. Mech. Appl. 2020, 540, 123237. [Google Scholar] [CrossRef]
- Bentaleb, D.; Harroudi, S.; Amine, S.; Allali, K. Analysis and optimal control of a multistrain SEIR epidemic model with saturated incidence rate and treatment. Differ. Equ. Dyn. Syst. 2023, 31, 907–923. [Google Scholar] [CrossRef]
- Capasso, V.; Serio, G. A generalization of the Kermack–McKendrick deterministic epidemic model. Math. Biosci. 1978, 42, 43–61. [Google Scholar] [CrossRef]
- Witbooi, P.J.; Mengistu, A.K. Mathematical analysis of TB model with vaccination and saturated incidence rate. Abstr. Appl. Anal. 2020, 2020, 6669997. [Google Scholar] [CrossRef]
- Rasheed, S.; Iyiola, O.S.; Oke, S.I.; Wade, B.A. Exploring a mathematical model with saturated treatment for the co-dynamics of tuberculosis and diabetes. Mathematics 2024, 12, 3765. [Google Scholar] [CrossRef]
- Lu, M.; Huang, J.; Ruan, S.; Yu, P. Bifurcation analysis of an SIRS epidemic model with a generalized nonmonotone and saturated incidence rate. J. Differ. Equ. 2019, 267, 1859–1898. [Google Scholar] [CrossRef] [PubMed]
- Mengistu, A.K.; Witbooi, P.J. Modeling the effects of vaccination and treatment on tuberculosis transmission dynamics. J. Appl. Math. 2019, 1, 7463167. [Google Scholar] [CrossRef]
- Kar, T.K.; Mondal, P.K. Global dynamics of a tuberculosis epidemic model and the influence of backward bifurcation. J. Math. Model. Algorithms 2012, 11, 433–459. [Google Scholar] [CrossRef]
- Egonmwan, A.O.; Okuonghae, D. Mathematical analysis of a tuberculosis model with imperfect vaccine. Int. J. Biomath. 2019, 12, 1950040. [Google Scholar] [CrossRef]
- Horsburgh, C.R.; Jo, Y.; Nichols, B.; Jenkins, H.E.; Russell, C.A.; White, L.F. Contribution of Reinfection to Annual Rate of Tuberculosis Infection (ARI) and Incidence of Tuberculosis Disease Free. Clin. Infect. Dis. 2023, 76, e965–e972. [Google Scholar] [CrossRef]
- Ragonnet, R.; Flegg, J.A.; Brilleman, S.L.; Tiemersma, E.W.; Melsew, Y.A.; McBryde, E.S.; Trauer, J.M. Revisiting the natural history of pulmonary tuberculosis: A Bayesian estimation of natural recovery and mortality rates. Clin. Infect. Dis. 2021, 73, e88–e96. [Google Scholar] [CrossRef]
- Sulayman, F.; Abdullah, F. Analysis of a Tuberculosis Infection Model considering the Influence of Saturated Recovery (Treatment). Complex 2021, 2021, 1805651:1–1805651:16. [Google Scholar] [CrossRef]
- Aldila, D.; Saslia, B.R.; Gayarti, W.; Tasman, H. Backward bifurcation analysis on Tuberculosis disease transmission with saturated treatment. J. Phys. Conf. Ser. 2021, 1821, 012002. [Google Scholar] [CrossRef]
- Zhou, L.; Fan, M. Dynamics of an SIR epidemic model with limited medical resources revisited. Nonlinear Anal. Real World Appl. 2012, 13, 312–324. [Google Scholar] [CrossRef]
- Castillo-Chavez, C.; Song, B. Dynamical models of tuberculosis and their applications. Math. Biosci. Eng. 2004, 1, 361–404. [Google Scholar] [CrossRef]
- Khan, M.A.; DarAssi, M.H.; Ahmad, I.; Seyam, N.M.; Alzahrani, E. Modeling the Dynamics of Tuberculosis with Vaccination, Treatment, and Environmental Impact: Fractional Order Modeling. Comput. Model. Eng. Sci. 2024, 141, 1365–1394. [Google Scholar] [CrossRef]
- Gemeda, A.E.; Obsu, L.L.; Gurmu, E.D. Mathematical modeling of tuberculosis transmission dynamics with vaccination and two lines of treatments: A Caputo fractional approach. J. Appl. Math. Comput. 2025, 71, 2017–2049. [Google Scholar] [CrossRef]
- Amilo, D. Analyzing the Dynamics of Tuberculosis through a Fractional-Order Model. J. Math. Model. Fract. Calc. 2024. [Google Scholar] [CrossRef]

| Symbol | Description | Value | Dimension | Source |
|---|---|---|---|---|
| Initial number of susceptible individuals | 21 millions | individuals | Assumed | |
| Initial number of vaccinated individuals | 1 million | individuals | Assumed | |
| Initial number of exposed individuals | 0.2 million | individuals | Assumed | |
| Initial number of actively infected individuals | 0.1 million | individuals | Assumed | |
| Initial number of recovered individuals | 8 million | individuals | Assumed | |
| Recruitment rate into susceptible class | 5 | individuals time−1 | [4] | |
| Transmission rate between susceptible and infected individuals | 0.12, 0.3 | time−1 individual−1 | [4] | |
| k | Saturation constant in incidence rate | 0.1 | individual−1 | [21] |
| p | Fraction of infections that become immediately infectious | 0.1 | dimensionless | [30] |
| Vaccination rate of susceptibles | 0.2, 0.8 | time−1 | [4] | |
| Rate at which vaccinated individuals lose immunity | 0.067 | time−1 | [4] | |
| Natural death rate | 0.15 | time−1 | [4] | |
| Reduction in infection risk due to vaccination | 0.2 | dimensionless | [4] | |
| Transmission rate between vaccinated and infected individuals | 0.024, 0.06 | time−1 individual−1 | [4] | |
| Rate of progression from exposed to infectious | 0.02 | time−1 | [4] | |
| r | Recovery rate from infection | 0.302 | time−1 | [32] |
| Disease-induced death rate of infectious individuals | 0.17 | time−1 | [28] | |
| Rate of reactivation (reinfection) from recovered to exposed | 0.0013 | time−1 | [28] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Saputra, H.L.; Ansori, M.F. Analysis of an SVEIR with Reinfection Model of Tuberculosis Disease Spread with Saturated Infected Rate and Imperfect Vaccination. AppliedMath 2025, 5, 163. https://doi.org/10.3390/appliedmath5040163
Saputra HL, Ansori MF. Analysis of an SVEIR with Reinfection Model of Tuberculosis Disease Spread with Saturated Infected Rate and Imperfect Vaccination. AppliedMath. 2025; 5(4):163. https://doi.org/10.3390/appliedmath5040163
Chicago/Turabian StyleSaputra, Handika Lintang, and Moch. Fandi Ansori. 2025. "Analysis of an SVEIR with Reinfection Model of Tuberculosis Disease Spread with Saturated Infected Rate and Imperfect Vaccination" AppliedMath 5, no. 4: 163. https://doi.org/10.3390/appliedmath5040163
APA StyleSaputra, H. L., & Ansori, M. F. (2025). Analysis of an SVEIR with Reinfection Model of Tuberculosis Disease Spread with Saturated Infected Rate and Imperfect Vaccination. AppliedMath, 5(4), 163. https://doi.org/10.3390/appliedmath5040163







