Whittaker-Type Differential Equation: A Solution via Integral Functions

Abstract

In this study, we consider and analyze an inhomogeneous Whittaker-type differential equation of the form ${\displaystyle \frac{d^{2}y\left(x\right)}{d{x}^2}}+{\displaystyle \frac{1}{x}}{\displaystyle \frac{dy\left(x\right)}{dx}}-{\alpha }^2\left(x^2-{\beta }^2\right)y\left(x\right)=g\left(x\right)$, where $\alpha$ and $\beta$ are given parameters. We investigate the analytical structure of its solution through the application of the Whittaker integral representation. The analysis encompasses both initial value problems (IVPs) and boundary value problems (BVPs), wherein appropriate conditions are imposed within a unified analytical framework. Furthermore, a systematic methodology is developed for constructing explicit solutions within the framework of Whittaker function theory. This approach not only elucidates the functional behaviour of the solutions but also provides a foundation for extending the analysis to more general classes of second-order linear differential equations.

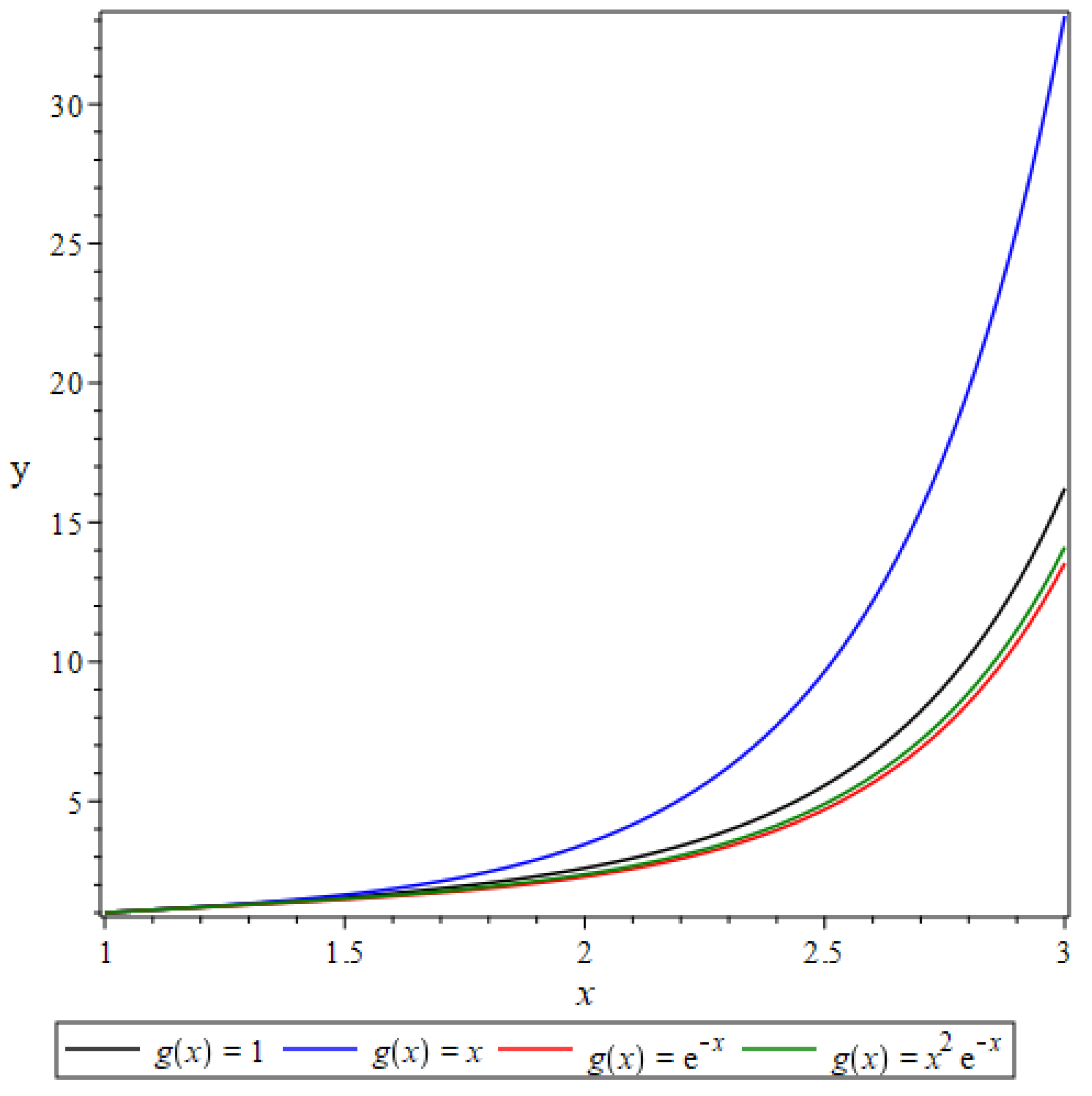
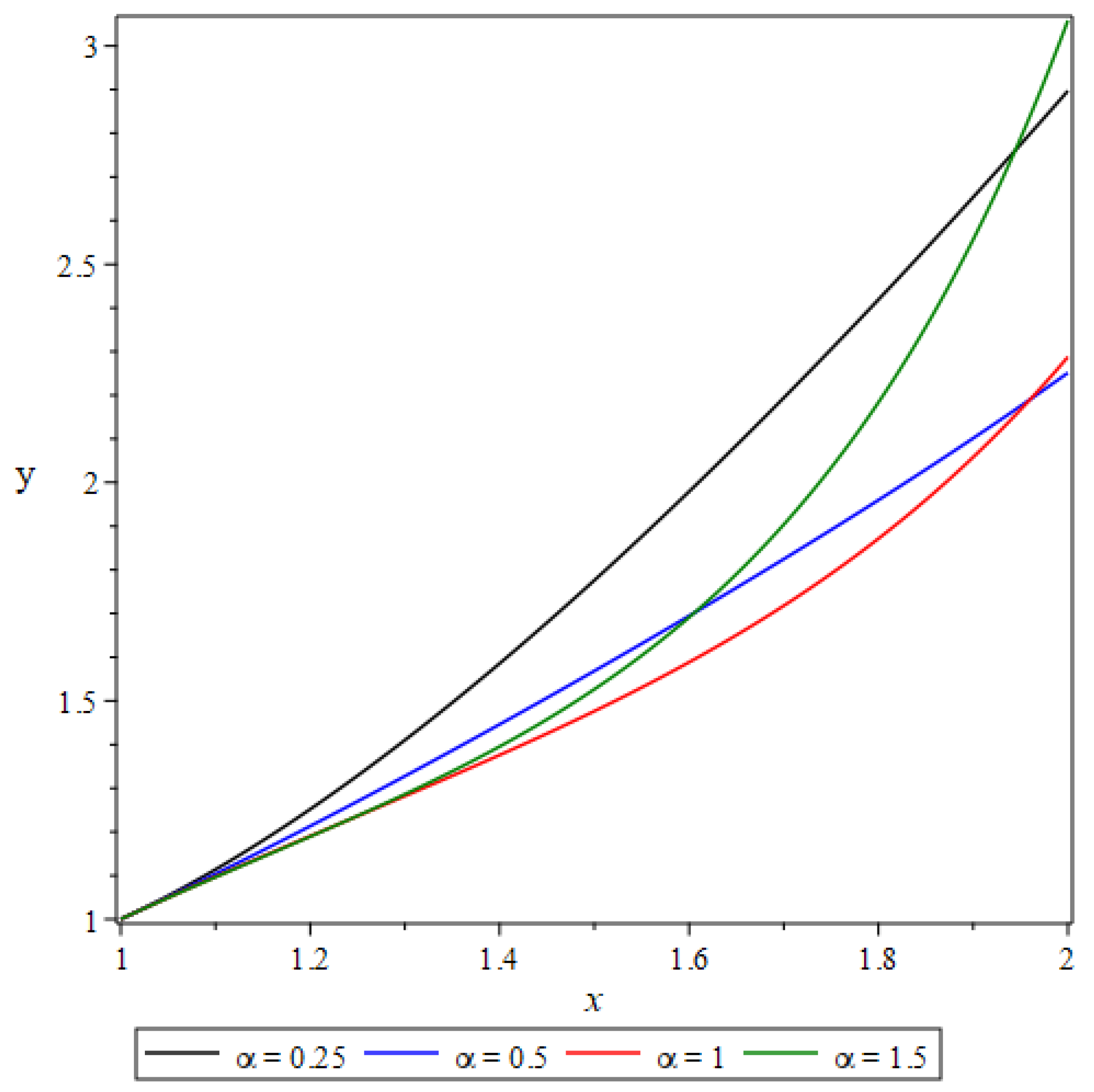
1. Introduction

A Whittaker-type differential equation refers to a class of ordinary and partial differential equations which, through suitable transformations of variables or dependent functions, can be reduced to the canonical form of the Whittaker differential equation. In the context of partial differential equations, such equations typically arise when the method of separation of variables is employed to construct solutions, particularly within the framework of mathematical physics and spectral theory. Whittaker’s equation itself arises as a special case of the confluent hypergeometric equation and is given by

$${\displaystyle \frac{d^2\mathrm{W}}{d{z}^2}}+\left(-{\displaystyle \frac{1}{4}}+{\displaystyle \frac{\kappa }{z}}+{\displaystyle \frac{\frac{1}{4}-{\mu }^2}{z^2}}\right)\mathrm{W}=0,$$

(1)

where $\kappa$ and $\mu$ are parameters. Equations reducible to this form are of significant interest due to their connections with special functions, quantum mechanics, and mathematical physics [1,2,3,4]. The transformation to Whittaker form often reveals underlying symmetries or allows for the use of well-established analytical techniques and known solutions. The Whittaker differential equation plays a fundamental role in the theory of special functions and quantum mechanics. A notable application is its connection to the initial value problem of the heat equation, where the heat equation can be transformed into a Whittaker form. This relationship enables the use of Whittaker functions to describe heat propagation under certain conditions, highlighting the equation’s importance in both theoretical and applied mathematical physics [5]. A rigorous analysis of integral transforms related to the initial Whittaker heat problem was presented by [5], wherein the theory of reproducing kernels was employed to examine the structure and properties of the associated kernel functions. Recent developments in the study of Whittaker and hypergeometric functions have focused on their generalization and extension. Nagar et al. [6] introduced an extended form of the Whittaker function via the extended confluent hypergeometric function of the first kind and explored its analytical properties, while Khan and Ghavasuddin [7] further investigated generalized extended Whittaker functions, providing additional insights and applications. Chaudhry et al. [8] developed extended hypergeometric and confluent hypergeometric functions, highlighting their structural properties and demonstrating their relevance in various applied mathematical contexts. Recent studies on extended hypergeometric functions have addressed their differential equations and integral representations. Mubeen et al. [9] solved the second-order linear k-hypergeometric differential equation using the Frobenius method at all regular singularities, providing eight solutions corresponding to various parameter cases. Mubeen [10] investigated solutions of integral equations involving confluent k-hypergeometric functions, and Mubeen and Habibullah [11] introduced new integral representations for both k-hypergeometric and k-confluent hypergeometric functions. Collectively, these works extend the classical framework of the Whittaker and hypergeometric functions, offering theoretical insights, practical tools, and potential applications in mathematical analysis and statistical distribution theory.

Solutions to the inhomogeneous Whittaker equation are rare (cf. [12] and the references therein). However, in a recent article, Abu Zaytoon et al. [12] introduced a semi-analytical approach capable of providing the particular and general solutions to the inhomogeneous Whittaker equation, whereby particular solutions were obtained by introducing a special integral function, denoted by ${}^f\mathrm{Zi}_{\kappa ,\mu }\left(x\right)$. For specific values of the parameters $\mu$ and $\kappa$, the function ${}^f\mathrm{Zi}_{\kappa ,\mu }\left(x\right)$ can be expressed in terms of other well-known special functions and is shown in this work to be well-suited for obtaining particular and general solutions to the inhomogeneous Whittaker-type equation of the form

$${\displaystyle \frac{d^{2}y\left(x\right)}{d{x}^2}}+{\displaystyle \frac{1}{x}}{\displaystyle \frac{dy\left(x\right)}{dx}}-{\alpha }^2\left(x^2-{\beta }^2\right)y\left(x\right)=g\left(x\right).$$

(2)

Various other analyses, representations and applications of the Whittaker and Whittaker-type equations have been reported in the literature (cf. [13,14,15,16,17] and the references therein). In particular, Lin et al. [15] analyzed the electronic structure of a hydrogenic impurity in a multilayer-coated quantum dot using the effective mass approximation, expressing the eigenfunctions analytically in terms of Whittaker functions. This approach reduces the Schrödinger equation to a Whittaker-type differential equation, allowing for efficient determination of ground and excited state energies and straightforward identification of bound states in $n-l$ layered quantum dots. Tas and Sahin [16] conducted a comprehensive investigation of the inter-sublevel optical properties in a core/shell/well/shell spherical quantum dot structure by numerically solving the Schrödinger equation using the shooting method within the framework of the effective mass approximation. Although their analysis is primarily computational, the corresponding radial Schrödinger equation inherently admits a Whittaker-type formulation when the confining potential includes Coulombic or exponentially varying components, thereby establishing a connection between their numerical approach and the broader class of analytically solvable Whittaker differential equations. Li and Xia [17] investigated the binding energies of hydrogenic donor impurities in rectangular quantum dots, demonstrating pronounced dependence on dot geometry, impurity position, and applied electric fields, encapsulating quantum confinement and Stark effects. The underlying radial Schrödinger equation, incorporating Coulomb and external field interactions, can be formally expressed as a Whittaker-type differential equation, bridging numerical plane-wave calculations with analytical approaches.

The main objective of this work is to analyze a particular form of the Whittaker-type differential equations, the type that can be transformed into a standard Whittaker’s equation through suitable changes of variables or functions, and to provide a methodology for obtaining its particular and general solutions. To achieve this objective, we provide a thorough exposition and extension of the solution methodology developed in [12] to the inhomogeneous Whittaker-type equation. It is envisaged that the obtained solutions and the solution methodology are of theoretical and practical significance with potential applications to applied physical problems, such as fluid flow and heat conduction problems.

To accomplish the proposed work, this manuscript is organized as follows. In Section 2, a brief overview of the inhomogeneous Whittaker’s equation, and of the integral function ${}^f\mathrm{Zi}_{\kappa ,\mu }\left(x\right)$ and its role in the particular solution of Whittaker’s equation, is provided. This is followed in Section 2 by the introduction of the inhomogeneous Whittaker-type equation, its transformation and its associated integral ${}^f\mathrm{Zi}_{\kappa ,\mu }\left(x\right)$ function, and the method of obtaining its particular and general solutions. Initial and boundary value problems associated with the Whittaker-type equation are considered in Section 4, together with associated sample graphs and solutions. Finally, in Section 5 we provide conclusions to this work and discuss what has been accomplished, and some recommendations for future work.

In carrying out the analysis in this work, we relied on the built-in functions and symbolic manipulation capabilities of the 2022 version of Maple^TM. It is worth noting that in the analysis of initial and boundary value problems, solutions were not obtained via any differential equations’ solver. Rather, the expressions in the initial and boundary value problems were evaluated using Maple^TM.

The highlights of this work are as follows.

• This work introduces a methodology for transforming and obtaining the general solution to a class of inhomogeneous Whittaker-type equations.
• Particular solutions to the problem are obtained using the recently introduced ${}^f\mathrm{Zi}_{\kappa ,\mu }\left(x\right)$ integral function.
• This work discusses the initial and boundary value problems associated with the inhomogeneous Whittaker-type equations, and provides their solutions without resorting to numerical techniques offered by any differential equation solver.

2. Inhomogeneous Whittaker Equation

The inhomogeneous Whittaker equation is a second-order linear differential equation of the form

$${\displaystyle \frac{d^2\mathrm{W}}{d{x}^2}}+\left(-{\displaystyle \frac{1}{4}}+{\displaystyle \frac{\kappa }{x}}+{\displaystyle \frac{\frac{1}{4}-{\mu }^2}{x^2}}\right)\mathrm{W}=f\left(x\right),$$

(3)

where $\kappa$ and $\mu$ are parameters, and $f\left(x\right)$ is a known forcing term. A comprehensive analysis of the solution to this differential equation is presented in [12], where both initial and boundary value problems are considered. Abu Zaytoon et al. [12] introduced an integral function, denoted by ${}^f\mathrm{Zi}_{\kappa ,\mu }\left(x\right)$, to express the solution of the inhomogeneous Whittaker Equation (3). The function ${}^f\mathrm{Zi}_{\kappa ,\mu }\left(x\right)$ is evaluated for various parameter values, which, in certain cases, reduce it to well-known special functions, including Bessel functions, Gamma functions, incomplete Gamma functions, and error functions.

A general solution of the inhomogeneous Whittaker equation is given by [12]

$$\begin{array}{cc}\hfill & \mathrm{W}\left(z\right)=C_1{\mathrm{M}}_{\kappa ,\mu }\left(z\right)+C_2{\mathrm{W}}_{\kappa ,\mu }\left(z\right)+{\displaystyle \frac{\Gamma \left(\frac{1}{2}+\mu -\kappa \right)}{\Gamma (1+2\mu )}}{}^f\mathrm{Zi}_{\kappa ,\mu }\left(z\right),\hfill \\ \hfill & 2\mu \ne -1,-2,\dots \hfill \end{array}$$

(4)

In Equation (4), $C_1$ and $C_2$ are arbitrary constants; the functions ${\mathrm{M}}_{\kappa ,\mu }\left(x\right)$ and ${\mathrm{W}}_{\kappa ,\mu }\left(x\right)$ denote the Whittaker functions, which constitute a fundamental set of solutions to the homogeneous Whittaker Equation (1), (c.f. [13]). The Whittaker function ${\mathrm{M}}_{\kappa ,\mu }\left(x\right)$ is defined as

$${\mathrm{M}}_{\kappa ,\mu }\left(x\right)=x^{\mu -1/2}{e^{-x/2}}_1{F}_1\left(\left.\begin{array}{c}\mu -\kappa +{\displaystyle \frac{1}{2}}\\ 1+2\mu \end{array}\right|x\right).$$

(5)

While the Whittaker function ${\mathrm{W}}_{\kappa ,\mu }\left(x\right)$ is defined in terms of confluent hypergeometric functions, it can also be expressed as a linear combination of the Whittaker functions of the first kind ${\mathrm{M}}_{\kappa ,\mu }\left(x\right)$, provided that $2\mu \notin \mathbb{Z}$, as follows [2,3]:

$${\mathrm{W}}_{\kappa ,\mu }\left(x\right)={\displaystyle \frac{\Gamma (-2\mu )}{\Gamma \left(\frac{1}{2}-k-\mu \right)}}{\mathrm{M}}_{\kappa ,\mu }\left(x\right)+{\displaystyle \frac{\Gamma \left(2\mu \right)}{\Gamma \left(\frac{1}{2}-k+\mu \right)}}{\mathrm{M}}_{\kappa ,-\mu }\left(x\right).$$

(6)

The function ${}^f\mathrm{Zi}_{\kappa ,\mu }\left(x\right)$ is defined as [12]

$${}^f\mathrm{Zi}_{\kappa ,\mu }\left(x\right)={\mathrm{M}}_{\kappa ,\mu }\left(x\right){}^f\mathrm{Mi}_{\kappa ,\mu }\left(x\right)-{\mathrm{W}}_{\kappa ,\mu }\left(x\right){}^f\mathrm{Wi}_{\kappa ,\mu }\left(x\right),$$

(7)

where

$$\begin{array}{c}{}^f\mathrm{Mi}_{\kappa ,\mu }\left(x\right)={\int }_0^{x}f\left(t\right){\mathrm{Mi}}_{\kappa ,\mu }\left(t\right)dt,\\ {}^f\mathrm{Wi}_{\kappa ,\mu }\left(x\right)={\int }_0^{x}f\left(t\right){\mathrm{Wi}}_{\kappa ,\mu }\left(t\right)dt.\end{array}$$

(8)

The derivatives of the Whittaker functions are given in [13] as

$${\mathrm{M}}_{\kappa ,\mu }^{\prime }\left(x\right)=\left({\displaystyle \frac{1}{2}}-{\displaystyle \frac{\kappa }{x}}\right){\mathrm{M}}_{\kappa ,\mu }\left(x\right)+\left({\displaystyle \frac{1}{2}}+\mu +\kappa \right){\displaystyle \frac{{\mathrm{M}}_{\kappa +1,\mu }\left(x\right)}{x}}.$$

(9)

$${\mathrm{W}}_{\kappa ,\mu }^{\prime }\left(x\right)=\left({\displaystyle \frac{1}{2}}-{\displaystyle \frac{\kappa }{x}}\right){\mathrm{W}}_{\kappa ,\mu }\left(x\right)-{\displaystyle \frac{{\mathrm{W}}_{\kappa +1,\mu }\left(x\right)}{x}}.$$

(10)

Furthermore, the derivative of the function ${}^f\mathrm{Zi}_{\kappa ,\mu }\left(x\right)$ is given by [12]

$$\begin{array}{cc}\hfill {}^f\mathrm{Z}_{\kappa ,\mu }^{\prime }\left(x\right)& =\left[\left({\displaystyle \frac{1}{2}}-{\displaystyle \frac{\kappa }{x}}\right){\mathrm{M}}_{\kappa ,\mu }\left(x\right)+\left({\displaystyle \frac{1}{2}}+\mu +\kappa \right){\displaystyle \frac{{\mathrm{M}}_{\kappa +1,\mu }\left(x\right)}{x}}\right]{}^f\mathrm{Wi}_{\kappa ,\mu }\left(x\right)\hfill \\ \hfill & -\left[\left({\displaystyle \frac{1}{2}}-{\displaystyle \frac{\kappa }{x}}\right){\mathrm{W}}_{\kappa ,\mu }\left(x\right)-{\displaystyle \frac{{\mathrm{W}}_{\kappa +1,\mu }\left(x\right)}{x}}\right]{}^f\mathrm{Mi}_{\kappa ,\mu }\left(x\right).\hfill \end{array}$$

(11)

3. Whittaker-Type Differential Equation

Whittaker-type differential equations form a broad class of second-order linear differential equations that encompass many well-known equations in mathematical physics, including Weber’s equation, the radial Schrödinger equation, and other confluent hypergeometric-type equations. These equations are characterized by their singularity structure and the presence of terms proportional to $1/x$ and $1/x^2$, which allows their solutions to be expressed in terms of Whittaker functions or related special functions. The Whittaker framework thus provides a unifying approach for analyzing a wide variety of physical and applied problems, ranging from quantum mechanics and wave propagation to statistical and engineering applications. In the remainder of this section, we focus on a special class of equations, namely Equation (2), and demonstrate that it belongs to the Whittaker-type differential equations. Through a series of appropriate transformations and analytical steps, we will show how it can be recast into the canonical form of the Whittaker’s differential equation. To solve Equation (2), we first establish that it belongs to the class of Whittaker-type differential equations. This is achieved by applying an appropriate transformation that demonstrates its equivalence to the inhomogeneous Whittaker equation. The result is summarized in the following corollary.

Corollary 1.

Equation (2) is identified as a Whittaker-type differential equation. Consequently, its solutions can be expressed in terms of Whittaker functions ${\mathrm{M}}_{\kappa ,\mu }\left(x\right)$, ${\mathrm{W}}_{\kappa ,\mu }\left(x\right)$, and the integral function ${}^f\mathrm{Zi}_{\kappa ,\mu }\left(x\right)$.

Proof. 

We begin by introducing the following transformation:

$$s=\alpha x^2,\mathrm{Y}\left(s\right)=xy\left(x\right).$$

(12)

Upon substituting the transformation (12) into Equation (2), we obtain the following equation:

$$\begin{array}{cc}\hfill & {\alpha }^{3/2}\left(4\sqrt{s}{\displaystyle \frac{d^{2}Y\left(s\right)}{d{s}^2}}-{\displaystyle \frac{2}{\sqrt{s}}}{\displaystyle \frac{dY\left(s\right)}{ds}}+{\displaystyle \frac{2}{s^{3/2}}}Y\left(s\right)\right)+{\alpha }^{3/2}\left({\displaystyle \frac{2}{\sqrt{s}}}{\displaystyle \frac{dY\left(s\right)}{ds}}-{\displaystyle \frac{1}{s^{3/2}}}Y\left(s\right)\right)\hfill \\ \hfill & -{\alpha }^{3/2}\left({\displaystyle \frac{s-\alpha {\beta }^2}{\sqrt{s}}}\right)Y\left(s\right)=g\left(s\right).\hfill \end{array}$$

(13)

Upon simplifying Equation (13), we obtain

$${\displaystyle \frac{d^{2}Y\left(s\right)}{d{s}^2}}+\left(-{\displaystyle \frac{1}{4}}+{\displaystyle \frac{\frac{\alpha {\beta }^2}{4}}{s}}+{\displaystyle \frac{\frac{1}{4}}{s^2}}\right)Y\left(s\right)={\displaystyle \frac{1}{4\alpha \sqrt{\alpha s}}}g\left(s\right).$$

(14)

□

Equation (14) is an inhomogeneous Whittaker equation, where

$$\kappa ={\displaystyle \frac{\alpha {\beta }^2}{4}},\mathrm{and}\mu =0.$$

(15)

Corollary 2.

The solution of Equation (14) is given by

$$Y\left(s\right)=C_1{\mathrm{M}}_{{\displaystyle \frac{\alpha {\beta }^2}{4}},0}\left(s\right)+C_2{\mathrm{W}}_{{\displaystyle \frac{\alpha {\beta }^2}{4}},0}\left(s\right)+\Gamma \left({\displaystyle \frac{1}{2}}-{\displaystyle \frac{\alpha {\beta }^2}{4}}\right){}^{{\displaystyle \frac{1}{4\alpha \sqrt{\alpha s}}}g\left(s\right)}\mathrm{Zi}_{{\displaystyle \frac{\alpha {\beta }^2}{4}},0}\left(s\right).$$

(16)

Proof. 

Proof of Corollary 2 follows directly from Equation (4), which represents the general solution to Equation (3). Upon substitution of the variables defined by (12) and (15) in (4), Equation (16) is obtained. □

The following theorem provides the solution to Equation (2). This solution will serve as a fundamental tool for expressing solutions to initial and boundary value problems.

Theorem 1.

General solution to Equation (2) can be expressed in the form

$$y\left(x\right)={\displaystyle \frac{1}{x}}\left(C_1{\mathrm{M}}_{{\displaystyle \frac{\alpha {\beta }^2}{4}},0}\left(\alpha x^2\right)+C_2{\mathrm{W}}_{{\displaystyle \frac{\alpha {\beta }^2}{4}},0}\left(\alpha x^2\right)+\Gamma \left({\displaystyle \frac{1}{2}}-{\displaystyle \frac{\alpha {\beta }^2}{4}}\right){}^{{\displaystyle \frac{1}{4{\alpha }^{2}x}}g\left(\alpha x^2\right)}\mathrm{Zi}_{{\displaystyle \frac{\alpha {\beta }^2}{4}},0}\left(\alpha x^2\right)\right).$$

(17)

Proof. 

Upon substituting Equation (12) into Equation (16), and simplifying, solution (17) is obtained. □

In the case where $\mu =0$, the Whittaker functions can be expressed in terms of confluent hypergeometric functions. In particular, ${\mathrm{M}}_{{\displaystyle \frac{\alpha {\beta }^2}{4}},0}\left(x\right)$ reduces to the confluent hypergeometric function of the first kind $M\left({\displaystyle \frac{\alpha {\beta }^2}{4}}+{\displaystyle \frac{1}{2}},1,x\right)$, and ${\mathrm{W}}_{{\displaystyle \frac{\alpha {\beta }^2}{4}},0}\left(x\right)$ corresponds to the confluent hypergeometric function of the second kind $\mathrm{U}\left({\displaystyle \frac{\alpha {\beta }^2}{4}}+{\displaystyle \frac{1}{2}},1,x\right)$, commonly known as Tricomi’s function [13], as follows:

$${\mathrm{M}}_{{\displaystyle \frac{\alpha {\beta }^2}{4}},0}\left(x\right)=e^{-x/2}{x}^{{\displaystyle \frac{\alpha {\beta }^2}{4}}+1/2}·M\left({\displaystyle \frac{\alpha {\beta }^2}{4}}+{\displaystyle \frac{1}{2}},1,x\right).$$

(18)

$${\mathrm{W}}_{{\displaystyle \frac{\alpha {\beta }^2}{4}},0}\left(x\right)=e^{-x/2}{z}^{{\displaystyle \frac{\alpha {\beta }^2}{4}}+1/2}·\mathrm{U}\left({\displaystyle \frac{\alpha {\beta }^2}{4}}+{\displaystyle \frac{1}{2}},1,x\right).$$

(19)

The function ${\mathrm{M}}_{{\displaystyle \frac{\alpha {\beta }^2}{4}},0}\left(x\right)$ admits the following integral representation, valid for $|{\displaystyle \frac{\alpha {\beta }^2}{4}}|<{\displaystyle \frac{1}{2}}$ (see [13]):

$${\mathrm{M}}_{{\displaystyle \frac{\alpha {\beta }^2}{4}},0}\left(x\right)={\displaystyle \frac{x^{\frac{1}{2}}}{\Gamma \left(\frac{1}{2}-\frac{\alpha {\beta }^2}{4}\right)\Gamma \left(\frac{1}{2}+\frac{\alpha {\beta }^2}{4}\right)}}{\int }_{-1}^1{\mathrm{e}}^{{\displaystyle \frac{1}{2}}xt}{(1+t)}^{-{\displaystyle \frac{1}{2}}-{\displaystyle \frac{\alpha {\beta }^2}{4}}}{(1-t)}^{-{\displaystyle \frac{1}{2}}+{\displaystyle \frac{\alpha {\beta }^2}{4}}}\mathrm{d}t.$$

(20)

An expansion of the function $\mathrm{U}$ yields the following representation of ${\mathrm{W}}_{{\displaystyle \frac{\alpha {\beta }^2}{4}},0}\left(x\right)$ that is particularly effective in analyzing the behaviour of the function in the regime of small x [13]:

$$\begin{array}{cc}\hfill W_{{\displaystyle \frac{\alpha {\beta }^2}{4}},0}\left(x\right)=x^{{\displaystyle \frac{1}{2}}}{e}^{-{\displaystyle \frac{x}{2}}}[& lnx·\sum _{n=0}^{\infty }{\displaystyle \frac{{\left(\frac{1}{2}-\frac{\alpha {\beta }^2}{4}\right)}_n}{{(n!)}^2}}{x}^n\hfill \\ \hfill & +\sum _{n=0}^{\infty }{\displaystyle \frac{{\left(\frac{1}{2}-\frac{\alpha {\beta }^2}{4}\right)}_n}{{(n!)}^2}}{x}^n\left(\psi (n+1)-\psi \left({\displaystyle \frac{1}{2}}-{\displaystyle \frac{\alpha {\beta }^2}{4}}+n\right)\right)],\hfill \end{array}$$

(21)

Here, ${\left(a\right)}_n$ denotes the Pochhammer’s Symbol, and $\psi \left(x\right)$ is the digamma function defined by

$$\psi \left(x\right)={\displaystyle \frac{d}{dx}}ln\Gamma \left(x\right)={\displaystyle \frac{{\Gamma }^{\prime }\left(x\right)}{\Gamma \left(x\right)}}.$$

(22)

When the parameters $\alpha$ and $\beta$ satisfy the inequality $\alpha {\beta }^2<2$, the function ${\mathrm{W}}_{{\displaystyle \frac{\alpha {\beta }^2}{4}},0}\left(x\right)$ admits the following integral representation for $x>0$ [13]:

$${\mathrm{W}}_{{\displaystyle \frac{\alpha {\beta }^2}{4}},0}\left(x\right)=x^{1/2}{e}^{-x/2}·{\displaystyle \frac{1}{\Gamma \left(\frac{1}{2}-\frac{\alpha {\beta }^2}{4}\right)}}{\int }_0^{\infty }{e}^{-xt}{t}^{-{\displaystyle \frac{\alpha {\beta }^2}{4}}-1/2}{(1+t)}^{{\displaystyle \frac{\alpha {\beta }^2}{4}}-1/2}dt.$$

(23)

Notably, the function ${\mathrm{W}}_{{\displaystyle \frac{\alpha {\beta }^2}{4}},0}\left(x\right)$ satisfies ${\mathrm{W}}_{{\displaystyle \frac{\alpha {\beta }^2}{4}},0}\left(0\right)=0$, indicating that it vanishes at the origin [5]. Further research is required to derive closed-form expressions for the functions ${\mathrm{M}}_{{\displaystyle \frac{\alpha {\beta }^2}{4}},0}\left(x\right)$ and ${\mathrm{W}}_{{\displaystyle \frac{\alpha {\beta }^2}{4}},0}\left(x\right)$, which would enhance the analytical tractability and efficiency of the solution process.

An important identity is provided in [13], where the Whittaker functions are expressed in terms of the generalized Laguerre polynomials, as given by

$$\begin{array}{cc}\hfill {\mathrm{W}}_{{\displaystyle \frac{1}{2}}\gamma +{\displaystyle \frac{1}{2}}+n,{\displaystyle \frac{1}{2}}\gamma }\left(x\right)& ={(-1)}^n{(\gamma +1)}_n{\mathrm{M}}_{{\displaystyle \frac{1}{2}}\gamma +{\displaystyle \frac{1}{2}}+n,{\displaystyle \frac{1}{2}}\gamma }\left(x\right)\hfill \\ \hfill & ={(-1)}^{n}n!{\mathrm{e}}^{-{\displaystyle \frac{1}{2}}z}{z}^{{\displaystyle \frac{1}{2}}\gamma +{\displaystyle \frac{1}{2}}}{L}_n^{\left(\gamma \right)}\left(x\right),\hfill \end{array}$$

(24)

where $L_n^{\left(\gamma \right)}\left(x\right)$ are the generalized Laguerre polynomials defined in [14]. Specifically, for $\gamma >-1$, the Laguerre polynomials $\left\{L_n^{\left(\gamma \right)}\left(x\right)\right\}$ are characterized by the orthogonality and normalization condition

$${\int }_0^{\infty }{e}^{-x}{x}^{\gamma }{L}_n^{\left(\gamma \right)}\left(x\right)L_m^{\left(\gamma \right)}\left(x\right)dx=\Gamma (\gamma +1)\left({\displaystyle \genfrac{}{}{0pt}{}{n+\gamma }{n}}\right){\delta }_{nm},n,m=0,1,2,\dots$$

(25)

Equivalently, they admit the following explicit representation [14]

$$L_n^{\left(\gamma \right)}\left(x\right)=\sum _{k=0}^n{(-1)}^k\left({\displaystyle \genfrac{}{}{0pt}{}{n+\gamma }{n-k}}\right){\displaystyle \frac{x^k}{k!}}.$$

(26)

When $\gamma =0$, the generalized Laguerre polynomials reduce to the standard Laguerre polynomials of the form

$$L_n\left(x\right)\equiv L_n^{\left(0\right)}\left(x\right)=\sum _{k=0}^n{(-1)}^k\left({\displaystyle \genfrac{}{}{0pt}{}{n}{n-k}}\right){\displaystyle \frac{x^k}{k!}}=\sum _{k=0}^n{(-1)}^k{\displaystyle \frac{n!}{(n-k)!k!}}{x}^k.$$

(27)

The connection between Laguerre polynomials and the ${}^f\mathrm{Zi}_{n+{\displaystyle \frac{1}{2}},0}\left(x\right)$ is through Equation (24), as can be seen in the proof of the following Corollary.

Corollary 3.

For non-negative integer n, the function ${}^f\mathrm{Zi}_{n+{\displaystyle \frac{1}{2}},0}\left(x\right)=0$.

Proof. 

Using (24) and (27) with $\gamma =0$, we have

$$\begin{array}{cc}\hfill & {\mathrm{M}}_{{\displaystyle \frac{1}{2}}+n,0}\left(x\right)=e^{-{\displaystyle \frac{1}{2}}x}{x}^{{\displaystyle \frac{1}{2}}}{L}_n\left(x\right),\hfill \\ \hfill & {\mathrm{W}}_{{\displaystyle \frac{1}{2}}+n,0}\left(x\right)={(-1)}^{n}n!{\mathrm{M}}_{{\displaystyle \frac{1}{2}}+n,0}\left(x\right).\hfill \end{array}$$

(28)

$$\begin{array}{cc}\hfill {}^f\mathrm{Zi}_{{\displaystyle \frac{1}{2}}+n,0}\left(x\right)& ={\mathrm{M}}_{{\displaystyle \frac{1}{2}}+n,0}\left(x\right){\int }_0^{x}f\left(t\right){\mathrm{W}}_{{\displaystyle \frac{1}{2}}+n,\mu }\left(t\right)dt-{\mathrm{W}}_{{\displaystyle \frac{1}{2}}+n,0}\left(x\right){\int }_0^{x}f\left(t\right){\mathrm{M}}_{{\displaystyle \frac{1}{2}}+n,0}\left(t\right)dt\hfill \\ \hfill & ={\mathrm{M}}_{{\displaystyle \frac{1}{2}}+n,0}\left(x\right){\int }_0^{x}f\left(t\right){(-1)}^{n}n!{\mathrm{M}}_{{\displaystyle \frac{1}{2}}+n,0}\left(x\right)dt\hfill \\ \hfill & -{(-1)}^{n}n!{\mathrm{M}}_{{\displaystyle \frac{1}{2}}+n,0}\left(x\right){\int }_0^{x}f\left(t\right){\mathrm{M}}_{{\displaystyle \frac{1}{2}}+n,0}\left(t\right)dt\hfill \\ \hfill & =0.\hfill \end{array}$$

(29)

□

The result obtained in Corollary 3 is consistent with the fact that the Whittaker functions are not linearly independent when $\mu =0$. This can be seen directly from Equation (6), where the representation of ${\mathrm{W}}_{\kappa ,\mu }\left(x\right)$ in terms of ${\mathrm{M}}_{\kappa ,\mu }\left(x\right)$ and ${\mathrm{M}}_{\kappa ,-\mu }\left(x\right)$ degenerates, leading to the loss of linear independence. As a consequence, for the inhomogeneous differential equation, the variation in parameter method no longer produces two distinct contributions from the Whittaker functions. Instead, the particular solution collapses into a form proportional to a single Whittaker function. In this case, the solution of the inhomogeneous equation reduces to the homogeneous solution only.

4. Initial and Boundary Value Problems

To advance toward the resolution of initial and boundary value problems involving Equation (2), it is necessary—particularly in the context of initial value problems—to determine the derivative of the solution $y\left(x\right)$. By differentiating both sides of Equation (17), we obtain the following expression for $y^{\prime }\left(x\right)$:

$$\begin{array}{cc}\hfill y^{\prime }\left(x\right)={\displaystyle \frac{1}{x^2}}& [\left(2\alpha x^2{\mathrm{M}}_{{\displaystyle \frac{\alpha {\beta }^2}{4}},0}^{\prime }\left(\alpha x^2\right)-{\mathrm{M}}_{{\displaystyle \frac{\alpha {\beta }^2}{4}},0}\left(\alpha x^2\right)\right)C_1\hfill \\ \hfill & +\left(2\alpha x^2{\mathrm{W}}_{{\displaystyle \frac{\alpha {\beta }^2}{4}},0}^{\prime }\left(\alpha x^2\right)-{\mathrm{W}}_{{\displaystyle \frac{\alpha {\beta }^2}{4}},0}\left(\alpha x^2\right)\right)C_2\hfill \\ \hfill & +\Gamma \left({\displaystyle \frac{1}{2}}-{\displaystyle \frac{\alpha {\beta }^2}{4}}\right)\left(2\alpha x^2{}^{{\displaystyle \frac{1}{4{\alpha }^{2}x}}g\left(\alpha x^2\right)}\mathrm{Zi}_{{\displaystyle \frac{\alpha {\beta }^2}{4}},0}^{\prime }\left(\alpha x^2\right)-{}^{{\displaystyle \frac{1}{4{\alpha }^{2}x}}g\left(\alpha x^2\right)}\mathrm{Zi}_{{\displaystyle \frac{\alpha {\beta }^2}{4}},0}\left(\alpha x^2\right)\right)].\hfill \end{array}$$

(30)

Upon substituting Equations (9)–(11) into Equation (30), we obtain the following:

$$\begin{array}{cc}\hfill & y^{\prime }\left(x\right)=\left(-{\displaystyle \frac{{\mathrm{M}}_{\frac{\alpha {\beta }^2}{4},0}\left(\alpha x^2\right)}{x^2}}+2\alpha \left[\left({\displaystyle \frac{1}{2}}-{\displaystyle \frac{{\beta }^2}{4x^2}}\right){\mathrm{M}}_{{\displaystyle \frac{\alpha {\beta }^2}{4}},0}\left(\alpha x^2\right)+{\displaystyle \frac{\left(\frac{1}{2}+\frac{\alpha {\beta }^2}{4}\right){\mathrm{M}}_{\frac{\alpha {\beta }^2}{4}+1,0}\left(\alpha x^2\right)}{\alpha x^2}}\right]\right)C_1\hfill \\ \hfill & +\left(-{\displaystyle \frac{{\mathrm{W}}_{\frac{\alpha {\beta }^2}{4},0}\left(\alpha x^2\right)}{x^2}}+2\alpha \left[\left({\displaystyle \frac{1}{2}}-{\displaystyle \frac{{\beta }^2}{4x^2}}\right){\mathrm{W}}_{{\displaystyle \frac{\alpha {\beta }^2}{4}},0}\left(\alpha x^2\right)-{\displaystyle \frac{{\mathrm{W}}_{\frac{\alpha {\beta }^2}{4}+1,0}\left(\alpha x^2\right)}{\alpha x^2}}\right]\right)C_2\hfill \\ \hfill & +2\alpha \Gamma \left({\displaystyle \frac{1}{2}}-{\displaystyle \frac{\alpha {\beta }^2}{4}}\right)\{\left[\left({\displaystyle \frac{1}{2}}-{\displaystyle \frac{\kappa }{\alpha x^2}}\right){\mathrm{M}}_{\kappa ,\mu }\left(\alpha x^2\right)+\left({\displaystyle \frac{1}{2}}+\kappa \right){\displaystyle \frac{{\mathrm{M}}_{\kappa +1,0}\left(\alpha x^2\right)}{\alpha x^2}}\right]{}^{{\displaystyle \frac{1}{4{\alpha }^{2}x}}g\left(\alpha x^2\right)}\mathrm{Wi}_{\kappa ,0}\left(\alpha x^2\right)\hfill \\ \hfill & -\left[\left({\displaystyle \frac{1}{2}}-{\displaystyle \frac{\kappa }{\alpha x^2}}\right){\mathrm{W}}_{\kappa ,0}\left(\alpha x^2\right)-{\displaystyle \frac{{\mathrm{W}}_{\kappa +1,0}\left(x\right)}{x}}\right]{}^{{\displaystyle \frac{1}{4{\alpha }^{2}x}}g\left(\alpha x^2\right)}\mathrm{Mi}_{\kappa ,0}\left(\alpha x^2\right)\}\hfill \\ \hfill & -{\displaystyle \frac{1}{x^2}}\Gamma \left({\displaystyle \frac{1}{2}}-{\displaystyle \frac{\alpha {\beta }^2}{4}}\right)\left[{\mathrm{M}}_{\kappa ,0}\left(x\right){}^{{\displaystyle \frac{1}{4{\alpha }^{2}x}}g\left(\alpha x^2\right)}\mathrm{Mi}_{\kappa ,0}\left(x\right)-{\mathrm{W}}_{\kappa ,0}\left(x\right){}^{{\displaystyle \frac{1}{4{\alpha }^{2}x}}g\left(\alpha x^2\right)}\mathrm{Wi}_{\kappa ,0}\left(x\right)\right].\hfill \end{array}$$

(31)

4.1. Initial Value Problems

Theorem 2.

Consider the inhomogeneous Whittaker-type differential equation given by Equation (2), subject to the following initial conditions:

$$y\left(a\right)=A;y^{\prime }\left(a\right)=B.$$

(32)

The solution to the above initial value problem is given by

$$y\left(x\right)={\displaystyle \frac{1}{x}}\left(C_1{\mathrm{M}}_{{\displaystyle \frac{\alpha {\beta }^2}{4}},0}\left(\alpha x^2\right)+C_2{\mathrm{W}}_{{\displaystyle \frac{\alpha {\beta }^2}{4}},0}\left(\alpha x^2\right)+\Gamma \left({\displaystyle \frac{1}{2}}-{\displaystyle \frac{\alpha {\beta }^2}{4}}\right){}^{{\displaystyle \frac{1}{4{\alpha }^{2}x}}g\left(\alpha x^2\right)}\mathrm{Zi}_{{\displaystyle \frac{\alpha {\beta }^2}{4}},0}\left(\alpha x^2\right)\right),$$

(33)

where the constants $C_1$ and $C_2$ satisfy

$$\begin{array}{c}\hfill C_1=-{\displaystyle \frac{a_{12}{b}_2-a_{22}{b}_1}{a_{11}{a}_{22}-a_{12}{a}_{21}}},\end{array}$$

(34)

and

$$\begin{array}{c}\hfill C_2=-{\displaystyle \frac{a_{11}{b}_2-a_{21}{b}_1}{a_{11}{a}_{22}-a_{12}{a}_{21}}},\end{array}$$

(35)

with

$$a_{11}={\displaystyle \frac{1}{a}}{\mathrm{M}}_{{\displaystyle \frac{\alpha {\beta }^2}{4}},0}\left(\alpha a^2\right),$$

$$a_{12}={\mathrm{W}}_{{\displaystyle \frac{\alpha {\beta }^2}{4}},0}\left(\alpha a^2\right),$$

$$a_{21}={\displaystyle \frac{1}{a^2}}\left(2\alpha a^2{\mathrm{M}}_{{\displaystyle \frac{\alpha {\beta }^2}{4}},0}^{\prime }\left(\alpha a^2\right)-{\mathrm{M}}_{{\displaystyle \frac{\alpha {\beta }^2}{4}},0}\left(\alpha a^2\right)\right),$$

$$a_{22}=\left(2\alpha a^2{\mathrm{W}}_{{\displaystyle \frac{\alpha {\beta }^2}{4}},0}^{\prime }\left(\alpha a^2\right)-{\mathrm{W}}_{{\displaystyle \frac{\alpha {\beta }^2}{4}},0}\left(\alpha a^2\right)\right),$$

$$b_1=A-\Gamma \left({\displaystyle \frac{1}{2}}-{\displaystyle \frac{\alpha {\beta }^2}{4}}\right){}^{{\displaystyle \frac{1}{4{\alpha }^{2}a}}g\left(\alpha a^2\right)}\mathrm{Zi}_{{\displaystyle \frac{\alpha {\beta }^2}{4}},0}\left(\alpha a^2\right),$$

$$b_2=B-\Gamma \left({\displaystyle \frac{1}{2}}-{\displaystyle \frac{\alpha {\beta }^2}{4}}\right)\left(2\alpha a^2{}^{{\displaystyle \frac{1}{4{\alpha }^{2}a}}g\left(\alpha a^2\right)}\mathrm{Zi}_{{\displaystyle \frac{\alpha {\beta }^2}{4}},0}^{\prime }\left(\alpha a^2\right)-{}^{{\displaystyle \frac{1}{4{\alpha }^{2}a}}g\left(\alpha a^2\right)}\mathrm{Zi}_{{\displaystyle \frac{\alpha {\beta }^2}{4}},0}\left(\alpha a^2\right)\right)$$

Proof. 

To solve the initial value problem, we start by substituting the initial conditions from (32) into Equations (17) and (30), yielding

$$A={\displaystyle \frac{1}{a}}\left(C_1{\mathrm{M}}_{{\displaystyle \frac{\alpha {\beta }^2}{4}},0}\left(\alpha a^2\right)+C_2{\mathrm{W}}_{{\displaystyle \frac{\alpha {\beta }^2}{4}},0}\left(\alpha a^2\right)+\Gamma \left({\displaystyle \frac{1}{2}}-{\displaystyle \frac{\alpha {\beta }^2}{4}}\right){}^{{\displaystyle \frac{1}{4{\alpha }^{2}a}}g\left(\alpha a^2\right)}\mathrm{Zi}_{{\displaystyle \frac{\alpha {\beta }^2}{4}},0}\left(\alpha a^2\right)\right),$$

(36)

$$\begin{array}{cc}\hfill B=& {\displaystyle \frac{1}{a^2}}[\left(2\alpha a^2{\mathrm{M}}_{{\displaystyle \frac{\alpha {\beta }^2}{4}},0}^{\prime }\left(\alpha a^2\right)-{\mathrm{M}}_{{\displaystyle \frac{\alpha {\beta }^2}{4}},0}\left(\alpha a^2\right)\right)C_1\hfill \\ \hfill & +\left(2\alpha a^2{\mathrm{W}}_{{\displaystyle \frac{\alpha {\beta }^2}{4}},0}^{\prime }\left(\alpha a^2\right)-{\mathrm{W}}_{{\displaystyle \frac{\alpha {\beta }^2}{4}},0}\left(\alpha a^2\right)\right)C_2\hfill \\ \hfill & +\Gamma \left({\displaystyle \frac{1}{2}}-{\displaystyle \frac{\alpha {\beta }^2}{4}}\right)\left(2\alpha a^2{}^{{\displaystyle \frac{1}{4{\alpha }^{2}a}}g\left(\alpha a^2\right)}\mathrm{Zi}_{{\displaystyle \frac{\alpha {\beta }^2}{4}},0}^{\prime }\left(\alpha a^2\right)-{}^{{\displaystyle \frac{1}{4{\alpha }^{2}a}}g\left(\alpha a^2\right)}\mathrm{Zi}_{{\displaystyle \frac{\alpha {\beta }^2}{4}},0}^{\prime }\left(\alpha a^2\right)\right)],\hfill \end{array}$$

(37)

which can be written in matrix form as

$$\left[\begin{array}{cc}{a}_{11}\hfill & a_{12}\hfill \\ a_{13}\hfill & a_{14}\hfill \end{array}\right]\left[\begin{array}{c}{C}_1\hfill \\ C_2\hfill \end{array}\right]=\left[\begin{array}{c}{b}_1\hfill \\ b_2\hfill \end{array}\right],$$

(38)

where

$$a_{11}={\displaystyle \frac{1}{a}}{\mathrm{M}}_{{\displaystyle \frac{\alpha {\beta }^2}{4}},0}\left(\alpha a^2\right),$$

$$a_{12}={\mathrm{W}}_{{\displaystyle \frac{\alpha {\beta }^2}{4}},0}\left(\alpha a^2\right),$$

$$a_{21}={\displaystyle \frac{1}{a^2}}\left(2\alpha a^2{\mathrm{M}}_{{\displaystyle \frac{\alpha {\beta }^2}{4}},0}^{\prime }\left(\alpha a^2\right)-{\mathrm{M}}_{{\displaystyle \frac{\alpha {\beta }^2}{4}},0}\left(\alpha a^2\right)\right),$$

$$a_{22}=\left(2\alpha a^2{\mathrm{W}}_{{\displaystyle \frac{\alpha {\beta }^2}{4}},0}^{\prime }\left(\alpha a^2\right)-{\mathrm{W}}_{{\displaystyle \frac{\alpha {\beta }^2}{4}},0}\left(\alpha a^2\right)\right),$$

$$b_1=A-\Gamma \left({\displaystyle \frac{1}{2}}-{\displaystyle \frac{\alpha {\beta }^2}{4}}\right){}^{{\displaystyle \frac{1}{4{\alpha }^{2}a}}g\left(\alpha a^2\right)}\mathrm{Zi}_{{\displaystyle \frac{\alpha {\beta }^2}{4}},0}\left(\alpha a^2\right),$$

$$b_2=B-\Gamma \left({\displaystyle \frac{1}{2}}-{\displaystyle \frac{\alpha {\beta }^2}{4}}\right)\left(2\alpha a^2{}^{{\displaystyle \frac{1}{4{\alpha }^{2}a}}g\left(\alpha a^2\right)}\mathrm{Zi}_{{\displaystyle \frac{\alpha {\beta }^2}{4}},0}^{\prime }\left(\alpha a^2\right)-{}^{{\displaystyle \frac{1}{4{\alpha }^{2}a}}g\left(\alpha a^2\right)}\mathrm{Zi}_{{\displaystyle \frac{\alpha {\beta }^2}{4}},0}\left(\alpha a^2\right)\right).$$

Upon solving the system, we get

$$\begin{array}{c}\hfill C_1=-{\displaystyle \frac{a_{12}{b}_2-a_{22}{b}_1}{a_{11}{a}_{22}-a_{12}{a}_{21}}},\end{array}$$

(39)

and

$$\begin{array}{c}\hfill C_2=-{\displaystyle \frac{a_{11}{b}_2-a_{21}{b}_1}{a_{11}{a}_{22}-a_{12}{a}_{21}}}.\end{array}$$

(40)

□

Having established the general analysis, we proceed to exemplify the solution of initial value problems governed by Equation (2). An illustrative case is defined by the parameters $\alpha =1$ and $\beta =1$, coupled with the initial conditions

$$\mathrm{y}\left(1\right)=1,y^{\prime }\left(1\right)=1.$$

(41)

The solutions to this initial value problem, corresponding to distinct definitions of the source term $\mathrm{g}\left(x\right)$, are computationally derived and plotted in Figure 1. In Figure 2, the solution is presented for $g\left(x\right)=e^{-x}$, $\alpha =1$ and various values of $\beta$. The effect of $\alpha$ on the solution is shown in Figure 3 for $\beta =1$, $g\left(x\right)=e^{-x}$ and different values of $\alpha$.

4.2. Boundary Value Problem

In this section, we consider boundary value problems associated with Equation (2), subject to appropriate boundary conditions. The main result is summarized in the following theorem.

Theorem 3.

Consider the inhomogeneous Whittaker-type differential equation given in Equation (2), subject to the following Boundary conditions:

$$\mathrm{y}\left(a\right)=A,y\left(b\right)=B.$$

(42)

The solution is given by

$$y\left(x\right)={\displaystyle \frac{1}{x}}\left(C_1{\mathrm{M}}_{{\displaystyle \frac{\alpha {\beta }^2}{4}},0}\left(\alpha x^2\right)+C_2{\mathrm{W}}_{{\displaystyle \frac{\alpha {\beta }^2}{4}},0}\left(\alpha x^2\right)+\Gamma \left({\displaystyle \frac{1}{2}}-{\displaystyle \frac{\alpha {\beta }^2}{4}}\right){}^{{\displaystyle \frac{1}{4{\alpha }^{2}x}}g\left(\alpha x^2\right)}\mathrm{Zi}_{{\displaystyle \frac{\alpha {\beta }^2}{4}},0}\left(\alpha x^2\right)\right),$$

(43)

where the Constants $C_1$ and $C_2$ satisfy

$$\begin{array}{c}\hfill C_1=-{\displaystyle \frac{a_{12}{b}_2-a_{22}{b}_1}{a_{11}{a}_{22}-a_{12}{a}_{21}}},\end{array}$$

(44)

and

$$\begin{array}{c}\hfill C_2=-{\displaystyle \frac{a_{11}{b}_2-a_{21}{b}_1}{a_{11}{a}_{22}-a_{12}{a}_{21}}},\end{array}$$

(45)

with

$$a_{11}={\displaystyle \frac{1}{a}}{\mathrm{M}}_{{\displaystyle \frac{\alpha {\beta }^2}{4}},0}\left(\alpha a^2\right),$$

$$a_{12}={\displaystyle \frac{1}{a}}{\mathrm{W}}_{{\displaystyle \frac{\alpha {\beta }^2}{4}},0}\left(\alpha a^2\right),$$

$$a_{21}={\displaystyle \frac{1}{b}}{\mathrm{M}}_{{\displaystyle \frac{\alpha {\beta }^2}{4}},0}\left(\alpha b^2\right)$$

$$a_{22}={\displaystyle \frac{1}{a}}{\mathrm{W}}_{{\displaystyle \frac{\alpha {\beta }^2}{4}},0}\left(\alpha b^2\right),$$

$$b_1=A-{\displaystyle \frac{1}{a}}\Gamma \left({\displaystyle \frac{1}{2}}-{\displaystyle \frac{\alpha {\beta }^2}{4}}\right){}^{{\displaystyle \frac{1}{4{\alpha }^{2}a}}g\left(\alpha a^2\right)}\mathrm{Zi}_{{\displaystyle \frac{\alpha {\beta }^2}{4}},0}\left(\alpha a^2\right),$$

$$b_2=B-{\displaystyle \frac{1}{b}}\Gamma \left({\displaystyle \frac{1}{2}}-{\displaystyle \frac{\alpha {\beta }^2}{4}}\right){}^{{\displaystyle \frac{1}{4{\alpha }^{2}b}}g\left(\alpha b^2\right)}\mathrm{Zi}_{{\displaystyle \frac{\alpha {\beta }^2}{4}},0}\left(\alpha b^2\right).$$

Proof. 

We will start by applying the boundary condition (42) to Equation (17) in order to obtain

$$A={\displaystyle \frac{1}{a}}\left(C_1{\mathrm{M}}_{{\displaystyle \frac{\alpha {\beta }^2}{4}},0}\left(\alpha a^2\right)+C_2{\mathrm{W}}_{{\displaystyle \frac{\alpha {\beta }^2}{4}},0}\left(\alpha a^2\right)+\Gamma \left({\displaystyle \frac{1}{2}}-{\displaystyle \frac{\alpha {\beta }^2}{4}}\right){}^{{\displaystyle \frac{1}{4{\alpha }^{2}a}}g\left(\alpha a^2\right)}\mathrm{Zi}_{{\displaystyle \frac{\alpha {\beta }^2}{4}},0}\left(\alpha a^2\right)\right),$$

(46)

$$B={\displaystyle \frac{1}{b}}\left(C_1{\mathrm{M}}_{{\displaystyle \frac{\alpha {\beta }^2}{4}},0}\left(\alpha b^2\right)+C_2{\mathrm{W}}_{{\displaystyle \frac{\alpha {\beta }^2}{4}},0}\left(\alpha b^2\right)+\Gamma \left({\displaystyle \frac{1}{2}}-{\displaystyle \frac{\alpha {\beta }^2}{4}}\right){}^{{\displaystyle \frac{1}{4{\alpha }^{2}a}}g\left(\alpha b^2\right)}\mathrm{Zi}_{{\displaystyle \frac{\alpha {\beta }^2}{4}},0}\left(\alpha b^2\right)\right),$$

(47)

which can be re-writen in matrix form as

$$\left[\begin{array}{cc}{a}_{11}\hfill & a_{12}\hfill \\ a_{13}\hfill & a_{14}\hfill \end{array}\right]\left[\begin{array}{c}{C}_1\hfill \\ C_2\hfill \end{array}\right]=\left[\begin{array}{c}{b}_1\hfill \\ b_2\hfill \end{array}\right].$$

(48)

where

$$a_{11}={\displaystyle \frac{1}{a}}{\mathrm{M}}_{{\displaystyle \frac{\alpha {\beta }^2}{4}},0}\left(\alpha a^2\right),$$

$$a_{12}={\displaystyle \frac{1}{a}}{\mathrm{W}}_{{\displaystyle \frac{\alpha {\beta }^2}{4}},0}\left(\alpha a^2\right),$$

$$a_{21}={\displaystyle \frac{1}{b}}{\mathrm{M}}_{{\displaystyle \frac{\alpha {\beta }^2}{4}},0}\left(\alpha b^2\right)$$

$$a_{22}={\displaystyle \frac{1}{a}}{\mathrm{W}}_{{\displaystyle \frac{\alpha {\beta }^2}{4}},0}\left(\alpha b^2\right),$$

$$b_1=A-{\displaystyle \frac{1}{a}}\Gamma \left({\displaystyle \frac{1}{2}}-{\displaystyle \frac{\alpha {\beta }^2}{4}}\right){}^{{\displaystyle \frac{1}{4{\alpha }^{2}a}}g\left(\alpha a^2\right)}\mathrm{Zi}_{{\displaystyle \frac{\alpha {\beta }^2}{4}},0}\left(\alpha a^2\right),$$

$$b_2=B-{\displaystyle \frac{1}{b}}\Gamma \left({\displaystyle \frac{1}{2}}-{\displaystyle \frac{\alpha {\beta }^2}{4}}\right){}^{{\displaystyle \frac{1}{4{\alpha }^{2}b}}g\left(\alpha b^2\right)}\mathrm{Zi}_{{\displaystyle \frac{\alpha {\beta }^2}{4}},0}\left(\alpha b^2\right).$$

Upon solving the system, we get

$$\begin{array}{c}\hfill C_1=-{\displaystyle \frac{a_{12}{b}_2-a_{22}{b}_1}{a_{11}{a}_{22}-a_{12}{a}_{21}}},\end{array}$$

(49)

and

$$\begin{array}{c}\hfill C_2=-{\displaystyle \frac{a_{11}{b}_2-a_{21}{b}_1}{a_{11}{a}_{22}-a_{12}{a}_{21}}}.\end{array}$$

(50)

□

Solutions corresponding to various functions $g\left(x\right)$ and boundary conditions $y\left(1\right)=1$ and $y\left(2\right)=1$ are shown in Figure 4, for illustration.

5. Conclusions

In the above work, particular and general solutions to the class of Whittaker-type differential equations of the form given by Equation (2) were semi-analytically obtained and presented, together with the methodology for obtaining these solutions. Both initial and boundary value problems were considered within the introduced framework. The analytical approach employed in this work is based on the function ${\mathrm{Zi}}_{{\displaystyle \frac{\alpha {\beta }^2}{4}},0}\left(x\right)$, introduced in [12]. Graphical representations of the solutions were provided for selected parameter values and corresponding external forcing functions $\mathrm{g}\left(\mathrm{x}\right)$ generated and evaluated using the symbolic manipulation capabilities of Maple^TM. The method developed herein contributes to the broader study of inhomogeneous Whittaker-type differential equations. While in the current work emphasis is placed on computational evaluations of the ${\mathrm{Zi}}_{{\displaystyle \frac{\alpha {\beta }^2}{4}},0}\left(x\right)$ function, a more in-depth future analytical investigation could yield closed form expressions for this function, particularly for the special case where $\mu =0$. The methodology developed in this work is not restricted to the specific differential equation under consideration; it might prove effective in deriving solutions to a broader class of Whittaker-type differential equations. Future work could benefit from extensions beyond linear Whittaker’s equation to include nonlinear Whittaker-type equations and fractional Whittaker-type systems of equations, in addition to extensions involving certain partial differential equations governing heat and fluid flow and their associated numerical schemes.