Heat Transfer Enhancement and Entropy Minimization Through Corrugation and Base Inclination Control in MHD-Assisted Cu–H₂O Nanofluid Convection

Abstract

Efficient management of heat transfer and entropy generation in nanofluid enclosures is essential for the development of high-performance thermal systems. This study employs the finite element method (FEM) to numerically analyze the effects of wall corrugation and base inclination on magnetohydrodynamic (MHD)-assisted natural convection of Cu–H₂O nanofluid in a trapezoidal cavity containing internal heat-generating obstacles. The governing equations for fluid flow, heat transfer, and entropy generation are solved for a wide range of Rayleigh numbers (10³–10⁶), Hartmann numbers (0–50), and geometric configurations. Results show that for square obstacles, the Nusselt number increases from 0.8417 to 0.8457 as the corrugation amplitude rises (a = 0.025 L–0.065 L) at Ra = 10³, while the maximum heat transfer (Nu = 6.46) occurs at Ra = 10⁶. Entropy generation slightly increases with amplitude (15.46–15.53) but decreases under stronger magnetic fields due to Lorentz damping. Higher corrugation frequencies (f = 9.5) further enhance convection, producing Nu ≈ 6.44–6.47 for square and triangular obstacles. Base inclination significantly influences performance: γ = 10° yields maximum heat transfer (Nu ≈ 6.76), while γ = 20° minimizes entropy (St ≈ 0.00139). These findings confirm that optimized corrugation and inclination, particularly with square obstacles, can effectively enhance convective transport while minimizing irreversibility, providing practical insights for the design of energy-efficient MHD-assisted heat exchangers and cooling systems.

1. Introduction

Natural convection within enclosures has long been a central focus of thermal fluid research owing to its widespread applications in geophysical and industrial processes, including electronic cooling, solar energy collection, thermal storage, and biomedical systems [1,2]. The emergence of nanofluid base fluids enhanced with high-conductivity nanoparticles such as Cu, Al₂O₃, TiO₂, and Ag has significantly improved the heat transfer characteristics of convective systems by increasing effective thermal conductivity and promoting stronger buoyancy-driven motion [3,4,5,6]. Among these, Cu–H₂O nanofluid has gained prominence due to its excellent stability, high thermal conductivity, and superior energy transport efficiency, making it a suitable working medium for microscale and compact thermal devices [7,8,9,10].

Cavity geometry and internal configuration exert substantial influence on natural and mixed convection behavior. Studies have demonstrated that parameters such as internal heat sources [11,12,13], obstacle shape [14,15,16], and boundary heating conditions [17,18,19] critically affect thermal distribution and flow circulation. Research on enclosures with corrugated or wavy walls has shown that geometric undulations effectively disrupt thermal boundary layers, induce secondary eddies, and enhance local convective transport [20,21,22,23]. Similarly, the inclination of cavity walls modifies buoyancy direction and alters flow symmetry, yielding significant variations in heat transfer rate and entropy generation [24,25,26].

In recent years, the application of magnetic fields in nanofluid-filled cavities has attracted considerable attention. Magnetohydrodynamic (MHD) effects can suppress or enhance convective transport depending on the Hartmann number, magnetic field strength, and orientation [27,28,29,30,31]. The Lorentz force generated by magnetic fields influences both velocity and temperature gradients, providing a controllable means to optimize thermal performance. Concurrently, entropy generation has emerged as a key thermodynamic metric for quantifying system irreversibility, enabling the assessment of the trade-off between increased heat transfer and enhanced viscous or Joule dissipation [32,33].

A recent investigation reported the behavior of a hybrid MWCNT–Fe₃O₄/water nanofluid convection in a porous wavy trapezoidal enclosure under the influence of MHD [34]. While that study primarily emphasized the effects of porosity and hybrid nanoparticle interaction, the present research focuses on a non-porous trapezoidal cavity containing Cu–H₂O nanofluid with corrugated walls, base inclination, and internal heat-generating obstacles. This work further extends the understanding of MHD-assisted nanofluid convection by integrating geometric and thermodynamic optimization. A related study on conjugate mixed convection in a lid-driven cavity with internal heat generation and a spinning solid cylinder [35] provides additional validation context and serves as a benchmark for the present numerical approach.

Despite extensive prior research, the combined influence of wall corrugation, base inclination, and magnetic field interaction on conjugate natural convection and entropy generation within non-porous trapezoidal nanofluid enclosures remains insufficiently explored. The present study addresses this gap by numerically analyzing MHD-assisted Cu–H₂O nanofluid convection using the finite element method. The goal is to identify geometric and magnetic configurations that simultaneously enhance heat transfer and minimize entropy production, thereby providing valuable insights for the development of efficient thermal management systems, advanced cooling technologies, and next-generation compact heat exchangers.

2. Materials and Methods

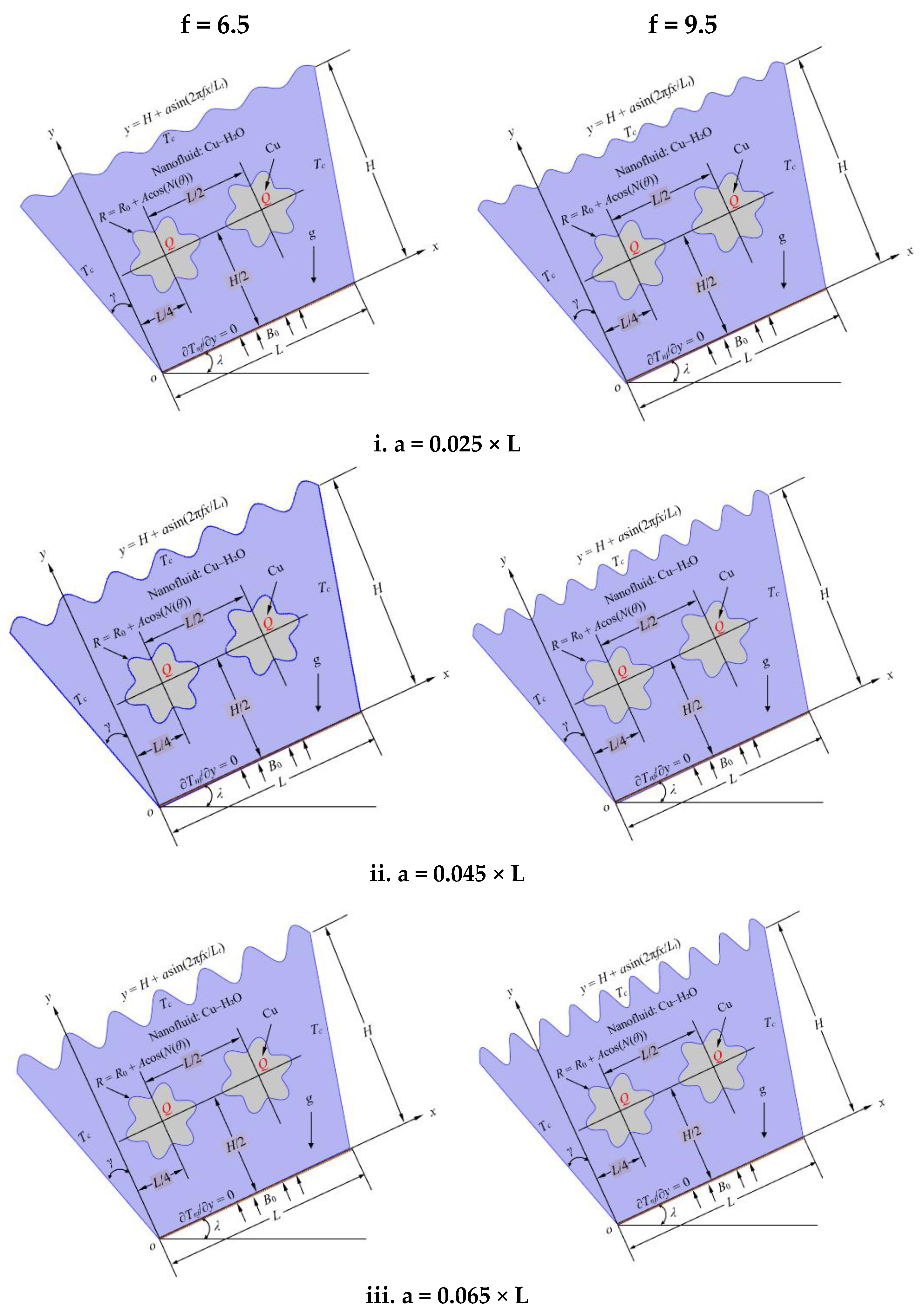
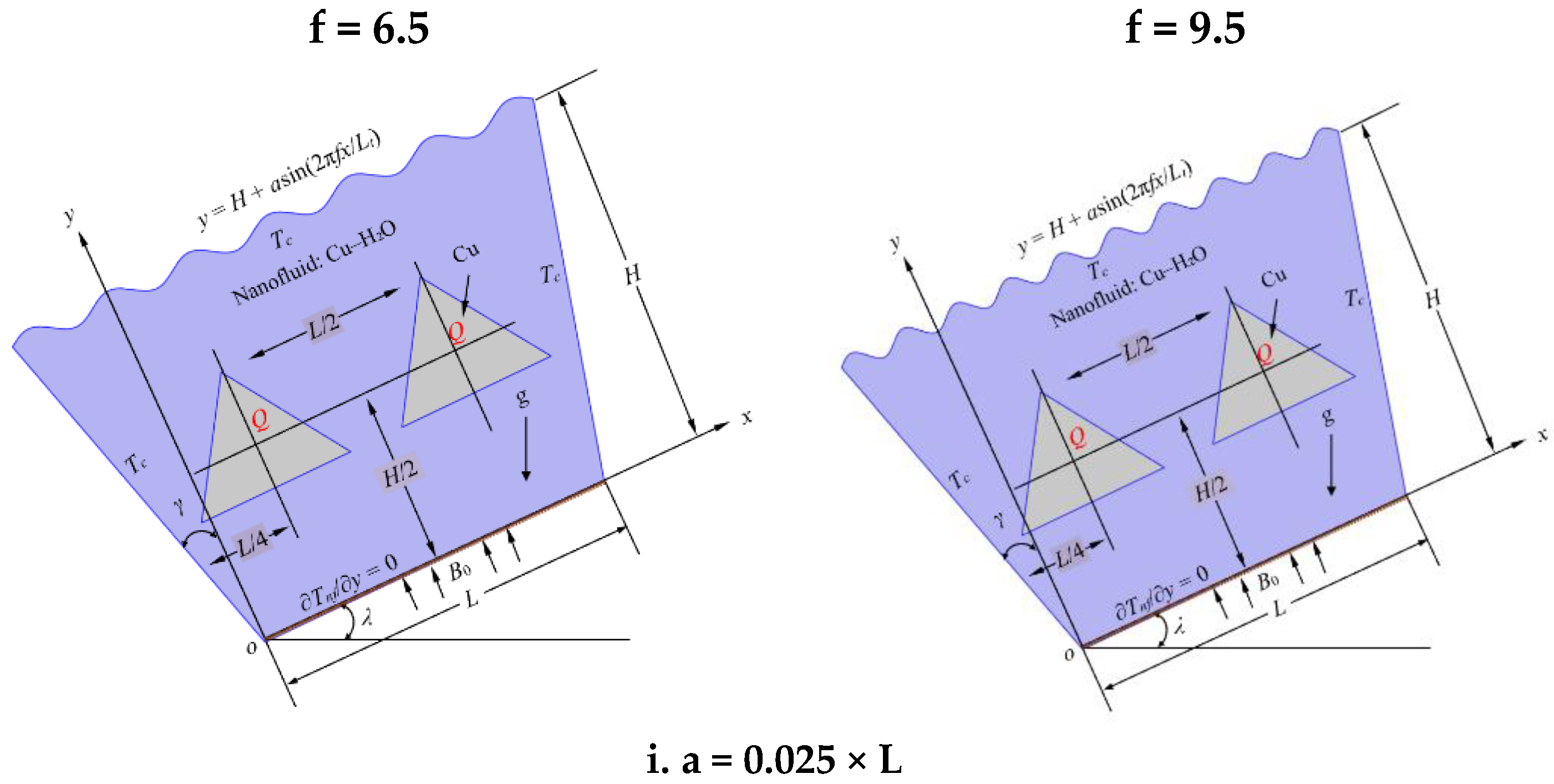
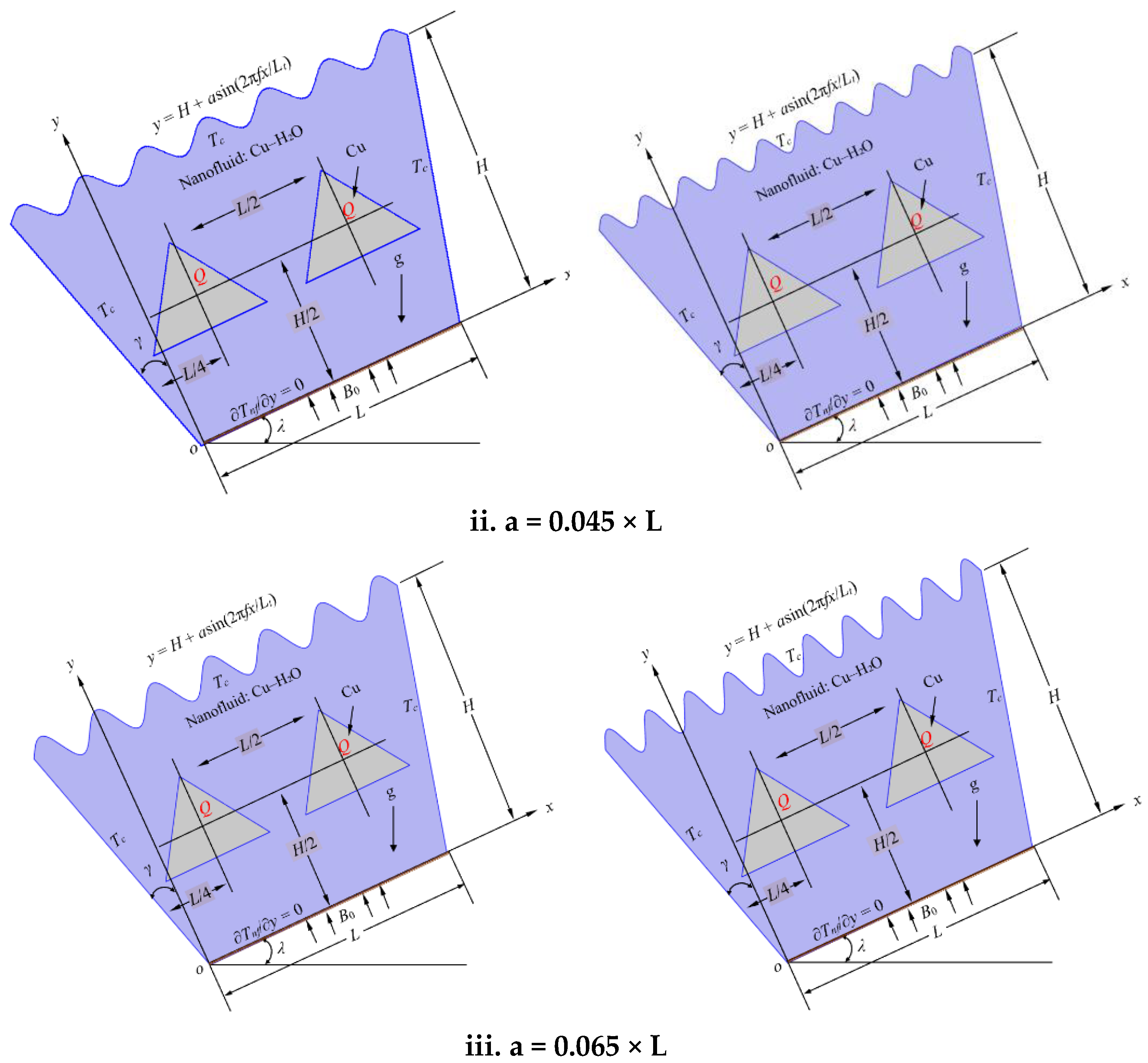
This study focuses on enhancing heat transfer and minimizing entropy generation in a two-dimensional trapezoidal cavity filled with Cu–H₂O nanofluid under the influence of a uniform horizontal magnetic field. The cavity features a cold sinusoidally corrugated top wall, an adiabatic inclined base, and two cold slanted side walls. Internally, heat-generating solid obstacles of various shapes are embedded symmetrically. The primary aim is to investigate the effects of top wall corrugation, base inclination angle, and internal obstacle geometry on natural convection and thermodynamic irreversibility in an MHD environment.

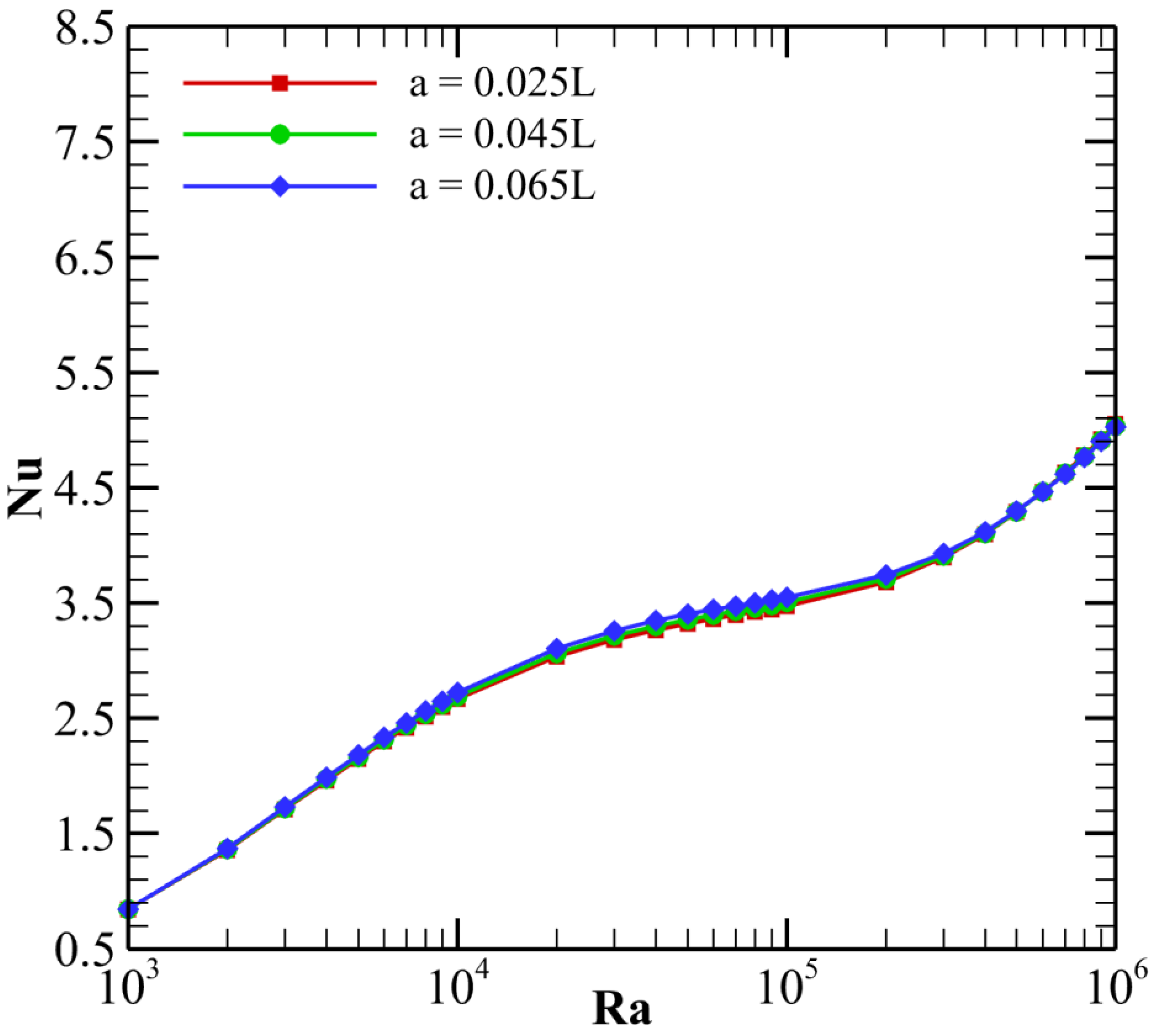
The sinusoidal top wall introduces surface complexity, mathematically defined by the function y = H + asin (2πfx/Lt), where a is the amplitude of corrugation and f is the frequency. In this study, three amplitudes (0.025 L, 0.045 L, and 0.065 L) and two frequencies (6.5 and 9.5) were selected to systematically examine the influence of wall corrugation intensity on the overall thermal performance of the enclosure. Lower amplitudes and frequencies correspond to smoother surfaces, which promote stable convection with limited boundary layer disruption. In contrast, higher values generate more pronounced undulations, enhancing local mixing and heat transfer but potentially increasing entropy generation. These selected ranges provide a balanced representation of convective behavior and thermodynamic efficiency. Figure 1, Figure 2 and Figure 3 show the geometries for square, star, and triangle-shaped obstacles, respectively, under various combinations of amplitude and frequency. These shapes were chosen to reflect a range of surface area-to-volume ratios and thermal interaction behaviors. 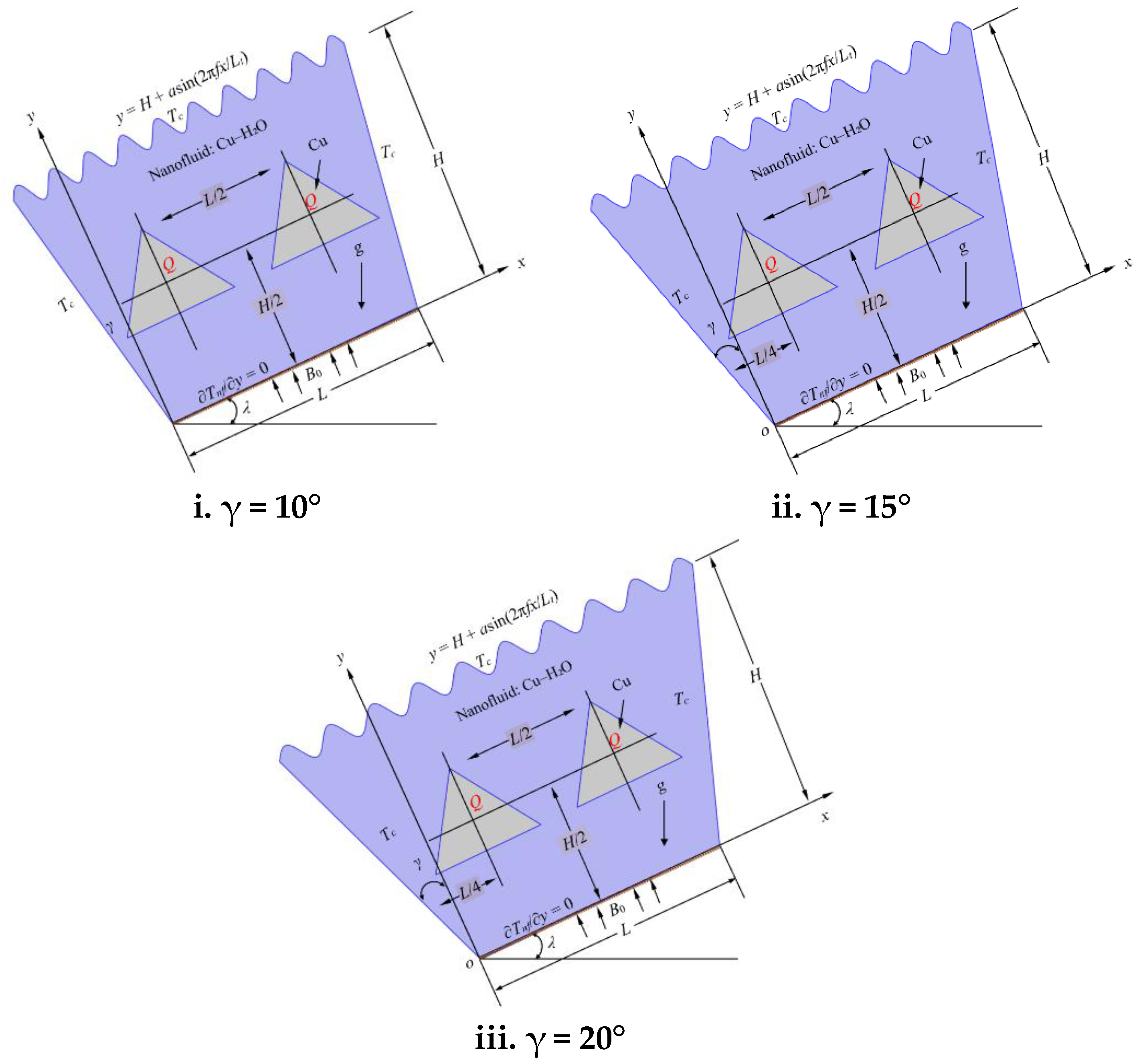Figure 4, Figure 5 and Figure 6 further illustrate how varying the base angle (γ = 10°, 15°, and 20°) affects the convective flow field and entropy production, particularly when the top wall corrugation is fixed at A = 0.045 L and f = 9.5.

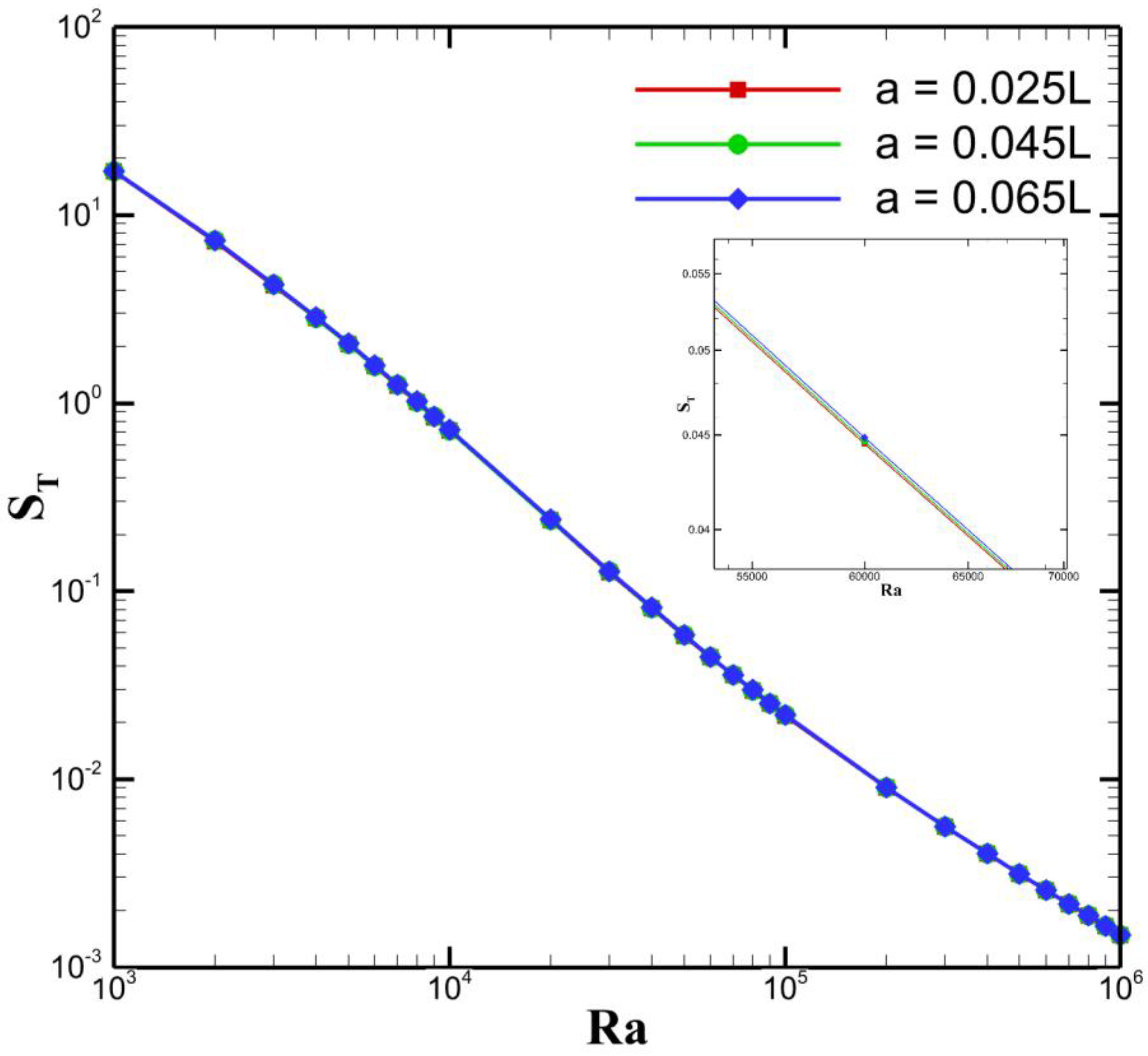
In this study, entropy generation and heat transfer are analyzed for Rayleigh numbers (10³–10⁶) and Hartmann numbers (0–50). The selected Rayleigh number range represents the transition from weak to strongly developed natural convection, while the chosen Hartmann numbers capture the shift from buoyancy-dominated to magnetically influenced regimes, enabling a comprehensive assessment of Lorentz force and buoyancy effects on flow behavior, heat transfer, and entropy generation within the cavity.

In this study, Joule heating and viscous dissipation were neglected because their effects are insignificant under laminar natural convection with internal heat-generating obstacles and low-to-moderate Hartmann number ranges, where buoyancy and thermal conduction predominantly govern the energy transport.

The computational model is based on a steady-state, laminar, two-dimensional formulation of the governing equations for fluid flow and heat transfer. The governing set consists of 22 equations, labeled Equations (1)–(22), including the continuity equation, momentum equations in the x and y directions (incorporating the Lorentz force), the energy equations for both fluid and solid regions, and the local entropy generation equation. Entropy generation is calculated from two main contributions: heat transfer irreversibility and fluid friction irreversibility. These equations are non-dimensionalized using characteristic scales for length, temperature, and velocity, and the magnetic field effect is quantified using the Hartmann number.

Boundary conditions for the model are detailed in

Table 1. Boundary Conditions.

Boundary Element	Label/Equation	Type	Mathematical Condition	Physical Description
Top Wavy Wall	y = H + asin(2πfx/Lt)	Isothermal (Cold)	T = Tc	Wavy top maintained at constant cold temperature; enhances surface area and mixing.
Bottom Inclined Wall	Inclined at angle λ	Thermally insulated (Adiabatic)	∂T/∂n = 0	The Bottom wall is thermally insulated, which prevents heat loss.
Left & Right Walls	Slanted at angle γ	Isothermal (Cold)	T = Tc	Left and Right walls are maintained at a constant cold temperature, which enhances surface area and mixing.
Internal Shaped Blocks	R = R0 + Acos(Nθ)	Heat Generation (Solid)	q = Q = const	Internal heat sources embedded in nanofluid; modeled with volumetric heat generation.
All Solid Surfaces	Cavity and block boundaries	No-slip Velocity	u = 0, v = 0	Viscous boundary layers form due to fluid-solid interaction.
Entire Fluid Domain	Volume enclosed by walls and blocks	Magnetic Field (MHD)	B = B0 î	Uniform horizontal magnetic field introduces Lorentz force; quantified via Hartmann number.
Gravity	g⃗↓	Buoyancy-driven flow	Acts in y direction	Drives natural convection from heated blocks to cold boundaries.

. The combined thermal and fluid boundary conditions ensure realistic heat exchange between solid blocks and the surrounding nanofluid. Thermophysical properties used in the model are presented in

Table 2. Thermo-physical properties of Water and Cu at T_m = 300K ([8,19]).

Name of Property	Symbol	Unit	Water	Cu
Mass Density	ρ	kgm−3	996.6	8933
Specific Heat at Constant Pressure	Cp	Jkg−1K−1	4179.2	385
Thermal Conductivity	k	Wm−1K−1	0.6102	401
Volumetric Thermal Expansion Coefficient	β	K−1	26.6 × 10−5	49.9 × 10−6
Electrical Conductivity	σ	Sm−1	0.05	59.6 × 10−6
Dynamic viscosity	μ	kgm−1s−1	8.538 × 10−4	-

. The effective properties of the Cu–H₂O nanofluid are calculated using established correlations that account for particle volume fraction and base fluid characteristics. The selection of Cu nanoparticles is motivated by their high thermal conductivity, which is expected to significantly improve the overall heat transfer rate in the cavity.

Fluid domain:

$${\displaystyle \frac{\mathsf{\partial }u}{\mathsf{\partial }x}}+{\displaystyle \frac{\mathsf{\partial }v}{\mathsf{\partial }y}}=0$$

(1)

$${\rho }_{nf}\left(u{\displaystyle \frac{\mathsf{\partial }u}{\mathsf{\partial }x}}+v{\displaystyle \frac{\mathsf{\partial }u}{\mathsf{\partial }y}}\right)=-{\displaystyle \frac{\mathsf{\partial }p}{\mathsf{\partial }x}}+{\mu }_{nf}\left({\displaystyle \frac{{\mathsf{\partial }}^{2}u}{\mathsf{\partial }{x}^2}}+{\displaystyle \frac{{\mathsf{\partial }}^{2}u}{\mathsf{\partial }{y}^2}}\right)+{\rho }_{nf}g{\beta }_{nf}\left(T_{nf}-T_c\right)\sin \left(\lambda \right)-{\sigma }_{nf}{B}_0^{2}u$$

(2)

$${\rho }_{nf}\left(u{\displaystyle \frac{\mathsf{\partial }v}{\mathsf{\partial }x}}+v{\displaystyle \frac{\mathsf{\partial }v}{\mathsf{\partial }y}}\right)=-{\displaystyle \frac{\mathsf{\partial }p}{\mathsf{\partial }y}}+{\mu }_{nf}\left({\displaystyle \frac{{\mathsf{\partial }}^{2}v}{\mathsf{\partial }{x}^2}}+{\displaystyle \frac{{\mathsf{\partial }}^{2}v}{\mathsf{\partial }{y}^2}}\right)+{\rho }_{nf}g{\beta }_{nf}\left(T_{nf}-T_c\right)\cos \left(\lambda \right)$$

(3)

$${\rho }_{nf}{C}_{p,nf}\left(u{\displaystyle \frac{\mathsf{\partial }{T}_{nf}}{\mathsf{\partial }x}}+v{\displaystyle \frac{\mathsf{\partial }{T}_{nf}}{\mathsf{\partial }y}}\right)=k_{nf}\left({\displaystyle \frac{{\mathsf{\partial }}^2{T}_{nf}}{\mathsf{\partial }{x}^2}}+{\displaystyle \frac{{\mathsf{\partial }}^2{T}_{nf}}{\mathsf{\partial }{y}^2}}\right)$$

(4)

Solid domains:

$$k_s\left({\displaystyle \frac{{\mathsf{\partial }}^2{T}_s}{\mathsf{\partial }{x}^2}}+{\displaystyle \frac{{\mathsf{\partial }}^2{T}_s}{\mathsf{\partial }{y}^2}}\right)+Q=0$$

(5)

Here, u and v denote velocity components in the x- and y-directions, respectively, and p and T represent pressure and temperature, respectively. The fluid properties are mass density (ρ), thermal conductivity (k), specific heat at constant pressure (C_p), volumetric thermal expansion coefficient (β), and electrical conductivity (σ).

$${\rho }_{nf}=(1-\varphi ){\rho }_f+\varphi {\rho }_s$$

(6)

$${(\rho c_p)}_{nf}=(1-\varphi ){(\rho c_p)}_f+\varphi {(\rho c_p)}_s$$

(7)

$${\mu }_{nf}={\displaystyle \frac{{\mu }_f}{{(1-\varphi )}^{2.5}}}$$

(8)

$$k_{nf}=k_f[{\displaystyle \frac{k_s+2k_f-2\varphi (k_f-k_s)}{k_s+2k_f+\varphi (k_f-k_s)}}]$$

(9)

$${\beta }_{nf}={\displaystyle \frac{(1-\varphi ){\rho }_f{\beta }_f+\varphi {\rho }_s{\beta }_s}{{\rho }_{nf}}}]$$

(10)

Entropy generation reflects the loss of energy due to irreversible effects, such as heat transfer, friction, and MHD forces. In buoyancy-driven MHD flow, entropy is generated through heat transfer, viscous dissipation, and magnetic fields. The local entropy generation due to heat transfer ($S_{ht}$) in solid and fluid domains, volumetric entropy production due to viscous flow dissipation ($S_{ff}$), and external magnetic effects ($S_{mf}$) can be described using the following formulas:

$$S_{ht}={\displaystyle \frac{k_s}{T_s^2}}\left[{\left({\displaystyle \frac{\mathsf{\partial }{T}_s}{\mathsf{\partial }x}}\right)}^2+{\left({\displaystyle \frac{\mathsf{\partial }{T}_s}{\mathsf{\partial }y}}\right)}^2\right]+{\displaystyle \frac{k_{nf}}{T_{nf}^2}}\left[{\left({\displaystyle \frac{\mathsf{\partial }{T}_{nf}}{\mathsf{\partial }x}}\right)}^2+{\left({\displaystyle \frac{\mathsf{\partial }{T}_{nf}}{\mathsf{\partial }y}}\right)}^2\right]+{\displaystyle \frac{Q_{gen}}{T_s}}$$

(11)

$$S_{ff}={\displaystyle \frac{{\mu }_{nf}}{T_{nf}}}\left[2{\left({\displaystyle \frac{\mathsf{\partial }u}{\mathsf{\partial }x}}\right)}^2+2{\left({\displaystyle \frac{\mathsf{\partial }v}{\mathsf{\partial }y}}\right)}^2+{\left({\displaystyle \frac{\mathsf{\partial }u}{\mathsf{\partial }y}}+{\displaystyle \frac{\mathsf{\partial }v}{\mathsf{\partial }x}}\right)}^2\right]$$

(12)

$$S_{mf}={\beta }_0^2{\displaystyle \frac{{\sigma }_{nf}}{T_{nf}}}{\nu }^2$$

(13)

To get the non-dimensional governing equations, the following scales are used:

$$X={\displaystyle \frac{x}{L}},Y={\displaystyle \frac{y}{L}},U={\displaystyle \frac{uL}{{\alpha }_f}},V={\displaystyle \frac{vL}{{\alpha }_f}},\theta ={\displaystyle \frac{T-T_c}{T_h-T_c}},P={\displaystyle \frac{p{L}^2}{{\mu }_{nf}}},Here,{\alpha }_f={\displaystyle \frac{k_f}{{\rho }_f{c}_{p,f}}}$$

(14)

$$Ra={\displaystyle \frac{g{\beta }_{nf}(T_h-T_c)L^3}{{\nu }_{nf}{\alpha }_{nf}}},Here,{\alpha }_{nf}={\displaystyle \frac{k_{nf}}{{\rho }_{nf}{c}_{p,nf}}},\mathrm{Pr}={\displaystyle \frac{{\nu }_{nf}}{{\alpha }_{nf}}},Ha=B_{0}L\sqrt{{\displaystyle \frac{{\sigma }_{nf}}{{\mu }_{nf}}}},Q^{\ast }={\displaystyle \frac{Q{L}^2}{k_{nf}(T_h-T_c)}}$$

(15)

Now, the Non-Dimensional governing equations are:

$${\displaystyle \frac{\mathsf{\partial }U}{\mathsf{\partial }X}}+{\displaystyle \frac{\mathsf{\partial }V}{\mathsf{\partial }Y}}=0$$

(16)

$$(U{\displaystyle \frac{\mathsf{\partial }U}{\mathsf{\partial }X}}+V{\displaystyle \frac{\mathsf{\partial }U}{\mathsf{\partial }Y}})=-{\displaystyle \frac{\mathsf{\partial }P}{\mathsf{\partial }X}}+{\displaystyle \frac{{\mu }_{nf}}{{\mu }_f}}\left({\displaystyle \frac{{\mathsf{\partial }}^{2}U}{\mathsf{\partial }{X}^2}}+{\displaystyle \frac{{\mathsf{\partial }}^{2}U}{\mathsf{\partial }{Y}^2}}\right)+Ra\mathrm{Pr}{\displaystyle \frac{{\rho }_{nf}{\beta }_{nf}}{{\rho }_f{\beta }_f}}\theta \sin (\lambda )-H{a}^{2}U$$

(17)

$$(U{\displaystyle \frac{\mathsf{\partial }V}{\mathsf{\partial }X}}+V{\displaystyle \frac{\mathsf{\partial }V}{\mathsf{\partial }Y}})=-{\displaystyle \frac{\mathsf{\partial }P}{\mathsf{\partial }X}}+{\displaystyle \frac{{\mu }_{nf}}{{\mu }_f}}\left({\displaystyle \frac{{\mathsf{\partial }}^{2}V}{\mathsf{\partial }{X}^2}}+{\displaystyle \frac{{\mathsf{\partial }}^{2}V}{\mathsf{\partial }{Y}^2}}\right)+Ra\mathrm{Pr}{\displaystyle \frac{{\rho }_{nf}{\beta }_{nf}}{{\rho }_f{\beta }_f}}\theta \cos (\lambda )-H{a}^{2}U$$

(18)

$$(U{\displaystyle \frac{\mathsf{\partial }\theta }{\mathsf{\partial }X}}+V{\displaystyle \frac{\mathsf{\partial }\theta }{\mathsf{\partial }Y}})={\displaystyle \frac{k_{nf}}{k_f}}{\displaystyle \frac{1}{\mathrm{Pr}}}\left({\displaystyle \frac{{\mathsf{\partial }}^2\theta }{\mathsf{\partial }{X}^2}}+{\displaystyle \frac{{\mathsf{\partial }}^2\theta }{\mathsf{\partial }{Y}^2}}\right)+Q^{\ast }$$

(19)

The thermal behavior of the chamber under different operating conditions is assessed by analyzing the Nusselt number (Nu) of the heated strips and the average fluid temperature (Θ_av) inside the domain. The definitions of these quantities are as follows:

$$Nu={\displaystyle \frac{L}{L_s}}\left[-{\displaystyle \underset{L_0/L}{\overset{2L_0/L}{\int }}{\left.\frac{\mathsf{\partial }\Theta }{\mathsf{\partial }Y}\right|}_{Y=0}dX}-{\displaystyle \underset{3L_0/L}{\overset{4L_0/L}{\int }}{\left.\frac{\mathsf{\partial }\Theta }{\mathsf{\partial }Y}\right|}_{Y=0}dX}\right],{\Theta }_{av}={\displaystyle \frac{1}{A}}{\displaystyle \underset{A}{\int }\Theta dA}$$

(20)

The total entropy generation, expressed as a dimensionless quantity, can be obtained using the following expression:

$$S_T={\displaystyle \frac{T_c^2{L}^2}{k_f\Delta T^{2}A}}{\displaystyle \underset{A}{\int }\left(S_{ht}+S_{ff}+S_{mf}\right)}dA$$

(21)

where A represents the surface area of the computational domain.

In this study, the thermo-physical properties (Table 2) of the Cu–H₂O nanofluid are considered constant at the mean temperature $T_m=300\hspace{0.17em}K$. The temperature variation within the cavity is relatively small, so changes in viscosity and thermal conductivity are negligible. This approach is consistent with previous laminar nanofluid convection studies [8,19], which have shown that constant properties provide accurate predictions of heat transfer and entropy generation behavior. Furthermore, the influence of nanoparticles on the electrical conductivity of the Cu–H₂O nanofluid was not explicitly modeled, as the variations in this property are negligible within the studied temperature range. The relations defining the effective thermo-physical properties of the nanofluid have been adopted from established models.

Numerical simulation is conducted using the finite element method (FEM). A structured and refined mesh is generated, with higher density near the corrugated top wall, internal obstacles, and boundary layers to ensure solution accuracy. The Galerkin method is employed to discretize the governing equations. A convergence criterion is set such that residuals for all governing equations fall below 10⁻⁶. The numerical model is validated through mesh independence and comparison with benchmark results, as discussed in the next section.

This modeling approach allows for a detailed parametric study of how geometric modifications (corrugation amplitude and frequency, base inclination, and obstacle shape) and electromagnetic forces interact to influence convective flow, heat transfer enhancement, and entropy generation inside nanofluid-filled enclosures.

3. Results

The numerical results of the investigation are presented in terms of the average Nusselt number (Nu) and entropy generation (St), which are the primary indicators of heat transfer efficiency and thermodynamic irreversibility.

Table 3. Nusselt Number with Amplitudes Variation for Different Obstacle Shapes (f = 6.5, Ra = 10³, λ = 30°).

Amplitudes	Obstacle	Nu
		Ha = 0	Ha = 15	Ha = 30	Ha = 50
0.025 L	Square	0.84174	0.84174	0.84173	0.84172
	Star	0.79179	0.79179	0.79179	0.79179
	Triangle	0.79107	0.79106	0.79106	0.79106
0.045 L	Square	0.84326	0.84325	0.84325	0.84324
	Star	0.79369	0.79369	0.79369	0.79369
	Triangle	0.79175	0.79175	0.79175	0.79174
0.065 L	Square	0.84572	0.84571	0.84571	0.8457
	Star	0.79609	0.79609	0.79609	0.79608
	Triangle	0.79252	0.79252	0.79252	0.79251

,

Table 4. Entropy Generation (S_T) with Amplitudes Variation for Different Obstacle Shapes (f = 6.5 Ra = 10³, λ = 30°).

Amplitudes	Obstacle	St
		Ha = 0	Ha = 15	Ha = 30	Ha = 50
0.025 L	Square	15.457	15.457	15.457	15.457
	Star	16.862	16.862	16.862	16.862
	Triangle	17.109	17.109	17.109	17.109
0.045 L	Square	15.491	15.491	15.491	15.491
	Star	16.898	16.898	16.898	16.898
	Triangle	17.131	17.131	17.131	17.131
0.065 L	Square	15.535	15.535	15.535	15.535
	Star	16.945	16.945	16.945	16.945
	Triangle	17.16	17.16	17.16	17.16

,

Table 5. Nusselt Number with Amplitudes Variation for Different Obstacle Shapes (f = 6.5, Ra = 10⁶, λ = 30°).

Amplitudes	Obstacle	Nu
		Ha = 0	Ha = 15	Ha = 30	Ha = 50
0.025 L	Square	6.4631	6.0489	5.5929	5.058
	Star	6.0291	5.622	5.1749	4.6582
	Triangle	6.4925	6.1805	5.6542	5.0606
0.045 L	Square	6.3086	5.9994	5.5697	5.0505
	Star	5.916	5.5713	5.1574	4.6587
	Triangle	6.4336	6.1422	5.6355	5.062
0.065 L	Square	6.2254	5.9552	5.551	5.0466
	Star	5.8015	5.5259	5.1413	4.6589
	Triangle	6.3795	6.1005	5.6126	5.061

,

Table 6. Entropy Generation (S_T) with Amplitudes Variation for Different Obstacle Shapes (f = 6.5 Ra = 10⁶, λ = 30°).

Amplitudes	Obstacle	St
		Ha = 0	Ha = 15	Ha = 30	Ha = 50
0.025 L	Square	0.0014932	0.0014866	0.0014791	0.0014712
	Star	0.0014874	0.0014814	0.0014726	0.0014626
	Triangle	0.0015062	0.0015016	0.0014932	0.0014821
0.045 L	Square	0.0014918	0.0014862	0.0014795	0.0014719
	Star	0.0014865	0.0014807	0.0014728	0.0014633
	Triangle	0.0015064	0.0015015	0.0014927	0.0014813
0.065 L	Square	0.0014896	0.0014852	0.0014794	0.0014723
	Star	0.001484	0.0014792	0.0014724	0.0014635
	Triangle	0.0015061	0.0015011	0.001492	0.0014806

,

Table 7. Nusselt Number with Amplitudes Variation for Different Obstacle Shapes (f = 9.5, Ra = 10³, λ = 30°).

Amplitudes	Obstacle	Nu
		Ha = 0	Ha = 15	Ha = 30	Ha = 50
0.025 L	Square	0.84176	0.84176	0.84175	0.84174
	Star	0.79215	0.79214	0.79214	0.79214
	Triangle	0.79125	0.79124	0.79124	0.79123
0.045 L	Square	0.844	0.84399	0.84398	0.84398
	Star	0.79441	0.79441	0.79441	0.79441
	Triangle	0.79212	0.79212	0.79212	0.79211
0.065 L	Square	0.84668	0.84667	0.84666	0.84666
	Star	0.79709	0.79709	0.79709	0.79709
	Triangle	0.79342	0.79342	0.79341	0.79341

,

Table 8. Entropy Generation (S_T) with Amplitudes Variation for Different Obstacle Shapes (f = 9.5 Ra = 10³, λ = 30°).

Amplitudes	Obstacle	St
		Ha = 0	Ha = 15	Ha = 30	Ha = 50
0.025 L	Square	15.464	15.464	15.464	15.464
	Star	16.869	16.869	16.869	16.869
	Triangle	17.113	17.113	17.113	17.113
0.045 L	Square	15.504	15.504	15.504	15.504
	Star	16.912	16.912	16.912	16.912
	Triangle	17.14	17.14	17.14	17.14
0.065 L	Square	15.554	15.554	15.554	15.554
	Star	16.965	16.965	16.965	16.965
	Triangle	17.172	17.172	17.172	17.172

,

Table 9. Nusselt Number with Amplitudes Variation for Different Obstacle Shapes (f = 9.5, Ra = 10⁶, λ = 30°).

Amplitudes	Obstacle	Nu
		Ha = 0	Ha = 15	Ha = 30	Ha = 50
0.025 L	Square	6.4422	6.0404	5.5864	5.0521
	Star	6.0062	5.6164	5.1689	4.6495
	Triangle	6.4702	6.1603	5.6366	5.0475
0.045 L	Square	6.2984	5.9869	5.5576	5.0364
	Star	5.8871	5.561	5.1428	4.6375
	Triangle	6.4061	6.1113	5.6047	5.0346
0.065 L	Square	6.2086	5.9396	5.5346	5.024
	Star	5.7749	5.5138	5.1206	4.6275
	Triangle	6.3514	6.0659	5.5769	5.0249

and

Table 10. Entropy Generation (S_T) with Amplitudes Variation for Different Obstacle Shapes (f = 9.5 Ra = 10⁶, λ = 30°).

Amplitudes	Obstacle	St
		Ha = 0	Ha = 15	Ha = 30	Ha = 50
0.025 L	Square	0.0014993	0.0014927	0.0014859	0.0014779
	Star	0.0014936	0.0014868	0.0014787	0.0014691
	Triangle	0.0015127	0.0015071	0.0014973	0.0014853
0.045 L	Square	0.0014968	0.0014916	0.0014858	0.0014782
	Star	0.0014913	0.0014854	0.0014784	0.0014693
	Triangle	0.001512	0.0015064	0.0014967	0.0014847
0.065 L	Square	0.0014936	0.0014895	0.0014845	0.0014772
	Star	0.0014879	0.0014834	0.0014772	0.0014684
	Triangle	0.0015101	0.0015046	0.0014951	0.0014833

summarize the variation of parameters under different corrugation amplitudes and frequencies for square, star, and triangle-shaped obstacles, subjected to different Hartmann numbers (Ha = 0–50). The discussion is organized to emphasize the role of corrugation geometry, obstacle shape, and magnetic field in modulating convective heat transfer and entropy generation.

3.1. Corrugation Amplitude Effect

3.1.1. Case I: Square Obstacle

From Table 3 and Table 5, the effect of wall corrugation on heat transfer depends on the Rayleigh number and flow regime. At low Ra (10³), increasing amplitude slightly raises Nu (e.g., from 0.84174 to 0.84572 at Ha = 0) because small waviness enhances surface area and thermal diffusion in conduction-dominated flow. At high Ra (10⁶), however, Nu decreases with amplitude as strong corrugations disrupt buoyant plumes, create stagnant zones, and increase Lorentz damping, thereby suppressing convection. Moreover, Table 5 shows a monotonic decrease in Nu with Ha (0 → 50), consistent with the absence of Joule heating. The Lorentz force (−Ha²u) only dampens motion—its effect is negligible at low Ra but significant at high Ra, where it reduces mixing and thickens the thermal boundary layer. Thus, Nu decreases with both amplitude and Ha at high Ra, but remains nearly constant at low Ra.

Entropy generation (Table 4 and Table 6) exhibits opposite trends due to the change in thermal–flow regimes. At Ra = 10³, entropy increases slightly with amplitude (e.g., from 15.457 to 15.535 for square obstacles) as enhanced wall corrugation increases heat transfer area and temperature gradients in conduction-dominated flow. At Ra = 10⁶, however, entropy generation decreases marginally with increasing Hartmann number because magnetic damping suppresses fluid motion and reduces velocity gradients. This indicates that while corrugation amplitude enhances convective transport, it also introduces additional irreversibilities at higher flow intensities, reflecting the transition from conduction-controlled to convection-controlled regimes.

3.1.2. Case II: Star Obstacle

For star-shaped obstacles (Table 3, Table 4, Table 5 and Table 6), the enhancement in Nusselt number with amplitude is less pronounced compared to square obstacles. At Ra = 10³, the increase in Nu from 0.79179 (a = 0.025 L) to 0.79609 (a = 0.065 L) is minimal. However, at Ra = 10⁶, heat transfer shows a decreasing trend with amplitude, where Nu drops from 6.0291 to 5.8015 as amplitude increases.

Entropy generation values (Table 4 and Table 6) are consistently higher for star obstacles compared to square ones, with S_T ranging between 16.862 and 16.945 at Ra = 10³. At higher Rayleigh numbers, entropy generation values remain in the order of 10⁻³, but magnetic damping reduces St, especially at Ha = 50. This indicates that star obstacles increase flow complexity, raising irreversibility while reducing thermal efficiency at higher amplitudes.

3.1.3. Case III: Triangle Obstacle

Triangle-shaped obstacles (Table 3, Table 4, Table 5 and Table 6) show intermediate behavior between square and star geometries. At Ra = 10³, the average Nusselt number increases marginally with amplitude (from 0.79107 at a = 0.025 L to 0.79252 at a = 0.065 L). At Ra = 10⁶, however, the triangular geometry demonstrates better heat transfer than stars, but lower than squares, with maximum Nu = 6.4925 at a = 0.025 L.

Entropy generation (Table 4 and Table 6) is the highest for triangular obstacles among all geometries, with St = 17.109–17.160 at Ra = 10³. Even at high Rayleigh numbers, triangles exhibit slightly higher entropy values compared to squares and stars, suggesting that sharper edges in triangular obstacles intensify fluid recirculation but at the cost of greater irreversibility.

Figure 7, Figure 8 and Figure 9 illustrate the variation in the average Nusselt number (Nu) with Rayleigh number (Ra) for square, star, and triangular obstacles at different corrugation amplitudes (a = 0.025 L, 0.045 L, 0.065 L). In all cases, Nu increases steadily with increasing Ra, confirming stronger convective transport at higher buoyancy forces. For the square obstacle (Figure 7), the enhancement in Nu is more pronounced, and larger amplitudes (0.065 L) yield slightly higher values compared to smaller amplitudes. The star obstacle (Figure 8) shows a similar growth trend, though its Nu remains consistently lower than that of the square case, indicating weaker convection. The triangular obstacle (Figure 9) performs between the square and star cases, with amplitude effects more visible at moderate to high Ra.

Figure 10, Figure 11 and Figure 12 present the entropy generation (St) as a function of Ra for the same obstacle geometries. In all cases, St decreases sharply with increasing Ra, demonstrating that thermodynamic irreversibility diminishes as buoyancy-driven convection becomes dominant over conduction and magnetic damping. The square obstacle (Figure 10) exhibits the lowest entropy production across amplitudes, confirming its efficiency in balancing heat transfer with reduced losses. The star obstacle (Figure 11) generates the highest S_T, indicating greater irreversibility and lower thermal efficiency, while the triangular obstacle (Figure 12) shows intermediate behavior but remains closer to the star obstacle in terms of performance. These results indicate that square obstacles combined with larger corrugation amplitudes achieve the most favorable balance of enhanced heat transfer and reduced entropy generation, whereas star-shaped obstacles suffer from higher irreversibility despite modest thermal improvements. Triangular obstacles provide moderate enhancement, but at the cost of increased entropy compared to the square case.

The investigation of corrugation amplitude reveals that increasing wall undulation enhances heat transfer performance, particularly for square-shaped obstacles, which consistently achieve the highest Nusselt numbers while maintaining relatively low entropy generation. Star-shaped obstacles, although responsive to amplitude variations, exhibit weaker thermal enhancement and are penalized by excessive entropy production, making them less efficient thermodynamically. Triangular obstacles provide moderate improvements in heat transfer but still show higher irreversibility compared to square geometries. Across all configurations, larger amplitudes strengthen convective transport at moderate Rayleigh numbers, but the associated increase in entropy is more pronounced in non-square obstacles. This confirms that optimizing corrugation amplitude is crucial, with square obstacles demonstrating the most effective balance between thermal augmentation and entropy minimization.

3.2. Corrugation Frequency Effect

3.2.1. Case I: Square Obstacle

Table 6 and Table 9 illustrate the effect of corrugation frequency on square obstacles. At Ra = 10³, the Nusselt number increases with frequency, reaching Nu = 0.84668 at f = 9.5, a = 0.065 L, compared to Nu = 0.84174 at f = 6.5, a = 0.025 L, indicating that higher frequencies promote stronger surface undulations and enhance convective mixing. Conversely, at Ra = 10⁶, the Nusselt number decreases progressively with increasing Hartmann number, showing that under strong magnetic damping, excessive corrugation suppresses circulation and weakens overall heat transport.

Entropy generation values (Table 8 and Table 10) indicate a gradual rise with frequency at Ra = 10³, but a significant reduction with increasing Ha at Ra = 10⁶. This demonstrates a trade-off where higher frequencies improve convective mixing but also enhance thermal irreversibility.

3.2.2. Case II: Star Obstacle

For star-shaped obstacles (Table 6 and Table 9), frequency variation shows a negligible effect on the Nusselt number at Ra = 10³, with a slight rise from Nu = 0.79179 (f = 6.5) to Nu = 0.79709 (f = 9.5). In contrast, at Ra = 10⁶, the Nusselt number drops sharply with increasing Hartmann number from 6.0291 (Ha = 0) to 4.6587 (Ha = 50), indicating that the star-shaped obstacle is highly susceptible to magnetic damping, particularly under high-frequency wall corrugations.

Entropy generation values (Table 8 and Table 10) confirm this inefficiency, as S_T for stars remains consistently higher than for square and triangular cases. The persistence of high entropy production suggests that while stars introduce greater flow disruption, they compromise overall thermodynamic efficiency, particularly under high-frequency undulations.

3.2.3. Case III: Triangle Obstacle

Triangular obstacles (Table 6 and Table 9) exhibit moderate sensitivity to variations in frequency. At Ra = 10³, the Nusselt number increases slightly with frequency from Nu = 0.79107 (f = 6.5, a = 0.025 L) to Nu = 0.79342 (f = 9.5, a = 0.065 L), indicating a mild enhancement in convective mixing. At Ra = 10⁶, the triangular configuration demonstrates greater resistance to magnetic damping than the star geometry, retaining relatively higher Nu values even at large Ha, signifying more stable heat transfer performance under strong magnetic influence.

Entropy generation trends show that triangular obstacles consistently generate the highest St values across all cases. At high frequencies and Ra = 10⁶, entropy reduction with Ha is observed, but the absolute magnitude remains larger than for squares. This underlines that while triangles offer better mixing than stars, they are thermodynamically less efficient than squares due to higher irreversibility.

The overall findings from the analysis reveal distinct thermal and entropy behaviors for the different obstacle shapes. Square obstacles demonstrate the most favorable balance between heat transfer and thermodynamic efficiency, as they consistently enhance the Nusselt number (Nu) while maintaining relatively lower entropy generation (S_T). In contrast, star-shaped obstacles exhibit poor thermal performance, as they generate excessive entropy and show high sensitivity to magnetic suppression, which significantly reduces their efficiency under strong magnetic fields. Triangular obstacles provide moderate improvement in heat transfer compared to star shapes; however, this comes at the cost of higher entropy production, making them less efficient from a thermodynamic standpoint. Furthermore, the influence of corrugation amplitude and frequency is found to be strongly dependent on the Rayleigh number (Ra). At lower Ra, higher amplitudes and frequencies enhance convective mixing and improve thermal transport, but at higher Ra, the combination of strong corrugations and elevated Hartmann numbers (Ha) suppresses convective transport and intensifies irreversibility, thereby limiting the overall efficiency of the system.

3.3. Base Angle Effect

The inclination of the cavity base plays a critical role in governing the interaction between buoyancy-driven convection, magnetic field suppression, and geometric confinement of the heated nanofluid.

Table 11. Nusselt Number with Base Angle Variation for Different Obstacle Shapes (Ra = 10³, λ = 30°).

Base Angle (γ)	Obstacle	Nu
		Ha = 0	Ha = 15	Ha = 30	Ha = 50
10°	Square	0.85888	0.85887	0.85887	0.85886
	Star	0.80902	0.80902	0.80902	0.80901
	Triangle	0.81386	0.81386	0.81386	0.81385
15°	Square	0.844	0.84399	0.84398	0.84398
	Star	0.79441	0.79441	0.79441	0.79441
	Triangle	0.79212	0.79212	0.79212	0.79211
20°	Square	0.83276	0.83275	0.83274	0.83273
	Star	0.78335	0.78335	0.78335	0.78334
	Triangle	0.77633	0.77632	0.77632	0.77632

,

Table 12. Nusselt Number with Base Angle Variation for Different Obstacle Shapes (Ra = 10⁶, λ = 30°).

Base Angle (γ)	Obstacle	Nu
		Ha = 0	Ha = 15	Ha = 30	Ha = 50
10°	Square	6.3016	5.9708	5.5627	5.0975
	Star	5.9225	5.6206	5.2248	4.7628
	Triangle	6.7566	6.5266	6.1018	5.5524
15°	Square	6.2984	5.9869	5.5576	5.0364
	Star	5.8871	5.561	5.1428	4.6375
	Triangle	6.4061	6.1113	5.6047	5.0346
20°	Square	6.3882	6.0592	5.5749	4.9767
	Star	5.9073	5.5824	5.1324	4.5738
	Triangle	6.1729	5.847	5.3399	4.7476

,

Table 13. Entropy Generation (S_T) with Base Angle Variation for Different Obstacle Shapes (Ra = 10³, λ = 30°).

Base Angle (γ)	Obstacle	St
		Ha = 0	Ha = 15	Ha = 30	Ha = 50
10°	Square	15.775	15.775	15.775	15.775
	Star	17.223	17.223	17.223	17.223
	Triangle	17.628	17.628	17.628	17.628
15°	Square	15.504	15.504	15.504	15.504
	Star	16.912	16.912	16.912	16.912
	Triangle	17.14	17.14	17.14	17.14
20°	Square	15.29	15.29	15.29	15.289
	Star	16.669	16.669	16.669	16.669
	Triangle	16.786	16.786	16.786	16.786

and

Table 14. Entropy Generation (S_T) with Base Angle Variation for Different Obstacle Shapes (Ra = 10⁶, λ = 30°).

Base Angle (γ)	Obstacle	Nu
		Ha = 0	Ha = 15	Ha = 30	Ha = 50
10°	Square	0.0016209	0.0016156	0.0016104	0.0016035
	Star	0.0016132	0.0016078	0.0016014	0.0015929
	Triangle	0.0016398	0.0016352	0.0016262	0.0016133
15°	Square	0.0014968	0.0014916	0.0014858	0.0014782
	Star	0.0014913	0.0014854	0.0014784	0.0014693
	Triangle	0.001512	0.0015064	0.0014967	0.0014847
20°	Square	0.0013884	0.0013829	0.0013758	0.0013666
	Star	0.001384	0.0013778	0.0013699	0.0013597
	Triangle	0.0013981	0.0013921	0.0013827	0.0013708

summarize the effect of base angles (γ = 10°, 15°, 20°) for square, star, and triangular obstacles under varying Hartmann numbers (Ha) at both low (Ra = 10³) and high (Ra = 10⁶) Rayleigh numbers. The results reveal that a smaller base angle promotes stronger convective circulation and enhanced heat transfer, while larger inclination angles dampen buoyant plumes and elevate entropy generation, particularly under high magnetic suppression. Obstacle shape continues to influence performance, with square configurations consistently demonstrating superior thermal transport efficiency compared to star and triangular geometries.

3.3.1. Case I: γ = 10°

At γ = 10°, the cavity maintains the most favorable orientation for buoyancy-driven flow, allowing strong plume circulation and enhanced wall interactions. From Table 11, the Nusselt number (Nu) for square obstacles reaches its peak values (~0.859) at Ra = 10³, outperforming star (~0.809) and triangular (∼0.814) shapes across all Hartmann numbers. At high Rayleigh number (Ra = 10⁶, Table 12), triangular obstacles achieve the highest Nu (~6.76) due to enhanced corner-driven vortex structures, though square obstacles remain competitive (~6.30).

Entropy generation trends, presented in Table 13, show that square obstacles yield the lowest entropy levels (~15.78), while triangular (~17.63) and star (~17.22) geometries incur greater irreversibility. At high Ra, Table 14 confirms that square obstacles continue to minimize St, whereas triangular shapes, despite favorable heat transfer, are penalized by entropy production. This suggests that a γ = 10° base angle provides the best compromise between convection enhancement and thermodynamic efficiency.

3.3.2. Case II: γ = 15°

Increasing the base angle to γ = 15° moderately reduces convective strength, as buoyant plumes are redirected along inclined walls, weakening circulation intensity. According to Table 11, square obstacles still dominate in terms of Nu (~0.844), followed by star (~0.794) and triangular (~0.792) shapes at low Ra. However, at high Ra (Table 12), triangular obstacles again record superior Nu (~6.41) due to geometric facilitation of thermal boundary layer disruption, though square obstacles maintain reasonably strong performance (~6.30).

Entropy results (Table 13) confirm that irreversibility decreases slightly compared to γ = 10°. Squares generate the lowest entropy (~15.50), while triangular and star shapes remain higher (~17.14 and ∼16.91, respectively). At Ra = 10⁶ (Table 14), square obstacles remain the most thermodynamically efficient with lower entropy production (~0.00150), compared to triangular (~0.00151) and star (~0.00149).

Overall, γ = 15° balances heat transfer moderately well, but convection efficiency weakens compared to γ = 10°.

3.3.3. Case III: γ = 20°

At the steepest inclination (γ = 20°), buoyancy-driven plumes are significantly suppressed, and flow circulation becomes weaker, leading to reduced Nu values. As seen in Table 11, square obstacles record the highest Nu (~0.833) but with a marked drop compared to smaller angles, while star (~0.783) and triangular (~0.776) obstacles perform poorly. At higher Rayleigh numbers (Table 12), triangular obstacles (~6.17) surpass squares (~6.39) in heat transfer, although both show reduced performance compared to shallower angles.

Entropy generation trends (Table 13) show that irreversibility slightly decreases for all obstacles at γ = 20°, with square obstacles yielding the lowest entropy (~15.29) compared to star (~16.67) and triangular (~16.79) geometries. At high Ra (Table 14), entropy values drop further, particularly for square obstacles (~0.00139), reinforcing their advantage in thermodynamic optimization. Thus, while larger base angles (γ = 20°) reduce convective heat transfer, they also suppress entropy generation, making them beneficial in scenarios where thermodynamic efficiency is prioritized over absolute heat transport.

The analysis of base angle variations (γ = 10°, 15°, 20°) reveals that cavity inclination strongly influences the balance between heat transfer enhancement and entropy minimization. At a smaller base angle of γ = 10°, buoyancy-driven circulation is more vigorous, leading to higher Nusselt numbers, particularly for square and triangular obstacles, although this comes at the expense of elevated entropy generation. Increasing the angle to γ = 15° moderately reduces heat transfer rates but also lowers entropy levels, providing a compromise between transport efficiency and thermodynamic losses. At the steepest inclination of γ = 20°, convective transport is significantly weakened, as indicated by reduced Nusselt numbers across all obstacle shapes. However, entropy generation is also minimized, particularly for square obstacles, highlighting their superior thermodynamic stability under inclined configurations.

Overall, square obstacles consistently provide the best performance across all inclination angles due to their ability to sustain favorable heat transfer while keeping entropy generation relatively low. Triangular obstacles demonstrate strong thermal transport at low base angles but are penalized by high entropy production, whereas star obstacles show the weakest performance due to persistent irreversibility and sensitivity to magnetic damping. These results confirm that selecting an optimal base angle is critical: γ = 10° is most suitable for maximizing convection, while γ = 20° favors entropy minimization, with γ = 15° serving as a balanced intermediate configuration.

4. Discussion

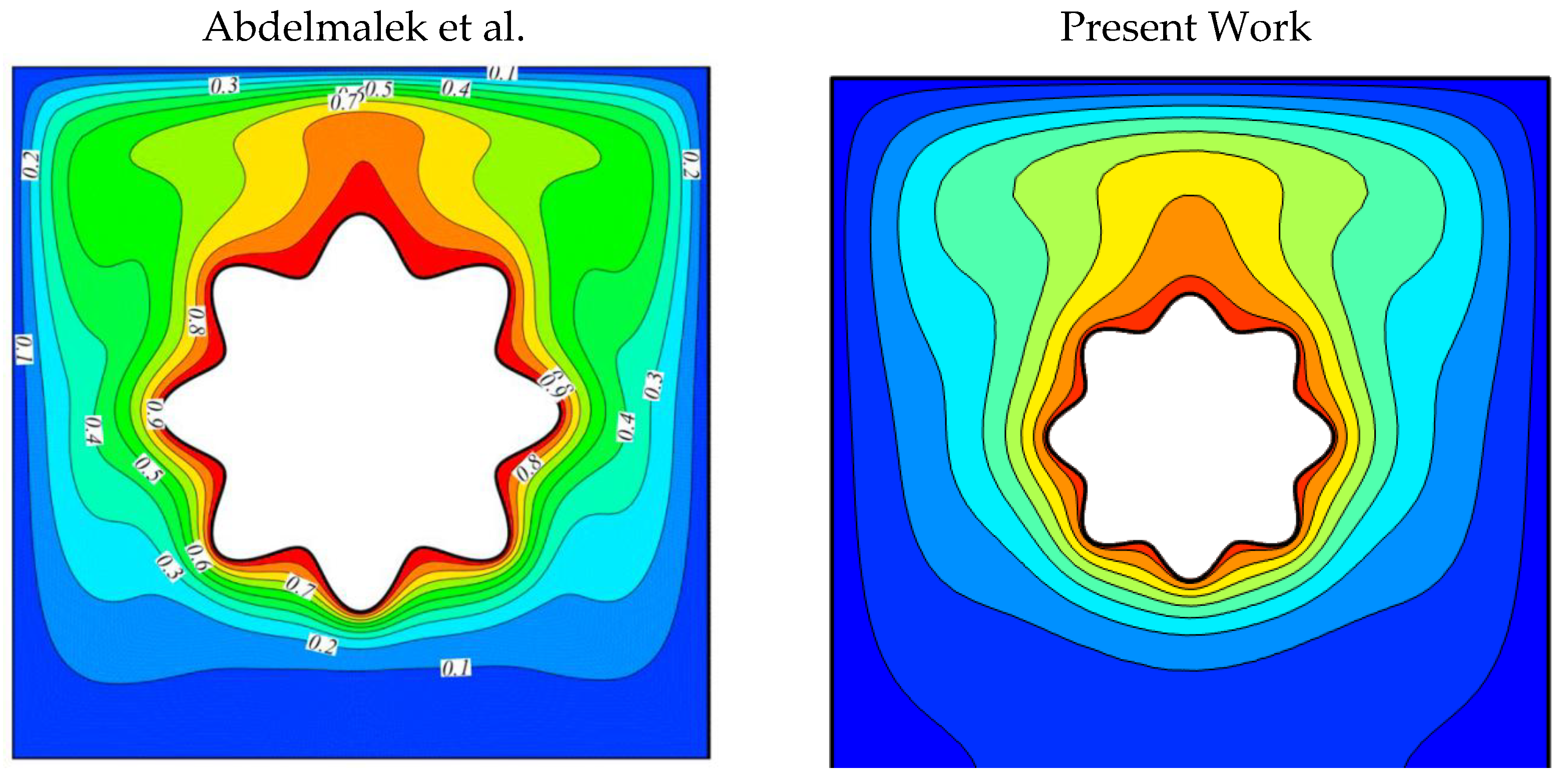
The present numerical investigation has been validated through a direct comparison with the benchmark study of Abdelmalek et al. [19], where natural convection of nanofluids in enclosures with star-shaped obstacles was considered. Figure 13 shows the isotherm distributions at Ra = 10⁴, N = 8, A = 0.15, and ϕ = 2%. The comparison demonstrates close similarity in the thermal plume development and boundary layer structure near the obstacle surface, confirming that the present model reliably reproduces the essential flow and thermal features reported previously. This agreement is further substantiated by

Table 15. Comparison of Nu Between Present Work and Abdelmalek et al. [19].

Ra	Nanoparticle Volume Fraction (ϕ%)	Present Study	Abdelmalek et al. [19]	Deviation (%)
103	2	1.1470	1.1307	1.44
104	2	2.2944	2.2674	1.19
105	2	4.6379	4.5851	1.15
106	2	8.9586	8.8341	1.41

, where the Nusselt numbers predicted in the current work deviate by less than 1.5% from Abdelmalek et al. [19] across the examined Rayleigh number range (Ra = 10³–10⁶). Such a low deviation validates both the governing equations and the numerical implementation used in this study.

From a broader perspective, the findings align with the general consensus in nanofluid convection research that the inclusion of solid nanoparticles enhances effective thermal conductivity, thereby promoting convective heat transfer. As seen in Table 15, the Nusselt number increases significantly with Rayleigh number, consistent with buoyancy-driven convection intensification at higher thermal gradients.

The present study extends these results by systematically examining how obstacle geometry, corrugation amplitude, frequency, and base inclination can be tuned to achieve both heat transfer enhancement and entropy minimization. Unlike Abdelmalek et al. [19], who primarily addressed nanofluid natural convection in smooth-walled enclosures, the current analysis highlights the interplay between obstacle-induced flow disturbances and magnetic field suppression in controlling system performance.

To further ensure the reliability and accuracy of the numerical model, an additional validation was performed against the benchmark results of Mahmud et al. [35], who studied conjugate mixed convection in a lid-driven cavity containing a rotating solid cylinder. As shown in Figure 14, the streamline patterns from the present simulation closely match the reference results for $R{e}_c=2$, $Ri=10$, and $Gr={10}^5$, demonstrating similar vortex structures and flow circulation behavior. This strong agreement verifies the precision and stability of the current finite element formulation, enhancing confidence in the adopted numerical scheme for modeling MHD-assisted Cu–H₂O nanofluid convection.

The implications of these findings are significant for thermal management systems where optimizing both energy efficiency and irreversibility reduction is crucial. Square obstacles consistently demonstrated a favorable balance between heat transfer enhancement and lower entropy generation, indicating their potential for practical applications in heat exchangers, electronic cooling, and solar thermal collectors. In contrast, star-shaped obstacles, although geometrically effective at disturbing flow, exhibited excessive entropy production, reducing their thermal efficiency. Triangular obstacles provided moderate improvements, but at the expense of higher irreversibility. This distinction in performance underscores the importance of obstacle geometry selection in engineering applications.

Future research should expand on these findings by incorporating more complex boundary conditions, such as oscillatory heating, non-uniform wall temperature distributions, or porous media filling. Additionally, extending the analysis to hybrid nanofluids (e.g., Cu–Al₂O₃/H₂O) and considering turbulent flow regimes would further enhance the practical relevance of this study. Experimental validation using advanced visualization and thermal imaging techniques would also strengthen confidence in the predictive capabilities of the present numerical model. Finally, exploring optimization frameworks that couple geometry, magnetic field intensity, and nanoparticle concentration could provide a pathway toward real-time adaptive thermal management systems.

The present work is valid and consistent with established literature, while also offering novel insights into corrugation and inclination effects under magnetohydrodynamic conditions. The outcomes reinforce the applicability of nanofluid convection control in advanced thermal engineering applications and set a foundation for future explorations into more intricate and realistic configurations.

5. Conclusions

This study numerically examined the combined effects of wall corrugation, base inclination, and internal obstacle geometry on heat transfer and entropy generation in a trapezoidal cavity filled with Cu–H₂O nanofluid under magnetohydrodynamic (MHD) influence. Using the finite element method, the investigation systematically assessed the interplay between Rayleigh number, Hartmann number, corrugation amplitude and frequency, and obstacle shape. Based on the results, the following conclusions can be drawn:

i. 

Corrugation Effects

Moderate wall corrugation (amplitude a = 0.045 L) and higher frequency (f = 9.5) enhance convective mixing by disrupting boundary layers and promoting stronger circulation, leading to higher Nusselt numbers. However, excessive corrugation at large amplitudes suppresses convection at high Rayleigh numbers due to increased flow resistance and magnetic damping.

ii. 

Obstacle Shape Influence

a.

Square obstacles provide the most balanced performance, combining strong thermal transport with relatively low entropy generation.

b.

Star-shaped obstacles increase entropy significantly, indicating poor thermodynamic efficiency despite modest heat transfer gains.

c.

Triangular obstacles show intermediate performance, enhancing heat transfer moderately but with higher irreversibility compared to squares.

iii. 

Base Angle Effects

a.

A smaller base angle (γ = 10°) promotes vigorous buoyancy-driven plumes and maximizes heat transfer, though with elevated entropy generation.

b.

An intermediate base angle (γ = 15°) offers a balanced configuration, with moderately high Nusselt numbers and reduced entropy production.

c.

A larger base angle (γ = 20°) weakens convective intensity but minimizes entropy generation, favoring thermodynamic stability over maximum thermal transport.

iv. 

Magnetic Field Suppression

Increasing Hartmann number (Ha) systematically damps convective circulation, reducing Nusselt number while lowering entropy generation. This indicates that MHD control can be used as a tuning mechanism to balance heat transfer enhancement against entropy minimization.

v. 

Thermal–Entropy Trade-off

The results highlight a clear trade-off between maximizing heat transfer and minimizing entropy generation. Optimal thermal performance is achieved with square obstacles, moderate corrugation amplitude, high frequency, and low-to-intermediate base inclination.

Geometric tailoring through the coordinated adjustment of wall corrugation, obstacle shape, and cavity inclination provides an effective strategy for enhancing thermal performance while minimizing irreversibility in MHD-assisted nanofluid enclosures. These findings have direct implications for the design of energy-efficient thermal management systems such as electronic cooling devices, solar collectors, and compact heat exchangers. Future work should extend this framework to hybrid nanofluids, oscillatory boundary conditions, and turbulent flow regimes, alongside experimental validation for practical implementation.