Numerical Discretization of Riemann–Liouville Fractional Derivatives with Strictly Positive Eigenvalues
Abstract
1. Introduction
Riemann–Liouville Fractional Derivative
2. Summation by Parts Operator
- 1.
- ;
- 2.
- ;
- 3.
- 4.
- .
- 1.
- Multiplying by the numerical solution from the left.
- 2.
- Add the transpose of the resulting equation from step 1. above.
Simultaneous Approximation Terms
3. Riemann–Liouville SBP-SAT Operator
Spectrum Analysis
4. Numerical Example
Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bhalekar, S.; Abdeljawad, M. Recent Advances in Fractional Calculus. Axioms 2024, 13, 310. [Google Scholar] [CrossRef]
- Alsidrani, F.; Kılıçman, A.; Senu, N. A comprehensive review of the recent numerical methods for solving FPDEs. Open Math. 2024, 22, 20240036. [Google Scholar] [CrossRef]
- Al-Maskari, A.O.; Al-Balushi, M. Review on Recent Advances in Fractional Differentiation and its Applications. Appl. Math. Inf. Sci. 2024, 11, 245–261. [Google Scholar]
- Bhatti, A.H.; Hussain, H.; Din, Q. Dynamics investigation and numerical simulation of fractional-order eco-epidemiological systems. Discret. Contin. Dyn. Syst. Ser. S 2024, 18, 181. [Google Scholar] [CrossRef]
- Kumar, D.; Singh, J.; Baleanu, D. Dynamical and computational analysis of a fractional predator–prey model with infectious disease and harvesting policy. Aims Math. 2024, 9, 36082–36101. [Google Scholar] [CrossRef]
- Singh, A.; Elsadany, A.A.; Elsonbaty, A. Complex dynamics of a discrete fractional–order Leslie–Gower predator–prey model with immigration and Holling II response. Nonlinear Dyn. 2025, 42, 3992–4007. [Google Scholar]
- Sharma, R.S.; Gupta, S. Chaotic analysis of a prey–predator population model with fractional derivatives. Chaos Solitons Fractals 2025, 114523. [Google Scholar]
- Khan, N.A.; Ali, M.; Ara, A.; Khan, M.I.; Abdullaeva, S.; Waqas, M. Optimizing pantograph fractional differential equations: A Haar-wavelet operational matrix approach. Appl. Numer. Math. 2024, 11, 100774. [Google Scholar] [CrossRef]
- Takhtipour, R.; Hooshangian, L.; Shokrolahi Yancheshmeh, S.; Esmaily, J. Haar Wavelet Method for Numerical Solution of Two-Dimensional Partial Fractional Integro-Differential Equations. Int. J. Math. Model. Comput. 2024, 14, 241–254. [Google Scholar] [CrossRef]
- Khan, N.A.; Altaf, S.; Khan, N.A.; Ayaz, M. Haar-wavelet Arctic Puffin Optimization Method (HWAPOM) for fractal–fractional Caputo–Fabrizio problems. J. Comput. Appl. Math. 2025, 13, 101114. [Google Scholar] [CrossRef]
- Al-Mazmumy, M.; Alyami, M.A.; Alsulami, M.; Alsulami, A.S.; Redhwan, S.S. An Adomian decomposition method with some orthogonal polynomials for fractional differential equations. Aims Math. 2024, 9, 30548–30571. [Google Scholar] [CrossRef]
- Bekela, A.S.; Deresse, A.T. A hybrid Yang-transform Adomian decomposition method for non-linear time-fractional PDEs. BMC Res. Notes 2024, 17, 226. [Google Scholar] [CrossRef]
- Mursaleen, R.; Khan, T.A. Mixed Erdélyi–Kober and Caputo fractional differential equations with nonlocal, non-separated boundary conditions: Existence via fixed points. Aims Math. 2024, 9, 32904–32920. [Google Scholar]
- Ali, R.; Zada, A.; Li, M. Novel exploration of topological degree method for noninstantaneous impulsive fractional integro-differential equations. Fixed Point Theory Algorithms Sci. Eng. 2024, 2024, 7645. [Google Scholar]
- Cui, R.; Shi, J.; Wang, Y. Existence and uniqueness of positive solutions for a class of semilinear elliptic systems. Acta Math. Sin. 2011, 27, 1079–1090. [Google Scholar] [CrossRef]
- Sajavičius, S.; Sapagovas, M. Numerical Analysis of the Eigenvalue Problem for One-Dimensional Differential Operator with Nonlocal Integral Conditions. Nonlinear Anal. Model. Control 2009, 14, 115–122. [Google Scholar] [CrossRef]
- Kreiss, H.O.; Scherer, G. Finite Element and Finite Difference Methods for Hyperbolic Partial Differential Equations; Elsevier: Amsterdam, The Netherlands, 1974; pp. 195–212. [Google Scholar]
- Svärd, M.; Carpenter, M.H.; Nordström, J. A stable high-order finite difference scheme for the compressible Navier-Stokes equations, far-field boundary conditions. J. Comput. Phys. 2007, 225, 1020–1038. [Google Scholar] [CrossRef]
- Linders, V. On an Eigenvalue Property of Summation-By-Parts Operators. J. Sci. Comput. 2022, 93, 82. [Google Scholar] [CrossRef]
- Eriksson, S.; Wang, S. Summation-by-parts approximations of the second derivative: Pseudoinverses of singular operators and revisiting the sixth order accurate narrow-stencil operator. arXiv 2020, arXiv:2011.03776. [Google Scholar]
- Hicken, J.E. Entropy-stable, high-order summation-by-parts discretizations without interface penalties. arXiv 2020, arXiv:2002.04653. [Google Scholar] [CrossRef]
- Ranocha, H. Generalised Summation-by-Parts Operators and Variable Coefficients. arXiv 2017, arXiv:1705.10541. [Google Scholar] [CrossRef]
- Hicken, J.E.; Fernández, D.C.D.R.; Zingg, D.W. Multidimensional Summation-By-Parts Operators: General Theory and Application to Simplex Elements. arXiv 2015, arXiv:1505.03125. [Google Scholar] [CrossRef]
- Luchko, Y. Fractional derivatives and the fundamental theorem of fractional calculus. Fract. Calc. Appl. Anal. 2020, 23, 939–966. [Google Scholar] [CrossRef]
- Carpenter, M.H.; Gottlieb, D.; Abarbanel, S. Time-stable boundary conditions for finite-difference schemes solving hyperbolic systems: Methodology and application to high-order compact schemes. J. Comput. Phys. 1994, 111, 220–236. [Google Scholar] [CrossRef]
- Nordström, J.; Carpenter, M.H. High-order finite difference methods, multidimensional linear problems, and curvilinear coordinates. J. Comput. Phys. 2001, 173, 149–174. [Google Scholar] [CrossRef]
- Hicken, J.E.; Zingg, D.W. Summation-by-parts operators and high-order quadrature. J. Comput. Appl. Math. 2013, 237, 111–125. [Google Scholar] [CrossRef]
- Diethelm, K.; Ford, N. A Predictor-Corrector Approach for the Numerical Solution of Fractional Differential Equations. Nonlinear Dyn. 2002, 29, 3–22. [Google Scholar] [CrossRef]
- Hairer, E.; Wanner, G. Solving Ordinary Differential Equations II. Stiff and Differential-Algebraic Problems; Springer: New York, NY, USA, 1996; Volume 14. [Google Scholar] [CrossRef]
- Garrappa, R. Trapezoidal methods for fractional differential equations: Theoretical and computational aspects. Math. Comput. Simul. 2015, 110, 96–112. [Google Scholar] [CrossRef]
- Svärd, M.; Nordström, J. On the convergence rates of energy-stable finite-difference schemes. J. Comput. Phys. 2019, 397, 108819. [Google Scholar] [CrossRef]
- Ranocha, H. Some notes on summation by parts time integration methods. Results Appl. Math. 2019, 1, 100004. [Google Scholar] [CrossRef]

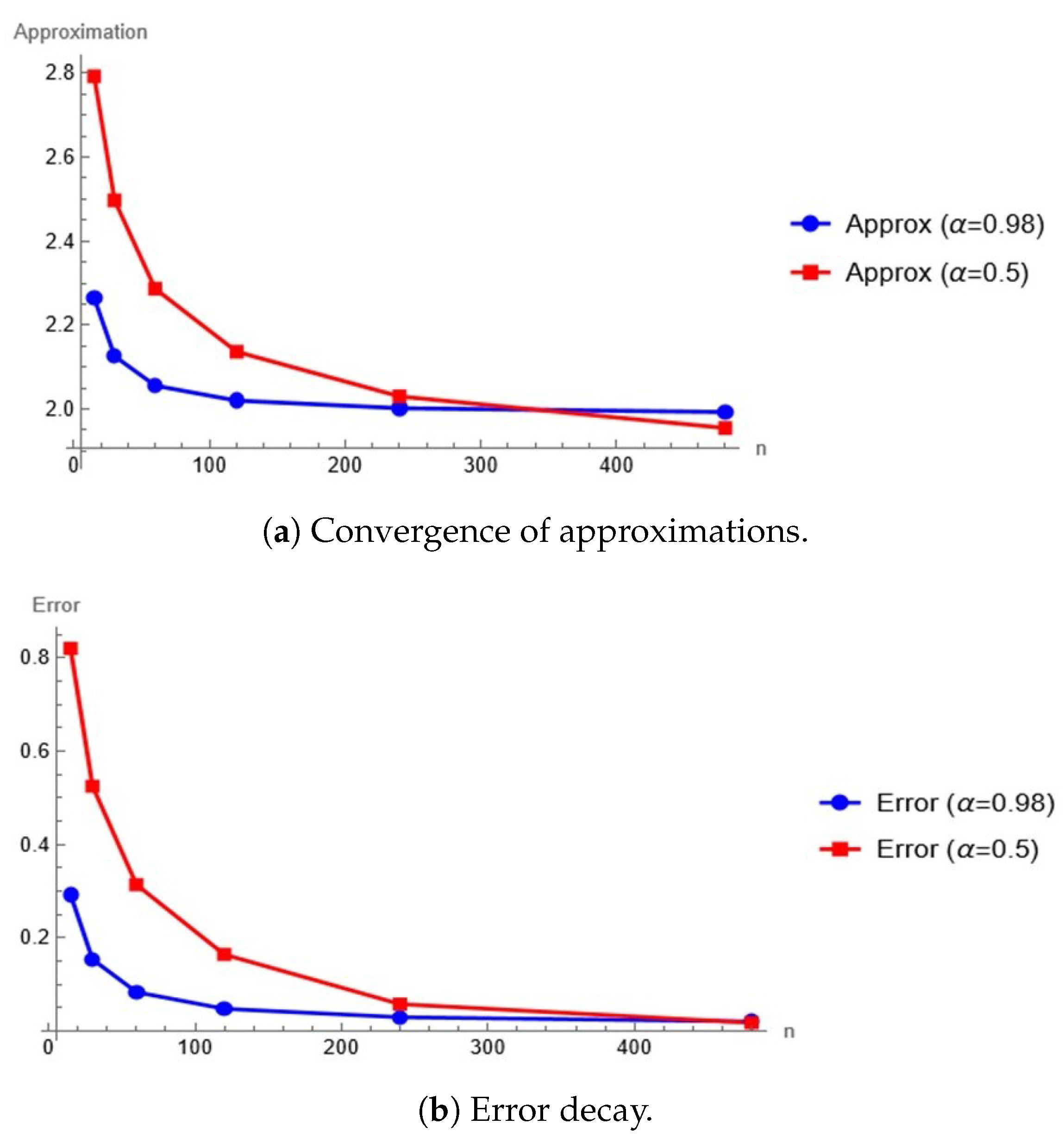
| n | ||||
|---|---|---|---|---|
| Approx | Error | Approx | Error | |
| 15 | 2.26456 | 0.29209 | 2.79234 | 0.81987 |
| 30 | 2.12596 | 0.15349 | 2.49693 | 0.52446 |
| 60 | 2.05569 | 0.08322 | 2.28618 | 0.31371 |
| 120 | 2.02006 | 0.04759 | 2.13635 | 0.16388 |
| 240 | 2.00199 | 0.02952 | 2.03006 | 0.05759 |
| 480 | 1.99283 | 0.02036 | 1.95474 | 0.01773 |
| Conv. Rate | ||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rametse, S.M.; Herbst, R.S. Numerical Discretization of Riemann–Liouville Fractional Derivatives with Strictly Positive Eigenvalues. AppliedMath 2025, 5, 130. https://doi.org/10.3390/appliedmath5040130
Rametse SM, Herbst RS. Numerical Discretization of Riemann–Liouville Fractional Derivatives with Strictly Positive Eigenvalues. AppliedMath. 2025; 5(4):130. https://doi.org/10.3390/appliedmath5040130
Chicago/Turabian StyleRametse, Sam Motsoka, and Rhameez Sheldon Herbst. 2025. "Numerical Discretization of Riemann–Liouville Fractional Derivatives with Strictly Positive Eigenvalues" AppliedMath 5, no. 4: 130. https://doi.org/10.3390/appliedmath5040130
APA StyleRametse, S. M., & Herbst, R. S. (2025). Numerical Discretization of Riemann–Liouville Fractional Derivatives with Strictly Positive Eigenvalues. AppliedMath, 5(4), 130. https://doi.org/10.3390/appliedmath5040130






