On Schröder-Type Series Expansions for the Lambert W Function
Abstract
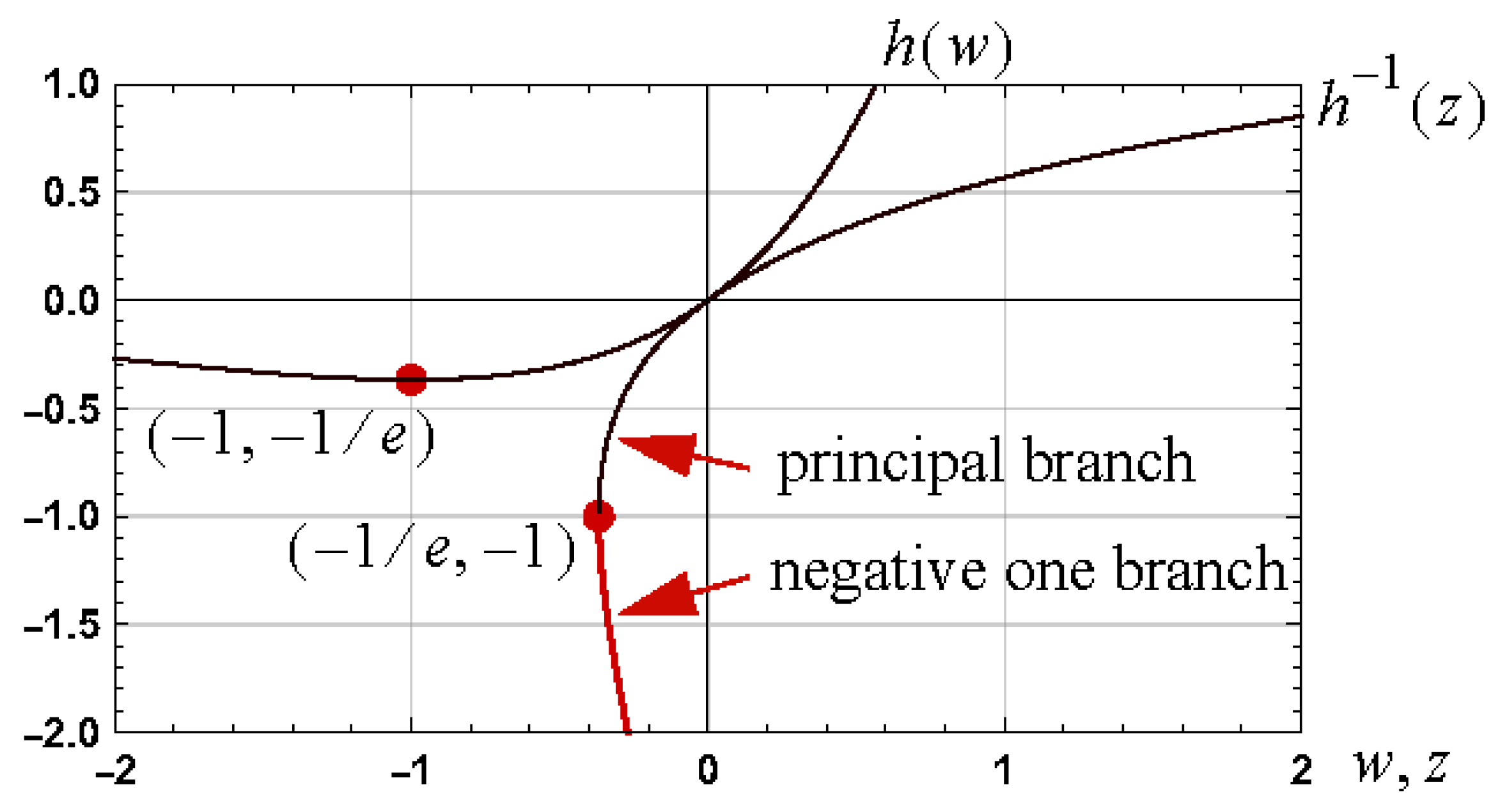
1. Introduction
1.1. Structure of Paper
1.2. Assumptions and Notation
2. Published Series Approximations
2.1. Taylor Series
Taylor Series at the Branch Point for the Negative One and Principal Branches
2.2. Asymptotic Series
Negative One Branch
2.3. Series Based on Exponential Arguments
2.4. Continued Fraction Expansion
2.5. Iterative Approximations
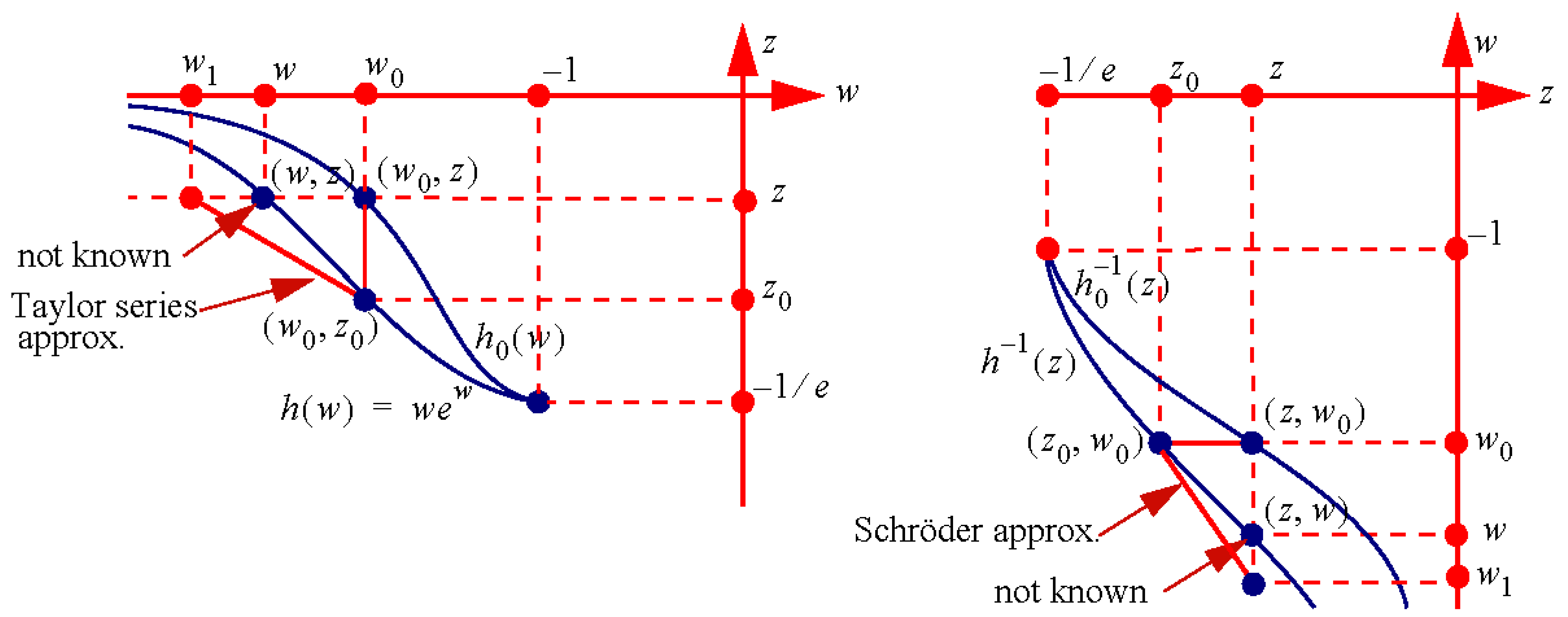
3. Schröder-Based Series
3.1. Notes
3.2. Explicit Expressions
3.3. Special Approximation Form
Explicit Expression
4. Initial Approximations for Negative One Branch
4.1. Notes
4.2. Published Approximations
5. Initial Approximations for Principal Branch
5.1. Initial Approximation
Improved Approximation
5.2. Published Results
6. Schröder-Based Approximations
6.1. Negative One Branch
6.2. Principal Branch
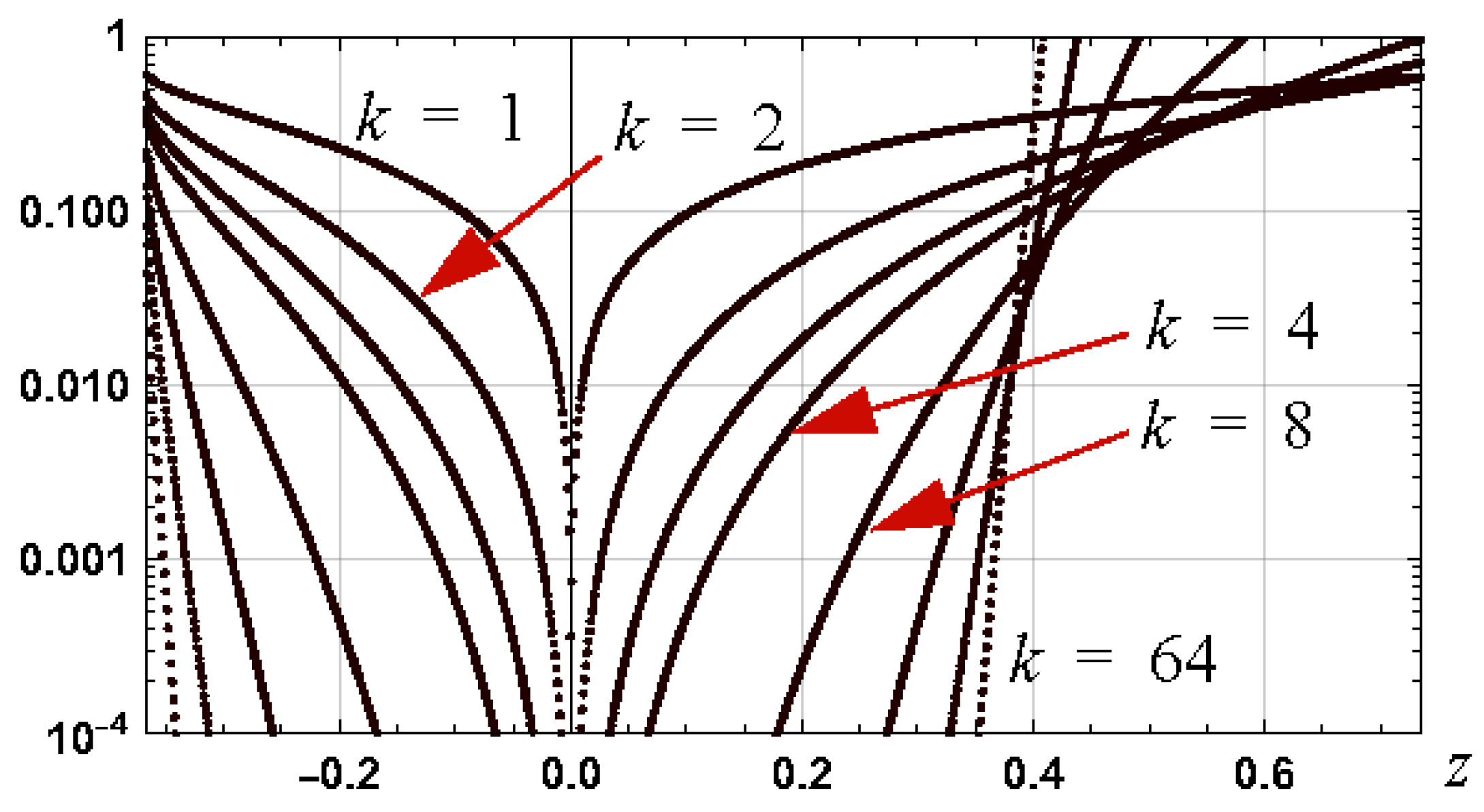
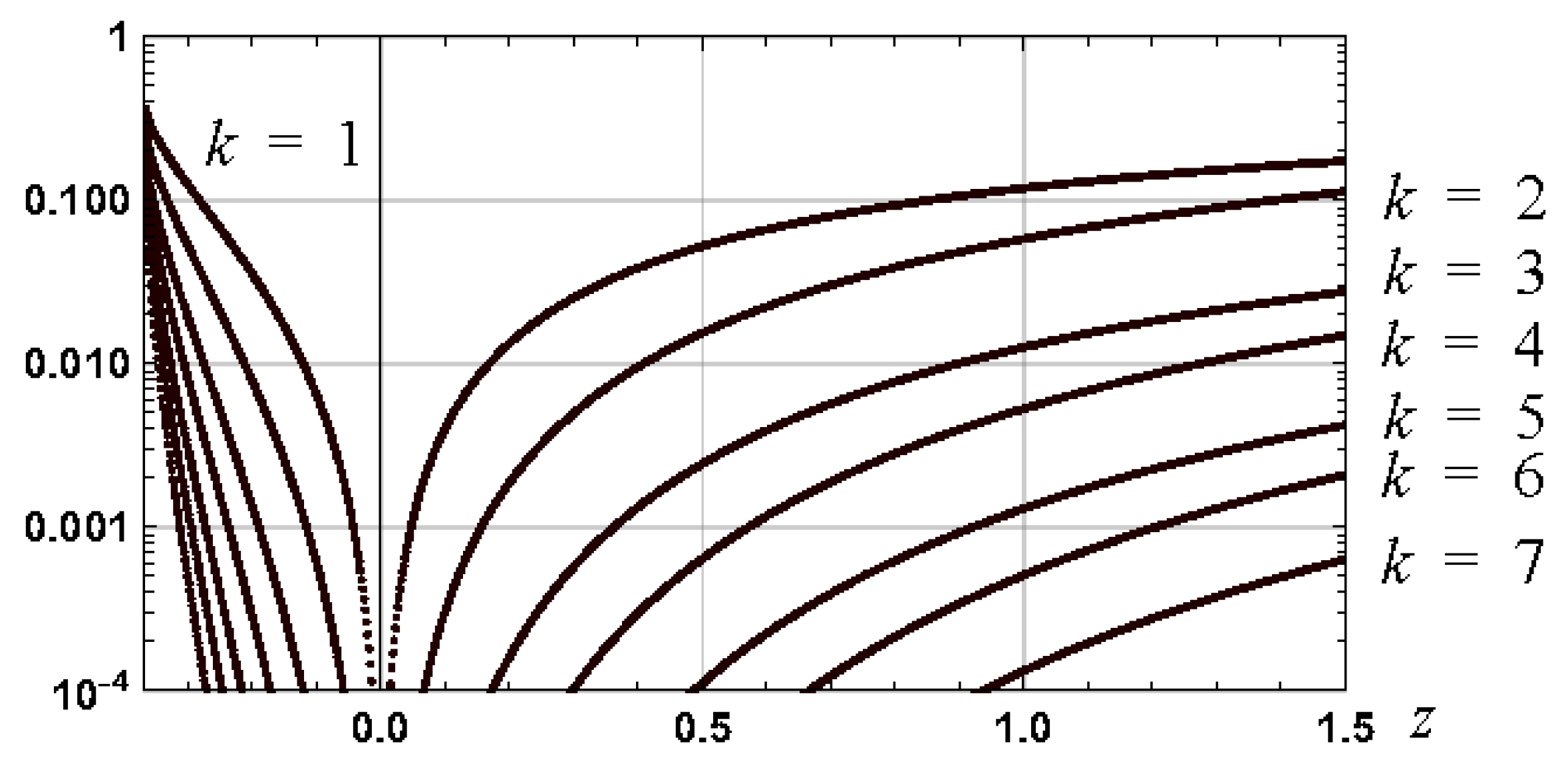
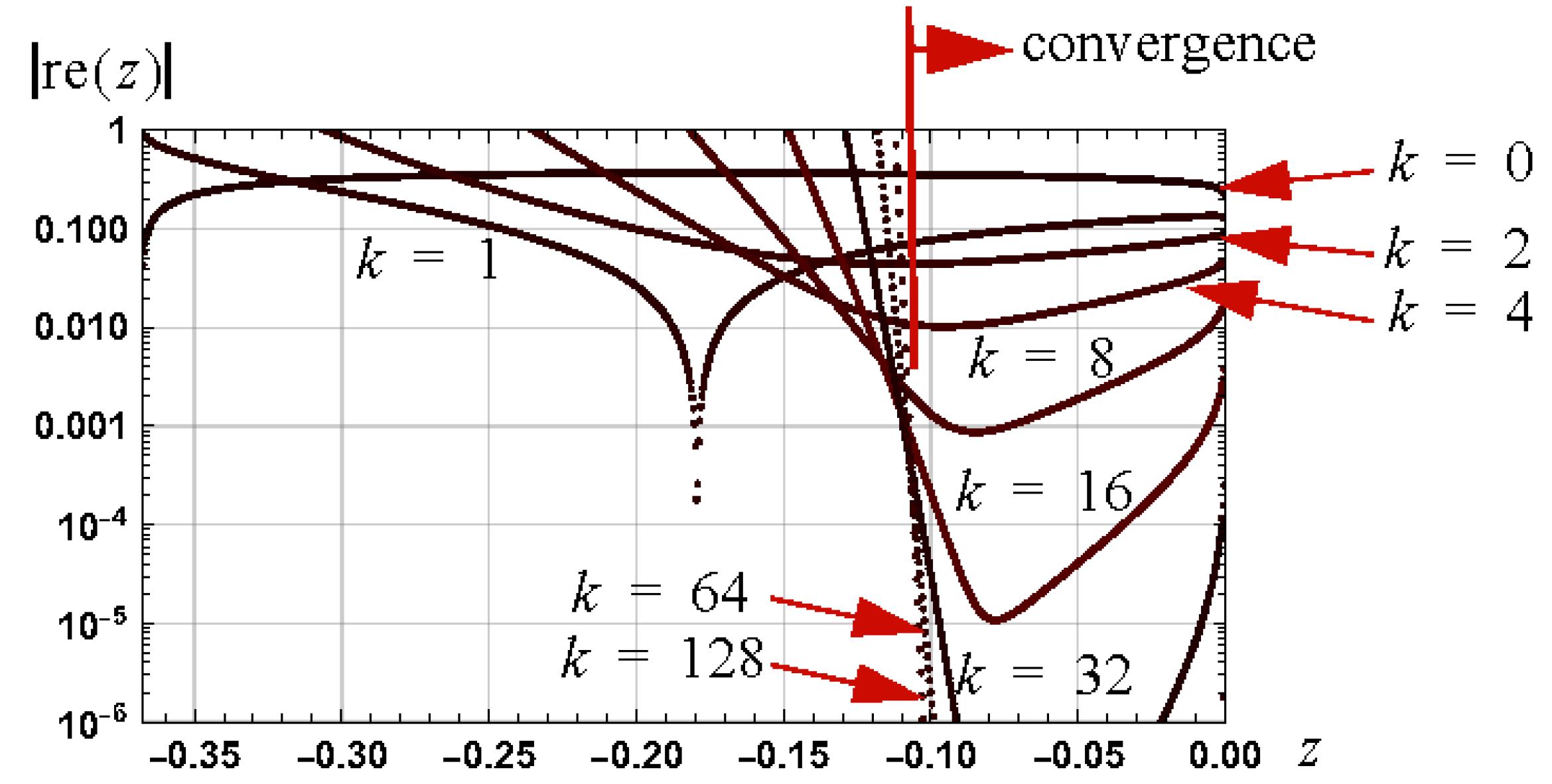
7. Convergence Analysis
Sufficient Condition for Convergence
8. Bounds on Approximation for Convergence
8.1. Bounds for Convergence for Negative One Branch
8.2. Bounds for Convergence for Principal Branch
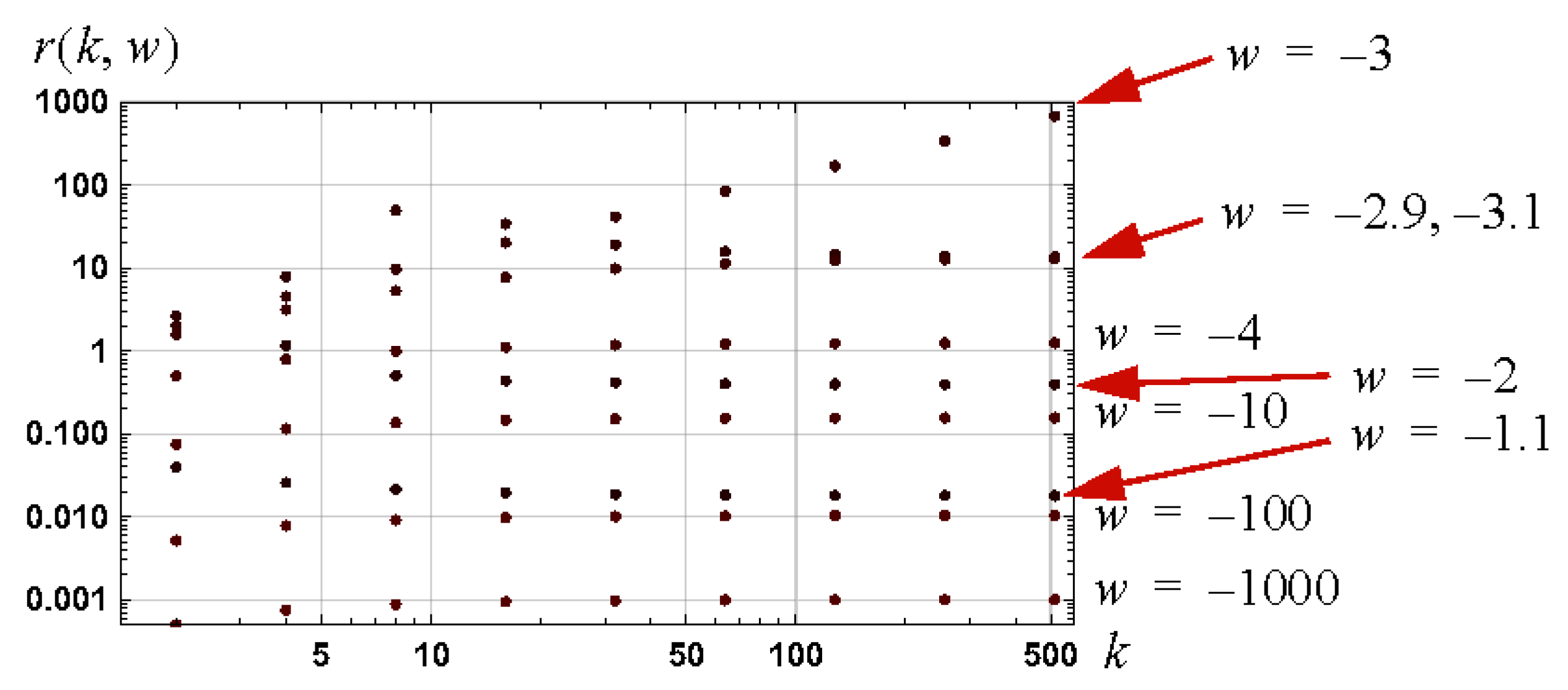
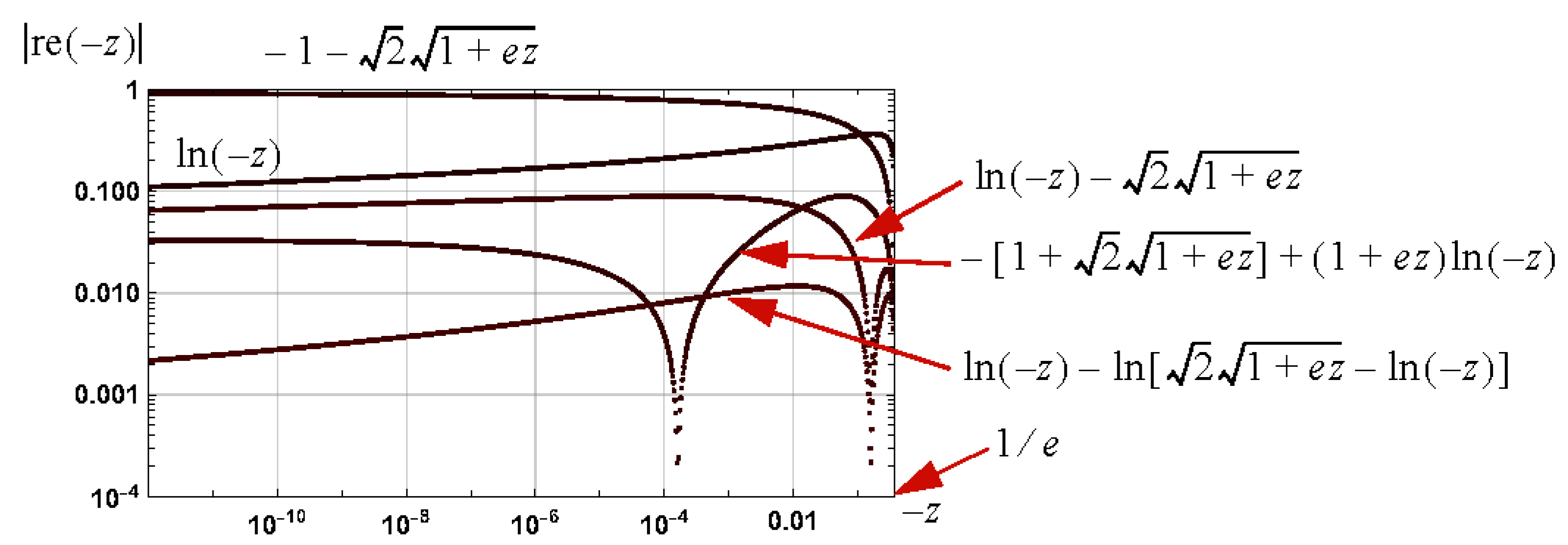
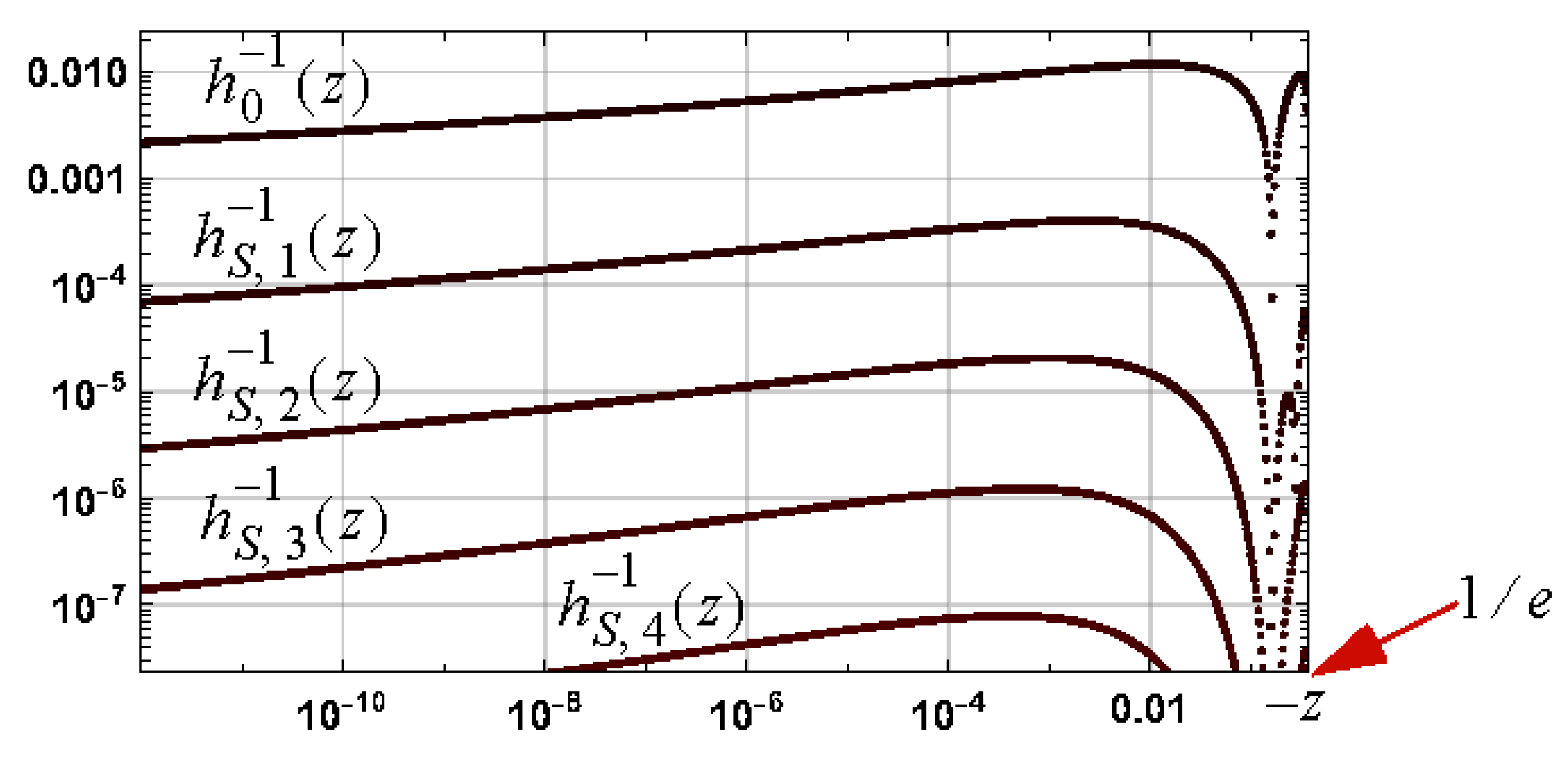
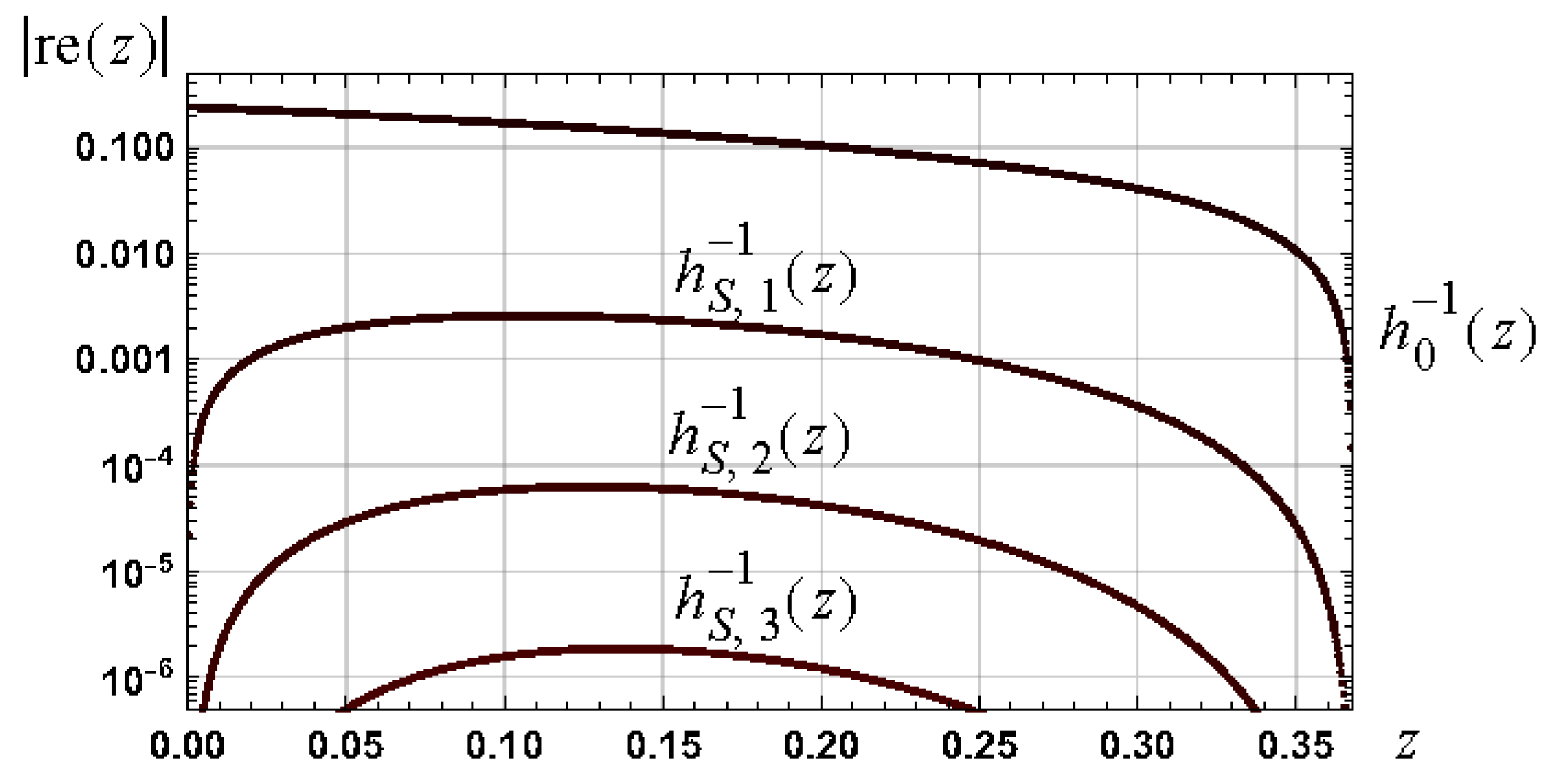
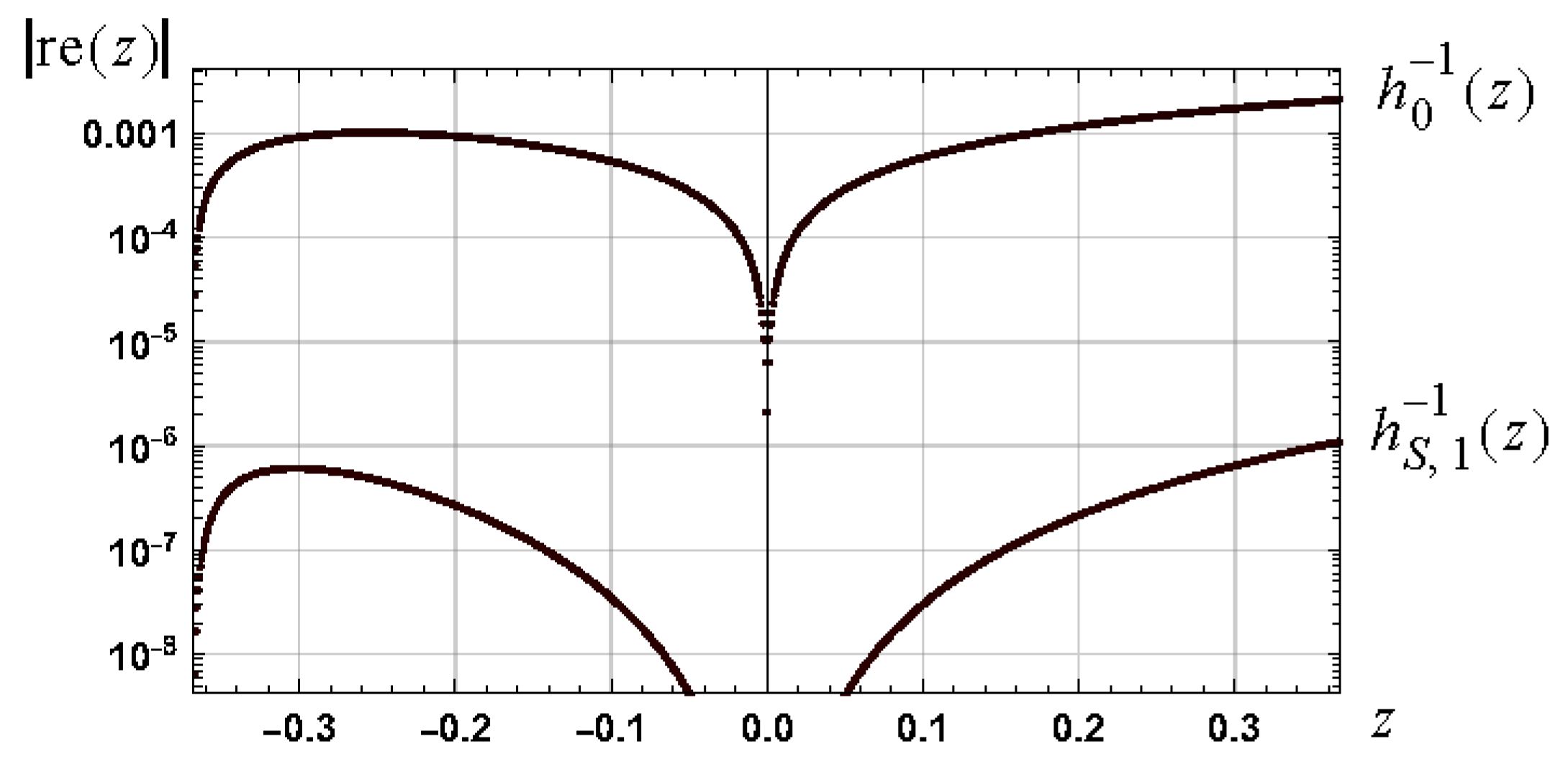
8.3. Confirmation of Bounds: Negative One Branch
Simulation Results
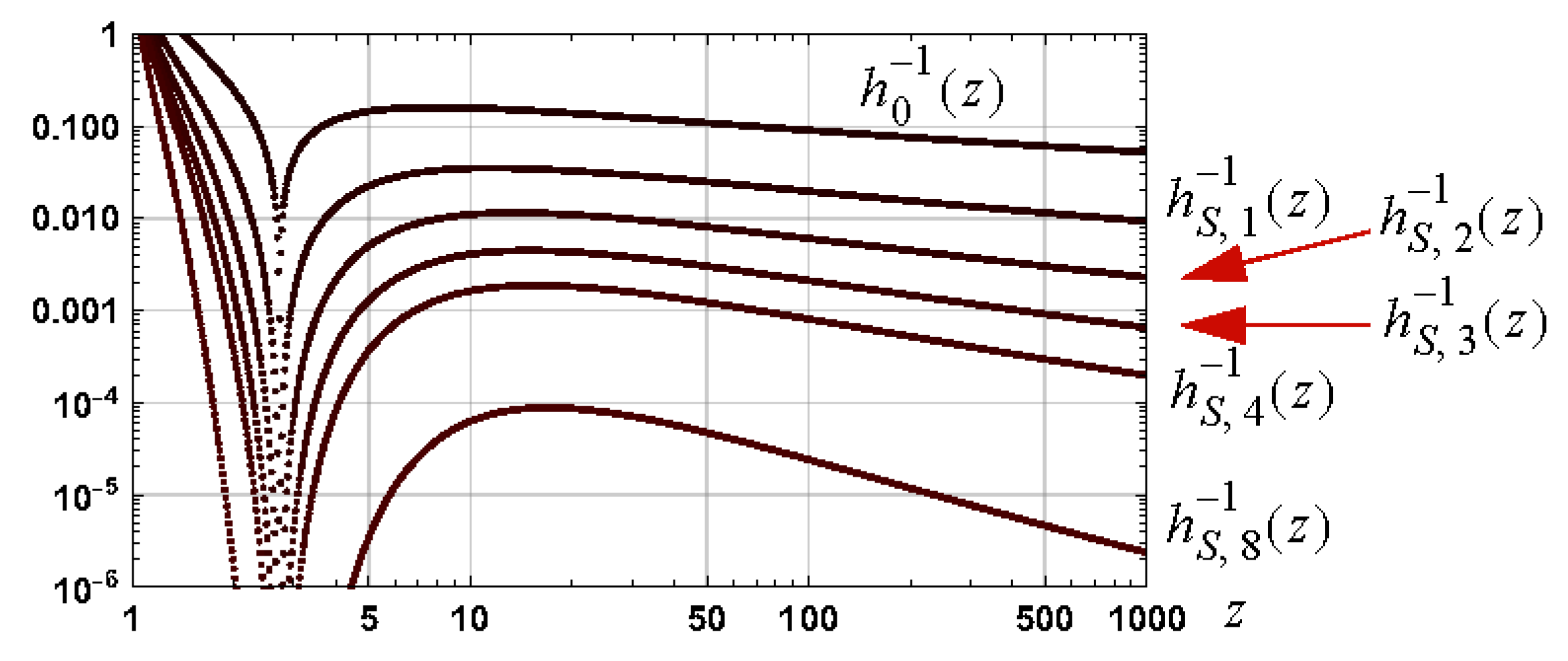
8.4. Confirmation of Bounds: Principal Branch
9. Applications
9.1. Approximations for Principal Branch
Approximation for Principal Branch and Interval [−1/e,1/e]
9.2. Upper/Lower Bounds
9.3. Integral Approximation
9.4. Principal Branch: Asymptotic-Based Approximation for z > 1
9.5. Approximations for a Power of the Lambert W Function
9.6. Approximation to Solutions of cc = y and CC = ev
10. Conclusions
Future Research
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Miscellaneous Results: Approximations for Principal Branch
Appendix A.1. Derivative Values
Appendix A.2. Approximation at Origin
Appendix A.3. Improved Approximation via Iteration
Appendix B. Proof of Theorem 4


Appendix B.1. Principal Branch
Appendix B.2. Negative One Branch


Appendix B.3. Independence of r(k,w) on k for the Case of w = 0
Appendix B.4. Independence of r(k,w) on k for w Fixed, w, k Large
References
- Mező, I. The Lambert W Function: Its Generalizations and Applications; Chapman and Hall/CRC: Boca Raton, FL, USA, 2022. [Google Scholar]
- Corless, R.M.; Gonnet, G.H.; Hare, D.E.G.; Jeffrey, D.J.; Knuth, D.E. On the Lambert W function. Adv. Comput. Math. 1996, 5, 329–359. [Google Scholar] [CrossRef]
- Veberič, D. Lambert W function for applications in physics. Comput. Phys. Commun. 2012, 183, 2622–2628. [Google Scholar] [CrossRef]
- Barry, D.A.; Parlange, J.Y.; Li, L.; Prommer, H.; Cunningham, C.J.; Stagnitti, F. Analytical approximations for real values of the Lambert W-function. Math. Comput. Simul. 2000, 53, 95–103. [Google Scholar] [CrossRef]
- Banwell, T.C. Bipolar transistor circuit analysis using the Lambert W-function. IEEE Trans. Circuits Syst. I Fundam. Theory Appl. 2000, 47, 1621–1633. [Google Scholar] [CrossRef]
- Lehtonen, J. The Lambert W function in ecological and evolutionary models. Methods Ecol. Evol. 2016, 7, 1110–1118. [Google Scholar] [CrossRef]
- Visser, M. Primes and the Lambert W function. Mathematics 2018, 6, 56. [Google Scholar] [CrossRef]
- Goličnik, M. On the Lambert W function and its utility in biochemical kinetics. Biochem. Eng. J. 2012, 63, 116–123. [Google Scholar] [CrossRef]
- Iacono, R.; Boyd, J.P. New approximations to the principal real-valued branch of the Lambert W-function. Adv. Comput. Math. 2017, 43, 1403–1436. [Google Scholar] [CrossRef]
- Howard, R.M. Analytical approximations for the principal branch of the Lambert W function. Eur. J. Math. Anal. 2022, 2, 14. [Google Scholar] [CrossRef]
- Lóczi, L. Guaranteed-and high-precision evaluation of the Lambert W function. Appl. Math. Comput. 2022, 433, 127406. [Google Scholar] [CrossRef]
- Barry, D.; Parlange, J.-Y.; Sander, G.; Sivaplan, M. A class of exact solutions for Richards’ equation. J. Hydrol. 1993, 142, 29–46. [Google Scholar] [CrossRef]
- Barry, D.A.; Parlange, J.Y.; Li, L.; Jeng, D.S. and Crapper, M. Green–ampt approximations. Adv. Water Resour. 2005, 28, 1003–1009. [Google Scholar] [CrossRef]
- Chatzigeorgiou, I. Bounds on the lambert function and their application to the outage analysis of user cooperation. IEEE Commun. Lett. 2013, 17, 1505–1508. [Google Scholar] [CrossRef]
- Corless, R.M.; Jeffrey, D.J.; Knuth, D.E. A sequence of series for the Lambert W function. In Proceedings of the 1997 International Symposium on Symbolic and Algebraic Computation, Kihei, HI, USA, 21–23 July 1997; pp. 197–204. [Google Scholar]
- De Bruijn, N.G. Asymptotic Methods in Analysis; North Holland: Amsterdam, The Netherlands, 1961. [Google Scholar]
- Corcino, C.B.; Corcino, R.B.; Mező, I. Continued fraction expansions for the Lambert W function. Aequationes Math. 2019, 93, 485–498. [Google Scholar] [CrossRef]
- Dubeau, F. Polynomial and rational approximations and the link between Schröder’s processes of the first and second kind. Abstr. Appl. Anal. 2014, 2014, 719846. [Google Scholar] [CrossRef]
- Howard, R.M. Schröder-based inverse function approximation. Axioms 2023, 12, 1042. [Google Scholar] [CrossRef]
- Schröder, E. Üeber unendlich viele Algorithmen zur Auflösung der Gleichungen. Math. Ann. 1870, 2, 317–365. [Google Scholar] [CrossRef]
- Kalugin, G.A.; Jeffrey, D.J. Unimodal sequences show Lambert W is Bernstein. arXiv 2010, arXiv:1011.5940. [Google Scholar]
- Kruchinin, V. Derivation of Bell polynomials of the second kind. arXiv 2011, arXiv:1104.5065. [Google Scholar]
- Barry, D.A.; Li, L.; Jeng, D.S. Comments on “numerical evaluation of the Lambert W function and application to generation of generalized Gaussian noise with exponent 1/2”. IEEE Trans. Signal Process. 2004, 52, 1456–1457. [Google Scholar] [CrossRef]
- Howard, R.M. Arbitrarily Accurate Analytical Approximations for the Error Function. Math. Comput. Appl. 2022, 27, 14. [Google Scholar] [CrossRef]

















| k | j = 0 | j = 1 | j = 2 | j = 3 | j = 4 | j = 5 | j = 6 | j = 7 |
|---|---|---|---|---|---|---|---|---|
| 1 | 1 | |||||||
| 2 | 2 | 1 | ||||||
| 3 | 9 | 8 | 2 | |||||
| 4 | 64 | 79 | 36 | 6 | ||||
| 5 | 625 | 974 | 622 | 192 | 24 | |||
| 6 | 7776 | 14,543 | 11,758 | 5126 | 1200 | 120 | ||
| 7 | 117,649 | 255,828 | 248,250 | 137,512 | 45,756 | 8640 | 720 | |
| 8 | 2,097,152 | 5,187,775 | 5,846,760 | 3,892,430 | 1,651,480 | 445,572 | 70,560 | 5040 |
| Order of Approx. | Equation (31): Relative Error Bound for the Interval | Equation (31): Relative Error Bound for the Interval | Equation (32): Relative Error Bound for the Interval |
|---|---|---|---|
| initial approx.: | |||
| first order: | |||
| second order: | |||
| third order: | |||
| fourth order: | |||
| eighth order: | |||
| 16th order: | |||
| 32nd order: | |||
| 64th order: | |||
| 128th order: |
| Order of Approx. | Equation (48). Relative Error Bound for the Interval . | Equation (48). Relative Error Bound for the Interval . | Equation (50). Relative Error Bound for the Interval . | Equation (50). Relative Error Bound for the Interval . |
|---|---|---|---|---|
| initial approx.: | ||||
| first order: | ||||
| second order: | ||||
| third order: | ||||
| fourth order: | ||||
| eighth order: | ||||
| 16th order: | ||||
| 32nd order: | ||||
| 64th order: | ||||
| 128th order: |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Howard, R.M. On Schröder-Type Series Expansions for the Lambert W Function. AppliedMath 2025, 5, 66. https://doi.org/10.3390/appliedmath5020066
Howard RM. On Schröder-Type Series Expansions for the Lambert W Function. AppliedMath. 2025; 5(2):66. https://doi.org/10.3390/appliedmath5020066
Chicago/Turabian StyleHoward, Roy M. 2025. "On Schröder-Type Series Expansions for the Lambert W Function" AppliedMath 5, no. 2: 66. https://doi.org/10.3390/appliedmath5020066
APA StyleHoward, R. M. (2025). On Schröder-Type Series Expansions for the Lambert W Function. AppliedMath, 5(2), 66. https://doi.org/10.3390/appliedmath5020066






