Solving Boundary Value Problems for a Class of Differential Equations Based on Elastic Transformation and Similar Construction Methods
Abstract
:1. Introduction
2. Preview Knowledge
2.1. The Definition and Geometric Meaning of Elasticity
2.2. Elastic Representation of the Derivative and Elastic Inverse Transformation
2.3. General Solution of the Tschebycheff Equation [21]
3. Main Theorems and Proofs
4. Flowchart
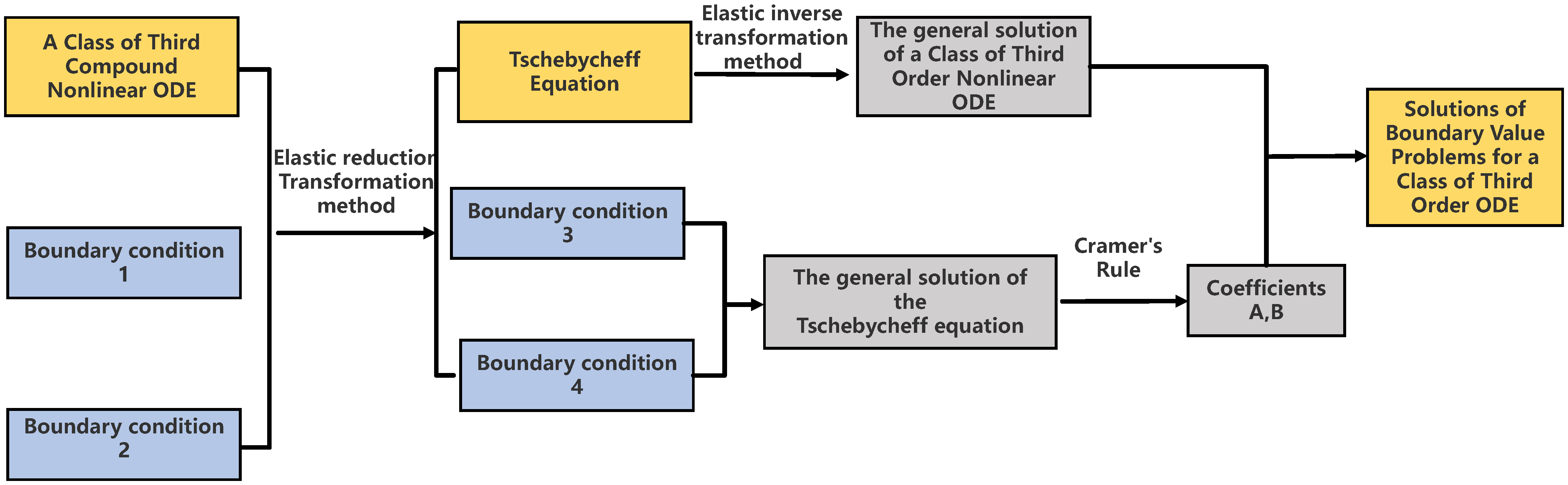
4.1. Flowchart for Solving a Class of Third-Order Nonlinear Variable Coefficient Constant Differential Square Boundary Value Problems Using the Elastic Transformation Method with the Similar Construction Method
- 1.
- Problem Formulation: Define the original third-order nonlinear ODE along with boundary conditions.
- 2.
- Elastic Transformation: Convert the nonlinear ODE into a Tschebycheff equation using an elastic reduction transformation.
- 3.
- Solve the Tschebycheff Equation: Obtain the general solution under transformed boundary conditions.
- 4.
- Inverse Transformation: Map the solution back to the original nonlinear ODE.
- 5.
- Coefficient Determination: Use Cramer’s law to compute coefficients ensuring boundary condition satisfaction.
- 6.
- Final Solution: Substitute coefficients into the general solution to obtain the final result.
4.2. Flowchart for Solving a Class of Third-Order Composite Nonlinear Variable Coefficient Constant Differential Square Boundary Value Problems by the Elastic Transformation Method with the Similar Construction Method
- 1.
- Problem Formulation: Set a class of third-order composite nonlinear ODEs as the target, along with two boundary and two cohesion conditions.
- 2.
- Elastic Transformation: Transform the ODEs, obtaining new boundary and cohesion conditions.
- 3.
- Tschebycheff Equation Solution: Solve the composite Tschebycheff equation using the new conditions to obtain its general solution.
- 4.
- Solution Conversion: Employ the SCM method to convert the Tschebycheff equation’s solution to that of the original ODEs.
- 5.
- Final Solution: Derive the boundary value problem solutions based on the converted general solution.
5. Example of Theorem
5.1. For a Class of Third-Order Nonlinear Ordinary Differential Equations with Boundary Value Problems
5.2. For a Class of Third-Order Nonlinear Composite Ordinary Differential Equations with Boundary Value Problems
6. Curve Analysis
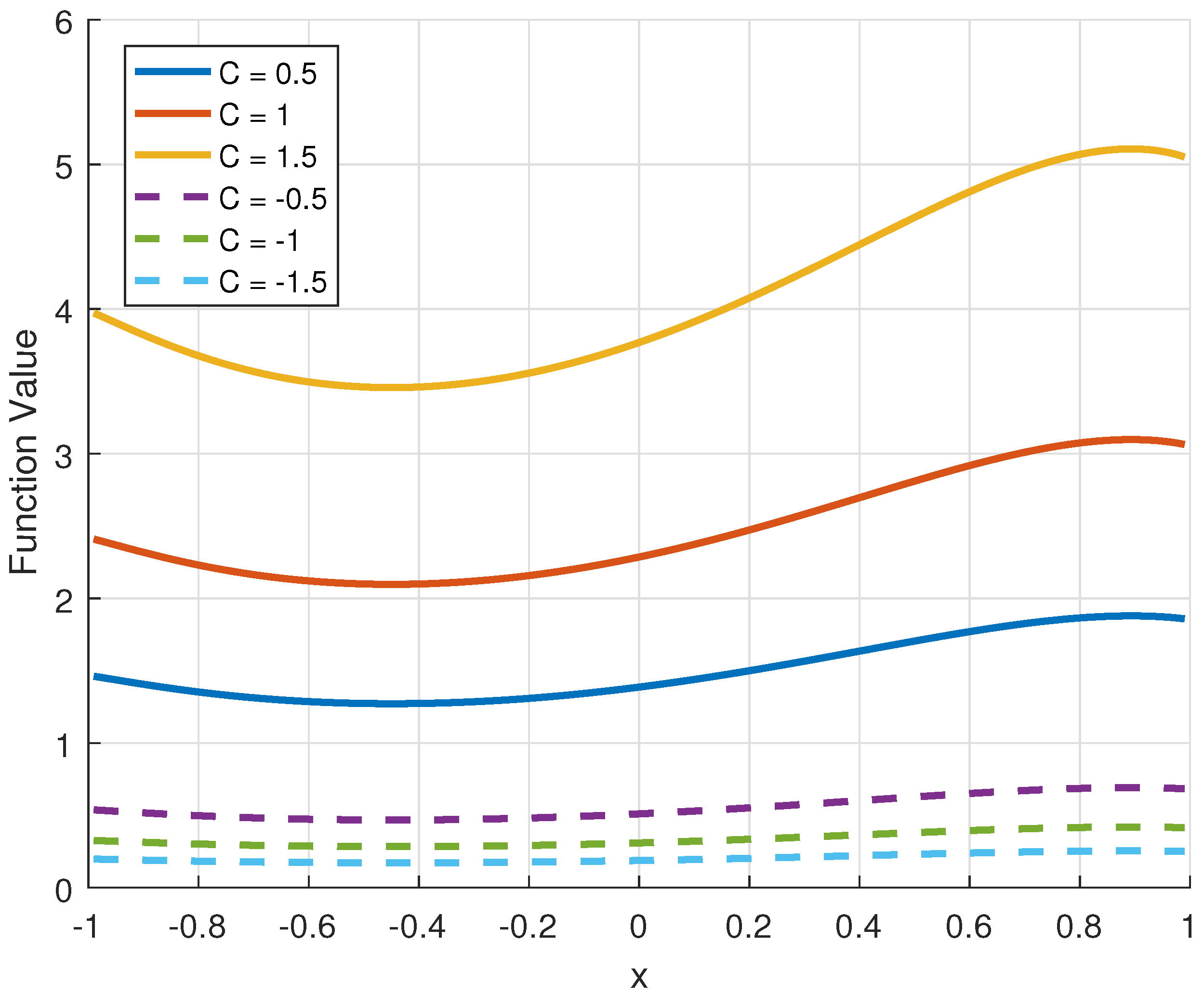
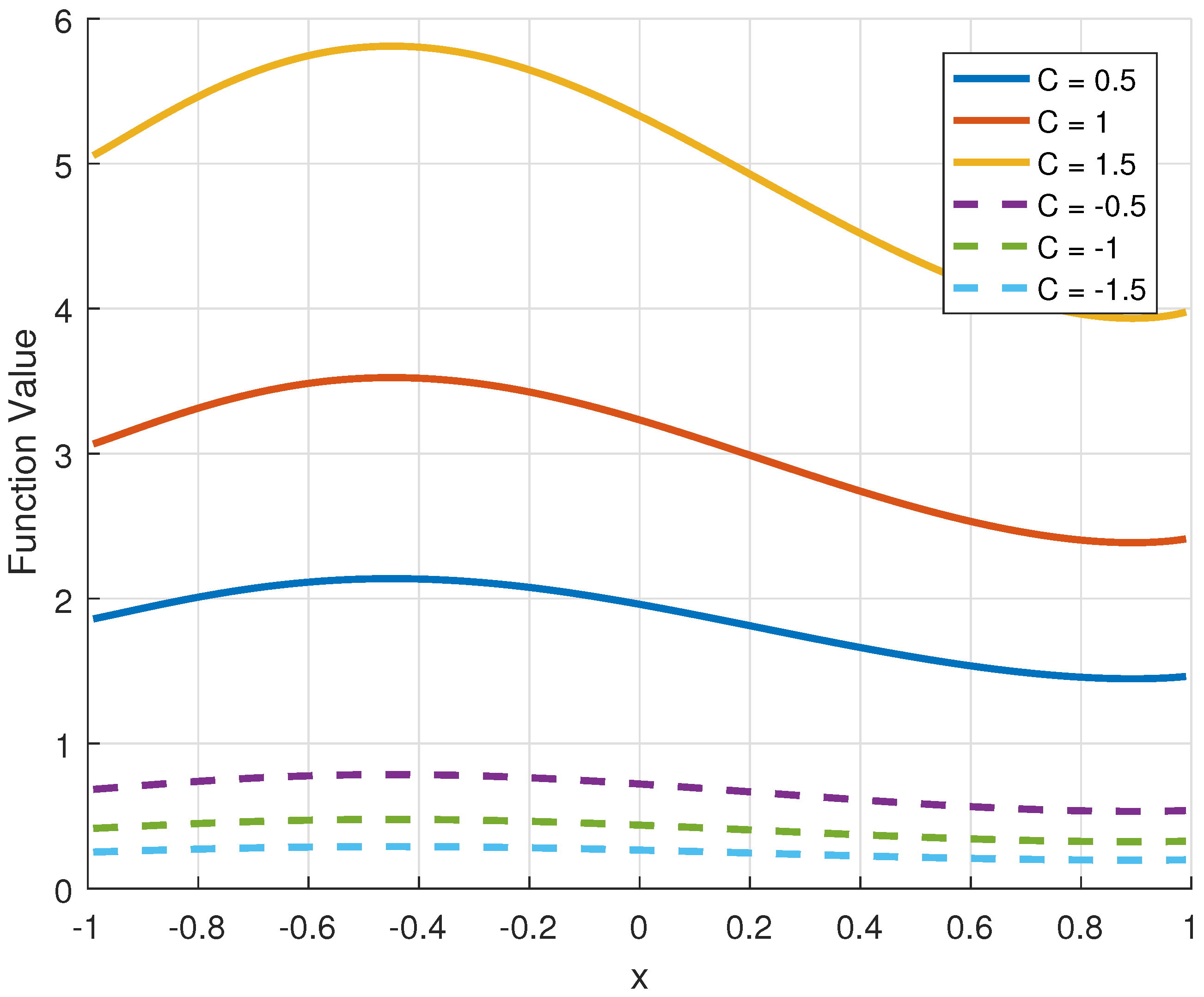
6.1. Considering the Effect of Different C Values on the Curve of the Original Function of a Class of Third-Order Nonlinear Ordinary Differential Equations
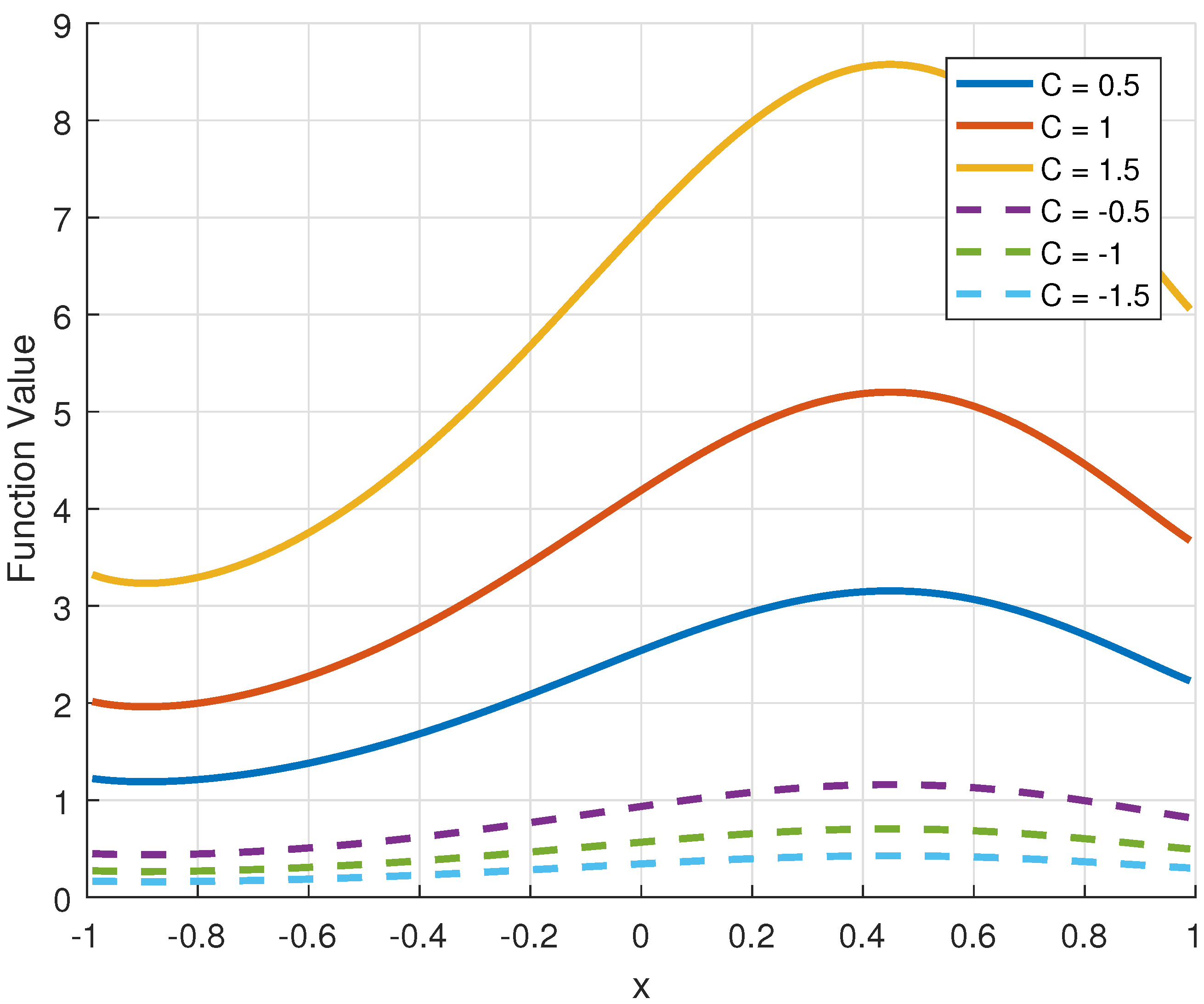
6.2. Considering the Effect of Different Initial C Values in the Region on the Left Side on the Curve of the Original Function of a Class of Third-Order Composite Nonlinear Ordinary Differential Equations
6.3. Considering the Effect of Different C Values in the Region on the Right Side on the Curve of the Original Function of a Class of Third-Order Composite Nonlinear Ordinary Differential Equations
7. Conclusions
- 1.
- This study employs the elastic transformation method (ETM) to transform the third-order boundary value problem and composite third-order nonlinear ordinary differential equations into second-order Tschebycheff equations. The boundary value problem of the Tschebycheff equation is then solved using the similar construction method (SCM). Finally, by applying the inverse elastic transformation method (EITM), the solution to the original third-order nonlinear ordinary differential equation is obtained.
- 2.
- The ETM effectively reduces the order of higher-order differential equations, simplifying their solution process. In contrast, the EITM elevates a lower-order equation to a higher order, transforming it into a solvable form. Moreover, the SCM ensures a systematic approach, eliminating the need for cumbersome computational procedures. The integration of these methods provides a novel strategy for solving nonlinear differential equations with variable coefficients.
8. Discussion
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wang, F.F.; Jiang, Z.S. Explicit Solutions of Some Nonlinear Evolution Equations through Separation of Variables. Sch. Math. 2024, 40, 58–62. [Google Scholar]
- Zhao, L.L. Integral Factors and Integral Factor Method. Sch. Math. Stat. 2023, 26, 19–22+25. [Google Scholar]
- Öziş, T.; Ağırseven, D. He’s homotopy perturbation method for solving heat-like and wave-like equations with variable coefficients. Phys. Lett. A 2008, 372, 5944–5950. [Google Scholar]
- Verma, A.K.; Kumar, N. A note on variation iteration method with an application on Lane–Emden equations. Eng. Comput. 2021, 38, 3932–3943. [Google Scholar]
- Jaiswal, J.P. Some Class of Third-and Fourth-Order Iterative Methods for Solving Nonlinear Equations. J. Appl. Math. 2014, 2014, 817656. [Google Scholar]
- Li, J.X.; Li, L. The Application of Variable Substitution in Ordinary Differential Equations. Sch. Math. Baoshan Univ. 2016, 35, 51–54. [Google Scholar]
- Liu, Q. Solutions and Integrability Analysis of Two Classes of Nonlinear Differential Equations. Master’s Thesis, North China Electric Power University, Beijing, China, 2021. [Google Scholar]
- Ouyang, T. Application of Three Methods in Solving Nonlinear Partial Differential Equations. Master’s Thesis, Xinjiang Normal University, Ürümqi, China, 2022. [Google Scholar]
- Li, S.C.; Yi, L.Z.; Zheng, P.S. The Similar Structure of Differential Equation on Fixed Solution Problem. J. Sichuan Univ. (Nat. Sci. Ed.) 2006, 43, 933–934. [Google Scholar]
- Li, S.C. The Similarity Structuring Method of Boundary Value Problems for Composite Differential Equations. J. Xihua Univ. Nat. Sci. 2013, 32, 27–31. [Google Scholar]
- Li, H.E.; Dong, X.X.; Li, S.C.; Fan, C.Y. A New Method and Applications of the Boundary Value Problem of Differential Equation. Adv. Mater. Res. 2014, 937, 695–699. [Google Scholar] [CrossRef]
- Shi, J. The Constructive Method and Its Applications of Solutions for the Boundary Value Problem of Composite Second-Order Differential Equation. Master’s Thesis, Xihua University, Chengdu, China, 2014. (In Chinese). [Google Scholar]
- Zheng, P.; Li, S.; Leng, L.; Gui, D. Similar Construction Method of Boundary Value Problems of a Nonlinear Composite Modified Bessel Equations. J. Xinyang Norm. Univ. (Nat. Sci. Ed.) 2014, 27, 490–492+504. [Google Scholar]
- Dong, X.X.; Liu, Z.B.; Li, S.C. Similar Constructing Method for Solving Nonlinear Spherical Seepage Model with Quadratic Pressure Gradient of Three-region Composite Fractal Reservoir. Comput. Appl. Math. 2019, 38, 83. [Google Scholar]
- Sheng, C.C.; Zhao, J.Z.; Li, Y.M.; Li, S.C.; Jia, H. Similar Construction Method of Solution for Solving the Mathematical Model of Fractal Reservoir with Spherical Flow. J. Appl. Math. 2013, 2013, 219218. [Google Scholar]
- Xu, L.; Liu, X.; Liang, L.; Li, S.; Zhou, L. The Similar Structure Method for Solving the Model of Fractal Dual-Porosity Reservoir. Math. Prob. Eng. 2013, 2013, 954106. [Google Scholar]
- Rosa, A.J.; Horne, R.H.N. Automated Type-Curve Matching in Well Test Analysis Using Laplace Space Determination of Parameter Gradients. In Proceedings of the SPE Annual Technical Conference and Exhibition, San Francisco, CA, USA, 5–8 October 1983. [Google Scholar]
- Roumboutsos, A.; Stewart, G. A Direct Deconvolution or Convolution Algorithm for Well Test Analysis. In Proceedings of the SPE Annual Technical Conference and Exhibition, Houston, TX, USA, 2–5 October 1988. [Google Scholar]
- Sahimi, M.; Yortsos, Y.C. Applications of Fractal Geometry to Porous Media: A Review. In Proceedings of the Annual Fall Meeting of the Society of Petroleum Engineers, New Orleans, LA, USA, 3–6 October 1990. [Google Scholar]
- Li, S.C.; He, Q.; Dong, X.X. The Elasticity of the Outer Boundary and the Solution of Two-Region Composite Reservoir Seepage Model. Pet. Sci. Technol. 2022, 40, 2773–2791. [Google Scholar] [CrossRef]
- Zheng, P.; Luo, J.; Li, S.; Dong, X. Elastic Transformation Method for Solving Ordinary Differential Equations with Variable Coefficients. AIMS Math. 2022, 7, 1307–1320. [Google Scholar] [CrossRef]
- Lin, F.; Li, S.; Shao, D.; Fu, X.; Liu, P.; Gui, Q. Elastic Transformation Method for Solving the Initial Value Problem of Variable Coefficient Nonlinear Ordinary Differential Equations. AIMS Math. 2022, 7, 11972–11991. [Google Scholar]
- Fan, L. Research on Solvable Classes of Riccati Equation Based on Elastic Transformation. Ph.D. Thesis, Xihua University, Chengdu, China, 2023. [Google Scholar]
- Jiang, T.; Zheng, P.; Xu, L.; Leng, L. Application of Elastic Transformation Method and Similarity Construction Method in Solving Ordinary Differential Equations. J. Appl. Math. Comput. 2023, 70, 175–195. [Google Scholar] [CrossRef]
- Xia, W.; Li, S.; Gui, D. Similar Structured Method of Solution to Boundary Value Problems of the Composite Tschebyscheff System. J. Shaanxi Univ. Technol. (Nat. Sci. Ed.) 2015, 31, 69–74. [Google Scholar]
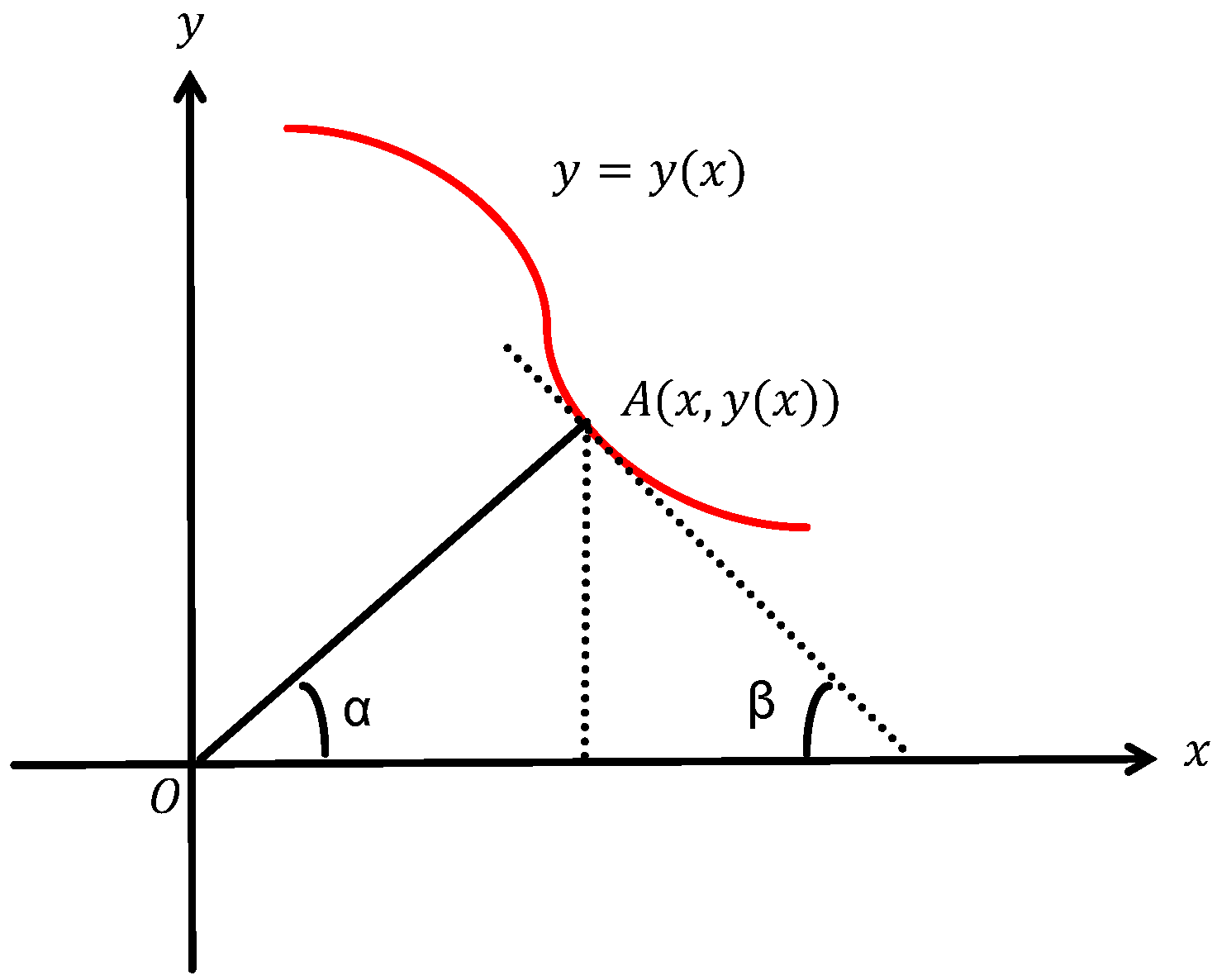

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, J.; Zheng, P.; Xie, J. Solving Boundary Value Problems for a Class of Differential Equations Based on Elastic Transformation and Similar Construction Methods. AppliedMath 2025, 5, 41. https://doi.org/10.3390/appliedmath5020041
Liu J, Zheng P, Xie J. Solving Boundary Value Problems for a Class of Differential Equations Based on Elastic Transformation and Similar Construction Methods. AppliedMath. 2025; 5(2):41. https://doi.org/10.3390/appliedmath5020041
Chicago/Turabian StyleLiu, Jinfeng, Pengshe Zheng, and Jiajia Xie. 2025. "Solving Boundary Value Problems for a Class of Differential Equations Based on Elastic Transformation and Similar Construction Methods" AppliedMath 5, no. 2: 41. https://doi.org/10.3390/appliedmath5020041
APA StyleLiu, J., Zheng, P., & Xie, J. (2025). Solving Boundary Value Problems for a Class of Differential Equations Based on Elastic Transformation and Similar Construction Methods. AppliedMath, 5(2), 41. https://doi.org/10.3390/appliedmath5020041





