Convergence Analysis of Jarratt-like Methods for Solving Nonlinear Equations for Thrice-Differentiable Operators
Abstract
1. Introduction
1.1. Motivation
- Proving the order of convergence of an iterative method is not a straightforward task. In [13], the authors proved that method (4) has an order of convergence of four by using the Taylor series expansion for the operators, which are at least five times differentiable. Even though higher-order derivatives of the involved operators are not present in the structure of the iterative methods, one needs the existence of higher-order derivatives to obtain the convergence order, which limits their applicability. For example, consider the equation , where and 0 otherwise. It is observed that is unbounded at and . Therefore, method (4) cannot guarantee the convergence if one uses the analysis in [13].
- The most important semi-local convergence analysis has not been given.
- A set that contains all suitable initial points for convergence of the process is not provided in earlier studies.
1.2. Originality
- (I)
- We prove that method (4) has an order of convergence of at least four without using the Taylor series expansion, only considering the existence of the third-order differentiability of the involved operator.
- (II)
- We present a ball of convergence and address the uniqueness of the solution, which is not provided in earlier works.
- (III)
- We extend method (4) to a sixth-order method given by
- (IV)
- (V)
- An upper bound for the asymptotic error constant is provided.
- (VI)
- The selection of initial points not previously available is now known.
- (VII)
- The analysis is conducted in Banach spaces.
- (a)
- The convergence conditions are sufficient but not necessary. It will be interesting to also find necessary conditions. This will be the direction of future research, even if we will have to impose additional conditions.
- (b)
- We can see if the second Lipschitz-type condition () for the semi-local case or the Lipschitz-type conditions on second and third derivative (see (), (), respectively) for the local convergence case can be weakened.
2. Basic Concepts
- (i)
- ,
- (ii)
- There exists , , and such that ;
3. Semi-Local Convergence Analysis of (4) and (5)
- ()
- There exists and such that with .
- ()
- There exists and an invertible operator such thatand the Lipschitz-like conditionwhere is given in Lemma 2.
- ()
- and .
- (i)
- The operator can be considered I (the identity operator) or . Other choices are possible if conditions () and () are satisfied.
- (ii)
- By condition (), we have
- (iii)
- From conditions () and (), we obtainBy using Lemma 1, the operator is invertible and
- (iv)
- Using (ii) and (iii), we obtain
- Let us define two scalar sequences and by
4. Local Convergence Analysis of (4) and (5)
- ;
- ;
- ;
- .
5. Numerical Examples
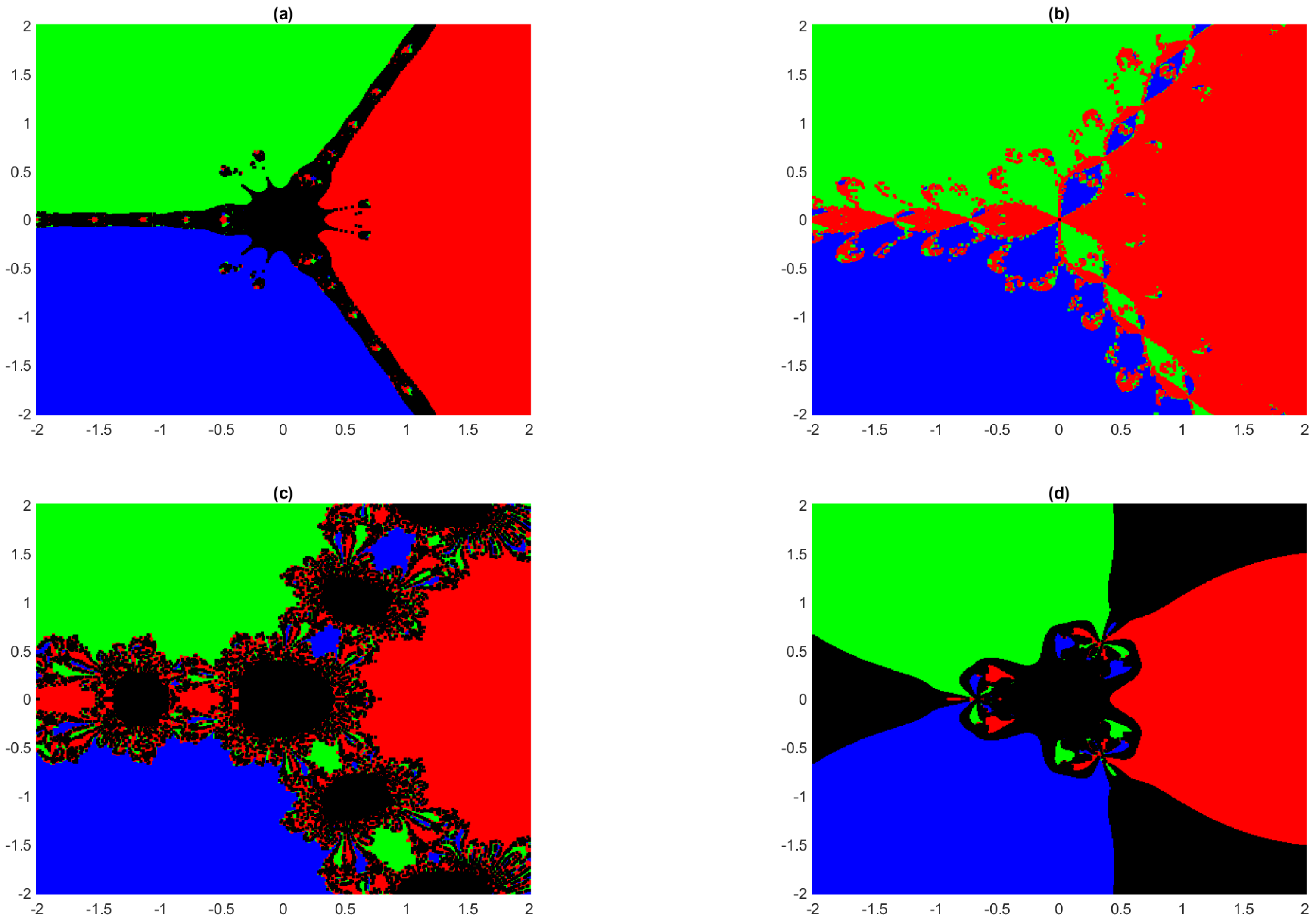
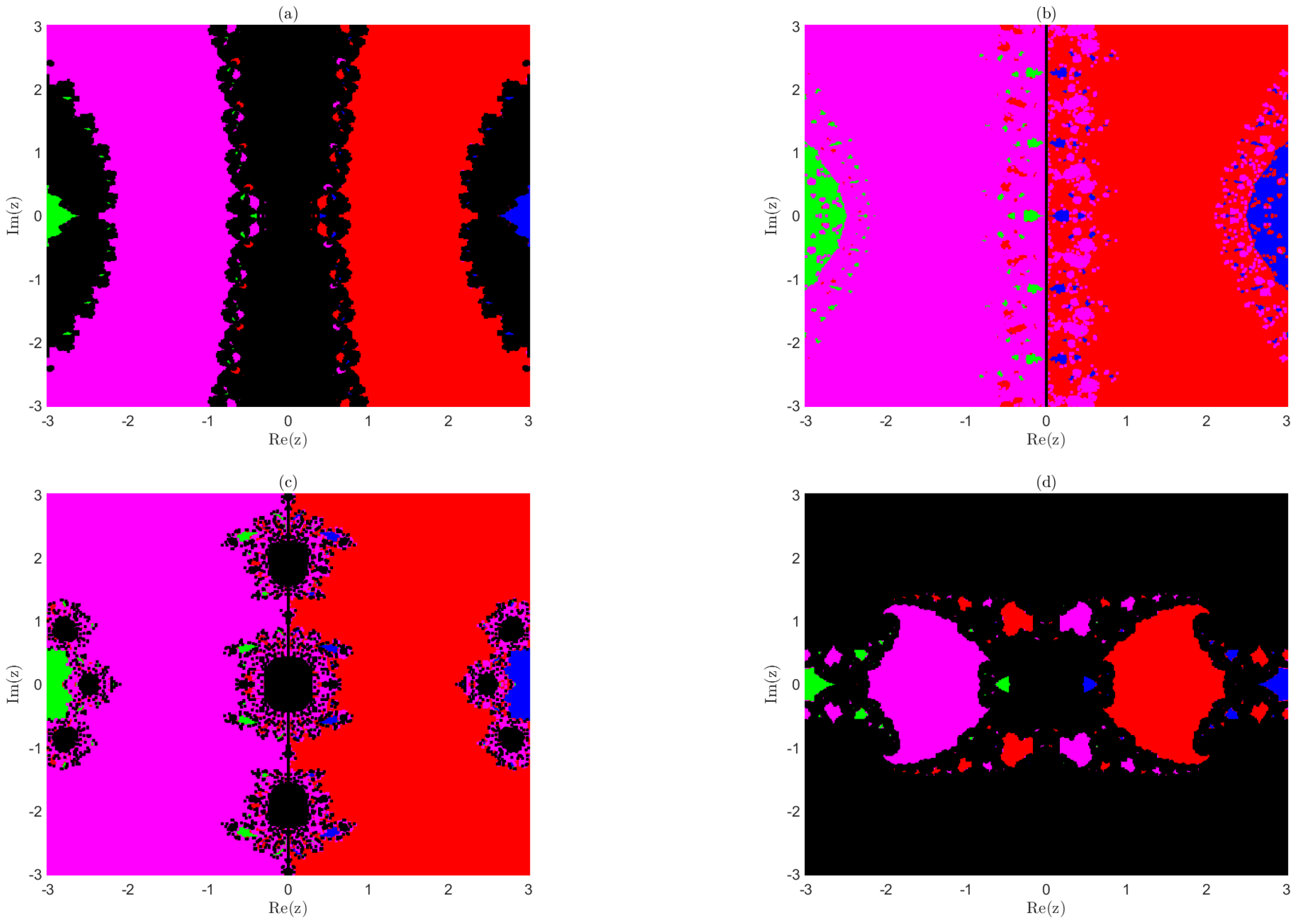
6. Dynamical Concepts
- Dividing the region R that contains all the solutions of the equation in equidistant grid points. The grid points are considered as the initial points for the convergence process.
- denotes the percentage of grid points for which the sequence converges to a solution of the given equation, and denotes the percentage of grid points for which the sequence does not converge to any of the solutions of the equation given in Examples 4 and 5.
- To obtain a visual picture, colors blue, green, red, and magenta are assigned to the grid points for which the sequence does not converge to , respectively, and black is assigned to grid points for which the sequence does not converge to any of the solutions of the given equation in Examples 4 and 5.
- An error tolerance of in a maximum of 50 iteration is considered.
7. Conclusions
- ⋆
- ⋆
- ⋆
- ⋆
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ostrowski, A.M. Solution of Equations and Systems of Equations, 2nd ed.; Pure and Applied Mathematics; Academic Press: New York, NY, USA; London, UK, 1966; Volume 9, pp. xiv+338. [Google Scholar]
- Kantorovich, L. Sur la méthode de Newton. Travaux De L’institut Des Mathématiques Steklov 1949, XXVIII, 104–144. [Google Scholar]
- Bartle, R.G.; Sherbert, D.R. Introduction to Real Analysis, 4th ed.; John Wiley & Sons, Inc.: New York, NY, USA, 2011; pp. xii+404. [Google Scholar]
- Argyros, I.K. Computational Theory of Iterative Methods; Studies in Computational Mathematics; Elsevier B. V.: Amsterdam, The Netherlands, 2007; Volume 15, pp. xvi+487. [Google Scholar]
- Ortega, J.M.; Rheinboldt, W.C. Iterative Solution of Nonlinear Equations in Several Variables; Classics in Applied Mathematics; SIAM: Philadelphia, PA, USA, 2000; Volume 30, pp. xxvi+572. [Google Scholar]
- Argyros, I.K. Convergence and Applications of Newton-Type Iterations; Springer: New York, NY, USA, 2008; pp. xvi+506. [Google Scholar]
- Bruck, R.E.; Reich, S. A general convergence principle in nonlinear functional analysis. Nonlinear Anal. 1980, 4, 939–950. [Google Scholar]
- Traub, J.F. Iterative Methods for the Solution of Equations; Prentice-Hall Series in Automatic Computation; Prentice-Hall, Inc.: Englewood Cliffs, NJ, USA, 1964; pp. xviii+310. [Google Scholar]
- Jarratt, P. Some fourth order multipoint iterative methods for solving equations. Math. Comput. 1966, 20, 434–437. [Google Scholar] [CrossRef]
- Narang, M.; Bhatia, S.; Kanwar, V. New two-parameter Chebyshev-Halley-like family of fourth and sixth-order methods for systems of nonlinear equations. Appl. Math. Comput. 2016, 275, 394–403. [Google Scholar] [CrossRef]
- Cordero, A.; Rojas-Hiciano, R.V.; Torregrosa, J.R.; Vassileva, M.P. A highly efficient class of optimal fourth-order methods for solving nonlinear systems. Numer. Algorithms 2024, 95, 1879–1904. [Google Scholar] [CrossRef]
- Bate, I.; Senapati, K.; George, S.; Muniyasamy, M.; Chandhini, G. Jarratt-type methods and their convergence analysis without using Taylor expansion. Appl. Math. Comput. 2025, 487, 1–28. [Google Scholar]
- Sharma, J.R.; Arora, H. Efficient Jarratt-like methods for solving systems of nonlinear equations. Calcolo 2014, 51, 193–210. [Google Scholar] [CrossRef]
- Ezquerro Fernández, J.A.; Hernández Verón, M.A. Newton’s Method: An Updated Approach of Kantorovich’s Theory; Frontiers in Mathematics; Birkhäuser/Springer: Cham, Switzerland, 2017; pp. xii+166. [Google Scholar]
- Weerakoon, S.; Fernando, T.G.I. A variant of Newton’s method with accelerated third-order convergence. Appl. Math. Lett. 2000, 13, 87–93. [Google Scholar]
- Sakawa, Y. Optimal control of a certain type of linear distributed-parameter systems. IEEE Trans. Autom. Control 1966, 11, 35–41. [Google Scholar] [CrossRef]
- Kumar, S.; Sloan, I.H. A new collocation-type method for Hammerstein integral equations. Math. Comput. 1987, 48, 585–593. [Google Scholar] [CrossRef]
- Dolph, C.L. Nonlinear integral equations of the Hammerstein type. Trans. Am. Math. Soc. 1949, 66, 289–307. [Google Scholar] [CrossRef]
- Hu, S.; Khavanin, M.; Zhuang, W. Integral equations arising in the kinetic theory of gases. J. Appl. Anal. 1989, 34, 261–266. [Google Scholar] [CrossRef]
- Amat, S.; Busquier, S.; Plaza, S. Review of some iterative root-finding methods from a dynamical point of view. Sci. Ser. A Math. Sci. (N.S.) 2004, 10, 3–35. [Google Scholar]
- Nayak, T.; Pal, S. Symmetry and Dynamics of Chebyshev’s Method. Mediterr. J. Math. 2025, 22, 1–25. [Google Scholar] [CrossRef]
- Varona, J.L. Graphic and numerical comparison between iterative methods. Math. Intell. 2002, 24, 37–46. [Google Scholar] [CrossRef]
- Campos, B.; Canela, J.; Vindel, P. Dynamics of Newton-like root finding methods. Numer. Algorithms 2023, 93, 1453–1480. [Google Scholar] [CrossRef]
- Hueso, J.L.; Martínez, E.; Teruel, C. Convergence, efficiency and dynamics of new fourth and sixth order families of iterative methods for nonlinear systems. J. Comput. Appl. Math. 2015, 275, 412–420. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bate, I.; Senapati, K.; George, S.; Argyros, I.K.; Argyros, M.I. Convergence Analysis of Jarratt-like Methods for Solving Nonlinear Equations for Thrice-Differentiable Operators. AppliedMath 2025, 5, 38. https://doi.org/10.3390/appliedmath5020038
Bate I, Senapati K, George S, Argyros IK, Argyros MI. Convergence Analysis of Jarratt-like Methods for Solving Nonlinear Equations for Thrice-Differentiable Operators. AppliedMath. 2025; 5(2):38. https://doi.org/10.3390/appliedmath5020038
Chicago/Turabian StyleBate, Indra, Kedarnath Senapati, Santhosh George, Ioannis K. Argyros, and Michael I. Argyros. 2025. "Convergence Analysis of Jarratt-like Methods for Solving Nonlinear Equations for Thrice-Differentiable Operators" AppliedMath 5, no. 2: 38. https://doi.org/10.3390/appliedmath5020038
APA StyleBate, I., Senapati, K., George, S., Argyros, I. K., & Argyros, M. I. (2025). Convergence Analysis of Jarratt-like Methods for Solving Nonlinear Equations for Thrice-Differentiable Operators. AppliedMath, 5(2), 38. https://doi.org/10.3390/appliedmath5020038







