1. Introduction
A person has a secret which they have shared with all of their friends except one. In fairness, they decide that they need to share the secret with this other friend. Repeated iterations of this algorithm will either propagate the secret across the entire network or stall where the secret will no longer be shared. This process, which can be applied to the spread of infection or diseases, can be described with zero-forcing. For a graph
G, the zero forcing number of
G,
, is the minimum size of a set
S of vertices in which repeated applications of the forcing algorithm (described below) ends with all vertices being in
S. The forcing algorithm is as follows: if a vertex
v is in
S, and there is exactly one neighbor
u of
v that is not in
S, then the vertex
u is added to
S in the subsequent iteration. Zero forcing numbers and related variants have been investigated and results have appeared in several papers, see for example Allison et al. [
1], Ansill, Jacob, Penzellna, and Saavedra [
2], Fallat and Hogben [
3], Fetcie, Jacob, and Saavedra [
4], Gomez et al. [
5], Gomez et al. [
6], Johnson, Vick, and Narayan [
7], and Karst, Shen, and Vu [
8]. An analogous problem is to investigate the maximum size of a set
S that fails to force all of the vertices in a graph to be in
S. This property is defined to be the failed zero-forcing number of a graph, and is denoted by
, and has sparked attention in recent years. Colorings can be used to represent failed zero forcing sets where the vertex in
S will be called colored and the vertices not in
S will be called uncolored. An interesting problem is how to determine the maximum size of a set
S that fails to force all of the vertices in a graph to be in
S. This threshold is called the failed zero forcing number of a graph, denoted by
, see [
4,
9]. Shitov [
10], proved that the problem of determining the failed zero forcing number of a graph is NP-complete. A classification of all graphs having a failed zero forcing number equal to 2 was determined by Gomez, Rubi, Terrazas, and Narayan [
6]. An nearly equivalent property known as the zero blocking number of a graph was independently obtained in 2020 by Beaudouin-Lafona, Crawford, Chen, Karst, Nielsen, and Sakai Troxell [
11] and Karst, Shen, and Vu [
8]. The zero blocking number of a graph
G equals
. In 2010, the IMA-ISU research group [
1] introduced the skew zero forcing. Here, any vertex that has all but one of its neighbors colored will force the last vertex to be forced. In 2016, Ansill, Jacob, Penzellna, and Saavedra [
2] defined the failed skew zero forcing number, which is the maximum size of a set of vertices that fails to force all of the vertices in the graph. The skew zero forcing number was introduced as an approach for finding the minimum rank among all skew-symmetric matrices associated with a prescribed graph [
1]. It also applies to the problem involving all symmetric matrices with zero diagonal. In skew zero forcing, if exactly one neighbor
u of
v is not in
S, then
u is added to
S in the next iteration. The difference between skew zero forcing and zero forcing is that vertices that are not in
S can force other vertices. This leads to the failed skew zero forcing number of a graph, which is denoted by
. They obtained a classification of all graphs where
. Johnson, Vick, and Narayan obtained a classification of all graphs where
[
7]. If a subset
of colored vertices forces all of the vertices
V in a graph, we say that
skew forces (or simply forces) the graph, or state that
. If a subset
of colored vertices fails to add more vertices at the next iteration, we will refer to the set
as skew stalled (or simply stalled).
The forcing rule can be formally described in Algorithm 1.
| Algorithm 1: Maximum-sized failed skew zero forcing set |
Input: A graph G and a subset of vertices S Output: Maximum sized failed skew zero forcing set While G has a vertex v with only one neighbor u that is not in S. (a) Choose a vertex v with only one neighbor u that is not in S. (b) Add u to S. |
We present an example of skew zero forcing in
Figure 1.
Failed skew zero forcing numbers have been determined for paths, cycles, complete multipartite graphs, grid graphs, wheel graphs, and certain subfamilies of trees [
2]. In 2023, Cooper and Fickes identified a connection between skew zero forcing and zero loci of null vectors [
12].
Our focus will be on graphs where there are sets of vertices in close proximity. In
Section 2, we investigate powers of paths. The
kth power of a path
is denoted
and is a graph with vertices
and edges between
and
if, and only if,
. We note that this family includes both paths and complete graphs, such as
and
. However, we can investigate intermediate cases of path powers to uncover unexplored families of graphs.
In
Section 3, we investigate circulant graphs. The circulant graph
, where
, is the graph with a set of
n vertices
and a set of edges equal to
. Circulant graphs are of interest in failed skew zero forcing, as they have applications to small world networks, as defined by Watts and Strogatz [
13], where nodes are able to reach most other nodes by paths with a small number of edges. In addition, circulant graphs have applications to deadlock-free routing. The multiple paths between vertices provide passage ways to avoid deadlocks, as noted by A. El-Mesady et al. [
14]. The impact of these multiple paths is that the failed skew-forcing numbers for circulant graphs will be larger than those for cycles. The question is, how much? Our results quantify how much failed skew zero forcing numbers will increase.
We extend work by Gomez et al. [
6] on failed zero forcing numbers of circulant graphs to failed skew zero forcing numbers. Certain sequences for failed skew zero forcing numbers path powers and circulant graphs are sequences A355067 and A355399 in the Online Encyclopedia for Integer Sequences [
15,
16].
2. Path Powers
The failed skew zero forcing number of paths was investigated by Ansill, Jacob, Penzellna, and Saavedra [
2]. An interesting aspect of some of these graphs is that
may not exist. The smallest example is
, where one vertex will force the second vertex and then the second vertex will force the first vertex. They proved that
if
n is odd and if
n is even then
does not exist. When
n is odd, the maximum-sized failed skew forcing set is obtained by starting with the second vertex and coloring every other vertex.
A path can be used to model a set of people arranged in a line where each person has one or two people in their proximity. We consider expanding the neighborhood of each person, so they can reach people that are not just adjacent but are within a prescribed distance
k. This can be modeled using path powers, where
is a graph with vertices
and
and
are adjacent if, and only if,
. An example of a maximum-sized failed skew zero forcing set of a path is shown in
Figure 2 and a maximum-sized failed skew zero forcing set of a square of a path is shown in
Figure 3.
We continue with some basic results regarding the failed skew forcing number of path powers. We will use the term prefix to indicate the initial vertices of a path power.
Lemma 1. For the graph , if where , then all of the vertices in the graph will be forced.
Proof. Assume that . Then will be forced one at a time by for all and will be forced one at a time by for all . □
The next lemma shows that if we have a string of three colored vertices, they must have a string of three uncolored vertices both preceding and succeeding the string.
Lemma 2. Let where . Assume we have a failed skew zero forcing set where ,, and are vertices that are colored. Then , , , , , and must all be uncolored.
Proof. It suffices to consider cases for each of the uncolored vertices:
If is colored, then will force and then will force ;
If is colored, then will force ;
If or is colored, then we will have four consecutive colored vertices, which forces the graph;
If is colored, then will force ;
If is colored, then will force and then will force to create four consecutive colored vertices.
□
In the next lemma, we present lower bounds for the failed skew forcing number of squares of paths.
Lemma 3. Let . Then , , and .
Proof. Let .
Coloring the vertices will result in a failed skew zero forcing set since every colored vertex will have two uncolored neighbors and the uncolored vertices will all have either zero or two uncolored neighbors. Hence, .
Coloring the vertices will result in a failed skew zero forcing set since every colored vertex will have two uncolored neighbors and the uncolored vertices will all have either zero or two uncolored neighbors. Hence, .
Coloring the vertices will result in a failed skew zero forcing set since every colored vertex will have two uncolored neighbors and the uncolored vertices will all have either zero or two uncolored neighbors. Hence, . □
In our next lemma, we consider different prefixes that force all of the vertices in the path.
Lemma 4. Let be our prefix of four vertices. If , , and will not skew force. If and , S will cause all of the vertices in the graph to be forced.
Proof. For this, we must consider the cases where , or are in S:
Case (i): Suppose . Then both neighbors of are in S and and have uncolored neighbors, and . So, and will not force.
Case (ii): Suppose . Then will force since it is its only uncolored neighbor. Now we have the case.
Case (iii): Suppose . Then will force since it is its only uncolored neighbor. Once again, we now have the case.
Case (iv): Now consider if . Then has only one neighbor not in S:. Now, . It follows that now only has one uncolored neighbor, . Thus, . By Lemma 1, all of the vertices in the graph will be forced.
Case (v): Suppose . Then has one uncolored neighbor, . Now, . Therefore, will skew force . Also, has one neighbor not in S, . Thus, and by Lemma 1, all of the vertices in the graph will be forced.
Case (vi): Suppose . Then has one neighbor not in , causing . Now has only one neighbor not in S, , causing , and by Lemma 1, all of the vertices in the graph will be forced.
Case (vii): Suppose . Then has one neighbor not in S, , which it will skew force, causing . Now has one neighbor outside S, , which it will skew force, causing , and by Lemma 1, all of the vertices in the graph will be forced.
Case (viii): Suppose . Then has one neighbor not in S, , which it will skew force into S, causing . Now has one neighbor not in S, . Thus, and by Lemma 1, all of the vertices in the graph will be forced.
All cases where have now been covered, except .
Case (ix): Suppose . Then has one uncolored neighbor, . Thus, and by Lemma 1, all of the vertices in the graph will be forced.
□
Next, we present upper bounds for the square of paths.
Lemma 5. Let . Then , , and .
Proof. We first consider when . By the pigeonhole principle, for the first vertices we must have at most vertices colored. We note that we cannot have colored with the first vertex in the graph colored. As a result, the fourth and fifth to the last vertices must be colored. Then, by Lemma 4, the last three vertices must be uncolored. Hence, .
Next, we consider when . By the pigeonhole principle, for the first vertices we must have, at most, vertices colored. We note that we cannot have colored with the first vertex in the graph colored. Hence, .
Finally, we consider when . Using the pigeonhole principle and trying to avoid three consecutively filled vertices, for the first vertices we must have, at most, vertices colored. We note that we cannot have colored with the first vertex in the graph colored. This then leaves five vertices at the other end. At most, one of these can be colored. Hence, □
Lemmas 3 and 5 can be combined into the following theorem.
Theorem 1. Let . Then if and otherwise.
We next consider the third powers of paths.
Lemma 6. Proof. First, consider . We know then that , and to see that S is skew stalled, note that for all for that are in S, they have neighbors and outside of S, such that and , so they will not skew force. Furthermore, any for will have no neighbors outside of S, since any neighbor would have , so they are not adjacent. So, we know that
Now, to show , suppose . We will show now that S will skew force all of V. So, if there are vertices in S, then there are white vertices to divide the colored vertices. If we color vertices and , then we have remaining vertices. So, we will place vertices across k sections. If we use 3 colored vertices in each section, then we have used a total of vertices and are left with a surplus of 5 vertices, which can be split into 1 and 4 or 2 and 3, both of which would cause . Furthermore, if we use only 1 vertex in a section, we use vertices, causing a surplus of 7 leftover colored vertices. Note that if we use only 1 vertex in more than one section, we are left with a surplus of 7 vertices or more across 2 sections, which would cause . For S to be a failed skew zero forcing set, . Therefore, . □
Lemma 7. Proof. Coloring all vertices except gives a failed skew forcing set of size since each vertex has either 0 or 2 uncolored neighbors. Hence, . Now, we want to show that . So, assume , implying that . First, we will focus on the first four vertices, , and mirror those results to the last four vertices through symmetry. We know that if and , will not skew force. Furthermore, we know that if only 2 vertices of these first 4 and last 4 are in S, then there remains vertices in S to be separated by vertices outside S, causing there to be a section of 3 vertices in S, one vertex outside S, and 4 more vertices in S, which would cause the uncolored vertex outside S to be forced by its neighbor in the longer string, which, by Lemma 2, would skew force the whole graph. Finally, if all 4 of the prefix vertices are in S, then will force , eventually causing .
So, we know that S must contain and and to have the maximum number of vertices. However, with this prefix, S can only be defined as it is in Lemma 4 without causing S to skew force V. So, . Since we know and , we conclude that . □
Lemma 8. for
Proof. Suppose . Then where . Notice that for all where , they have neighbors , such that and , which implies that will not skew force. Note that for any , where , has no neighbors not in S. Notice that , which is not in S, has neighbors ; therefore, cannot skew force. This also shows that and have at least two neighbors not in S meaning they cannot skew force. Similarly, , which is not in S, also has neighbors ; therefore, cannot skew force. Thus, S is skew stalled and . Now consider . So, there are uncolored vertices to color on the graph. If we color and outside S, we have sections to include the colored vertices, spaced out by k uncolored vertices. Leaving the last section open, we are left with sections to initially color. Suppose we include 3 colored vertices in each of these sections, using colored vertices. We are left with 3 vertices to color in our last 2 sections. However, this will cause ; either will force , or vice-versa. If we have one section with 1 colored vertex, we then have vertices used, so we are left with 5 vertices in our surplus, which is taken care of by our surplus 5 Lemma. If we have more than 1 section with 1 colored vertex, we use vertices and thus have a surplus of 7, which we know we cannot have without skew forcing the entire graph. So, we know that to prevent the whole graph from being skew forced, we must have □
Lemma 9. for
Proof. Suppose . Then where . Notice that for all where , they have neighbors , such that and , which implies that will not skew force. Notice that for any where has no neighbors outside of S, since for any neighbor , which means they are not adjacent. For , they all have two neighbors not in S. S is skew stalled. Therefore, .
Now, suppose . So, we have vertices outside of S to place on the graph and divide S. If we use 2 vertices outside S on and , we have a total of vertices, to create k sections of colored vertices. If all sections are filled with 3 colored vertices, we use colored vertices and are left with 4 to place, which can be split between 2 sections as 1–3, 2–2, or 0–4. In each situation, will force and , causing all of the vertices in the graph to be forced. Now suppose we put a single colored vertex in a section. Then we have used , giving us 6 surplus vertices to use, splitting it 3–3, 2–4, or 1–5, all of which would cause . So, we know that in order to prevent , we can have, at a maximum,
So, we can conclude . □
We can combine Lemmas 8–11 to create the following theorem.
Theorem 2. Let . Then .
When , the failed skew zero forcing numbers, in order, are 0, 1, 3, 3, 4, 4, 6, 5, 6, 7, 9, 8, 9, 10. This was submitted to the Online Encyclopedia of Integer Sequences and was approved as sequence A355067.
Now we consider the failed skew forcing number of .
Lemma 10. Let . If and and , then the entire graph will be forced.
Proof. We will prove the first case and the second case will follow by symmetry. Here, will force the vertex in that is not in S, which will result in the first five vertices of the graph being in S. Then, if is not in S, it will be forced by . Then, if is not in S, it will be forced by . Then, if is not in S, it will be forced by . This creates 8 consecutively filled vertices in G which will force the graph. □
Lemma 11. .
Proof. First, to prove that , let . Then . Notice that for all where , there exists two neighbors , such that and . Therefore, will not skew force. Notice that for any where , has no neighbors outside S because for any , which shows they are not adjacent. Note that is not in S, but is adjacent to ; therefore, it cannot skew force. This also shows that and will not skew force. Thus, S is skew stalled.
To show that , consider when . Then, optimally, we can place strings with 4 vertices across sections, leaving 7 vertices to place between 2 sections. □
Lemma 12. .
Proof. Coloring vertices for and leaving the remaining vertices uncolored shows that .
To prove that , consider when . Then, optimally, we can place strings of 4 vertices in sections, leaving 13 vertices to place between 3 sections. If we place 0 vertices on the end, then by the pigeonhole principle, one of these sections would be a string with 7 vertices, causing the all of the vertices in the graph to be forced. Furthermore, if we configure the 13 vertices across 3 sections, then we must have, for a string with a vetices being the furthest from the end, that and, by Lemma 4, for , . So, we must have that , which would cause the whole graph to be skew forced. Therefore, , and we can conclude that . □
Lemma 13. .
Proof. To prove that , let Then . Notice that for all where , there exists neighbors , such that and . Therefore, will not skew force. Also note that for any where and for any , which shows they are not adjacent, i.e., cannot skew force. Now consider the vertex , which has neighbors ; therefore, it cannot skew force. This also shows that and cannot skew force. By looking at the final vertices, , we can see they both have as neighbors, which implies that they cannot skew force. Thus, S is skew stalled.
To show that , consider when . Then, we can place strings with 4 vertices across sections, leaving 9 vertices to be placed between 3 sections. If we leave no colored vertices on the end of the graph, then by the pigeonhole principle, one of these sections would be a string with 5 vertices, causing all of the vertices in the graph to be forced. If we have three sections, then with a string of a vertices being furthest from the end, we have that and, by Lemma 4, . So, , which would cause the entire graph to be skew forced. Thus, , and we can conclude that . □
Lemma 14. .
Proof. First, we prove that . Consider . Then . Notice that for all where , there exists neighbors , such that and . Therefore, will not skew force. Also note that for any where and for any , , which shows they are not adjacent, i.e., cannot skew force. Now consider the vertex which has neighbors ; therefore, it cannot skew force. This also shows that and cannot skew force. By looking at the final vertices, , we can see that they all have as neighbors, which implies that they cannot skew force. Thus, S is skew stalled.
To prove that , consider when . At a maximum, we can fit sections of strings with 4 vertices, leaving 10 vertices to place across 3 sections. Having a string with 6 vertices would cause all of the vertices in the graph to be forced. So, consider when the sections are two strings with 5 vertices. Then, will only have an uncolored neighbor, , causing the whole graph to be skew forced. Furthermore, if we place the 10 across 3 sections, then by Lemma 4, the ending 5 vertices must have no more than 3 vertices in S, leaving a string with 7 vertices before them that would skew force the entire graph. Therefore, . □
Lemma 15. .
Proof. First, to prove that , consider . Then . Notice that for all where , there exists neighbors , such that and . Therefore, will not skew force. Also note that for any where and for any , , which shows they are not adjacent, i.e., cannot skew force. Now consider the vertex which has neighbors , which implies that it cannot skew force. This also shows that and cannot skew force. By looking at the final vertex , which has neighbors , i.e., it cannot skew force, we know that S is skew stalled.
To prove , consider when . We will attempt to configure S in sections with consecutive colored vertices such that it does not skew force the entire vertex set. So, distributing these as strings with 4 vertices leaves 6 vertices to place across 2 sections. If we place these at two adjacent sections with 3 consecutively colored vertices, will skew force , causing the entire graph to become skew forced. If we place these as strings with 4 vertices and a string with 2 vertices then the vertex following the strings with 2 vertices will skew force the vertex before the strings with 2 vertices, causing the entire graph to become skew forced. Finally, if we have the vertices as a strings with 5 vertices and a string with a single vertex, then the vertex after the string with a single vertex will skew force the vertex before the string with a single vertex, causing the entire graph to be skew forced. Now consider that if we are placing the vertices across three sections, we should consider placing in S. Then, for a string with a vertices being our section furthest from , we know that , so a must be a string with 3 vertices. Then, the vertex before the string with 3 vertices will skew force the vertex after, as it is preceded by a string with 4 vertices. This skew force will cause the whole graph to become skew forced. Therefore, . □
General Results for Path Powers
Next, we extend results from earlier in the section to state some general results involving failed skew zero forcing numbers of path powers.
Lemma 16. .
Proof. First, to prove
, consider
. For any two
and
that are outside
S, they are not neighbors since they are both in
S:
Furthermore, any vertex will always have two neighbors outside S, since and . So, S is skew stalled with , creating the upper bound that .
Next we give another general result. □
Theorem 3. Let . Then .
Proof. Let . Each vertex is a neighbor to if . Let . Then, for any , they will not be neighbors since . Then, for each , either has two neighbors outside S such that will not skew force since and .
Now, assume . Then we would have blue vertices and l white vertices. We need to place vertices into sections. We first assume that the first section is empty. Then, we are left to place vertices into l sections. Placing k vertices in the first sections gives a total of blue vertices. This leaves blue vertices to place in the last three sections, a, b, and c. By Lemma 4, we must have that if then . This implies that , which would force the entire graph. We next consider if the first section has one or more vertices. By Lemma 4, in order for the graph not to be stalled, the first two sections must contain, at most, a total of vertices. The same is true for the last two sections. Then, we would need to place at least blue vertices in the middle sections. By the pigeonhole principle, if we have more than vertices over sections then we will have two consecutive sections with k or more vertices, which will force the graph. Since we are placing vertices and , the graph will be forced. □
3. Circulant Graphs
Failed skew zero forcing number of cycles were investigated by Ansill, Jacob, Penzellna, and Saavedra [
2], where they proved that
if
and
n is even and if
and
n is odd then
.
The circulant graph , where , is the graph with set of n vertices and set of edges equal to
We will refer to the cycle
and edges
,
,
…,
,
as the ‘main cycle’ of the circulant graph. Applications of circulant graphs have been noted by Monakhova, Monakhov, and Yu [
17] and Monakhov, Monakhova, and Kireev [
18].
We will refer to a set of consecutively colored vertices as a string and a set of strings with vertices separated by an uncolored vertex as a as a configuration.
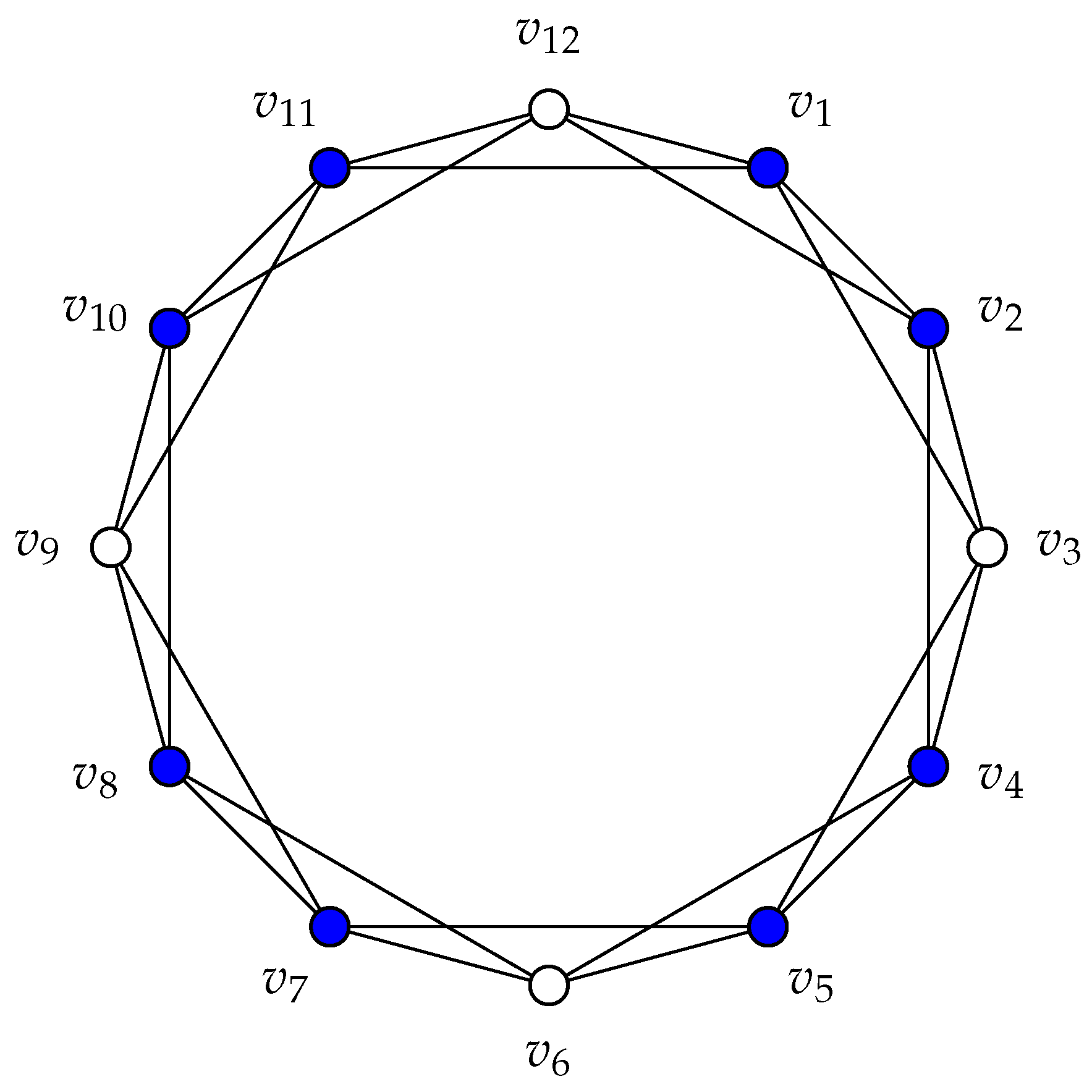
In
Figure 4, we give an example of graph where six consecutively colored vertices force the entire graph.
We recall a result of [
5], which we restate as our next lemma.
Lemma 17. A coloring of , where , with a string of filled vertices along the main cycle forms a zero forcing set.
The next lemma shows that if a failed skew zero forcing set contains a string of 3 colored vertices then there must be a string of 3 uncolored vertices both preceding and succeeding this string. We note that this limits the number of colored vertices in the graph, as it only allows for a third of the vertices to be colored.
Lemma 18. In , if , , and , and if any of the following vertices , , , , , or , then by skew forcing. Furthermore, if or with only the first 3 vertices, S will be stalled.
Proof. Let , , and . By symmetry, it suffices to show that if , , or , then and that if or , where , then S will be stalled. Cases (i)–(iii) cover the cases where one of the three vertices preceding (or succeeding) , , and are in S and the last case shows that the graph is stalled if none of these vertices are in S:
Case (i): Suppose . Then has only one neighbor not in S, . Then, by the forcing rule, . Then will force . By Lemma 17, this will lead to .
Case (ii): Suppose . Then has only one neighbor not in S, . Thus, it will force . By Lemma 17 this will lead to .
Case (iii): Suppose . By Lemma 17, we have .
Case (iv): Suppose or , where . Then neither new vertex will be able to skew force. Furthermore, each uncolored vertex between or and the rest of S will have at least two neighbors outside of S. Finally, will each have two neighbors not in S. So, no vertex will force any other vertex.
Thus, unless there exists 3 vertices not in S both preceding and succeeding the 3 vertices in S.
□
Lemma 19. For , there cannot be vertices in S that fit into sections without causing .
Proof. We will prove this using two cases, both of which involve sets of three colored vertices that will force all vertices in the graph. It suffices to consider a set of four consecutive vertices three of which are colored and another case involving three consecutively colored vertices.
Case i: We know that if we have , and , that will skew force into S. Then, if , we need in n sections, which is more difficult than fitting into sections. If , we have a string of 4 vertices which will cause all vertices in the graph to be forced.
Case ii: Suppose there exists at least one string with 3 colored vertices. This implies that the next three vertices are not in
S and the previous 3 are not in
S if we desire
S to stall. So after a configuration of
i strings of 3 vertices, we are left with
vertices and
sections. This shows us that, at its minimum,
which contradicts the assumption that
. Hence, the inequality holds for any positive number of strings of 3 vertices. So, after considering all strings with 3 vertices, the average number of vertices in a section is greater than 2, implying that there must be a string of 4 vertices, which would skew force the entire graph.
□
Lemma 20. For , there cannot be vertices in S that fit into sections without causing .
Proof. The proof is similar to the proof of Lemma 19. We will prove this using two cases, both of which involve sets of three colored vertices that will force all of the vertices in the graph. It suffices to consider a set of four consecutive vertices, three of which are colored, and another case involving three consecutively colored vertices:
Case i: We know that if we have , and , that will skew force into S. Then, if , we need colored vertices in sections, which is more difficult than fitting colored vertices into sections. If , we have a string of four colored vertices which leads to by Lemma 17.
Case ii: Suppose there exists at least one string with 3 vertices. This implies that the next three vertices are not in
S and the previous 3 are not in
S if we desire
S to stall. So, after a configuration with
i strings with 3 vertices, we are left with
vertices and
sections. This shows us that, at its minimum,
and
, so the inequality holds for copies of strings with 3 vertices. So, after considering all strings with 3 vertices, the average number of vertices in a section is greater than 2, implying that there must be four consecutive colored vertices, which would force the entire graph.
□
We precede our next result with an example in
Figure 5.
Lemma 21. for
Proof. To show that , consider . If , we must have either a string of 4 vertices or a string of 3 vertices that does not have 3 uncolored vertices on either side. Hence, by Lemma 17 or Lemma 18, the graph will be forced. □
Lemma 22. for .
Proof. We must show that . To do this, consider . Here, S is stalled, as no vertex will have exactly one neighbor outside of S.
By the above lemma, we know that vertices cannot be placed onto without causing by Lemma 17 or Lemma 18. □
For the case with vertices, we first consider small cases where and 2.
When , so coloring two non-adjacent vertices gives . This size is a maximum since .
When , so coloring vertices , , and gives . This size is a maximum since would imply there is a pair of consecutively colored vertices. There cannot be two pairs of consecutively colored vertices separated by a single uncolored vertex, since a vertex that is adjacent to a vertex in exactly one of the pairs of colored vertices would have exactly one colored neighbor.
Lemma 23. for .
Proof. We will first show that . Consider −. Then, each vertex does not have exactly one neighbor in S, so S is skew stalled. To show that , note that by the lemma regarding fitting vertices in S onto the graph without , there is not way to fit vertices onto the graph without skew forcing all vertices by Lemma 17 or Lemma 18. So, .
Therefore, .
Case i: Consider or ; because of symmetry, they are handled the same. Without loss of generality, choose . This would cause 3 vertices in S to be in a row: , , and . However, there would only be 3 vertices not in S on one side and not the other, which would cause all of the vertices in the graph to be forced.
Case ii: Now suppose or ; again because of symmetry, they are handled the same. Without loss of generality, choose . Then, would only have one neighbor not in S, , which it would force into S. It follows that would then force into S which would force into S as well. This creates more than 4 vertices in a row which would force all of the vertices in the graph.
Case iii: Finally, suppose . Then, would have one neighbor not in S, , which would force it into S. Now, would force . This creates 3 vertices in a row without 3 vertices not in S on both sides, which forces all of the vertices in the graph to be forced.
Therefore, . Thus, . □
Lemmas 21–23 can be combined to form the following theorem.
Theorem 4. When , .
For , the failed skew zero forcing numbers, in order, are 0, 1, 2, 4, 3, 4, 6, 5, 6, 8, 6, 8, 10, 8, 10. This was submitted to the Online Encyclopedia of Integer Sequences (OEIS) and is now listed as sequence A355067.
When , the failed skew zero forcing numbers of are and when , the number is .
Lemma 24. If there exist partitions of vertices on a , then all of the vertices in the graph will be forced.
Proof. (By induction) First, consider the case where and 7 vertices on are colored. Then, by Lemma 17, all vertices in the graph will be forced.
Now consider . To show that 13 vertices cannot fit in 3 partitions, first see that by the pigeonhole principle, there must be a partition with 5 or more vertices inside. However, if it is then adjacent to a partition with 2 or more vertices, it will cause all vertices in the graph to be forced. So, assume its neighboring partition has 1 vertex. Then the third partition will contain 7 vertices and by case, this will cause all vertices in the graph to be forced.
Suppose that the result holds for . Then, this will imply that the theorem also holds for . Suppose partitions of vertices on a causes . That is, suppose there are partitions and need to fit vertices into the partitions, for . Note that for all . So, by the pigeonhole principle, there exists at least one partition with 4 or more vertices. Then if its neighboring partition has 2 or more vertices inside, . So, assume its neighbor partition has one vertex. Then, there remain vertices to place in partitions. By the case, this is impossible to achieve without all of the vertices in the graph being forced. So, . So, the result holds for all .
Now suppose there n partitions in which we need to place vertices into. By the pigeonhole principle, there exists at least one partition with 4 or more vertices inside. Then, if its neighboring partition has 2 or more vertices inside, . So, assume its neighboring partition has 1 vertex. Then there remains vertices to fit into partitions. However, we know that we cannot do this without since, by inductive hypothesis, the theorem holds for , since .
By induction, the lemma holds for all n. □
Theorem 5. , and .
Proof. We have by using a configuration of alternating strings of 3 followed by an uncolored vertex. The upper bound follows by Lemma 24. We have by using two configurations of alternating strings of 2 vertices followed by an uncolored vertex, and configurations of alternating strings of 3 vertices followed by an uncolored vertex. The upper bound follows by Lemma 24. □
Theorem 6. , , .
Proof. First, we will show that .
Let ; . So, without loss of generality, we know that has neighbors . We know , and . We also know that and . So, does not have exactly one neighbor outside of S. Therefore, cannot skew force. Additionally, has neighbors , , , and . Note that has neighbors ; has zero neighbors in S which implies that is stalled. Therefore, .
The upper bound
follows since
(Theorem 4.1 in [
2]) and
(Theorem 15 in [
6]). □