Symmetry Analysis of the 3D Boundary-Layer Flow of a Non-Newtonian Fluid

Abstract

This study investigates the three-dimensional, steady, laminar boundary-layer equations of a non-Newtonian fluid over a flat plate in the absence of body forces. The classical boundary-layer theory, introduced by Prandtl in 1904, suggests that fluid flows past a solid surface can be divided into two regions: a thin boundary layer near the surface, where steep velocity gradients and significant frictional effects dominate, and the outer region, where friction is negligible. Within the boundary layer, the velocity increases sharply from zero at the surface to the freestream value at the outer edge. The boundary-layer approximation significantly simplifies the Navier–Stokes equations within the boundary layer, while outside this layer, the flow is considered inviscid, resulting in even simpler equations. The viscoelastic properties of the fluid are modeled using the Rivlin–Ericksen tensors. Lie group analysis is applied to reduce the resulting third-order nonlinear system of partial differential equations to a system of ordinary differential equations. Finally, we determine the admissible forms of the freestream velocities in the x- and z-directions.

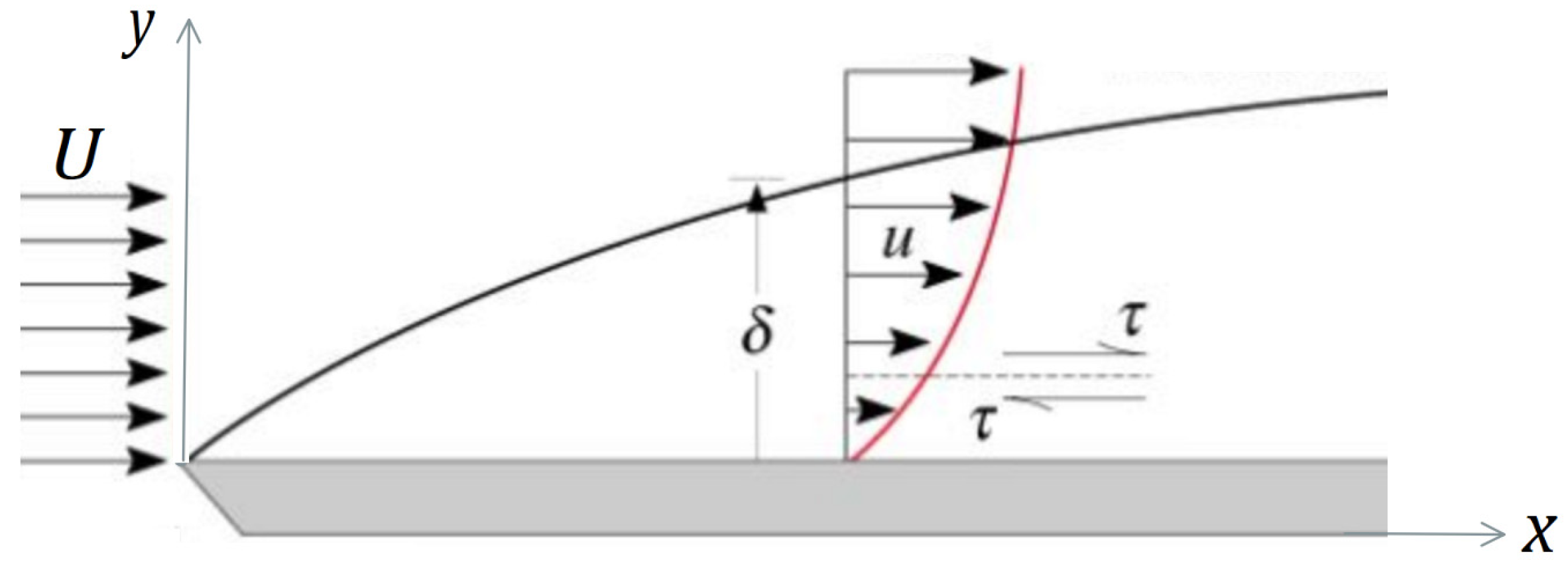
1. Introduction

In many engineering applications—including drilling muds, certain oils and greases, polymer melts, suspensions, blood, and other biological fluids—fluid flow often exhibits unexpected behaviors that cannot be adequately described by the classical Newtonian theory of incompressible viscous flow, which is based on the following constitutive equation:

$$T_{ij}=-p{\delta }_{ij}+2\mu D_{ij}$$

(1)

Here, $T_{ij}$ is the symmetric Cauchy stress tensor, $D_{ij}$ is the stretching tensor, $\mu$ is the viscosity of the fluid, $p$ is the indeterminate pressure, and ${\delta }_{ij}=\left\{\begin{array}{c}0, if i\ne j\\ 1, if i=j\end{array}\right.$.

These fluids are classified as non-Newtonian or viscoelastic. The various viscoelastic properties observed in such fluids include the following [1]:

(a)

Shear-rate-dependent viscosity: most of these fluids display “shear thinning”; that is, the viscosity decreases with increasing shear rate.

(b)

Normal stress effects: unequal normal stresses in the different directions in steady shear flow and related simple flows.

(c)

Elastic and tensile properties: the resistance of the fluid to stretching.

As a result, Equation (1) requires a suitable generalization to account for non-Newtonian fluid behavior. However, these fluids exhibit significant variability in both their physical properties and their responses to stress. Consequently, numerous constitutive equations have been proposed, as discussed in the works of Storer and Green, Walters, Oldroyd, Coleman and Noll [2], Rivlin [3], Denn [4], Truesdell (cited in Showalter [5]), and others. A comprehensive review of these constitutive equations can be found in references [1,5].

In order to study the effects of elasticity, several authors have employed boundary-layer-type analyses with different idealized constitutive equations. Rivilin [3] has investigated the flow of ordered fluids along a straight, non-circular pipe. He (see Ref. [3]) has also studied torsional flow between parallel discs and between coaxial cones and the helical flow of such fluids. Ting [6] has studied various non-steady flows, including channel and pipe flows under a constant pressure gradient, as well as flow between infinite parallel planes in an incompressible second-order fluid. Beard and Walters [7] numerically solved the boundary-layer equations for two-dimensional flow near a stagnation point, while Sarpkaya and Rainey [8] approached the same problem with a slightly different method. Huilgol [9] investigated slow, steady flows of second-order fluids where inertia terms are negligible. Rajagopal and Gupta [10,11] identified exact solutions for such fluids, where nonlinearities either cancel out or the equations simplify to linear forms. Siddiqui [12] used the hodograph transformation method to study the flow of ordered fluids. H. Stephani and T. Wolf [13] considered the motion of expanding shear-free perfect fluids in general relativity and performed a complete symmetry analysis of the governing ordinary differential equation. J. M. Cervero and O. Zurron [14] devised algorithmic procedures dealing with an integrable non-linear partial differential equation arising from the field of two-layer fluid dynamics, which cannot be solved using procedures based upon Painleve Tests, Lie Classical Symmetries, Non-Classical Blumen and Cole Symmetries, or Contact Symmetries. C. Alexa and D. Vrinceanu [15] discussed the flow of a relativistic imperfect fluid in two dimensions. They calculated the symmetry group of the energy–momentum tensor conservation equation in the ultra-relativistic limit and obtained Group-invariant solutions for the incompressible fluid. I. T. Habibullin [16] considered the problem of constructing boundary conditions for nonlinear equations compatible with their higher symmetries. They discussed boundary conditions for the sine-Gordon, Zhiber–Shabat and KdV equations and found new examples for the JS equation.

The investigations mentioned above primarily focused on two-dimensional flows. However, their results are known to lack accuracy in many engineering applications. For instance, Hansen and Herzig [17] observed that in turbomachine boundary layers, two-dimensional boundary-layer flows often transition into three-dimensional flows due to the generation of secondary flows. Therefore, considering three-dimensional boundary layers is far more desirable for obtaining physically accurate solutions.

In their article [18], Sacheti and Chandran studied the steady three-dimensional boundary-layer flow of a certain kind of second-order fluid over a flat plate. R. E. Hewitt and P. W. Duck [19] investigated three-dimensional laminar boundary layers with a spanwise scale comparable to the boundary-layer thickness, concluding that, in such flows, viscous momentum diffusion must be considered in both the transverse and spanwise directions. M. Uddin, W. Khan, and A. I. Ismail [20] presented a mathematical model for two-dimensional unsteady magneto-convective flows with heat and mass transfer under a time-dependent magnetic field. They used a two-parameter scaling group transformation combined with an implicit finite difference method to solve the resulting equations. Their findings showed that the magnetic field increases the rates of heat and mass transfer, while the buoyancy ratio enhances heat transfer and reduces mass transfer. T. Aziz, A. Aziz, and C. Khalique [21] studied the time-dependent flow of an incompressible, thermodynamically compatible, non-Newtonian, third-grade nanofluid, generated by the motion of a plate with an impulsive velocity. They applied Lie theory to obtain exact closed-form exponential solutions for the model equations.

More recently, Lie group analysis has been extended to fractional differential equations. In their book Symmetry Analysis of Fractional Differential Equations [22], M. S. Hashemi and D. Baleanu discuss different aspects of fractional Lie symmetries and related conservation laws and find the exact solutions of a fractional partial differential equation. Also, they develop Lie symmetries for fractional integro-differential equations. G. Iskenderoglu and D. Kaya [23] conducted a Lie symmetry analysis of initial and boundary value problems for partial differential equations with Caputo fractional derivatives, determining the symmetries of these equations in general form. They applied this analysis to fractional diffusion and a third-order fractional partial differential equation, obtaining several solutions. In their 2019 paper [24], Y. Chatibi, E. El Kinani, and A. Ouhadan used the Hydon method to identify discrete symmetries for a range of differential equations, including ordinary, partial, and fractional types, and demonstrated how these symmetries can be applied to generate new solutions from known ones. K. Sethukumarasamy, P. Vijayaraju, and P. Prakash [25] extended Lie symmetry analysis to n-coupled systems of FODEs with R-L fractional derivatives, deriving the Lie point symmetries for scalar and coupled systems, including the fractional Thomas–Fermi equation, the Bagley–Torvik equation, and a two-coupled system of fractional quartic oscillators.

On the experimental side, there has been a recent surge in studies on all kinds of non-Newtonian fluids, such as Kelvin material, Maxwell material, Rheopectic fluids, Thixotropic fluids, shear thickening (dilatant), shear thinning (pseudoplastic), and generalized Newtonian fluids, both naturally occurring or manufactured for specific purposes. For instance, C. M. Ionescu et al. [26] proposed a mathematical framework for the use of fractional-order impedance models to capture fluid dynamic properties in frequency-domain experimental datasets. They tested four classes of fluids: oil, sugar, detergent, and liquid soap. Their experimental results suggested that the proposed model is useful for characterizing various degrees of viscoelasticity in NN fluids. They concluded that the advantage of the proposed model is that it is compact while capturing fluid properties and can be identified in real time for further use in prediction or control applications.

In their work, “Experimental and Numerical Analysis of a Non-Newtonian Fluids Processing Pump” [27], Aldi et al. showed that at high flow rates, their two non-Newtonian fluids had the lowest kaolin powder concentrations. They found that there was a slight increase in head with respect to water, while with kaolin 40% (which has the higher apparent viscosity), there was a high derating of pump performance compared to the water curves. With kaolin 35% and 40%, at a lower flow rate, the pump head decreased, with a significant modification in the pump performance trend. Subsequently, the pump performance was calculated by means of numerical simulations and compared with the experimental data. The numerical results agreed well with the experimental data for water and kaolin 30% and 35%, but they showed an overestimated head with kaolin 40%.

P. Akbarzadeh et al. [28] experimentally investigated the entry of hydrophobic/hydrophilic spheres into Newtonian and Boger fluids. Using a PcoDimaxS high-speed camera, they captured the spheres’ trajectory from impact to the end of their path. Their results showed that more air was drawn in during the sphere’s impact with the Newtonian liquid than with the non-Newtonian fluid, and pinch-off occurred later. The bubbles shed in the Boger fluid were cusped-shaped, while in the Newtonian fluid, they were elliptical. The most significant impact of surface wettability was observed in the Newtonian fluid. The study also found that the sphere moved faster and traveled a longer distance in the Newtonian fluid within a specified time interval. They concluded that these differences are closely related to the viscoelastic fluid’s elasticity and extensional viscosity.

Yaxin Liu et al. [29] experimentally studied the motion of a single Taylor bubble rising in stagnant and downward-flowing non-Newtonian fluids in inclined pipes. Their results showed that bubble velocity increases with the inclination angle and decreases as the liquid viscosity increases. Additionally, the length of the Taylor bubble decreases as the downward flow velocity and viscosity increase. The bubble velocity was found to be independent of bubble length. A new drift velocity correlation that incorporates inclination angle and apparent viscosity was developed which is applicable to non-Newtonian fluids with Eötvös numbers (E₀) ranging from 3212 to 3405 and an apparent viscosity (µ_app) ranging from 0.001 Pa·s to 129 Pa·s.

In a paper published recently [30], P. Dorner, W. Schroder, and M. Klass investigated complex flow in arteries by analyzing the fluid–structure interaction between the time-dependent velocity field, the non-Newtonian fluid, and elastic blood vessels. Their results showed that the wall shear stress maximum increases up to 32–38% for the non-Newtonian fluid despite a 10–45% higher wall shear rate for the Newtonian reference fluid. Furthermore, the amplitudes of the dilatation and the pressure in the vessel were more pronounced for the non-Newtonian fluid.

In a paper published last year [31], Asghar et al. integrated magnetohydrodynamics, Hall effects, and porous medium with cilia-driven flow and examined graphical illustrations of streamlines, pressure drop, and axial velocity under the influence of relevant parameters. Their results suggested that when a high magnetic field (Hall current) and porous media are combined with the Carreau–Yasuda fluid, the pumping equipment operates better than the viscous liquid. In addition, they showed that fluid movement in biological organs is improved by metachronal ciliary motion.

In this paper, we investigate the flow of a steady three-dimensional boundary layer for a non-Newtonian fluid model that has gained considerable support from researchers in the field: the Rivilin–Ericksen model. In this model, the stress tensor, $T_{ij},$ is given by [5]

$$T_{ij}=-p{\delta }_{ij}+\mu A_1+{\mu }_1{A}_2+{\mu }_2{A}_1^2$$

(2)

where $\mu$ is the coefficient of viscosity, ${\mu }_1$ is the coefficient of viscoelasticity, and ${\mu }_2$ is the coefficient of cross-viscosity. Furthermore, the Rivilin–Erickson tensors $A_1$ and $A_2$ are defined by

$$A_1=A_{ij}=\left(V_{i,j}+V_{j,i}\right)$$

(2a)

$$A_2={\displaystyle \frac{\partial }{\partial t}}{A}_{ij}+V_k{A}_{ij,k}+A_{im}{V}_{m,j}+A_{jm}{V}_{m,i}$$

(2b)

$$A_1^2=A_{ik}{A}_{kj}$$

(2c)

where $V_i=\left(u,v,w\right)$ is the velocity vector field.

The employment of (2) in the momentum equations results in highly nonlinear equations of motion. As a result, it is very difficult to obtain exact solutions to these equations unless either there are some simplifying features to the problem or some simplifying assumptions are made.

2. Basic Equations and Ordering Analysis

The equations of motion for an incompressible flow in the absence of body forces are as follows:

Linear momentum:

$${\displaystyle \frac{{\partial T}_{ij}}{{\partial x}_j}}=\rho \left({\displaystyle \frac{{\partial V}_i}{\partial t}}+V_j{\displaystyle \frac{{\partial V}_i}{{\partial x}_j}}\right), i=1, 2, 3$$

(3a)

Continuity:

$${\displaystyle \frac{{\partial V}_j}{{\partial x}_j}}=0$$

(3b)

Here, we used the Einstein summation notation, where j runs from 1 to 3.

If we substitute (2) in (3a) and make use of Equations (2a)–(2c), we obtain

$$\begin{gathered} \begin{array}{c}\rho \left({\displaystyle \frac{{\partial V}_i}{\partial t}}+V_j{\displaystyle \frac{{\partial V}_i}{{\partial x}_j}}\right)={\displaystyle \frac{\partial }{{\partial x}_j}}\left({p\delta }_{ij}\right)+\mu {\displaystyle \frac{{\partial }^2{V}_i}{{\partial x}_j{\partial x}_j}}+{\mu }_1\left[{\displaystyle \frac{\partial }{\partial t}}\left({\displaystyle \frac{{\partial }^2{V}_i}{{\partial x}_j{\partial x}_j}}\right)+{\displaystyle \frac{{\partial V}_k}{{\partial x}_j}}{\displaystyle \frac{{\partial }^2{V}_i}{{\partial x}_j{\partial x}_k}}+V_k{\displaystyle \frac{{\partial }^3{V}_i}{{\partial x}_j{\partial x}_j{\partial x}_k}}\right.+{\displaystyle \frac{{\partial V}_k}{{\partial x}_j}}\left({\displaystyle \frac{{\partial }^2{V}_j}{{\partial x}_i{\partial x}_k}}\right) +\\ {\displaystyle \frac{{\partial }^2{V}_m}{{\partial x}_j{\partial x}_j}}\left({\displaystyle \frac{{\partial V}_i}{\partial x_m}}+{\displaystyle \frac{{\partial V}_m}{{\partial x}_i}}\right)+{\displaystyle \frac{{\partial V}_m}{{\partial x}_j}}\left({\displaystyle \frac{{\partial }^2{V}_i}{{\partial x}_j{\partial x}_m}}+{\displaystyle \frac{{\partial }^2{V}_m}{{\partial x}_i{\partial x}_j}}\right)+{\displaystyle \frac{{\partial }^2{V}_m}{{\partial x}_i{\partial x}_j}}\left({\displaystyle \frac{{\partial V}_j}{{\partial x}_m}}+{\displaystyle \frac{{\partial V}_m}{{\partial x}_j}}\right)+{\displaystyle \frac{{\partial V}_m}{{\partial x}_i}}\left.{\displaystyle \frac{{\partial }^2{V}_m}{{\partial x}_j{\partial x}_j}}\right]+{\mu }_2\left[{\displaystyle \frac{{\partial }^2{V}_k}{{\partial x}_j{\partial x}_j}}\left({\displaystyle \frac{{\partial V}_i}{{\partial x}_k}}+{\displaystyle \frac{{\partial V}_k}{{\partial x}_i}}\right)+ \\ \left({\displaystyle \frac{{\partial }^2{V}_i}{{\partial x}_k{\partial x}_j}}+{\displaystyle \frac{{\partial }^2{V}_k}{{\partial x}_i{\partial x}_j}}\right)\left.\left({\displaystyle \frac{{\partial V}_k}{{\partial x}_j}}+{\displaystyle \frac{{\partial V}_j}{{\partial x}_k}}\right)\right]\right.\end{array} \end{gathered}$$

(4)

where $x_i=\left(x,y,z\right)$ are the usual Cartesian coordinates.

Let $U_0(x, z)$ and $W_0(x, z)$ be the velocity components of the potential flow in the x- and z-directions, respectively, and introduce the following non-dimensional variables:

$$t={\displaystyle \frac{U_{0}t}{L}}, {\overline{x}}_i={\displaystyle \frac{x_i}{L}}, \overline{P}=\rho {\displaystyle \frac{L^2}{{\mu }^2}}P, \overline{U}={\displaystyle \frac{U}{U_0}}, \overline{W}={\displaystyle \frac{W}{W_0}}, \mathrm{and} {\overline{V}}_i=\rho {\displaystyle \frac{V_{i}L}{\mu }},$$

where U and W are the x- and z-freestream velocities.

We now make the usual boundary-layer assumptions [32]. Within the boundary layer, $u, w,{\displaystyle \frac{\partial u}{\partial x}}, {\displaystyle \frac{\partial u}{\partial z}}, {\displaystyle \frac{\partial w}{\partial x}}, {\displaystyle \frac{\partial w}{\partial z}}, {\displaystyle \frac{\partial p}{\partial x}}, \mathrm{a}\mathrm{n}\mathrm{d} {\displaystyle \frac{\partial p}{\partial z}}$ are assumed to be O(1) and y is assumed to be $O\left(\delta \right)$, where $\delta$ is the boundary-layer thickness, as shown in Figure 1.

From the equation of continuity, we find that ${\displaystyle \frac{\partial v}{\partial y}}=O\left(1\right);$ therefore, $v=O\left(\delta \right)$. We also have ${\displaystyle \frac{\partial P}{\partial y}}=O(\delta )$, so we can assume that the pressure within the boundary layer can be approximated by the pressure outside. Therefore, from Bernoulli’s equation, we have

$$-{\displaystyle \frac{1}{\rho }}{\displaystyle \frac{\partial P}{\partial x}}=U{\displaystyle \frac{\partial U}{\partial x}}+W{\displaystyle \frac{\partial U}{\partial z}}$$

(5a)

and

$$-{\displaystyle \frac{1}{\rho }}{\displaystyle \frac{\partial P}{\partial z}}=U{\displaystyle \frac{\partial W}{\partial x}}+W{\displaystyle \frac{\partial W}{\partial z}}$$

(5b)

The Steady-State Case

If we let ${\overline{\mu }}_1={\displaystyle \frac{{\mu }_1}{\rho L^2}}$, ${\overline{\mu }}_2={\displaystyle \frac{{\mu }_2}{\rho L^2}}$, the steady-state equations of motion, in dimensionless form, become

$$u_x+v_y+w_z=0$$

(6a)

$$\begin{array}{cc}\hfill u{u}_x+v{u}_y+w{u}_z& =U{U}_x+W{U}_z+u_{yy}+{\overline{\mu }}_1[u{u}_{xyy}+v{u}_{yyy}+w{u}_{yyz}+u_y\left(3u_{xy}-w_{yz}\right)+u_{yy}\left(u_x-2w_z\right)\hfill \\ & + 2w_y\left(u_{yz}+w_{xy}\right)+w_{yy}(u_z+2w_x)]+{\overline{\mu }}_2\left[{\left\{\left(u_z+w_x\right)w_y-2u_y{w}_z\right\}}_y+\left.{\left(u_y{w}_y\right)}_z+{{\left(u_y\right)}^2}_x\right]\right.\end{array}$$

(6b)

$$\begin{array}{cc}\hfill u{w}_x+v{w}_y+w{w}_z& =U{W}_x+W{W}_z+w_{yy}+{\overline{\mu }}_1[u{w}_{xyy}+v{w}_{yyy}+w{w}_{yyz}+w_y\left(3w_{zy}-u_{yx}\right)+u_{yy}\left(w_x+2u_z\right)\hfill \\ & + 2u_y\left(u_{yz}+w_{xy}\right)+w_{yy}(w_z-2u_x)]+{\overline{\mu }}_2\left[{\left\{\left(u_z+w_x\right)u_y-2u_x{w}_y\right\}}_y\right.+\left.{\left(u_y{w}_y\right)}_x+{{\left(w_y\right)}^2}_z\right]\hfill \end{array}$$

(6c)

subject to the boundary conditions

$$\begin{gathered} \mathrm{At} y=0: u=v=w=0 \mathrm{and} \\ \mathrm{as} y\to \infty :u\to U, w\to W \end{gathered}$$

(6d)

In the above equations, the overbars have been dropped for convenience.

3. Lie Group Analysis

The classical Lie symmetry group of a system of differential equations is a local group of point transformations, or diffeomorphisms, on the space of independent and dependent variables that map solutions of the system into other solutions. Lie group theory is employed to find the symmetries of the governing equations. For a detailed discussion of the theory, one can consult [33,34].

Let

$$\begin{gathered} \mathbf{x}=(x,y,z), \mathbf{u}=(u,v,w), {\mathbf{u}}_1=(u_x,v_y,w_z), \\ {\mathbf{u}}_2=(u_{yy},w_{yy},u_{xy},u_{yz},w_{xy},w_{yz}), \mathrm{and} \\ {\mathbf{u}}_3=(u_{yyy},u_{xyy},u_{yyz},w_{xyy},w_{yyy},w_{yyz}) \end{gathered}$$

Then, the system of PDEs (6) is expressed as ${\psi }^i={\mathsf{\Psi }}^i(\mathbf{x},\mathbf{u},{\mathbf{u}}_1{,\mathbf{u}}_2,{\mathbf{u}}_3)=0$, a vector of locally analytic functions of the differentiable variables $\mathbf{x},\mathbf{u},{\mathbf{u}}_1{,\mathbf{u}}_2, \mathrm{a}\mathrm{n}\mathrm{d} {\mathbf{u}}_3$.

We consider a one-parameter group of infinitesimal transformations [Cantwell] given by the thrice extended group:

$$\begin{gathered} {\tilde{x}}^j=x^j+s{\xi }^j\left(\mathbf{x},\mathbf{u}\right)+O\left(s^2\right) \\ {\tilde{u}}^i=u^i+s{\eta }^i\left(\mathbf{x},\mathbf{u}\right)+O\left(s^2\right) \\ {\tilde{u}}_{j_1}^i=u_{j_1}^i+s{\eta }_{\left\{j_1\right\}}^i\left(\mathbf{x},\mathbf{u},{\mathbf{u}}_1\right)+O\left(s^2\right) \end{gathered}$$

(7)

$$\begin{gathered} {\tilde{u}}_{j_1{j}_2}^i=u_{j_1{j}_2}^i+s{\eta }_{\left\{j_1{j}_2\right\}}^i\left(\mathbf{x},\mathbf{u},{\mathbf{u}}_1,{\mathbf{u}}_2\right)+O\left(s^2\right) \\ {\tilde{u}}_{j_1{j}_2{j}_3}^i=u_{j_1{j}_2{j}_3}^i+s{\eta }_{\left\{j_1{j}_2{j}_3\right\}}^i\left(\mathbf{x},\mathbf{u},{\mathbf{u}}_1,{\mathbf{u}}_2,{\mathbf{u}}_3\right)+O(s^2) \end{gathered}$$

(8)

where s is the group parameter, ${\xi }^j$ and ${\eta }^i$ are the infinitesimals of the group,

$${\eta }_{\left\{j_1{j}_2{j}_3\right\}}^i=D_{j_3}{\eta }_{\left\{j_1{j}_2\right\}}^i-u_{j_1{j}_2\alpha }^i{D_{j_3}\xi }^{\alpha },$$

$\alpha$ is a dummy index summed over $1 \mathrm{t}\mathrm{o} 3$, and

$$D_{j_3}={\partial }_{x^{j_3}}+u_{j_3}^i{\partial }_{u^i}+u_{j_1{j}_3}^i{\partial }_{u_{j_1}^i}+u_{j_1{j}_2{j}_3}^i{\partial }_{u_{j_1{j}_2}^i}.$$

Now, ${\mathsf{\Psi }}^i(\mathbf{x},\mathbf{u},{\mathbf{u}}_1{,\mathbf{u}}_2,{\mathbf{u}}_3)$ is expanded in a Lie series:

$${\mathsf{\Psi }}^i\left(\mathbf{x},\mathbf{u},{\mathbf{u}}_1{,\mathbf{u}}_2,{\mathbf{u}}_3\right)={\psi }^i\left(\mathbf{x},\mathbf{u},{\mathbf{u}}_1{,\mathbf{u}}_2,{\mathbf{u}}_3\right)+s{X}_{\left\{3\right\}}{\mathsf{\psi }}^i+{\displaystyle \frac{s^2}{2!}}{X}_{\left\{3\right\}}\left(X_{\left\{3\right\}}{\psi }^i\right)+O(s^3)$$

(9)

The prolonged infinitesimal group operator is

$$X_{\left\{3\right\}}={\xi }^i{\partial }_{x^j}+{\eta }^i{\partial }_{u^i}+{\eta }_{\left\{j_1\right\}}^i{\partial }_{u_{j_1}^i}+{\eta }_{\left\{j_1{j}_2\right\}}^i{\partial }_{u_{j_1{j}_2}^i}+{\eta }_{\left\{j_1{j}_2{j}_3\right\}}^i{\partial }_{u_{j_1{j}_2{j}_3}^i}$$

(10)

The system ${\mathsf{\Psi }}^i$ is invariant under the action of the group $({\xi }^i,{\eta }^i)$ if and only if

$$X_{\left\{3\right\}}{\mathsf{\Psi }}^i=0,\hspace{1em}i=1,2,3.$$

(11)

The characteristic equations corresponding to (11) are

$${\displaystyle \frac{d{x}^j}{{\xi }^j}}={\displaystyle \frac{d{u}^i}{{\eta }^i}}={\displaystyle \frac{d{u}_{j_1}^i}{{\eta }_{\left\{j_1\right\}}^i}}={\displaystyle \frac{d{u}_{j_1{j}_2}^i}{{\eta }_{\left\{j_1{j}_2\right\}}^i}}={\displaystyle \frac{d{u}_{j_1{j}_2{j}_3}^i}{{\eta }_{\left\{j_1{j}_2{j}_3\right\}}^i}}$$

(12)

Thus, we end up with an overdetermined system of linear homogeneous PDEs in the unknown infinitesimals, but many of them will likely be redundant and, ultimately, few play a role in determining the ${(\xi }^j,{\eta }^i).$ The calculations are straightforward but long, tedious, and error-prone when carried out by hand. They are usually performed using sophisticated computer algebra systems (CASs) such as Maple, Mathematica, MACSYMA, REDUCE, and others.

Algorithms designed to address overdetermined systems generally fall into two categories: heuristic and non-heuristic. Heuristic algorithms integrate the determining equations by starting with specific assumptions about the structure of the desired solutions. For example, it is often assumed that certain solution functions are polynomials in the independent variables. Non-heuristic algorithms, on the other hand, aim to integrate the determining system without relying on any predefined assumptions. These algorithms typically begin by reducing the system of linear PDEs to a simplified, triangular, or canonical form, ensuring that integrability conditions are preserved and satisfied. This standard form is usually more conducive to both numerical and analytical solution techniques compared to the original system. Additionally, the dimensions of the solution space, as well as the consistency or inconsistency of the system, can be directly determined from its standard form [35,36,37,38,39,40].

Non-heuristic algorithms always provide the complete solution set for the system. However, the computational difficulty increases exponentially with the complexity of the system. Additionally, since deriving the canonical form relies on the theory of differential algebra, such as differential Gröbner bases, these algorithms are typically applicable only when the system of PDEs is polynomial with respect to the unknown functions and their derivatives. While heuristic algorithms are generally faster, they do not, in most cases, yield the full solution space of the determining equations [41]. In this paper, we utilized Maple to obtain the similarity variables [42].

4. Symmetry Reductions and the Similarity Solution

Based on the above analysis, we introduce similarity variables that will isolate (6a) by providing a formula for determining $v$ and reduce the nonlinear third-order PDE system (6b) and (6c) to a system of ordinary differential equations:

Let

$$\eta =y\varphi (x,z).$$

(13a)

$$u=U(x,z)F^{\prime }\left(\eta \right)$$

(13b)

$$w=W(x,z)G^{\prime }\left(\eta \right)$$

(13c)

The continuity Equation (6a) becomes

$$v_y=-\left(u_x+w_z\right)=-\left[U_x{F}^{\prime }+{\left(\ln \varphi \right)}_{x}U\eta F^{″}+W_z{G}^{\prime }+{\left(\ln \varphi \right)}_{z}W\eta G^{″}\right]$$

Hence,

$$v=-\int \left(U_x{F}^{\prime }+{\left(\ln \varphi \right)}_{x}U\eta F^{″}+W_z{G}^{\prime }+{\left(\ln \varphi \right)}_{z}W\eta G^{″}\right){\displaystyle \frac{1}{\varphi }}d\eta$$

or

$$\varphi v=\left[U{\left(\ln \varphi \right)}_x-U_x\right]F+\left[W{\left(\ln \varphi \right)}_z-W_z\right]-U{\left(\ln \varphi \right)}_x\eta F^{\prime }-W{\left(\ln \varphi \right)}_z\eta G^{\prime }.$$

(14)

The x-momentum equation becomes

$$\begin{gathered} {\displaystyle \frac{1}{{\varphi }^2}}{U}_x\left({F^{\prime }}^2-F{F}^{″}-1\right)+{\displaystyle \frac{W}{{\varphi }^2}}{\left(\ln U\right)}_z\left(F^{\prime }{G}^{\prime }-1\right)+{\displaystyle \frac{U}{{\varphi }^2}}{\left(\ln \varphi \right)}_{x}F F^{″}+{\displaystyle \frac{1}{{\varphi }^2}}\left[W{\left(\ln \varphi \right)}_z-W_z\right]F^{″}G-F^{‴} \\ -{\overline{\mu }}_1\left[{\left(\ln \varphi \right)}_{x}U\left(2F^{\prime }{F}^{‴}+3{F^{″}}^2+2\eta F^{″}{F}^{‴}\right)+U_x\left(2F^{\prime }{F}^{‴}-F{F}^{iv}+{F^{″}}^2\right)+{\left(\ln \varphi \right)}_{x}UF{F}^{iv}\right. \\ +{\left(\ln \varphi \right)}_{z}W\left(G{F}^{iv}+2G^{\prime }{F}^{‴}+F^{″}{G}^{″}\right)-W_z\left(G{F}^{iv}+G^{″}{F}^{″}+2G^{\prime }{F}^{‴}\right) \\ +{\displaystyle \frac{W}{U}}{U}_z\left(F^{‴}{G}^{\prime }+2F^{″}{G}^{″}+F^{\prime }{G}^{‴}\right)+{\left(\ln \varphi \right)}_x{\displaystyle \frac{W^2}{U}}\left(2{G^{″}}^2+4\eta G^{″}{G}^{‴}\right)+2{\displaystyle \frac{W}{U}}{W}_x\left.\left({G^{″}}^2+G^{\prime }{G}^{‴}\right)\right] \\ -{\overline{\mu }}_2\left[{\displaystyle \frac{W}{U}}{U}_z\right.\left(2F^{″}{G}^{″}+F^{\prime }{G}^{‴}\right)+{\displaystyle \frac{W}{U}}{W}_x\left(G^{\prime }{G}^{‴}+{G^{″}}^2\right)+{\left(\ln \varphi \right)}_x{\displaystyle \frac{W^2}{U}}\left(2\eta G^{″}{G}^{‴}+{G^{″}}^2\right) \\ -W_z(2F^{‴}{G}^{\prime }+F^{″}{G}^{″})+{\left(\ln \varphi \right)}_{z}W{F}^{″}{G}^{″}+2{\left(\ln \varphi \right)}_{x}U\left({F^{″}}^2+\eta F^{″}{F}^{‴}\right)\left.+2U_x{F^{″}}^2\right]=0 \end{gathered}$$

(15a)

and the z-momentum equation is

$$\begin{gathered} {\displaystyle \frac{1}{{\varphi }^2}}{W}_z\left({G^{\prime }}^2-G{G}^{″}-1\right)+{\displaystyle \frac{U}{{\varphi }^2}}{\left(\ln W\right)}_x\left(F^{\prime }{G}^{\prime }-1\right)+{\displaystyle \frac{W}{{\varphi }^2}}{\left(\ln \varphi \right)}_{z}G{G}^{″}+{\displaystyle \frac{1}{{\varphi }^2}}\left[U{\left(\ln \varphi \right)}_x-U_x\right]F{G}^{″}-G^{‴} \\ -{\overline{\mu }}_1\left[{\left(\ln \varphi \right)}_{z}W\left(2G^{\prime }{G}^{‴}+3{G^{″}}^2+2\eta G^{″}{G}^{‴}\right)+W_x\left(2G^{\prime }{G}^{‴}-G{G}^{iv}+{G^{″}}^2\right)+{\left(\ln \varphi \right)}_{z}WG{G}^{iv} \\ +{\left(\ln \varphi \right)}_{x}U\left({FG}^{iv}+2F^{\prime }{G}^{‴}+F^{″}{G}^{″}\right)\right.-W_z\left(F{G}^{iv}+F^{″}{G}^{″}+2F^{\prime }{G}^{‴}\right) \\ +{\displaystyle \frac{U}{UE}}{W}_x\left(G^{‴}{F}^{\prime }+2F^{″}{G}^{″}+G^{\prime }{F}^{‴}\right)+{\left(\ln \varphi \right)}_z{\displaystyle \frac{U^2}{W}}\left(2{F^{″}}^2+4\eta F^{″}{F}^{‴}\right)+2{\displaystyle \frac{U}{W}}{U}_z\left.\left({F^{″}}^2+F^{\prime }{F}^{‴}\right)\right] \\ -{\overline{\mu }}_2\left[{\displaystyle \frac{U}{W}}{W}_x\right.\left(2F^{″}{G}^{″}+G^{\prime }{GF}^{‴}\right)+{\displaystyle \frac{U}{W}}{U}_z\left(F^{\prime }{F}^{‴}+{F^{″}}^2\right)+{\left(\ln \varphi \right)}_z{\displaystyle \frac{U^2}{W}}\left(2\eta F^{″}{F}^{‴}+{F^{″}}^2\right) \\ -U_x(2G^{‴}{F}^{\prime }+F^{″}{G}^{″})+{\left(\ln \varphi \right)}_{x}U{F}^{″}{G}^{″}+2{\left(\ln \varphi \right)}_{z}W\left({G^{″}}^2+\eta G^{″}{G}^{‴}\right)\left.+2W_z{G^{″}}^2\right]=0 \end{gathered}$$

(15b)

The partial differential Equation (9) will be transformed into a system of ordinary differential equations provided that the coefficients of F, G, and their derivatives are made proportional. In this case, the following must hold:

$${\varphi }^2=c_1$$

(16a)

$$U_x=c_2$$

(16b)

$$W_z=c_3$$

(16c)

$${\displaystyle \frac{W}{U}}{U}_z=c_4$$

(16d)

$${\displaystyle \frac{W}{U}}{W}_x=c_5$$

(16e)

$${\displaystyle \frac{U}{W}}{W}_x=c_6$$

(16f)

$${\displaystyle \frac{U}{W}}{U}_z=c_7$$

(16g)

From (10b) and (10c), we obtain

$$U=c_{2}x+a_1\left(z\right)$$

(17a)

$$W=c_{3}z+a_2\left(x\right)$$

(17b)

Also, Equations (10d)–(10g) yield

$$U=c_{8}W$$

(17c)

where the $c_i^{\prime }s$ are constants.

Therefore, $a_2\left(x\right)={\displaystyle \frac{c_2}{c_8}}x$ and $a_1\left(z\right)=c_3{c}_{8}z,$ and Equation (11) becomes

$$U=c_{2}x+c_3{c}_{8}z$$

(18a)

$$W=c_{3}z+{\displaystyle \frac{c_2}{c_8}}x$$

(18b)

The flows described by (12) represent flows near a stagnation point.

Using (10) in (9a), we obtain (for $c_1=1)$

$$\begin{gathered} c_2\left({F^{\prime }}^2-F{F}^{″}-1\right)+c_4\left(F^{\prime }{G}^{\prime }-1\right)-c_3{F}^{″}G-F^{‴}-{\overline{\mu }}_1[c_2\left(2F^{\prime }{F}^{‴}-F{F}^{iv}+3{F^{″}}^2\right)-c_3(F^{iv}G+F^{″}{G}^{″} \\ +2F^{‴}{G}^{\prime })+c_4\left(F^{‴}{G}^{\prime }+2F^{″}{G}^{″}+F^{\prime }{G}^{‴}\right)+2c_5({G^{″}}^2+G^{\prime }{G}^{‴}\left)\right]-{\overline{\mu }}_2[c_4\left(2F^{″}{G}^{″}+F^{\prime }{G}^{‴}\right) \\ +c_5(G^{\prime }{G}^{‴}+{G^{″}}^2)-c_3\left(2F^{‴}{G}^{\prime }+F^{″}{G}^{″}\right)+2c_2{F^{″}}^2]=0 \end{gathered}$$

(19a)

and

$$\begin{gathered} c_3\left({G^{\prime }}^2-G{G}^{″}-1\right)+c_6\left(F^{\prime }{G}^{\prime }-1\right)-c_2{G}^{″}F-G^{‴} \\ -{\overline{\mu }}_1[c_3\left(2G^{\prime }{G}^{‴}-G{G}^{iv}+3{G^{″}}^2\right)-c_2(G^{iv}F+F^{″}{G}^{″}+2G^{‴}{F}^{\prime }) \\ +c_6\left(G^{‴}{F}^{\prime }+2F^{″}{G}^{″}+G^{\prime }{F}^{‴}\right)+2c_7({F^{″}}^2+F^{\prime }{F}^{‴})] \\ -{\overline{\mu }}_2[c_6\left(2F^{″}{G}^{″}+G^{\prime }{F}^{‴}\right)+c_7(F^{\prime }{F}^{‴}+{F^{″}}^2) \\ -c_2\left(2G^{‴}{F}^{\prime }+F^{″}{G}^{″}\right)+2c_3{G^{″}}^2]=0 \end{gathered}$$

(19b)

The boundary conditions are

$$\begin{gathered} \mathrm{At} \eta =0:F=0,F^{\prime }=0,G=0,G^{\prime }=0 \\ \mathrm{As} \eta \to \mathrm{\infty }:F^{\prime }\to 1,G^{\prime }\to 1. \end{gathered}$$

Usually, a perturbation technique is applied to the similarity functions, or they are approximated by nth-degree polynomials before a numerical solution is calculated.

Values for the velocities can, then, be found from

$$u\left(x,y,z\right)=\left(c_{2}x+c_3{c}_{8}z\right)F^{\prime }\left(y\right)$$

(20a)

$$w\left(x,y,z\right)=\left(c_{3}x+{\displaystyle \frac{c_2}{c_8}}z\right)G^{\prime }(y)$$

(20b)

$$v\left(y\right)=-c_{2}F\left(y\right)-c_{3}G\left(y\right)$$

(20c)

5. Concluding Remarks

When ${\overline{\mu }}_1={\overline{\mu }}_2=0$, we have the purely viscous case (Newtonian flow), which has been treated by Hansen and Herzig [17]. Equation (13) becomes

$$c_2\left({F^{\prime }}^2-F{F}^{″}-1\right)+c_4\left(F^{\prime }{G}^{\prime }-1\right)-c_3{F}^{″}G-F^{‴}=0$$

(21a)

$$c_3\left({G^{\prime }}^2-G{G}^{″}-1\right)+c_6\left(F^{\prime }{G}^{\prime }-1\right)-c_2{G}^{″}F-G^{‴}$$

(21b)

subject to the same boundary conditions.

By comparing Equations (13) and (15), it is obvious that the salient feature of the viscoelastic fluid is the increased order of the governing equations. In Equation (15), the formulae are of order three, whereas those in Equation (13) are of order four. The presence of elasticity greatly alters the boundary-layer equations and, hence, the flow from the purely viscous case.

Instead of dealing with the third-order system of nonlinear partial differential equations given in Equation (6), we now work with a nonlinear system of ordinary differential equations, which is easier to handle in terms of both solution procedure and error control. Although numerous numerical techniques and types of software are available for solving partial differential equations, the theory, methods, and tools for solving ODEs are far more advanced. By 1980, the field of numerical solutions for ODEs was so well developed that a 1981 paper [43] was provocatively titled “Numerical Solution of Ordinary Differential Equations: Is There Anything Left to Do?” The answer, of course, was yes. The numerical solution of ODEs has deep roots in 18th- and 19th-century mathematics and saw substantial progress throughout the 20th century. In contrast, the mathematical foundations for solving PDEs numerically are comparatively recent [44]. Furthermore, the truncation error caused by numerical approximations in one dimension is inherently smaller than that in higher dimensions, making ODEs more manageable for precise computations.

The resulting set of ordinary differential equations in Equation (13) is of order four, while the original system of partial differential equations is of order two. This increase in order is due to the symmetry transformation. This increases the number of boundary conditions needed to solve the system. On the theoretical side, the works of Coscia, Sequeira, and Videman and Galdi, Grobbelaar, and Sauer, refs. [45,46], imply that for a certain class of flows, the usual boundary conditions of no slip and impermeability at a solid wall are sufficient to prove that the solution is unique. On the other hand, the works of Rajagopal [47,48] and Rajagopal and Kaloni [49] show that the “no-slip” boundary conditions are, in general, quite inadequate for producing the desired solution. However, it has been shown that extra conditions can be obtained based on perturbations of the velocity and/or stress fields. In problems involving unbounded domains, boundary conditions may be supplemented by requiring the flow to be bounded. A detailed discussion of these issues can be found in the references [49,50,51].

In the next paper, we will numerically solve the system of ODEs and the system of PDEs and compare the results to any available experimental results.

We will also consider non-Newtonian fluid flow past a circular cylinder and an airfoil. These investigations could lead to a better understanding of rotating flows such as flows past industrial fans and rotating mills.