Mathematical Analysis of a Navier–Stokes Model with a Mittag–Leffler Kernel
Abstract
1. Introduction
2. Preliminaries
3. Existence and Uniqueness of Nonlinear Fractional Derivatives with Respect to the ABCFD
4. Analysis of the Fractional Navier–Stokes Equation with the ABCFD
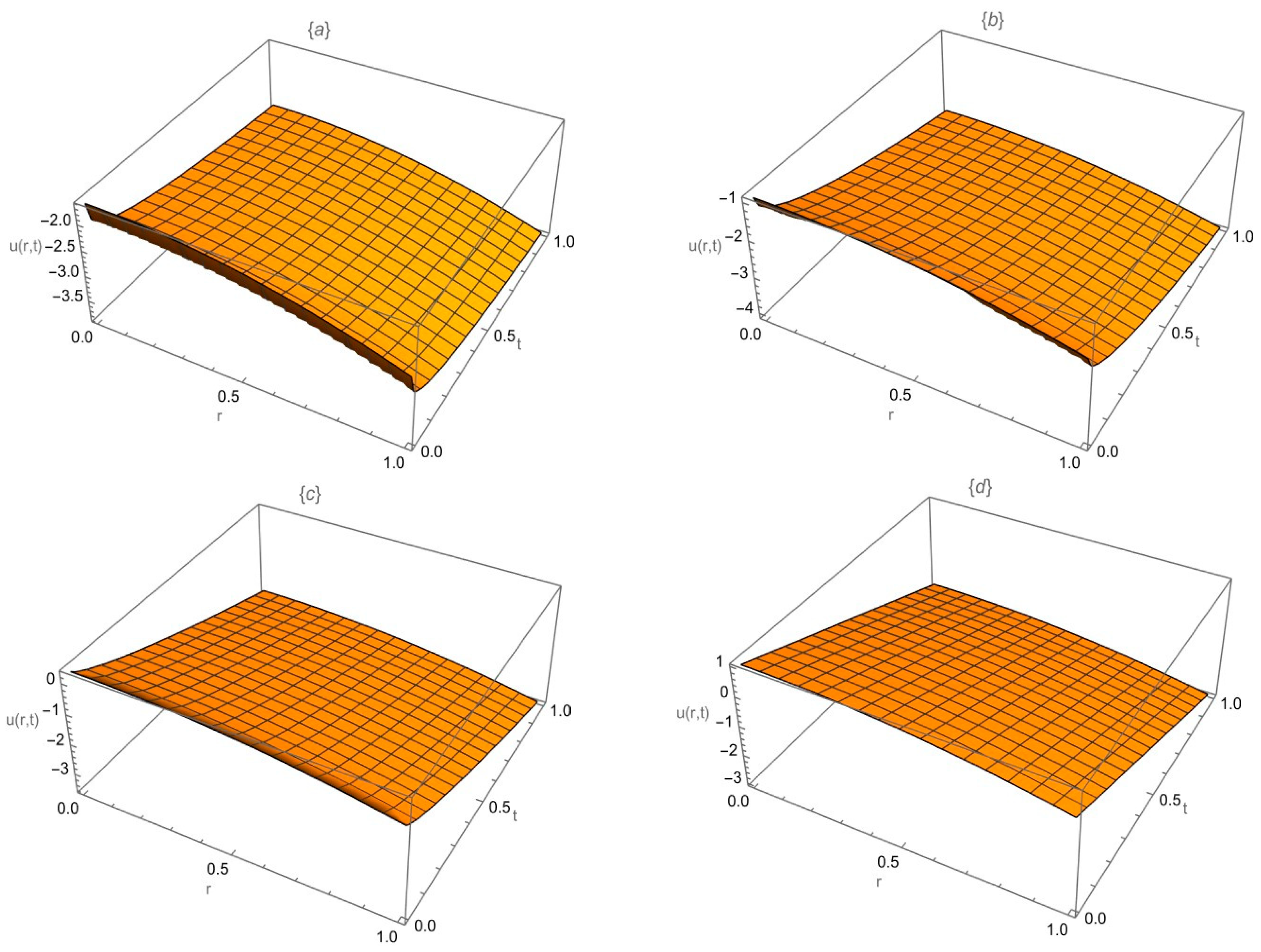
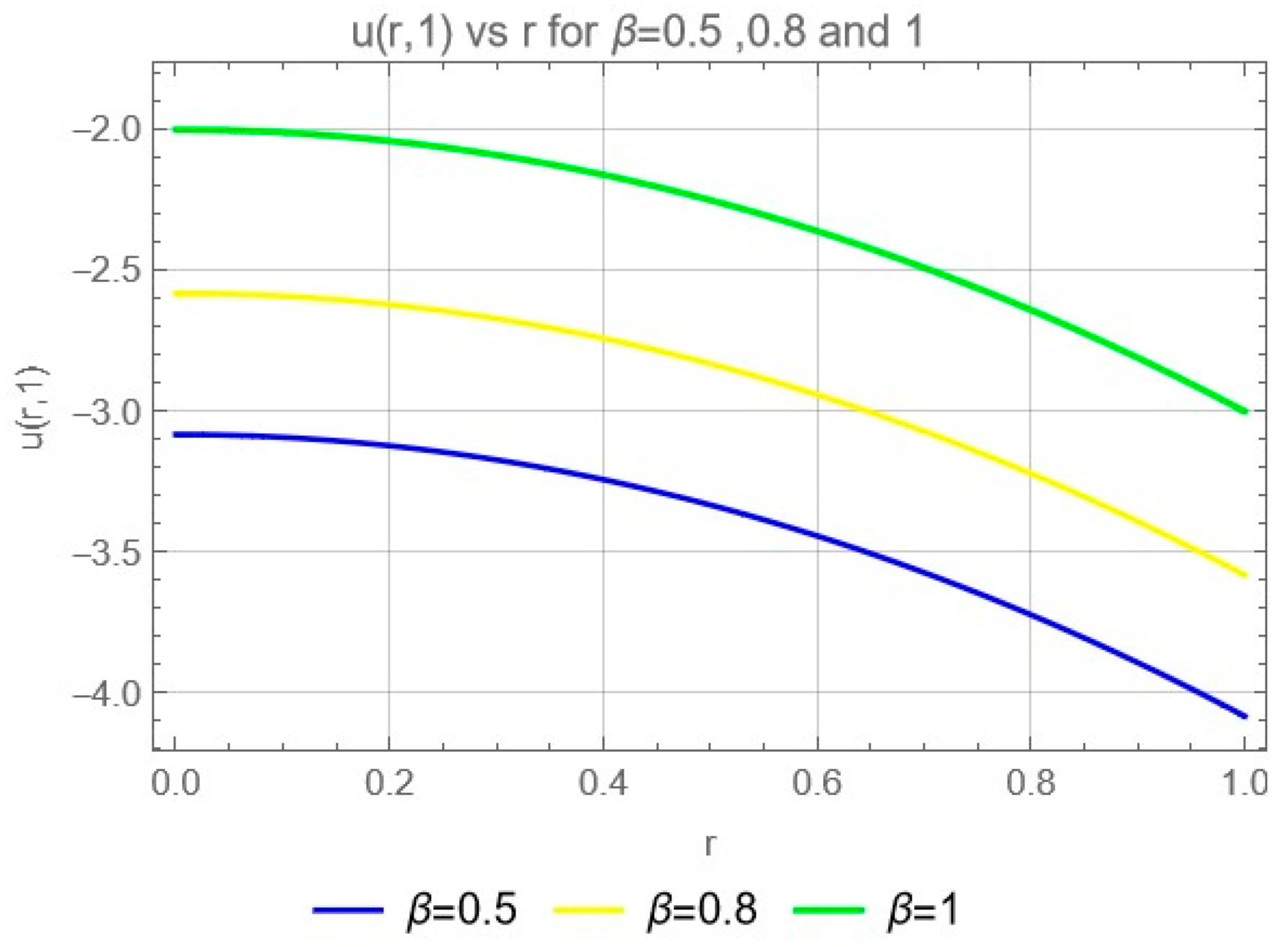
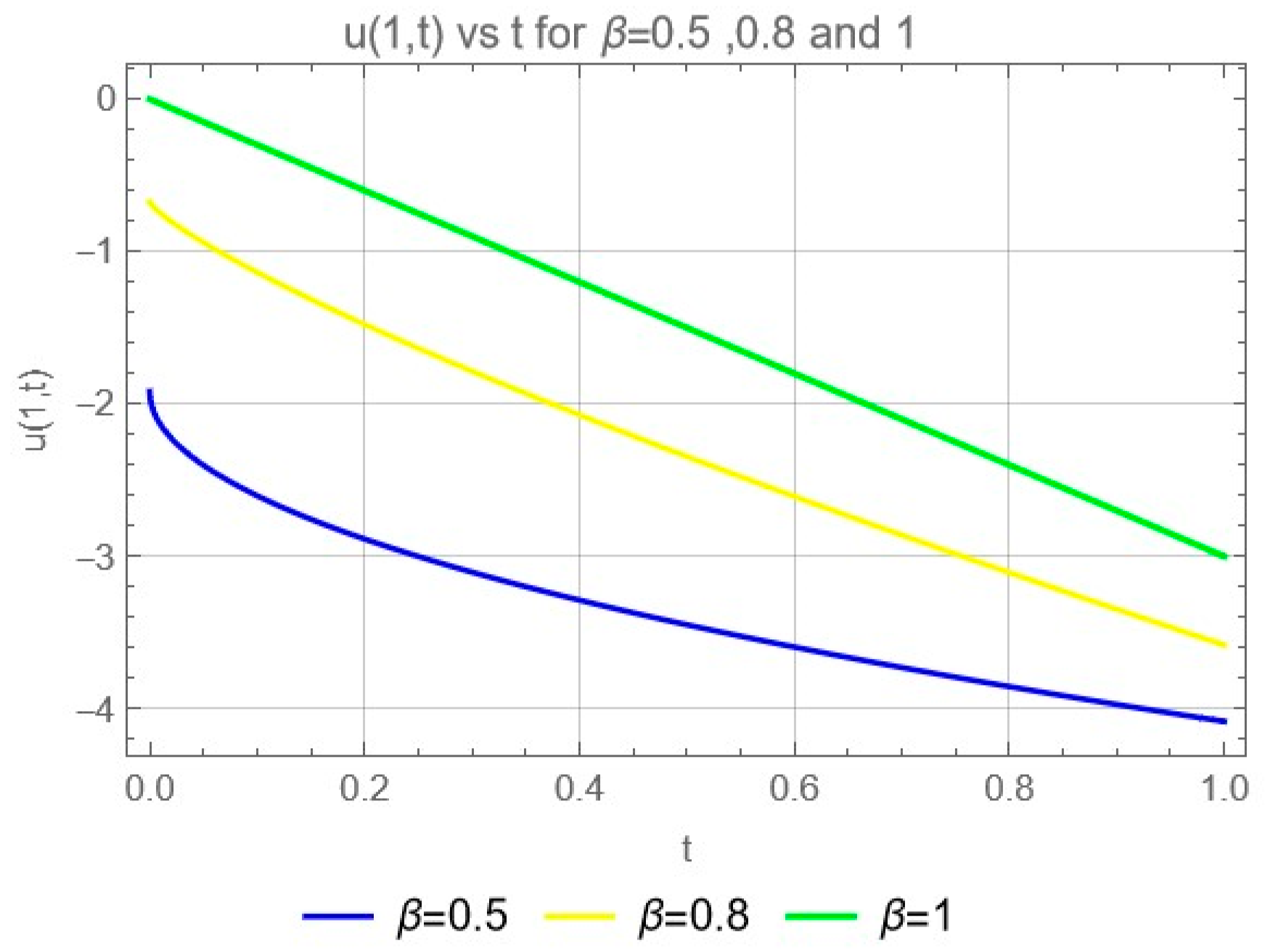
Numerical Examples
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| ABCFD | Atangana–Baleanu–Caputo fractional derivatives. |
| ABFI | Atangana–Baleanu fractional integral. |
| IM | Iterative method. |
| MLF | Mittag–Leffler function. |
| N-S | Navier–Stokes |
References
- Akbar, T.; Zia, Q.M.Z. Some Exact Solutions of Two-Dimensional Navier–Stokes Equations by Generalizing the Local Vorticity. Adv. Mech. Eng. 2019, 11, 168781401983189. [Google Scholar] [CrossRef]
- Kumar, D.; Singh, J.; Kumar, S. A Fractional Model of Navier–Stokes Equation Arising in Unsteady Flow of a Viscous Fluid. J. Assoc. Arab. Univ. Basic. Appl. Sci. 2015, 17, 14–19. [Google Scholar] [CrossRef]
- Yadav, L.K.; Agarwal, G.; Kumari, M. Study of Navier-Stokes Equation by Using Iterative Laplace Transform Method (ILTM) Involving Caputo- Fabrizio Fractional Operator. J. Phys. Conf. Ser. 2020, 1706, 012044. [Google Scholar] [CrossRef]
- Kumar, S.; Kumar, D.; Abbasbandy, S.; Rashidi, M.M. Analytical Solution of Fractional Navier–Stokes Equation by Using Modified Laplace Decomposition Method. Ain Shams Eng. J. 2014, 5, 569–574. [Google Scholar] [CrossRef]
- Zhou, Y.; Peng, L. On the Time-Fractional Navier–Stokes Equations. Comput. Math. Appl. 2017, 73, 874–891. [Google Scholar] [CrossRef]
- Ashmawy, E.A. Unsteady Translational Motion of a Slip Sphere in a Viscous Fluid Using the Fractional Navier-Stokes Equation. Eur. Phys. J. Plus 2017, 132, 142. [Google Scholar] [CrossRef]
- Momani, S.; Odibat, Z. Analytical Solution of a Time-Fractional Navier–Stokes Equation by Adomian Decomposition Method. Appl. Math. Comput. 2006, 177, 488–494. [Google Scholar] [CrossRef]
- Biazar, J.; Babolian, E.; Kember, G.; Nouri, A.; Islam, R. An Alternate Algorithm for Computing Adomian Polynomials in Special Cases. Appl. Math. Comput. 2003, 138, 523–529. [Google Scholar] [CrossRef]
- Burqan, A.; El-Ajou, A.; Saadeh, R.; Al-Smadi, M. A New Efficient Technique Using Laplace Transforms and Smooth Expansions to Construct a Series Solution to the Time-Fractional Navier-Stokes Equations. Alex. Eng. J. 2022, 61, 1069–1077. [Google Scholar] [CrossRef]
- Iqbal, S.; Martínez, F. An Approach for Approximating Analytical Solutions of the Navier-Stokes Time-Fractional Equation Using the Homotopy Perturbation Sumudu Transform’s Strategy. Axioms 2023, 12, 1025. [Google Scholar] [CrossRef]
- Djennadi, S.; Shawagfeh, N.; Arqub, O.A. Well-Posedness of the Inverse Problem of Time Fractional Heat Equation in the Sense of the Atangana-Baleanu Fractional Approach. Alex. Eng. J. 2020, 59, 2261–2268. [Google Scholar] [CrossRef]
- Atangana, A.; Baleanu, D. New Fractional Derivatives with Nonlocal and Non-Singular Kernel: Theory and Application to Heat Transfer Model. Therm. Sci 2016, 20, 763–769. [Google Scholar] [CrossRef]
- Atangana, A.; Owolabi, K.M. New Numerical Approach for Fractional Differential Equations. Math. Model. Nat. Phenom. 2018, 13, 3. [Google Scholar] [CrossRef]
- Bokhari, A.; Baleanu, D.; Belgacem, R. Application of Shehu Transform to Atangana-Baleanu Derivatives. J. Math. Comput. Sci. 2019, 20, 101–107. [Google Scholar] [CrossRef]
- Alomari, A.K. Homotopy-Sumudu Transforms for Solving System of Fractional Partial Differential Equations. Adv. Differ. Equ. 2020, 2020, 222. [Google Scholar] [CrossRef]
- Syam, M.I.; Al-Refai, M. Fractional Differential Equations with Atangana–Baleanu Fractional Derivative: Analysis and Applications. Chaos Solitons Fractals X 2019, 2, 100013. [Google Scholar] [CrossRef]




Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Monyayi, V.T.; Doungmo Goufo, E.F.; Tchangou Toudjeu, I. Mathematical Analysis of a Navier–Stokes Model with a Mittag–Leffler Kernel. AppliedMath 2024, 4, 1230-1244. https://doi.org/10.3390/appliedmath4040066
Monyayi VT, Doungmo Goufo EF, Tchangou Toudjeu I. Mathematical Analysis of a Navier–Stokes Model with a Mittag–Leffler Kernel. AppliedMath. 2024; 4(4):1230-1244. https://doi.org/10.3390/appliedmath4040066
Chicago/Turabian StyleMonyayi, Victor Tebogo, Emile Franc Doungmo Goufo, and Ignace Tchangou Toudjeu. 2024. "Mathematical Analysis of a Navier–Stokes Model with a Mittag–Leffler Kernel" AppliedMath 4, no. 4: 1230-1244. https://doi.org/10.3390/appliedmath4040066
APA StyleMonyayi, V. T., Doungmo Goufo, E. F., & Tchangou Toudjeu, I. (2024). Mathematical Analysis of a Navier–Stokes Model with a Mittag–Leffler Kernel. AppliedMath, 4(4), 1230-1244. https://doi.org/10.3390/appliedmath4040066





