Abstract
The two-parameter logistic (2PL) item response theory (IRT) model is frequently applied to analyze group differences for multivariate binary random variables. The item parameters in the 2PL model are frequently fixed when estimating the mean and the standard deviation for a group of interest. This method is also called fixed item parameter calibration (FIPC). In this article, the bias and the linking error of the FIPC approach are analytically derived in the presence of random uniform differential item functioning (DIF). The adequacy of the analytical findings was validated in a simulation study. It turned out that the extent of the bias and the variance in distribution parameters increases with increasing variance of random DIF effects.
Keywords:
item response theory; 2PL model; bias; linking error; fixed item parameter calibration; differential item functioning MSC:
62H12; 62H17; 62H25; 62P25
1. Introduction
Item response theory (IRT) models [1,2,3,4,5,6,7] represent a statistical framework to model multivariate discrete random variables. IRT models are frequently employed in the context of educational or psychological research. Let be the vector of dichotomous (i.e., binary) random variables that are typically referred to as (scored) items (or scored item responses). A unidimensional IRT model [8,9] is a statistical model for the probability distribution for , where
In (1), denotes the density of the univariate normal distribution with mean and standard deviation . The parameters of the distribution for the latent (factor) variable , also labeled as trait or ability, define the parameter of interest . The vector collects all estimated item parameters of item response functions (IRF) (). The two-parameter logistic (2PL) model [10,11,12] has the IRF:
where and are the item discrimination and item difficulty, respectively, and the logistic distribution function is given by the following:
In this case, the item parameters in (1) are given as . The model parameters in the IRT model (1) are frequently estimated using (marginal) maximum likelihood estimation [13,14].
IRT models are frequently used to compare the distribution of a particular group, such as a country, in a test (i.e., on a set of items) with a reference distribution with respect to the factor variable in the IRT model (1). Fixed item parameter calibration (FIPC, [15,16,17,18,19]) is frequently use. It assumes that item parameters are known (or estimated) in the total sample, and only the distribution parameters must be estimated. The application of the FIPC method using the 2PL model can be assumed to provide consistent distribution parameter estimates if the item parameters also hold for the group under study. However, it could be that the item parameters were group-specific. This property is referred to as differential item functioning (DIF) in the literature (see, for example, [20,21,22,23,24]). It has been shown in the linking literature that DIF produces additional variability in the estimated mean and standard deviation [25,26,27,28,29,30,31]. Moreover, it has been demonstrated that the occurrence of DIF can introduce bias in the distribution parameters [32,33]. In particular, bias in FIPC due to random DIF can emerge, because a misspecified IRF is assumed that ignores DIF effects. Importantly, bias in distribution parameter estimates emerges, even if DIF effects are random (i.e., average to zero in the population). Moreover, the presence of random DIF also includes additional variability of the FIPC method.
In this article, the performance of FIPC is investigated in the presence of random DIF [34,35,36,37,38,39,40]. An analytical derivation and a simulation study show that biased estimates can result in the presence of random DIF. The analytical derivation utilizes standard techniques from calculus. However, to our knowledge, such a derivation of the bias and the variance of the FIPC estimates in the presence of DIF have not yet been presented in the literature.
The rest of this article is organized as follows. Section 2 presents an analytical derivation of the bias and the variance of the parameter estimate of the FIPC method. Section 3 reports the findings of a simulation study that aims to confirm the analytical findings of Section 2. Finally, the article closes with a discussion in Section 4.
2. Analytical Derivation of Bias and Linking Error
In this section, we compute approximations of the bias and the variance (i.e., the square of the linking error) for the FIPC method in the presence of random uniform DIF. The derivation operates on the assumption of an infinite sample size of persons. Hence, the effects of sampling error (i.e., sampling of subjects) are neglected.
Let be a vector of item responses. The index h of an item response pattern can be defined as , where . In total, there are item response patterns for I items. The likelihood of the item response pattern is given by (see [41])
where are known weights that are proportional to the standard normal distribution, and the likelihood (4) is evaluated at a discrete grid for of points. The distribution parameters consists of the mean and the standard deviation . is the vector of item discriminations, and is the vector of item difficulties. Note that and also enter item response probabilities in (4) because the prior probability weights follow a standard normal distribution.
The item response data are generated by additionally assuming uniform DIF effects. The probability of a pattern is given by the following (see [41]):
and the notation and indicates that the distribution parameters are fixed for data generation. Note that is a function of random uniform DIF effects , where .
The log-likelihood function l is used to obtain parameter estimates for the population parameter . The log-likelihood function is given by the following:
The parameter estimate is obtained as the maximizer of l, which means that is the root of a score equation:
Importantly, DIF effects only affect probabilities , and the DIF effects are not modelled.
We now derive an approximation of the parameter estimate as a function of random uniform DIF effects . A Taylor expansion of partial derivative in (8) is utilized in the approximation (see [42] for an extensive usage of this technique). We assume independent random uniform DIF effects with and DIF variance (i.e., a standard deviation ; see [38,43]) and use a Taylor expansion around and
Because we also have (i.e., the true parameter is obtained if DIF effects are absent), we arrive at the following:
while omitting arguments in the corresponding partial derivatives. Then, we can obtain the expected bias (due to and ) from (10)) by taking the expectation operator as follows:
Note that because and both increases with I, the bias is asymptotically independent of the number of items I. The variance of can be computed as follows:
The linking error is is defined as the square root of the variance [26].
We can now more explicitly compute the appearing terms in (11) and (12). The partial derivatives of l with respect to are given by the following:
while the partial derivatives (denoted by the operator ∂) with respect to uniform DIF effects can be computed as follows:
In detail, the estimating equation for is given by the following:
Moreover, we obtain the estimating equation for as follows:
The second-order derivatives in are given as follows:
where . Furthermore, we now compute the derivatives of with respect to . We obtain the following for the derivatives evaluated at :
It appears that the bias-determining term in (11) is mainly affected by partial derivatives with respect to the standard deviation . The bias-determining term can be computed as follows:
This expression can be simplified to the following:
It is difficult to obtain clear insights in the expression (23). However, the sign of this term can be reasoned via simplified assumptions. Assume item difficulties are close to . First, we investigate the first factor of (23) that involves the following term:
Assume that . Then, we expect , and will typically be positive. In this case, the term will be positive. If , we expect , and will typically be negative. Again, will be positive. Second, we investigate the second factor:
If , we expect , and is positive. If , we expect , which also implies that is positive. Because there is a negative sign for in (23), we expect a negative contribution of . Furthermore, the second-order derivative matrix is negative definite for a maximizer. Moreover, from (11), we have the total bias contribution , which includes an additional negative sign. By taking these three negative signs into account, we reason that the bias in can be expected to be negative.
3. Simulation Study
3.1. Methods
The 2PL model was used as the IRT model to simulate item responses. We fixed the mean and the SD for the normally distributed ability variable at 0.3 and 1.2, respectively.
The number I of items was fixed at 15 in the simulation. The item discriminations of the 15 items had a mean of 1.007 and a standard deviation of 0.225 and ranged between 0.6 and 1.3. The item difficulties had a mean of 0.000, a standard deviation of 1.272, and ranged between −2.0 and 2.0. The concrete item parameters can be found at https://osf.io/uf2xc (accessed on 4 August 2024). These item parameters were used in the FIPC scaling model.
For data generation using the 2PL model, random uniform DIF effects () were added to item difficulties . The standard deviation was chosen at seven factor levels: 0 (indicating no DIF), 0.1, 0.2, 0.3, 0.4, 0.5, and 0.6. Note that random DIF effects were simulated in each replication of the simulation study.
Item responses were simulated according to the 2PL model for sample sizes N of 250, 500, 1000, 2000, and an infinite sample size of subjects (denoted by Inf). In the case of an infinite sample size, the probabilities for all item response patterns according to the data-generating model were directly computed, and no item responses were simulated.
FIPC was applied as the analysis model in all conditions. The item parameters of the 2PL model were fixed at the prespecified and values, as described above.
In each of the 5 (sample size N) × 7 (DIF standard deviation ) = 35 cells of the simulation study, 20,000 replications were conducted. We computed the empirical bias and the root mean square error (RMSE) for the estimated mean and the estimated standard deviation to assess the estimation quality of parameter estimates (see [44]).
The R software (version 4.4.1) [45] was used for the entire analysis in this simulation study. The 2PL model was fitted using the R package TAM [46]. Dedicated R functions for this simulation study were written by the author of this article. These functions and replication material for this Simulation study can be found at https://osf.io/uf2xc (accessed on 4 August 2024).
3.2. Results
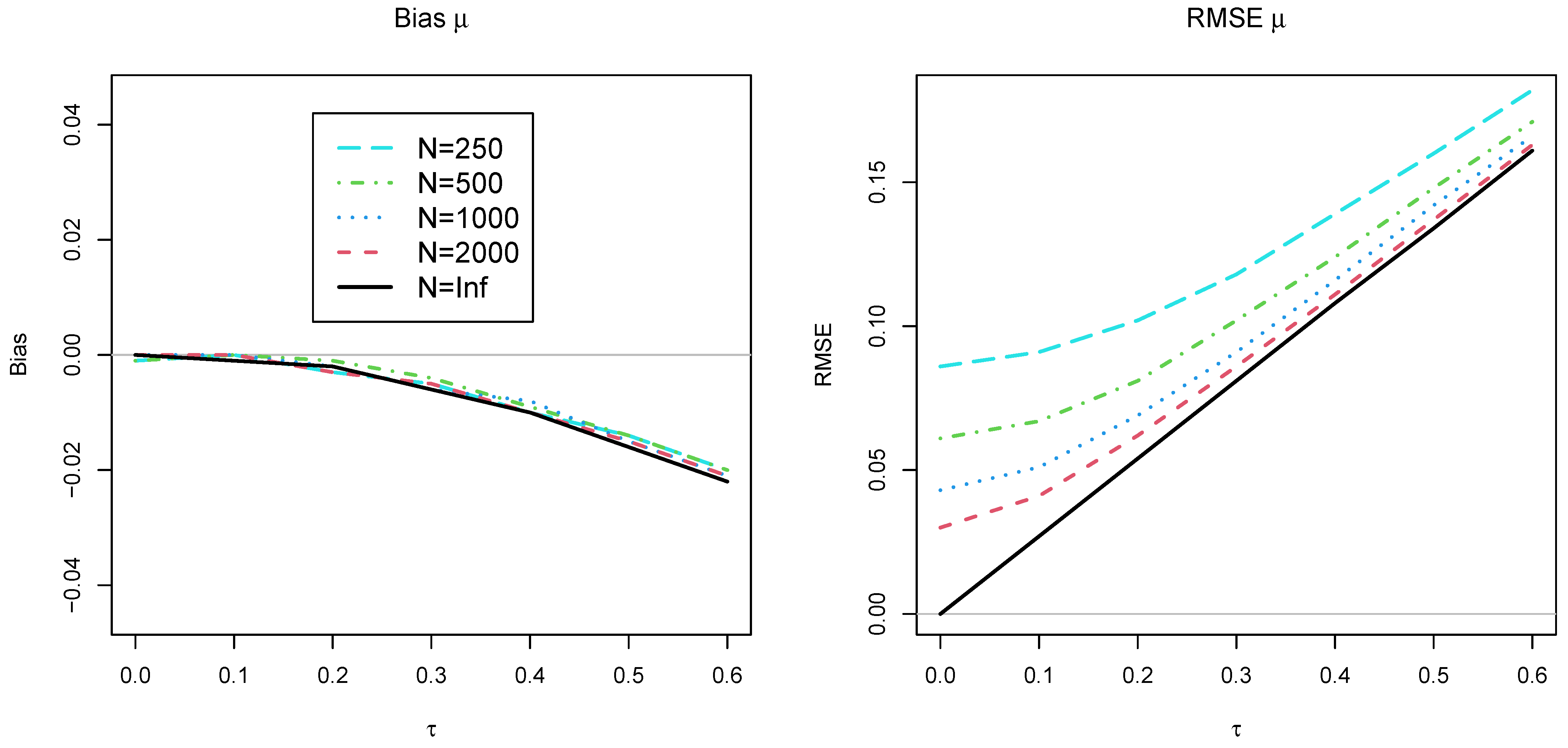
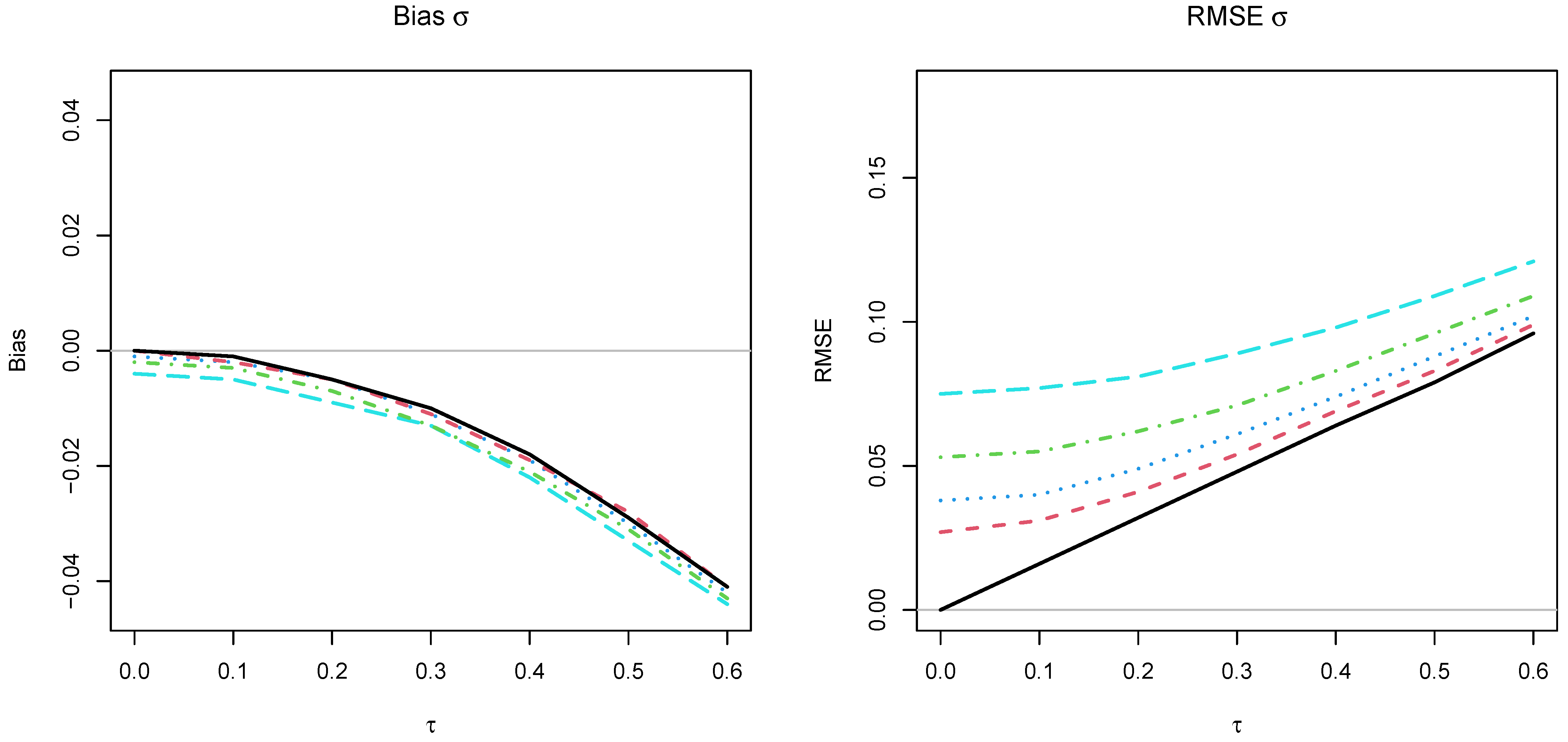
Table 1 reports the bias and the RMSE for the estimates of the mean and the standard deviation . Overall, it turned out that the bias was larger for than for . Moreover, the bias increased as a function of the standard deviation . The bias exceeded a non-negligible cutoff value of 0.010 (in absolute value) for for and for for . Also, the bias was slightly larger for smaller sample sizes compared to large sample sizes or an infinite sample size. For a fixed value of DIF standard deviation , the RMSE was the smallest for infinite sample sizes. On the other hand, the RMSE was zero in the case of an infinite sample size of subjects (i.e., ) and no DIF standard deviation (i.e., ).

Table 1.
Simulation study: Bias and root mean square error (RMSE) for the estimate of the mean and standard deviation as a function of the uniform DIF standard deviation and sample size N.
The results in Table 1 are also graphically displayed in Figure 1. Notably, bias and RMSE for and increase with increasing DIF standard deviation . The bias is hardly affected by sample size. Moreover, the RMSE is almost perfectly linearly related to in an infinite sample size. Moreover, the RMSE increases with decreasing sample size N.
Figure 1.
Simulation study: Graphical visualization of the bias and root mean square error (RMSE) for the estimate of the mean and standard deviation as a function of the uniform DIF standard deviation and sample size N.
4. Discussion
Through analytical arguments and a simulation study, this article shows that the FIPC method provides biased estimates in the presence of random uniform DIF. Analytical arguments demonstrated that the bias was a function of the DIF standard deviation . The analytically obtained results were also confirmed based on a simulation study. Overall, the bias in the estimated standard deviation was larger than in the estimated mean .
Note that we derived the bias of distribution parameter estimates under a random DIF assumption. The derivation of the bias under fixed DIF could also rely on the Taylor Expansion (9). However, it is likely that only the linear expansion with respect to must be considered because we now cannot assume as in the random DIF case. Note that identification assumptions must be imposed in the fixed DIF case (e.g., all DIF effects sum to zero; see [47,48,49]). This property illustrates the circularity of the DIF definition in the case of fixed DIF, and general statements of the bias of a linking method like FIPC crucially depend on the chosen identification assumptions imposed by individual researchers [50].
Our derivation of the bias and the variance only involved uniform DIF effects (i.e., DIF effects in item difficulty). However, the Taylor expansion could be extended to include nonuniform DIF effects (i.e., DIF effects in item discriminations). Future research might focus on generalizing the findings to the more general DIF case.
Moreover, we only investigated the 2PL model with random DIF. The findings regarding the FIPC method can most likely be transferred to more complex IRT models, such as the three-parameter logistic (3PL) models [51] or other IRT models [52,53,54].
It should be emphasized that our findings were also observed for the nonlinear Haebara and Stocking–Lord linking methods [32]. These linking methods (see [55,56,57,58] for general treatments) also result in biased mean and standard deviations in the presence of random uniform DIF. In contrast, the mean–geometric mean linking method [55,59] that directly operates on estimated item parameters typically provides unbiased estimates [32]. Except for very small sample sizes, we believe that mean–geometric mean linking should be the preferred scaling (i.e., linking) method in applications if researchers cannot exclude the situation of random DIF.
Our study did not consider the estimation of the variance of distribution parameters in FIPC estimation, which is important for statistical inference. Linking errors for the FIPC method can be obtained by using an item jackknife that repeatedly estimates the IRT model with FIPC while excluding one item or one group of items [60]. Computational shortcuts for item jackknife for the FIPC method using the 2PL model were discussed in [61]. In the statistical inference of distribution parameters, standard errors due to the sampling of persons and linking errors due to randomness in item parameters must be disentangled. Ref. [28] addressed this topic for linking methods, but the estimation technique does not apply to the FIPC method.
By interpreting the findings of FIPC and the Haebara and Stocking–Lord linking methods, it appears that the source of the bias is the attempt to align a misspecified item response function that contains DIF onto an item response function that does not represent the DIF in their item parameters. A misfitting item results in a smaller estimated item discrimination. Because the estimated standard deviation represents an average estimated item discrimination, the bias in the estimated mean and standard deviation can be explained as a consequence of item misfit. Hence, the bias of FIPC also transfers to the recalibration linking technique [62,63] that is used in some large-scale educational studies [64,65].
Our findings also shed some light on the practical applications of linking methods to educational large-scale assessment studies [66], like programme for international student assessment (PISA; [67]). Older PISA studies effectively implemented the FIPC method for country comparisons [68]. More recent PISA studies opted for a partial invariance approach in which only the largest DIF effects and country-specific item parameters were assumed in the 2PL model [68,69,70]. Hence, an item with a large DIF effect in one country is essentially excluded from country comparisons that involve this country [50]. Nevertheless, there is very likely random DIF in the remaining items, which will subsequently (slightly) bias the distribution parameters. Hence, there is no statistical evidence for preferring scaling models with invariant item parameters (i.e., using the FIPC method for a country) or partially invariant item parameters (i.e., using the FIPC method for a subset of items for a country) instead of linking methods that allow for DIF effects in all items. However, identification assumptions are imposed by model choice, and any assumption can, in principle, be defended due to the definitional ambiguity.
Funding
This research received no external funding.
Data Availability Statement
No new data were created or analyzed in this study.
Conflicts of Interest
The author declares no conflict of interest.
Abbreviations
- The following abbreviations are used in this manuscript:
| 2PL | two-parameter logistic |
| FIPC | fixed item parameter calibration |
| Inf | infinite sample size |
| IRF | item response function |
| IRT | item response theory |
| RMSE | root mean square error |
References
- Bock, R.D.; Moustaki, I. Item response theory in a general framework. In Handbook of Statistics, Vol. 26: Psychometrics; Rao, C.R., Sinharay, S., Eds.; Elsevier: Amsterdam, The Netherlands, 2007; pp. 469–513. [Google Scholar] [CrossRef]
- Chen, Y.; Li, X.; Liu, J.; Ying, Z. Item Response Theory—A Statistical Framework for Educational and Psychological Measurement. 2024. Ahead of Print. Available online: https://arxiv.org/abs/2108.08604 (accessed on 4 August 2024).
- De Ayala, R.J. The Theory and Practice of Item Response Theory; Guilford Publications: New York, NY, USA, 2022. [Google Scholar]
- Formann, A.K.; Kohlmann, T. Structural latent class models. Sociol. Methods Res. 1998, 26, 530–565. [Google Scholar] [CrossRef]
- Martinková, P.; Hladká, A. Computational Aspects of Psychometric Methods: With R; Chapman and Hall/CRC: Boca Raton, FL, USA, 2023. [Google Scholar] [CrossRef]
- Noventa, S.; Heller, J.; Kelava, A. Toward a unified perspective on assessment models, part I: Foundations of a framework. J. Math. Psychol. 2024, 122, 102872. [Google Scholar] [CrossRef]
- Yen, W.M.; Fitzpatrick, A.R. Item response theory. In Educational Measurement; Brennan, R.L., Ed.; Praeger Publishers: Westport, WA, USA, 2006; pp. 111–154. [Google Scholar]
- van der Linden, W.J. Unidimensional logistic response models. In Handbook of Item Response Theory, Volume 1: Models; van der Linden, W.J., Ed.; CRC Press: Boca Raton, FL, USA, 2016; pp. 11–30. [Google Scholar] [CrossRef]
- Meijer, R.R.; Tendeiro, J.N. Unidimensional item response theory. In The Wiley Handbook of Psychometric Testing: A Multidisciplinary Reference on Survey, Scale and Test; Irwing, P., Booth, T., Hughes, D.J., Eds.; Wiley: New York, NY, USA, 2018; pp. 413–443. [Google Scholar] [CrossRef]
- Birnbaum, A. Some latent trait models and their use in inferring an examinee’s ability. In Statistical Theories of Mental Test Scores; Lord, F.M., Novick, M.R., Eds.; MIT Press: Reading, MA, USA, 1968; pp. 397–479. [Google Scholar]
- von Davier, M. A general diagnostic model applied to language testing data. Br. J. Math. Stat. Psychol. 2008, 61, 287–307. [Google Scholar] [CrossRef] [PubMed]
- von Davier, M.; Yamamoto, K. Partially observed mixtures of IRT models: An extension of the generalized partial-credit model. Appl. Psychol. Meas. 2004, 28, 389–406. [Google Scholar] [CrossRef]
- Bock, R.D.; Aitkin, M. Marginal maximum likelihood estimation of item parameters: Application of an EM algorithm. Psychometrika 1981, 46, 443–459. [Google Scholar] [CrossRef]
- Glas, C.A.W. Maximum-likelihood estimation. In Handbook of Item Response Theory, Vol. 2: Statistical Tools; van der Linden, W.J., Ed.; CRC Press: Boca Raton, FL, USA, 2016; pp. 197–216. [Google Scholar] [CrossRef]
- Kang, T.; Petersen, N.S. Linking item parameters to a base scale. Asia Pac. Educ. Rev. 2012, 13, 311–321. [Google Scholar] [CrossRef]
- Kim, K.Y. Two IRT fixed parameter calibration methods for the bifactor model. J. Educ. Meas. 2020, 57, 29–50. [Google Scholar] [CrossRef]
- Kim, S. A comparative study of IRT fixed parameter calibration methods. J. Educ. Meas. 2006, 43, 355–381. [Google Scholar] [CrossRef]
- Kim, S.; Kolen, M.J. Application of IRT fixed parameter calibration to multiple-group test data. Appl. Meas. Educ. 2019, 32, 310–324. [Google Scholar] [CrossRef]
- König, C.; Khorramdel, L.; Yamamoto, K.; Frey, A. The benefits of fixed item parameter calibration for parameter accuracy in small sample situations in large-scale assessments. Educ. Meas. Issues Pract. 2021, 40, 17–27. [Google Scholar] [CrossRef]
- Magis, D.; Béland, S.; Tuerlinckx, F.; De Boeck, P. A general framework and an R package for the detection of dichotomous differential item functioning. Behav. Res. Methods 2010, 42, 847–862. [Google Scholar] [CrossRef]
- Mellenbergh, G.J. Item bias and item response theory. Int. J. Educ. Res. 1989, 13, 127–143. [Google Scholar] [CrossRef]
- Millsap, R.E. Statistical Approaches to Measurement Invariance; Routledge: New York, NY, USA, 2011. [Google Scholar] [CrossRef]
- Penfield, R.D.; Camilli, G. Differential item functioning and item bias. In Handbook of Statistics, Vol. 26: Psychometrics; Rao, C.R., Sinharay, S., Eds.; Elsevier: Amsterdam, The Netherlands, 2007; pp. 125–167. [Google Scholar] [CrossRef]
- Soares, T.M.; Gonçalves, F.B.; Gamerman, D. An integrated Bayesian model for DIF analysis. J. Educ. Behav. Stat. 2009, 34, 348–377. [Google Scholar] [CrossRef]
- Michaelides, M.P.; Haertel, E.H. Selection of common items as an unrecognized source of variability in test equating: A bootstrap approximation assuming random sampling of common items. Appl. Meas. Educ. 2014, 27, 46–57. [Google Scholar] [CrossRef]
- Monseur, C.; Berezner, A. The computation of equating errors in international surveys in education. J. Appl. Meas. 2007, 8, 323–335. Available online: https://bit.ly/2WDPeqD (accessed on 4 August 2024). [PubMed]
- Robitzsch, A. Linking error in the 2PL model. J 2023, 6, 58–84. [Google Scholar] [CrossRef]
- Robitzsch, A. Estimation of standard error, linking error, and total error for robust and nonrobust linking methods in the two-parameter logistic model. Stats 2024, 7, 592–612. [Google Scholar] [CrossRef]
- Sachse, K.A.; Roppelt, A.; Haag, N. A comparison of linking methods for estimating national trends in international comparative large-scale assessments in the presence of cross-national DIF. J. Educ. Meas. 2016, 53, 152–171. [Google Scholar] [CrossRef]
- Sachse, K.A.; Haag, N. Standard errors for national trends in international large-scale assessments in the case of cross-national differential item functioning. Appl. Meas. Educ. 2017, 30, 102–116. [Google Scholar] [CrossRef]
- Wu, M. Measurement, sampling, and equating errors in large-scale assessments. Educ. Meas. Issues Pract. 2010, 29, 15–27. [Google Scholar] [CrossRef]
- Robitzsch, A. Bias-reduced Haebara and Stocking-Lord linking. J 2024, 7, 373–384. [Google Scholar] [CrossRef]
- Robitzsch, A. SIMEX-based and analytical bias corrections in Stocking-Lord linking. Analytics 2024, 3, 368–388. [Google Scholar] [CrossRef]
- De Boeck, P. Random item IRT models. Psychometrika 2008, 73, 533–559. [Google Scholar] [CrossRef]
- Fox, J.P. Bayesian Item Response Modeling; Springer: New York, NY, USA, 2010. [Google Scholar] [CrossRef]
- Fox, J.P.; Verhagen, A.J. Random item effects modeling for cross-national survey data. In Cross-Cultural Analysis: Methods and Applications; Davidov, E., Schmidt, P., Billiet, J., Eds.; Routledge: London, UK, 2010; pp. 461–482. [Google Scholar] [CrossRef]
- de Jong, M.G.; Steenkamp, J.B.E.M.; Fox, J.P. Relaxing measurement invariance in cross-national consumer research using a hierarchical IRT model. J. Consum. Res. 2007, 34, 260–278. [Google Scholar] [CrossRef]
- Longford, N.T.; Holland, P.W.; Thayer, D.T. Stability of the MH D-DIF statistics across populations. In Differential Item Functioning; Holland, P.W., Wainer, H., Eds.; Routledge: London, UK, 1993; pp. 171–196. [Google Scholar] [CrossRef]
- Van den Noortgate, W.; De Boeck, P. Assessing and explaining differential item functioning using logistic mixed models. J. Educ. Behav. Stat. 2005, 30, 443–464. [Google Scholar] [CrossRef]
- Robitzsch, A. Robust and nonrobust linking of two groups for the Rasch model with balanced and unbalanced random DIF: A comparative simulation study and the simultaneous assessment of standard errors and linking errors with resampling techniques. Symmetry 2021, 13, 2198. [Google Scholar] [CrossRef]
- Bock, R.D.; Gibbons, R.D. Item Response Theory; Wiley: Hoboken, NJ, USA, 2021. [Google Scholar] [CrossRef]
- Boos, D.D.; Stefanski, L.A. Essential Statistical Inference; Springer: New York, NY, USA, 2013. [Google Scholar] [CrossRef]
- Penfield, R.D.; Algina, J. A generalized DIF effect variance estimator for measuring unsigned differential test functioning in mixed format tests. J. Educ. Meas. 2006, 43, 295–312. [Google Scholar] [CrossRef]
- Morris, T.P.; White, I.R.; Crowther, M.J. Using simulation studies to evaluate statistical methods. Stat. Med. 2019, 38, 2074–2102. [Google Scholar] [CrossRef]
- R Core Team. R: A Language and Environment for Statistical Computing; R Core Team: Vienna, Austria, 2023; Available online: https://www.R-project.org (accessed on 15 March 2023).
- Robitzsch, A.; Kiefer, T.; Wu, M. TAM: Test Analysis Modules. 2024. R Package Version 4.2-21. Available online: https://doi.org/10.32614/CRAN.package.TAM (accessed on 19 February 2024).
- Bechger, T.M.; Maris, G. A statistical test for differential item pair functioning. Psychometrika 2015, 80, 317–340. [Google Scholar] [CrossRef]
- Camilli, G. The case against item bias detection techniques based on internal criteria: Do item bias procedures obscure test fairness issues? In Differential Item Functioning: Theory and Practice; Holland, P.W., Wainer, H., Eds.; Erlbaum: Hillsdale, NJ, USA, 1993; pp. 397–417. [Google Scholar]
- Doebler, A. Looking at DIF from a new perspective: A structure-based approach acknowledging inherent indefinability. Appl. Psychol. Meas. 2019, 43, 303–321. [Google Scholar] [CrossRef]
- Robitzsch, A.; Lüdtke, O. A review of different scaling approaches under full invariance, partial invariance, and noninvariance for cross-sectional country comparisons in large-scale assessments. Psychol. Test Assess. Model. 2020, 62, 233–279. Available online: https://bit.ly/3ezBB05 (accessed on 4 August 2024).
- Lord, F.M.; Novick, R. Statistical Theories of Mental Test Scores; Addison-Wesley: Reading, MA, USA, 1968. [Google Scholar]
- Bolt, D.M.; Deng, S.; Lee, S. IRT model misspecification and measurement of growth in vertical scaling. J. Educ. Meas. 2014, 51, 141–162. [Google Scholar] [CrossRef]
- Loken, E.; Rulison, K.L. Estimation of a four-parameter item response theory model. Br. J. Math. Stat. Psychol. 2010, 63, 509–525. [Google Scholar] [CrossRef] [PubMed]
- Shim, H.; Bonifay, W.; Wiedermann, W. Parsimonious asymmetric item response theory modeling with the complementary log-log link. Behav. Res. Methods 2023, 55, 200–219. [Google Scholar] [CrossRef]
- Kolen, M.J.; Brennan, R.L. Test Equating, Scaling, and Linking; Springer: New York, NY, USA, 2014. [Google Scholar] [CrossRef]
- Lee, W.C.; Lee, G. IRT linking and equating. In The Wiley Handbook of Psychometric Testing: A Multidisciplinary Reference on Survey, Scale and Test; Irwing, P., Booth, T., Hughes, D.J., Eds.; Wiley: New York, NY, USA, 2018; pp. 639–673. [Google Scholar] [CrossRef]
- von Davier, M.; von Davier, A.A. A unified approach to IRT scale linking and scale transformations. Methodology 2007, 3, 115–124. [Google Scholar] [CrossRef]
- von Davier, A.A.; Carstensen, C.H.; von Davier, M. Linking Competencies in Educational Settings and Measuring Growth; (Research Report No. RR-06-12); Educational Testing Service: Princeton, NJ, USA, 2006. [Google Scholar] [CrossRef]
- Haberman, S.J. Linking Parameter Estimates Derived from an Item Response Model through Separate Calibrations; (Research Report No. RR-09-40); Educational Testing Service: Princeton, NJ, USA, 2009. [Google Scholar] [CrossRef]
- Monseur, C.; Sibberns, H.; Hastedt, D. Linking errors in trend estimation for international surveys in education. IERI Monogr. Ser. 2008, 1, 113–122. [Google Scholar]
- Robitzsch, A. Analytical approximation of the jackknife linking error in item response models utilizing a Taylor expansion of the log-likelihood function. AppliedMath 2023, 3, 49–59. [Google Scholar] [CrossRef]
- Martin, M.O.; Mullis, I.V.S.; Foy, P.; Brossman, B.; Stanco, G.M. Estimating linking error in PIRLS. IERI Monogr. Ser. 2012, 5, 35–47. [Google Scholar]
- Robitzsch, A. A comparison of linking methods for two groups for the two-parameter logistic item response model in the presence and absence of random differential item functioning. Foundations 2021, 1, 116–144. [Google Scholar] [CrossRef]
- Foy, P.; Yin, L. Scaling the PIRLS 2016 achievement data. In Methods and Procedures in PIRLS 2016; Martin, M.O., Mullis, I.V., Hooper, M., Eds.; IEA: Boston College, Chestnut Hill, MA, USA, 2017. [Google Scholar]
- Foy, P.; Fishbein, B.; von Davier, M.; Yin, L. Implementing the TIMSS 2019 scaling methodology. In Methods and Procedures: TIMSS 2019 Technical Report; Martin, M.O., von Davier, M., Mullis, I.V., Eds.; IEA: Boston College, Chestnut Hill, MA, USA, 2020. [Google Scholar]
- Rutkowski, L.; von Davier, M.; Rutkowski, D. (Eds.) A Handbook of International Large-Scale Assessment: Background, Technical Issues, and Methods of Data Analysis; Chapman Hall/CRC Press: London, UK, 2013. [Google Scholar] [CrossRef]
- OECD. PISA 2018. Technical Report; OECD: Paris, France, 2020; Available online: https://bit.ly/3zWbidA (accessed on 4 August 2024).
- OECD. PISA 2012. Technical Report; OECD: Paris, France, 2014; Available online: https://bit.ly/2YLG24g (accessed on 4 August 2024).
- Oliveri, M.E.; von Davier, M. Investigation of model fit and score scale comparability in international assessments. Psychol. Test Assess. Model. 2011, 53, 315–333. Available online: https://bit.ly/3k4K9kt (accessed on 4 August 2024).
- von Davier, M.; Yamamoto, K.; Shin, H.J.; Chen, H.; Khorramdel, L.; Weeks, J.; Davis, S.; Kong, N.; Kandathil, M. Evaluating item response theory linking and model fit for data from PISA 2000–2012. Assess. Educ. Princ. Policy Pract. 2019, 26, 466–488. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).