Readability across Time and Languages: The Case of Matthew’s Gospel Translations

Abstract

We have studied how the readability of a text can change in translation by considering Matthew’s Gospel, written in Greek, translated into Latin and 35 modern languages. We have found that the deep-language parameters $C_P$ (characters per word), $P_F$ (words per sentence), $I_P$ (words per interpunctions), $M_F$ (interpunctions per sentence) and a universal readability index $G_U$ of each translation are so diverse from language to language, and even within a given language for which there are many versions of Matthew—such as in English and Spanish—that the resulting texts mathematically seem to be diverse. The several tens of versions of Matthew’s Gospel studied appear to address very diverse audiences. If a reader could understand all of them well, he/she would have the impression of reading texts written by diverse authors, although all of them tell the same story.

1. A Common Ground for Measuring Readability across Time and Languages

Readability formulae [1,2,3,4,5,6,7,8,9] are applicable to any alphabetical language. Based on the length of words and sentences, they allow for the comparison of diverse texts automatically and objectively to assess the difficulty that readers may find in reading them. From the point of view of the writer, a readability formula allows one to better match readers and texts. Many readability formulae have been proposed for English [5], but only a few have been proposed for a very small number of other languages [9].

In response to the need to provide a readability formula applicable to any alphabetical language and the interest to compare the readability of texts written in diverse languages, including translations, in Reference [10], we have proposed a universal readability index which includes, for the first time, an estimate of the short-term memory (STM) processing capacity of readers. This capacity seems to be linked to the response of readers’ STM to the partial stimuli contained in a sentence, singled out by interpunctions, a process described by the so-called word interval $I_P$, i.e., the number of words between two following interpunctions [11,12]. In fact, all other readability formulae neglect the empirical connection found between readers’ STM processing capacity (described by Miller’s $7\pm 2$ law [13]) and the word interval $I_P$, which appears, at least empirically, justified and natural [10,11,12,14,15,16].

The possibility of comparing the readability of texts written in any alphabetical language, including ancient languages such as Greek and Latin, can be very useful in cognitive psychology, theory of communication, information theory, phonics and linguistics. Before Reference [10], however, scholars had never considered $I_p$, but the scatterplots of $I_p$ versus any readability index show that texts sharing the same readability index can have very diverse values of $I_p$ [11]. Now, it is unlikely that $I_P$ has no impact on reading difficulty; therefore, by introducing $I_P$ in the mathematical definition of a readability index, the readability index is better “fine-tuned” to readers and reveals their STM processing capacity.

In Reference [10], the global readability index $G$ that was developed from Italian [12] was transformed into the universal readability index $G_U$ after showing that the popular Flesch’s Reading Ease Index [1] and the Automated Readability Index [2], largely used in assessing the readability of English texts, are connected to $G$.

As the title of this article claims, our purpose is to assess whether the translation of an ancient text written in Greek—namely, in our exercise, the Gospel according to Matthew—into Latin and 35 modern languages may reveal similarities or differences in the reading ability required to readers for understanding it across time and translation. The mathematical parameters we use for this study are the deep-language parameters recalled in Section 2 and the universal readability index recalled in Section 3. We have studied Matthew’s Gospel because of its great heritage value and its multiple translations [14].

After this introductory section, Section 2 deals with Matthew’s Gospel translations in Latin and in 35 modern languages, together with their representation in a vector plane; Section 3 deals with a universal readability index in translated texts; Section 4 deals with many diverse translations of Matthew within the same language (English and Spanish); finally, Section 5 summarizes some final remarks and proposes further developments.

2. Matthew’s Gospel Translations and the Vector Plane of Deep-Language Parameters

The defined deep-language parameters $C_P$ (number of characters per word), $P_F$ (number of words per sentence), $I_P$ (word interval, number of words per interpunctions) and $M_F$ (number of interpunctions per sentence) [11] are listed in

Table 1. Average values of $C_P$ (characters per word), $P_F$ (words per sentence), $I_P$ (words per interpunction), $M_F$ (interpunctions, or number of $I_P$, per sentence), $G_U$ (universal readability index, recalled and calculated in Section 3) in Matthew in the indicated languages and listed according to their belonging to a language family. The source of these texts is reported in Reference [14].

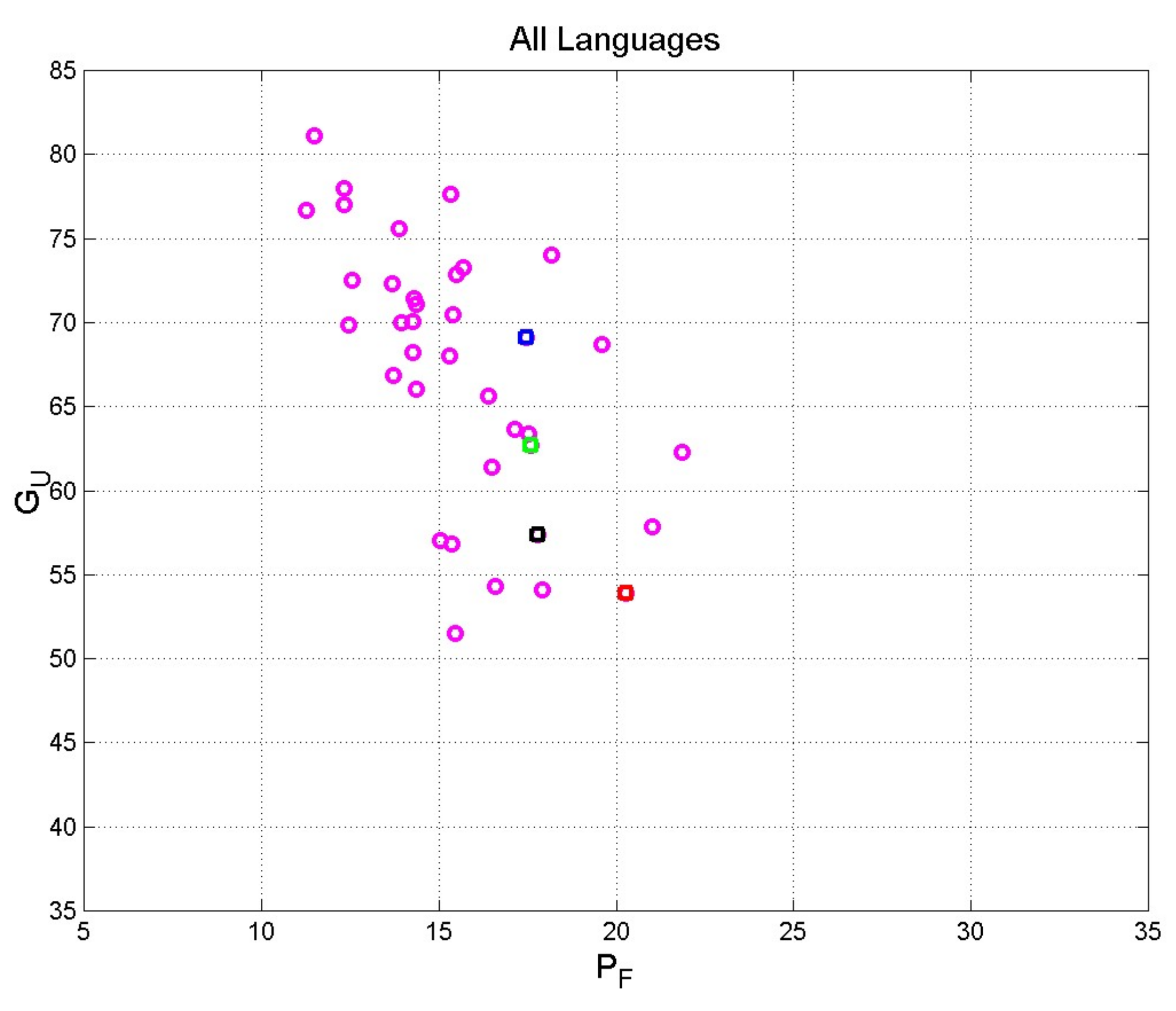
Language	Language Family	${\mathit{C}}_{\mathit{p}}$	${\mathit{P}}_{\mathit{F}}$	${\mathit{I}}_{\mathit{P}}$	${\mathit{M}}_{\mathit{F}}$	${\mathit{G}}_{\mathit{U}}$
1. Greek	Hellenic	4.896	20.270	7.182	2.825	53.90
2. Latin	Italic	5.132	17.450	5.051	3.465	69.08
3. Esperanto	Constructed	4.468	19.586	4.798	4.083	68.72
4. French	Romance	4.170	17.917	7.468	2.404	54.13
5. Italian	“	4.281	17.534	5.982	2.931	63.41
6. Portuguese	“	4.445	14.302	5.292	2.709	71.41
7. Romanian	“	4.283	16.495	6.493	2.542	61.42
8. Spanish	“	4.246	17.605	6.091	2.903	62.68
9. Danish	Germanic	4.123	14.266	5.838	2.449	68.19
10. English	“	4.031	17.774	6.947	2.578	57.39
11. Finnish	“	5.844	15.509	4.784	3.248	72.83
12. German	“	4.646	16.403	5.805	2.830	65.65
13. Icelandic	“	4.381	14.363	5.331	2.706	71.09
14. Norwegian	“	4.073	15.377	7.474	2.062	56.86
15. Swedish	“	4.202	15.045	7.513	2.012	57.05
16. Bulgarian	Balto-Slavic	4.375	14.284	5.522	2.590	70.06
17. Czech	“	4.519	12.326	4.755	2.605	78.00
18. Croatian	“	4.379	13.674	5.307	2.585	72.29
19. Polish	“	5.088	11.486	4.531	2.536	81.12
20. Russian	“	4.665	18.185	4.107	4.426	74.05
21. Serbian	“	4.196	13.943	5.614	2.484	70.02
22. Slovak	“	4.635	12.330	4.912	2.512	77.05
23. Ukrainian	“	4.590	13.891	4.696	2.960	75.61
24. Estonian	Uralic	4.847	15.411	5.199	2.969	70.46
25. Hungarian	“	5.287	15.347	4.013	3.832	77.66
26. Albanian	Albanian	4.032	21.013	6.434	3.287	57.86
27. Armenian	Armenian	4.487	15.316	5.625	2.726	68.03
28. Welsh	Celtic	4.071	21.863	5.603	3.911	62.29
29. Basque	Isolate	4.671	15.702	4.672	3.365	73.26
30. Hebrew	Semitic	4.125	11.261	5.359	2.103	76.68
31. Cebuano	Austronesian	4.695	15.464	8.351	1.862	51.48
32. Tagalog	“	4.779	16.584	7.664	2.168	54.30
33. Chichewa	Niger-Congo	6.084	12.464	6.067	2.071	69.86
34. Luganda	“	6.236	12.543	5.599	2.254	72.51
35. Somali	Afro-Asiatic	5.308	17.137	6.003	2.872	63.68
36. Haitian	French Creole	3.343	14.351	6.181	2.326	66.01
37. Nahuatl	Uto-Aztecan	6.699	13.725	6.197	2.228	66.87

alongside their average values in the original Greek Matthew and its translation into Latin and 35 modern languages [14].

Notice that verses 1.1 to 1.17 (genealogy) have been deleted every time for not biasing the statistics of $P_F$, $I_P$ and $M_F$ [14,16,17], as with all titles, notes and other characters not belonging to the pure text. This work was done manually with WinWord.

Similar to in References [14,15,16,17], the 28 chapters of Matthew were statistically weighted with the fraction of total words. For example, the original Greek Matthew contains $18,121$ total words; therefore, each sample does not weigh $1/128=0.0078$ but the number of its words divided by the total words: Chapter 5, for example, is made of $824$ words; therefore, its weight is $824/18,121=0.0455$. This choice is mandatory to avoid a short chapter (or, in general, a short text) affecting the statistical results as though it were a long one.

The averages of the four deep-language parameters can be used to represent each text graphically in the first Cartesian quadrant [11], thereby allowing a first assessment of whether texts are mathematically similar or “close” according to these parameters.

Let us consider the following six vectors of the indicated components, made of the average values of Table 1$,$ $\overrightarrow{R_1}=(C_P,P_F$), $\overrightarrow{R_2}=(M_F,P_F$), $\overrightarrow{R_3}=(I_P,P_F$), $\overrightarrow{R_4}=(C_P,M_F$), $\overrightarrow{R_5}=(I_P,M_F$), $\overrightarrow{R_6}=(I_P,C_P$), and their resulting ending point:

$$\overrightarrow{R}={{\displaystyle \sum }}_{k=1}^6\overrightarrow{R_k}$$

(1)

Figure 1 shows the ending point of vector (1) of the original Greek text and its translations. We notice a very large spread, as discussed in Reference [14], because most translations are not verbatim, although they all maintain the conventional division in chapters and verses of the Greek text. The spread is so large to be almost identical to that shown by seven centuries of Italian literature [11]. In other words, the texts of Table 1, mathematically, could describe an entire culture’s literature, not a single text.

For two texts to be mathematically similar, the vicinity in this plane is only a necessary condition. Because based on averages only, the “vicinity” of two texts should be further studied and assessed with Communication Theory involving the “sentences channel”, the “interpunctions channel” and the “likeness index”, as shown in [12,14,15,16].

After showing this large spread, let us recall and apply the concept of a universal readability index proposed in Reference [10] to Matthew’s translations.

3. Universal Readability Index in Translations

As shown in Reference [10], the universal readability index is given by the following formula:

$$G_U=G-6\left(I_P-6\right)$$

(2)

with $G$:

$$G=89-10k{C}_P+300/P_F$$

(3)

(4)

The symbol $<>$ indicates average values, as with those reported in Table 1; $C_{P,ITA}$ refers to Italian. Notice that since, in the following, we calculate Equation (4) according to average values, hence .281 for all languages.

The rationale for this latter choice is that $C_P$ is a parameter typical of a language which, if not scaled before calculating Equation (2), would bias any readability index without really quantifying the change in reading difficulty experimented by readers used to reading, in their language, shorter or longer words than those found in Italian. This scaling, therefore, avoids changing $G$ and $G_{U }$ for the only reason that a language has, on average, words shorter or longer than their Italian counterparts. In any case, as shown in Reference [11], $C_p$ affects readability much less than $P_F$.

Figure 2 shows the scatterplot of $I_P$ versus $P_F$ concerning the translations listed in Table 1. Since $G$ is mostly affected by $P_F$, the rationale for introducing $I_P$ in Equation (2) becomes clear [10,11]. For example, if $P_F\approx 15$, $I_P$ can range from 4 to 8.5, practically by Miller’s range of $7\pm 2$.

In conclusion, a readability formula that does not consider $I_p$ assumes, unrealistically, that a text with a given readability index is readable, with the same effort, both by readers who display powerful STM processing capacity (large $I_p$) and by readers who do not (small $I_p$).

Equation (2) sets $G_U=G$ for $I_P=6$—a center value for texts according to the equivalence between $I_P$ and Miller’s $7\pm 2$ law, see [18,19,20,21,22,23,24,25,26,27]—$G_U<G$ for $I_P>6$ and $G_U>G$ for $I_P<6$. In other words, if a text has a small word interval $I_P$ (therefore matched to readers gifted with average-to-weak STM processing capacity), then it should be read more easily than a text with the same $G$ but larger $I_P$ (matched to readers gifted with an average-to-powerful STM processing capacity). These changes quantify and introduce important aspects of readers’ STM; therefore, $G_U$ should better “measure” relative reading difficulties, which are very likely linked to readers’ schooling.

In fact, $G_U$ can be related to the number of years of school attended in Italy’s school system [10,11]—assumed as a reference school system for any language if $G_U$ is adopted as a universal readability index—as shown in Figure 3. From it, we notice that the larger $G_U$, the more readable the text for a given number of school years. The continuous lines divide the quadrant into areas of the same reading performance, such as “almost unintelligible”, “very difficult”, etc. For example, the area labelled “easy” indicates all combinations of values of $G_U$ and school years required to declare a text “easy” to read. In all cases, as readers’ schooling increases, they can read more difficult texts as far as readability is concerned.

The rightmost column of Table 1 reports $G_U$ calculated with the average values of $P_F$ and $I_P$ listed there.

Table 2. Average values and range (minimum–maximum) of $P_F$ (words per sentence), $I_P$ (words per interpunction) and $G_U$ (universal readability index) found in the texts listed in Table 1.

	${\mathit{P}}_{\mathit{F}}$	${\mathit{I}}_{\mathit{P}}$	${\mathit{G}}_{\mathit{U}}$
Minimum	$11.26$ Hebrew	$4.01$ Hungarian (Short STM capacity)	$51.48$ Cebuano (Least readable)
Average	$15.63$	$5.80$	$67.18$
Maximum	$21.86$ Welsh	$8.35$ Cebuano (Long STM capacity)	$81.12$ Polish (Most readable)

reports the overall average values and ranges of $P_F$, $I_P$ and $G_U$ calculated from Table 1. We can notice a large range for each parameter. In other words, if there were a reader who could understand all languages equally well, he/she would experiment with quite diverse reading difficulties, not to mention he/she would read texts which would appear diverse, with diverse lengths of sentences and diverse distribution of interpunctions, although they all convey the same story.

For example, the Cebuano version (least readable) requires at least 10 years of schooling to be considered “easy” to read (Figure 3), while the Polish version (most readable) requires less than 5.

Figure 4 shows the scatterplot of $G_U$ versus $P_F$ and Figure 5 shows the scatterplot of $G_U$ versus $I_P$. Figure 4 clearly shows, in agreement with Equation (2), that $G_U$ decreases as $P_F$ increases. Figure 5 enhances the linear decrease of $G_U$ as $I_P$ increases. In all cases, notice that translations show values that are quite diverse compared to that of the original Greek text.

The large spread found in translating Matthew’s Gospel into diverse languages is also found in translating it into the same language by diverse teams of translators—as is the case for the multiple versions in English and Spanish—discussed in the next section.

4. Many Diverse Translations within the Same Language

It may be curious to notice that within the same language, there are many diverse translations of the Bible. In most cases, the reason for this proliferation is not that the existing translation has become obsolete because of particularly convoluted sentences and/or old words no longer clearly understood. The reason, as it becomes clear in this section, is that each translation seems to be addressed to diverse contemporary readers. The most striking cases are English and Spanish, for which there are tens of translations, some of which we have studied.

Table 3. Average values of $C_P$ (characters per word), $P_F$ (words per sentence), $I_P$ (words per interpunction), $M_F$ (interpunctions, or number of $I_P$, per sentence) and $G_U$ (universal readability index) in Matthew in the indicated English translations, updated to the indicated year. Source: https://www.biblegateway.com/versions/ (last access, 15 April 2023).

Translation	${\mathit{C}}_{\mathit{p}}$	${\mathit{P}}_{\mathit{F}}$	${\mathit{I}}_{\mathit{P}}$	${\mathit{M}}_{\mathit{F}}$	${\mathit{G}}_{\mathit{U}}$
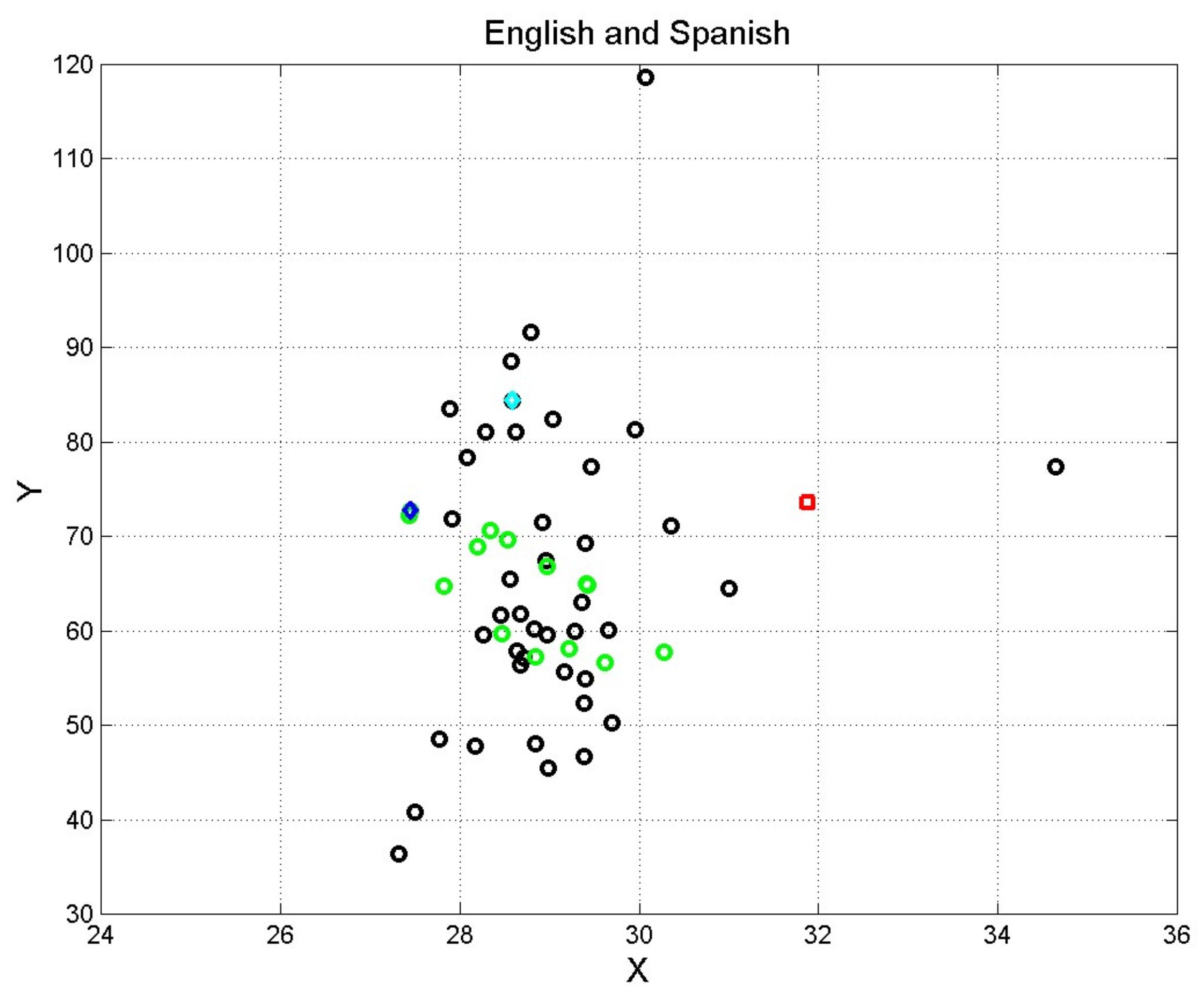
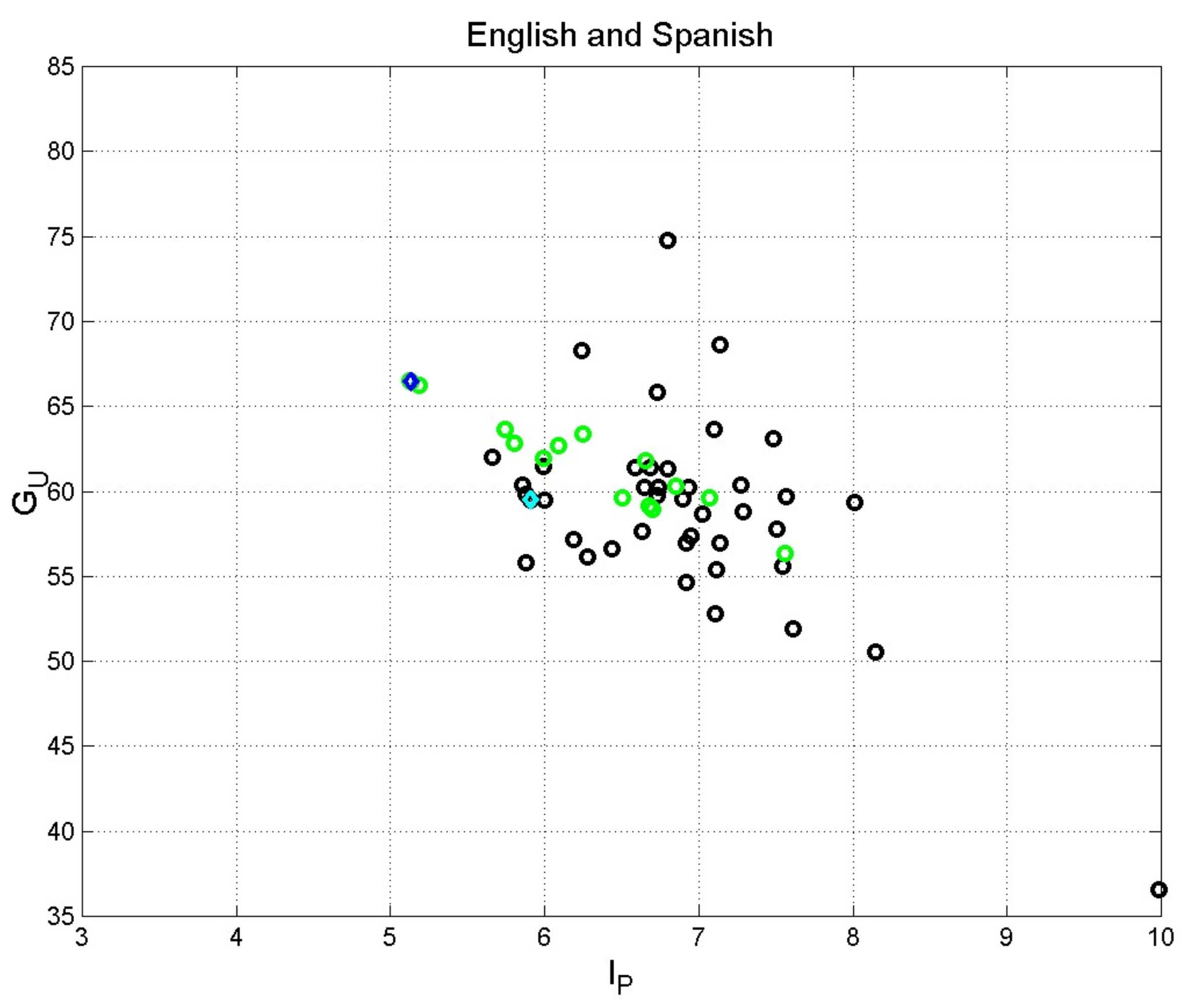
New American Bible (Vatican, 2002)	4.03	17.78	6.96	2.58	57.39
King James (1611)	4.27	23.51	5.91	3.98	59.51
21st Century King James (1994)	4.23	19.66	6.63	2.96	57.64
American Standard Version (1881)	4.29	22.51	6.00	3.75	59.51
Amplified Bible (1987)	4.05	25.73	6.28	4.10	56.18
Amplified Bible, Classic Edition (1987)	4.06	24.80	6.19	4.01	57.17
Blue Red & Gold Bible (2012)	4.25	22.50	5.85	3.84	60.41
Christian Standard Bible (2017)	4.32	16.22	6.74	2.40	60.24
Common English Bible (2011)	4.32	13.78	7.27	1.90	60.35
Complete Jewish Bible (1998)	4.29	16.01	6.90	2.32	59.54
Contemporary English Version (1995)	4.28	13.08	7.57	1.73	59.72
Darby Translation (1890)	4.20	22.97	6.44	3.57	56.62
Disciples’ Literal New Testament (2011)	4.29	16.70	6.65	2.51	60.26
Douay-Rheims 1899 American Edition	4.21	19.75	5.99	3.30	61.45
Easy-to-Read Version (2006)	4.16	11.64	7.45	1.56	63.09
Evangelical Heritage Version (2019)	4.22	15.27	6.94	2.20	60.22
English Standard Version (2016)	4.15	18.41	6.91	2.66	57.00
English Standard Version Anglicised (1971)	4.17	18.93	7.11	2.66	55.36
1599 Geneva Bible	4.31	21.70	5.66	3.83	62.04
God’s Word Translation (2020)	4.29	12.46	6.73	1.85	65.86
Good News Translation (1992)	4.15	16.10	7.54	2.13	55.58
Holman Christian Standard Bible (2009)	4.32	15.53	6.68	2.32	61.41
International Standard Version (2014)	4.31	16.13	7.02	2.30	58.66
J.B. Phillips New Testament (1972)	4.19	17.38	8.15	2.13	50.56
Jubilee Bible 2000	4.19	22.60	7.10	3.18	52.84
Legacy Standard Bible (2021)	4.17	21.43	6.92	3.10	54.67
Lexham English Bible (2012)	4.19	19.45	7.61	2.55	51.93
Living Bible (1971)	4.29	15.05	6.80	2.21	61.32
The Message (2018)	4.42	12.74	6.24	2.04	68.30
Modern English Version (2014)	4.17	16.68	6.73	2.48	59.79
Names of God Bible (2011)	4.30	12.47	7.10	1.76	63.64
New American Standard Bible 1995	4.19	21.05	9.98	2.11	36.54
New Catholic Bible (2019)	4.23	17.04	7.14	2.39	56.96
New Century Version (2005)	4.15	14.53	7.51	1.94	57.81
New International Reader’s Version (2014)	4.13	8.99	6.80	1.32	74.75
New Life Version (2003)	3.96	11.89	8.01	1.49	59.37
New Living Translation (2015)	4.19	14.76	7.29	2.03	58.80
Tree of Life Version (2015)	4.22	16.03	6.58	2.43	61.41
Worldwide English New Testament (1998)	3.93	10.25	7.14	1.44	68.63
Wycliffe Bible (2001)	4.06	23.25	5.88	3.95	59.82
Young’s Literal Translation (1898)	4.19	33.75	5.88	5.74	55.80

lists 40 English translations and their parameters, including the classical King James (1611),

Table 4. Average values of $C_P$ (characters per word), $P_F$ (words per sentence), $I_P$ (words per interpunction), $M_F$ (interpunctions, or number of $I_P$, per sentence), $G_U$ (universal readability index) in Matthew in the indicated English translations, updated to the indicated year. Source: https://www.biblegateway.com/versions/ (last access, 15 April 2023).

Translation	${\mathit{C}}_{\mathit{p}}$	${\mathit{P}}_{\mathit{F}}$	${\mathit{I}}_{\mathit{P}}$	${\mathit{M}}_{\mathit{F}}$	${\mathit{G}}_{\mathit{U}}$
La Biblia (Vatican, traducción argentina, 1990)	4.25	17.615	6.09	2.90	62.68
La Biblia de las Américas (1997)	4.47	19.37	5.80	3.34	62.85
Biblia del Jubileo (2020)	4.42	19.80	5.19	3.82	66.22
Dios Habla Hoy (1996)	4.39	18.23	6.50	2.80	59.64
Nueva Biblia de las Américas (2005)	4.45	19.09	5.99	3.19	61.94
Nueva Traducción Viviente (2010)	4.45	15.10	7.07	2.14	59.62
Nueva Versión Internacional (Castilian, 2015)	4.41	15.33	6.65	2.30	61.84
Palabra de Dios para todos (2015)	4.38	15.37	7.56	2.03	56.37
La Palabra (España, 2010)	4.48	17.63	6.68	2.64	59.13
La Palabra (Hispanoamérica, 2010)	4.46	17.69	6.70	2.64	58.97
Reina Valera 1995	4.48	18.87	5.74	3.29	63.63
Traducción en lenguaje actual (2000)	4.41	15.58	6.85	2.27	60.33
Spanish Blue Red and Gold Letter Edition (2012)	4.44	19.94	5.12	3.89	66.51
Reina Valera Antigua (1602)	4.44	19.93	5.13	3.88	66.46
Reina Valera Actualizada (2015)	4.46	16.09	6.25	2.58	63.35

lists 15 Spanish translations, including the classical Reina Valera Antigua. Both sets are freely available, along with other translations, on the website https://www.biblegateway.com/versions/ (accessed on 15 April 2023) The deep-language parameters and the universal readability indices calculated for each translation are extremely variable, especially in English.

Figure 6 shows the scatterplot of $I_P$ versus $P_F$ concerning the English (black circles, Table 3) and Spanish (green circles, Table 4) translations. Again, we notice $I_P$ can vary in the full Miller’s range $7\pm 2$ and the necessity and usefulness of introducing $I_P$ in readability formulae.

Figure 7 shows the ending point of vector (1) of the original Greek text compared with the English and Spanish translations. The spread is similar to that found in Figure 1 concerning diverse languages.

Table 5. Average values and range (minimum–maximum) of $P_F$ (words per sentence), $I_P$ (words per interpunction) and $G_U$ (universal readability index) found in the English translations listed in Table 3.

	${\mathit{P}}_{\mathit{F}}$	${\mathit{I}}_{\mathit{P}}$	${\mathit{G}}_{\mathit{U}}$
Minimum	$8.99$ New International Reader’s Version	$5.66$ 1599 Geneva Bible (Short STM capacity)	$36.54$ New American Standard Bible (Least readable)
Average	$17.82$	$6.89$	$58.98$
Maximum	$33.75$ Young’s Literal Translation	$9.98$ New American Standard Bible (Long STM capacity)	$74.75$ New International Reader’s Version (Most readable)

and

Table 6. Average values and range (minimum–maximum) of $P_F$ (words per sentence), $I_P$ (words per interpunction) and $G_U$ (universal readability index) found in the Spanish translations listed in Table 5.

	${\mathit{P}}_{\mathit{F}}$	${\mathit{I}}_{\mathit{P}}$	${\mathit{G}}_{\mathit{U}}$
Minimum	$15.10$ Nueva Traducción Viviente	$5.12$ Spanish Blue Red and Gold Letter Edition (Short STM capacity)	$56.37$ Palabra de Dios para todos (Least readable)
Average	$17.71$	$6.22$	$61.97$
Maximum	$19.94$ Spanish Blue Red and Gold Letter Edition	$7.56$ Palabra de Dios para todos (Long STM capacity)	$66.51$ Spanish Blue Red and Gold Letter Edition (Most readable)

report the main statistics for these two sets. As noticed, the English translations are more varied than the Spanish ones, a find confirmed in Figure 8 and Figure 9 showing the scatterplot of $G_U$ versus $P_F$ and $G_U$ versus $I_P$.

From Table 5 and Figure 3, in English, the least readable version (New American Standard Bible) requires more than 13 years of schooling for “easy” reading; the most readable version (New International Reader’s Version) only requires 6 years. The historical King James’ version (1611) requires 8 years.

Similarly, in Spanish (Table 6 and Figure 3), the least readable version (Palabra de Dios para todos) requires 9 years of schooling for “easy” reading, while the most readable version (Spanish Blue Red and Gold Letter Edition) requires about 7. The historical Reina Valera Antigua (1602) requires 7 years of schooling.

In conclusion, multiple translations within the same languages are likely addressed to readers with very different STM processing capacities and schooling.

5. Conclusions

We have studied how the readability of a text can change in translation. To arrive at a sound conclusion, we have considered the translation of an ancient text written in Greek—the Gospel according to Matthew (very important for its heritage value)—into Latin and 35 modern languages. We have found that the deep-language parameters $C_P$, $P_F$, $I_P$, $M_F$ and a universal readability index $G_U$ of each translation are so diverse from language to language, and even within a given language for which there are many versions of Matthew—such as in English and in Spanish—that the resulting texts mathematically seem to be diverse texts. All the analyses performed confirm this extremely marked scattering, which does not depend on the year of translation.

What is really striking is the large range of the readability index, which does not depend on the year of translation. This index “measures” how difficult a text is to read and how many years of schooling it requires for “easy” reading. The several tens of versions of Matthew’s Gospel studied here appear to address very diverse audiences. If a reader could understand all the 37 languages considered well, he/she, on the one hand, would be surely guided by the traditional division in chapters and verses of Matthew common to all versions, but on the other hand, would also have the impression of reading texts written by diverse authors, although all of them tell the same story.

Future work should study how readability changes in translations of modern novels, which tend to be more verbatim than that of Matthew and, in general, of the New Testament.