Machine-Learning Classification Models to Predict Liver Cancer with Explainable AI to Discover Associated Genes
Abstract
1. Introduction
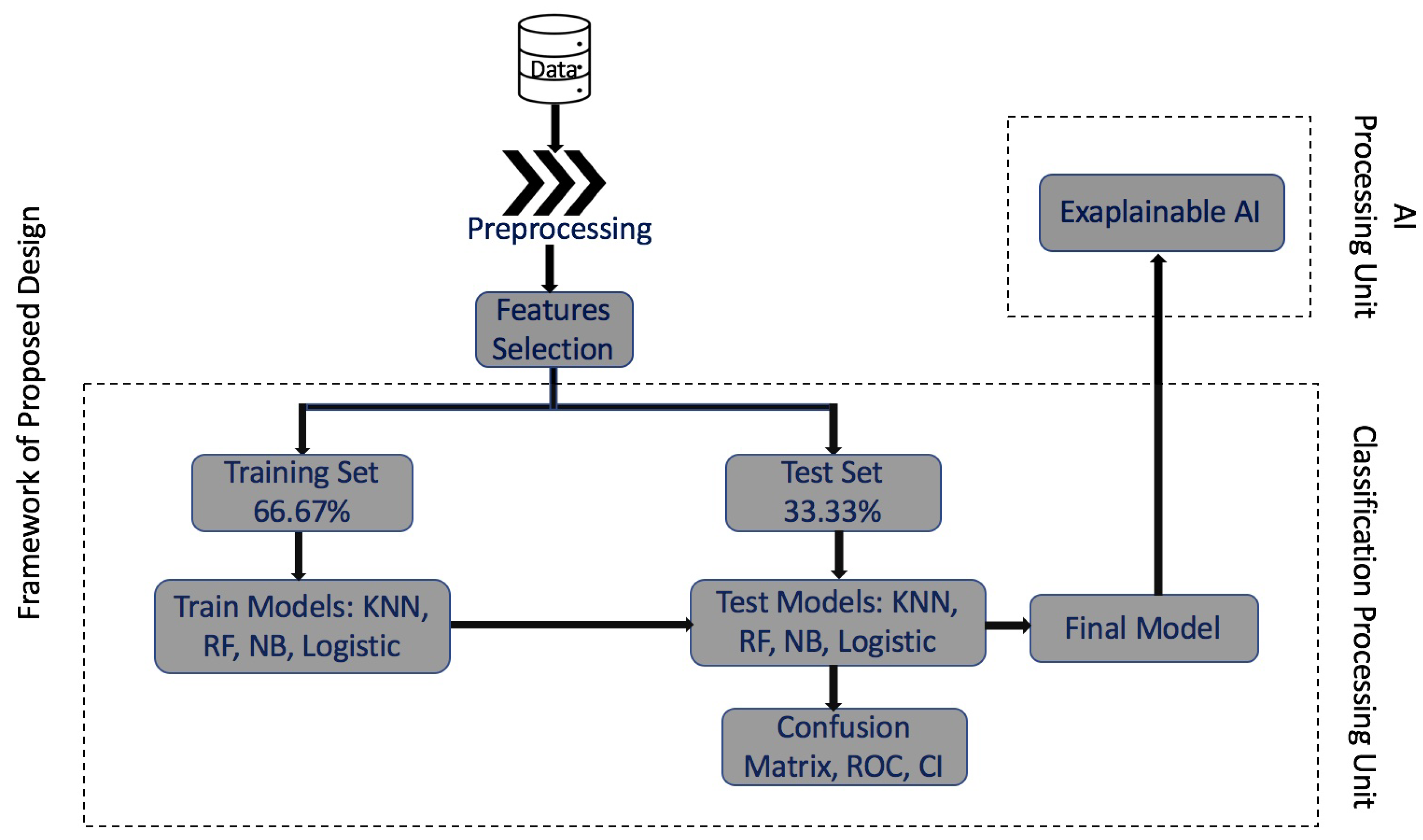
2. Methodology and Framework
2.1. Samples from Gene Data
2.2. Mathematical Framework Machine-Learning Approaches
2.3. Variable Selection for Classification, Pathway Analysis, and Statistical Analysis
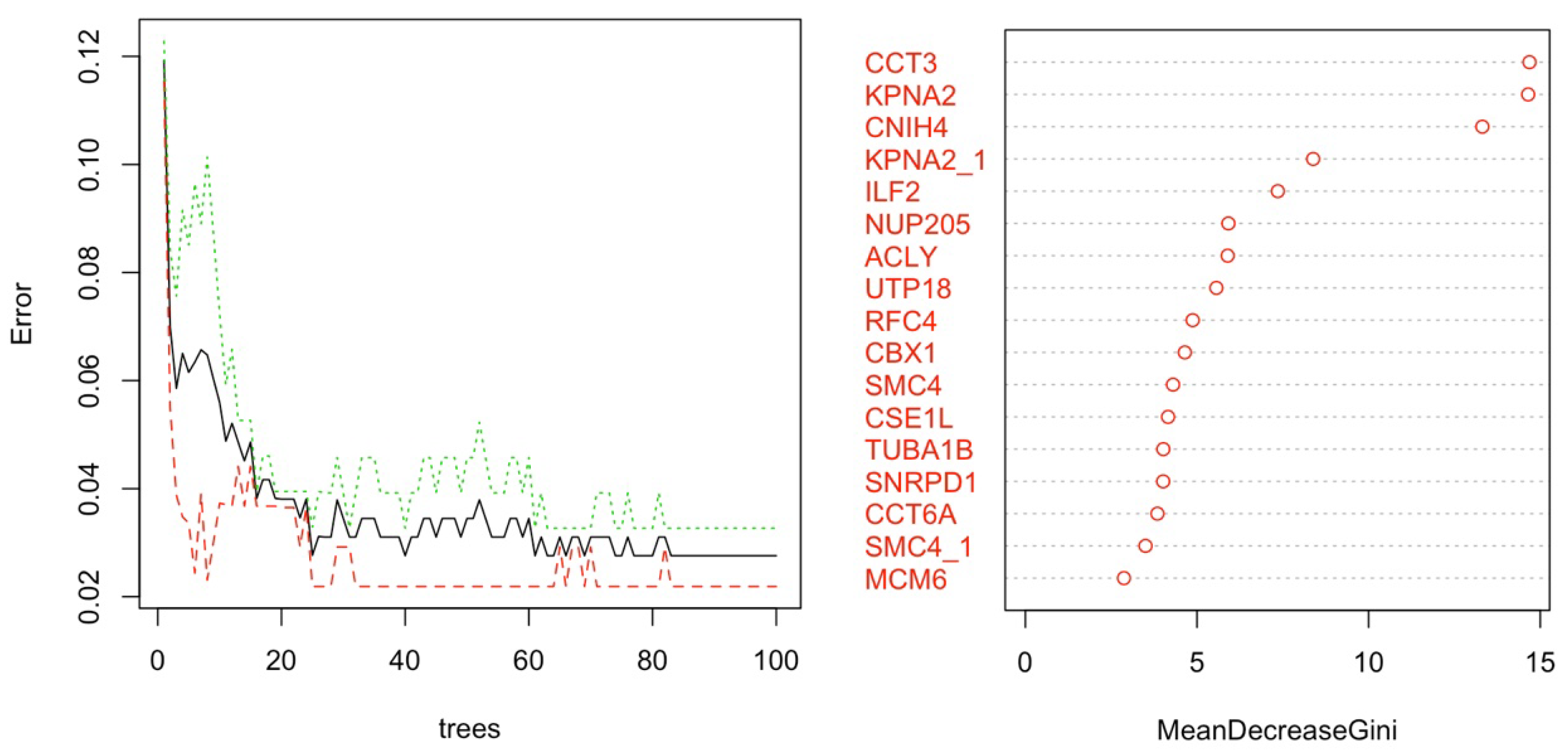
2.3.1. Dimension Reduction and HCC Gene Mining
2.3.2. Classification of Gene Expression Data
Naïve Bayes Classifier for HCC Classification:
Logistic Regression Classifier for HCC Classification:
k-NN Classifier for HCC Classification:
Random Forest Classifier for HCC Classification:
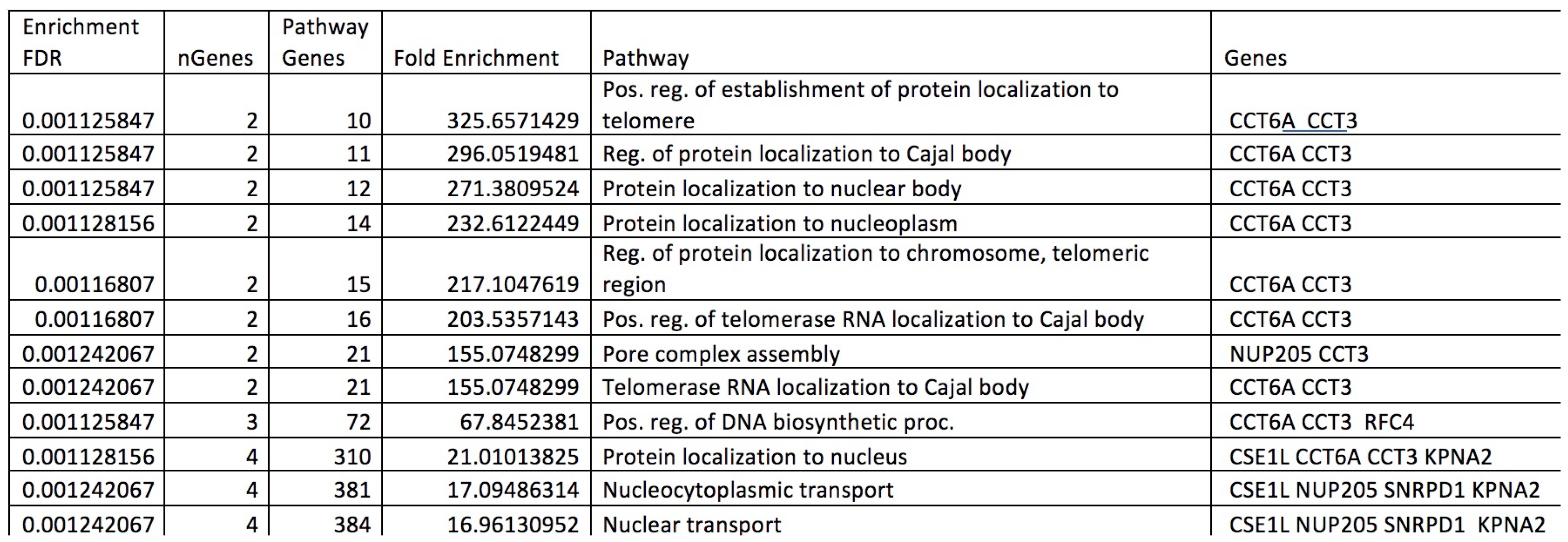
2.4. Pathway Analysis
2.5. Statistical Hypothesis Test on Accuracy
2.6. Model Accuracy and Analysis of the Receiver Operating Characteristic Curve
2.7. Explainable AI among Best Predictive Model Applied to Gene Expression Data
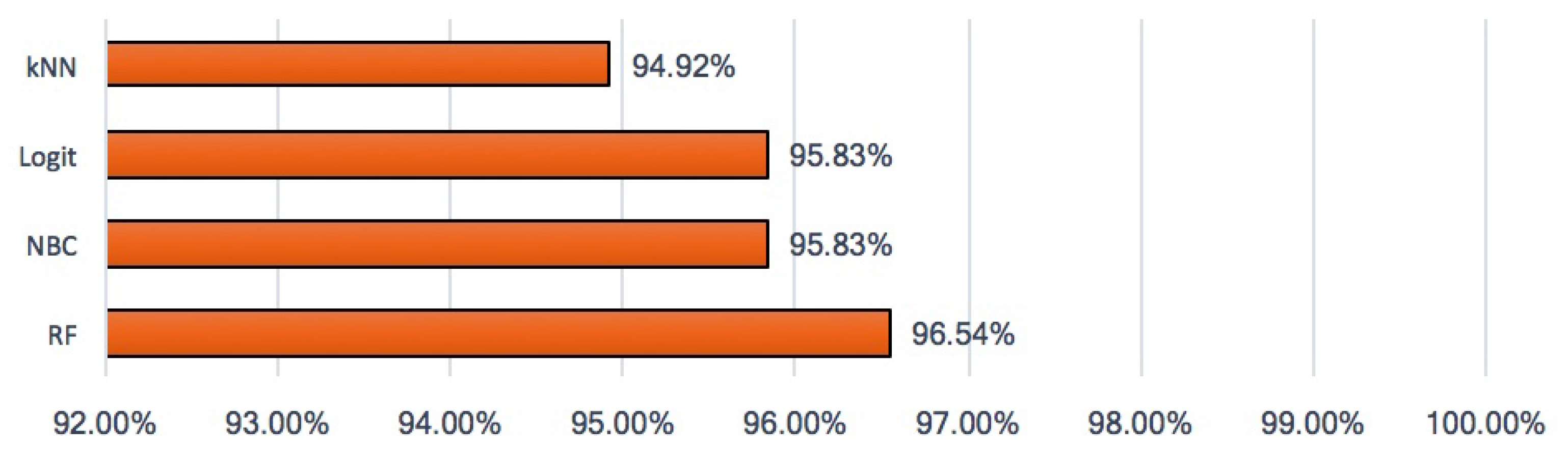
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A. Used Python and R Packages
Appendix A.1
Appendix A.2
Appendix B. Hyper-Parameters in the ML Models
- Method: RF
- Method: NBC
- Method: k-NN
| Algorithm A1: The algorithm for the proposed framework. |
Input: HCC dataset. Output: Final trained and tested model. Step 1: Initialize the dataset. - Load the HCC dataset. Step 2: Preprocess the full dataset. - Remove missing data and duplicates and normalize the dataset. Step 3: Feature selection of the HCC dataset. - Perform PCA to select the top 100 genes. Step 4: Divide the dataset into two sets: i. Training Set (66.67% of the dataset). ii. Test Set (33.37% of the dataset). - Randomly split the dataset into training and test sets. Step 5: Train the models with the Training Set. - Train multiple machine-learning models, such as random forest, SVM, logistic regression, and NBC using the 16 top genes by variable importance ranking. Step 6: Test the trained models with the Test Set. - Evaluate the performance of the trained models on the test set. Step 7: Generate the confusion matrix and ROC analysis. - Calculate the confusion matrix, ROC curve, and confidence interval. Step 8: Generate the final trained and tested model. - Select the best-performing model based on evaluation metrics. Step 9: Send the final model to Explainable AI. - Use the LIME algorithm to generate the top 16 genes that contribute to the final model’s decision. |
Appendix C. HCC Gene Mining
| AFFYMETRIX 3PRIME IVT ID | Name | Species | Column ID |
| 210987_x_at | tropomyosin 1 (TPM1) | Homo sapiens | V10434 |
| 210986_s_at | tropomyosin 1 (TPM1) | Homo sapiens | V10433 |
| 220917_s_at | WD repeat domain 19 (WDR19) | Homo sapiens | V20281 |
| 221223_x_at | cytokine-inducible SH2 containing protein (CISH) | Homo sapiens | V20586 |
| 215605_at | nuclear receptor coactivator 2 (NCOA2) | Homo sapiens | V14978 |
| 204718_at | EPH receptor B6 (EPHB6) | Homo sapiens | V4245 |
| 219828_at | RAB, member RAS oncogene family like 6 (RABL6) | Homo sapiens | V19192 |
| 211072_x_at | tubulin alpha 1b (TUBA1B) | Homo sapiens | V10516 |
| 204690_at | syntaxin 8 (STX8) | Homo sapiens | V4217 |
| 201327_s_at | chaperonin containing TCP1 subunit 6A (CCT6A) | Homo sapiens | V855 |
| 200750_s_at | RAN, member RAS oncogene family (RAN) | Homo sapiens | V278 |
| 218421_at | ceramide kinase (CERK) | Homo sapiens | V17786 |
| 213455_at | family with sequence similarity 114 member A1 (FAM114A1) | Homo sapiens | V12836 |
| 202146_at | interferon related developmental regulator 1 (IFRD1) | Homo sapiens | V1674 |
| 221351_at | 5-hydroxytryptamine receptor 1A (HTR1A) | Homo sapiens | V20714 |
| 200052_s_at | interleukin enhancer binding factor 2 (ILF2) | Homo sapiens | V73 |
| 214037_s_at | coiled-coil domain containing 22 (CCDC22) | Homo sapiens | V13416 |
| 203721_s_at | UTP18 small subunit processome component (UTP18) | Homo sapiens | V3248. |
| 221760_at | mannosidase alpha class 1A member 1 (MAN1A1) | Homo sapiens | V21120 |
| 209030_s_at | cell adhesion molecule 1 (CADM1) | Homo sapiens | V8524 |
| 212168_at | RNA-binding motif protein 12 (RBM12) | Homo sapiens | V11554 |
| 203477_at | collagen type XV alpha 1 chain (COL15A1) | Homo sapiens | V3004 |
| 201112_s_at | chromosome segregation 1 like (CSE1L) | Homo sapiens | V640 |
| 212519_at | ubiquitin conjugating enzyme E2 E1 (UBE2E1) | Homo sapiens | V11904 |
| 217889_s_at | cytochrome b reductase 1 (CYBRD1) | Homo sapiens | V17254 |
| 202291_s_at | matrix Gla protein (MGP) | Homo sapiens | V1819 |
| 221664_s_at | F11 receptor (F11R) | Homo sapiens | V21025 |
| 216867_s_at | platelet derived growth factor subunit A (PDGFA) | Homo sapiens | V16237 |
| 205463_s_at | platelet derived growth factor subunit A (PDGFA) | Homo sapiens | V4990 |
| 200612_s_at | adaptor related protein complex 2 subunit beta 1 (AP2B1) | Homo sapiens | V140 |
| 200910_at | chaperonin containing TCP1 subunit 3 (CCT3) | Homo sapiens | V438 |
| 210385_s_at | endoplasmic reticulum aminopeptidase 1 (ERAP1) | Homo sapiens | V9863 |
| 218010_x_at | pancreatic progenitor cell differentiation and proliferation factor (PPDPF) | Homo sapiens | V17375 |
| 218728_s_at | cornichon family AMPA receptor auxiliary protein 4 (CNIH4) | Homo sapiens | V18092 |
| 209071_s_at | regulator of G protein signaling 5 (RGS5) | Homo sapiens | V8565 |
| 218353_at | regulator of G protein signaling 5 (RGS5) | Homo sapiens | V17718 |
| 202011_at | tight junction protein 1 (TJP1) | Homo sapiens | V1539 |
| 201873_s_at | ATP-binding cassette subfamily E member 1 (ABCE1) | Homo sapiens | V1401 |
| 209373_at | mal, T cell differentiation protein like (MALL) | Homo sapiens | V8866 |
| 202469_s_at | cleavage and polyadenylation specific factor 6 (CPSF6) | Homo sapiens | V1997 |
| 212473_s_at | microtubule associated monooxygenase, calponin and LIM domain containing 2 (MICAL2) | Homo sapiens | V11858 |
| 218622_at | nucleoporin 37 (NUP37) | Homo sapiens | V17987 |
| 201128_s_at | ATP citrate lyase (ACLY) | Homo sapiens | V656 |
| 201909_at | ribosomal protein S4 Y-linked 1 (RPS4Y1) | Homo sapiens | V1437 |
| 55872_at | uridine-cytidine kinase 1 like 1 (UCKL1) | Homo sapiens | V22108 |
| 204020_at | purine rich element binding protein A (PURA) | Homo sapiens | V3547 |
| 202565_s_at | supervillin (SVIL) | Homo sapiens | V2093 |
| 208683_at | calpain 2 (CAPN2) | Homo sapiens | V8178 |
| 211974_x_at | recombination signal binding protein for immunoglobulin kappa J region (RBPJ) | Homo sapiens | V11361 |
| 203021_at | secretory leukocyte peptidase inhibitor (SLPI) | Homo sapiens | V2550 |
| 213139_at | snail family transcriptional repressor 2 (SNAI2) | Homo sapiens | V12522 |
| 218531_at | transmembrane protein 134 (TMEM134) | Homo sapiens | V17896 |
| 201663_s_at | structural maintenance of chromosomes 4 (SMC4) | Homo sapiens | V1191 |
| 201664_at | structural maintenance of chromosomes 4 (SMC4) | Homo sapiens | V1192 |
| 211833_s_at | BCL2 associated X, apoptosis regulator (BAX) | Homo sapiens | V11229 |
| 201177_s_at | ubiquitin-like modifier activating enzyme 2 (UBA2) | Homo sapiens | V705 |
| 200985_s_at | CD59 molecule (CD59 blood group) (CD59) | Homo sapiens | V513 |
| 212463_at | CD59 molecule (CD59 blood group) (CD59) | Homo sapiens | V11848 |
| 213911_s_at | H2A.Z variant histone 1 (H2AZ1) | Homo sapiens | V13290 |
| 200853_at | H2A.Z variant histone 1 (H2AZ1) | Homo sapiens | V381 |
| 201518_at | chromobox 1 (CBX1) | Homo sapiens | V1046 |
| 202543_s_at | glia maturation factor beta (GMFB) | Homo sapiens | V2071 |
| 204347_at | adenylate kinase 4 (AK4) | Homo sapiens | V3874 |
| 205968_at | potassium voltage-gated channel modifier subfamily S member 3 (KCNS3) | Homo sapiens | V5495 |
| 219215_s_at | solute carrier family 39 member 4 (SLC39A4) | Homo sapiens | V18579 |
| 201930_at | minichromosome maintenance complex component 6 (MCM6) | Homo sapiens | V1458 |
| 203041_s_at | lysosomal associated membrane protein 2 (LAMP2) | Homo sapiens | V2570 |
| 202597_at | interferon regulatory factor 6 (IRF6) | Homo sapiens | V2125 |
| 212766_s_at | interferon stimulated exonuclease gene 20 like 2 (ISG20L2) | Homo sapiens | V12151 |
| 217755_at | Jupiter microtubule associated homolog 1 (JPT1) | Homo sapiens | V17120 |
| 208789_at | caveolae associated protein 1 (CAVIN1) | Homo sapiens | V8284 |
| 205361_s_at | prefoldin subunit 4 (PFDN4) | Homo sapiens | V4888 |
| 200795_at | SPARC-like 1 (SPARCL1) | Homo sapiens | V323 |
| 201181_at | G protein subunit alpha i3 (GNAI3) | Homo sapiens | V709 |
| 212371_at | desumoylating isopeptidase 2 (DESI2) | Homo sapiens | V11756 |
| 203953_s_at | claudin 3 (CLDN3) | Homo sapiens | V3480 |
| 202790_at | claudin 7 (CLDN7) | Homo sapiens | V2318 |
| 204440_at | CD83 molecule (CD83) | Homo sapiens | V3967 |
| 221578_at | Ras association domain family member 4 (RASSF4) | Homo sapiens | V20940 |
| 204023_at | replication factor C subunit 4 (RFC4) | Homo sapiens | V3550 |
| 213882_at | TM2 domain containing 1 (TM2D1) | Homo sapiens | V13262 |
| 201200_at | cellular repressor of E1A stimulated genes 1 (CREG1) | Homo sapiens | V728 |
| 213506_at | F2R-like trypsin receptor 1 (F2RL1) | Homo sapiens | V12887 |
| 218418_s_at | KN motif and ankyrin repeat domains 2 (KANK2) | Homo sapiens | V17783 |
| 204106_at | testis associated actin remodelling kinase 1 (TESK1) | Homo sapiens | V3633 |
| 202690_s_at | small nuclear ribonucleoprotein D1 polypeptide (SNRPD1) | Homo sapiens | V2218 |
| 208541_x_at | transcription factor A, mitochondrial (TFAM) | Homo sapiens | V8039 |
| 211754_s_at | solute carrier family 25 member 17 (SLC25A17) | Homo sapiens | V11154 |
| 207996_s_at | low density lipoprotein receptor class A domain containing 4 (LDLRAD4) | Homo sapiens | V7507 |
| 213242_x_at | centrosomal protein 170B (CEP170B) | Homo sapiens | V12624 |
| 202072_at | heterogeneous nuclear ribonucleoprotein L (HNRNPL) | Homo sapiens | V1600 |
| 205542_at | STEAP family member 1 (STEAP1) | Homo sapiens | V5069. |
| 220264_s_at | G protein-coupled receptor 107 (GPR107) | Homo sapiens | V19628 |
| 209917_s_at | TP53 target 1 (TP53TG1) | Homo sapiens | V9403 |
| 210740_s_at | inositol-tetrakisphosphate 1-kinase (ITPK1) | Homo sapiens | V10201 |
| 212043_at | trans-golgi network protein 2 (TGOLN2) | Homo sapiens | V11429 |
| 212247_at | nucleoporin 205 (NUP205) | Homo sapiens | V11633 |
| 211762_s_at | karyopherin subunit alpha 2 (KPNA2) | Homo sapiens | V11161 |
| 201088_at | karyopherin subunit alpha 2 (KPNA2) | Homo sapiens | V616 |
| 222344_at | Information Unknown | V21703 |
Appendix D. Pathway Analysis



References
- El-Serag, H.B.; Kanwal, F. Epidemiology of hepatocellular carcinoma in the United States: Where are we? Where do we go? Hepatology 2014, 60, 1767. [Google Scholar] [CrossRef] [PubMed]
- Guan, X. Cancer metastases: Challenges and opportunities. Acta Pharm. Sin. B 2015, 5, 402–418. [Google Scholar] [CrossRef] [PubMed]
- Roessler, S.; Jia, H.L.; Budhu, A.; Forgues, M.; Ye, Q.H.; Lee, J.S.; Thorgeirsson, S.S.; Sun, Z.; Tang, Z.Y.; Qin, L.X.; et al. A unique metastasis gene signature enables prediction of tumor relapse in early-stage hepatocellular carcinoma patients. Cancer Res. 2010, 70, 10202–10212. [Google Scholar] [CrossRef] [PubMed]
- Roessler, S.; Long, E.L.; Budhu, A.; Chen, Y.; Zhao, X.; Ji, J.; Walker, R.; Jia, H.L.; Ye, Q.H.; Qin, L.X.; et al. Integrative genomic identification of genes on 8p associated with hepatocellular carcinoma progression and patient survival. Gastroenterology 2012, 142, 957–966. [Google Scholar] [CrossRef]
- Zhao, X.; Parpart, S.; Takai, A.; Roessler, S.; Budhu, A.; Yu, Z.; Blank, M.; Zhang, Y.E.; Jia, H.L.; Ye, Q.H.; et al. Integrative genomics identifies YY1AP1 as an oncogenic driver in EpCAM+ AFP+ hepatocellular carcinoma. Oncogene 2015, 34, 5095–5104. [Google Scholar] [CrossRef]
- Wang, Y.; Gao, B.; Tan, P.Y.; Handoko, Y.A.; Sekar, K.; Deivasigamani, A.; Seshachalam, V.P.; Ouyang, H.Y.; Shi, M.; Xie, C.; et al. Genome-wide CRISPR knockout screens identify NCAPG as an essential oncogene for hepatocellular carcinoma tumor growth. FASEB J. 2019, 33, 8759–8770. [Google Scholar] [CrossRef]
- Lu, Y.; Xu, W.; Ji, J.; Feng, D.; Sourbier, C.; Yang, Y.; Qu, J.; Zeng, Z.; Wang, C.; Chang, X.; et al. Alternative splicing of the cell fate determinant Numb in hepatocellular carcinoma. Hepatology 2015, 62, 1122–1131. [Google Scholar] [CrossRef]
- Chen, S.; Fang, H.; Li, J.; Shi, J.; Zhang, J.; Wen, P.; Wang, Z.; Yang, H.; Cao, S.; Zhang, H.; et al. Microarray analysis for expression profiles of lncRNAs and circRNAs in rat liver after brain-dead donor liver transplantation. BioMed Res. Int. 2019, 2019, 5604843. [Google Scholar] [CrossRef]
- Chen, S.L.; Zhu, Z.X.; Yang, X.; Liu, L.L.; He, Y.F.; Yang, M.M.; Guan, X.Y.; Wang, X.; Yun, J.P. Cleavage and polyadenylation specific factor 1 promotes tumor progression via alternative polyadenylation and splicing in hepatocellular carcinoma. Front. Cell Dev. Biol. 2021, 9, 616835. [Google Scholar] [CrossRef]
- Ashburner, M.; Ball, C.A.; Blake, J.A.; Botstein, D.; Butler, H.; Cherry, J.M.; Davis, A.P.; Dolinski, K.; Dwight, S.S.; Eppig, J.T.; et al. Gene ontology: Tool for the unification of biology. Nat. Genet. 2000, 25, 25–29. [Google Scholar] [CrossRef]
- García-Campos, M.A.; Espinal-Enríquez, J.; Hernández-Lemus, E. Pathway analysis: State of the art. Front. Physiol. 2015, 6, 383. [Google Scholar] [CrossRef]
- Folger, O.; Jerby, L.; Frezza, C.; Gottlieb, E.; Ruppin, E.; Shlomi, T. Predicting selective drug targets in cancer through metabolic networks. Mol. Syst. Biol. 2011, 7, 501. [Google Scholar] [CrossRef]
- Hansen, M.; Dubayah, R.; DeFries, R. Classification trees: An alternative to traditional land cover classifiers. Int. J. Remote Sens. 1996, 17, 1075–1081. [Google Scholar] [CrossRef]
- Huang, C.; Davis, L.; Townshend, J. An assessment of support vector machines for land cover classification. Int. J. Remote Sens. 2002, 23, 725–749. [Google Scholar] [CrossRef]
- Rogan, J.; Miller, J.A.; Stow, D.A.; Franklin, J.; Levien, L.M.; Fischer, C. Land-Cover Change Monitoring with Classification Trees Using Landsat TM and Ancillary Data. Photogramm. Eng. Remote. Sens. 2003, 69, 793–804. [Google Scholar] [CrossRef]
- Foody, G.M. Land cover classification by an artificial neural network with ancillary information. Int. J. Geogr. Inf. Syst. 1995, 9, 527–542. [Google Scholar] [CrossRef]
- Friedl, M.A.; Brodley, C.E. Decision tree classification of land cover from remotely sensed data. Remote Sens. Environ. 1997, 61, 399–409. [Google Scholar] [CrossRef]
- Breiman, L. Randomizing outputs to increase prediction accuracy. Mach. Learn. 2000, 40, 229–242. [Google Scholar] [CrossRef]
- Kleinberg, E.M. On the algorithmic implementation of stochastic discrimination. IEEE Trans. Pattern Anal. Mach. Intell. 2000, 22, 473–490. [Google Scholar] [CrossRef]
- Santos, M.S.; Abreu, P.H.; García-Laencina, P.J.; Simão, A.; Carvalho, A. A new cluster-based oversampling method for improving survival prediction of hepatocellular carcinoma patients. J. Biomed. Inform. 2015, 58, 49–59. [Google Scholar] [CrossRef]
- Acharya, U.R.; Faust, O.; Molinari, F.; Sree, S.V.; Junnarkar, S.P.; Sudarshan, V. Ultrasound-based tissue characterization and classification of fatty liver disease: A screening and diagnostic paradigm. Knowl.-Based Syst. 2015, 75, 66–77. [Google Scholar] [CrossRef]
- Muflikhah, L.; Widodo, N.; Mahmudy, W.F.; Solimun; Wahibah, N.N. Detection of Hepatoma based on Gene Expression using Unitary Matrix of Singular Vector Decomposition. Int. J. Adv. Comput. Sci. Appl. 2021, 12, 8. [Google Scholar] [CrossRef]
- Książek, W.; Hammad, M.; Pławiak, P.; Acharya, U.R.; Tadeusiewicz, R. Development of novel ensemble model using stacking learning and evolutionary computation techniques for automated hepatocellular carcinoma detection. Biocybern. Biomed. Eng. 2020, 40, 1512–1524. [Google Scholar] [CrossRef]
- Zhang, H. The optimality of naive Bayes. Aa 2004, 1, 3. [Google Scholar]
- Caruana, R.; Niculescu-Mizil, A. An empirical comparison of supervised learning algorithms. In Proceedings of the 23rd International Conference on Machine Learning, Virtual, 26–28 August 2006; pp. 161–168. [Google Scholar]
- Ribeiro, M.T.; Singh, S.; Guestrin, C. “Why should i trust you?” Explaining the predictions of any classifier. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; pp. 1135–1144. [Google Scholar]
- Palatnik de Sousa, I.; Maria Bernardes Rebuzzi Vellasco, M.; Costa da Silva, E. Local interpretable model-agnostic explanations for classification of lymph node metastases. Sensors 2019, 19, 2969. [Google Scholar] [CrossRef]
- Kumarakulasinghe, N.B.; Blomberg, T.; Liu, J.; Leao, A.S.; Papapetrou, P. Evaluating local interpretable model-agnostic explanations on clinical machine learning classification models. In Proceedings of the 2020 IEEE 33rd International Symposium on Computer-Based Medical Systems (CBMS), Rochester, MN, USA, 28–30 July 2020; pp. 7–12. [Google Scholar]
- Davagdorj, K.; Li, M.; Ryu, K.H. Local interpretable model-agnostic explanations of predictive models for hypertension. In Advances in Intelligent Information Hiding and Multimedia Signal Processing; Springer: Berlin/Heidelberg, Germany, 2021; pp. 426–433. [Google Scholar]
- W3Techs. Geo Accession Viewer. 2010. Available online: https://www.ncbi.nlm.nih.gov/geo/query/acc.cgi (accessed on 1 November 2022).
- Reinhardt, J.; Landsberg, J.; Schmid-Burgk, J.L.; Ramis, B.B.; Bald, T.; Glodde, N.; Lopez-Ramos, D.; Young, A.; Ngiow, S.F.; Nettersheim, D.; et al. MAPK signaling and inflammation link melanoma phenotype switching to induction of CD73 during immunotherapy. Cancer Res. 2017, 77, 4697–4709. [Google Scholar] [CrossRef]
- Abdi, H.; Williams, L.J. Principal component analysis. Wiley Interdiscip. Rev. Comput. Stat. 2010, 2, 433–459. [Google Scholar] [CrossRef]
- Watson, D.S. Interpretable machine learning for genomics. Hum. Genet. 2021, 141, 1499–1513. [Google Scholar] [CrossRef]
- Strobl, C.; Boulesteix, A.L.; Kneib, T.; Augustin, T.; Zeileis, A. Conditional variable importance for random forests. BMC Bioinform. 2008, 9, 307. [Google Scholar] [CrossRef]
- Raileanu, L.E.; Stoffel, K. Theoretical comparison between the gini index and information gain criteria. Ann. Math. Artif. Intell. 2004, 41, 77–93. [Google Scholar] [CrossRef]
- Tangirala, S. Evaluating the impact of GINI index and information gain on classification using decision tree classifier algorithm. Int. J. Adv. Comput. Sci. Appl. 2020, 11, 612–619. [Google Scholar] [CrossRef]
- Leung, K.M. Naive bayesian classifier. Polytechnic University Department of Computer Science/Finance and Risk Engineering. 2007, 2007, 123–156. Available online: https://cse.engineering.nyu.edu/~mleung/FRE7851/f07/naiveBayesianClassifier.pdf (accessed on 2 October 2022).
- Langarizadeh, M.; Moghbeli, F. Applying naive bayesian networks to disease prediction: A systematic review. Acta Inform. Medica 2016, 24, 364. [Google Scholar] [CrossRef]
- Komarek, P. Logistic Regression for Data Mining and High-Dimensional Classification; Carnegie Mellon University: Pittsburgh, PA, USA, 2004. [Google Scholar]
- Mucherino, A.; Papajorgji, P.J.; Pardalos, P.M. K-nearest neighbor classification. In Data Mining in Agriculture; Springer: Berlin/Heidelberg, Germany, 2009; pp. 83–106. [Google Scholar]
- Laaksonen, J.; Oja, E. Classification with learning k-nearest neighbors. In Proceedings of the International Conference on Neural Networks (ICNN’96), Washington, DC, USA, 3–6 June 1996; Volume 3, pp. 1480–1483. [Google Scholar]
- Jiang, L.; Cai, Z.; Wang, D.; Jiang, S. Survey of improving k-nearest-neighbor for classification. In Proceedings of the Fourth International Conference on Fuzzy Systems and Knowledge Discovery (FSKD 2007), Haikou, China, 24–27 August 2007; Volume 1, pp. 679–683. [Google Scholar]
- Zhang, C.; Ma, Y. Ensemble Machine Learning: Methods and Applications; Springer: Berlin/Heidelberg, Germany, 2012. [Google Scholar]
- Wu, M.; Liu, Z.; Zhang, A.; Li, N. Identification of key genes and pathways in hepatocellular carcinoma: A preliminary bioinformatics analysis. Medicine 2019, 98, e14287. [Google Scholar] [CrossRef]
- Raschka, S. Model evaluation, model selection, and algorithm selection in machine learning. arXiv 2018, arXiv:1811.12808. [Google Scholar]
- Pratt, J.W. Remarks on zeros and ties in the Wilcoxon signed rank procedures. J. Am. Stat. Assoc. 1959, 54, 655–667. [Google Scholar] [CrossRef]
- Wilcoxon, F. Individual comparisons by ranking methods. In Breakthroughs in Statistics; Springer: Berlin/Heidelberg, Germany, 1992; pp. 196–202. [Google Scholar]
- Fawcett, T. An introduction to ROC analysis. Pattern Recognit. Lett. 2006, 27, 861–874. [Google Scholar] [CrossRef]
- Zou, K.H.; O’Malley, A.J.; Mauri, L. Receiver-operating characteristic analysis for evaluating diagnostic tests and predictive models. Circulation 2007, 115, 654–657. [Google Scholar] [CrossRef]
- Taherdoost, H. Sampling methods in research methodology; how to choose a sampling technique for research; How to choose a sampling technique for research. Int. J. Acad. Res. Manag. 2016, 5, 18–27. [Google Scholar]
- Lu, C.; Zhang, J.; He, S.; Wan, C.; Shan, A.; Wang, Y.; Yu, L.; Liu, G.; Chen, K.; Shi, J.; et al. Increased α-tubulin1b expression indicates poor prognosis and resistance to chemotherapy in hepatocellular carcinoma. Dig. Dis. Sci. 2013, 58, 2713–2720. [Google Scholar] [CrossRef]
- Zeng, G.; Wang, J.; Huang, Y.; Lian, Y.; Chen, D.; Wei, H.; Lin, C.; Huang, Y. Overexpressing CCT6A contributes to cancer cell growth by affecting the G1-To-S phase transition and predicts a negative prognosis in hepatocellular carcinoma. OncoTargets Ther. 2019, 12, 10427. [Google Scholar] [CrossRef] [PubMed]
- Cheng, S.; Jiang, X.; Ding, C.; Du, C.; Owusu-Ansah, K.G.; Weng, X.; Hu, W.; Peng, C.; Lv, Z.; Tong, R.; et al. Expression and critical role of interleukin enhancer binding factor 2 in hepatocellular carcinoma. Int. J. Mol. Sci. 2016, 17, 1373. [Google Scholar] [CrossRef]
- Wang, Z.; Pan, L.; Guo, D.; Luo, X.; Tang, J.; Yang, W.; Zhang, Y.; Luo, A.; Gu, Y.; Pan, Y. A novel five-gene signature predicts overall survival of patients with hepatocellular carcinoma. Cancer Med. 2021, 10, 3808–3821. [Google Scholar] [CrossRef] [PubMed]
- Yan, J.; Cao, J.; Chen, Z. Mining prognostic markers of Asian hepatocellular carcinoma patients based on the apoptosis-related genes. BMC Cancer 2021, 21, 175. [Google Scholar] [CrossRef] [PubMed]
- Skawran, B.; Steinemann, D.; Weigmann, A.; Flemming, P.; Becker, T.; Flik, J.; Kreipe, H.; Schlegelberger, B.; Wilkens, L. Gene expression profiling in hepatocellular carcinoma: Upregulation of genes in amplified chromosome regions. Mod. Pathol. 2008, 21, 505–516. [Google Scholar] [CrossRef]
- Xu, Y.; Zhang, Z.; Xu, D.; Yang, X.; Zhou, L.; Zhu, Y. Identification and integrative analysis of ACLY and related gene panels associated with immune microenvironment reveal prognostic significance in hepatocellular carcinoma. Cancer Cell Int. 2021, 21, 1–20. [Google Scholar] [CrossRef]
- Yang, Y.F.; Pan, Y.H.; Tian, Q.H.; Wu, D.C.; Su, S.G. CBX1 indicates poor outcomes and exerts oncogenic activity in hepatocellular carcinoma. Transl. Oncol. 2018, 11, 1110–1118. [Google Scholar] [CrossRef]
- Liu, M.; Hu, Q.; Tu, M.; Wang, X.; Yang, Z.; Yang, G.; Luo, R. MCM6 promotes metastasis of hepatocellular carcinoma via MEK/ERK pathway and serves as a novel serum biomarker for early recurrence. J. Exp. Clin. Cancer Res. 2018, 37, 1–13. [Google Scholar] [CrossRef]
- Han, Y.; Wang, X. The emerging roles of KPNA2 in cancer. Life Sci. 2020, 241, 117140. [Google Scholar] [CrossRef]
- Li, Y.; Gan, S.; Ren, L.; Yuan, L.; Liu, J.; Wang, W.; Wang, X.; Zhang, Y.; Jiang, J.; Zhang, F.; et al. Multifaceted regulation and functions of replication factor C family in human cancers. Am. J. Cancer Res. 2018, 8, 1343. [Google Scholar]
- Lee, C.F.; Ling, Z.Q.; Zhao, T.; Fang, S.H.; Chang, W.C.; Lee, S.C.; Lee, K.R. Genomic-wide analysis of lymphatic metastasis-associated genes in human hepatocellular carcinoma. World J. Gastroenterol. WJG 2009, 15, 356. [Google Scholar] [CrossRef]
- Deng, Z.; Huang, K.; Liu, D.; Luo, N.; Liu, T.; Han, L.; Du, D.; Lian, D.; Zhong, Z.; Peng, J. Key Candidate Prognostic Biomarkers Correlated with Immune Infiltration in Hepatocellular Carcinoma. J. Hepatocell. Carcinoma 2021, 8, 1607. [Google Scholar] [CrossRef]
- Yao, X.; Lu, C.; Shen, J.; Jiang, W.; Qiu, Y.; Zeng, Y.; Li, L. A novel nine gene signature integrates stemness characteristics associated with prognosis in hepatocellular carcinoma. Biocell 2021, 45, 1425. [Google Scholar] [CrossRef]
- Lu, Q.; Guo, Q.; Xin, M.; Lim, C.; Gamero, A.M.; Gerhard, G.S.; Yang, L. LncRNA TP53TG1 Promotes the Growth and Migration of Hepatocellular Carcinoma Cells via Activation of ERK Signaling. Non-Coding RNA 2021, 7, 52. [Google Scholar] [CrossRef]
- Lee, B.K.B.; Tiong, K.H.; Chang, J.K.; Liew, C.S.; Abdul Rahman, Z.A.; Tan, A.C.; Khang, T.F.; Cheong, S.C. DeSigN: Connecting gene expression with therapeutics for drug repurposing and development. BMC Genom. 2017, 18, 934. [Google Scholar] [CrossRef]
- Trevisani, F.; Cantarini, M.; Wands, J.; Bernardi, M. Recent advances in the natural history of hepatocellular carcinoma. Carcinogenesis 2008, 29, 1299–1305. [Google Scholar] [CrossRef] [PubMed]


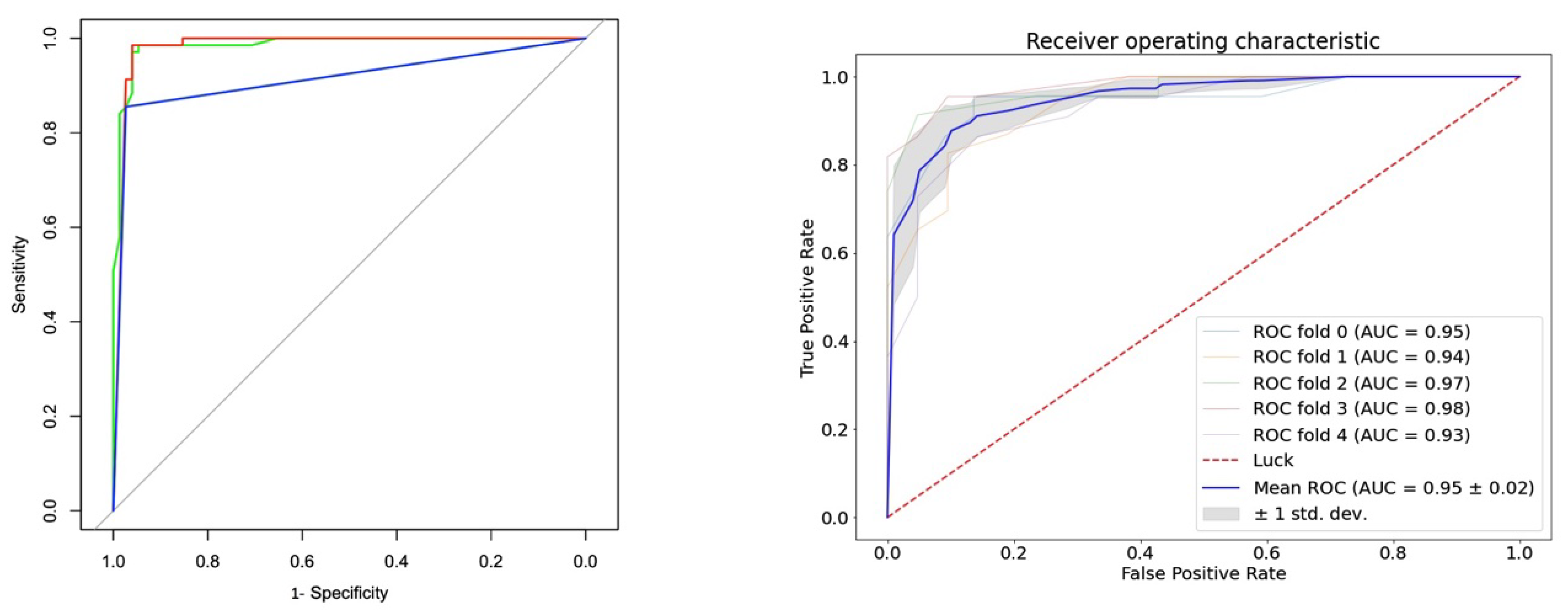
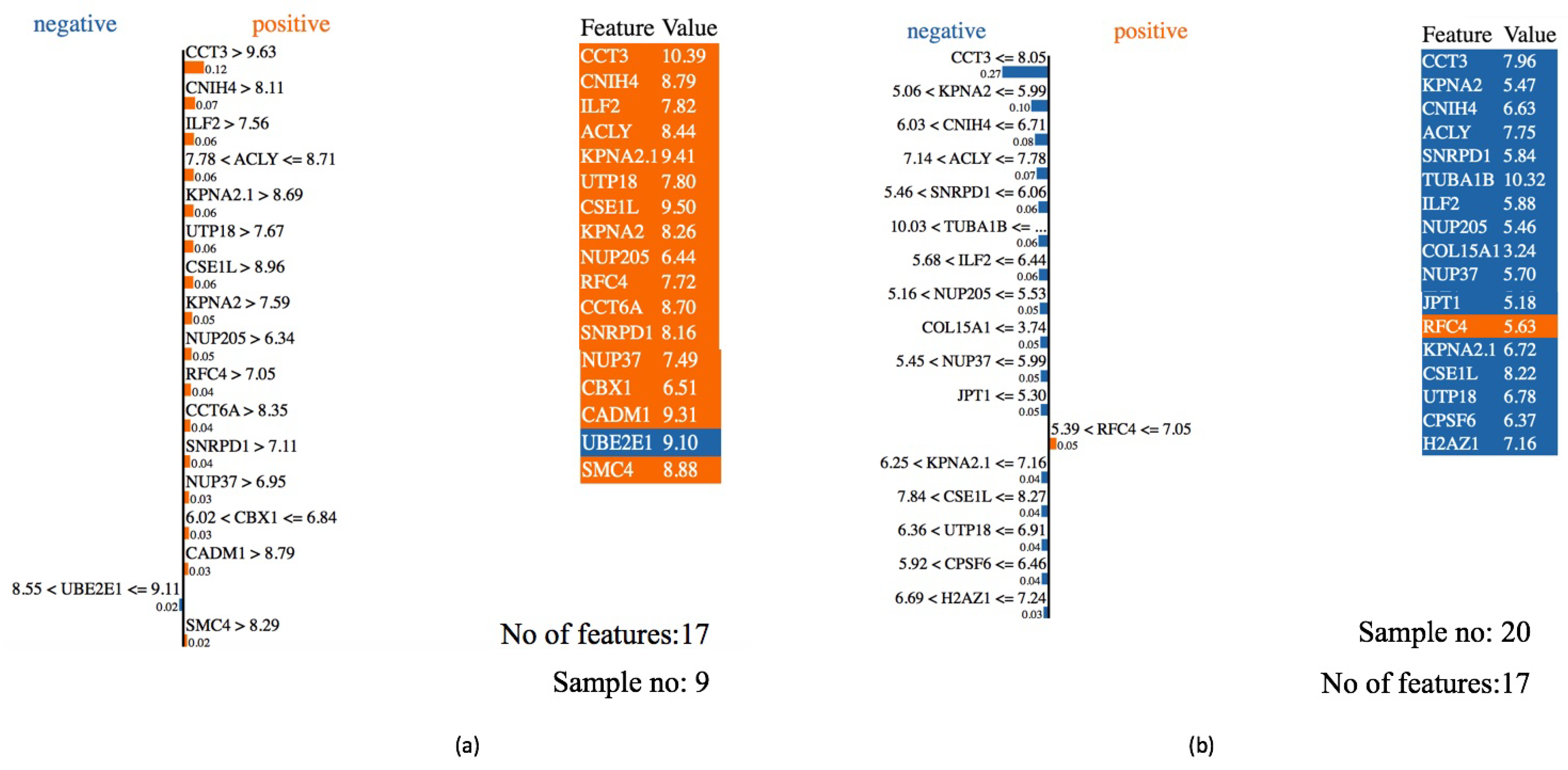
| Methods | ||||||
|---|---|---|---|---|---|---|
| RF | ||||||
| NBC | ||||||
| Logistic Regression | ||||||
| k-NN |
| Methods | RF & NBC Are Equivalent | RF & k-NN Are Equivalent | NBC & k-NN Are Equivalent |
|---|---|---|---|
| p-value |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hasan, M.E.; Mostafa, F.; Hossain, M.S.; Loftin, J. Machine-Learning Classification Models to Predict Liver Cancer with Explainable AI to Discover Associated Genes. AppliedMath 2023, 3, 417-445. https://doi.org/10.3390/appliedmath3020022
Hasan ME, Mostafa F, Hossain MS, Loftin J. Machine-Learning Classification Models to Predict Liver Cancer with Explainable AI to Discover Associated Genes. AppliedMath. 2023; 3(2):417-445. https://doi.org/10.3390/appliedmath3020022
Chicago/Turabian StyleHasan, Md Easin, Fahad Mostafa, Md S. Hossain, and Jonathon Loftin. 2023. "Machine-Learning Classification Models to Predict Liver Cancer with Explainable AI to Discover Associated Genes" AppliedMath 3, no. 2: 417-445. https://doi.org/10.3390/appliedmath3020022
APA StyleHasan, M. E., Mostafa, F., Hossain, M. S., & Loftin, J. (2023). Machine-Learning Classification Models to Predict Liver Cancer with Explainable AI to Discover Associated Genes. AppliedMath, 3(2), 417-445. https://doi.org/10.3390/appliedmath3020022





