1. Introduction
The term mereology originates from the Ancient Greek word, μέρος (méros, “part”) + −logy (“study, discussion, science”), while the term topology originates from the Ancient Greek word, τόπος (tópos, “place, locality”) + −(o)logy (“study of, a branch of knowledge”). The combined expression, mereotopology (MT), thus stands for a theory combining mereology (M) and topology (T). The term mereology was first coined by Stanisław Leśniewski as one of three formal systems: protothetic, ontology, and mereology. “Leśniewski was also a radical nominalist: he rejected axiomatic set theory at a time when that theory was in full flower. He pointed to Russell’s paradox and the like in support of his rejection, and devised his three formal systems as a concrete alternative to set theory”. (
https://en.wikipedia.org/wiki/Stanisław_Leśniewski (accessed on 1 November 2021)). “Parts” in mereology do not necessarily have to be spatial parts but may also represent, e.g., parts of energy. The top axiom of mereology seems to form a basis to quantify parthood and even to derive a number of physics equations from this philosophical concept [
1].
Mereotopology, as a philosophical branch, aims at investigating relations between parts and wholes, the connections between parts, and the boundaries between them. Mereology and topology are based on primitive relations, such as
isPartOf or
isConnectedTo (throughout this article the CamelCase notation is used for objects/classes, while the lowerCamelCase is used for relations), upon which the mereotopology axiomatic systems can be built. An introduction to mereotopology, its fundamental concepts, and possible axiomatic systems can be found in the book “Parts & Places“ [
2] together with the definition of most of the mereotopological relations and numerous references therein.
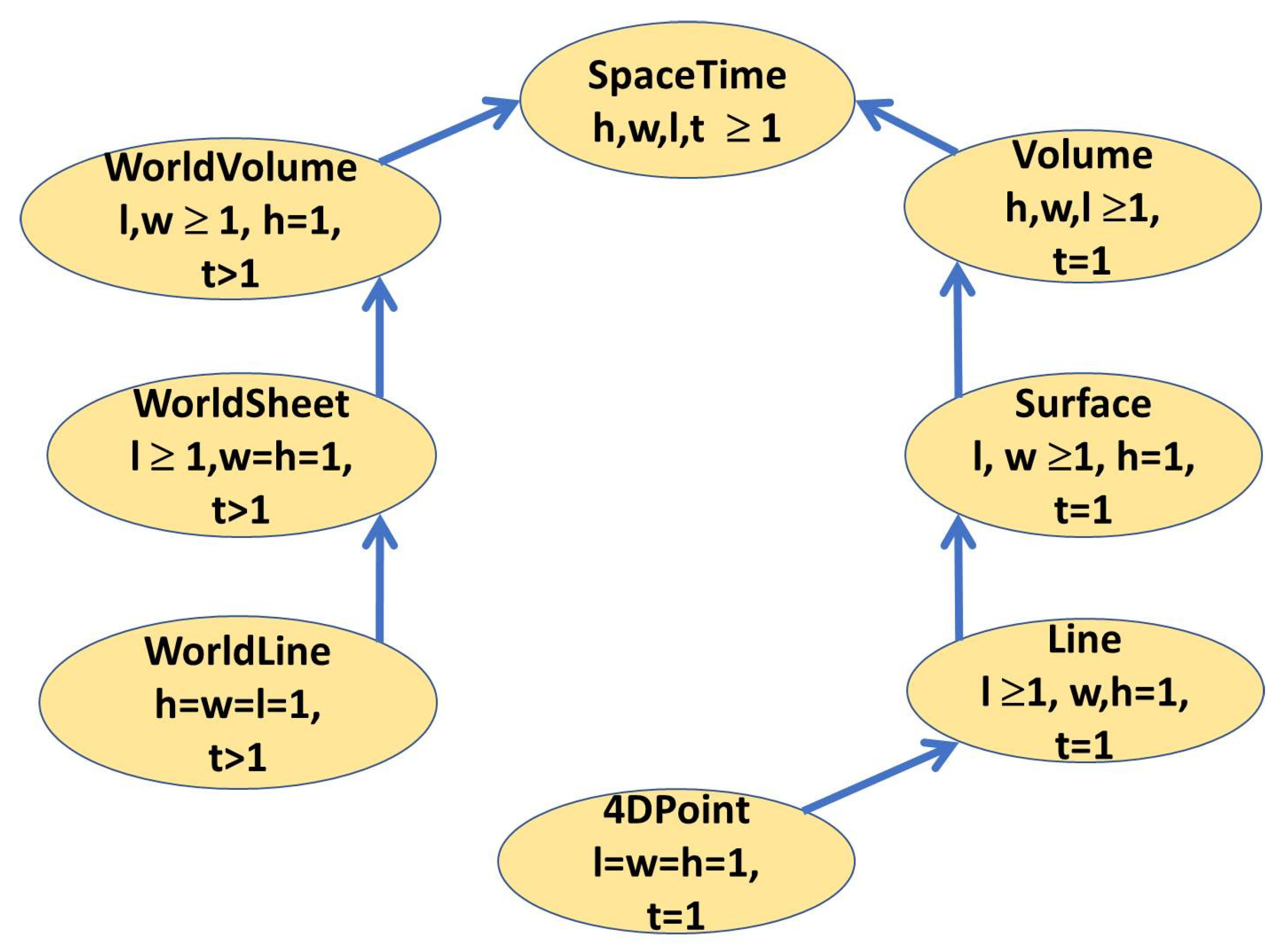
Thus, mereotopology formalizes the description of parthood and connectedness. Mereology maps well onto the hierarchical structure of physical objects, such as materials and enables to represent materials at different levels of granularity. Any part of a Material
isA Material. Any Material
hasPart of some Material. Any part of a 3DSpace
isA 3DSpace. Any part of a Region
isA Region. This matches Whitehead’s view [
3,
4] that “points”, as well as the other primitive notions in Euclidean geometry, such as “lines” and “planes”, do not have a separate existence in reality. As all of them are parts of a 4D-spacetime any of them—from a fundamental perspective—must have a 4D nature as well. Any (4D) SpaceTimeRegion
isA 4DRegion, any 3DVolume
isA 4DRegion being “thin” in the time dimension, any 2DPlane
isA 4DRegion being “thin” in the time dimension and in one spatial dimension, and so forth (see
Appendix A). Topology formalizes whether space–time regions (3D and/or 4D or even higher dimensional spaces) are connected items or not. If they are connected, some finite boundary region exists where they coexist and collocate.
Mereotopology finds application in the development of ontologies. Several foundational ontologies are based on mereotopology as one of the underlying concepts for the specification of relations between individuals and classes, with the most recent example being the Elementary Multiperspective Material Ontology EMMO [
5]. Further standardized upper ontologies currently available for use include e.g., BFO [
6], BORO method [
7], Dublin Core [
8], GFO [
9], Cyc/OpenCyc/ResearchCyc [
10], SUMO [
11], UMBEL [
12], UFO [
13], DOLCE [
14,
15] and OMT/OPM [
16,
17].
The following section is adapted from [
18] with slight modifications and amendments. In classical Euclidean geometry, the notion of “point” is taken as one of the basic primitive notions. In contrast, the Region-Based Theory of Space (RBTS), going back to Whitehead [
3] and de Laguna [
19], has as primitives the more realistic notion of a region as an abstraction of a finite-sized physical body, together with some basic relations and operations on regions, such as the
isConnected or
isPartOf relations. This is one of the reasons why the extension of mereology, complemented by these new relations, is commonly called mereotopology “MT”. There is no clear difference in the literature between RBTS and mereotopology, and by some authors RBTS is related, rather, to the so-called mereogeometry [
20,
21], while mereotopology is considered only as a kind of point-free topology, considering mainly topological properties of things. RBTS has applications in computer science because of its more simple way of representing qualitative spatial information. It initiated a special field in knowledge representation (KR) [
22], called qualitative spatial representation and reasoning (QSRR) [
23]. One of the most popular systems in QSRR is the Region Connection Calculus (RCC), introduced in [
24]. The notion of Contact Algebra (CA) is one of the main tools in RBTS. This notion appears in the literature under different names and formulations as an extension of Boolean algebra with some mereotopological relations [
25,
26,
27,
28,
29,
30,
31,
32]. The simplest system, only called Contact Algebra (CA), was introduced in [
31] as an extension of the Boolean algebra with a binary relation called “contact” and satisfying several simple axioms. Recent work addresses extensions of contact algebra [
33].
Most of above approaches are based on monadic relations, such as P
x (
x isA Part), and dyadic relations, such as
xC
y (
x isConnected y), and thus are limited to relations between two things. In the case of multiple things, higher-order relations may exist. An example might be a triadic relation, such as
x isConnected y forSome z. A simple instance for such a relation would be, e.g., a motorway bridge connecting two cities on two sides of a river. If this bridge exists, the cities are connected for a car. Another example is catalysis, where the two chemical states,
x and
y, are connected (i.e., the reaction occurs) if a catalyst
z is present. Otherwise, they are disconnected. These simple examples for triadic relations surely need a further formalization. According to Peirce’s Reduction Thesis, however, it can be stated, “(a)
triads are necessary because genuinely triadic relations cannot be completely analyzed in terms of monadic and dyadic predicates, and (b)
triads are sufficient because there are no genuinely tetradic or larger polyadic relations—all higher-arity n-adic relations can be analyzed in terms of triadic and lower-arity relations” (
https://en.wikipedia.org/wiki/Semiotic_theory_of_Charles_Sanders_Peirce (accessed on 1 November 2021)). Proofs for Peirce’s Reduction Thesis are available, e.g., in [
34,
35].
The relation of an n-ary contact is described in a generalization of Contact Algebra called Sequent Algebra, which is considered as an extended mereotopology [
36,
37]. Sequent Algebra replaces the contact between two regions with a binary relation between
finite sets of regions and
a region satisfying some formal properties of the Tarski consequence relation. Another approach to multiple connected regions is, e.g., the mereology for connected structures [
38].
Another important aspect, not yet covered by classical mereotopology, relates to the description of time-dependent relations and transitions. In normal language, this would refer to the specification of relations, such as “
isConnected”, “
wasConnected”, and
hasBeenConnected”, or similar. The 4D-mereotopology [
39] specifying, e.g., relations, such as “
isHistoricalPartOf”, dynamic contact algebra DCA [
40,
41], and dynamic relational mereotopology [
42], are current first approaches to tackle this challenge.
All of the above approaches to mereotopology are—to the best of the author’s knowledge—based on some Boolean algebra and additional relations. They thus only allow for qualitative descriptions, such as x isConnected y (or isNotConnected as the binary alternative). In contrast, the phase-field approach to mereotopology, depicted in the present article, allows the quantitative description of different “degrees of connectivity”, ranging, e.g., from 0% to 100%. The phase-field perspective thus provides a much higher expressivity and, in particular, allows for describing transitions—e.g., temporal changes—between classes that are disjoint in binary and Boolean relations. An example would be a transition from “isDisconnected” via different states of “isConnected” to “isProperPartOf” with a physics example for such a process being a cherry dropping into a region of whipped cream. Eventually, the formulation of relations, such as “wasConnected”, “hasBeenConnected” and many more, also becomes possible based on the same approach.
In the spirit of Whitehead’s Region-Based Theory of Space (RBTS), the regions in the phase-field model are defined by values of the phase-field. The phase-field is a scalar field that is defined over a continuous or discretized Euclidian space and thus has some relations with Discrete Mereotopology (DM) [
43,
44] and Mathematical Morphology MM [
45]. An essay that also describes the discretized Euclidean space–time itself, based on mereology, is attempted in the
Appendix B of the present article.
The major focus and innovative topics of the present article are (i) a step-by-step comparison of the logical (FOL) concepts of Boolean Algebra as used in mereology, region connect calculus and contact algebra with the algebraic and field theoretic concepts of the phase-field method, (ii) the identification of similarities and discrepancies between these two concepts for each of these steps, and (iii) the identification and preliminary discussion of the shortcomings of either method in a summarizing conclusion.
2. Scope and Outline
It is not the scope of the present article to review all the types of concepts mereotopology beyond what has shortly been summarized in the introduction. In addition, no comparison will be made with other important algebraic and numerical concepts addressing topology without explicitly drawing on fields, such as the cell method [
46,
47,
48,
49].
Mereotopology, mereogeometry and Region Connect Calculus all are based on logical expressions having only the logical values “true” or “false”. The phase-field concept—in contrast—allows for a quantitative and continuous description, particularly of the transitions between different regions. Following George Boolos: “to be is to be the value of a variable or some values of some variables” [
50]; the value of the phase-field variable identifies anything as being a fraction of the universe or of a region under consideration. Any phase-field variable, accordingly, takes values from the closed interval [0, 1] of the real numbers, though in a strict sense “fractions” are all members of the set of rationale numbers.
The article starts from a short introduction into time-independent phase-field models, which represent objects/regions as scalar fields, namely, the so-called phase-fields. It will be demonstrated how boundaries can be represented as correlations of such scalar fields. Along with this basic introduction, analogies and correspondences to mereotopology will be indicated wherever possible and meaningful. A special section will discuss the extension of the description of dual-boundaries towards higher-order junctions, such as triple junctions and quadruple junctions, in which more than two things collocate and coexist.
A dedicated chapter—in a summarizing way—then compares expressions derived from the phase-field concept with their counterparts in region connect calculus and in classical mereotopology, respectively. It is, however, beyond the scope of the present article to discuss implications of the phase-field perspective for all types of more complex MT theories.
Current applications of the multiphase-field concept particularly address the evolution of complex structures in space and time. A dedicated section of the present article thus introduces the time perspective of the phase-field approach, leading to extended notions of isConnected, such as isTimeConnected (“coexistence”), isSpaceConnected (“collocation”), isPhysicallyConnected, and isCausallyConnected. Further notions become possible on the basis of the phase-field concept, such as wasPhysicallyConnected; isPathConnected, or isEnergeticallyConnected are shortly introduced and provide a promising outlook on possible future developments of mereotopology towards “mereophysics”.
4. Comparison with Mereotopological Concepts
Based on the specifications of bulk areas, boundaries, triple junctions, and quadruple junctions depicted in the preceding section, especially in
Table 2, mereotopological relations can easily be formulated and visualized based on some simple configurations, as outlined in the following.
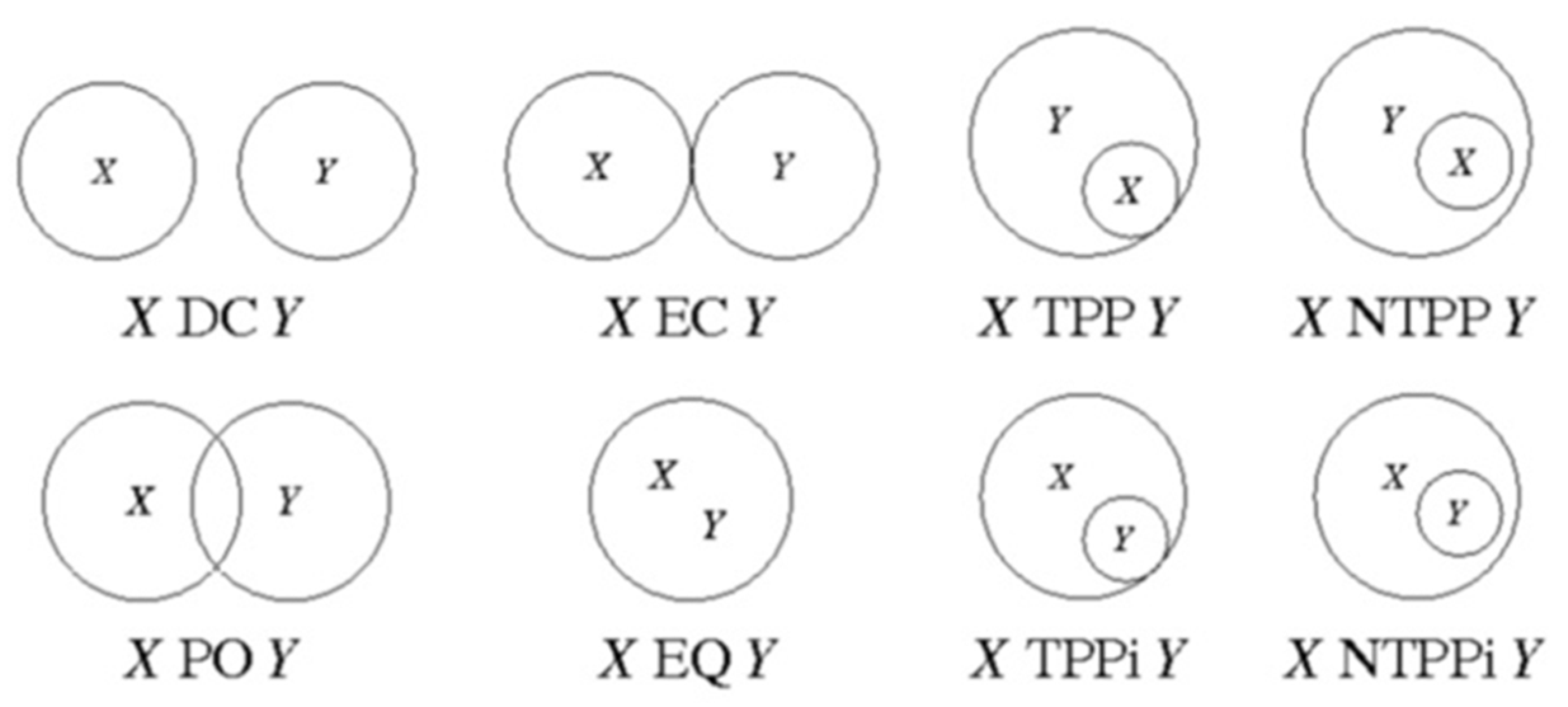
4.1. Comparison with Region Connect Calculus
Some simple region connect calculus (RCC) situations, as shown in
Figure 11, are individually discussed based on the description of boundary terms, as introduced in
Section 3.
The discussion of these boundary terms will intentionally not follow the sequence as indicated in
Figure 11. In contrast, it will start from the easily identifiable configurations (X DC Y, X NTTPi Y, X NTTP Y, and X PO Y), and then address the more complex situations involving only
one Triple Junction (X EC Y, X TPP Y, and X TPPi Y). The most attention is eventually paid to X EQ Y.
Case: X DC Y: X and Y do not have any common boundary:
For X DC Y, parts X AND Y both have boundaries with the background thing 0 (not shown in the figure)
only. Thus, their total boundary hasPart
only of the boundary to the thing 0:
In addition, as there exists no dual boundary between X and Y, no triple junctions involving either of the two parts exist:
Case: X NTPP Y: X has a boundary with Y
only while Y has a boundary to thing 0 as well:
Although there exists a boundary between both things, there is no region where both things are connected to the 0-thing as well. Thus, there are no triple junctions:
Case: X NTPPi Y: Y has a boundary with X
only while X has a boundary to thing 0 as well:
Though there exists a boundary between both parts, there is no region where both things are connected to the 0-thing as well. There are no triple junctions:
All of the three cases above do not comprise any triple junction. The easiest case, including the triple junctions (X PO Y), will be discussed first, as this discussion is helpful in understanding the cases revealing only one single triple junction (i.e., the cases X EC Y, X TPP Y, and X TPPi Y).
Case: X PO Y: X and Y reveal a region of coexistence/collocation—the overlap region. A boundary between X and Y thus exists:
Further, both things X and Y in this case also have boundaries to thing 0:
X PO Y further comprises two regions (“points”), where all three things X AND Y AND the 0-thing collocate: there exist two triple junctions. Their total boundary thus
hasPart of the boundaries to thing 0, to X (resp. to Y), and further, the
two triple junctions, where X, Y, and 0 coexist/collocate. These two triple junctions, however, do NOT collocate—i.e., they exist in different volumes,
xl and
xm—and are distinguished by different helicities for the two different locations; see
Section 3.4. A correlation of the two triple junctions does not exist in any volume element
xn:
Case: X EC Y
In this case, there seemingly exists a
single triple junction in a discretized
single volume
xn. This defines a “point” (a finite-sized smallest volume in two dimensions):
In the case of X PO Y, as discussed above, two triple junctions are coexistent—but not collocated. In the case of X DC Y, no triple junctions exist. X EC Y describes a transition between X DC Y and X PO Y, and thus benefits from being capable of describing both cases—each of them as a limit. Looking at the reverse process the two separated—i.e., not collocated—triple junctions in the X PO Y case then have to condense into a single state of coexistence AND collocate for the X EC Y case (and also for the TPP cases):
Case: X EQ Y
X and Y obviously have the same total boundary:
Both have a boundary with 0
only:
Further, they both have identical phase fields:
This expression directly implies that the two things are identical i.e., the “same thing” in a mereological sense. They have the same geometry, as defined by their individual phase fields. In terms of being fractions of a universe, both things are also identical. They can be treated as a single thing representing twice the fraction of one of the two things but losing their identity, then:
Further, there may be additional attributes beyond the mere geometric shape, which may still allow distinguishing them in spite of being geometrically identical.
4.2. Phase-Field Perspective of Contact Algebra
The topology axioms of contact algebra are (adapted from [
18]):
- (C1)
If aCb, then a > 0 and b > 0,
- (C2)
If aCb and a ≤ c and b ≤ d, then cCd,
- (C3)
If aC(b + c), then aCb or aCc,
- (C4)
If aCb, then bCa,
- (C5)
If a●b ≠ 0, then aCb.
In the following, these axioms are related and compared to the phase-field formulations for time-independent situations. The phase-field formulations introduced in the preceding section are shortly recovered in the following for this purpose. A thing
Φa is
globally present in a region under consideration if it takes a non-zero value in this region:
A thing
Φa is
locally present in a region
xj, which is a sub-region of the region under consideration, if it takes a non-zero value in that sub-region:
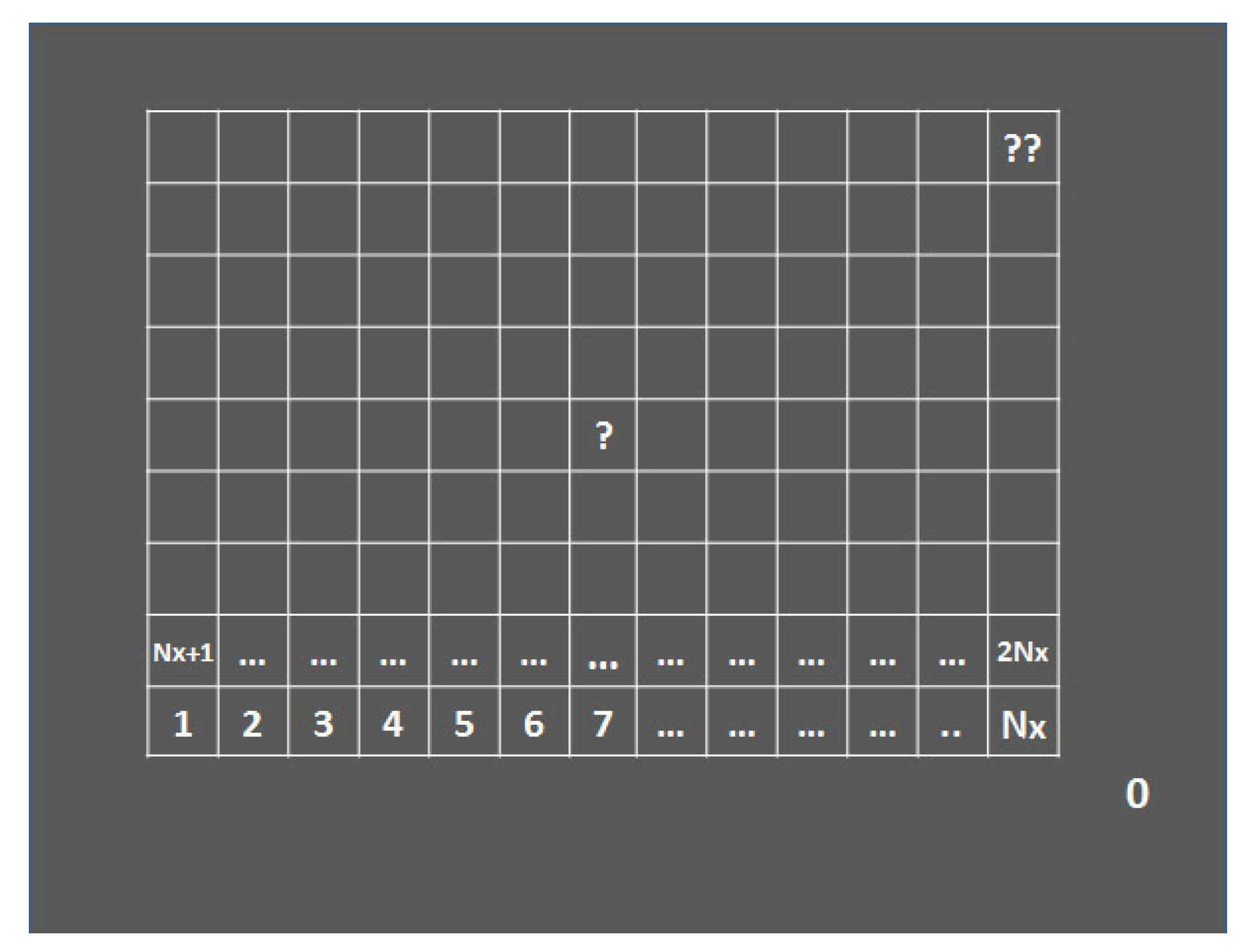
The
global value
Φa is the normalized
sum of all local values in the
Nx sub-regions:
Eventually the definition of “
collocation” is:
This implies that there exists a boundary between the two things:
“
Collocated” in this context (i.e., time independent) means “
isSpatiallyConnected” or just
isConnected, i.e.,
, in the nomenclature of contact algebra.
The
Axiom (C1) of
Contact Algebra—using the phase-field definition of
isSpatiallyConnected—then translates into:
Expressed in words, this reads: “If two things are locally connected, both things must at least globally exist”. Thus, Axiom (C1) is recovered by the phase-field perspective.
Axiom (C3) covers the case of one thing being connected to two other things, which both
globally exist:
Expressed in words, this reads: “If a thing is connected to two other things, it is connected to at least one of them”. Thus, Axiom (C3) is also recovered by the phase-field perspective. For multiple things this can be even further refined as: “Any thing is connected to at least one of the other things” or “Any thing is connected to its complement”.
Axiom (C4) relates to the symmetry of the connected relation:
Expressed in words, this reads: “If thing “a” is connected to thing “b”, then thing “b” is also connected to thing “a””. Thus, Axiom (C4) is also recovered by the phase-field perspective for time-independent correlations.
The situation, however, may be—and probably is—different for time-dependence and other situations. A “path” connecting two things, “
a” and “
b”, may exist for some time, while the return path might not exist anymore, when attempting to go back from “
b” to “
a”. An example would be a bridge connecting “
a” and “
b”, which breaks down when crossing it for the first time. The concept of asymmetric connectivity has major implications for a number of areas in physics and chemistry, such as chemical reactions preferentially proceeding into one direction, entropy always increasing, or osmotic processes, to name a few. A simple example from everyday life is a one-way in traffic. To the best of the author’s knowledge a concept of asymmetric connectivity has not yet been discussed in any of the contemporary mereotopology endeavors. “Symmetric connectivity” can be retained by defining the two things,
a and
b, as
isConnected, if at least one path direction does exist. This allows for a more general—even symmetric—formulation:
This expression, which is still symmetric, can be satisfied by following three configurations:
The last expression indicates the existence of a reversible path, while both other expressions lead to irreversible situations, where there is a path from “
a” to “
b” (or vice versa), but no way back. Path connectivity is an important concept, introduced by Richard P. Feynman, and it finds applications in the principles of least action and/or Fermat’s principle. It is discussed in a little more detail in
Section 5.5.
In a last but single step,
Axiom (C5) is discussed
, which essentially states that if two things
globally exist, they are connected:
The second sum contains correlations between the volume elements
xj and
xk of the reference frame, when re-expressing the fields as products (i.e.,
see
Appendix B.5). Neglecting such correlations (i.e.,
= 0 for all
i,
j), the second term on the RHS vanishes and only the first sum remains:
As a side remark: In the spirit of the present article, such correlations will exist between volumes being in contact with each other, i.e., between neighboring positions. They are neglected here to show under which conditions the axioms of contact algebra can be recovered. These terms thus open options for a future refinement of the concept.
Expressed in words, this reads: “If
two things
globally exist, they are connected”. Thus,
Axiom (C5) is also recovered by the phase-field perspective for the case of
exactly two coexisting things. However, for three (and more things) existing
globally, i.e., for:
a number of options occurs which can be identified when using
Axiom (C3):
Thus—even if the two things,
a and
b, do exist globally (i.e., have non-zero values)—these two things,
a and
b, do not necessarily need to be connected if more than two things are globally present. In the case of
a and
b not being mutually connected, both have to be connected to—or separated by—a third thing,
c. This directly implies the following
global relations:
Expressed in words, this reads: “If
three things
globally exist, each of them is connected to at least one of the two other things”. Two things that are mutually connected directly imply that both
exist globally (see Axiom C1):
Their individual
global existence—in contrast, however—does NOT imply that they are connected if
more than two things are considered. In the case of the three things,
a, b, and
c, two of them, e.g.,
a and
b, may be mutually connected or may be disconnected (i.e., then separated by the third thing
c):
If
one of these boundaries does NOT exist (i.e., equals to 0) both other boundaries must exist (i.e., take non-zero values):
If a triple junction exists, all three dual boundaries do exist:
Thus, Axiom (C5) of contact algebra is recovered for exactly two existing things. The phase-field perspective depicted above seems, however, to imply that this axiom might have to be re-considered for the case of more than two things.
Eventually,
Axiom (C2) will be discussed. This seems to be the most complicated discussion, as it involves four different things. The
Axiom (C2): “if
aC
b and
a ≤
c and
b ≤
d, then
cC
d” expressed in words reads: If
a isConnected b and
a isPartOf c and if
b isPartof d then
c isConnected b. The individual expressions formulated in phase-field boundary terms translate into:
If
a isPartOf c, there exists a boundary between
a and
c:
The total boundary of “
a” then hasPart of the two dual boundaries, but
inevitably then also comprises a triple junction,
a,
b, and
c:
Then, further,
b isPartOf d implies the existence of a boundary between
b and
d:
The total boundary of “
b” then hasPart of the two dual boundaries, but
inevitably also has a triple junction of
a,
b, and
d:
If
aCb Accordingly, Axiom C2 can also be recovered by the phase-field perspective.
In summary, all five axioms of the axiomatic system of contact algebra can be expressed in terms of dual and higher order boundaries as described by the phase-field perspective.
4.3. Comparison with Mereology
While “connections” as used in region connect calculus and topology have been described as “boundaries” between things in the preceding chapter, the description of a “part” being at the heart of mereology is related to the phase field itself, in the phase-field perspective. The section starts with a short overview of mereology, as it is described in detail in [
2].
4.3.1. Mereological Axioms and Definitions
Part: The monadic relation:
This defines “
x” to be a part. This expression implies the existence of “
x”, as in order to be a part, “
x” must exist. It finds its phase-field counterpart in the expression.
By intention, the phase-field notation here deviates from using “
x” to denote a part as usual in mereology. In the context of the phase-field perspective,
a,
b, and
c, etc., will be used instead. This is to avoid confusion with the
xi being used to denote elementary spatial regions in the phase-field perspective. This implies that “
a” (denoted as
in the phase-field perspective) is a non-zero fraction of a system under consideration. The thing
exists if it has a non-zero value and if the thing does not exist it takes the exact value of 0 [
50]:
Parthood: Mereology further builds on a dyadic relation specifying parthood:
This parthood relation is considered as primitive following some basic axioms, such as (see, e.g., [
2]):
Some commonly used definitions based on these axioms are
Above axioms of ground mereology (M) are further complemented by a strong supplementation in extensional mereology (EM):
Then, extensional mereology is further complemented by the following closure extensional axioms, leading to closure extensional mereology (CEM):
Specifically, the
individual z matching the upper-bound axiom fixes a universe
u under consideration as a thing
havingPart all parts:
4.3.2. An Essay towards a First-Order Logic Description of the Phase-Field Concept
The phase-field method to the best of knowledge of the author has not, by now, been formulated as an axiomatic system. The following section thus can be considered as a first essay towards formalizing the phase-field concept. It does not reveal the degree of maturity of the mereological axioms and is subject to future review. Before formulating the phase-field concept in FOL it is instructive to summarize the major concepts in their algebraic form.
In the phase-field concept all existing things are fractions and sum up to form the “whole” (i.e., the value 1). Non-existing things do not contribute to this sum, as their values are identical to 0.
The “complement thing”,
has been added to this sum to account for all the un-named or un-identified—but existing—fractions of the universe. The “complement thing” accordingly can be defined as:
The result is the
basic equation already being introduced in [
1] with the summation starting from
i = 0:
Without rigorous proof—which is beyond the scope of the present article—a number of implications can be directly inferred:
Postulating the number of things to be finite (NΦ) directly implies the existence of the smallest fraction that has no parts (i.e., an “atom”) and of the largest fraction (an “upper bound”);
If a thing is the only thing (the “whole”), it takes the value of 1 and its complement is 0 meaning that the complement does not exist;
If a thing is not the only thing, the complement exists (i.e., it has a non-zero value);
The basic equation corresponds to the mereological sum of all existing things (including the complement);
If both—a thing and its complement thing—exist, their—mereological—product (or their “boundary” or “correlation”) does exist and they are connected (see
Section 4.2):
Note that this correlation term between a thing and its complement is found in a number of areas. Examples are the logistic differential equation, where it corresponds to the derivative of the logistic function (
https://en.wikipedia.org/wiki/Logistic_function (accessed on 1 November 2021)) and is named the logistic distribution:
The expression, interestingly, also corresponds to the lowest order Taylor approximation of entropy type terms [
1]:
In the following, a FOL description of the above concepts is attempted. For this purpose, the conventions of FOL are adapted and the are thus denoted as x, y, and z, etc., again in the following.
In the phase-field perspective all things—whether existing or non-existing (e.g., not yet or no longer existing)—are fractions (of a whole):
The closed interval [0, 1] here is the interval of rationale numbers
, because any fraction by definition is a rationale number. In contrast to selecting the same interval of the real numbers
this implies that things are countable, as the set of rationale numbers is countable. In a refined axiomatization even a
finite cardinality of the collection of N things could be postulated. If a thing exists it takes a non-zero value, if it does not exist it takes the value of 0:
This provides a link between “Boolean Logics” and more general types of logic, such as Heyting logic (
https://en.wikipedia.org/wiki/Intuitionistic_logic (accessed on 1 November 2021)) or Fuzzy logic (
https://en.wikipedia.org/wiki/Fuzzy_logic (accessed on 1 November 2021)), allowing for multiple logic states beyond the binary Boolean alternative of ”true” and/or ”false”. The Boolean view is recovered if selecting the values from the interval of the natural numbers
which only has the two elements 0 and 1 instead of
For the rationale numbers we have for an existing thing:
Expressed in words, this reads: if x exists (i.e., has a non zero value) it is either the whole (with a value of 1) or a part (with a value between 0 and 1). This allows for the specification of a whole and of a part in the following.
The
whole corresponds to a unique, single object (universe) with no further objects existing, then:
The
monadic part relation, as used, e.g., in mereology, is recovered by specifying “parts” as
existing fractions (of a whole) with values
smaller than one:
which is equivalent to
x having a value in the open interval (0,1):
If
x is a part or
x does not exist, there exists at least one other fraction/thing:
If
x is a part, the “other” thing
y is also a part:
These two fractions
either supplement each other to form a part, which still is not the whole:
or the two fractions
x and y complement each other to form the whole:
The thing and its complement always complement each other to form the universe:
The Universal Union allows inferring that the whole has no complement:
In contrast to Boolean logic, a thing and its complement can coexist, i.e., they both can have non-zero values:
This expression decomposes into two cases:
Case (a)
For a binary interval of the natural numbers—i.e., the Boolean case—the only alternative for selecting “not being equal 1” is to be equal to 0. Case (a) thus reflects the Boolean view that a thing and its complement do not coexist:
The Boolean view thus is recovered in this special case. From the phase-field logic this expression reads:
Expressed in words, this reads that a thing and its complement do not coexist if either the thing or its complement do not exist individually.
Case (b)
Case (b) is possible in a non-Boolean perspective only. In the phase-field formulation, one gets:
Note that
does NOT mean that
x does not exist but
denotes the complement of
x. In contrast: if
x does not exist, its complement does exist and vice versa, via the General Supplement Axiom:
In the phase-field perspective, thus anything (!) which is a part overlaps (i.e.,
isConnectedTo) its complement part:
This fundamental overlap is given by the algebraic product of the two non-zero fractions of the thing and its complement:
The general overlap between two parts is defined as:
The overlap in the phase-field perspective corresponds to the situation of two things being connected, being collocated resp. two things having a boundary. Any part is connected to its complement in view of the fundamental overlap. If the complement of
x has two parts,
y and
z,
x is connected to at least one of them (see also the discussion of the
Axiom C3 of contact algebra in
Section 4.2):
A full FOL (First-Order Logic (
https://en.wikipedia.org/wiki/First-order_logic (accessed on 1 November 2021))) or IPL (intuitionistic propositional logic (
https://en.wikipedia.org/wiki/Intuitionistic_logic (accessed on 1 November 2021))) description of the phase-field concept is beyond the scope of the present article and will be the subject of a future, separate publication. It will include the definition of objects, such as triple and quadruple junctions, and interesting objects, such as the ratio of things.
4.3.3. Further Useful Definitions
The following section defines some further objects based on the closure extensional mereology (CEM) framework described in
Section 4.3.1. The definition of these objects is helpful for a comparison with the phase-field perspective. The three objects being discussed for this purpose are the
self-sum, the
triple overlap, and the
triple product.
Self-Sum: Formally interpreting the minimal underlap (i.e., the mereological sum) of a thing with itself leads to the following specification, which has not yet been used in mereology formulations to the best of the author’s knowledge:
This expression reduces to:
This “self-sum” is observed to be identical with the fraction the part takes of the whole in the phase-field perspective.
Triple Overlap: A closer look at the “equivalence” in the expression for the mereological sum:
unveils three different options for
Owz to be “true”:
The last expression suggests—and allows for—a definition of a triple junction in the form of a triadic relation, which is not part of any mereology formulation by now. It is introduced here for the first time:
Expressed in words, this definition reads: “There exists a region w which overlaps with three regions x,y,z”. This region is denoted as a “triple overlap”.
Triple Product: Further, a maximum triple overlap—a “triple product”—comprising all regions w with triple overlaps of the same three things can be defined:
The definitions of triple product and triple overlap are amended to classical mereology here, as they find their counterparts in the phase-field perspective (see table in
Section 3.4).
4.3.4. Graphical Visualization of Mereological Expressions
Before eventually discussing mereology from the phase-field perspective, a graphical visualization of the different definitions in mereology is very instructive. Numerous graphical representations of the classical definitions and relations are available, e.g.,
Figure 12.
Some further graphics are added in the following allowing the discussion of some of the terms in more detail or trying to illustrate some of the terms graphically.
Underlap: The mereological underlap, Uxy, denotes a thing z, which has the two things, x and y, as parts. The two extremes are the whole (i.e., the universe individual) representing the
maximum object comprising both things and the mereological sum representing the
minimum object comprising both things, as shown in
Figure 13.
However, there is no “unique underlap”. A variety of different objects fulfill the condition to be an underlap of two things. Between the two extremes depicted in
Figure 13, a variety of different underlap objects can accordingly be defined, as shown in
Figure 14.
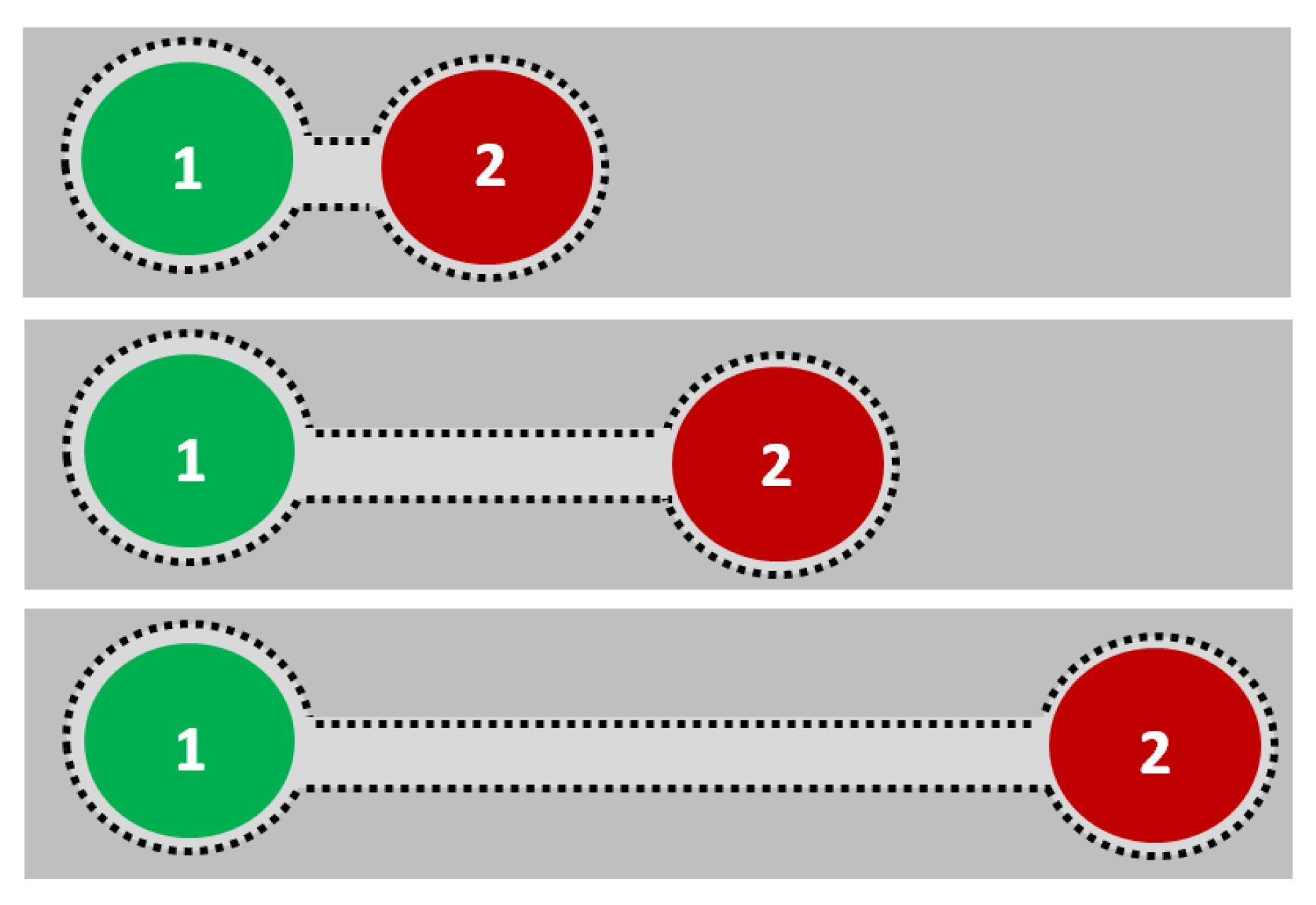
Self-Connected Underlaps of Disconnected Parts
If the underlap is postulated to be self-connected for both connected and also for disconnected things, a minimum of such a self-connected underlap can be used as a measure for distance, as shown in
Figure 15. Further separating the two things will increase this minimal volume, while approaching them will decrease it. A distance,
d, which also is a fraction of the universe, can thus be defined as the difference of the minimum self-connected underlap “MSCU” region and the “Mereological Sum”(MS, which is not self-connected for disconnected things). The value of
d will become 0 in the case of external contact between the two things.
The volume of the minimum self-connected underlap (MSCU) will correspond to the sum of the underlaps of the individual parts (i.e., their mereological sum) plus a volume corresponding to the minimal string/path connecting the two parts (the path volume; see also
Section 5.6) minus the total volume of their overlap (i.e., their mereological product). This concept is not addressed in current mereology, but can most probably be related to a concept of “potential energy”. Further discussion of this idea is beyond the scope of the current article and will be the subject of future work.
4.3.5. The Phase-Field Perspective of Mereological Expressions
An intuitive approach to a translation of mereological expressions to their phase-field counterparts starts from the mereological definition of the overlap:
The overlap in the phase-field perspective corresponds to the coexistence of the object
Φ (denoted as
x in the mereology expression) and an object of the reference frame
xn (denoted y in the mereology expression). In the case of coexistence, both things are non-zero fractions of a universe, i.e., both have values in the open interval (0,1) of the rationale numbers. Their algebraic product (their correlation, “
z” in the mereology expression, i.e., the overlap) thus exists:
This allows defining the phase-field (or even any scalar field) as being the overlap of an object
Φ and an object
xn as being part of a reference frame. Without loss of generality,
xn can exemplarily be imagined as a simple, individual voxel in a cubic grid.
The mereological self-sum, which was introduced as the special case of the mereological sum in
Section 4.3.3, can then be used to identify the total fraction of the object in the entire reference frame, being composed of “all
xnIdentifying “all
xn” (phase-field perspective) with “all
w” (mereology) and
x (mereology) with the object
Φ (phase-field), facilitates the translation between the phase-field perspective and mereological expressions. The object
z in this case is the total fraction of the object
Φ. Assuming further “all
xn” and thus “all
w” to be countable and finite allows specifying the total fraction
Φ of the object, which sums all
xn where
Φ is present.
Having thus related the phase-field expressions
and
Φ (see Equation (1) in the table in
Section 3.6) to mereological expressions, in the next steps the two expressions
(see Equation (3) in table in
Section 3.6) will be discussed. They can be identified to relate to the mereological product. The mereological product is the largest overlap of two-phase fields describing the two things
a and
b, i.e., the region formed by all
xn where the two things coexist. Things have been named
a and
b here in order not to generate confusion with the
x denoting an existing object of the reference frame in the phase field perspective. The smallest region of coexistence—the smallest overlap—is defined by coexistence of the two things, at least in a single
xn:
Expressed words: There exists a volume
xn which
hasPart finite fractions of both parts
a and
b (or which
isPart of both
a and
b):
This is the exact mereological definition of overlap and is also the phase-field definition of an interface in an elementary volume of the reference frame:
The maximum overlap—i.e., the
mereological product—is the object comprising all
xn, which contribute to the total boundary between the two things,
a and
b:Recovering the definition of the phase-field as the correlation (overlap) between the thing and a volume element
xn of a reference frame (see
Appendix B):
This allows the rewriting of which can eventually be interpreted as a triadic relation: . Expressed in words, this triadic relation reads: : a and b collocate in x. It can likewise be formulated for coexistence as : a and b coexist during t. Eventually, a quartic relation, Qabxt, for a physical contact, which corresponds to coexistence (during t) and collocation (in x) can be formulated: Q: a and b coexist in x during t.
The
mereological sum—i.e., a possible, minimum thing,
c, having the part two things,
a and
b—from a phase-field perspective—can directly be identified as the sum of the two individual phase-fields describing the two things,
a and
b, coexisting in an
xn. The thing
c—the sum—described by its own phase-field, then
only has
a and
b as parts and no further thing:
4.3.6. Graphical Comparison of Mereological and Phase-Field Descriptions
Boundary “areas” in mereotopology MT and in the region connect calculus RCC correspond to overlaps. External contact (EC) and tangential proper parts (TPP) both relate to triple junctions. There is no equivalent to quadruple junctions provided in either of these two concepts. The phase-field approach allows the description of mereotopological relations between things on the basis of the boundaries and the higher-order junctions they form, as shown in
Figure 16 and
Figure 17. Examples for three or more things forming a whole are depicted in
Figure 18.
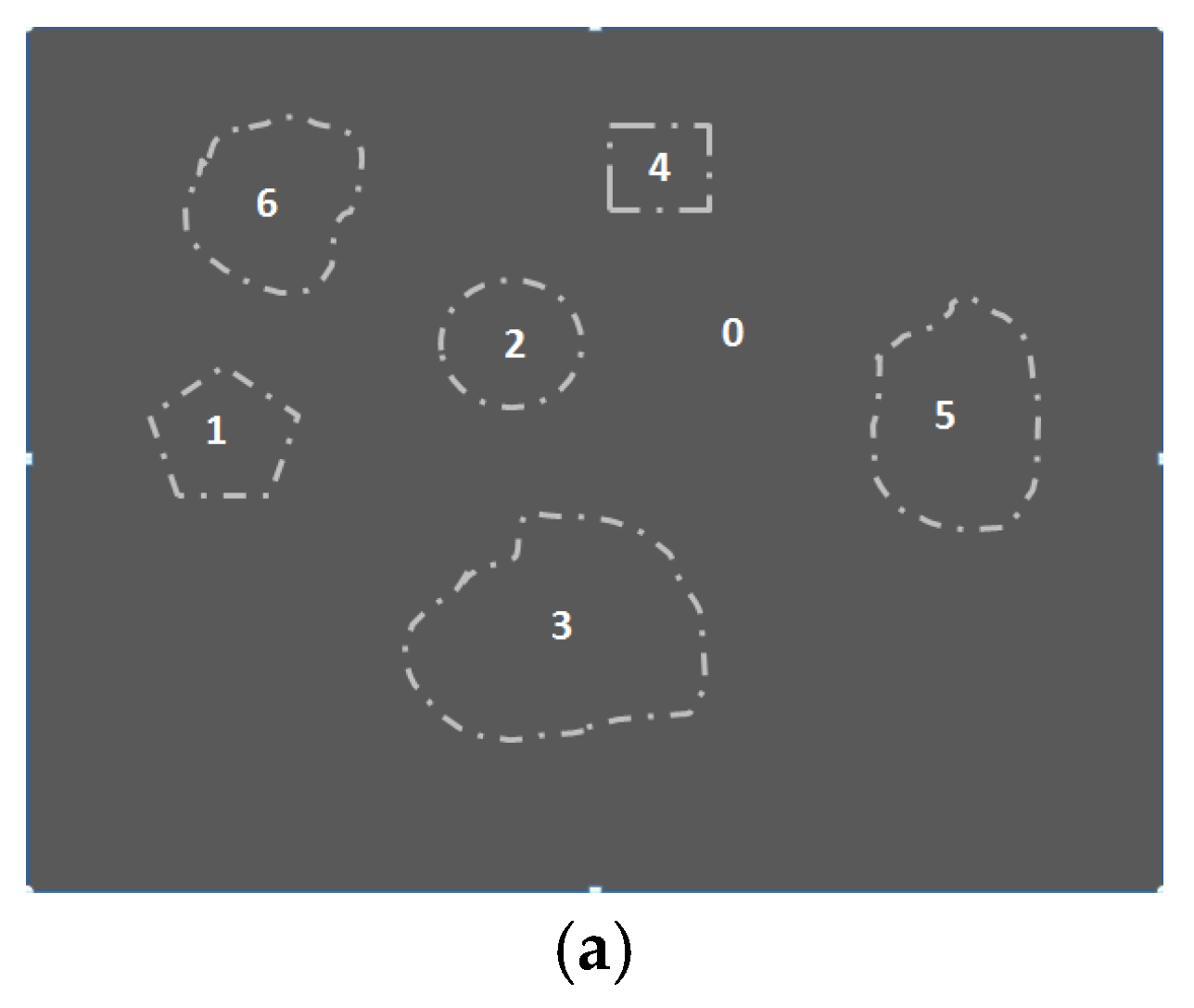
Based on boundaries, the topological relations between the things being depicted in
Figure 16 can easily described. For example, thing 10 has an interface with the matrix 0 only:
. Thing 1 is proper part of thing 2 and thus has an interface with 2 only:
. Thing 2 (in the absence of thing 1) is a direct part of the universe (thing 0) and thus has an interface with 0 only:
. In the presence of thing 1, however, thing 2 has an above external boundary with thing 0 but also a further internal boundary with thing 1:
. Thing 4 is tangential part of thing 3 and thus has an interface with 3 only but also a single triple-junction:
. Things 5 and 6 represent a “bound state” and their boundaries are
=
and
=
.
6. Summary, Conclusions and Outlook
The present article has related and compared the concepts of mereotopology, region connect calculus and contact algebra to a field-theoretic description of objects, their shapes, and their boundaries by the phase-field concept. The concepts underlying mereotopology, on the one hand, seemed to be similar to the principles underlying the phase-field concept, on the other hand, a number of differences/complementarities became obvious.
In the first place, some limitations of Boolean algebra were identified. Boolean algebra does not allow for the coexistence of a thing and its complement. Such a coexistence, however, is essential not only in the phase-field perspective, where coexistence and collocation are actually measures for the physical boundary between things. Mereotopology is based on Boolean algebra and thus considers the different types of connectivity as logically—and thus qualitatively—disjoint. Transitions, e.g., from “x isDisconnected y” to “x isProperPartof y”—with a cherry dropping into whipped cream being an example—thus cannot or can only hardly be addressed. Transitions, however, are ubiquitous processes and thus need a formal description. Such a description may widen the field of applications of contemporary mereology, mereotopology and mereogeometry, towards new grounds of mereophysics.
A “dynamic” view on contacts and boundaries and the notion of time were thus introduced. This is first reflected in time-dependent relations allowing one to semantically describe “historicalParthood” via “isConnected” or “wasConnected” relations. Separating the description of 4D connectivity into “isSpatiallyConnected” and “isTemporallyConnected” allowed for the definition of “isPhysciallyConnected” and eventually also of “isCausallyConnected”. As a consequence, the formulation of the relativistic space–time interval could be derived from mere logical inference.
Eventually the symmetry of the connectivity relation was discussed, where an “isPathConnected” and an “isEnergeticallyConnected” relation provide the grounds for describing reversible and/or irreversible paths.
In a generalized notion, the “isConnected” relation, according to the present article might be interpreted as some generalized “distance” between two things to be equal to 0. This generalized distance may be a spatial distance, a temporal distance, an energetic distance or any other type of general distance. All these distances are expressed as the difference between two values. Thus the status of “isConnected” is reached if two values are equal, i.e., if two values satisfy the equation of type A − B = 0. A possible notion of “distance” was introduced, which could be described in mereological terms as minimal self-connected underlap minus the mereological sum of two disconnected things.
Concepts of higher-order junctions were discussed. These relate to the connectivity of more than two things. The benefits of describing triple junctions with triadic relations and the importance of triadic relations in general were highlighted as well as the notion of helicity and aspects of 3D connectivity of triple junctions being seemingly disconnected in 2D. A potential need to reconsider/reformulate one of the axioms in contact algebra was identified when discussing the connectivity of multiple objects.