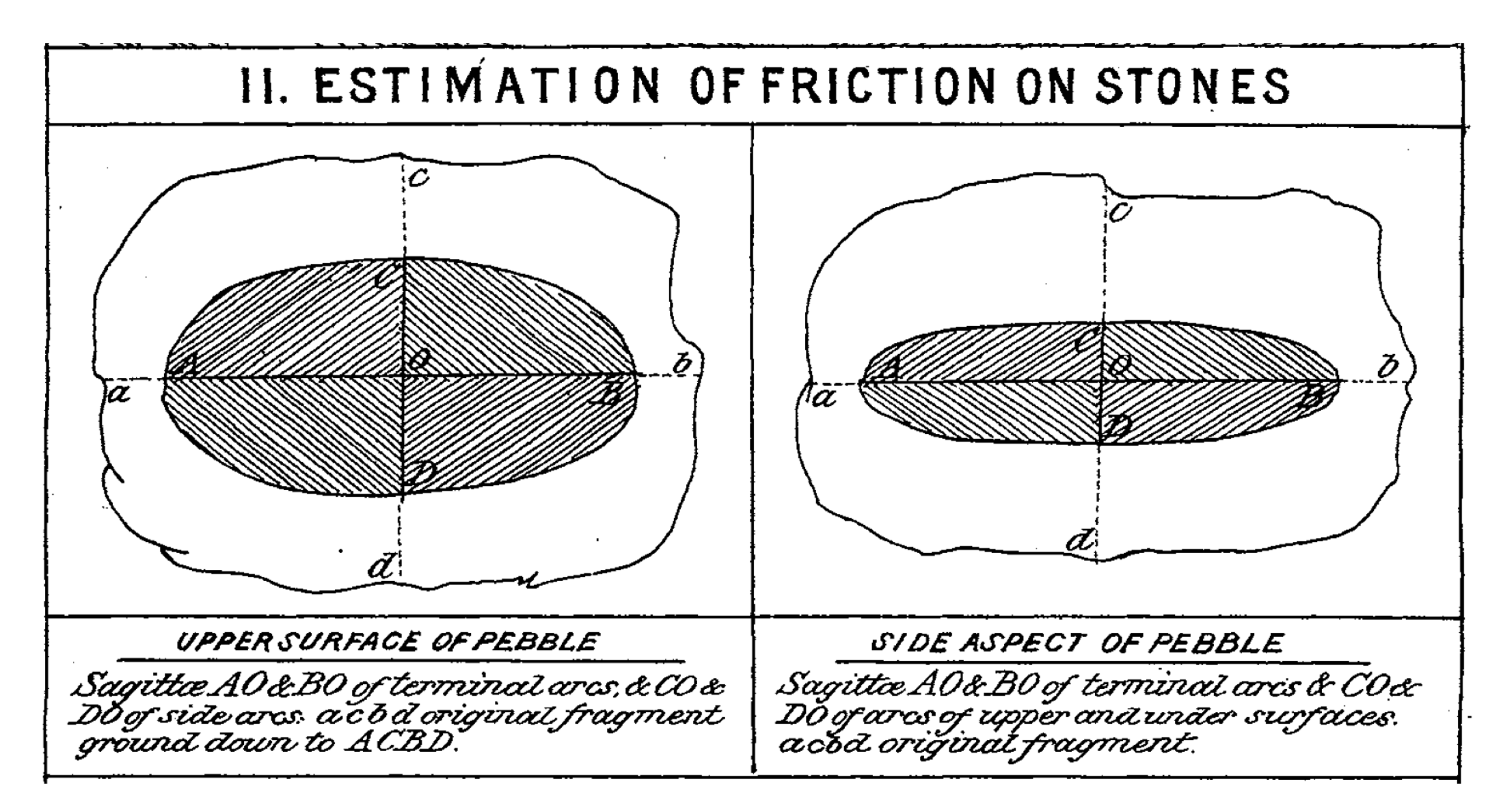
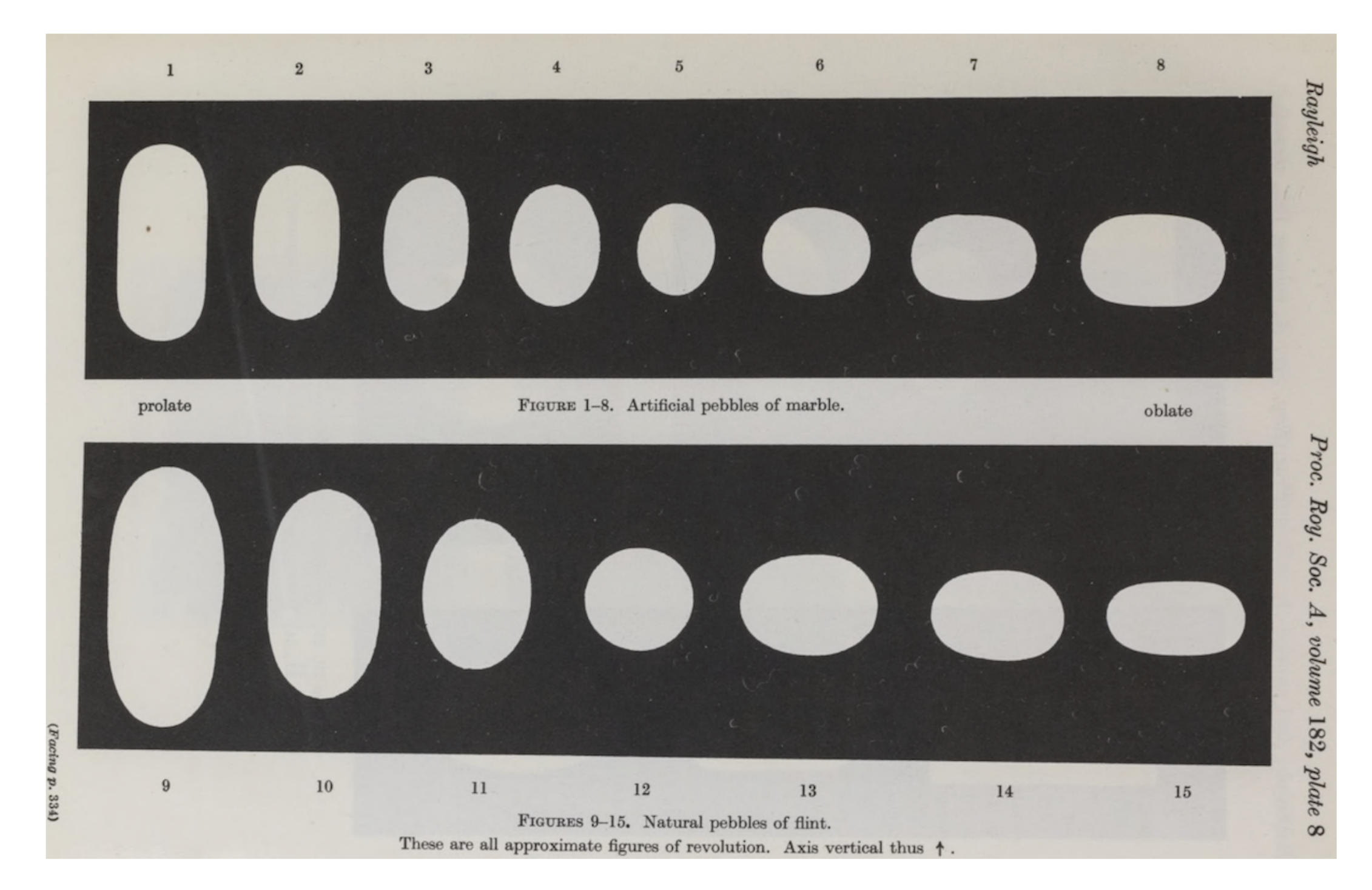
On the Oval Shapes of Beach Stones

Abstract

This article introduces a new stochastic non-isotropic frictional abrasion model, in the form of a single short partial integro-differential equation, to show how frictional abrasion alone of a stone on a planar beach might lead to the oval shapes observed empirically. The underlying idea in this theory is the intuitive observation that the rate of ablation at a point on the surface of the stone is proportional to the product of the curvature of the stone at that point and the likelihood the stone is in contact with the beach at that point. Specifically, key roles in this new model are played by both the random wave process and the global (non-local) shape of the stone, i.e., its shape away from the point of contact with the beach. The underlying physical mechanism for this process is the conversion of energy from the wave process into the potential energy of the stone. No closed-form or even asymptotic solution is known for the basic equation, which is both non-linear and non-local. On the other hand, preliminary numerical experiments are presented in both the deterministic continuous-time setting using standard curve-shortening algorithms and a stochastic discrete-time polyhedral-slicing setting using Monte Carlo simulation.

1. Introduction

“The esthetic shapes of mature beach pebbles”, as geologists have remarked, “have an irresistible fascination for sensitive mankind” [1]; see Figure 1, Figure 2 and Figure 3. This fascination dates back at least to Aristotle ([2]; see [3]), and has often been discussed in the scientific literature (e.g., [4,5,6,7,8,9,10,11,12,13,14,15,16]).

In studying the evolving shapes of beach stones, Aristotle conjectured that spherical shapes dominate (see [18]). In support of his theory, he proposed that the inward rate of abrasion in a given direction is an increasing function of the distance from the center of mass of the stone to the tangent plane (the beach) in that direction, the intuition being that the further from the center of mass a point is, the more likely incremental pieces are to be worn off, since the moment arm is larger.

1.1. Aristotle’s Distance-Driven Model

Aristotle’s model may be formalized mathematically as the following distance-driven flow (cf. [18] (Equation (1.1); [8] (Equation (1)):

$$\frac{\partial h}{\partial t}=-f(h),$$

(1)

where f is an increasing function of the distance $h=h(t,u)$ from the center of mass of the stone to the tangent plane in unit direction u at time t.

As observed in [18], since the location of the center of gravity is determined by time-dependent integrals, (1) is a non-local (cf. [19]) partial integro-differential equation. For many natural choices of f, the shape of a convex stone eroding under (1) apparently becomes spherical in the limit; see numerical experiments below.

1.2. Curvature-Driven Model

Modern mathematical models for the evolving shapes of stones often assume, as Aristotle did, that the ablation is normal to the surface of the stone, but unlike Aristotle, many assume that the rate of ablation is proportional to the curvature at the point of contact. Both Aristotle’s and these modern models typically assume that the stones are undergoing isotropic abrasion, i.e., the stones are being abraded uniformly from all directions, and each point on the surface of a convex stone is equally likely to be in contact with the abrasive plane. A typical real-life example of isotropic frictional abrasion of a stone is the abrasion of a stone in a standard rock tumbler.

The assumption that the rate of abrasion at a given point on the surface of the stone is proportional to the curvature at that point is analogous to the assumption that equal volumes (areas) are ablated in equal time (see Figure 4). This is physically realistic in that sharp points tend to erode more rapidly than flat regions. Note that under the assumption that the inward rate of abrasion is proportional to the curvature, the stone in Figure 4 will erode inward at rates less rapidly from A to C when it is in contact with the beach at those points.

Taking the constant of proportionality to be 1, and using the notation of [20], the basic assumption that the rate of ablation is proportional only to the curvature at the point of contact yields the classical curvature-driven flow, the local geometric PDE:

$$\frac{\partial h_0}{\partial t}=-\kappa$$

(2)

where $h_0=h_0(t,u)$ is the distance from a fixed origin to the tangent plane in unit direction u at time t and $\kappa =\kappa (t,u)$ is the (Gaussian) curvature of the body at the point of contact with the supporting hyperplane in unit direction u at time t.

(The interested reader is referred to [21] for the evolution of shapes under an even broader class of curvature-driven geometric flows).

Various models for the evolving shapes of 2 and 3-dimensional “stones”, both purely mathematical models on curve-shortening flows and physical models under frictional abrasion, also contain hypotheses guaranteeing that the shapes will become spherical in the limit (e.g., [20,22,23,24,25]). Observations of beach stones in nature, however, suggest that the “esthetically fascinating” shapes of beach stones are almost never spherical. Instead, real beach stones and artificial pebbles from laboratory experiments typically have the oval shapes seen in Figure 1, Figure 2 and Figure 3.

Furthermore, in his analysis of these oval shapes, Black reported that this “ovoid shape seems to be taken by all sorts of stones, from the soft sandstone to the hard quartzite, and may, therefore, be independent of mineral composition or relative hardness of the stone” [5] (p. 122). Recall that the evolution of the shapes of stones under frictional abrasion in distance-driven models, such as (1), and curvature-driven models, such as (2), are both isotropic, and both are independent of the underlying wave dynamics.

As for the shape of the stone playing a role, Rayleigh noted that based on his observations in nature and in laboratory experiments, “this abrasion cannot be merely a function of the local curvature” [13] (p. 207). Firey similarly observed that the shape of the stone “surely has a dynamic effect on the tumbling process and so on the distribution of contact directions at time t” [20] (p. 1). The distance-driven and curvature-driven models (1) and (2) do not provide physically realistic frameworks for the evolving shapes of stones undergoing frictional abrasion on a flat beach simply because they are isotropic; that is, they assume that abrasion of the stone is equally likely to occur in every direction regardless of the shape of the stone and the dynamics of the wave process. Thus, a more physically realistic model of the evolving shapes of beach stones under frictional abrasion will necessarily be non-isotropic and stochastic.

In some models, such as (1) (with $f(h)=h^{\alpha }$ for some $\alpha >1$) and (2), a spherical stone is in stable (attracting) equilibrium, and any shape close to a sphere will become more spherical. Among real beach stones, however, researchers have reported that “Pebbles never approach the spherical” [14] (p. 211), “one will never find stones in spherical form” [16] (p. 1), and “there is little or no tendency for a pebble of nearly spherical form to get nearer to the sphere” [26] (p. 169). In fact, Landon reported that “round pebbles become flat” [11] (p. 437), and Rayleigh observed, “a tendency to change away from a sphere” [13] (p. 114), i.e., that spheres are in unstable (repelling) equilibrium.

To see intuitively how a sphere could be in unstable equilibrium under frictional abrasion alone, consider the thought experiment of the abrasion of a sphere as illustrated in Figure 5.

Initially, all points on the surface of the spherical stone are in equilibrium, and the abrasion is isotropic. However, as soon as a small area has been ablated at a point on the surface, then that flattened direction is more likely to be in contact with the beach than any other direction, so the abrasion process now has become non-isotropic. That direction of contact with the beach has now entered stable equilibrium, as shown at point B in Figure 5. Moreover, since the center of gravity of the ablated stone has now moved directly away from B, point A is now also in stable equilibrium, and the stone is more likely to be ablated at A than at any other point except the B side. Thus, if a sphere is subject solely to frictional abrasion with a plane (the beach), the abrasion process will immediately become non-isotropic, and the stone will initially tend to flatten out on two opposite sides.

In a stone undergoing frictional abrasion on a beach, not only the shape of the stone but also the dynamics of the ocean (or lake) waves play a crucial role. If the waves are consistently very small, the stones will tend to rest in one stable position, and the low energy of the waves will cause the stones to grind down to a flat face on that side, much like a standard flat lap polisher is designed to do. The likelihood that other points on the surface of the stone will come into contact with the abrasive beach plane is very small. At the other extreme, if the waves are consistently huge, then it is likely that all exposed surface points of the stone will come into contact with the beach about equally often, i.e., the stone will be undergoing nearly isotropic abrasion as in a rock tumbler and will become more spherical.

In the basic non-isotropic model presented below, an isolated beach stone is eroding as it is being tossed about by incoming waves (e.g., the beach may be thought of as a plane of sandpaper set at a slight angle against the incoming waves), and the only process eroding the stone is frictional abrasion with the beach (e.g., no collisional or precipitation factors as in [24] or [27]). As with the curvature-driven model (2) above, it is assumed that the rate of ablation per unit time at the point of contact with the beach is proportional to its curvature at that point—that is, sharp points will wear faster than flat regions. Unlike a stone eroding in a rock tumbler, the likelihood that abrasive contact of a stone with a beach occurs in different directions generally depends on both the shape of the stone and the wave dynamics (see Figure 6). That is, in any physically realistic model, the ablation process is not isotropic.

The main goal of this paper is to introduce a simple mathematical equation based on physically intuitive heuristics that may help explain the limiting (non-elliptical) oval shapes of stones wearing down solely by frictional abrasion by waves on a flat sandy beach. Although very easy to state, this new equation is technically challenging, and no closed-form solution is known to the author for most starting stone shapes or distributions of wave energies, even in a 2-d setting.

On the other hand, two different types of numerical approximations of solutions of this equation for various starting shapes indicate promising conformity with the classical experimental and empirical shapes of beach stones found by Lord Rayleigh, as shown in Figure 2. One type of numerical solution of the equation models the evolving shapes of various isolated beach stones in a deterministic continuous-time setting using standard techniques for solving curve-shortening problems, and the other type uses Monte Carlo simulation to approximate typical changes in the stone shape in a discrete-time discrete-state “chipping” setting.

2. Methods

In the new frictional abrasion model introduced below, both the shape of the stone and the wave dynamics play key roles in the subsequent evolution of the shape of the stone. It is assumed that the energy required for the frictional abrasion of a beach stone is provided solely by the energy of the incoming waves, a time-dependent random process. Thus, the point of contact of the stone with the beach is also a time-varying random variable, and if the inward ablation of a stone at a given point on its surface is an infinitesimal distance d every time that point hits the abrasive surface (beach), then in n hits at that point, the resulting inward abrasion will be $nd$, the product of the inward rate and the number of times it is abraded at that point.

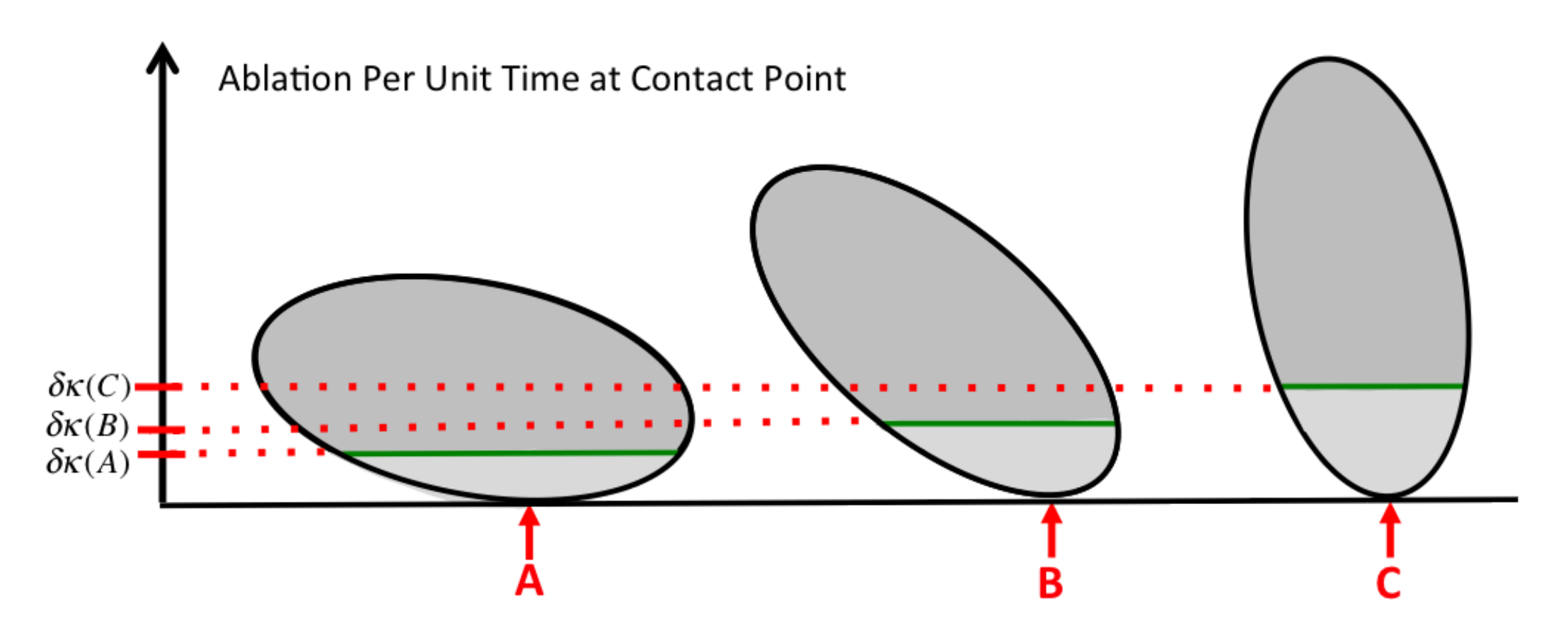
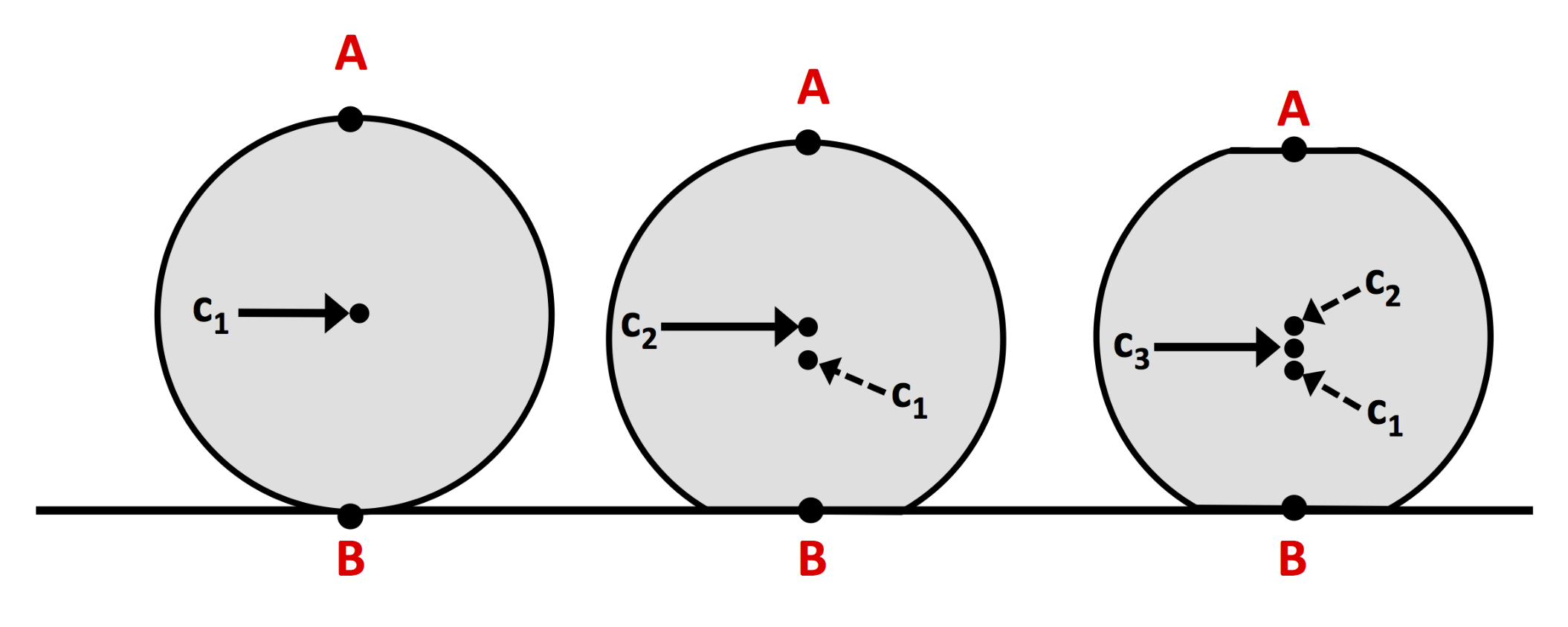
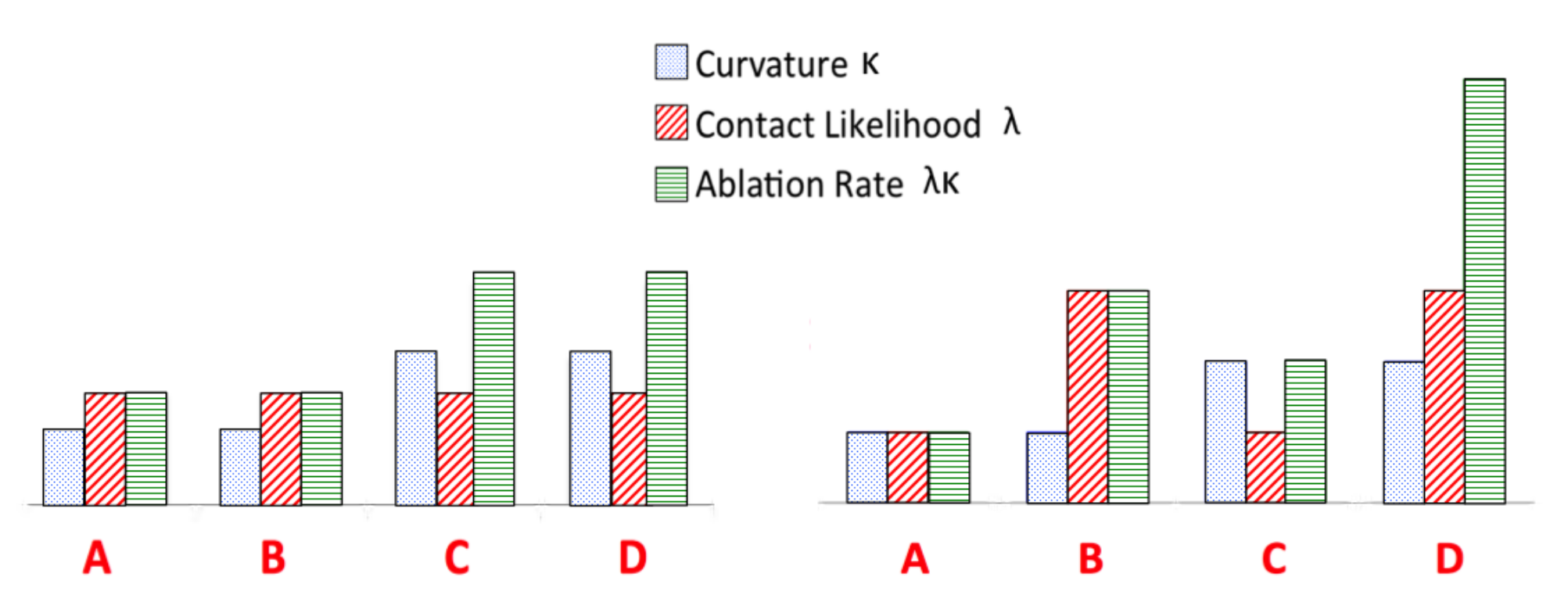
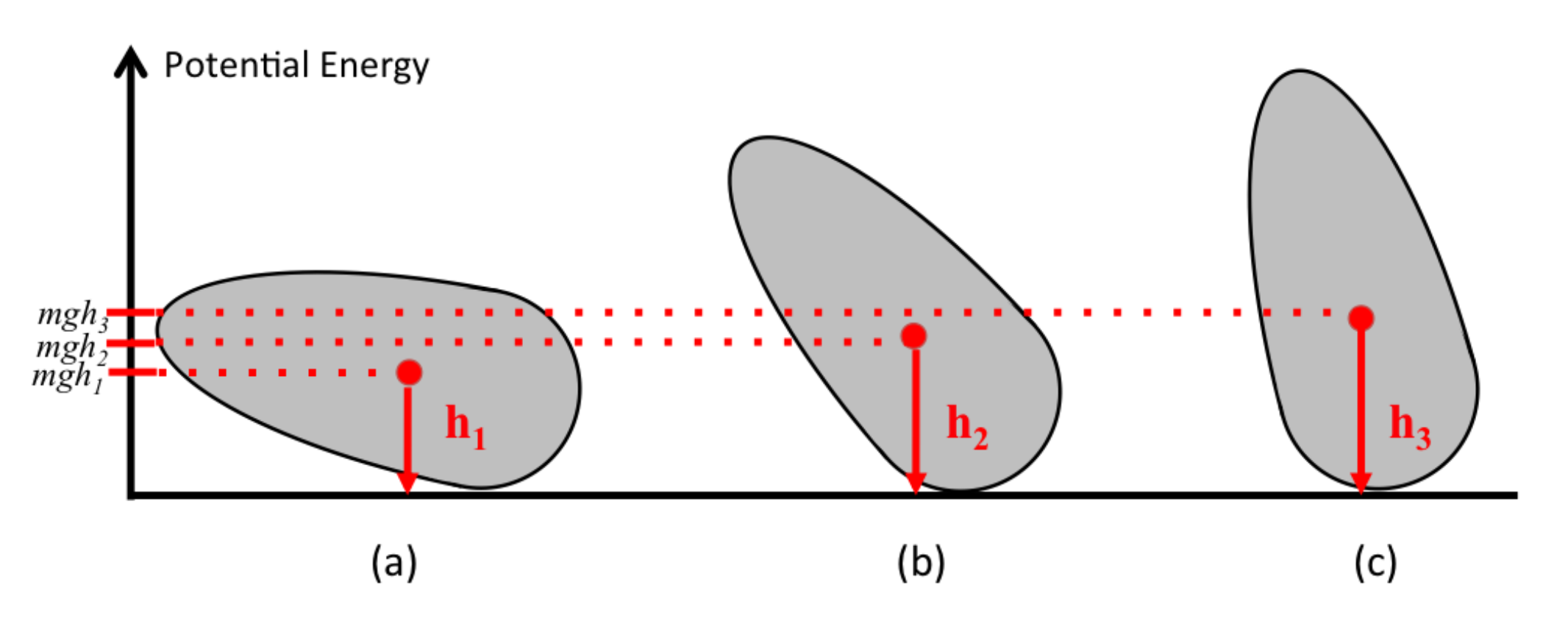
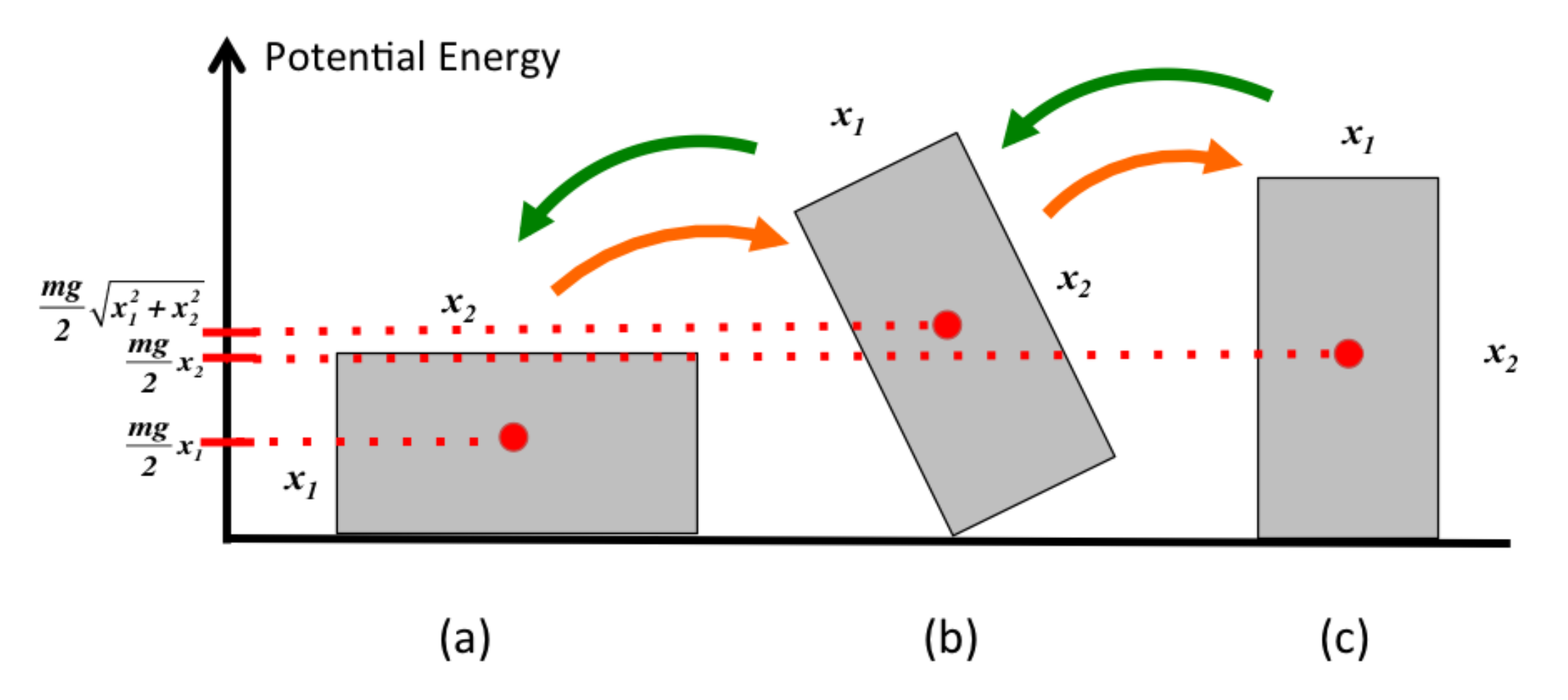
2.1. Curvature and Contact-Likelihood Model

Assuming that abrasion is proportional to curvature, this simple product principle implies that the expected rate of ablation at a point is the product of the curvature there and the average time that point is in contact with the beach, i.e., the likelihood of contact at that point. With Aristotle’s intuition that ablation should be toward the center of mass of the stone, this suggests the following conceptually natural curvature and contact-likelihood equation:

$$\begin{array}{c}\hfill \frac{\partial h}{\partial t}=-\lambda \kappa \end{array}$$

(3)

where $h=h(t,u)$ is the distance from the center of mass to the tangent plane in unit direction u at time t, $\kappa$ is the curvature as in (2), and $\lambda =\lambda (t,u)$ is the likelihood of abrasion in unit direction u at time t.

Note that Equation (3) is analogous to Aristotle’s Equation (1) in that the variable of interest is the distance h from the point of contact with the beach to the center of mass and is analogous to the curvature-driven geometric flow (2) in that the rate of change is proportional to the curvature. Furthermore, note that the functions h and $h_0$ in (1)–(3) are the support functions of the stone (simple closed curve or surface) with the origin taken as the center of mass (barycenter) and with the origin fixed, respectively. As is well-known, the limiting (renormalized) support function $h_0$ under the curve-shortening flow (2) is constant for essentially all (smooth) convex starting shapes (e.g., [20,28,29]). Since support functions uniquely determine convex bodies (e.g., [30]), and since spheres are the only convex bodies with constant support functions (with the origin at the center), this implies that the shape of a convex stone eroding under (2) also becomes spherical in the limit; see numerical experiments below.

The hypothetical convex 2-d stone in Figure 6 has the curvatures $\kappa$ at A and B equal to and exactly half the curvatures at C and D, as depicted by the osculating circles. In isotropic models of abrasion, where the likelihood function $\lambda$ is constant (dotted black line), the stone is assumed to be in contact with the beach with equal frequency (likelihood) at all points on its surface. In the non-isotropic setting shown (solid blue curve), however, B and D are more often in contact than A or C. Under the curvature and contact-likelihood model (3), the inward ablation rate at D will be strictly larger than the rates at A, B, and C (see Figure 7).

As will be seen below, $\lambda$ may sometimes be viewed as the local time of the limiting occupation measure (cf. [31]) of the time-dependent random process that reflects which direction the abrasive planar beach will be eroding the stone at that time. This crucial contact-likelihood function $\lambda$ in (3) may, in general, be very complicated since it can depend on both the shape of the stone away from the point of contact and on the dynamics of the underlying wave process.

2.2. Wave Dynamics

The first step in formalizing the fundamental role played by the waves in this non-isotropic curvature and contact-likelihood frictional abrasion model (3) is to define formally what is meant by a wave process. Real-life ocean or lake waves are random processes whose components (velocity, direction, height, temperature, etc.) vary continuously in time. For the purposes of the elementary abrasion model introduced here, it will be assumed that the critical component of the wave is its energy, and for simplicity, that this is proportional to its height.

From a realistic standpoint, it is also assumed that wave energies are bounded, i.e., not infinitely large, and that the wave crests (local maxima) are isolated; that is, no finite time interval contains an infinite number of crests. These simple notions lead to the following working definition.

Definition 1.

A wave process W is a bounded, continuous, real-valued stochastic process with isolated local maxima on an underlying probability space $(\mathsf{\Omega },\mathcal{F},P)$, i.e., $W:\mathsf{\Omega }\times {\mathbb{R}}^{+}\to \mathbb{R}$ is such that:

$$for each \omega \in \mathsf{\Omega },W(\omega ,·):{\mathbb{R}}^{+}\to \mathbb{R} is bounded and continuous with isolated local maxima$$

(4)

and

$$for each t\ge 0,W(·,t) is a random variable.$$

(5)

A standard assumption in oceanography (e.g., see [32,33,34,35]), is that the wave crests have a Pareto distribution. The next example describes a wave process with this property, and, as seen above, this Pareto distribution plays a key role in the basic heuristics underlying the physical intuition for the prototypical Equation (11) below.

Example 1.

$W(t)=X_{⌊t⌋}sin(2\pi t)$, where $⌊t⌋=max\{n:n\le t\}$, and $X_1, X_2,$ $X_3,\dots$ are i.i.d. Pareto random variables with c.d.f. $P(X_j\le x)=1-{(x_0/x)}^2$ for all $x\ge x_0>0$; see Figure 8. In contrast to the wave models in [16,36], here W is not exactly periodic (as real waves are not), since the sequence of wave crest heights of W are i.i.d. Pareto random variables.

Note that unlike Brownian motion, which is also a continuous-time continuous-state stochastic process, a wave process is in general not Markov for the simple reason that the current instantaneous state of the process alone may not indicate whether the wave is rising or falling.

Another key assumption about the wave process necessary for a physically realistic frictional abrasion process to follow the curvature and contact-likelihood model (3) is that the long-term behavior of the wave process is in equilibrium (steady-state). To put this in context, recall that for a continuous function $X:{\mathbb{R}}^{+}\to \mathbb{R}$, the occupation measure (or occupation time of X up to time s) is the function $T_{X,s}=T_s$ defined by:

$$T_s(B)=m(\{0\le t\le s:X(t)\in B\})={\int }_0^s{I}_B(X(t))dt\mathrm{for} \mathrm{all} \mathrm{Borel} B\subset \mathbb{R},$$

where m denotes the Lebesgue measure on ${\mathbb{R}}^1$, and $I_B$ is the indicator function of B.

2.3. Wave Steady-State Assumption

In addition to the wave continuity assumption (4), it is assumed that the wave process $\{W(\omega ,t):t\ge 0\}$ has a limiting average occupation measure ${\mu }_W$, i.e., there is a Borel probability measure ${\mu }_W$ on $\mathbb{R}$ satisfying:

$${\mu }_W(B)=\underset{s\to \infty }{lim}\frac{1}{s}m(\{0\le t\le s:W(·,t)\in B\})\mathrm{a}.\mathrm{s}. \mathrm{for} \mathrm{all} \mathrm{Borel} B\subset \mathbb{R}.$$

(6)

Note that assumption (6) is essentially a strong law of large numbers, and implies for instance, that W is not going off to infinity, or forever oscillating on average between several different values.

Example 2.

Suppose W is a wave process with a Pareto distribution, as in Example 1. Then the maximum heights of the wave intervals $\{X_{j}sin(2\pi t):t\in [j,j+1);j\ge 1\}$ are $X_1,X_2,\dots ,$ respectively, which by assumption are i.i.d. Pareto with $P(X_j>x)={(x_0/x)}^2$ for all $x\ge x_0$. Thus, by the Glivenko–Cantelli Theorem, the equilibrium-limiting distribution of the wave crests of W has this same Pareto distribution.

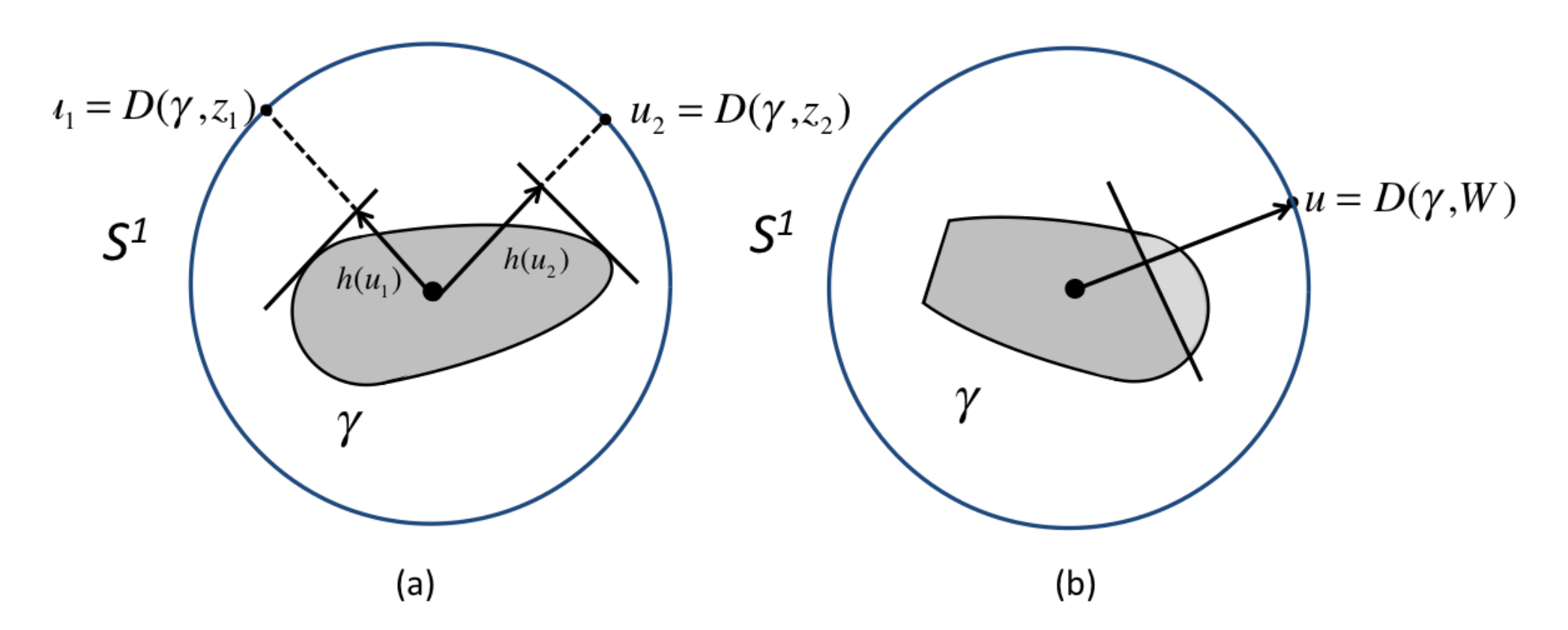
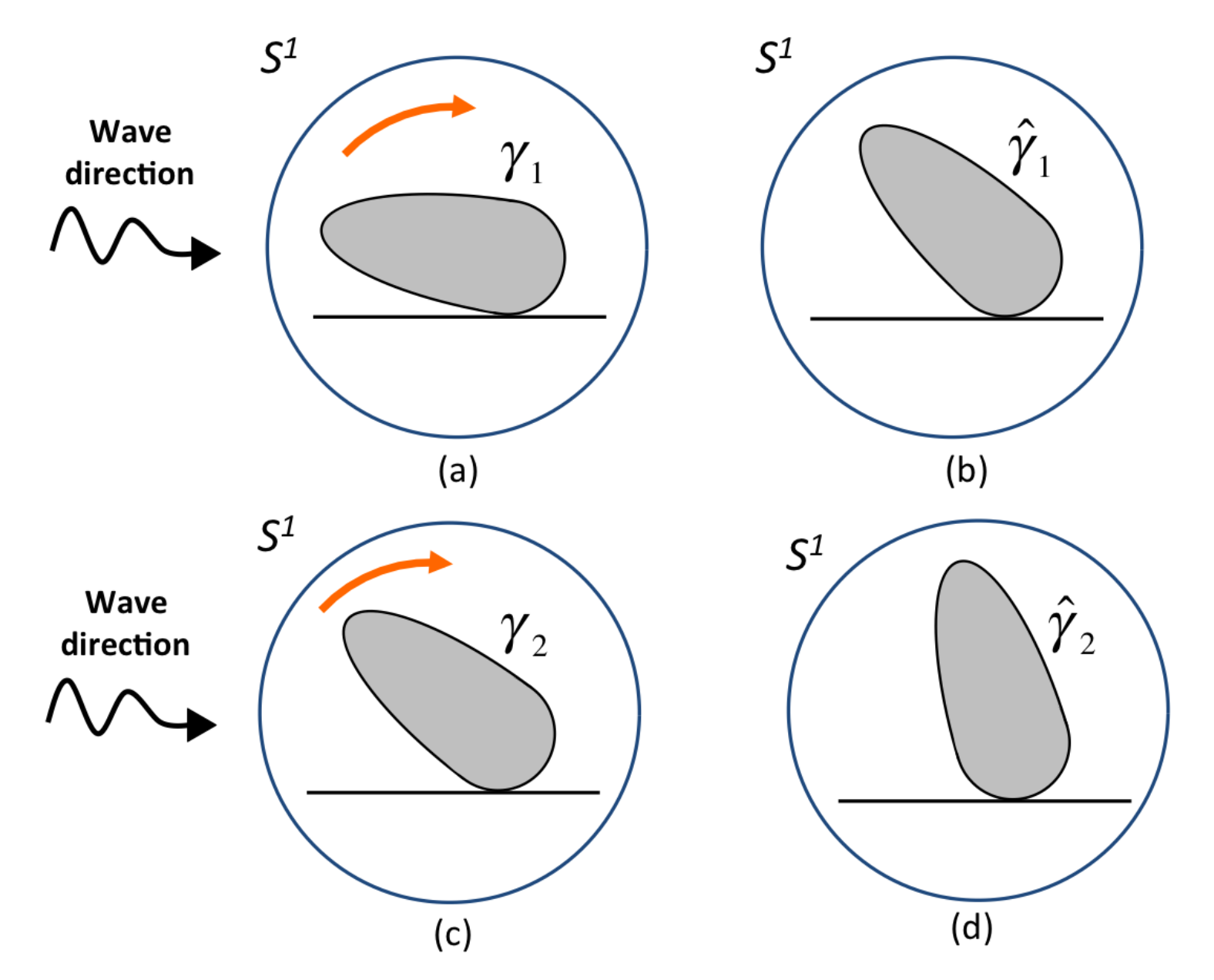
2.4. Contact-Likelihood Functions

The next step in relating the underlying wave process W to Equation (3) is to describe the relationship of W to the contact-likelihood function $\lambda$, which involves the direction of the point of abrasion on the stone as a function of the underlying time-dependent stochastic wave process W. For ease of exposition and graphical illustration, in this section, “stones” will be depicted in a 2-d setting.

Even for homogeneous and strictly convex stones, the role played by the contact-likelihood function $\lambda$ distinguishes the dynamics of the evolution of shape given by the non-isotopic model (3) from isotropic distance-driven models, such as (1), and from isotropic curvature-driven models, such as (2).

A (2-dimensional) stone is a compact convex set $K\subset {\mathbb{R}}^2$ with non-empty interior $int(K)$. Let $c=c_K\in int(K)$ denote the center of mass (barycenter) of K, and let $S^1$ denote the unit ball $S^1=\{(x,y)\in {\mathbb{R}}^2:x^2+y^2=1\}$.

Definition 2.

An oriented stone γ is an embedding $\gamma :S^1\to {\mathbb{R}}^{+}$ with the origin taken as the barycenter of the convex hull of the graph of γ. Let $\mathbb{S}$ denote the set of all oriented stones.

The point of abrasion of a stone with the beach as a result of an incoming wave depends not only on the size and shape of the stone but also on the wave energy and the orientation of the stone with the beach when the wave hits. Note that different waves hitting a stone in the same orientation may result in different directions of contact with the beach, as illustrated in Figure 9a. Moreover, note that the same wave may act on different orientations of the same stone to bring it into contact with the beach at different points on its surface, as depicted in Figure 10.

Definition 3.

An abrasion direction function D is a continuous function $D:\mathbb{S}\times \mathbb{R}\to S^1$.

The value $D(\gamma ,z)$ specifies the unit direction of the abrasion plane (the beach) resulting from a wave with energy $z\in \mathbb{R}$ acting on the oriented stone $\gamma$. In other words, $D(\gamma ,z)$ specifies which direction of $\gamma$ will be “down” after $\gamma$ is hit by a wave with energy z. Figure 9a illustrates typical values of $u_1$ and $u_2$ of the abrasion function D of the oriented stone $\gamma$ after impact by two waves with different wave energies $z_1$ and $z_2$, respectively, resulting in two different points of contact with the beach, $u_1$ and $u_2$, at distances $h(u_1)$ and $h(u_2)$ from the center of mass.

Recall that m denotes the Lebesgue measure.

Proposition 1.

Given an oriented stone γ, a wave process W, and an abrasion direction function D, the function $\mathsf{\Lambda }=\mathsf{\Lambda }(\gamma ,W,D):(\mathsf{\Omega },\mathcal{F})\to [0,1]$ given by:

$$\mathsf{\Lambda }(B)=\underset{s\to \infty }{lim}\frac{1}{s}m(\{0\le t\le s:D(\gamma ,W(·,t))\in B\})\mathrm{for} \mathrm{all} \mathrm{Borel} B\subset S^1$$

(7)

almost surely defines a Borel probability measure on $S^1$.

Proof. 

Fix a Borel set B in $S^1$. Recall by (5) that for all $t\ge 0$, $W(·,t)$ is a random variable. By (4) and Definition 3, $D(\gamma ,·)$ is continuous, and hence Borel measurable, so there exists a Borel set $\widehat{B}$ in $\mathbb{R}$ such that:

$$D(\gamma ,W(·,t))\in B)\iff W(·,t)\in \widehat{B}\mathrm{for} \mathrm{all} t\ge 0.$$

(8)

By the wave steady-state assumption (6), the limit in (7) exists and equals ${\mu }_W(B)$ a.s., so since ${\mu }_W$ is a probability measure, $0\le \mathsf{\Lambda }(B)\le 1$ a.s. The demonstration that $\mathsf{\Lambda }$ is a.s. a measure is routine. □

The probability measure $\mathsf{\Lambda }$ in Proposition 1 is the occupation measure (cf. [31]) of the steady-state likelihood (average time) that the oriented stone $\gamma$ is in contact with the abrasive plane in various directions, assuming that the rate of abrasion is negligible. For example, if $I\in S^1$ is an interval of unit directions, then $\mathsf{\Lambda }(I)$ is the probability that the oriented stone $\gamma$ is in contact with the beach in direction u for some $u\in I$.

2.4.1. Continuous Contact-Likelihood Functions

If $\mathsf{\Lambda }$ is absolutely continuous (with respect to the Lebesgue measure on $S^1$), then $\lambda$, the Radon–Nikodym derivative of $\mathsf{\Lambda }$ with respect to the uniform distribution on $S^1$, is the local time (cf. [37]) of the stochastic process $D(\gamma ,W)$. That is, $\lambda =d\mathsf{\Lambda }/dm$ is the density function of the distribution of the occupation measure. In some instances, as will be seen below, $\lambda$ may be approximated by a simple function of $\gamma$, in particular, of the support function h of $\gamma$.

Here, the energy required to produce frictional abrasion of a stone on the beach is assumed to come only from the waves, which lift and slide the stone against the beach (recall that in this simple model, collisional abrasion with other stones is assumed negligible). To lift the stone in Figure 11 to abrasion position (c) requires more energy than to lift it to position (b), and (b) requires more energy than (a). Thus, the expected likelihood (or frequency that) the stone is in position (c) is less than that in (b), and (b) less than (a). This means that for these three points of contact, the value of the contact-likelihood function $\lambda$ is decreasing from (a) to (c); the actual numerical values of $\lambda$ at these points, of course, also depend on the external wave process.

Consider the curvature and contact-time ablation Equation (3) when the ablation process is assumed to be continuous in time and space, i.e., a curve-shortening process (cf. [38]). As before, the incoming wave crest of W lifts the stone to a position determined by the wave parameters (e.g., kinetic energy of the crest), where its surface is ablated incrementally.

Fix $t>0$, and suppose that the oriented stone $\gamma =\gamma (t)$ is smooth and strictly convex, i.e., the non-empty interior of $\gamma$ is strictly convex with a smooth $(C^{\infty })$ boundary. Since the support function h is continuous, there exist $0<h_{min}<h_{max}<\infty$ so that on $\gamma$:

$$\mathrm{range}(h)=[h_{min},h_{max}]\subset {\mathbb{R}}^{+}.$$

(9)

Let $\mathsf{\Lambda }$ denote the occupation measure of the likelihood function of the abrasion direction process as in Proposition 1, and let $X_{\mathsf{\Lambda }}$ denote a random variable with values in the unit sphere and with distribution $\mathsf{\Lambda }$, i.e., for all intervals of unit directions I, $P(X_{\mathsf{\Lambda }}\in I)=\mathsf{\Lambda }(I)$ represents the likelihood that $\gamma$’s direction of contact with the planar beach at time t is in I. Assuming that W and D are continuous ((4) and Definition 3), it is routine to check that since $\gamma$ is strictly convex, the random direction $X_{\mathsf{\Lambda }}$ is absolutely continuous. Thus, $X_{\mathsf{\Lambda }}$ has a (Borel) density function $\lambda :S^1\to {\mathbb{R}}^{+}$ satisfying $P(X_{\mathsf{\Lambda }}\in I)={\int }_I\lambda (u)du$ for all intervals $I\subset S^1$.

Let $Y_{\mathsf{\Lambda }}$ denote the random variable $Y_{\mathsf{\Lambda }}=mgh{X}_{\mathsf{\Lambda }}$, where m is the mass (e.g., volume, or area in the 2-d setting) of $\gamma$ and g is the force of gravity. Thus, $Y_{\mathsf{\Lambda }}$ represents the potential energy of $\gamma$ when $X_{\mathsf{\Lambda }}$ is the direction of contact of the stone $\gamma$ with the abrasive plane, i.e., when $X_{\mathsf{\Lambda }}$ is the “down” direction at time t. Then (9) implies that:

$$\mathrm{range}(Y_{\mathsf{\Lambda }})=[mg{h}_{min},mg{h}_{max}]\subset {\mathbb{R}}^{+}.$$

(10)

Assuming that the wave crest energies (relative maxima) are converted into the potential energy of the stone in the corresponding “down” positions (see Figure 11), this implies that the distribution of $Y_{\mathsf{\Lambda }}$, given that $Y_{\mathsf{\Lambda }}$ is in $[mg{h}_{min},mg{h}_{max}]$, is the same as the distribution of the successive wave crests of W (see Figure 8) given that they are in $[mg{h}_{min},mg{h}_{max}]$. Ignoring secondary effects, such as multiple rolls of the stone, yields an intuitive physical explanation for the prototypical model to be described in Section 3 below.

2.4.2. Discrete Contact-Likelihood Functions

In actual physical frictional abrasion, of course, the evolution of the exact shape of a stone is not continuous in time since the ablated portions occur in discrete packets of atoms or molecules. For isotropic frictional abrasion, this has been studied in [39,40,41], where analysis of the evolution of the rounding of stones uses Monte Carlo simulation and a “stochastic chipping” process. The goal of this subsection is to present an analogous stochastic discrete-time analog of the evolution of a stone’s shape under the basic isotropic curvature and contact-likelihood Equation (3), where discrete portions of the stone are removed at discrete steps (see Figure 9b), but now where the effects of both the global shape of the stone and the wave dynamics (via $\lambda$) are also taken into account.

In this “chipping” setting, as illustrated in Figure 9b, an oriented stone $\gamma$ is hit by a wave W resulting in the unit direction of contact $u=D(\gamma ,W)$ of $\gamma$ with the abrasive plane, at which time a small fixed fraction $\delta$ of the volume of the stone is ground off in that direction. (Recall as illustrated in Figure 4 that removing a fixed fraction of the stone in a given direction is analogous to removing a portion proportional to its curvature there.) The evolving stones in this discrete stochastic framework are eventually random convex polygons (polyhedra), for which almost every point on the surface has curvature zero. Thus, this assumption that fixed proportions are removed, rather than portions proportional to curvature, seems physically plausible.

To see how a contact-likelihood function $\lambda$ may sometimes be discrete and explicitly calculated (or approximated), consider the 2-dimensional rectangular “stone” in Figure 12. Without loss of generality, $x_1<x_2$ and $m=2/g$, so the potential energy of the stone in position (a) is $x_1$, and the potential energy in position (c) is $x_2$.

Let W be a Pareto wave process, as in Example 1; recall Figure 8 for a sample path. Then the crests (maximum wave heights) of W are the i.i.d. random variables $\{X_j;j\in \mathbb{N}\}$. Let $\overline{F}$ denote the complementary cumulative distribution function of $X_1$, i.e., $\overline{F}=P(X_1>x)$ for all $x\ge 0$.

Suppose first that the stone is on a longer $x_2$-side (Figure 12a) at time $j\in \mathbb{N}$. Then it flips onto an $x_1$-side (Figure 12c) during the time interval $[j,j+1)$ if, and only if, the value of $X_j$ is greater than the energy required to lift the stone from position (a) to position (b), i.e., is enough to increase the potential energy of the stone from $x_1$ to more than $\sqrt{{x_1}^2+{x_2}^2}$.

Since the $\left\{X_j\right\}$ are i.i.d., this implies (ignoring multiple flips) that the number of waves until a flip occurs from (a) to (c) is a geometric random variable $N_1$ with parameter $\overline{F}(\sqrt{{x_1}^2+{x_2}^2}-x_1):=p_1$, so the expected value of $N_1$ is $E(N_1)=1/p_1$. Similarly, the expected number of waves $E(N_2)$ until a flip occurs from a shorter $x_1$-side (Figure 12c) to an $x_2$-side is $1/p_2$, where $p_2=\overline{F}(\sqrt{{x_1}^2+{x_2}^2}-x_2)>p_1$.

Thus, by the strong law of large numbers, the limiting frequency of time that the stone is on side $x_1$ is less than the relative frequency of time the stone is on side $x_2$, since:

$$\frac{E(N_2)}{E(N_1)+E(N_2)}=\frac{1/p_2}{1/p_1+1/p_2}=\frac{p_1}{p_1+p_2}<\frac{p_2}{p_1+p_2}=\frac{E(N_1)}{E(N_1)+E(N_2)}.$$

The next example illustrates how the resulting discrete contact-likelihood function $\lambda$ may sometimes be explicitly calculated.

Example 3.

Suppose the 2-dimensional stone is as in Figure 12 with $x_1=6$ and $x_2=8$, and the relative maxima (crests) of the wave process W are as in Example 1. Then:

$$p_1=\overline{F}(4)=\frac{c}{4^2}>\frac{c}{2^2}=\overline{F}(2)=p_2,$$

so the likelihood that the stone is on a short side ($x_1$ or its opposite side) is $\frac{2^2/c}{2^2/c+4^2/c}=0.2$ and the likelihood the stone is on a long side ($x_2$ or its opposite) is $0.8$. This implies that in terms of the oriented stone as in Figure 12a, the contact likelihood function λ at time t satisfies $\lambda (t,(1,0))=\lambda (t,(-1,0))=0.1,\lambda (t,(0,1))=\lambda (t,(0,-1))=0.4$, and $\lambda (t,u)=0$ for $u\notin \{(1,0),(-1,0),(0,1),(0,-1)\}$.

3. A Prototypical Non-Isotropic Model under Pareto Wave Distribution

In choosing a mathematical model to represent a physical process, such as frictional abrasion of a beach stone, there is typically a trade-off between maximal precision and simplicity. For example, the abrasion of beach stones also depends on small aerodynamic and hydrodynamic forces and even on tiny variabilities in gravitational forces, but these are ignored in most classical models, such as (1) and (2). As noted by Fields Medallist Timothy Gowers, “When choosing a model, one priority is to make its behaviour correspond closely to the actual, observed behaviour of the world. However, other factors, such as simplicity and mathematical elegance, can often be more important” [42] (p. 5). Similarly, the emphasis on the models presented here is on simplicity and elegance, just as those in (1) and (2).

In cases where the wave process and stone satisfy standard regularity conditions, as will be seen next, the contact-likelihood function $\lambda$ may sometimes be approximated by a very simple function of the distance from the center of mass of the stone. A concrete example of this is $\lambda =h^{-\alpha }$ for some $\alpha \ge 1$, in which case the curvature and contact-likelihood function (3) becomes the curvature and distance-driven flow

$$\frac{\partial h}{\partial t}=-\frac{\kappa }{h^{\alpha }}$$

(11)

where $h=h(t,u)$ is the distance from the center of mass to the tangent plane in unit direction u at time t, $\kappa$ is the curvature as in (2), and $\alpha \ge 1$.

The novelty of this model (11) is that it considers the product (rather than the sum) of curvature and distance-driven terms, and it derives the distance-driven term from the Pareto distribution of waves.

In the partial integro-differential Equation (11), the different roles of the three essential rate-of-abrasion factors—curvature at the point of contact, global shape of the stone, and wave dynamics—are readily distinguishable in the three variables $\kappa$, h, and $\alpha$. The variable $\kappa$ reflects the curvature at the point of contact, h reflects the global shape of the stone via its evolving center of mass, and $\alpha$ reflects the intensity of the wave process (in fact, in the interpretation in Example 4 below, $\alpha$ is an explicit decreasing function of the expected (mean) value of the wave crests). For example, increasing the curvature at the point of contact affects neither the center of mass nor the wave dynamics, changing the center of mass affects neither the curvature at the point of contact nor the wave dynamics, and changing the wave dynamics affects neither the center of mass nor the curvature of the stone.

3.1. Thought Experiment for Equation (11)

Consider a single fist-sized non-spherical convex stone (such as one of those in Figure 2 and Figure 3) that is eroding by friction as it is rolled about by waves on a flat sandy beach. Assume that when a wave comes in, it rolls/lifts the stone to the point of contact with the beach such that the potential energy of the stone in that position is proportional to the wave crest height—larger waves lift the center of mass of the stone higher.

Next, note that if the expected number of waves needed until the stone comes into contact with the beach at point B on the surface of the stone is twice the expected number of waves needed until point A comes into contact, then over time, point B will be in contact with the beach half as often as point A. That is, the likelihood of the stone being in contact with the beach at a given point on the surface of the stone is proportional to the reciprocal of the expected waiting time to hit that point.

As will be seen in the next example, assuming the random wave crest heights follow a Pareto distribution (a standard assumption; see below), the expected number of waves until a crest of height at least h occurs is proportional to $h^{\alpha }$, so the contact-likelihood is proportional to its reciprocal $1/h^{\alpha }$. Since the instantaneous rate of ablation at a point of contact is assumed to be proportional to the curvature $\kappa$ at that point (again, sharper points erode faster), taking the constant of proportionality to be 1 gives $\kappa /h^{\alpha }$, which yields the shape evolution Equation (11).

As suggested in this thought experiment, the new PDE model (11) is only intended to model the shape evolution of intermediate macroscopic-sized beach stones, not huge boulders or grain-sized particles, e.g., when the size of the beach stone is below the Pareto threshold $x_0$ of the wave. Intuitively, when the beach stone becomes extremely small, it is comparable to one of the grains of sand that make up the beach and is subject to different dynamics, such as collisional abrasion and fracturing. Moreover, (11) does not address the changing size of the abrading stone, which in some river rock models has been shown to decrease exponentially in time (e.g., see [8,43]).

Example 4.

Suppose that γ is smooth and strictly convex and that W is a wave process as in Example 1, with the $\left\{X_j\right\}$ i.i.d. Pareto random variables satisfying $P(X_j>x)={(x_0/x)}^2$ for all $x\ge x_0$ for some $x_0>0$. Then the sequence $X_1,X_2,\dots$ represents the values of the successive crests (relative maxima) of W, i.e., $X_j=max\{W(·,t):t\in [j,j+1)\}$ (see Figure 8).

This implies that for all $x_0<x_1<x_2$, the conditional distribution of each $X_j$, given that $X_j$ has values in $[x_1,x_2]$, is an absolutely continuous random variable with density proportional to $1/x^3$ for $x\in [x_1,x_2]$, i.e., there is a $c>0$ so that:

$$P(X_j\in I\mid X_j\in [x_1,x_2])=c{\int }_I\frac{1}{x^3}dx for all I=(a_1,a_2)\subset [x_1,x_2].$$

(12)

Letting $Y_j$ denote the maximum potential energy of the stone γ during time period $[j,j+1)$, then $Y_j=mgh(X_j)$ (see Figure 11). Again assuming that the wave energy at its crests is converted into the potential energy of the stone (see Figure 12), (12) implies that $Y_j$ is also absolutely continuous with density proportional to $1/h^3$ for $h\in [h_{min},h_{max}]$, so (3) yields (11) with $\alpha =3$. Note that as the stone gets smaller, the factor $1/h^3$ remains unchanged but is applied to new values of $h_{min}$ and $h_{max}$. This suggests that stones of different sizes on the same beach, i.e., subject to the same (Pareto) wave process, will abrade toward the same (renormalized) shapes.

As noted above, the contact-likelihood function $\lambda$ in basic Equation (3) may also reflect the observed evolving oval shapes of natural non-homogeneous and/or non-convex stones (see Figure 13) under frictional abrasion with a rough plane, perhaps also via the model in (11) directly. Furthermore, as observed by Krynine, “on the seashore the similar pebbles are seen in the same places” [3], and evidence of this is also apparent in Figure 3. Note that stones from the same beach (left and center) appear to have roughly the same shape independent of size—smaller stones do not appear to be becoming spherical or cigar-shaped. However, the shapes of stones from different beaches (right) may vary significantly. In fact, the new model presented here predicts exactly this behavior—that the shapes of stones on the same beach, i.e., subject to the same wave action, tend to evolve toward the same shape, independent of size.

Remark 3.

Replacing the curvature term κ in Equations (2), (3), and (11) by its positive part ${\kappa }^{+}=max\{\kappa ,0\}$ allows those abrasion models to be extended to non-convex initial shapes, and this is left to the interested reader. For informal empirical evidence, see Figure 13.

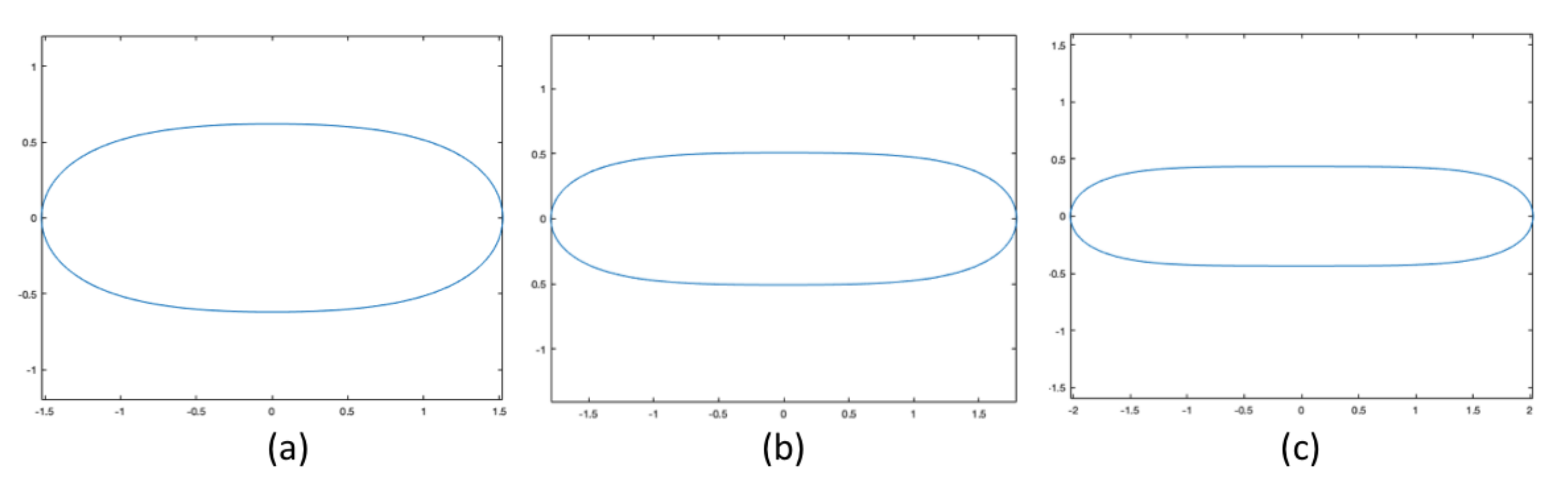
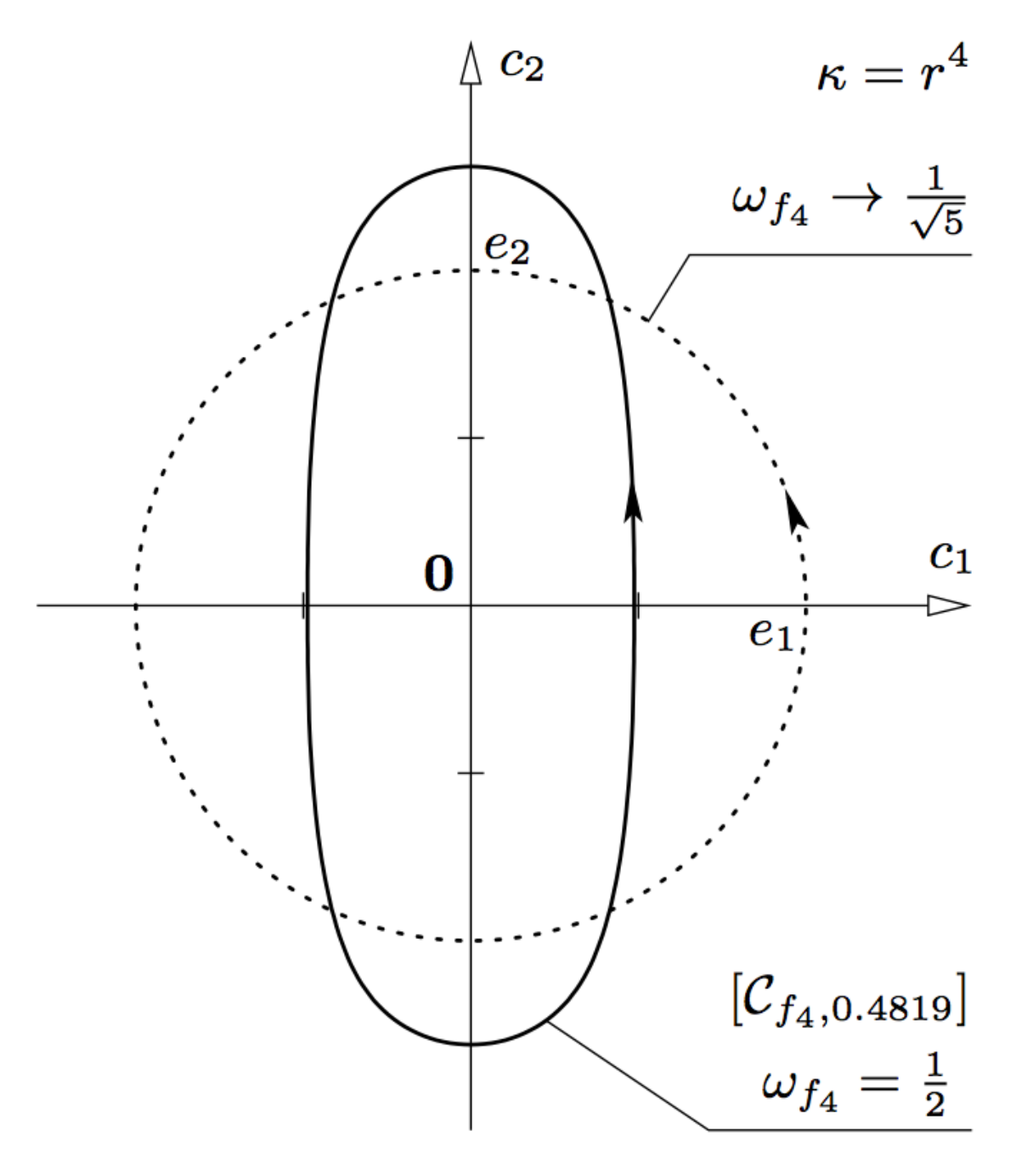
3.2. Limiting Shapes

Recall that the limiting shape of stones under curvature-only ablation (2) is spherical, and when normalized, is the unit sphere. Thus, if the contact-likelihood function $\lambda$ in (3) is constant, for example, then the process is isotropic, and the limiting shape will also be spherical. For non-isotropic (non-constant) contact likelihood functions $\lambda$, however, the limiting shape depends on $\lambda$, and this shape may sometimes be determined or approximated as follows.

First, it is routine to check that the renormalized shapes will remain the same if and only if $h=h(u,t)$ satisfies:

$$\frac{\partial h}{\partial t}=-ch$$

(13)

for some $c>0$. Renormalizing time by taking $c=1$ and equating the term $\partial h/\partial t$ in Equation (13) with the same term in (3) yields the shape equation:

$$\kappa =\frac{h}{\lambda }.$$

(14)

Suppose that the underlying wave crests have a Pareto distribution with $\alpha >1$, and that the ablation process results solely from the conversion of the energy of the wave process W into the potential energy of the stone by lifting it to the position where abrasion will occur. Then, as seen in Example 4, $\lambda$ is proportional to $h^{-\alpha }$. With (14) this yields the limiting shape equation:

$$\kappa =h^{\alpha +1}.$$

(15)

Since $\kappa ={(h+h^{″})}^{-1}$, and since h is the distance to the center of mass, note that (15) is a non-local ordinary differential equation. Numerical solutions of (15) for $c=1$ and $\alpha =2.5,3,4$ are shown in Figure 14. Note that flatter ovals correspond to Pareto waves with smaller means (i.e., with lighter tails); that is, as physical intuition suggests, more powerful waves produce more spherical limiting shapes.

Note also that the oval shapes in Figure 14 appear very similar to the non-elliptical ovals found by Rayleigh shown in Figure 2 in his empirical data in both natural specimens of beach stones and in his laboratory experiments. There is also a close resemblance of these same shapes to those in Figure 4 of [27], which studies the evolving shapes of carbonate particles that are both growing from chemical precipitation and eroding from physical abrasion.

The equations for these ovals, the solutions of (15), are not known to the author. Moreover, as Rayleigh noted, “the principal section of the pebble lies outside the ellipse drawn to the same axes, and I have not so far found any exception to this rule among artificial pebbles shaped by mutual attrition, or among natural pebbles” [17].

Equation (15) is analogous to Berger’s planar equation:

$$\begin{array}{c}\hfill \kappa =r^{\alpha +1},\end{array}$$

(16)

where $\kappa =\kappa (u)$ and $r=r(u)$ are the curvature and distance from the origin in unit direction u.

In Equation (16) with $\alpha =3$, Berger proved [44] (Theorem 5.6) that there are, modulo rotations, precisely two solutions in the plane that are simple closed (counter-clockwise oriented) curves: the unit circle and one non-circular oval (see Figure 15). Moreover, the unique non-circular, oval solution of $\kappa =r^4$ is “readily seen to not be an ellipse, an observation that nicely contrasts the ellipticity of all limit shapes for the affine curve-shortening” [44] (p. 2). That unique oval solution is strikingly similar to the empirical oval solutions of $\kappa =h^4$ found here; compare Figures 1 and 9 of [44] with Figure 14b.

Several other theories have also been proposed to model the evolution of non-spherical stone shapes. For example, [27] shows the existence of non-spherical limits for a process that involves a model with a combination of collisional abrasion, frictional abrasion, and isotropic surface growth, and [39] is a PDE model for purely collisional abrasion that also predicts non-spherical limit shapes. In fact, as will be seen in the next section, the apparent evolving form of an egg-shaped stone abrading under (11) is similar to that depicted in Figure 4 in [36], which is based on a model leading to the formation of elliptical stones by both grinding and rolling abrasion. For an overview of existing models of the geometry of abrasion, including their history, new extensions, and the mathematical relationship between various models, the reader is referred to [8].

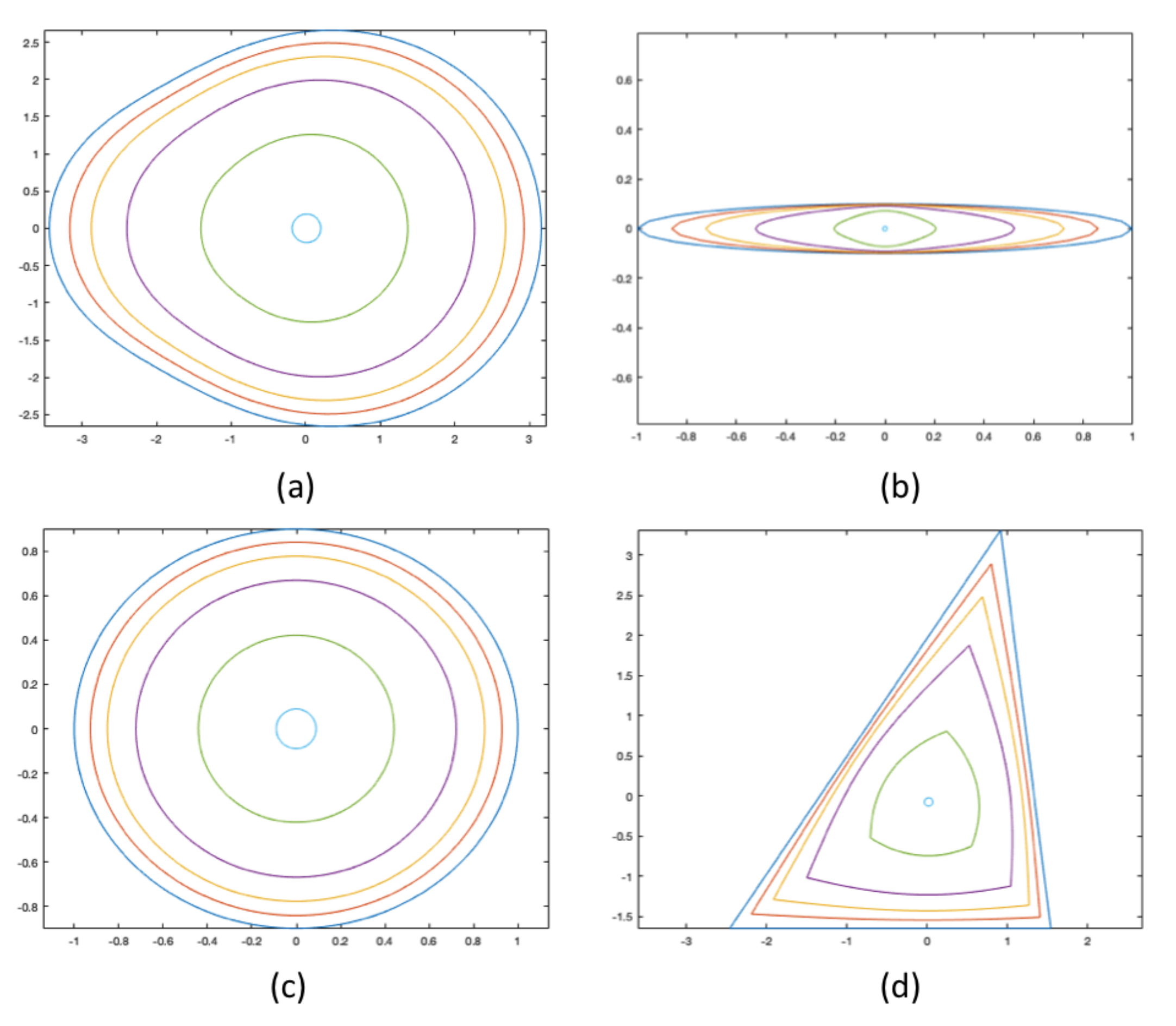
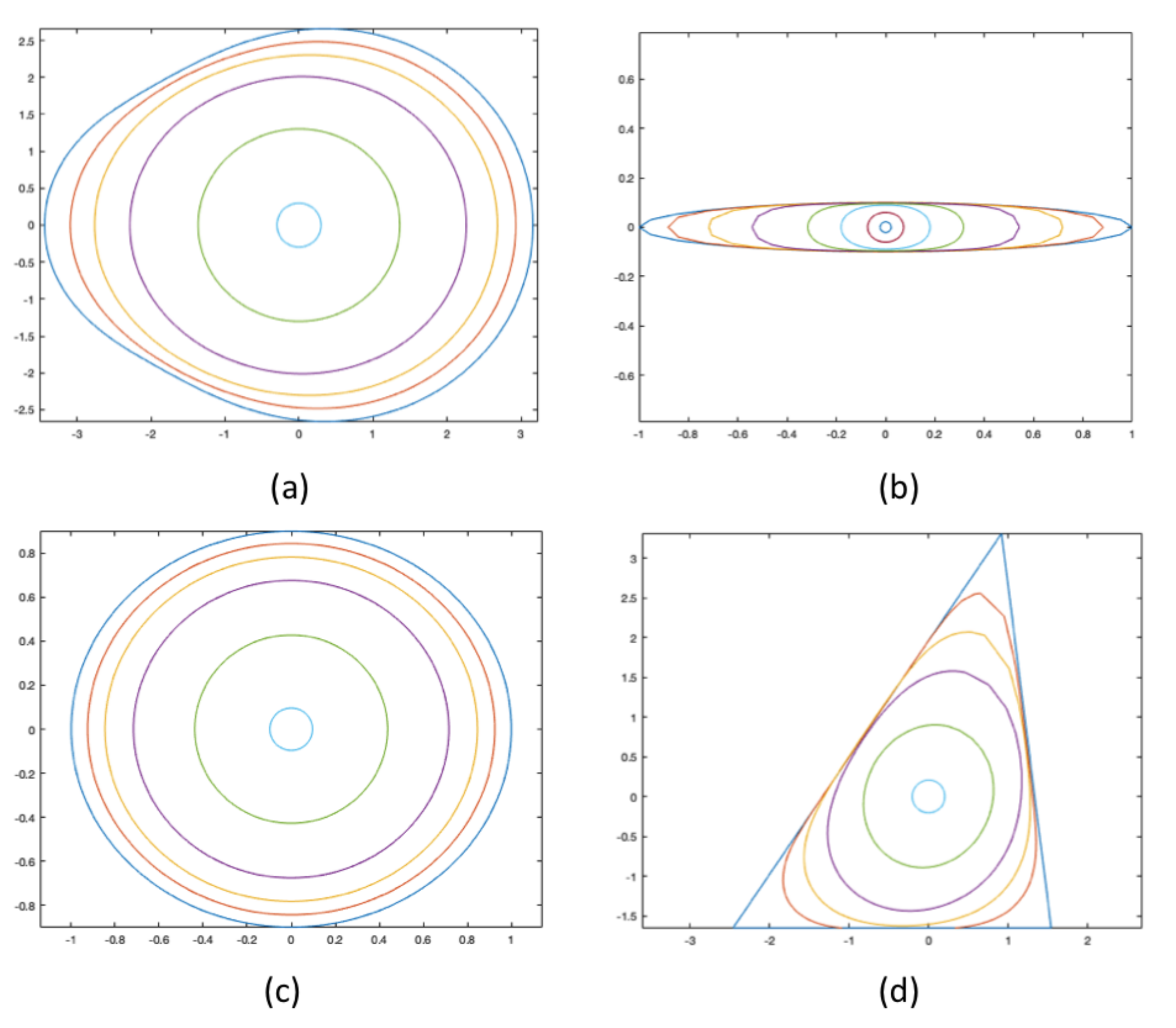
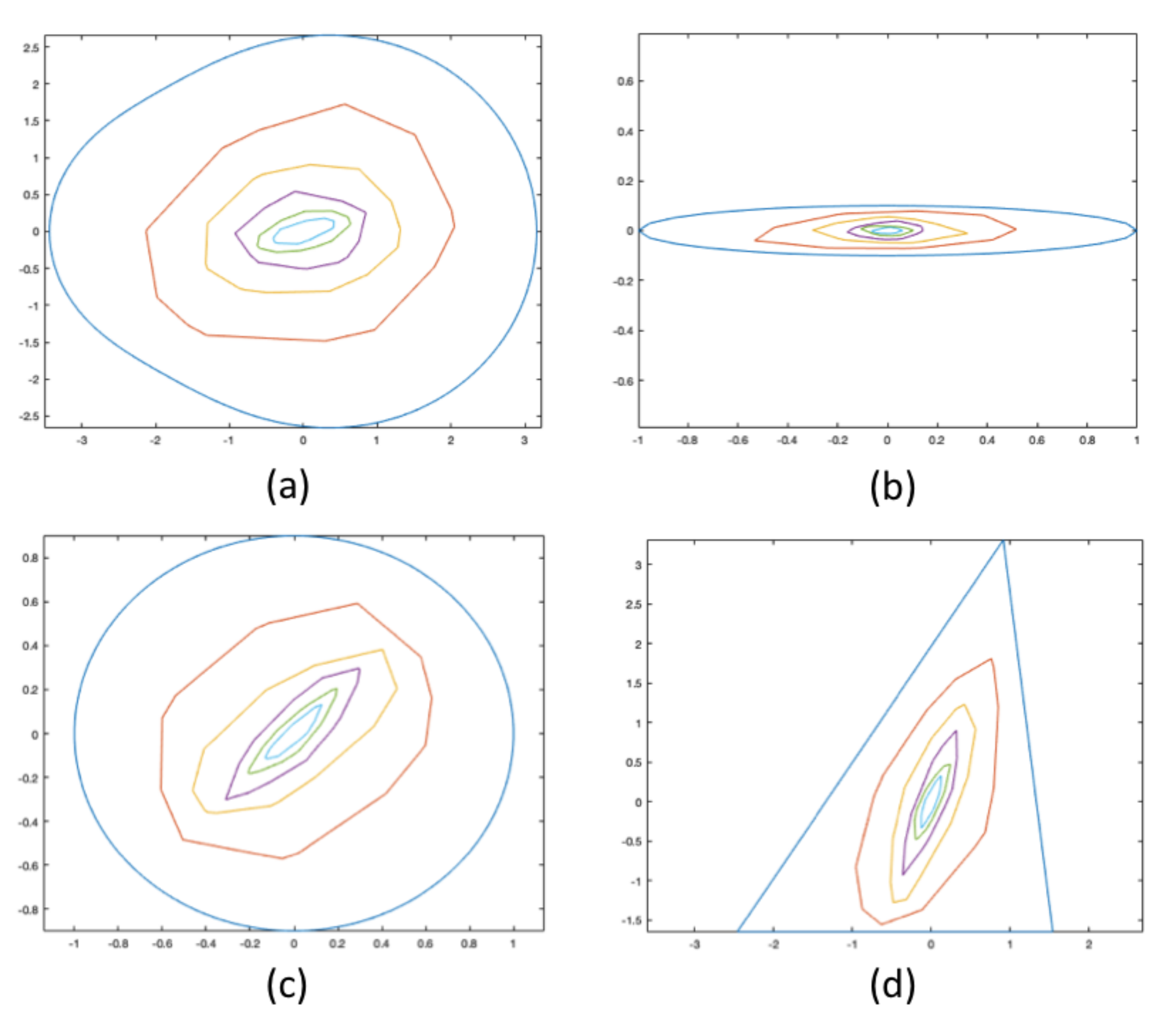
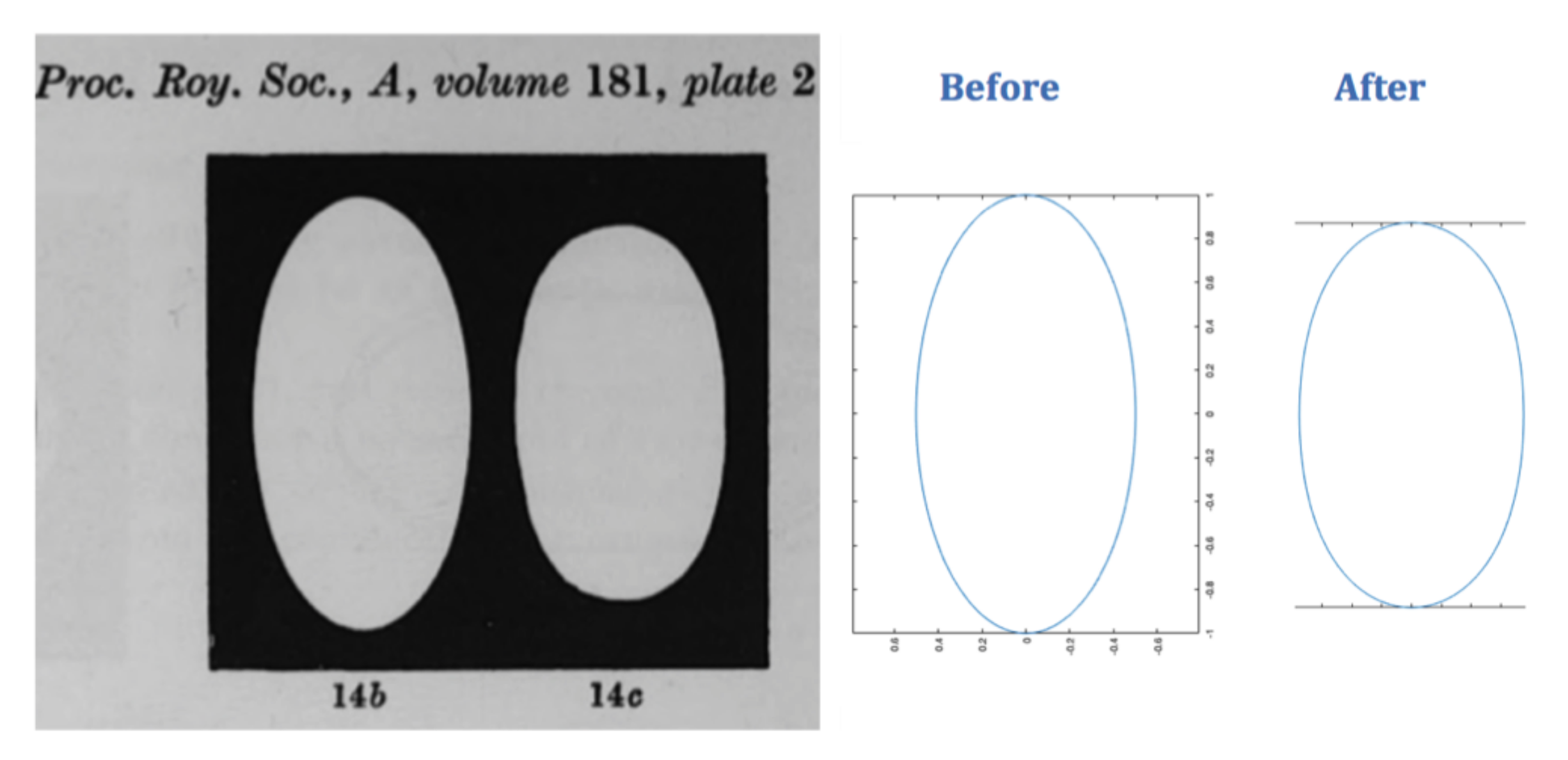
4. Preliminary Numerical Experiments

The graphics in this section were generated in Matlab using standard semi-implicit curve-shortening techniques (as described in [38]) and random number (Monte Carlo) generators. These only yield basic approximations of the evolving shapes, not state-of-the-art renditions. The pseudocode for these numerics can be found in Appendix A, and the Matlab code is available in the Supplementary Materials.

Figure 16 illustrates numerical solutions of Aristotle’s Equation (1) in the 2-dimensional setting for four different initial shapes (egg-shaped, ellipses with large and small eccentricities, and triangle) for the function $f(h)=h^2$. Note that in this case, shapes appear to become circular in the limit, which is not the case for some other choices of f, such as $f(h)=h$. Under this model (1), the further from the center of mass, the faster the stone is eroding.

Similarly, Figure 17 shows analogous approximations of the evolution of the same four initial shapes under the curvature-driven flow (2). Note again the apparent convergence to circles, as predicted by theory (cf. [20,22,23,28]).

Figure 18 depicts numerical approximations of those same four initial shapes under the new curvature and distance-driven flow (11). Note that a nearly-circular ellipse apparently becomes more elongated (e.g., circles or spheres may be in unstable equilibrium), and conversely, the very thin ellipses abrade towards less elongated ovals.

Figure 19 illustrates the results of a Monte Carlo simulation of the stochastic-slicing process evolving under the discrete-time analog of Equation (3) in the special case (11), with $\alpha =3$ for the same four initial 2-d stone shapes as in Figure 16, Figure 17 and Figure 18. Here, the direction of ablation is again selected at random, not uniformly (isotropically), but inversely proportional to the cube of the distance in that direction from the center of mass to the tangent plane (line). Note the apparent similarity of the evolving oval shapes in both the continuous and discrete settings.

An analogous Monte Carlo simulation of this same frictional abrasion process is illustrated in the 3-d setting in Figure 20, where a non-regular tetrahedron is undergoing a discrete-time analog of the same basic non-isotropic curvature, and contact-likelihood model (11) with $\alpha =3$. Similar to the analysis in [41], where a discrete-time stochastic chipping model of the isotropic curvature-driven Equation (2) was used to study the rate at which initial 3-d shapes converge toward spheres the evolving body here repeatedly has sections of a fixed proportion $\delta$ of the volume removed at each step by a planar cut, in a random direction, normal to the support function in that direction. In this case, however, in sharp contrast to that in [41], the abrasion is non-isotropic with the likelihood of abrasion in a given direction inversely proportional to the cube of the distance from the center of mass of the stone to the supporting plane in that direction (cf. Example 4).

Moreover, note that the chipping process depicted in Figure 20, even when renormalized at each step, does not have a limiting shape since at each successive iteration, a fixed proportion of the volume is chipped off. In this scenario, the author conjectures that there is a limiting distribution of (convex polyhedral) shapes, and that illustrated in Figure 20 is a representative case.

As one final example, Figure 21 illustrates the limiting shapes predicted by the prototypical model in Equation (11) with the empirical laboratory data reported by Rayleigh [13]. The stone (14b) in Figure 21 is the near-elliptical actual stone he subjected to frictional abrasion, and to its right (14c) is the same stone after ablation. In the two curves on the right in Figure 21, the one on the left is an exact ellipse with minor axis 0.5 and major axis 1.0 centered at the origin, and to its right is the evolved shape after curve shortening via the new curvature and contact-likelihood Equation (11) with $\alpha =2.2$. Note the striking resemblance of the experimental results with the model presented in basic Equation (11), i.e., (3) with $\lambda =h^{-\alpha }$.

5. Discussion

The stochastic non-isotropic model of the evolution of the shapes of beach stones introduced here is meant as a starting point to include the effects of both the global (non-local) shape of the stone and the wave dynamics into the process. The main equations are simple to state, but as both non-local and non-linear partial integro-differential equations, they are difficult to solve exactly, and no solutions are known to the author. Numerical approximations in the continuous-time continuous-state framework using standard curve-shortening algorithms and in the discrete-time discrete-state framework using Monte Carlo simulation both indicate remarkably good agreement with the shapes of both natural and artificial stones undergoing frictional abrasion on a flat plane.

Future Research Directions

The following is a list of some of the mathematical problems related to the models above that this author does not know how to solve.

• Prove or disprove that in the 2-d version of Aristotle’s Equation (1) with $f(h)=h^{\alpha }$, for all convex initial shapes, the renormalized shapes converge to a circle for all $\alpha >1$ and remain the same for $\alpha =1$. Determine the limiting renormalized shapes for $0<\alpha <1$, and for all $\alpha >0$ for which there is convergence, identify the rates of convergence.
• Prove or disprove that besides the circle, there is only one simple closed solution to the 2-d equation $\partial h/\partial t=-\kappa /h^3$ when the sizes are renormalized; identify the equation for the non-circular solution if there is one. Prove or disprove that the circle is in unstable equilibrium and that the other simple closed solution is in stable equilibrium. More generally, do the same for solutions of Equation (11) for $\alpha \ne 3$.
• Prove or disprove that besides the circle, there is only one simple closed solution to the 2-d equation $\kappa =h^4$; identify the equation for the non-circular solution if there is one. More generally, do the same for $\kappa =h^{\alpha }$ for $\alpha \ne 4$.
• Identify the equation for the unique (modulo rotations) simple closed non-circular solution to Berger’s 2-d equation $\kappa =r^4$ (where r is the radius in polar coordinates), the existence of which is proved in [44]. More generally, do the same for $\kappa =r^{\alpha }$ for all $3<\alpha <8$.
• Prove or disprove that when the sizes (areas) are renormalized, the 2-d “stochastic slicing” process illustrated in Figure 19 converges in distribution, and if it converges, identify the limiting distribution and the rate of convergence.
• Prove or disprove that there is exactly one (modulo rotations) non-circular simple closed solution to (15) for $2<\alpha <7$, and that this interval is sharp.
• Extend all of the above to the 3-d setting and by replacing h by $h_0$. (Same for the 3-d process in Figure 20).
• Investigate non-linear generalizations and extensions of (3) and (11) to try to identify better models for the evolution of the shapes of beach stones.
• Perform detailed numerical analysis (e.g., using standard finite element methods) of the non-linear and non-local partial integro-differential equations (3) and (11), in both 2-d and 3-d, for various values of lambda and alpha. Present the results of this analysis in both tabular and graphical forms.

The numerical results in this paper also suggest a comparison of these theoretical frictional abrasion evolving shape models with the empirical evolving shapes of beach stones, both natural and in laboratory experiments. For example, is the theoretical observation of a 3-d stone’s shape evolving toward an oval body with three different cross-sections as in Figure 20 consistent with natural beach stones undergoing only frictional abrasion on a flat beach and with laboratory experiments modeling this process?