The Modelling of Pt-Bearing ORR and OER-Active Alloys
Abstract
1. Introduction
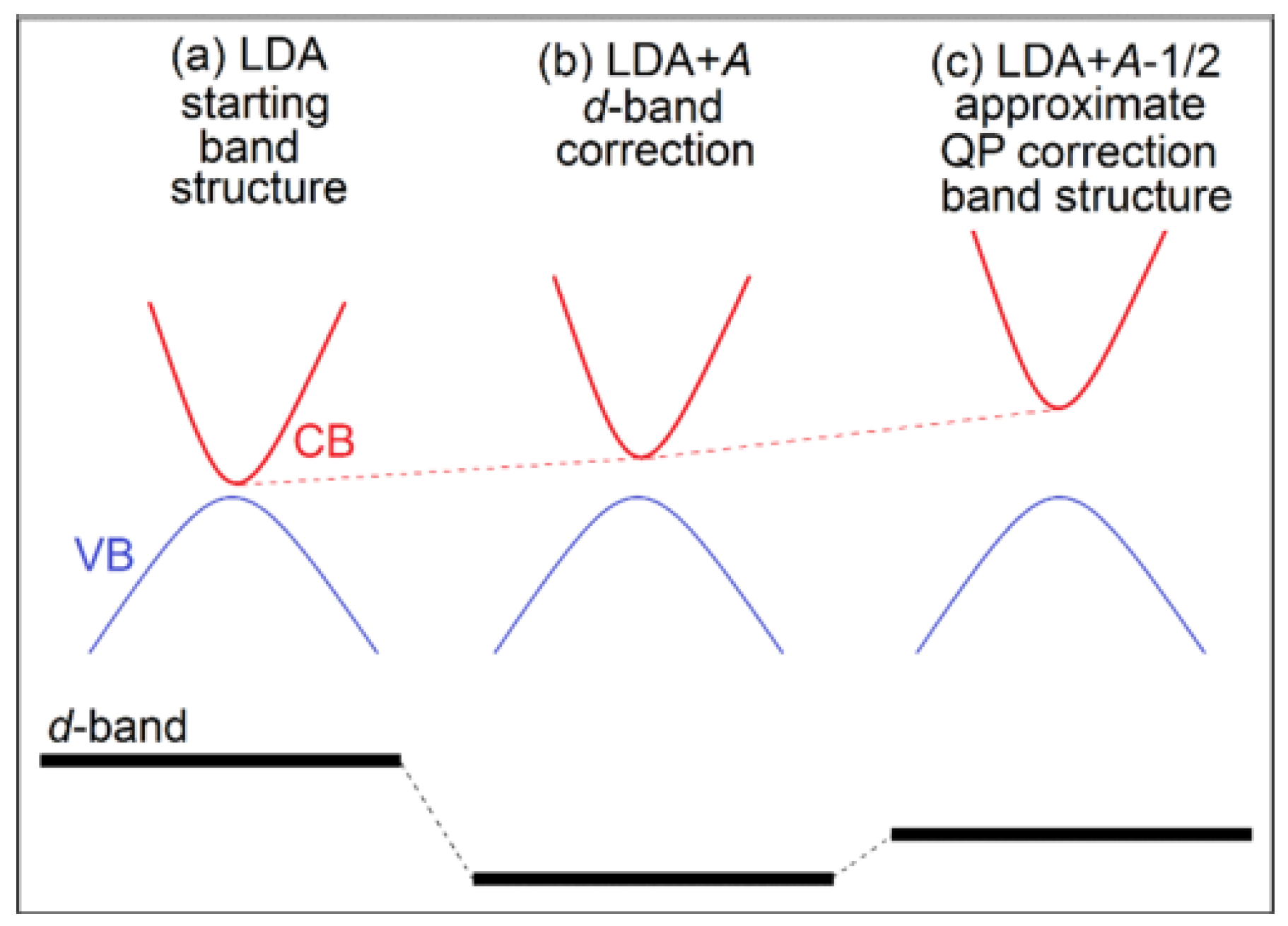
2. Band Structure Estimation Using DFT and Post-DFT Methods
3. The Band Structures of Crystals for the ORR/OER
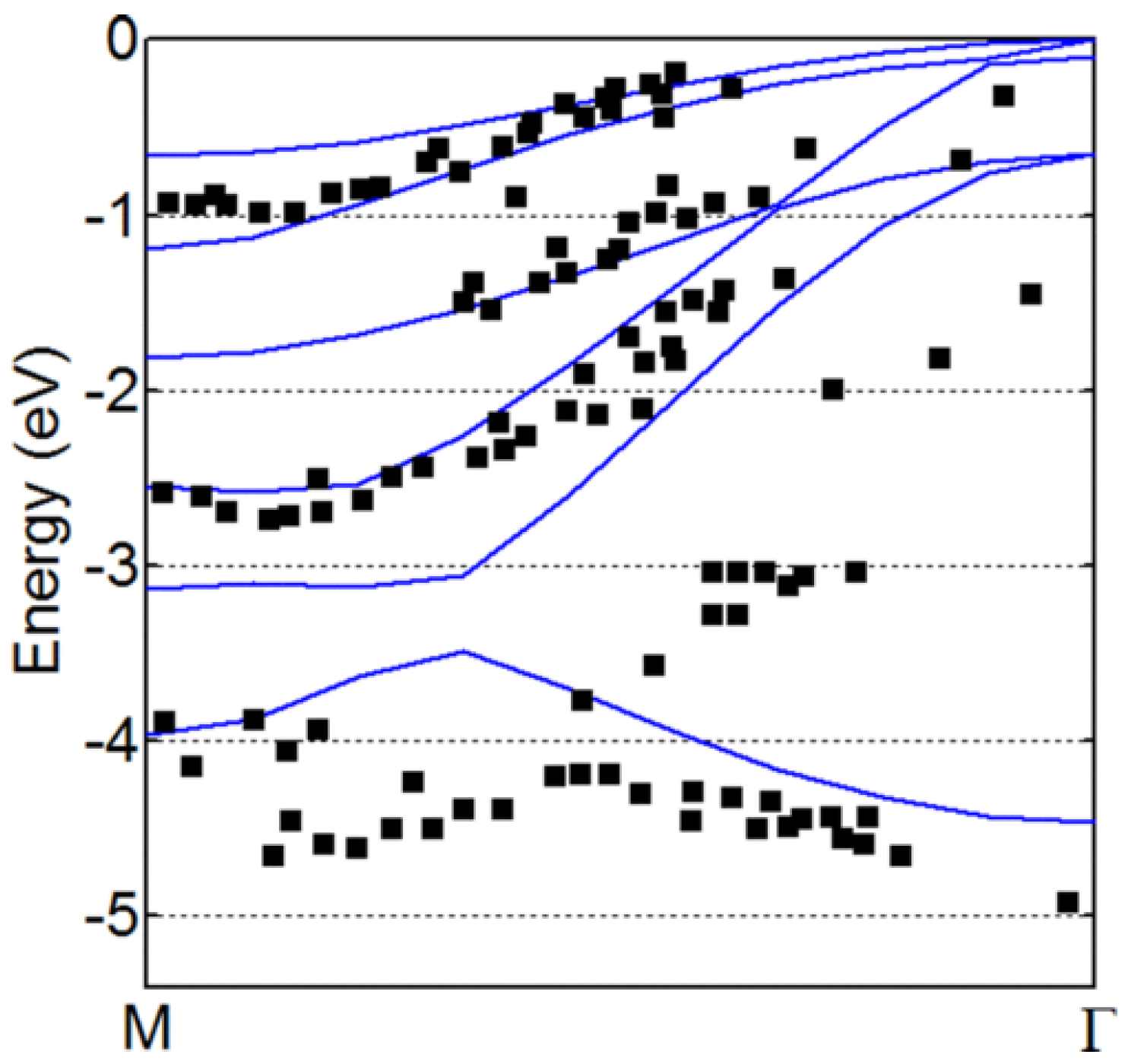
3.1. Oxidic Crystals
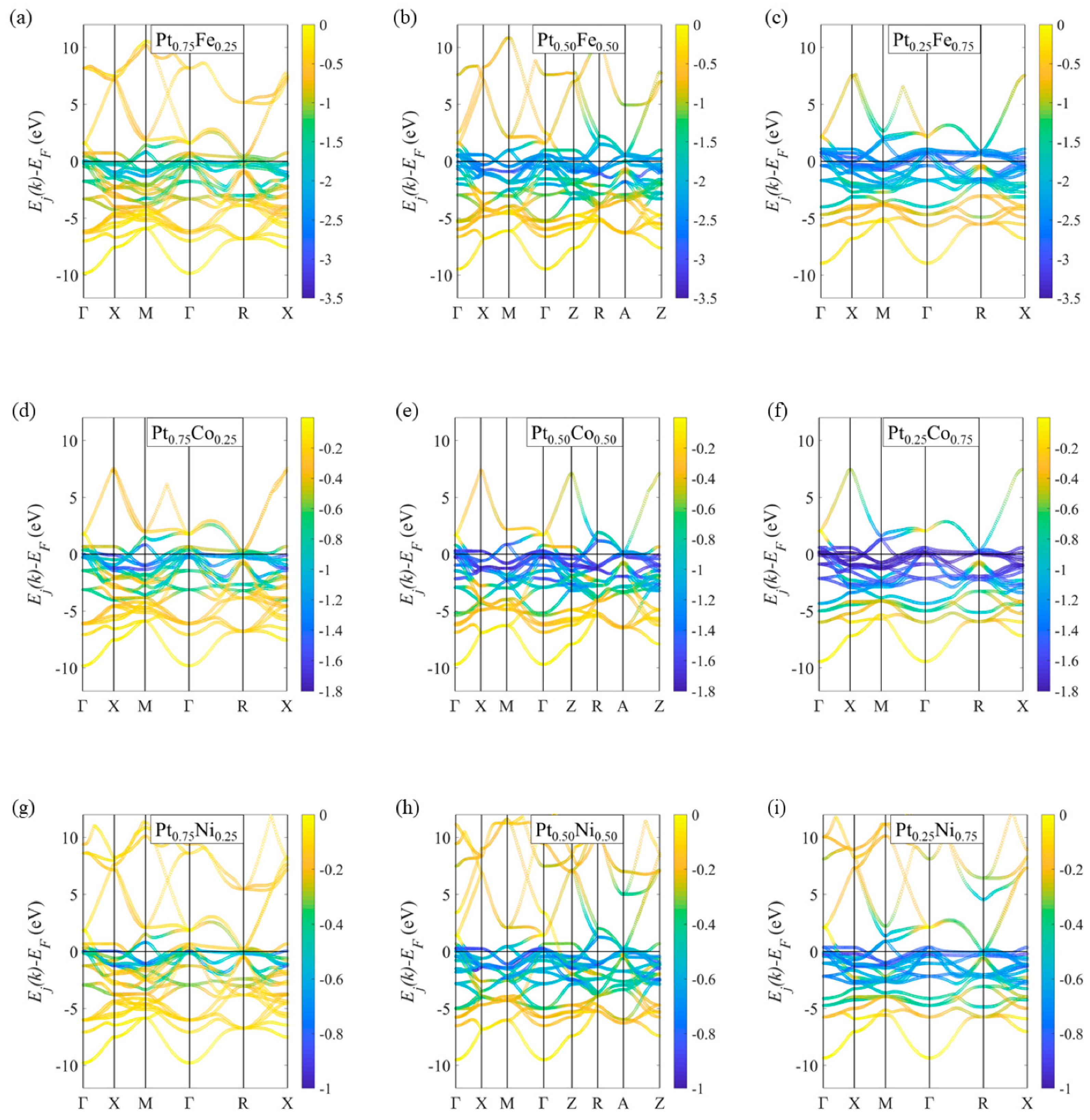
3.2. Metallic Alloy Crystals
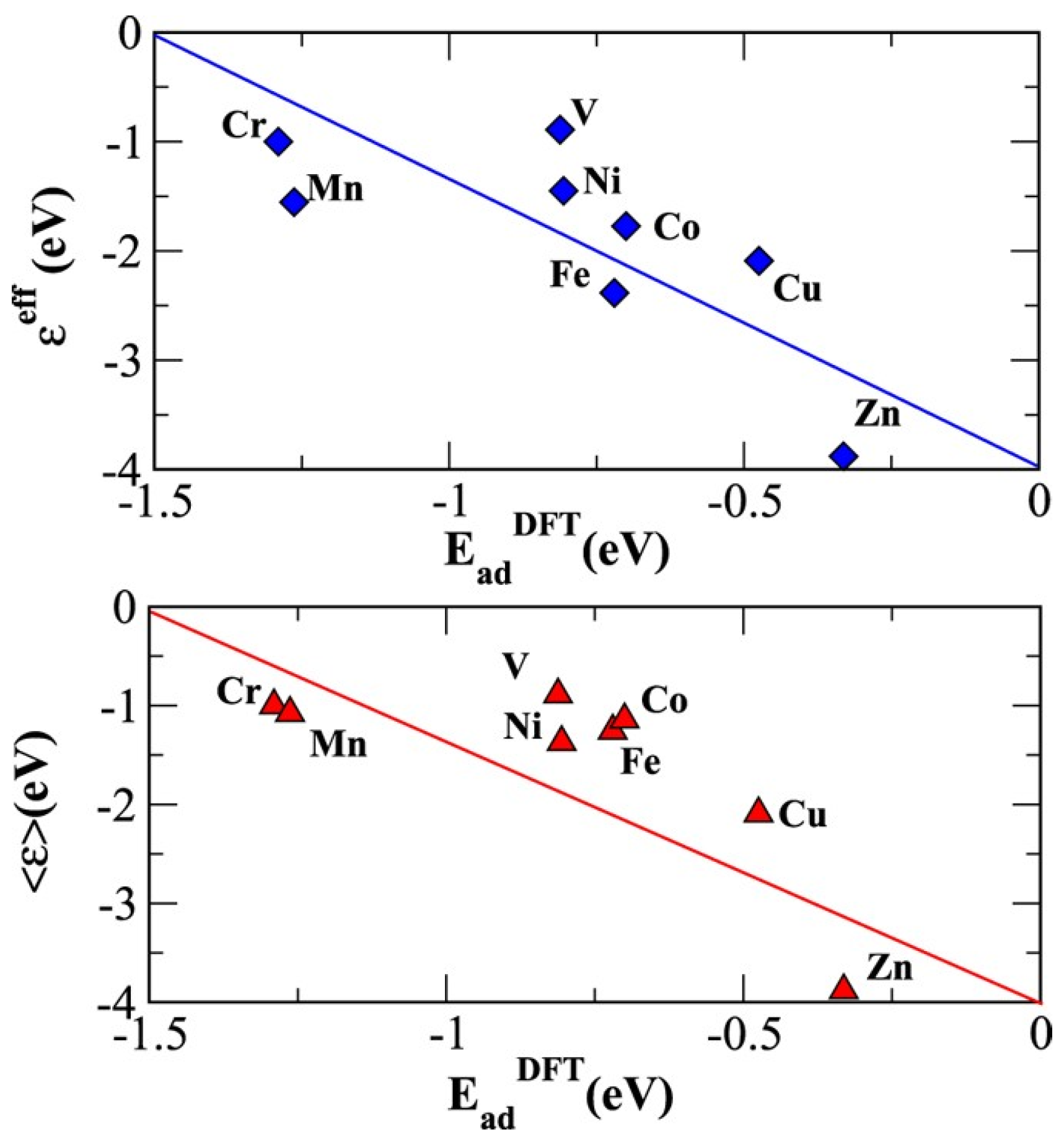
4. Energetic and Structural Models of the ORR/OER and Its Reactants
5. Summary and Future Directions
Funding
Data Availability Statement
Conflicts of Interest
References
- Lim, C.; Fairhurst, A.R.; Ransom, B.J.; Haering, D.; Stamenkovic, V.R. Role of Transition Metals in Pt Alloy Catalysts for the Oxygen Reduction Reaction. ACS Catal. 2023, 13, 14874–14893. [Google Scholar] [CrossRef] [PubMed]
- Stamenkovic, V.R.; Fowler, B.; Mun, B.S.; Wang, G.; Ross, P.N.; Lucas, C.A.; Marković, N.M. Improved Oxygen Reduction Activity on Pt3Ni(111) via Increased Surface Site Availability. Science 2007, 315, 493–497. [Google Scholar] [CrossRef] [PubMed]
- Stamenkovic, V.R.; Mun, S.B.; Arenz, M.; Mayrhofer, K.J.J.; Lucas, C.A.; Wang, G.; Ross, P.N.; Markovic, N.M. Trends in electrocatalysis on extended and nanoscale Pt-bimetallic alloy surfaces. Nat. Mater. 2007, 6, 241–247. [Google Scholar] [CrossRef] [PubMed]
- Shuttleworth, I.G. The Catalytic Activity of Magnetic Surfaces. Magnetochemistry 2024, 10, 40. [Google Scholar] [CrossRef]
- Biz, C.; Gracia, J.; Fianchini, M. Experimental Evidences on Magnetism-Covalent Bonding Interplay in Structural Properties of Solids and during Chemisorption. Int. J. Mol. Sci. 2024, 25, 1793. [Google Scholar] [CrossRef]
- Alaswad, A.; Omran, A.; Sodre, J.R.; Wilberforce, T.; Pignatelli, G.; Dassisti, M.; Baroutaji, A.; Olabi, A.G. Technical and Commercial Challenges of Proton-Exchange Membrane (PEM) Fuel Cells. Energies 2021, 14, 144. [Google Scholar] [CrossRef]
- Cullen, D.A.; Neyerlin, K.C.; Ahluwalia, R.K.; Mukundan, R.; More, K.L.; Borup, R.L.; Weber, A.Z.; Myers, D.J.; Kusoglu, A. New roads and challenges for fuel cells in heavy-duty transportation. Nat. Energy 2021, 6, 462–474. [Google Scholar] [CrossRef]
- Wang, X.X.; Swihart, M.T.; Wu, G. Achievements, challenges and perspectives on cathode catalysts in proton exchange membrane fuel cells for transportation. Nat. Catal. 2019, 2, 578–589. [Google Scholar] [CrossRef]
- Grigoriev, S.A.; Fateev, V.N.; Bessarabov, D.G.; Millet, P. Current status, research trends, and challenges in water electrolysis science and technology. Int. J. Hydrog. Energy 2020, 45, 26036–26058. [Google Scholar] [CrossRef]
- Santos, R.M.D.; Ornelas, I.; Dias, A.C.; Lima, M.P.; Da Silva, J.L.F. Theoretical Investigation of the Role of Mixed A+ Cations in the Structure, Stability, and Electronic Properties of Perovskite Alloys. ACS Appl. Energy Mater. 2023, 6, 5259–5273. [Google Scholar] [CrossRef]
- Noman, M.; Khan, Z.; Jan, S.T. A comprehensive review on the advancements and challenges in perovskite solar cell technology. RSC Adv. 2024, 14, 5085–5131. [Google Scholar] [CrossRef] [PubMed]
- Afre, R.A.; Pugliese, D. Perovskite Solar Cells: A Review of the Latest Advances in Materials, Fabrication Techniques, and Stability Enhancement Strategies. Micromachines 2024, 15, 192. [Google Scholar] [CrossRef] [PubMed]
- Kumari, P.; Gupta, A.K.; Mishra, R.K.; Ahmad, M.S.; Shahi, R.R. A Comprehensive Review: Recent Progress on Magnetic High Entropy Alloys and Oxides. J. Magn. Magn. Mater. 2022, 554, 169142. [Google Scholar] [CrossRef]
- George, E.P.; Raabe, D.; Ritchie, R.O. High-entropy alloys. Nat. Rev. Mater. 2019, 4, 515–534. [Google Scholar] [CrossRef]
- Miracle, D.B.; Senkov, O.N. A critical review of high entropy alloys and related concepts. Acta Mater. 2017, 122, 448–511. [Google Scholar] [CrossRef]
- Zhang, D.; Hou, Z.; Mi, W. Progress in magnetic alloys with kagome structure: Materials, fabrications and physical properties. J. Mater. Chem. C 2022, 10, 7748–7770. [Google Scholar] [CrossRef]
- Staunton, J.B.; Razee, S.S.A.; Ling, M.F.; Johnson, D.D.; Pinski, F.J. Magnetic alloys, their electronic structure and micromagnetic and microstructural models. J. Phys. D Appl. Phys. 1998, 31, 2355. [Google Scholar] [CrossRef]
- Thonhauser, T. Theory of Orbital Magnetization in Solids. Int. J. Mod. Phys. B 2011, 25, 1429–1458. [Google Scholar] [CrossRef]
- Kakehashi, Y. Modern Theory of Magnetism in Metals and Alloys; Springer Series in Solid-State Sciences 175; Springer: Berlin/Heidelberg, Germany, 2013; ISBN 9783642334009. [Google Scholar]
- Wang, C.; Li, D.; Chi, M.; Pearson, J.; Rankin, R.B.; Greeley, J.; Duan, Z.; Wang, G.; van der Vliet, D.; More, K.L.; et al. Rational Development of Ternary Alloy Electrocatalysts. J. Phys. Chem. Lett. 2012, 3, 1668–1673. [Google Scholar] [CrossRef]
- Perdew, J.P.; Schmidt, K. Jacob’s ladder of density functional approximations for the exchange-correlation energy. AIP Conf. Proc. 2001, 577, 1–20. [Google Scholar] [CrossRef]
- Borlido, P.; Schmidt, J.; Huran, A.W.; Tran, F.; Marques, M.A.L.; Botti, S. Exchange-correlation functionals for band gaps of solids: Benchmark, reparametrization and machine learning. NPJ Comput. Mater. 2020, 6, 96. [Google Scholar] [CrossRef]
- Aulbur, W.G.; Jönsson, L.; Wilkins, J.W. Quasiparticle calculations in solids. In Solid State Physics; Academic Press: San Diego, CA, USA, 2000; Volume 54, pp. 1–218. [Google Scholar] [CrossRef]
- Onida, G.; Reining, L.; Rubio, A. Electronic excitations: Density-functional versus many-body Green’s-function approaches. Rev. Mod. Phys. 2002, 74, 601–659. [Google Scholar] [CrossRef]
- López, N.; Reichertz, L.A.; Yu, K.M.; Campman, K.; Walukiewicz, W. Engineering the Electronic Band Structure for Multiband Solar Cells. Phys. Rev. Lett. 2011, 106, 028701. [Google Scholar] [CrossRef]
- Curély, J. The Microscopic Mechanisms Involved in Superexchange. Magnetochemistry 2022, 8, 6. [Google Scholar] [CrossRef]
- Marini, A.; Hogan, C.; Grüning, M.; Varsano, D. Yambo: An ab initio tool for excited state calculations. Comput. Phys. Commun. 2009, 180, 1392–1403. [Google Scholar] [CrossRef]
- Sangalli, D.; Ferretti, A.; Miranda, H.; Attaccalite, C.; Marri, I.; Cannuccia, E.; Melo, P.; Marsili, M.; Paleari, F.; Marrazzo, A.; et al. Many-body perturbation theory calculations using the yambo code. J. Phys. Condens. Matter 2019, 31, 325902. [Google Scholar] [CrossRef]
- Giannozzi, P.; Andreussi, O.; Brumme, T.; Bunau, O.; Nardelli, M.B.; Calandra, M.; Car, R.; Cavazzoni, C.; Ceresoli, D.; Cococcioni, M.; et al. Advanced capabilities for materials modelling with Quantum ESPRESSO. J. Phys. Condens. Matter 2017, 29, 465901. [Google Scholar] [CrossRef]
- Deslippe, J.; Samsonidze, G.; Strubbe, D.A.; Jain, M.; Cohen, M.L.; Louie, S.G. BerkeleyGW: A massively parallel computer package for the calculation of the quasiparticle and optical properties of materials and nanostructures. Comput. Phys. Commun. 2012, 183, 1269–1289. [Google Scholar] [CrossRef]
- Gonze, X.; Amadon, B.; Anglade, P.-M.; Beuken, J.-M.; Bottin, F.; Boulanger, P.; Bruneval, F.; Caliste, D.; Caracas, R.; Côté, M.; et al. ABINIT: First-principles approach to material and nanosystem properties. Comput. Phys. Commun. 2009, 180, 2582–2615. [Google Scholar] [CrossRef]
- Klein, M.; Nuber, A.; Schwab, H.; Albers, C.; Tobita, N.; Higashiguchi, M.; Jiang, J.; Fukuda, S.; Tanaka, K.; Shimada, K.; et al. Coherent Heavy Quasiparticles in a CePt5 Surface Alloy. Phys. Rev. Lett. 2011, 106, 186407. [Google Scholar] [CrossRef]
- Fujimori, S. Band structures of 4f and 5f materials studied by angle-resolved photoelectron spectroscopy. J. Phys. Condens. Mat. 2016, 28, 153002. [Google Scholar] [CrossRef]
- Goremychkin, E.A.; Park, H.; Osborn, R.; Rosenkranz, S.; Castellan, J.-P.; Fanelli, V.R.; Christianson, A.D.; Stone, M.B.; Bauer, E.D.; McClellan, K.J.; et al. Coherent band excitations in CePd3: A comparison of neutron scattering and ab initio theory. Science 2018, 359, 186–191. [Google Scholar] [CrossRef]
- Koitzsch, A.; Kim, T.K.; Treske, U.; Knupfer, M.; Büchner, B.; Richter, M.; Opahle, I.; Follath, R.; Bauer, E.D.; Sarrao, J.L. Band-dependent emergence of heavy quasiparticles in CeCoIn5. Phys. Rev. B 2013, 88, 035124. [Google Scholar] [CrossRef]
- Iizuka, T.; Mizuno, T.; Min, B.H.; Kwon, Y.S.; Kimura, S. Existence of Heavy Fermions in the Antiferromagnetic Phase of CeIn3. J. Phys. Soc. Jpn. 2012, 81, 043703. [Google Scholar] [CrossRef]
- Zhang, Y.; Feng, W.; Lou, X.; Yu, T.; Zhu, X.; Tan, S.; Yuan, B.; Liu, Y.; Lu, H.; Xie, D.; et al. Direct observation of heavy quasiparticles in the Kondo-lattice compound CeIn3. Phys. Rev. B 2018, 97, 045128. [Google Scholar] [CrossRef]
- Ochi, M.; Arita, R.; Matsumoto, M.; Kino, H.; Miyake, T. Robust flat bands in R Co5 (R = rare earth) compounds. Phys. Rev. B 2015, 91, 165137. [Google Scholar] [CrossRef]
- Spencer, J.A.; Mock, A.L.; Jacobs, A.G.; Schubert, M.; Zhang, Y.; Tadjer, M.J. A review of band structure and material properties of transparent conducting and semiconducting oxides: Ga2O3, Al2O3, In2O3, ZnO, SnO2, CdO, NiO, CuO, and Sc2O3. Appl. Phys. Rev. 2022, 9, 011315. [Google Scholar] [CrossRef]
- Pearton, S.J.; Yang, J.; Cary, P.H., IV; Ren, F.; Kim, J.; Tadjer, M.J.; Mastro, M.A. A review of Ga2O3 materials, processing, and devices. Appl. Phys. Rev. 2018, 5, 011301. [Google Scholar] [CrossRef]
- Playford, H.Y.; Hannon, A.C.; Barney, E.R.; Walton, R.I. Structures of Uncharacterized Polymorphs of Gallium Oxide from Total Neutron Diffraction. Chem. Eur. J. 2013, 19, 2803–2813. [Google Scholar] [CrossRef]
- Binet, L.; Gourier, D. Origin of the blue luminescence of β-Ga2O3. J. Phys. Chem. Solids 1998, 59, 1241–1249. [Google Scholar] [CrossRef]
- Desgreniers, S. High-density phases of ZnO: Structural and compressive parameters. Phys. Rev. B 1998, 58, 14102. [Google Scholar] [CrossRef]
- Ni, H.Q.; Lu, Y.F.; Ren, Z.M. Quasiparticle band structures of wurtzite and rock-salt ZnO. J. Appl. Phys. 2002, 91, 1339–1343. [Google Scholar] [CrossRef]
- Ataide, C.A.; Pelá, R.R.; Marques, M.; Teles, L.K.; Furthmüller, J.; Bechstedt, F. Fast and accurate approximate quasiparticle band structure calculations of ZnO, CdO, and MgO polymorphs. Phys. Rev. B 2017, 95, 045126. [Google Scholar] [CrossRef]
- Jaffe, J.E.; Pandey, R.; Kunz, A.B. Kunz Electronic structure of the rocksalt-structure semiconductors ZnO and CdO. Phys. Rev. B 1991, 43, 14030. [Google Scholar] [CrossRef]
- Sans, J.; Segura, A.; Manjón, F.; Marí, B.; Muñoz, A.; Herrera-Cabrera, M. Optical properties of wurtzite and rock-salt ZnO under pressure. Microelectron. J. 2005, 36, 928–932. [Google Scholar] [CrossRef]
- Nahm, T.-U.; Noh, J.; Kim, J.-Y.; Oh, S.-J. Electron spectroscopic evidence of electron correlation in Ni-Pt alloys: Comparison with specific heat measurement. J. Phys. Condens. Mat. 2003, 15, 3191. [Google Scholar] [CrossRef]
- Kumar, U.; Mukhopadhyay, P.K.; Sanyal, B.; Eriksson, O.; Nordblad, P.; Paudyal, D.; Tarafder, K.; Mookerjee, A. Experimental and theoretical study of annealed Ni-Pt alloys. Phys. Rev. B 2006, 74, 064401. [Google Scholar] [CrossRef]
- Pinski, F.J.; Ginatempo, B.; Johnson, D.D.; Staunton, J.B.; Stocks, G.M.; Gyorffy, B.L. Origins of compositional order in NiPt alloys. Phys. Rev. Lett. 1991, 66, 766. [Google Scholar] [CrossRef]
- Staunton, J.; Weinberger, P.; Gyorffy, B.L. On the electronic structure of paramagnetic NicPt1-c alloys: A relativistic calculation. J. Phys. F Met. Phys. 1983, 13, 779. [Google Scholar] [CrossRef]
- Shuttleworth, I.G. The magnetic band-structures of ordered PtxFe1−x, PtxCo1−x, and PtxNi1−x (x = 0.25, 0.50, and 0.75). Magnetochemistry 2020, 6, 61. [Google Scholar] [CrossRef]
- Aledealat, K.; Aladerah, B.; Obeidat, A. Study of structural, electronic, and magnetic properties of L10-ordered CoPt and NiPt: An ab initio calculations and Monte Carlo simulation. Solid. State Commun. 2023, 363, 115112. [Google Scholar] [CrossRef]
- Shuttleworth, I.G. The effects of strain on the ordered phases of NixPt1−x (x = 0.25, 0.5, and 0.75). Chem. Phys. Lett. 2017, 689, 41–47. [Google Scholar] [CrossRef]
- Shuttleworth, I.G. Magnetism in the strained ordered phases of PtxFe1−x and PtxCo1−x. (x = 0.25, 0.5, and 0.75). J. Phys. Chem. Solids 2018, 114, 153–162. [Google Scholar] [CrossRef]
- Pisanty, A.; Amador, C.; Ruiz, Y.; de la Vega, M. Band structures of Ni3Pt and NiPt3. Z. Phys. B Condens. Matter 1990, 80, 237–239. [Google Scholar] [CrossRef]
- Shuttleworth, I.G. The quasiparticle band structures of ordered NixPt1−x (x = 0.25, 0.5, and 0.75). Heliyon 2018, 4, e01000. [Google Scholar] [CrossRef]
- Hammer, B.; Nørskov, J.K. Electronic factors determining the reactivity of metal surfaces. Surf. Sci. 1995, 343, 211–220. [Google Scholar] [CrossRef]
- Bhattacharjee, S.; Waghmare, U.V.; Lee, S.-C. An improved d-band model of the catalytic activity of magnetic transition metal surfaces. Sci. Rep. 2016, 6, 35916. [Google Scholar] [CrossRef]
- Schnur, S.; Groß, A. Strain and coordination effects in the adsorption properties of early transition metals: A density-functional theory study. Phys. Rev. B 2010, 81, 033402. [Google Scholar] [CrossRef]
- Shuttleworth, I.G. Non-linear moments modelling of metal, oxygen and hydrogen binding to strained FCC (111) and (100) surfaces. Chem. Phys. Lett. 2023, 813, 140310. [Google Scholar] [CrossRef]
- Shuttleworth, I.G. Moments analysis of the binding of metal, oxygen and hydrogen atoms to strained Co(0001), Ru(0001) and Os(0001). Chem. Phys. 2023, 566, 111788. [Google Scholar] [CrossRef]
- Biz, C.; Gracia, J.; Fianchini, M. Review on Magnetism in Catalysis: From Theory to PEMFC Applications of 3d Metal Pt-Based Alloys. Int. J. Mol. Sci. 2022, 23, 14768. [Google Scholar] [CrossRef] [PubMed]
- Moguchikh, E.; Paperzh, K.; Pankov, I.; Belenov, S.; Alekseenko, A. Durability of Commercial Catalysts within Relevant Stress Testing Protocols. Catalysts 2023, 13, 923. [Google Scholar] [CrossRef]
- Zlatar, M.; Escalera-López, D.; Rodríguez, M.G.; Hrbek, T.; Götz, C.; Joy, R.M.; Savan, A.; Tran, H.P.; Nong, H.N.; Pobedinskas, P.; et al. Standardizing OER Electrocatalyst Benchmarking in Aqueous Electrolytes: Comprehensive Guidelines for Accelerated Stress Tests and Backing Electrodes. ACS Catal. 2023, 13, 15375–15392. [Google Scholar] [CrossRef]
- Zhang, Y.; Chen, S.; Wang, Y.; Ding, W.; Wu, R.; Li, L.; Qi, X.; Wei, Z. Study of the degradation mechanisms of carbon-supported platinum fuel cells catalyst via different accelerated stress test. J. Power Sources 2015, 273, 62–69. [Google Scholar] [CrossRef]
- Yang, X.; Lin, L.; Guo, X.; Zhang, S. Design of Multifunctional Electrocatalysts for ORR/OER/HER/HOR: Janus Makes Difference. Small 2024, 20, e2404000. [Google Scholar] [CrossRef]
- Sun, T.; Zang, W.; Sun, J.; Li, C.; Fan, J.; Liu, E.; Wang, J. SACs on Non-Carbon Substrates: Can They Outperform for Water Splitting? Adv. Funct. Mater. 2023, 33, 2301526. [Google Scholar] [CrossRef]
- Guo, J.-X.; Wu, S.-Y.; Zhang, G.-J.; Yan, L.; Hu, J.-G.; Li, X.-Y. Single noble metals (Pd, Pt and Ir) anchored Janus MoSSe monolayers: Efficient oxygen reduction/evolution reaction bifunctional electrocatalysts and harmful gas detectors. J. Colloid. Interf. Sci. 2022, 616, 177–188. [Google Scholar] [CrossRef]
- Jacob, T.; Goddard, W.A., III. Adsorption of atomic H and O on the (111) surface of Pt3Ni alloys. J. Phys. Chem. B 2004, 108, 8311–8323. [Google Scholar] [CrossRef]
- Shuttleworth, I.G. Strain engineering of H/transition metal systems. Surf. Sci. 2017, 661, 49–59. [Google Scholar] [CrossRef]
- Shuttleworth, I.G. Controlled FCC/on-top binding of H/Pt(111) using surface stress. App Surf. Sci. 2016, 378, 286–292. [Google Scholar] [CrossRef]
- Shuttleworth, I.G. A comparative study of oxygen and hydrogen adsorption on strained and alloy-supported Pt(111) monolayers. Magnetochemistry 2021, 7, 101. [Google Scholar] [CrossRef]
- Aladerah, B.; Obeidat, A. Pressure-dependent magnetic properties of FeNi alloy: Theoretical study. Solid. State Sci. 2024, 148, 107437. [Google Scholar] [CrossRef]
- Shuttleworth, I.G. Strain engineering of the CeNi5 system. Magnetochemistry 2016, 2, 39. [Google Scholar] [CrossRef]
- Cao, L.; Mueller, T. Rational Design of Pt3Ni Surface Structures for the Oxygen Reduction Reaction. J. Phys. Chem. C 2015, 119, 17735–17747. [Google Scholar] [CrossRef]
- Zhao, L.; Liu, H.; Liu, Y.; Han, X.; Xu, J.; Xing, W.; Guo, W. Mechanistic Insights into the Hydrogen Oxidation Reaction on PtNi Alloys in Alkaline Media: A First-Principles Investigation. ACS Appl. Mater. Interfaces 2020, 12, 40248–40260. [Google Scholar] [CrossRef] [PubMed]
- Aledealat, K.; Aladerah, B.; Obeidat, A.; Rawashdeh, A.-M.M. Enhancing the performance of rare-earth free permanent magnets: A computational study of nitrogen and oxygen defects in CoPt, CoFePt2, and CoNiPt2 alloys. J. Phys. Chem. Solids 2023, 183, 111649. [Google Scholar] [CrossRef]
- Hizi, A.; Garbouj, H.; Mottet, C.; Said, M. Chemical ordering and surface segregation in Ni1-cPtc system: A theoretical study from the alloys to the nanoalloys. Results Phys. 2019, 14, 102493. [Google Scholar] [CrossRef]
- Amador, C.; Lambrecht, W.R.L.; van Schilfgaarde, M.; Segall, B. Internal strain effects on the phase diagram of Ni-Pt alloys. Phys. Rev. B 1993, 47, 15276. [Google Scholar] [CrossRef]
- Wang, G.; Van Hove, M.A.; Ross, P.N.; Baskes, M.I. Quantitative prediction of surface segregation in bimetallic Pt-M alloy nanoparticles (M = Ni, Re, Mo). Prog. Surf. Sci. 2005, 79, 28–45. [Google Scholar] [CrossRef]
- Vitos, L.; Ruban, A.V.; Skriver, H.L.; Kollár, J. The surface energy of metals. Surf. Sci. 1998, 411, 186. [Google Scholar] [CrossRef]
- Tyson, W.R.; Miller, W.A. Surface free energies of solid metals: Estimation from liquid surface tension measurements. Surf. Sci. 1977, 62, 267. [Google Scholar] [CrossRef]
- de Boer, F.R.; Room, R.; Mattens, W.C.; Miedema, A.R.; Niessen, A.K. Cohesion in Metals. Transition Metal Alloys; North Holland: Amsterdam, The Netherlands, 1988. [Google Scholar]
- Vojvodic, A.; Nørskov, J.K.; Abild-Pedersen, F. Electronic Structure Effects in Transition Metal Surface Chemistry. Top. Catal. 2014, 57, 25–32. [Google Scholar] [CrossRef]
- Ehrenreich, H.; Schwartz, L.M. The Electronic Structure of Alloys. Solid. State Phys. 1976, 31, 149–286. [Google Scholar] [CrossRef]
- Popescu, V.; Zunger, A. Effective Band Structure of Random Alloys. Phys. Rev. Lett. 2010, 104, 236403. [Google Scholar] [CrossRef] [PubMed]
- Popescu, V.; Zunger, A. Extracting E versus k effective band structure from supercell calculations on alloys and impurities. Phys. Rev. B 2012, 85, 085201. [Google Scholar] [CrossRef]
- Massalski, T.B.; Okamoto, H.; Subramanian, P.R.; Kacprzak, L. (Eds.) Binary Alloy Phase Diagrams, 2nd ed.; ASM International: Materials Park, Ohio, USA, 1990; p. 2844. [Google Scholar] [CrossRef]
- Popov, A.A.; Varygin, A.D.; Plyusnin, P.E.; Sharafutdinov, M.R.; Korenev, S.V.; Serkova, A.N.; Shubin, Y.V. X-ray diffraction reinvestigation of the Ni-Pt phase diagram. J. Alloy Compd. 2022, 891, 161974. [Google Scholar] [CrossRef]
- Fedorov, P.P.; Popov, A.A.; Shubin, Y.V.; Chernova, E.V. Phase Diagram of the Nickel—Platinum System. Russ. J. Inorg. Chem. 2022, 67, 2018–2022. [Google Scholar] [CrossRef]
- Cadeville, M.; Dahmani, C.; Kern, F. Magnetism and spatial order in Ni-Pt and Co-Pt alloys. Magn. Magn. Mater. 1986, 54–57, 1055–1056. [Google Scholar] [CrossRef]
- Cadeville, M.C.; Morán-López, J.L. Magnetism and spatial order in transition metal alloys: Experimental and theoretical aspects. Phys. Rep. 1987, 153, 331–399. [Google Scholar] [CrossRef]
- Lu, X.-G.; Sundman, B.; Ågren, J. Thermodynamic assessments of the Ni-Pt and Al-Ni-Pt systems. Calphad 2009, 33, 450–456. [Google Scholar] [CrossRef]
- Camilos, P.; Varvenne, C.; Mottet, C. Size and shape effects on chemical ordering in Ni-Pt nanoalloys. Phys. Chem. Chem. Phys. 2024, 26, 15192–15204. [Google Scholar] [CrossRef] [PubMed]







| Catalytic reaction | Catalyst | Reference |
|---|---|---|
| Oxygen reduction reaction (ORR) | Platinum (Pt) | [6] |
| L10 Platinum-Cobalt (PtCo) | [7,8] | |
| Hydrogen evolution reaction (HER) | Platinum (Pt) | [9] |
| Nickel-Molybdenum (Ni-Mo) alloys | ||
| Nickel (Ni), Nickel (Ni) foam | ||
| Oxygen evolution reaction (OER) | Iridium dioxide (IrO2) | [9] |
| Ruthenium dioxide (RuO2) | ||
| Cobalt nickel oxide (CoNi2O4) |
| a (Å) | c (Å) | Etot (eV/Atom) | μPt (μB) | μNi (μB) | ΔHf (eV/atom) | |
|---|---|---|---|---|---|---|
| Ni | ||||||
| DFT (GGA) | 3.51 [79] 3.517 [61] | −5.467 | ||||
| Exp | 3.524 [61] | −4.44 | ||||
| Pt | ||||||
| DFT (GGA) | 3.98 [79] 3.963 [61] | −6.097 | ||||
| Exp | 3.9242 [61] | −5.84 | ||||
| NiPt3 (L12) | ||||||
| DFT (GGA) | 3.88 [79] 3.919 [57] | 0.348 | 1.284 | −0.068 [79] | ||
| (LDA) | 3.825 [57] | 0.262 | 1.043 | |||
| Exp | 3.836 [56] | −0.063 [80] | ||||
| NiPt (L10) | ||||||
| DFT (GGA) | 3.84 [79] 3.922 [57] | 3.644 [57] | 0.397 | 1.243 | −0.096 [79] | |
| (LDA) | 3.812 [57] | 3.539 [57] | 0.418 | 1.044 | ||
| Exp | 3.814 [56] | 3.533 [56] | −0.096 [80] | |||
| Ni3Pt (L12) | ||||||
| DFT (GGA) | 3.66 [79] 3.752 [57] | 0.177 | 1.198 | −0.072 [79] | ||
| (LDA) | 3.604 [57] | 0.384 | 0.973 | |||
| Exp | 3.645 [56] | −0.07 [80] |
| Element | Lattice | Surface | MEAM [81] | First Principles [82] | Experiment |
|---|---|---|---|---|---|
| Pt | FCC | (111) | 1651 | 2299 | 2489 [83] 2475 [84] |
| (100) | 2155 | 2734 | |||
| (110) | 1963 | 2819 | |||
| Ni | FCC | (111) | 2039 | 2011 | 2380 [83] 2450 [84] |
| (100) | 2438 | 2426 | |||
| (110) | 2362 | 2368 |
| Facet | Pt3Ni(111) | Pt(111) | Pt3Ni(111) | Pt(100) | Pt3Ni(111) | Pt(110) |
|---|---|---|---|---|---|---|
| d-band centre (eV) | −3.10 | −2.76 (Expt) −2.42 (DFT, [85]) | −3.14 | −2.90 | −2.70 | −2.54 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shuttleworth, I. The Modelling of Pt-Bearing ORR and OER-Active Alloys. Oxygen 2024, 4, 449-469. https://doi.org/10.3390/oxygen4040028
Shuttleworth I. The Modelling of Pt-Bearing ORR and OER-Active Alloys. Oxygen. 2024; 4(4):449-469. https://doi.org/10.3390/oxygen4040028
Chicago/Turabian StyleShuttleworth, Ian. 2024. "The Modelling of Pt-Bearing ORR and OER-Active Alloys" Oxygen 4, no. 4: 449-469. https://doi.org/10.3390/oxygen4040028
APA StyleShuttleworth, I. (2024). The Modelling of Pt-Bearing ORR and OER-Active Alloys. Oxygen, 4(4), 449-469. https://doi.org/10.3390/oxygen4040028






