Modelling the Effects of Oyster Tables on Estuarine Tidal Flow
Abstract
1. Introduction
2. Materials and Methods
2.1. Default Model Version
2.2. Modified Chézy Coefficient
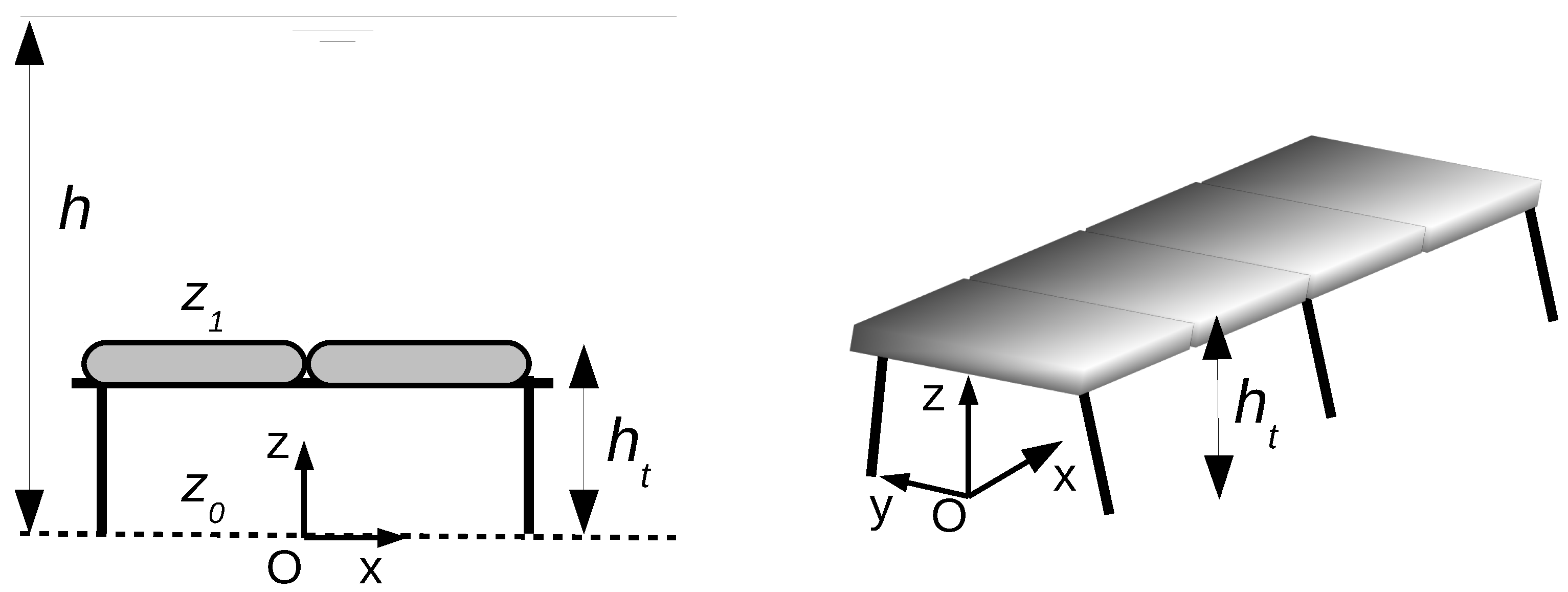
2.2.1. Unsubmerged Structures
2.2.2. Submerged Structures
2.2.3. Synthesis
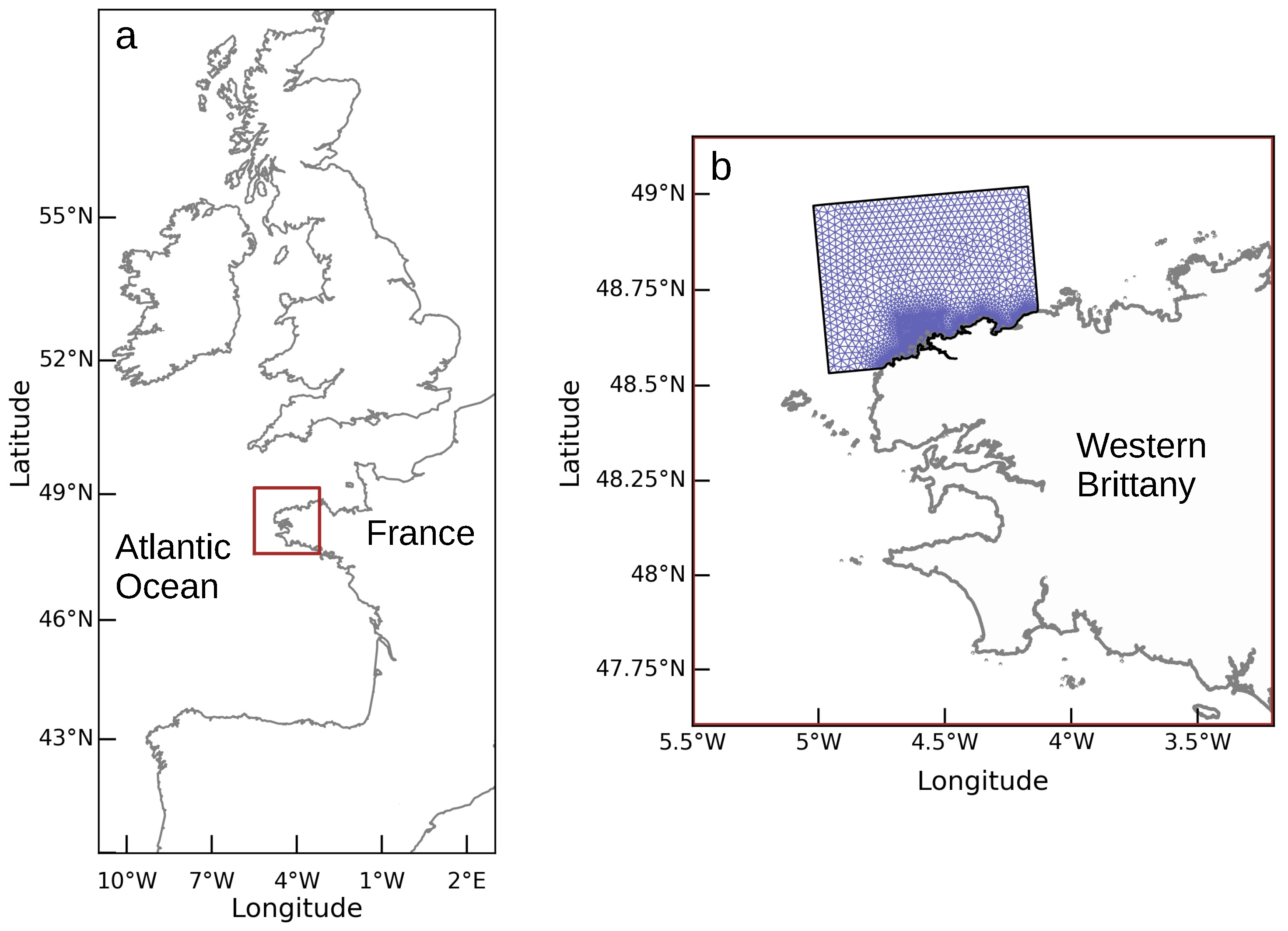
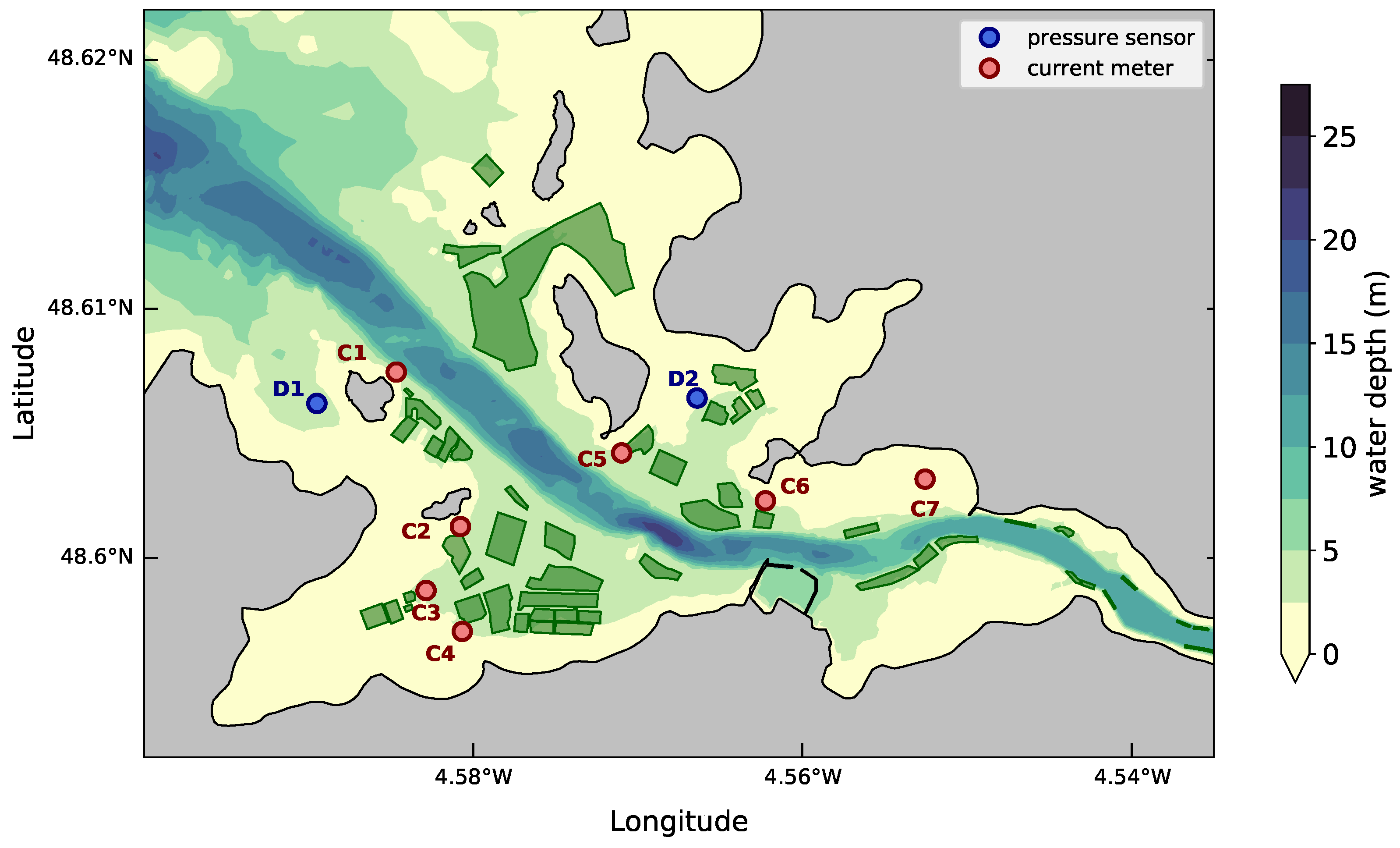
2.3. Model Setup
3. Results and Discussion
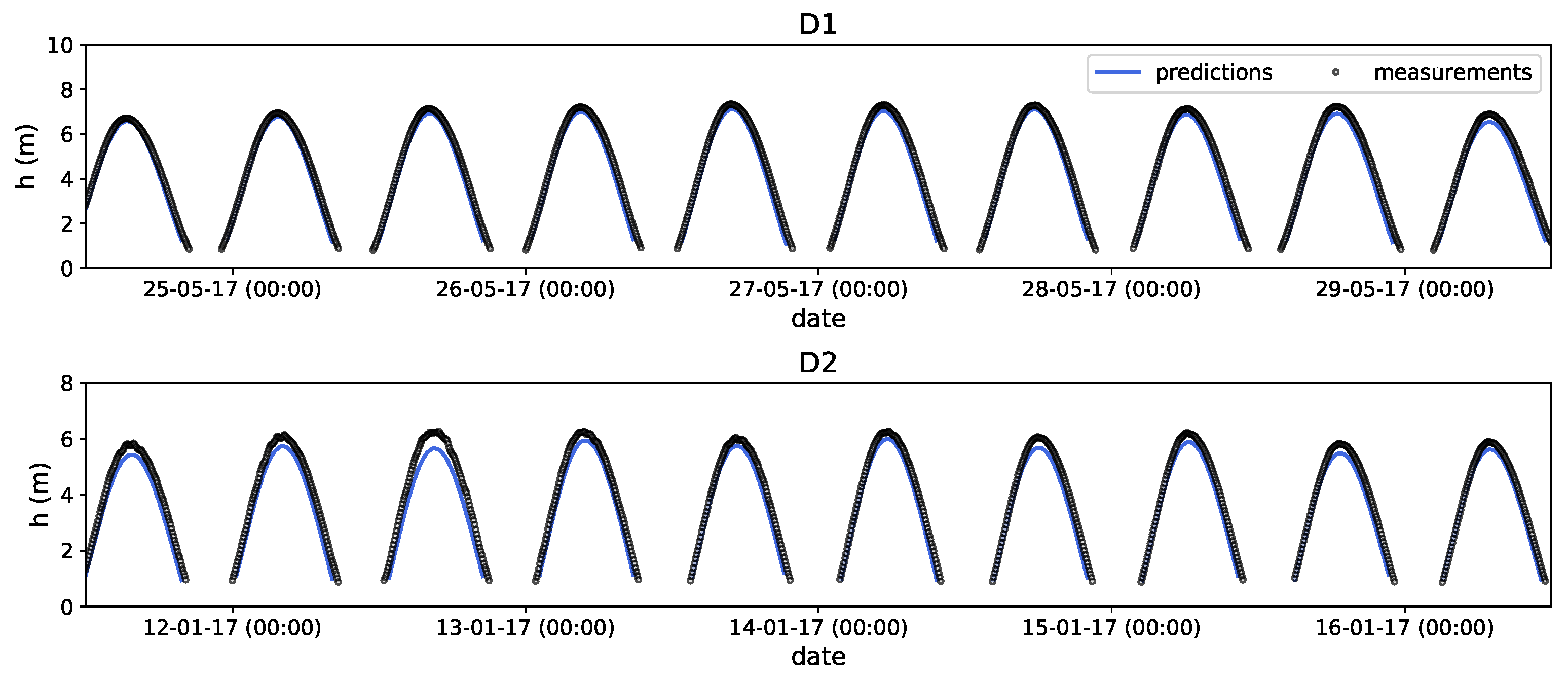
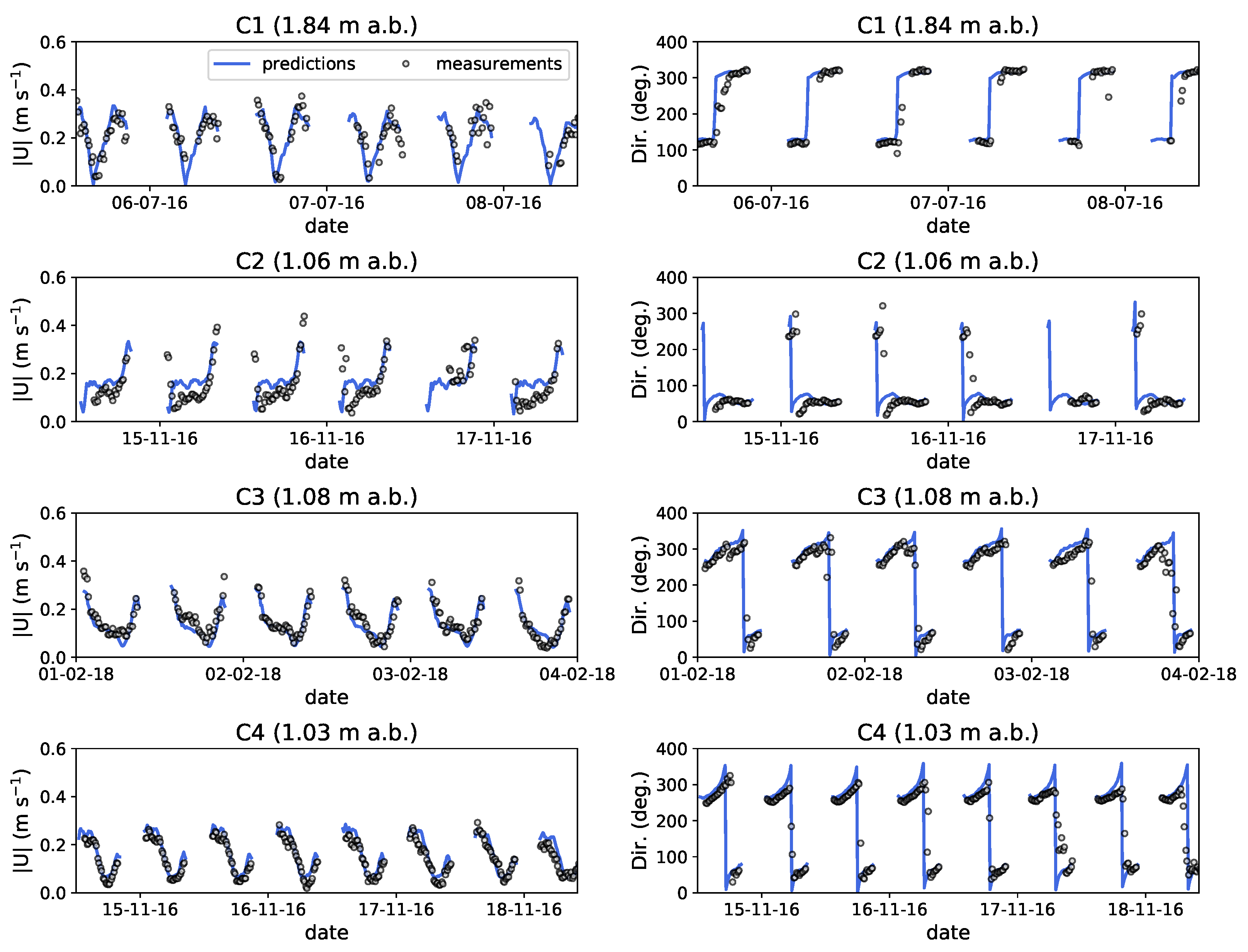
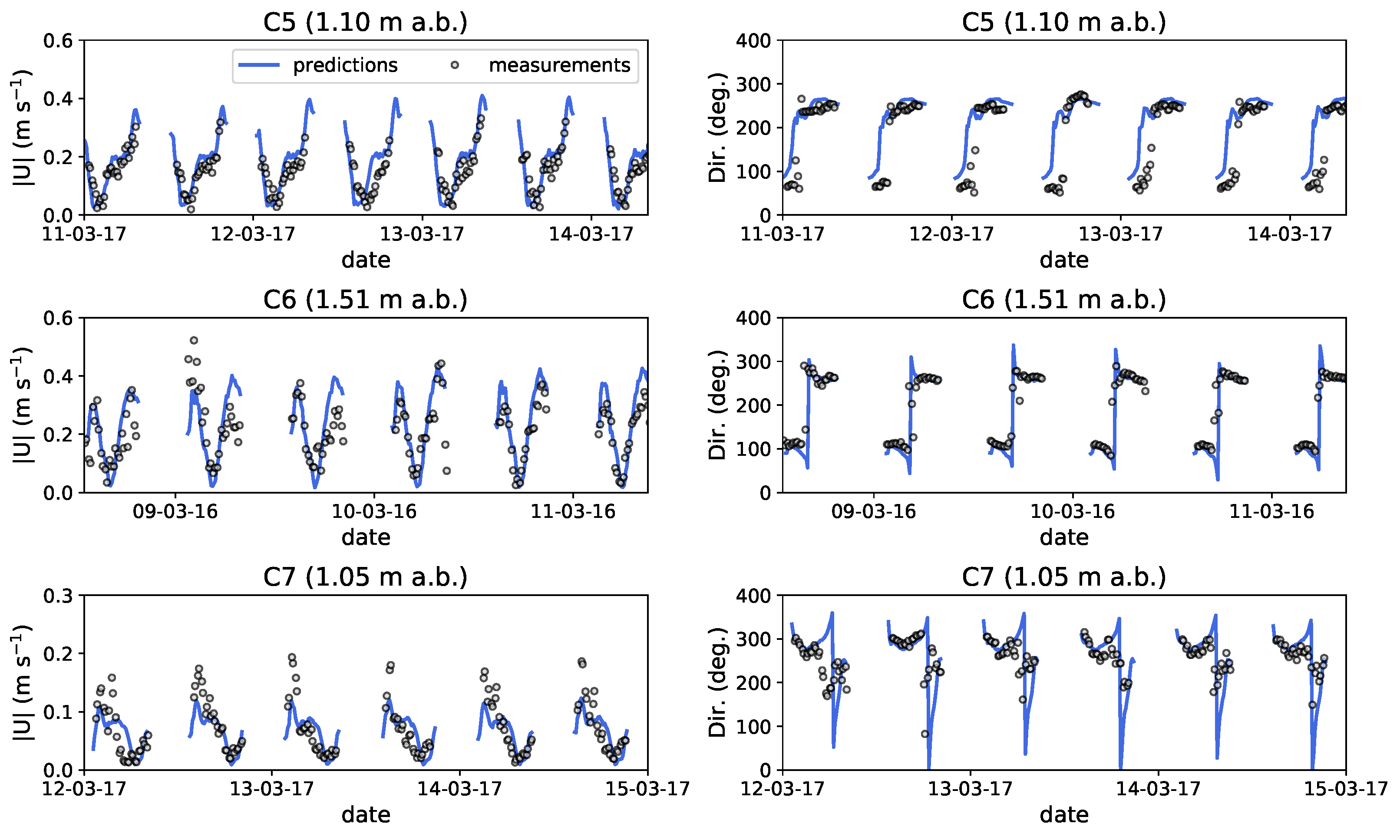
3.1. Assessment of Model Predictions
3.1.1. Sea Surface Elevation
3.1.2. Current Velocity
3.2. Model Sensitivity to Bottom Friction Formulations
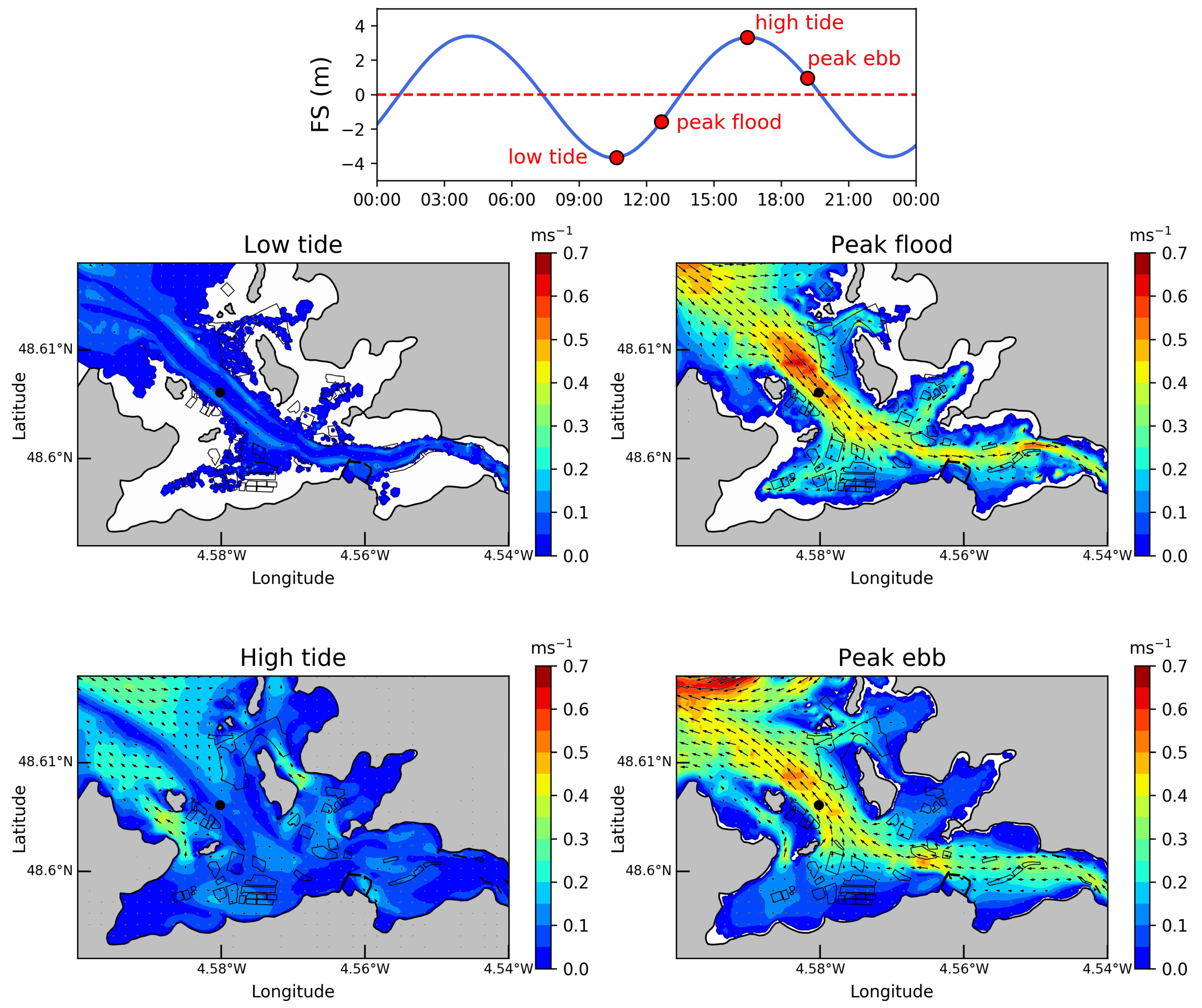
3.2.1. Global Tidal Circulation
3.2.2. Global Influence of Chézy Formulations on Tidal Current Magnitudes
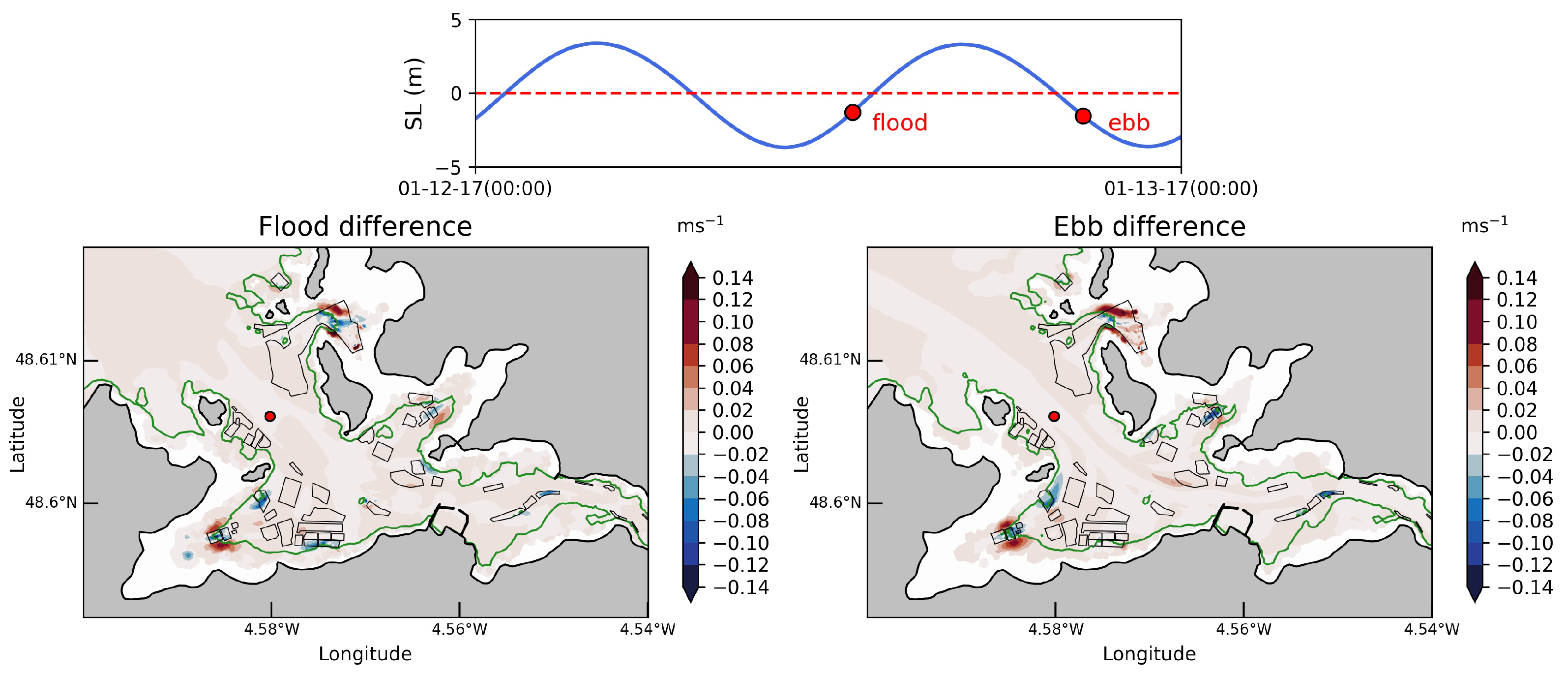
3.3. Effects of Oyster Tables
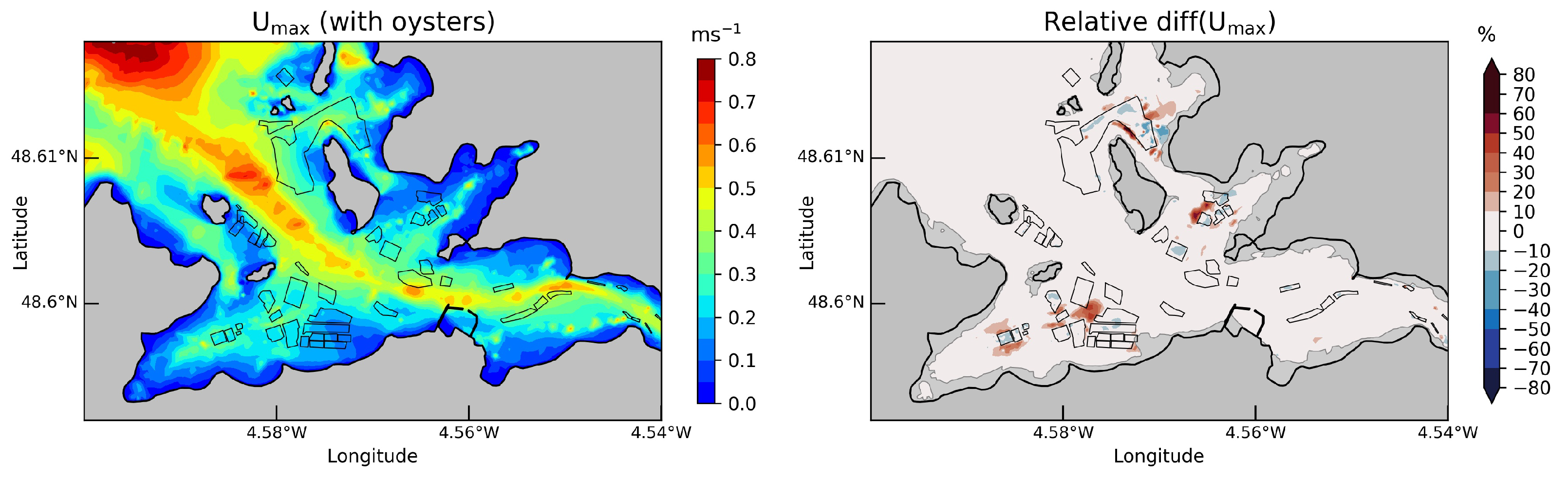
3.3.1. Tidal Current Magnitudes
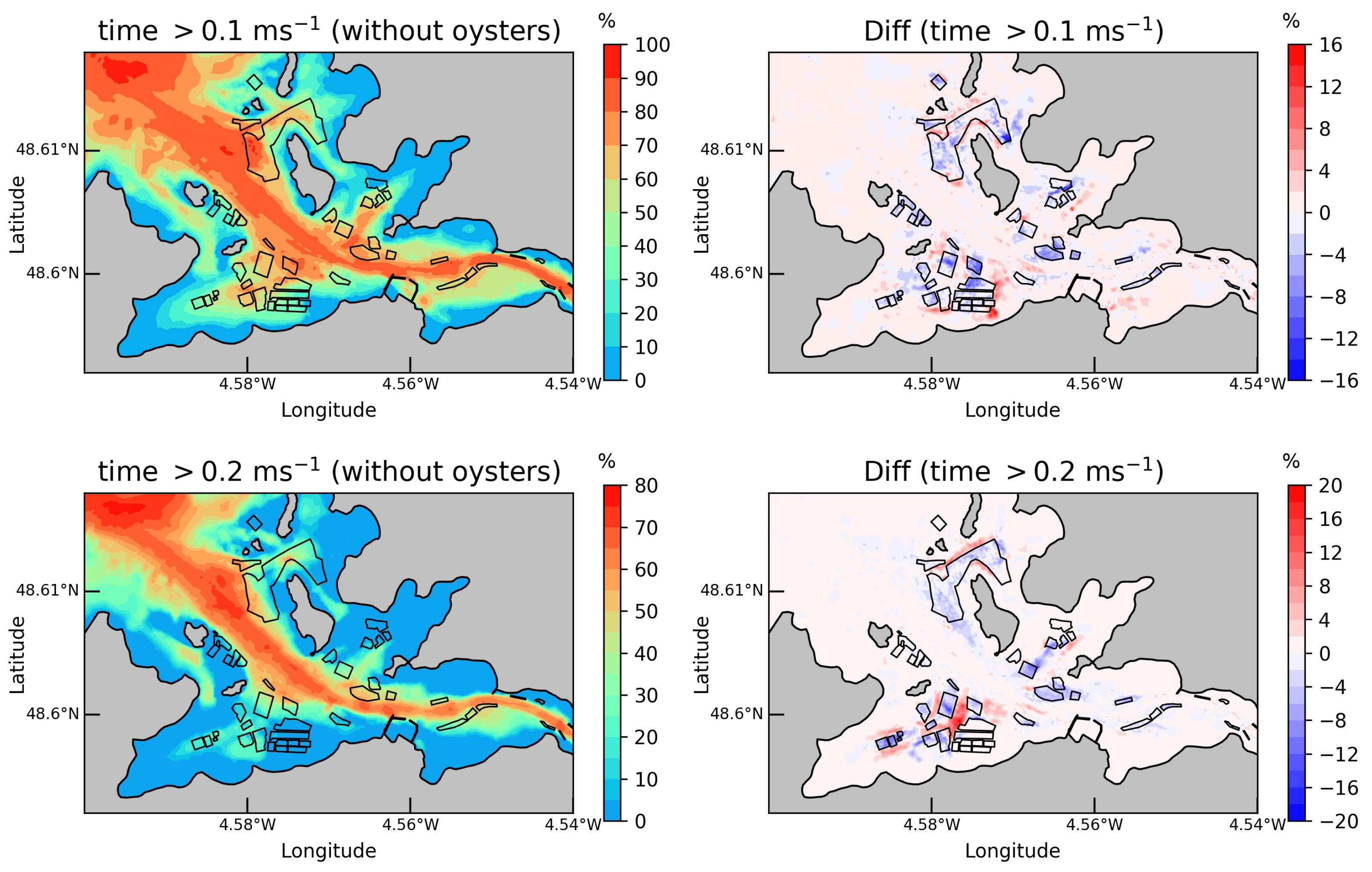
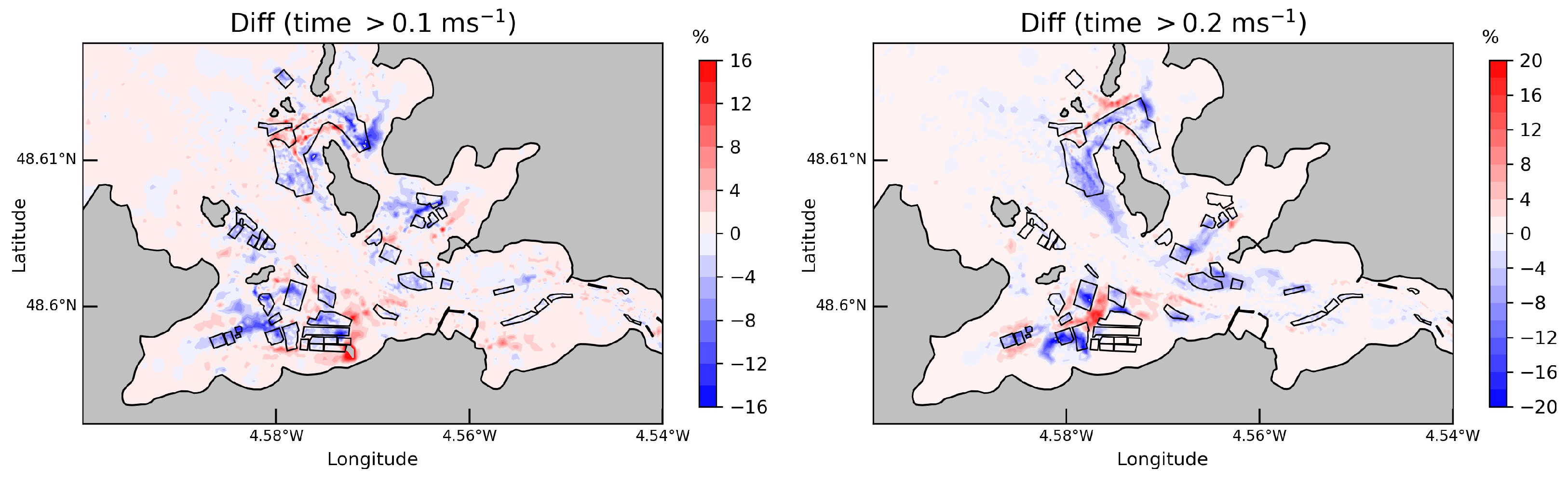
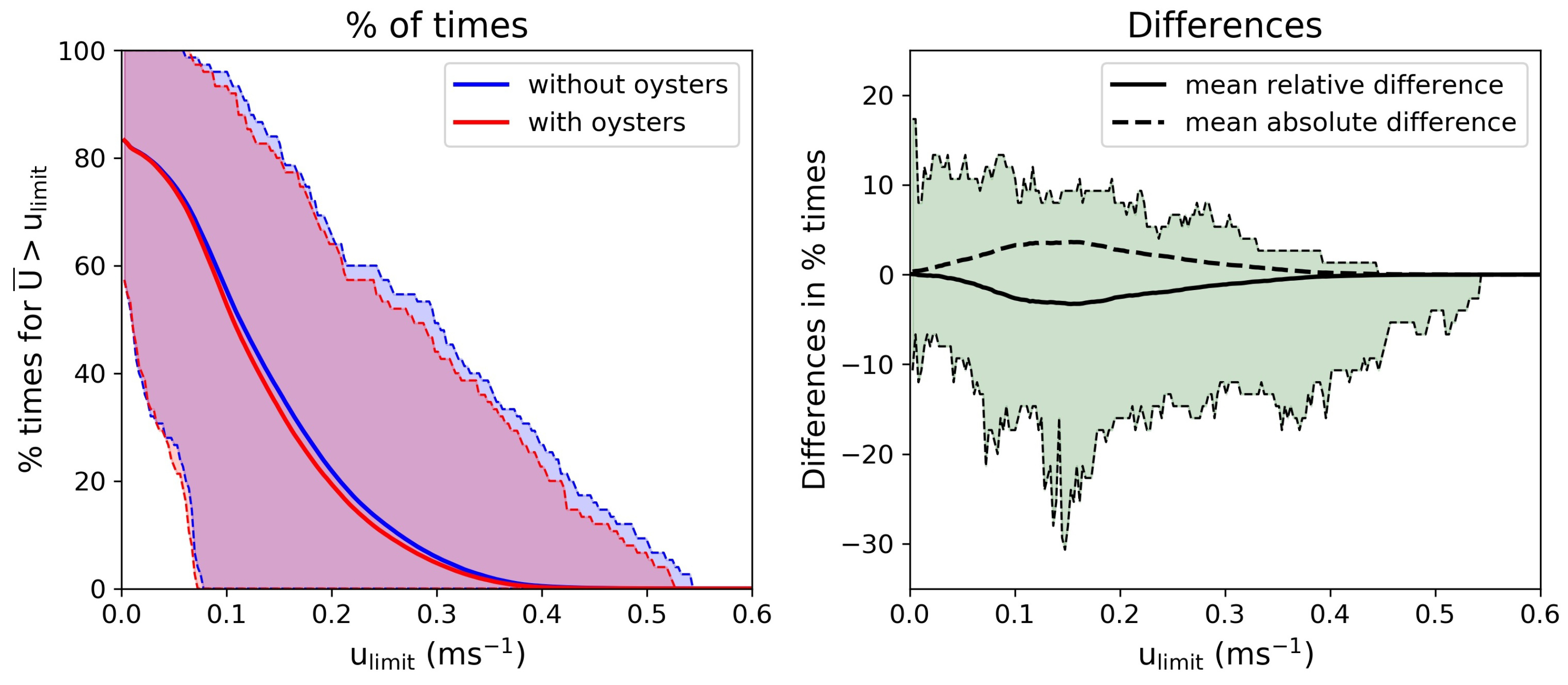
3.3.2. Velocities Exceedance
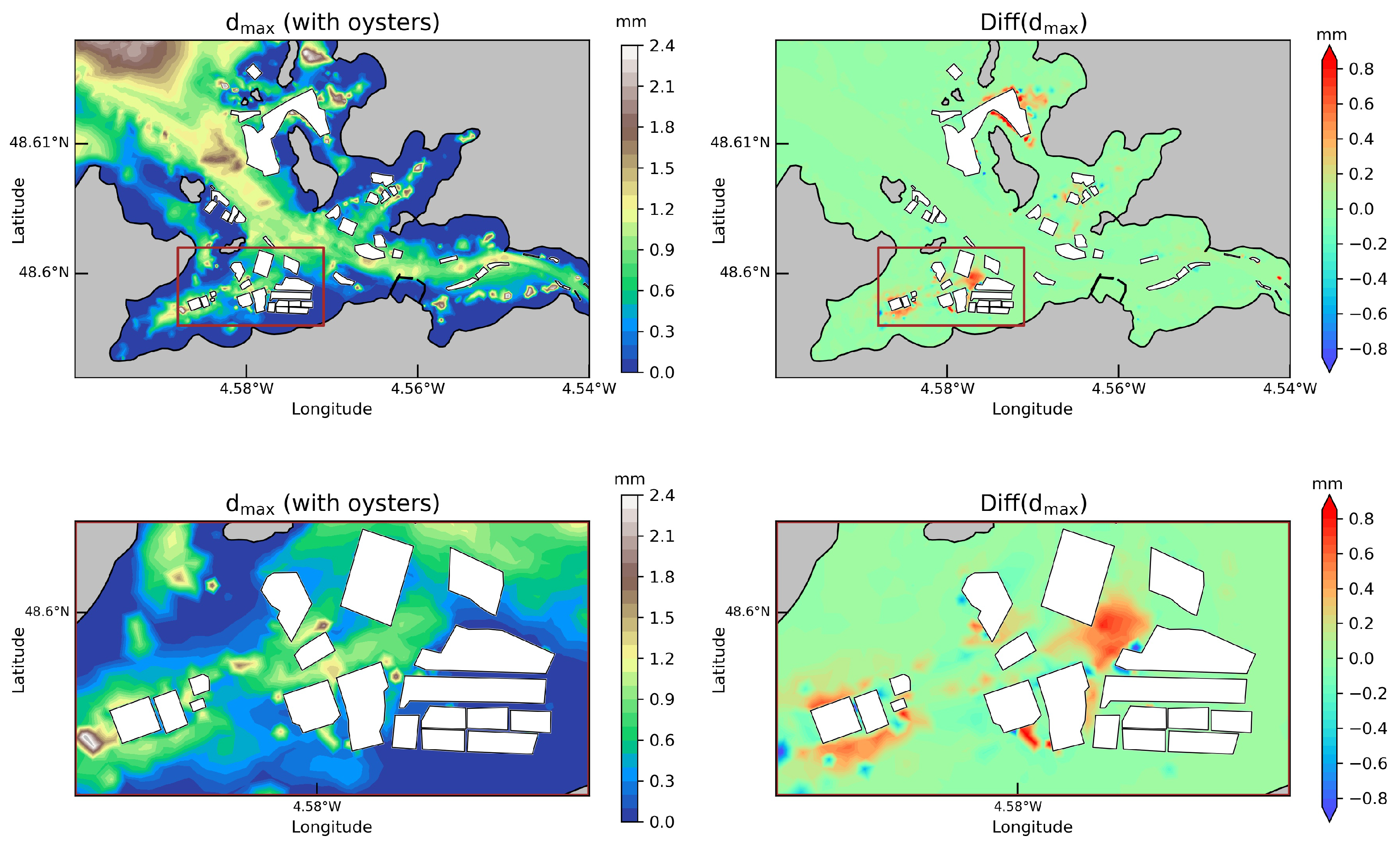
3.3.3. Sediment Transport
4. Conclusions
- The new Chézy formulation, here considered, relied on numerous approximations, including the alignment of current with table orientation, the development of vertical wakes and boundary layers, and the estimation of the minimal velocity within oyster bags. However, the associated analytical velocity profile (proposed here to express the Chézy coefficient) appeared consistent with experimental measurements and CFD predictions on a 1/2 scaled model. In preliminary studies, this revised formulation may, thus, be an interesting alternative to classical formulations based on a simple increase of the bottom friction, which neglected the conditions of submerged and unsubmerged structures in macro-tidal environments.
- Differences in the predictions of tidal current magnitudes were obtained between the two formulations of the Chézy coefficients considered in the vicinity of oyster structures at times of local peak flood and ebb. These effects were particularly noticeable for water depth near the height of oyster tables, thus exhibiting the limitation of the classical formulation to account for the temporal variations of the friction coefficient during the different phases of the tidal cycle.
- Predictions obtained with the revised formulation exhibited potential modifications of tidal velocities with (i) a reduction of current magnitudes over oyster farming areas and (ii) an acceleration of the tidal flow on both sides of these areas. Taking into account the reduced velocity magnitudes in intertidal areas, these modifications represented notable changes of current magnitudes with potential environmental effects.
- Thus, particular attention was dedicated to the fraction of time that the current magnitude was exceeding a given threshold value as an indicator of increased food delivery and water quality. However, despite the local high modifications, reduced changes of these velocities exceedance were obtained at the scale of areas covered by oyster tables.
- More important changes were finally exhibited on the surrounding sediment transport, in relation to the increased current magnitudes. Predictions suggested variations up to 0.7 mm of the maximum diameters of bed sediments liable to be moved in mean spring conditions. These effects were particularly noticeable in the south-western bay for structures bordering the access channel to the estuary. This suggested potential effects on seabed morphology and water quality.
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Gallardi, D. Effects of Bivalve Aquaculture on the Environment and Their Possible Mitigation: A Review. Fish. Aquac. J. 2014, 5, 8245. [Google Scholar] [CrossRef]
- O’Beirn, F.X.; Mckindsey, C.W.; Landry, T.; Costa-Pierce, B. Methods for Sustainable Shellfish Culture; Springer: Berlin/Heidelberg, Germany, 2012; pp. 9174–9196. [Google Scholar]
- FAO. The State of World Fisheries and Aquaculture—Meeting the Sustainable Development Goals; Food and Agriculture Organization of the United Nations: Rome, Italy, 2018. [Google Scholar]
- Yang, H.; Sturmer, L.; Baker, S. Molluscan Shellfish Aquaculture and Production. IFAS Extension, University of Florida, 2019. Available online: https://edis.ifas.ufl.edu/publication/FA191 (accessed on 1 January 2023).
- Solomon, O.; Ahmed, O. Ecological Consequences of Oysters Culture: A Review. Int. J. Fish. Aquat. Stud. 2016, 4, 01–06. [Google Scholar]
- DeFur, P.L.; Rader, D.N. Aquaculture in Estuaries: Feast or Famine? Estuaries 1995, 18, 2–9. [Google Scholar] [CrossRef]
- Read, P.; Fernandes, T. Management of environmental impacts of marine aquaculture in Europe. Aquaculture 2003, 226, 139–163. [Google Scholar] [CrossRef]
- Campbell, M.; Hall, S. Hydrodynamic effects on oyster aquaculture systems: A review. Rev. Aquac. 2019, 11, 896–906. [Google Scholar] [CrossRef]
- Forrest, B.M.; Keeley, N.B.; Hopkins, G.A.; Webb, S.C.; Clement, D.M. Bivalve aquaculture in estuaries: Review and synthesis of oyster cultivation effects. Aquaculture 2009, 298, 1–15. [Google Scholar] [CrossRef]
- Kirby, R. Sediments 2-oysters 0: The case histories of two legal disputes involving fine sediments and oysters. J. Coast. Res. 1994, 10, 466–487. [Google Scholar]
- Goslin, E. Marine Bivalve Molluscs, 2nd ed.; John Wiley & Sons: West Sussex, UK, 2015. [Google Scholar]
- Wildish, D.; Kristmanson, D. Benthic Suspension Feeders and Flow; Cambridge University Press: Cambridge, UK, 1997. [Google Scholar]
- Kervella, Y.; Germain, G.; Gaurier, B.; Facq, J.V.; Cayocca, F.; Lesueur, P. Experimental study of the near-field impact of an oyster table on the flow. Eur. J. Mech. B/Fluids 2010, 29, 32–42. [Google Scholar] [CrossRef]
- Nugues, M.; Kaiser, M.; Spencer, B.; Edwards, D. Benthic community changes associated with intertidal oyster cultivation. Aquac. Res. 1996, 27, 913–924. [Google Scholar] [CrossRef]
- Kervella, Y. Impact des Installations ostrÉicoles sur l’Hydrodynamique et la Dynamique Sédimentaire. Ph.D. Thesis, Université de Caen, Caen, France, 2010. [Google Scholar]
- Gaurier, B.; Germain, G.; Kervella, Y.; Davourie, J.; Cayocca, F.; Lesueur, P. Experimental and numerical characterization of an oyster farm impact on the flow. Eur. J. Mech. B/Fluids 2011, 30, 513–525. [Google Scholar] [CrossRef]
- Soletchnik, P.; Lambert, C.; Costil, K. Summer mortality of Crassostrea gigas (Thunberg) in relation to environmental rearing conditions. J. Shellfish. Res. 2005, 24, 197–207. [Google Scholar]
- SHOM. Courants de Marée et Hauteurs d’eau. La Manche de Dunkerque à Brest; Technical Report 564-UJA; Service Hydrographique et Océanographique de la Marine: Brest, France, 2000. [Google Scholar]
- Rollet, C.; Bonnot-Courtois, C.; Hamon, N.; Loarer, R. Réseau de Surveillance Benthique. Région Bretagne. Approche Sectorielle Intertidale. Cartographie des Habitats Benthiques, Secteur des Abers; Technical Report DYNECO/AG/11-06/CR; Ifremer: Brest, France, 2011; 47p. [Google Scholar]
- Hervouet, J.M. Hydrodynamics of Free Surface Flows, Modelling with the Finite Element Method; Cambridge University Press: Cambridge, UK, 2007; p. 311. [Google Scholar]
- EDF R&D. TELEMAC Modelling System—TELEMAC-3D Software—Release 6.2; Technical Report; EDF: Paris, France, 2013. [Google Scholar]
- Robins, P.; Lewis, M.; Simpson, J.; Howlett, E.; Malham, S. Future variability of solute transport in a macrotidal estuary. Estuarine Coast. Shelf Sci. 2014, 151, 88–99. [Google Scholar] [CrossRef]
- Guillou, N.; Thiébot, J. The impact of seabed rock roughness on tidal stream power extraction. Energy 2016, 112, 762–773. [Google Scholar] [CrossRef]
- Soulsby, R. The bottom boundary layer of shelf seas. In Physical Oceanography of Coastal and Shelf Seas; Johns, B.E., Ed.; Elsevier: Amsterdam, The Netherlands, 1983; pp. 189–266. [Google Scholar]
- Meijer, D.; Velzen, E.V. Prototype-scale flume experiments on hydraulic roughness of submerged vegetation. In Proceedings of the 28th International IAHR Conference, Paris, France, 25–28 August 1999. [Google Scholar]
- Jourdan, D.; Paradis, D.; Pasquet, A.; Michaud, H.; Gouillon, F.; Baraille, R.; Biscara, L.; Voineson, G.; Ohl, P. Le projet HOMONIM. Une contribution à l’amélioration de la prévision des submersions marines pour la Vigilance Vagues-Submersion. In Proceedings of the COCORISCO Conference, Brest, France, 3–4 July 2014. [Google Scholar]
- Louvart, L.; Grateau, C. The Litto3D project. In Proceedings of the Oceans 2005—Europe, Brest, France, 20–23 June 2005. [Google Scholar]
- Guillou, N.; Thiébot, J.; Chapalain, G. Turbines’ effects on water renewal within a marine tidal stream energy site. Energy 2019, 189, 116113. [Google Scholar] [CrossRef]
- Egbert, G.; Bennett, A.; Foreman, M. TOPEX/POSEIDON tides estimated using a global inverse model. J. Geophys. Res. 1994, 99, 24821–24852. [Google Scholar] [CrossRef]
- Merceron, M.; Gaffet, J.D. Température et Salinité dans l’Aber Benoît et l’Aber Wrac’h - été 1991—Rapport de Mesures; Technical Report; Ifremer: Plouzané, France, 1991. [Google Scholar]
- Souchu, P.; Vaquer, A.; Collos, Y.; Landrein, S.; Deslous-Paoli, J.M.; Bibent, B. Influence of shellfish farming activities on the biogeochemical composition of the water column in Thau Lagoon. Mar. Ecol. Prog. Ser. 2001, 218, 141–152. [Google Scholar] [CrossRef]
- Mitchell, I.M. In situ biodeposition rates of Pacific oysters (Crassostrea gigas) on a marine farm in Southern Tasmania (Australia). Aquaculture 2006, 257, 194–203. [Google Scholar] [CrossRef]
- Newell, C.; Hawkins, A.; Morris, K.; Richardson, J.; Davis, C.; Getchis, T. ShellGIS: A dynamic tool for shellfish farm site selection. J. World Aquac. Soc. 2013, 44, 50–53. [Google Scholar]
- Pearson, T.H.; Black, K.D. The environmental impact of marine fish cage culture. In Environmental Impacts of Aquaculture; Black, K.D.E., Ed.; Academic Press: Sheffield, UK, 2001; pp. 1–31. [Google Scholar]
- Soulsby, R.L.; Whitehouse, R.J.S.W. Threshold of sediment motion in coastal environments. In Proceedings of the Pacific Coasts and Ports ’97 Conference, Cristchurch, New Zealand, 7–11 September 1997; pp. 149–154. [Google Scholar]
- Everett, R.A.; Ruiz, G.M.; Carlton, J.T. Effects of oyster mariculture on submerged aquatic vegetation: An experimental test in a Pacific northwester estuary. Mar. Ecol. Prog. Ser. 1995, 125, 2205–2217. [Google Scholar] [CrossRef]
- Forrest, B.; Creese, R. Benthic impacts of intertidal oyster culture, with consideration of taxonomic sufficiency. Environ. Monit. Assess. 2006, 112, 159–176. [Google Scholar] [CrossRef] [PubMed]




| Parameters | Definition | Value |
|---|---|---|
| height of the upper side of oyster bags | 0.8 m | |
| m | number of rods per unit area | |
| D | diameter of iron rods | 0.016 m |
| drag coefficient of iron rods | 1.0 | |
| coefficient for calibrating | 0.4 | |
| seabed bottom roughness | ||
| roughness of upper part of oyster tables |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guillou, N. Modelling the Effects of Oyster Tables on Estuarine Tidal Flow. Coasts 2023, 3, 2-23. https://doi.org/10.3390/coasts3010002
Guillou N. Modelling the Effects of Oyster Tables on Estuarine Tidal Flow. Coasts. 2023; 3(1):2-23. https://doi.org/10.3390/coasts3010002
Chicago/Turabian StyleGuillou, Nicolas. 2023. "Modelling the Effects of Oyster Tables on Estuarine Tidal Flow" Coasts 3, no. 1: 2-23. https://doi.org/10.3390/coasts3010002
APA StyleGuillou, N. (2023). Modelling the Effects of Oyster Tables on Estuarine Tidal Flow. Coasts, 3(1), 2-23. https://doi.org/10.3390/coasts3010002






