Exploiting the Regularized Greedy Forest Algorithm Through Active Learning for Predicting Student Grades: A Case Study
Abstract
1. Introduction
2. Related Works
2.1. Recent Works on EDM
2.2. Related Works on Active Learning
3. Research Methodology
3.1. Research Motivation
3.2. The RGF Classification Algorithm
3.3. Active Learning
3.4. Proposed Methodology
4. Experiments and Results
4.1. Dataset
4.2. Experimental Setup
- The C4.5 decision tree algorithm: A well-known extension of ID3, which was introduced by Quinlan [35]. We used the J4.8 decision tree learning implementation.
- Multilayer perceptron: an artificial neural network architecture (ANN) [36] that utilizes feedforward connections and backpropagation for training learning models.
- Naïve Bayes: a probabilistic machine learning algorithm that is based on the Bayes theorem [37].
- Bagging: The bagging predictor first generates multiple instances of a predictive model and then combines them to obtain a more accurate predictor [38]. We tested bagging with Naïve Bayes, multilayer perceptron, and C4.5 classifiers.
- Random forests (RF): an ensemble learning method consisting of multiple decision trees, widely utilized for both classification and regression problems [40].
5. Results
5.1. First Phase of Experiments: Comparing the Performance of the RGF Classifier
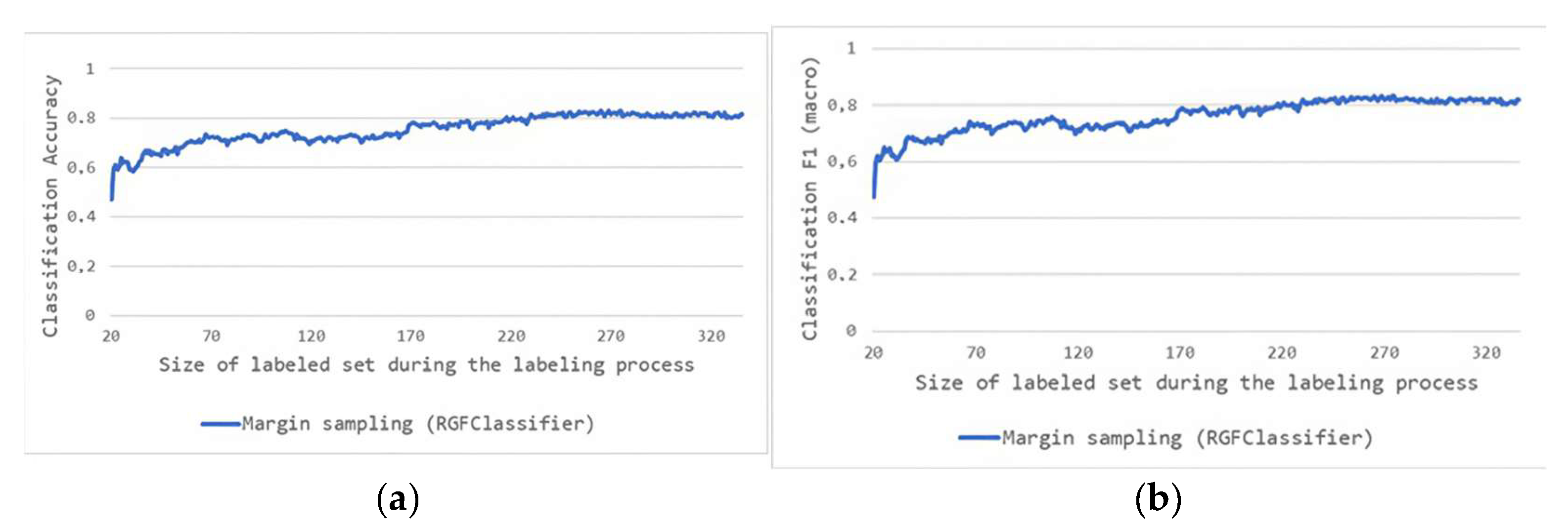
5.2. Second Phase of Experiments: Incorporating the RGF Classifier Within an Active Learning Scenario
6. Discussion
- Enhanced Prediction Accuracy: The Regularized Greedy Forest (RGF) is recognized for its effective feature selection capabilities, which enhance the construction of accurate predictive models by concentrating on the most relevant features. Additionally, RGF is adept at handling complex interactions and non-linearities within the data, thereby improving the model’s predictive accuracy.
- Efficient Use of Data: Active learning optimizes the training process by selecting the most informative data points for labeling, ensuring that the model is trained on instances that yield the greatest improvements. This approach reduces the amount of labeled data required while strategically querying only the most valuable samples, thereby conserving resources and minimizing effort.
- Regularization Benefits: The Regularized Greedy Forest (RGF) algorithm incorporates regularization techniques, such as L1 and L2 regularization, to prevent overfitting and ensure that the model generalizes effectively to new, unseen data. These regularization methods help maintain model simplicity by penalizing complexity, which enhances interpretability and further reduces the risk of overfitting.
- Scalability: The Regularized Greedy Forest (RGF) algorithm is capable of efficiently processing large datasets with high-dimensional feature spaces, making it particularly suitable for educational datasets that frequently encompass numerous variables. Additionally, the iterative nature of the active learning framework enables incremental updates to the model, enhancing its scalability and adaptability to new data.
- Adaptability: The active learning framework enables the model to dynamically adapt to new data and evolving patterns, ensuring high prediction accuracy over time. Its versatility allows it to accommodate different types of data and acquisition functions, making it suitable for a wide range of educational settings and requirements.
- Although our study focused on one strategy, we propose to explore other methods, such as uncertainty sampling, query by committee, and density-weighted strategies, in future research to provide more comprehensive results.
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Romero, C.; Ventura, S. Educational data mining: A survey from 1995 to 2005. Expert Syst. Appl. 2007, 33, 135–146. [Google Scholar] [CrossRef]
- Rahman, M.M.; Watanobe, Y.; Kiran, R.U.; Thang, T.C.; Paik, I. Impact of practical skills on academic performance: A data-driven analysis. IEEE Access 2021, 9, 139975–139993. [Google Scholar] [CrossRef]
- Romero, C.; Ventura, S. Educational data mining: A review of the state of the art. IEEE Trans. Syst. Man Cybern. Part C (Appl. Rev.) 2010, 40, 601–618. [Google Scholar] [CrossRef]
- Charitopoulos, A.; Rangoussi, M.; Koulouriotis, D. On the use of soft computing methods in educational data mining and learning analytics research: A review of years 2010–2018. Int. J. Artif. Intell. Educ. 2020, 30, 371–430. [Google Scholar] [CrossRef]
- Kabathova, J.; Drlik, M. Towards predicting students dropout in university courses using different machine learning techniques. Appl. Sci. 2021, 11, 3130. [Google Scholar] [CrossRef]
- Du, X.; Yang, J.; Shelton, B.E.; Hung, J.-L.; Zhang, M. A systematic meta-review and analysis of learning analytics research. Behav. Inf. Technol. 2021, 40, 49–62. [Google Scholar] [CrossRef]
- Rafique, A.; Khan, M.S.; Jamal, M.H.; Tasadduq, M.; Rustam, F.; Lee, E.; Washington, P.B.; Ashraf, I. Integrating learning analytics and collaborative learning for improving students academic performance. IEEE Access 2021, 9, 167812–167826. [Google Scholar] [CrossRef]
- Wolff, A.; Zdrahal, Z.; Herrmannova, D.; Knoth, P. Predicting student performance from combined data sources. In Educational Data Mining: Applications and Trends; Springer: Cham, Switzerland, 2014; pp. 175–202. [Google Scholar]
- ANDRADE, T.L.D.; Rigo, S.J.; Barbosa, J.L.V. Active Methodology, Educational Data Mining and Learning Analytics: A Systematic Mapping Study. Inform. Educ. 2021, 20, 171–204. [Google Scholar] [CrossRef]
- Dien, T.T.; Luu, S.H.; Thanh-Hai, N.; Thai-Nghe, N. Deep Learning with Data Transformation and Factor Analysis for Student Performance Prediction. Int. J. Adv. Comput. Sci. Appl. (IJACSA) 2020, 11, 711–721. [Google Scholar] [CrossRef]
- Campbell, J.P.; DeBlois, P.B.; Oblinger, D.G. Academic analytics: A new tool for a new era. EDUCAUSE Rev. 2007, 42, 40. [Google Scholar]
- Vachkova, S.N.; Petryaeva, E.Y.; Kupriyanov, R.B.; Suleymanov, R.S. School in digital age: How big data help to transform the curriculum. Information 2021, 12, 33. [Google Scholar] [CrossRef]
- Johnson, R.; Zhang, T. Learning nonlinear functions using regularized greedy forest. IEEE Trans. Pattern Anal. Mach. Intell. 2013, 36, 942–954. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Dai, Q. A cost-sensitive active learning algorithm: Toward imbalanced time series forecasting. Neural Comput. Appl. 2022, 34, 6953–6972. [Google Scholar] [CrossRef]
- Settles, B. Active Learning Literature Survey; Department of Computer Sciences, University of Wisconsin-Madison: Madison, Wisconsin, 2009. [Google Scholar]
- Settles, B. From theories to queries: Active learning in practice. PMLR 2011, 16, 1–18. [Google Scholar]
- Mai, T.T.; Crane, M.; Bezbradica, M. Students learning behaviour in programming education analysis: Insights from entropy and community detection. Entropy 2023, 25, 1225. [Google Scholar] [CrossRef]
- Altaf, S.; Asad, R.; Ahmad, S.; Ahmed, I.; Abdollahian, M.; Zaindin, M. A Hybrid Framework of Deep Learning Techniques to Predict Online Performance of Learners during COVID-19 Pandemic. Sustainability 2023, 15, 11731. [Google Scholar] [CrossRef]
- Hussain, S.; Khan, M.Q. Student-performulator: Predicting students academic performance at secondary and intermediate level using machine learning. Ann. Data Sci. 2023, 10, 637–655. [Google Scholar] [CrossRef]
- Villegas-Ch, W.; Mera-Navarrete, A.; García-Ortiz, J. Data Analysis Model for the Evaluation of the Factors That Influence the Teaching of University Students. Computers 2023, 12, 30. [Google Scholar] [CrossRef]
- Asad, R.; Altaf, S.; Ahmad, S.; Mohamed, A.S.N.; Huda, S.; Iqbal, S. Achieving personalized precision education using the Catboost model during the COVID-19 lockdown period in Pakistan. Sustainability 2023, 15, 2714. [Google Scholar] [CrossRef]
- Liu, Y.; Fan, S.; Xu, S.; Sajjanhar, A.; Yeom, S.; Wei, Y. Predicting student performance using clickstream data and machine learning. Educ. Sci. 2022, 13, 17. [Google Scholar] [CrossRef]
- Xing, W.; Li, C.; Chen, G.; Huang, X.; Chao, J.; Massicotte, J.; Xie, C. Automatic assessment of students engineering design performance using a Bayesian network model. J. Educ. Comput. Res. 2021, 59, 230–256. [Google Scholar] [CrossRef]
- Kostopoulos, G.; Lipitakis, A.-D.; Kotsiantis, S.; Gravvanis, G. Predicting student performance in distance higher education using active learning. In Engineering Applications of Neural Networks. EANN 2017. Communications in Computer and Information Science; Springer: Cham, Switzerland, 2017. [Google Scholar]
- Kostopoulos, G.; Kotsiantis, S.; Ragos, O.; Grapsa, T.N. Early dropout prediction in distance higher education using active learning. In Proceedings of the 2017 8th International Conference on Information, Intelligence, Systems & Applications (IISA), Larnaca, Cyprus, 27–30 August 2017. [Google Scholar]
- Rolim, V.; Mello, R.F.; Nascimento, A.; Lins, R.D.; Gasevic, D. Reducing the size of training datasets in the classification of online discussions. In Proceedings of the 2021 International Conference on Advanced Learning Technologies (ICALT), Tartu, Estonia, 12–15 July 2021. [Google Scholar]
- Yang, T.-Y.; Baker, R.S.; Studer, C.; Heffernan, N.; Lan, A.S. Active learning for student affect detection. In Proceedings of the 12th International Conference on Educational Data Mining, EDM 2019, Montréal, QC, Canada, 2–5 July 2019. [Google Scholar]
- Karumbaiah, S.; Lan, A.; Nagpal, S.; Baker, R.S.; Botelho, A.; Heffernan, N. Using past data to warm start active machine learning: Does context matter? In LAK21: 11th International Learning Analytics and Knowledge Conference; Association for Computing Machinery: New York, NY, USA, 2021. [Google Scholar]
- Hamalainen, W.; Vinni, M. Classifiers for educational data mining. In Handbook of Educational Data Mining, Chapman & Hall/CRC Data Mining and Knowledge Discovery Series; CRC Press: Boca Raton, FL, USA, 2021; pp. 57–71. [Google Scholar]
- Hodges, J.; Lehmann, E. Ranks methods for combination of independent experiments in analysis of variance. Ann. Math. Stat. 1962, 33, 482–497. [Google Scholar] [CrossRef]
- Friedman, J.H. Greedy function approximation: A gradient boosting machine. Ann. Stat. 2001, 29, 1189–1232. [Google Scholar] [CrossRef]
- Amrieh, E.A.; Hamtini, T.; Aljarah, I. Mining educational data to predict students academic performance using ensemble methods. Int. J. Database Theory Appl. 2016, 9, 119–136. [Google Scholar] [CrossRef]
- Campbell, C.; Cristianini, N.; Smola, A. Query learning with large margin classifiers. In ICML ‘00: Proceedings of the Seventeenth International Conference on Machine Learning; Morgan Kaufmann Publishers Inc.: San Francisco, CA, USA, 2000. [Google Scholar]
- Schohn, G.; Cohn, D. Less is more: Active learning with support vector machines. In ICML ‘00: Proceedings of the Seventeenth International Conference on Machine Learning; Morgan Kaufmann Publishers Inc.: San Francisco, CA, USA, 2000. [Google Scholar]
- Quinlan, J.R. C4.5 Programs for Machine Learning; Morgan Kaufmann: Burlington, MA, USA, 1993. [Google Scholar]
- Witten, I.H.; Frank, E.; Hall, M.A. Data Mining: Practical Machine Learning Tools and Techniques, 3rd ed.; Morgan Kaufmann: Burlington, MA, USA, 2011. [Google Scholar]
- Mitchell, T.M. Machine Learning; McGraw-Hill: New York, NY, USA, 1997. [Google Scholar]
- Breiman, L. Bagging predictors. Mach. Learn. 1996, 24, 123–140. [Google Scholar] [CrossRef]
- Freund, Y.; Schapire, R.E. A decision-theoretic generalization of on-line learning and an application to boosting. J. Comput. Syst. Sci. 1997, 55, 119–139. [Google Scholar] [CrossRef]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Holmes, G.; Donkin, A.; Witten, I.H. Weka: A machine learning workbench. In Proceedings of the ANZIIS ‘94—Australian New Zealnd Intelligent Information Systems Conference, Brisbane, QLD, Australia, 29 November–2 December 1994. [Google Scholar]
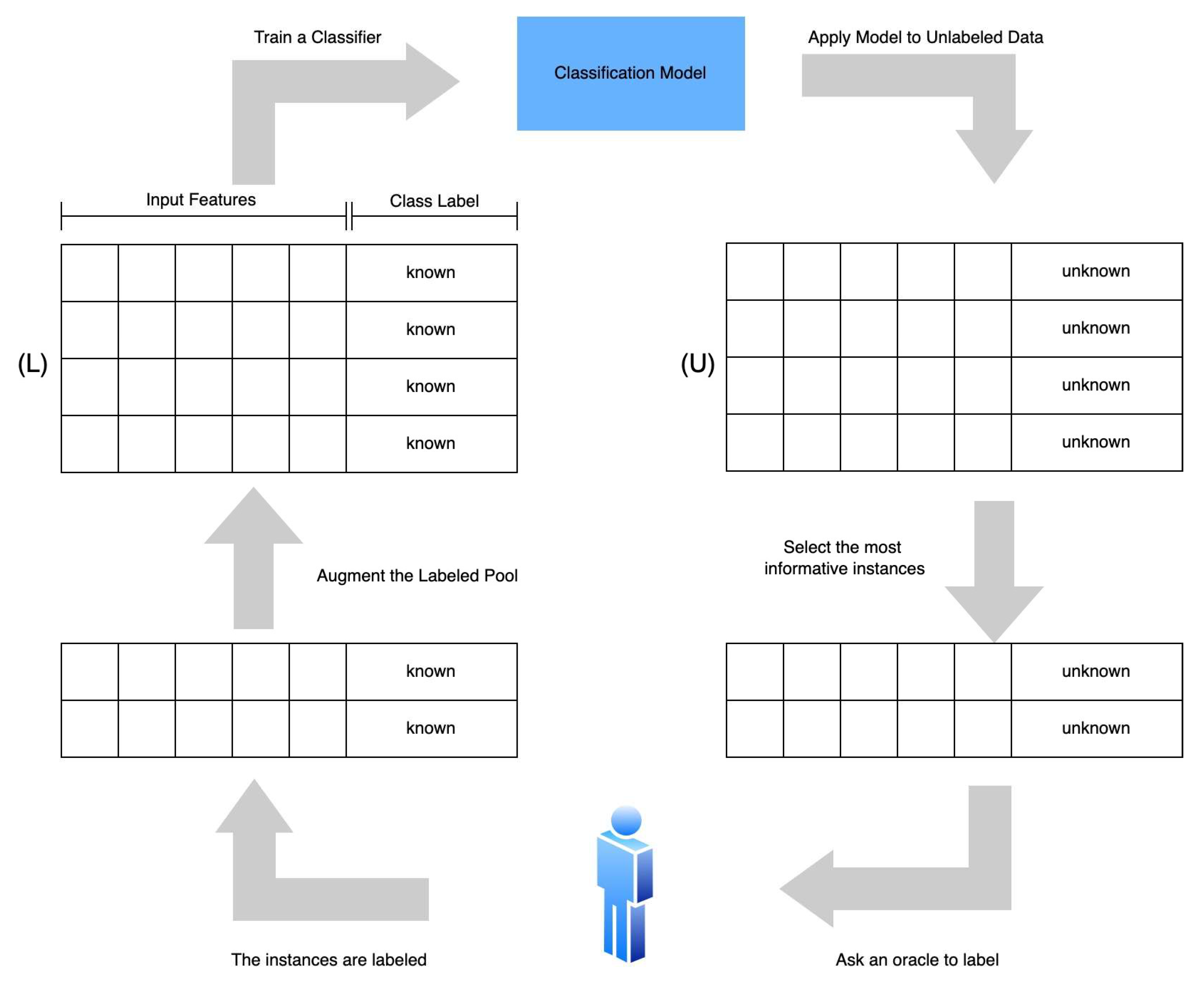

| Initialize: - Set of labeled data (X_l, y_l) - Set of unlabeled data X_u - Set of base learners (trees) F = {} - Initial model f(x) = 0 - Learning rate η - Regularization parameters λ1 and λ2 - Maximum number of iterations T - Budget B (number of data points to label) - Acquisition function A(x, f) to measure informativeness of data points Algorithm: 1. While budget B is not exhausted: a. Train the RGF model on the labeled data (X_l, y_l): i. For t = 1 to T: - Compute gradients and hessians for current model predictions: - Gradient: g_i = ∂L(y_i, f(x_i))/∂f(x_i) - Hessian: h_i = ∂²L(y_i, f(x_i))/∂f(x_i)² - Initialize new tree: - Tree t_new = {} - For each node split in the tree: - Select the best split that maximizes the gain: - Gain = ∑ g_i²/(∑ h_i + λ2) − λ1 - Choose split with the highest gain - Update the tree structure with the best split - Add the new tree to the forest: - F = F ∪ {t_new} - Update the model with the new tree: - f(x) = f(x) + η * t_new(x) b. Select the most informative unlabeled data points using the acquisition function: - Calculate informativeness score for each x in X_u: A(x, f) - Select top B’ points with highest scores (B’ ≤ B) c. Query the oracle to obtain labels for the selected points: - Get labels y_selected for X_selected d. Update the labeled and unlabeled datasets: - X_l = X_l ∪ X_selected - y_l = y_l ∪ y_selected - X_u = X_u\X_selected e. Reduce the budget: - B = B − B’ 2. Output the final model: - f(x) = ∑ t∈F η * t(x) |
| Category | Features | Value Types |
|---|---|---|
| Demographics | Student’s nationality, gender, place of birth, parent responsible (4 features) | Categorical |
| Academic background | educational stage, grade level, section, semester, course topic, absence days (6 features) | Categorical |
| Parent’s participation | parent answering survey, parent’s school satisfaction (2 features) | Categorical |
| Behavioral | discussion groups, visited resources, raised hand in class, announcement viewing (4 features) | Numerical |
| Class | student performance {high, medium, low} | Categorical |
| Feature | Description | Values |
|---|---|---|
| nationality | student’s nationality | {Egypt, Kuwait, …, USA, Venzuela} |
| gender | student’s gender | {m, f} |
| place of birth | student’s place of birth | {Egypt, Kuwait, …, USA, Venzuela} |
| parent responsible | student’s parent responsible | {father, mother} |
| educational stage | student’s level of schooling | {primary, middle, high} |
| grade level | student’s grade | {G-01, G-02, …, G-12} |
| section | student’s classroom | {A, B, C} |
| semester | school year semester | {first, second} |
| course topic | course topic | {math, biology, …, science} |
| absence days | total student’s absence days | {under 7 days, above 7 days} |
| parent answering survey | whether parent answers the surveys provided at school | {y, n} |
| parent school satisfaction | the degree of parent’s satisfaction with the school | {good, bad} |
| discussion groups | total number of visiting discussion groups | numeric |
| visited resources | total number of visiting resources | numeric |
| raised hand in class | total number of hand raises in class | numeric |
| announcement viewing | total number of viewing announcements | numeric |
| class | students’ total grade | {high, medium, low} |
| Female | Male | Low | Medium | High | Total | |
|---|---|---|---|---|---|---|
| Dataset | 175 | 305 | 127 | 211 | 142 | 480 |
| 36.5% | 63.5% | 26% | 44% | 30% | 100% |
| Tuned RGF Hyperparameters for Training |
|---|
| max_leaf = 10,000, test_interval = 100, algorithm = “RGF_Sib”, loss = “Log”, reg_depth = 1.0, l2 = 1.0, sl2 = 0.001, min_samples_leaf = 10, learning_rate = 0.001 |
| Classifiers | Evaluation Measure | ||||
|---|---|---|---|---|---|
| Accuracy | Recall | Precision | F1 | ||
| C4.5 (J4.8) | 0.7583 | 0.758 | 0.760 | 0.759 | |
| ANN | 0.7937 | 0.794 | 0.793 | 0.793 | |
| NB | 0.6770 | 0.677 | 0.675 | 0.671 | |
| Bagging | J4.8 | 0.7437 | 0.744 | 0.743 | 0.743 |
| ANN | 0.7812 | 0.781 | 0.781 | 0.781 | |
| NB | 0.6770 | 0.677 | 0.676 | 0.672 | |
| Boosting | J4.8 | 0.7791 | 0.779 | 0.779 | 0.779 |
| ANN | 0.7937 | 0.794 | 0.793 | 0.793 | |
| NB | 0.7229 | 0.723 | 0.724 | 0.718 | |
| RF | 0.7666 | 0.767 | 0.766 | 0.766 | |
| RGF | 0.8160 * | 0.8181 * | 0.8229 * | 0.8186 * | |
| Rank | Algorithm |
|---|---|
| 2.50000 | RGF |
| 8.50000 | Boosting (ANN) |
| 8.50000 | ANN |
| 14.50000 | Bagging (ANN) |
| 18.50000 | Boosting (J4.8) |
| 22.50000 | RF |
| 26.50000 | C4.5 (J4.8) |
| 30.50000 | Bagging (J4.8) |
| 34.50000 | Boosting (NB) |
| 40.25000 | Bagging (NB) |
| 40.75000 | NB |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tsiakmaki, M.; Kostopoulos, G.; Kotsiantis, S. Exploiting the Regularized Greedy Forest Algorithm Through Active Learning for Predicting Student Grades: A Case Study. Knowledge 2024, 4, 543-556. https://doi.org/10.3390/knowledge4040028
Tsiakmaki M, Kostopoulos G, Kotsiantis S. Exploiting the Regularized Greedy Forest Algorithm Through Active Learning for Predicting Student Grades: A Case Study. Knowledge. 2024; 4(4):543-556. https://doi.org/10.3390/knowledge4040028
Chicago/Turabian StyleTsiakmaki, Maria, Georgios Kostopoulos, and Sotiris Kotsiantis. 2024. "Exploiting the Regularized Greedy Forest Algorithm Through Active Learning for Predicting Student Grades: A Case Study" Knowledge 4, no. 4: 543-556. https://doi.org/10.3390/knowledge4040028
APA StyleTsiakmaki, M., Kostopoulos, G., & Kotsiantis, S. (2024). Exploiting the Regularized Greedy Forest Algorithm Through Active Learning for Predicting Student Grades: A Case Study. Knowledge, 4(4), 543-556. https://doi.org/10.3390/knowledge4040028








