Use of Patterns of Service Utilization and Hierarchical Survival Analysis in Planning and Providing Care for Overdose Patients and Predicting the Time-to-Second Overdose

Abstract

Individuals from a variety of backgrounds are affected by the opioid crisis. To provide optimal care for individuals at risk of opioid overdose and prevent subsequent overdoses, a more targeted response that goes beyond the traditional taxonomical diagnosis approach to care management needs to be adopted. In previous works, Graph Machine Learning and Natural Language Processing methods were used to model the products for planning and evaluating the treatment of patients with complex issues. This study proposes a methodology of partitioning patients in the opioid overdose cohort into various communities based on their patterns of service utilization (PSUs) across the continuum of care using graph community detection and applying survival analysis to predict time-to-second overdose for each of the communities. The results demonstrated that the overdose cohort is not homogeneous with respect to the determinants of risk. Moreover, the risk for subsequent overdose was quantified: there is a 51% higher chance of experiencing a second overdose for a high-risk community compared to a low-risk community. The proposed method can inform a more efficient treatment heterogeneity approach for a cohort made of diverse individuals, such as the opioid overdose cohort. It can also guide targeted support for patients at risk of subsequent overdoses.

1. Introduction

1.1. Use of Patterns of Service Utilization in Planning and Providing Care to Complex Patients

Regarding factors that govern the achievement of outcomes for patients with complex problems, solely relying on traditional taxonomic diagnostic approaches to care management can be limiting [1]. More challenges arise when the cohort of patients sharing the same diagnosis is not homogeneous with respect to other factors affecting their health. Multiple emerging conditions and distinctive distal and proximal determinants of health profiles can affect how patients respond to the treatment [2].

The overdose crisis has had a devastating impact [3,4,5]. Individuals affected come from diverse socioeconomic statuses, education levels, and cultural backgrounds [6]. Studies have shown that individuals suffering from substance use disorders, mental health disorders, or homelessness are at a higher risk of overdose [7,8,9,10,11,12]. However, there are cases where individuals who are not in a high-risk group are impacted by opioid overdoses [13,14,15]. Hence, determining whether the programs designed to combat this crisis are effective is challenging, as they clearly benefit some patients but not others [16], as the overdose cohort is not homogeneous with respect to determinants of risk [17].

The ultimate objectives are to (1) provide the best care for persons at risk for overdoses, (2) reduce the rate of overdoses, and (3) prevent subsequent overdoses. There is a need to look beyond the traditional taxonomic diagnostic approach to care management. One of the venues that need to be explored is the dynamics of engagement of individuals constituting the opioid overdose cohort with the health service system to understand their Patterns of Service Utilization (PSUs) across the continuum of care. PSUs are fundamentally descriptive and consist of channels that are etched progressively across the service system by groups of individuals who share some common set of needs. This may open an opportunity to effectively respond to the opioid crisis by providing a more targeted response to the individuals affected.

1.2. Evidence-Based Care: Machine Learning and Statistical Analysis

Significant effort has been devoted to supporting evidence-based care through both statistical and machine learning (ML) approaches to analyze healthcare data, generate insights, and inform care delivery. ML focuses on iterative construction and validation of models using algorithms to find patterns in high-dimensional data [18]. In contrast, statistical models focus on inference based on properties of the datasets as a whole (e.g., measures of central tendency for parametric methods; marginal distributions for some non-parametric tests) [18].

Survival analysis has been a standard method in statistics used to assess risk or survival probability over time [19]. For example, it can be used in cancer studies to compare time from complete remission to relapse among several treatments. Other examples include the use of survival analysis to model medical prognosis [20], model factors associated with length of stay for patients [21], and examine the influence of living arrangements and healthcare utilization on patients’ mortality [22].

1.3. Objectives

Individuals that have taken an overdose and/or are at risk of a second overdose present a different constellation of risk factors that bias the odds of overdosing. These different constellations of risk factors may reflect the fact that this group of individuals is not homogeneous. Understanding these differences is a first step in providing better care for opioid overdose patients and/or preventing subsequent overdoses.

In our previous works [23,24,25,26], the consideration of PSUs in planning and evaluating the treatment of patients with complex issues was proposed. Using Clinical Information System (CIS) encounters data, PSUs represent pathways etched into the service system terrain by the journeys of a patient or cohort of patients as they interact with a cross-continuum health service system. Various ML algorithms, including graph community detection and Natural Language Processing (NLP), are used to (1) group related health services based on PSUs, (2) compare/contrast the effectiveness/existence of a service model in caring for various cohorts of patients, and (3) evaluate access disparity for vulnerable patients.

To achieve this, different approaches were considered, including the following: (1) The use of an iterative graph community detection, combined with input from clinical subject matter experts (SMEs) to identify patterns in patient–service encounter data that are difficult to detect via classic statistical methods, resulting in a grouping of related health services based on PSUs [23]. In this case, services were connected when used by the same patients. The generated communities of services provide a possibility of influencing the reorganization of services within the health service structure to provide better care for vulnerable patients with mental and other complex healthcare challenges. (2) To show the similarity of results across different approaches for cross-validation and to demonstrate that the grouping of related services demonstrated in [23] was not an artifact of the method employed, NLP clustering was used–where each patient’s history of service utilization was generated as a sentence [24]. Following this, term frequency-inverse document frequency and cosine similarity were used to measure similarity between services, and a series of clustering algorithms were used to group similar services. The results in [23,24] were determined from a clinical perspective by clinical SMEs and service system operations experts to be similar. (3) The work in [23,24] modeled products of service system dynamics as temporal entities. In [25], the order of events was added to the data model to provide topological depictions of the dynamics that are embodied in patients’ movement across a complex healthcare system. Using a directed graph and applying various topological visualizations of the graph [25], we identified the way diverse components of the healthcare service system are functionally connected or disconnected by patient journeys. This methodology provided a preliminary step in addressing the challenge of locating potential operational problems for patients with complex problems engaging with a complex healthcare service system. (4) Expanding on [25] and using directed graph and logistic regression, a methodology to identify and quantify cohort-specific disparities in accessing healthcare services across the continuum of care was proposed in [26]. The result in [26] demonstrated that a more nuanced approach to assessing access-to-care disparity is feasible using PSUs from a longitudinal cross-continuum healthcare dataset.

As previously stated, survival analysis is a standard method in statistics that has been used to assess risk or survival probability over time, related to several clinical settings [19,20,21,22]. Additionally, regarding opioid overdose risk assessment, many studies have been conducted in areas such as: (1) the understanding of risk factors for a population of patients receiving opioids for pain [27], (2) the assessment of opioid overdose risk using patient data level [28], (3) the assessment of risk and protective factors for repeated overdose [29], and (4) the intersectionality of characteristics such as demographics, socioeconomics, and service use among individuals who experienced opioid overdose [17]. What is missing in the literature is a methodological approach for performing a comparison of risks of survival probability for a cohort of opioid overdose patients, based on their pattern of service engagement with the healthcare system across the full continuum of care, well beyond the emergency department and hospital admission.

Using graph community detection and survival analysis and relying on patients’ encounters data collected from a host organization, CIS, the work in this paper will expand on the use of PSUs, as outlined in [23,24,25,26], to answer the following questions:

• Using PSUs, to what extent can we determine whether the opioid overdose cohort is homogeneous or not with respect to determinants of risk?
• How many communities constitute the opioid overdose cohort, based on how patients within this cohort interact with the host organization’s cross-continuum service system?
• To what extent can we determine the risk of a subsequent opioid overdose based on the community an opioid overdose patient belongs to and quantify it using survival analysis?

Answering the above questions will provide an opportunity for the health service system to effectively respond to the opioid crisis by providing a more targeted response to the individuals affected.

2. Methods

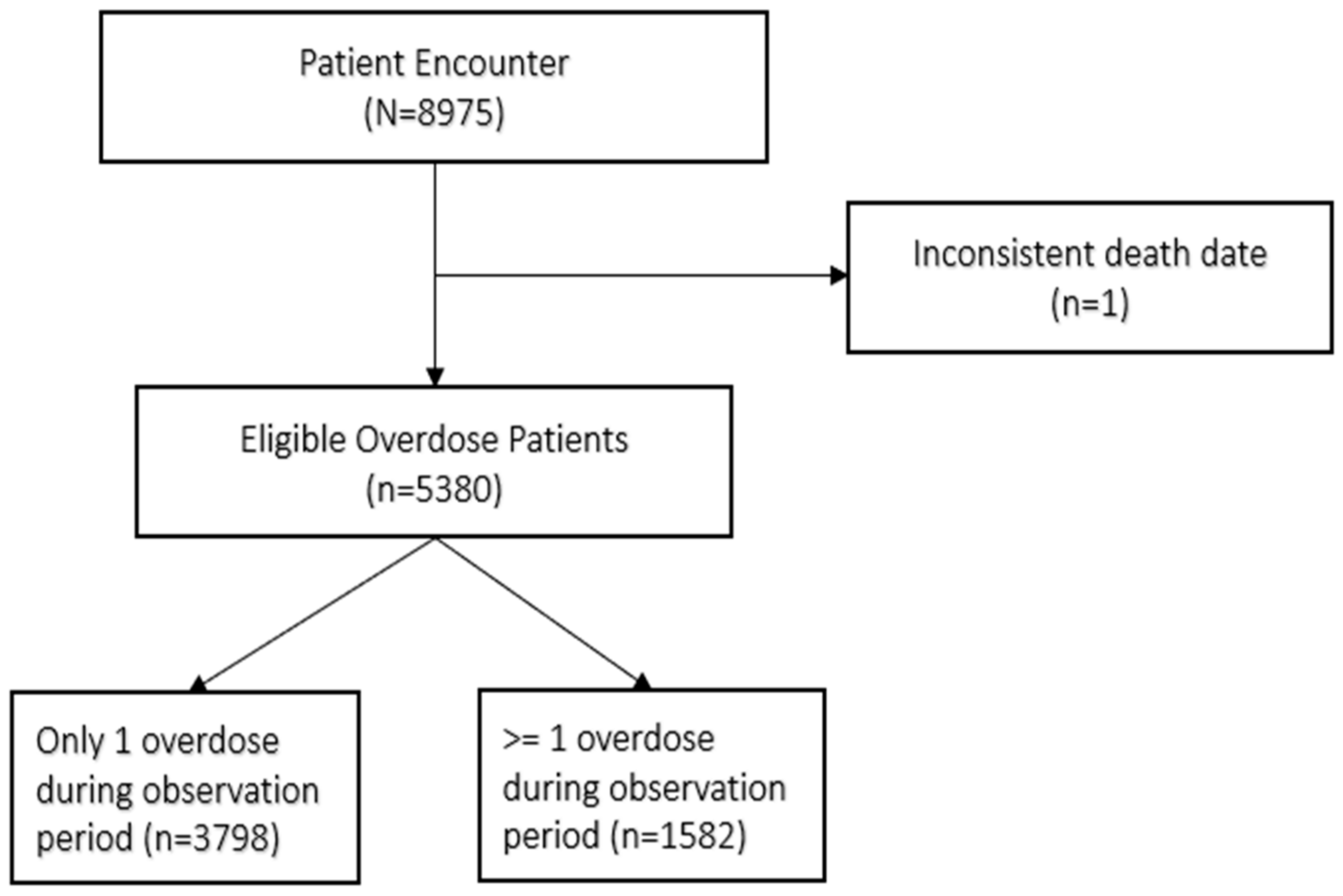
2.1. Addressing Data Granularity Issues

We use data supplied by a health organization that provides a comprehensive array of secondary and tertiary health services [30]. These services include acute care/intensive care services, hospital and community-based emergency response, ambulatory services, residential care services for older adults or persons contending with mental health issues, case management services, and a range of addictions harm reduction or rehab and recovery-oriented services. A certificate of approval was provided by the Research Ethics Board to conduct this research project.

One or more services provided are encapsulated into an array of roughly two thousand Service Units within the location of the host organization’s clinical information system used to support the delivery of care. To address the data granularity issues, following our previous works [23,24,25,26], a semantic layer, Clinical Context Coding Scheme [31], consisting of a scheme organized around six sets of codes, was applied to all the two thousand Service Units. The approximately two hundred Service Classes employed for the modeling in this paper consist of equivalence classes formed by the application of these code sets to the Service Units.

2.2. Community Detection

Healthcare encounter data can be viewed as a bipartite graph between patients and health services. This bipartite graph can then be projected either onto patients or services. These bipartite projections are illustrated in Figure 1. In this example, we have four patients (A, B, C, D) and three services (x, y, z). Upon projection onto patients, two patients are connected, or, in other words, there will be an edge between them in the projected graph if they use some common services. Furthermore, the weight of that edge is determined by the number of services that the two patients have in common. For example, Patient A and Patient C are connected by an edge because they both use Service y. In this case, there is only one common service, hence the weight of the edge AC is one. Between A and D, there are two common services (x and y), hence the weight of edge AD is two. As an alternative, we can also consider the number of times each patient used each service. For example, if Patient A used Service x five times and Patient D used Service x three times, then Service x contributes three units to the weight of the edge between A and D. On the other hand, for projection onto services, two services are connected if they have some common patients. In this paper, we group the patients based on their patterns of service utilization. Thus, we project the graph onto patients.

Having a weighted, undirected graph with patients as the nodes, we can then apply the Louvain community detection algorithm [32] to group the patients into communities. Roughly speaking, each community contains patients who have commonalities in their usage of services. Therefore, we can label each community based on the most dominant services used in the community. This becomes the characteristic of the patients in each community. We will show below that, in the case of the opioid overdose cohort, the differences in these characteristics are correlated to different risk levels for repeat overdose. The Louvain algorithm works by maximizing the modularity value, defined as follows:

$$Q={\displaystyle \frac{1}{2m}}\sum _{i,j}\left[A_{ij}-{\displaystyle \frac{k_i{k}_j}{2m}}\right]\mathsf{\delta }\left(c_i,c_j\right)$$

where $A_{ij}$ is the weight of the edge between node $i$ and node $j$; $k_i$ is the sum of the edge weights over all the edges that are connected to the node $i$; and $m$ is the total edge weights in the graph. Here, $c_i$ is the label of the community in which node $i$ belongs to. The delta function has a value equal to one if its two arguments are equal, i.e., if $c_i=c_j$, otherwise the value is 0.

At the initiation phase, each node has its own community. The algorithm starts by randomly choosing a node and then checks other nodes attached to that node to see if merging the communities would result in a higher $Q$. If yes, then the communities are merged. It would continue iteratively through all the communities until it could not increase $Q$ anymore, and then the algorithm would stop.

2.3. Survival Models

Survival analysis refers to the methods of modeling data where the outcome is the time until an event of interest occurs. One of the main challenges is the presence of instances whose event outcomes become unobservable after a certain time point, or when some instances do not experience any event during the study period. An important feature of survival analysis called censoring is the event of interest that may not have occurred for all subjects before the completion of the follow-up study. In this study, our main goal is to predict time-to-second overdose. In this case, patients who did not have a second overdose before the entire study period are rightly censored. In this section, we describe the model for longitudinal data with heterogeneous distribution such that the longitudinal data can be clustered into distinct groups.

Let $y_i$ be the longitudinal response for the subject $i$ monitored over a time $t_i;i=1,\dots ,n$; and $n$ is the number of subsets. Let $T_i^{*}$ denote the true event time (the time an individual leaves the study or has the second overdose) and $C_i$ be the censoring time. The true event $T_i=\min \left(C_i,T_i^{*}\right)$ represents the estimated survival time for the $i$th individual. Also, let ${\mathsf{\delta }}_i^{*}$ denote a censoring indicator $I\left(T^{*}\le C_i\right)$. Therefore, the observed data for the outcome consist of the pairs $\left(T_i,{\mathsf{\delta }}_i^{*}\right),i=\mathrm{1,2},\dots ,n$. The survival function, which represents the probability that the time to the event of interest is not earlier than a specified time $t$ [33,34] is one of the main goals in survival analysis. The survival function is given as follows:

$$S\left(t\right)=P\left(T^{*}\ge t\right).$$

The survival function monotonically decreases with time $t$, and the initial value is $1$ when $t=0$, which signifies that, at the beginning of the observation, $100\%$ of the observed subjects have not experienced a second overdose; in other words, none of the events of interest have occurred. In contrast, the cumulative distribution function, $F\left(t\right)$, which represents the probability that the event of interest occurs earlier than $t$, is $F\left(t\right)=1-S\left(t\right)$. Additionally, hazard function $h\left(t\right)$ refers to instantaneous rate [35]. Like $S\left(t\right)$, $h\left(t\right)$ is a non-negative function. While all the survival functions $S\left(t\right)$ decrease over time, the hazard function can have different shapes. The hazard function represents $h\left(t\right)=f\left(t\right)/S\left(t\right)$ where $f\left(t\right)=-\mathsf{\delta }S\left(t\right)/\mathsf{\delta }t$.

Survival analysis is generally performed with statistical or ML methods. Both can make predictions of the expected remaining “lifespan” and estimate the survival probability at the estimated survival time. However, the former focuses more on characterizing the distribution of the event times and the statistical properties of the parameter estimation by estimating the survival curves, while the latter focuses primarily on the prediction of the event occurrence at a given time. Depending on assumptions made, traditional statistical methods can be either non-parametric, semi-parametric, or parametric. ML methods are often more efficient in their ability to learn dependencies, including non-linear relationships, between covariates and survival times. In survival analysis, the main challenge facing ML methods is the difficulty of dealing appropriately with censored data. ML methods are effective when there are many instances in a reasonable dimensional feature space, a feat that proves difficult for survival analysis [36]. In non-parametric methods, an empirical estimate of the survival function can be obtained using the Kaplan–Meier (KM) method [37,38]. In the semi-parametric category, the Cox model is the most used regression analysis approach, built on the proportional hazards assumption and employing partial likelihood for the parameter estimation. Parametric methods are more efficient and accurate when the time of event follows a specific, known distribution. It is easier to estimate the time to event with parametric models, while it is impossible with the Cox model [39].

Also, Kaplan and Meier [37] developed the Kaplan–Meier (KM) curve to estimate the survival function using the actual length of the observed time. This method is the most widely used for estimating survival function. Let $T_1<T_2<\dots <T_k$ be a set of distinct ordered event times observed for $n\left(k\le n\right)$ instances. In addition to this, there are censored times for instances whose event times are not observed.

For a given instance $i$, represented by the triplet $\left(x_i,T_i,{\mathsf{\delta }}_i\right)$, the hazard function $h\left(t,x_i\right)$ in the Cox model follows the proportional hazards assumption, given by

$$h\left(t,x_i\right)=h_0\left(t\right)\mathrm{e}\mathrm{x}\mathrm{p}\left(x_i\mathsf{\beta }\right), \mathrm{for} i=1,\dots ,n,$$

where the baseline hazard function $h_0\left(t\right)$ can be any arbitrary non-negative function of time; $x_i=\left(x_{i1},\dots ,x_{ip}\right)$ is the corresponding covariate vector, for instance $i$; and ${\mathsf{\beta }}^T=\left({\mathsf{\beta }}_1,\dots ,{\mathsf{\beta }}_p\right)$ is the coefficient vector. Based on the assumption of shared baseline hazard function, the survival function is given as follows:

$$S\left(t\right)=exp\left(-H_0\left(t\right)exp\left(x\mathsf{\beta }\right)\right)=S_0{\left(t\right)}^{exp\left(x\mathsf{\beta }\right)}$$

where $H_0\left(t\right)$ is the cumulative baseline hazard function, and $S_0\left(t\right)=exp\left(-H_0\left(t\right)\right)$ is the baseline survival function. Among the parametric models used for survival analysis, the exponential model is characterized by a single parameter, the constant hazard rate $\mathsf{\lambda }$. In this case, the failure or death is assumed to be a random event that is independent of time. A large value of lambda indicates a higher risk and a shorter survival time. We have $logS\left(t\right)=-\mathsf{\lambda }t$, in which the relationship between the logarithm of the survival function and time $t$ is linear, with $\mathsf{\lambda }$ as the slope. The Weibull model, a generalized exponential model, is characterized by two parameters $\mathsf{\lambda }>0$ and $\mathsf{\gamma }>0$. The shape of the hazard function is determined using the shape parameter $\mathsf{\gamma }$, which provides more flexibility compared to the exponential model. If $\mathsf{\gamma }=1$, the hazard function will decrease over time. The scaling of the hazard function is determined by the scaling parameter $\mathsf{\lambda }$.

2.4. Combining Community Detection and Survival Analysis

As previously mentioned, ML focuses on iterative construction and validation of models using algorithms to find patterns in often rich and unwieldy data, whereas statistics rely on inference to compute various quantitative measures [18]. For this study, graph community detection was used to group patients into communities based on their patterns of service engagement with the health service system. This was followed using survival analysis to quantify the risk of a second overdose for each of the communities of patients. To achieve this, the following steps were followed:

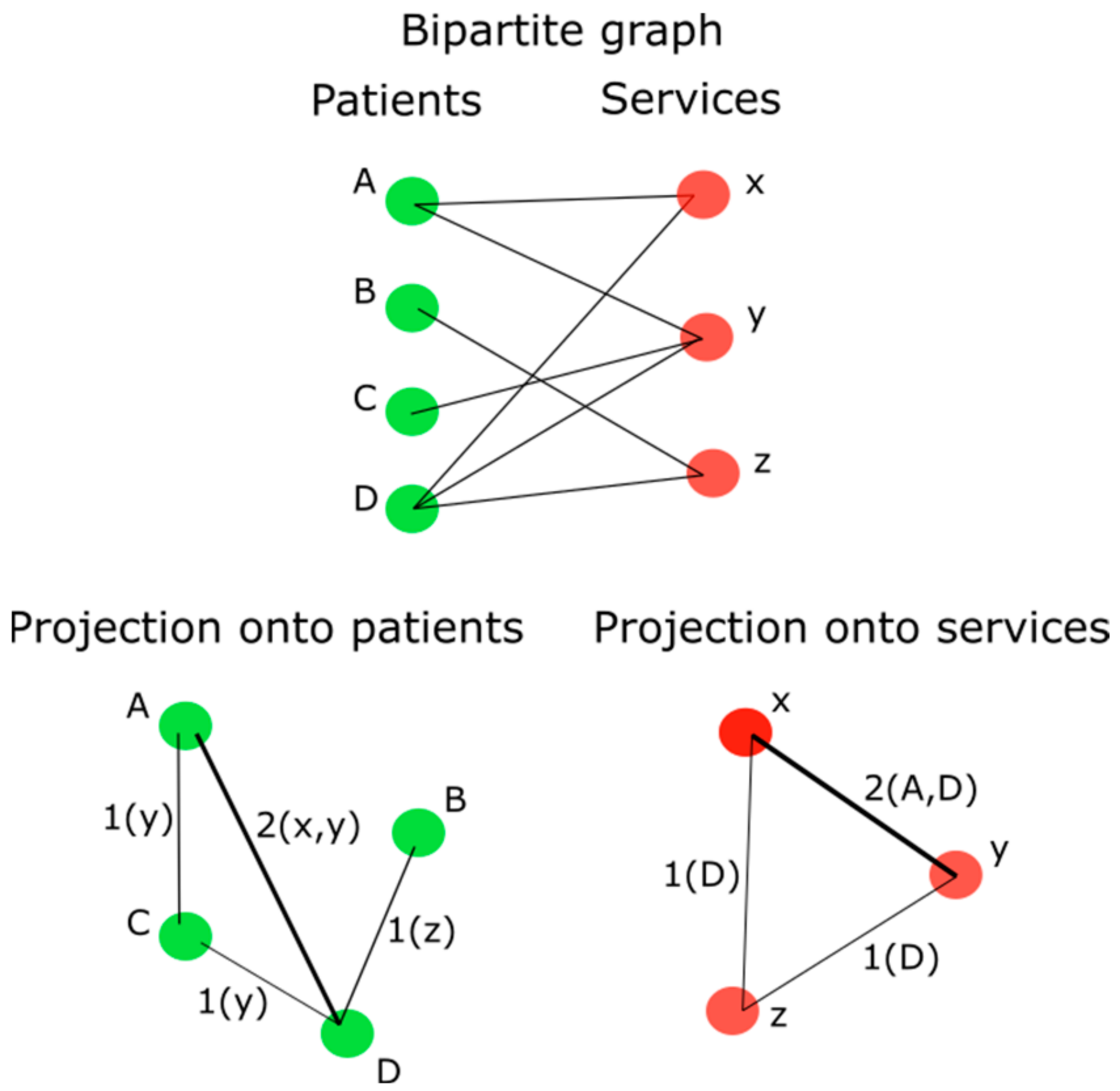
• The encounter data were engineered as a bipartite graph consisting of nodes with edges connecting patients to Service Classes. A patient (node) is connected to a Service Class (node) when they use a service represented by the Service Class. Recall that roughly two hundred Service Classes employed for modeling in this paper consist of equivalence classes formed by the application of six code sets to the host organization Service Units to reduce granularity.
• A bipartite projection onto patients was applied (Figure 1) to the bipartite graph to create a weighted graph, where the number of services that were used by two connected patients became the weight of the edge.
• The Louvain community detection algorithm was applied to the weighted graph to uncover the communities of patients that reflect high-prevalent PSUs by Service Classes.
• For each of the generated communities, both the service engagement profile and the diagnosis profile were appended.
• Collaborating with team members with clinical backgrounds, each community of patients was labeled based on their prevalent service engagement and diagnosis profile.
• Using community belonging as a characteristic of a patient, survival analysis was used to quantify the risk of a second overdose.
• Using other patient-related characteristics, such as age, gender, and homelessness status, survival analysis was used to further quantify the risk of a second overdose.

3. Analysis

The data that were analyzed contain records of opioid-overdose-related encounters with the emergency department at a regional health authority, from 30 March 2016 to 29 March 2022. The data contain about nine thousand $\left(8975\right)$ encounters, of around six thousand $\left(5381\right)$ individuals. Out of these individuals, one patient with inconsistent data was excluded. Thus, the number of eligible overdose patients is $5380$. From the eligible patients selected, around a quarter $\left(1582\right)$ have more than one overdose (OD) and $3798$ have only one overdose within the observation period (Figure 2). Furthermore, we also have demographic data, which contain information such as age group, gender, and homelessness. In addition, we have more complete encounter records, which include encounters with all healthcare services within the health authority for those patients. In our analysis, we consider the date of the first overdose event as the zero/start date for each patient. The second overdose is the event of interest. We form a data frame with one row for each patient, and the attributes include the status and the length in days from the first overdose to the second overdose. A patient has status one if observed as having a second overdose; otherwise, the patient has status zero. A patient is censored (i.e., has status zero but no longer contributes to the ‘at risk’ group) when no longer being observed—i.e., by the latest date of observation (29 March 2022), had not been observed to have a second overdose, or had died before 29 March 2022 and had not had a second overdose before.

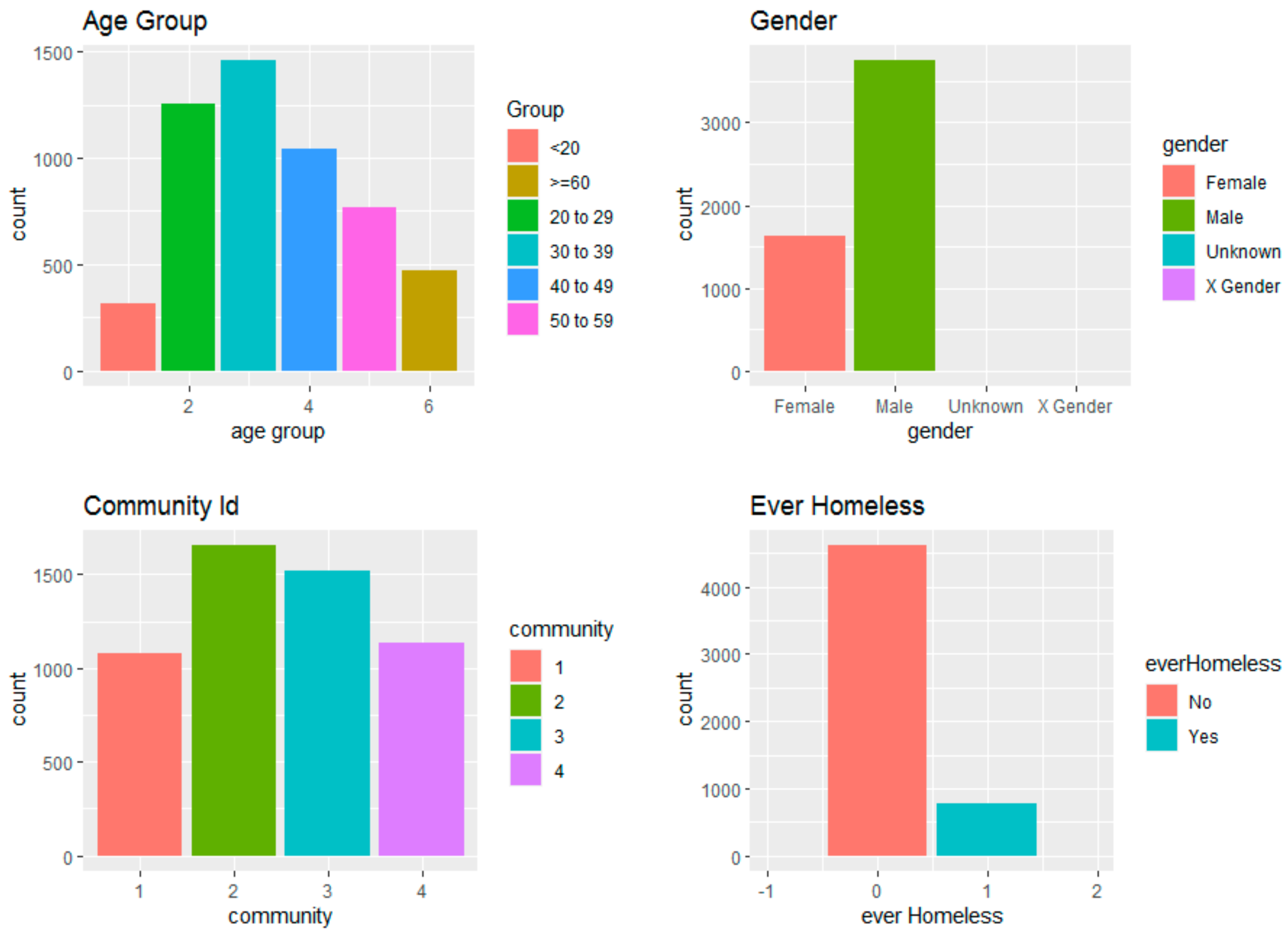
3.1. Patient Characteristics

The distribution of the overdose (OD) cohort by grouping attributes is provided in

Table 1. Distribution of overdose patients by grouping attributes.

Groups	Total OD %	No Second OD	Second OD	Hazard Ratio
	%(n) (N = 5380)	%(n) (N = 3798)	%(n) (N = 1582)	(95% CI)
Age
0−20	05.84 (314)	05.58 (212)	06.45 (102)	1.00
20–29	23.35 (1256)	21.70 (823)	27.37 (433)	0.77 (0.61, 0.97)
30–39	27.06 (1456)	25.70 (977)	30.28 (479)	0.77 (0.61, 0.97)
40–49	19.33 (1040)	19.50 (742)	18.84 (298)	0.67 (0.52, 0.85)
50–59	14.28 (768)	14.90 (565)	12.84 (203)	0.64 (0.50, 0.83)
60–100	08.75 (471)	10.60 (404)	04.24 (67)	0.45 (0.32, 0.62)
Gender
Male	69.65 (3747)	68.14 (2588)	73.30 (1159)	1.34 (1.18, 1.51)
Female	30.29 (1630)	31.78 (1207)	26.70 (423)	1.00
Unknown	00.06 (3)	00.08 (3)	−	−
Community ID
Community ID 1	20.00 (1076)	15.70 (0595)	30.40 (481)	1.00
Community ID 2	30.72 (1653)	35.00 (1331)	20.40 (322)	0.49 (0.42, 0.58)
Community ID 3	$28.23 \left(1519\right)$	$30.70 \left(1167\right)$	$22.20 \left(352\right)$	$0.60 (0.51,0.70)$
Community ID 4	$21.04 \left(1132\right)$	$18.60 \left(750\right)$	$27.00 \left(427\right)$	$0.72 (0.62,0.83)$
Ever Homeless
No (0)	$85.67\left(4609\right)$	$90.18\left(3425\right)$	$74.80\left(1184\right)$	$1.00$
Yes (1)	$14.33 \left(771\right)$	$09.82 \left(373\right)$	$25.20 \left(398\right)$	$1.65 (1.45,1.88)$

. From the demographic data, we have age, gender, and homelessness status. We can see that most have an age between twenty and sixty years old. The overall mean age of OD patients was $38$ years, the minimum age was $13$ years, and the maximum age was $97$ years. There are more males $(69.65\%)$ than females, and the majority $(85.67\%)$ had never been homeless.

In addition, we also group the patients by the graph community, which we will discuss more below. There are four communities, and each of the patients belongs to a single community (one to four). Community one has 1076 patients, Community two has 1653 patients, Community three has 1519 patients, and Community four has 1132 patients. The largest is Community two with 30.72%.

3.2. Community Characteristics

In this study, we examined the health service interactions of individuals within a cohort experiencing opioid overdose. Using a bipartite projection on patient data and applying the Louvain algorithm, we generated four distinct communities. For each of the communities, the services across the continuum of care that each community engaged with were reviewed in collaboration with clinical SMEs, and each community was labeled based on the most predominant and distinguishing services. The clinical SMEs that guided the annotation process have extensive experience in health service system operation, healthcare, and computer science. The following are details about the clinical SMEs: (Dr. Ken Moselle (PhD) and Dr. Ernie Chang (MD, PhD) have played a key role in guiding the annotation of the generated communities of patients constituting the overdose cohort, as described in this section. Dr. Ken Moselle is a registered clinical psychologist with extensive experience (25+ years) in health service systems operations. Dr. Ernie Chang is a retired family physician who also holds a PhD in Computer Science. They are both clinical SMEs on the team and co-authors of this manuscript.)

Once each community was labeled, each patient was tied to one of the four communities and assigned a community with a corresponding label. These labels include the following:

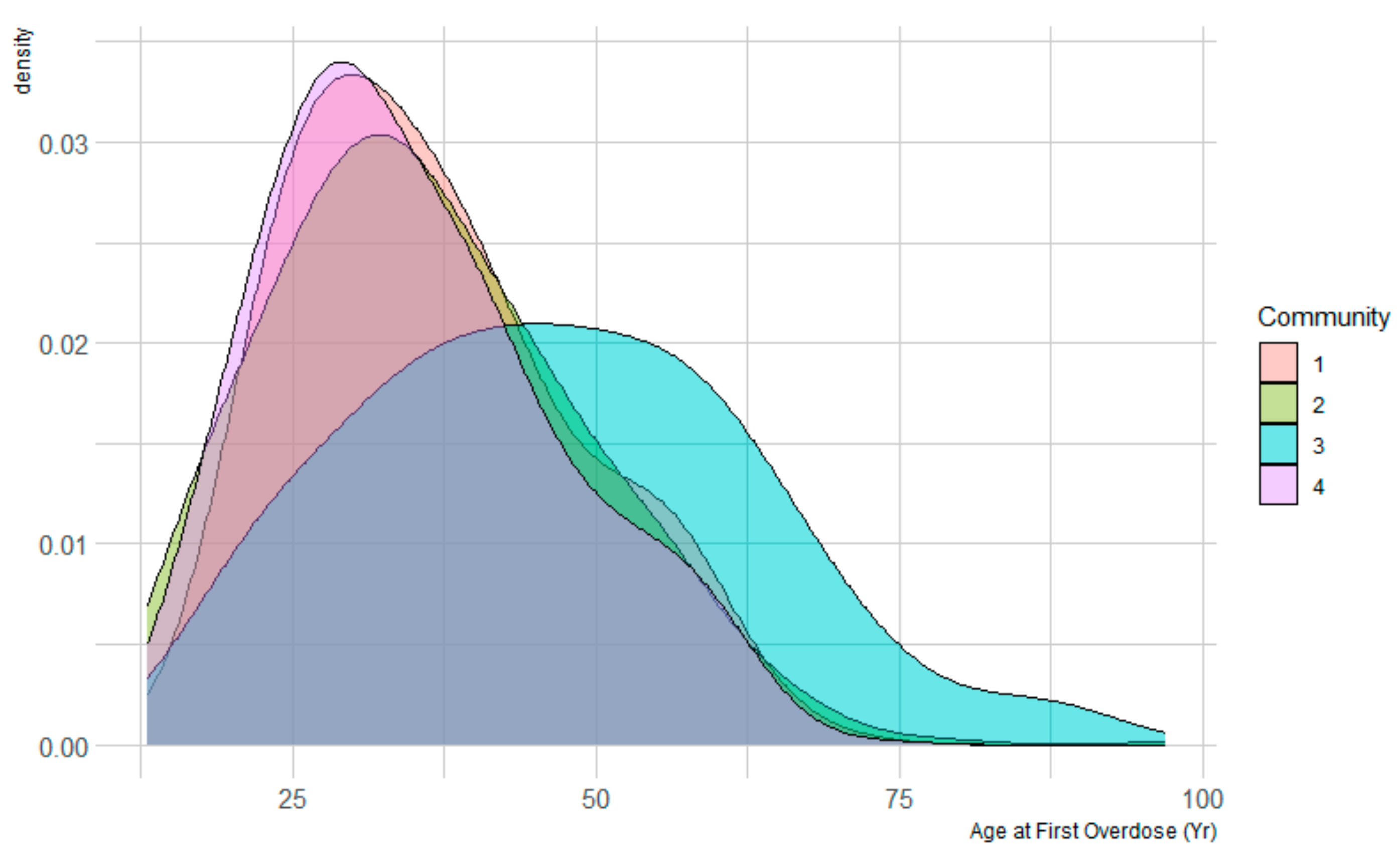
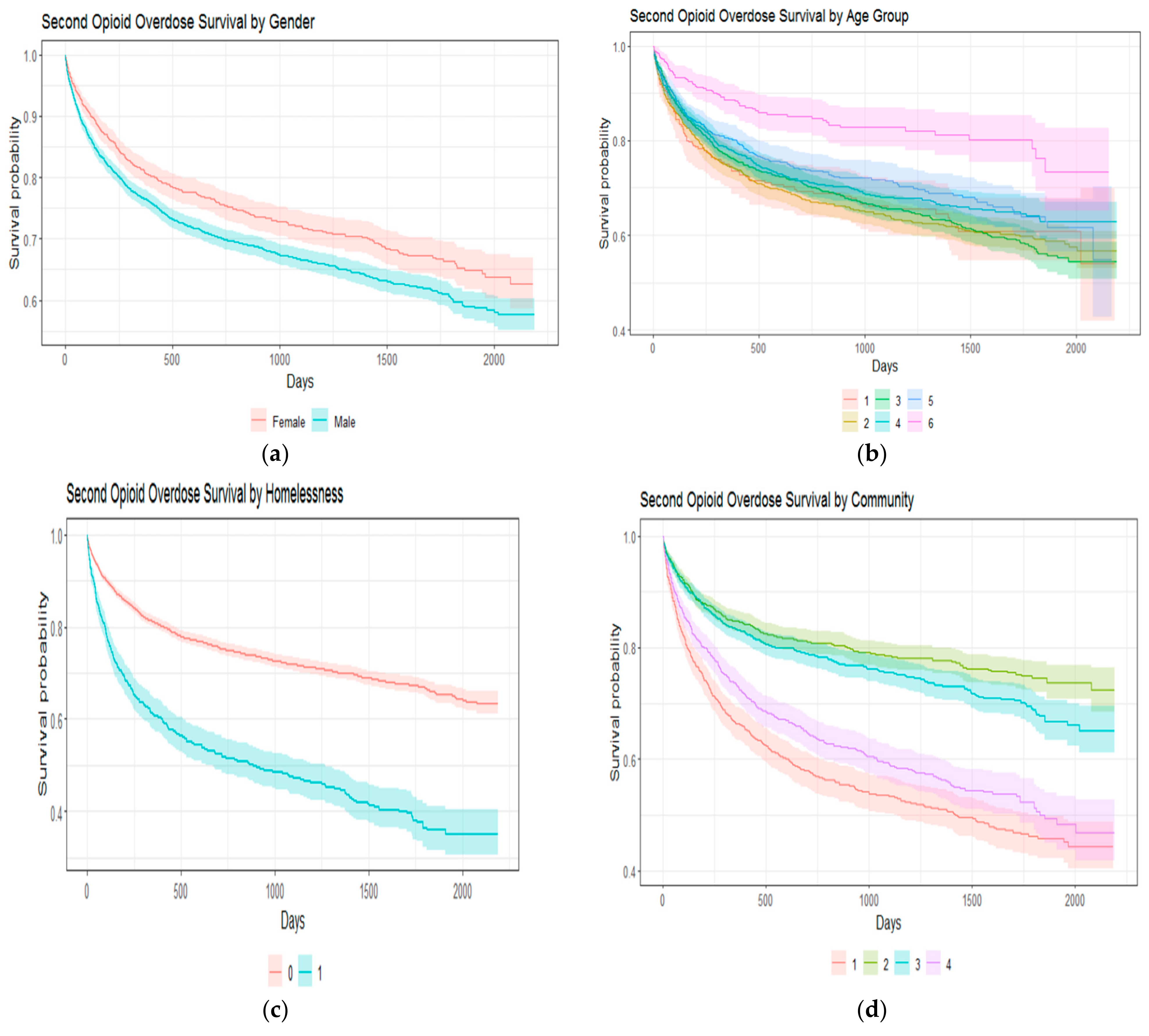
• Community one, termed the “reciprocal group”, exhibited a proactive approach to accessing health services, for example, self-referred ambulatory addiction services. They demonstrated higher utilization rates within the service system overall, including Mental Health, and Substance Use (MHSU) and Medical/Surgical (Med/Surg) services. Notably, 80% of patients in this community utilized MHSU clinical intake and addiction clinical intake services. Predominant diagnoses within this group centered around severe addiction issues, with minimal occurrences of schizophrenia-related diagnoses. The average age of patients in this community was $35$ years.
• Community two, characterized as the “service-disengaged group”, displayed lower engagement with the service system compared to other communities. They accessed overdose-related and addiction outreach services prior to the overdose events. Diagnostic profiles within this group were not pronounced, with only 8% reporting homelessness and an average age of $36$ years.
• Community three, labeled as the “group with complex/serious health problems”, exhibited a higher frequency of encounters with Med/Surg services, particularly laboratory and medical imaging procedures. Engagement with MHSU services was comparatively lower, indicating that their engagement with the service system focused on addressing complex medical conditions rather than substance use. Diagnostic data suggested a variety of medical issues, including high rates of palliative care and alterations of awareness. The average age within this community was 46 years, with a considerable number of patients being 60 years or older.
• Community four, characterized as the “group with severe psychiatric issues”, demonstrated a high engagement with psychiatric services but low involvement with addiction services. This group exhibited a younger average age of 35 years and a notably high prevalence of schizophrenia diagnoses. Engagement with MHSU services was more prominent than with Med/Surg services.

In Figure 3 and Figure 4, we compared the normalized age distribution (density) of each community. We found that they all have a similar profile, except for Community three, which has a broader and older age distribution. We further showed the density for the age at first overdose of the individuals in the community. We observe that community three has a wider age distribution at first overdose compared to the age distribution of other groups.

3.3. Statistical Analyses

Our analysis began by examining cohort demographics, which included patient grouping based on a community detection algorithm, as well as factors such as gender, age, and homelessness status. Subsequently, Cox proportional hazard models were used to calculate the unadjusted and adjusted hazard ratios (HR and aHR) for patients experiencing a second overdose during the study period. The adjusted hazard model controlled for gender, community ID group, and homelessness status, given previous associations between opioid overdose death rates and older age groups [40] and male gender [41]. Following this, we conducted Kaplan–Meier curve analyses to determine the time to a second overdose event based on gender, age group, homelessness status, and community ID group.

In our analysis, we observed that out of $4515$ patients at risk of overdose, $455$ experienced a second overdose, resulting in a survival probability of less than $90\%$ within the first hundred study periods. However, when considering the effects of patient grouping, particularly through the community detection algorithm, we identified significant differences in vulnerability within the cohort. Group one, comprising $854$ individuals at the start of the study, exhibited the lowest survival probability among the four groups, indicating it as the most vulnerable group despite having a smaller number of at-risk individuals compared to group two, which had the highest number of individuals at risk. All statistical analyses were conducted using the R programming language [42].

4. Results

The cohort under investigation comprised $5380$ patients who collectively accounted for $8975$ service encounters. Among these patients, $1582$ experienced at least one overdose within a span of two thousand days. Notably, in the population experiencing a second overdose, age group three constituted $30.28\%$, while age group one comprised only $6.45\%$. Additionally, $73.30\%$ of individuals were male and $25.20\%$ had a history of homelessness.

Regarding community ID grouping, $30.40\%$ belonged to the “reciprocal group”. Age groupings were categorized as follows: group one ($<$20 years), group two (from 20 to $29$ years), group three (from $30$ to $39$ years), group from ($40$ to $49$ years), group five (from $50$ to $59$ years), and group six ($\le$60 years) at the time of the first overdose.

Analyzing the grouping by age of patients experiencing a second overdose, we observed that individuals aged 60 years or older had the highest probability of avoiding subsequent overdoses compared to other age groups. Conversely, age groups two and three (from 20 to $29$ years and from $30$ to $39$ years, respectively) exhibited similar, lower survival probabilities.

Figure 5 shows the analysis without grouping. The five-year probability of avoiding a second overdose was approximately $60\%$. However, after adjusting for various attributes, including gender, homelessness status, age, and community ID, the hazard of experiencing a second overdose increased for male patients (HR $=1.34; 95\%$ CI: $1.18, 1.51$) and individuals with a history of homelessness (HR $=1.65; 95\%$ CI: $1.45, 1.88$). Conversely, Table 1 shows that the hazard was relatively lower for individuals aged over 20 years, excluding those in community ID group one (e.g., >60 years: HR $=0.45; 95\%$ CI $0.32, 0.62$; community ID two: HR $=0.49; 95\%$ CI $0.42, 0.58$).

The hazard ratios (HRs) provide crucial insights into the associations between various demographic and contextual factors and the likelihood of experiencing a second overdose within the study period. A hazard ratio represents the relative risk of an event occurring in one group compared to another, with a value greater than one indicating an increased risk and a value less than one indicating a decreased risk. The aHR of $1.34$ for male patients suggests that males are $1.34$ times more likely to experience a second overdose compared to females, holding all other variables constant. This finding underscores the heightened vulnerability of male individuals within the cohort to repeat overdose events. The $95\% \mathrm{C}\mathrm{I} (1.18, 1.51)$ indicates the range within which we can be confident that the true hazard ratio lies, with values above 1 indicating statistical significance. Similarly, an aHR of 1.65 for individuals with a history of homelessness reveals a substantial increase in the likelihood of experiencing a second overdose compared to those who have not experienced homelessness. This result highlights the profound impact of housing instability on the risk of overdose recurrence, suggesting a critical intersection between social determinants of health and substance use outcomes. Again, the narrow 95% confidence interval $\mathrm{C}\mathrm{I} (1.45, 1.88$) indicates a statistically significant association.

Conversely, hazard ratios for age groups older than 20 years present interesting findings. Individuals aged 60 years or older exhibit a notably lower hazard of experiencing a second overdose, with aHR of $0.45$. This indicates that older individuals are approximately $55\%$ less likely to experience a second overdose compared to younger individuals, after adjusting for other variables. Table 1 shows the confidence interval ($95\%$ CI: $0.32, 0.62$), which confirms the statistical significance of this effect.

Moreover, individuals in community ID groups other than group one, particularly those in community ID group two, demonstrate a reduced hazard of experiencing a second overdose. The aHR of $0.49$ suggests that individuals in community ID group two are approximately $51\%$ less likely to experience a second overdose compared to those in community ID group one, after adjusting for other factors. Again, the narrow confidence interval ($95\%$ CI: $0.42, 0.58$) underscores the statistical significance of this finding.

Overall, these hazard ratios provide valuable insights into the differential risks associated with demographic and contextual factors, emphasizing the importance of tailored interventions targeting vulnerable subpopulations to mitigate the burden of opioid overdose recurrence.

Figure 6 depicts the survival probability of patients experiencing a second overdose over time, stratified by gender, age group, and community ID, to illustrate these associations. The hazard rate of $1.34$ for male gender indicates an $34\%$ increase in the likelihood of a second overdose within two thousand days, while the hazard rate of $1.65$ for individuals who have ever experienced homelessness signifies an $65\%$ increase. Notably, there was a significant decrease in the hazard rate among age groups two and three, with over a 50% reduction observed among individuals aged over 60 years. Cumulative proportion plots further illustrate these trends, demonstrating the impact of gender, age, community ID, and homelessness status on the likelihood of experiencing a second overdose. In a comprehensive model encompassing all covariates, male sex (aHR $=1.30; 95\%$ CI $1.15, 1.46$), homelessness (aHR $=1.86; 95\%$ CI: $1.63, 2.11$), and community ID were identified as significant factors associated with a second overdose, Figure 7.

In this analysis, incorporating all relevant covariates, it becomes evident that certain factors emerge as particularly influential in shaping the likelihood of repeated overdose. Specifically, male sex carries a statistically significant aHR of $1.30$ ($95\%$ CI $1.15, 1.46$), indicating that male individuals are $1.30$ times more likely to experience a second overdose compared to their female counterparts, after accounting for others.

Overall, these hazard ratios provide valuable insights into the differential risks associated with demographic and contextual factors, emphasizing the importance of tailored interventions targeting vulnerable subpopulations to mitigate the burden of opioid overdose recurrence. Figure 6 shows the survival probability of patients experiencing a second overdose over time, stratified by gender, age group, and community ID, and illustrates these associations. The hazard rate of 1.34 for male gender indicates a 34% increase in the likelihood of a second overdose within two thousand days, while the hazard rate of 1.65 for individuals who have ever experienced homelessness signifies a 65% increase. Notably, there was a significant decrease in the hazard rate among age groups two and three, with over a 50% reduction observed among individuals aged over 60 years. Cumulative proportion plots further illustrate these trends, demonstrating the impact of gender, age, community ID, and homelessness status on the likelihood of experiencing a second overdose. In a comprehensive model encompassing all covariates, male sex (aHR = 1.30; 95% CI 1.15, 1.46), homelessness (aHR = 1.86; 95% CI 1.63, 2.11), and community ID were identified as significant factors associated with a second overdose, Figure 7.

In this analysis, incorporating all relevant covariates, it becomes evident that certain factors emerge as particularly influential in shaping the likelihood of repeated overdose. Specifically, male sex carries a statistically significant aHR of 1.30 (95% CI1.15, 1.46), indicating that male individuals are 1.30 times more likely to experience a second overdose compared to their female counterparts, after accounting for other variables. This also measures the level of vulnerability of males to repeated overdose events and emphasizes the importance of gender-sensitive interventions in addressing this disparity.

Similarly, homelessness status emerges as a significant predictor of second overdose risk, with an aHR of $1.86 (95\%$ CI $1.63, 2.11)$. This suggests that individuals with a history of homelessness are nearly twice as likely to experience a second overdose compared to those who have not experienced homelessness, even after controlling for other factors. 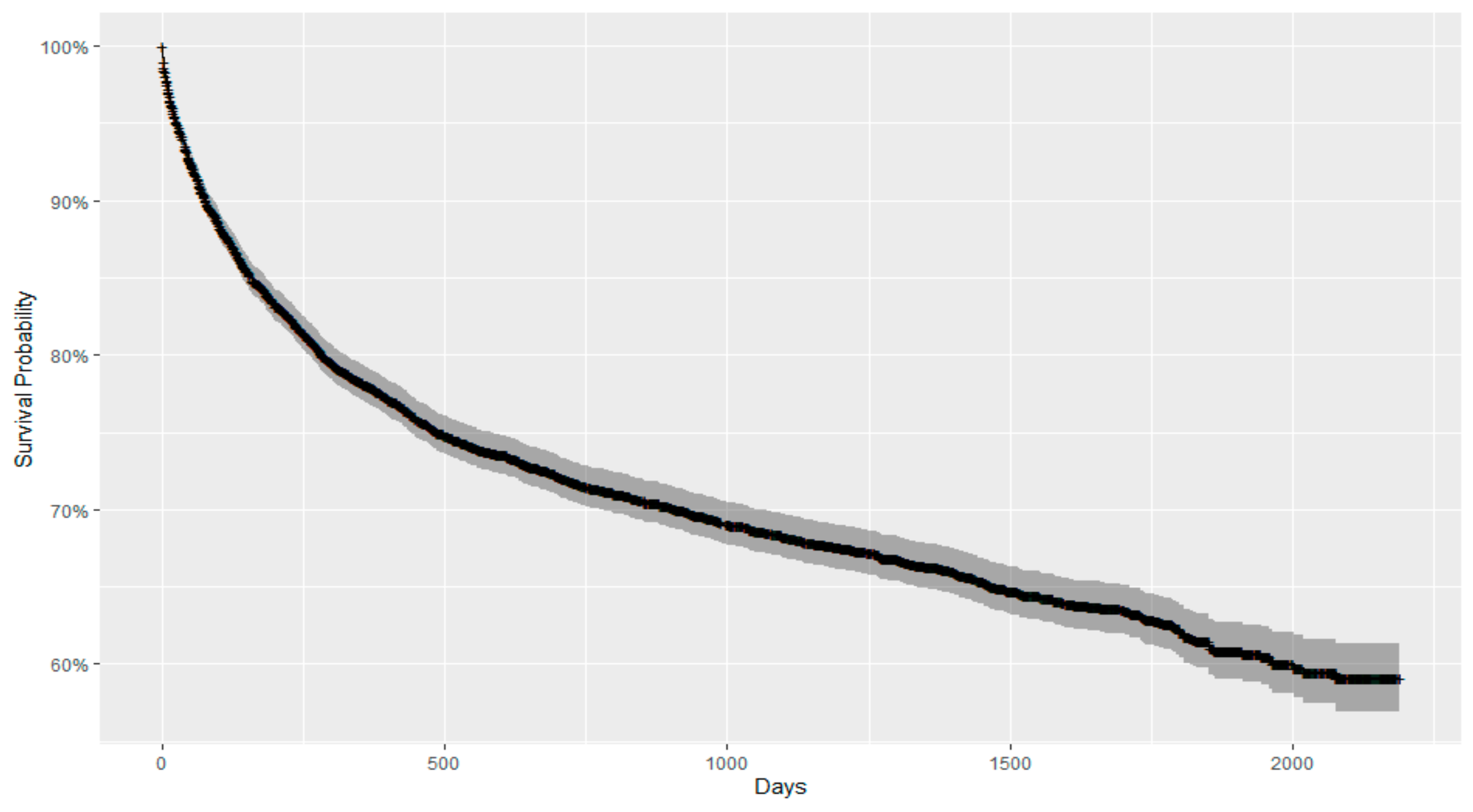This also highlights the profound impact of housing instability on overdose risk and underscores the urgent need for targeted interventions to support individuals experiencing homelessness in managing their substance use disorders.

5. Discussion

Treatment homogeneity may not work in all circumstances. For a cohort of patients that are suffering from an organ-bound illness such as diabetes or kidney disease, treatment homogeneity may be the appropriate approach to use. However, for a cohort of patients suffering from opioid overdose, treatment homogeneity may not work: Healthcare programs benefit certain opioid overdose patients but not others. This is mostly due to the fact that a cohort of opioid patients is heterogeneous with regard to a variety of factors, and as such, it requires a different approach than the traditional taxonomic diagnostic approach to care management.

In this study, we used a graph community detection to systematically partition the OD cohort based on their pattern of engagement with the health service system across the continuum of care. Additionally, we used diagnosis profiles to fine-tune the partition and facilitate the labeling of the groups from the community detection. Our result has shown that there are four distinct communities of patients that constitute the OD cohort. Working with team members with clinical and service system operation backgrounds, the communities were labeled as follows: (1) high risk and reciprocally engaged with the service system; (2) relatively disengaged with the service system; (3) complex health problems and heavy users of Med/Surg services; and (4) high risk with psychiatric issues and unilaterally engaged with the service system. Additionally, their age profile demonstrates a younger population for Communities one, two, and four, with an average age varying between $35$ and $36$ years. However, Community three is older with an average age of $46$ years, and a considerable number of patients are over $60$ years.

Focusing on the generated communities of patients and applying survival analysis has shown that the risk profile among these communities is not the same. Two of the communities, including Communities one and four, have a risk twice as great as Communities two and three in experiencing a second overdose. The high-risk Community one has a $51\%$ chance of experiencing a second overdose compared to Community two.

In this study, the combination of the emergency department and acute care (hospital admission) is not used as a proxy for full cross-continuum service utilization. Instead, access to all comprehensive services, including secondary and tertiary services provided by the host organization, is considered and brought into focus. Hence, services such as rehab recovery and harm reduction are brought into focus and are used to distinguish characteristics between the patients constituting the opioid cohort. This made it possible to fine-tune the clustering of patients. Using access to the emergency department and acute care as a proxy for full cross-continuum service utilization would not make such a fine-tuning of the communities possible to enable a more targeted response to their respective needs.

Moreover, the behaviors of individuals are an important determinant of the prevalence of a disease, treatment adherence, as well as health outcome [43]. Opioid overdoses are conditioned by patients’ behavior [27]. Bringing individuals’ behaviors into focus can be analytically challenging. However, patterns of service utilization reflect the behavior of individuals in relation to the behavior of the system. Hence, PSUs across the continuum of care can be used to bring proximal determinants and behavioral determinants of health into focus. This allows a fine-tuning of clusters, making it possible to distinguish characteristics between high-risk communities, as an example. Although both communities (Communities one and four) are considered high-risk, their behavior vis-à-vis the service system is dissimilar. As a result, a potentially useful approach to reach out and support the “high-risk and reciprocally engaged community” is going to be different from one considered for the “high-risk with psychiatric issues and unilaterally engaged with the service system community”. If one looks at the emergency department and acute care (hospital admission) only, it would be impossible to bring into focus the proximal determinants of the health profile of individuals into the analysis.

Other factors outside the use of patterns of service engagement as the basis for partitioning the OD cohort were used. Overall, the result has shown that the identification of male sex, homelessness status, and community ID as significant factors associated with second overdose risk. This underscores the complex interplay of individual, social, and environmental factors in shaping substance use outcomes. By understanding and addressing these factors comprehensively, healthcare providers and policymakers can develop more effective strategies to prevent overdose recurrence and improve the long-term health outcomes of individuals affected by substance use disorders.

Given the data used for this analysis, not all factors that can influence predisposition for a second opioid overdose were included in the analysis. These include patients’ distal determinants of health and social determinants that were not collected by the host organization. Moreover, the cohort used for the analysis only captures patients whose overdose was reported and recorded by the host organization. Any unreported overdose that took place in the community was not included in the analysis. Finally, due to incomplete/inconsistent collection of demographic data at source, as well as strict privacy limitations, information on race or ethnicity was not available for this study. These factors limit the findings of this study. Additionally, the findings of this study are limited to the host organization and hence not immediately generalizable/transferable to other jurisdictions. This is another limitation of the findings from this study. However, the methods outlined in this study are generalizable. to other healthcare jurisdictions.

6. Conclusions

This paper has provided a methodology that can help inform a treatment heterogeneity approach that is likely to be more efficient for a cohort made of diverse individuals, such as an opioid overdose cohort. By grouping opioid overdose patients into different communities informed by their PSUs for the healthcare services across the continuum of care, it is providing an opportunity for the healthcare service system to apply a more targeted approach to care that is likely to be more efficient for each of the communities constituting the overdose cohort.

Using PSUs, the findings from the paper demonstrated that the overdose cohort is not homogeneous with respect to the determinant of risk. This conclusion corroborates results reported in other studies, including [17]. In addition to previous studies findings, the number of groups constituting the various communities that make up the overdose cohort was determined and labeled based on their healthcare service engagement across the continuum of care and clinical characteristics. Finally, the risk for a subsequent overdose was quantified for each of the communities constituting the opioid overdose cohort. Providing such information to a healthcare organization will equip the organization with required information to provide a more differentiated package of services to different fractions of the overdose-at-risk population that are distinguishable on the basis of their proximal determinants of risk profiles, specifically, patterns of interacting with the service system. The intent is better evidence-informed efforts to prevent opioid overdoses.