Application of Back-Propagation Neural Network in the Post-Blast Re-Entry Time Prediction
Abstract
1. Introduction
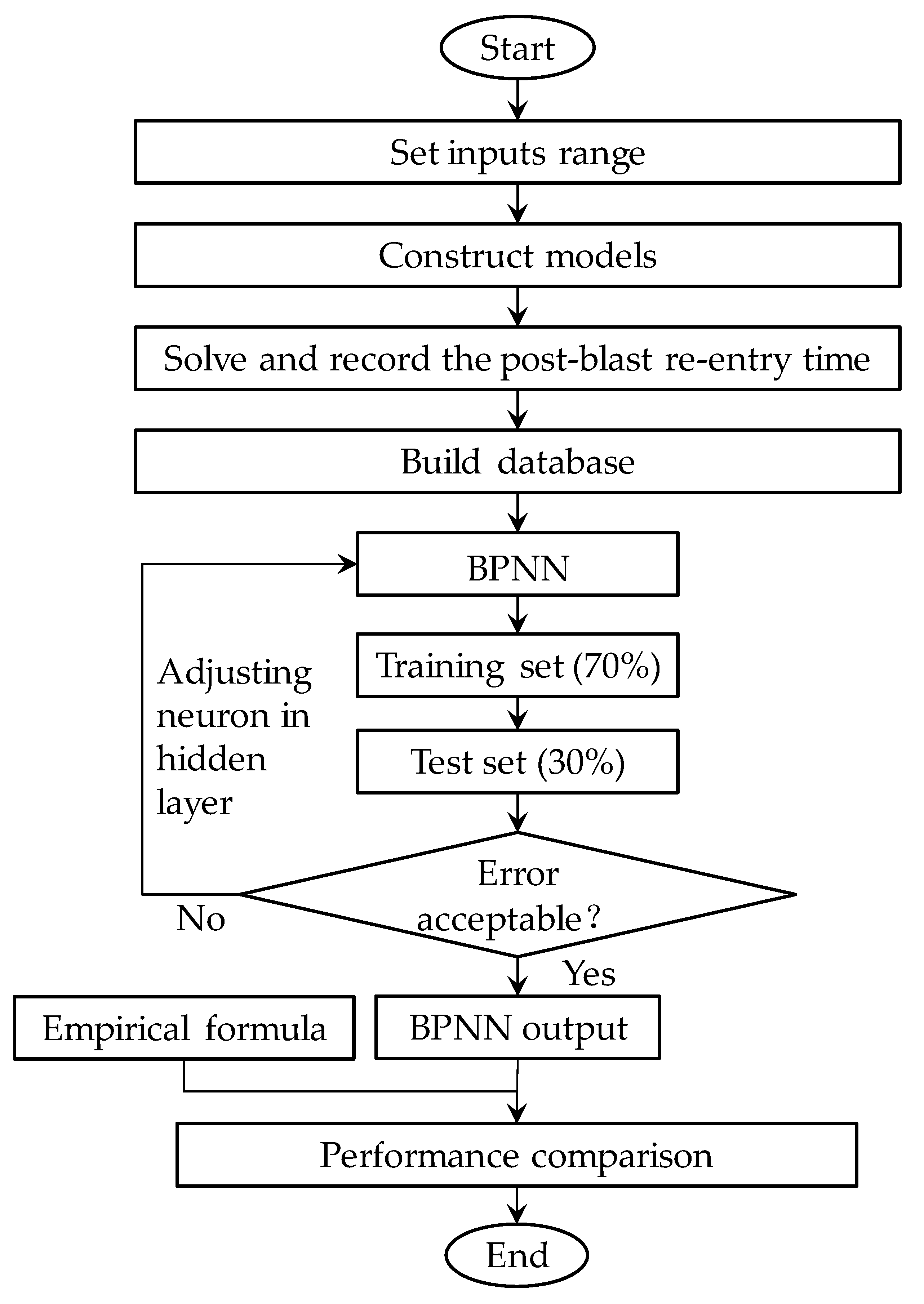
2. Model Process and Data Preparation
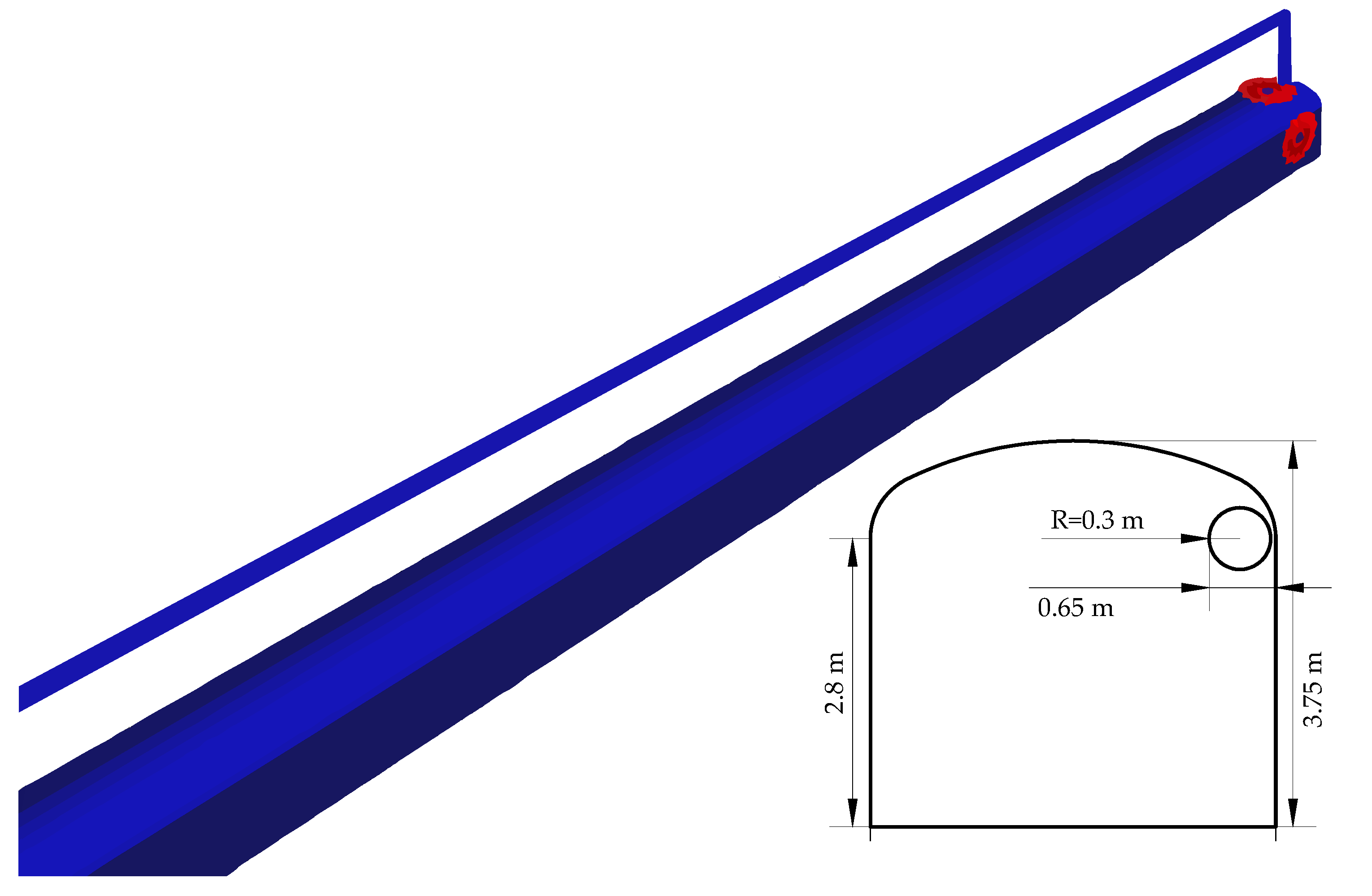
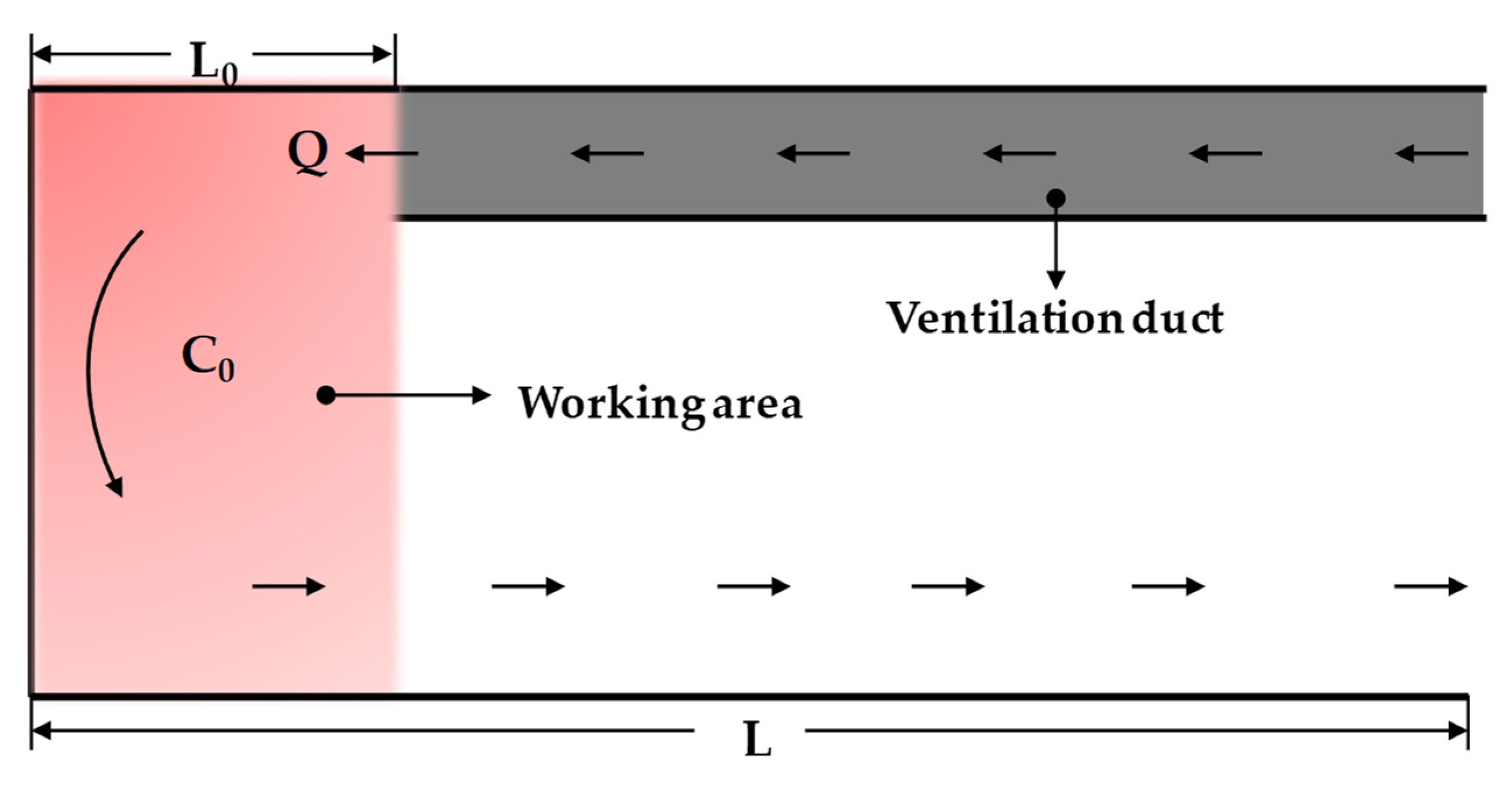
2.1. Model Construction
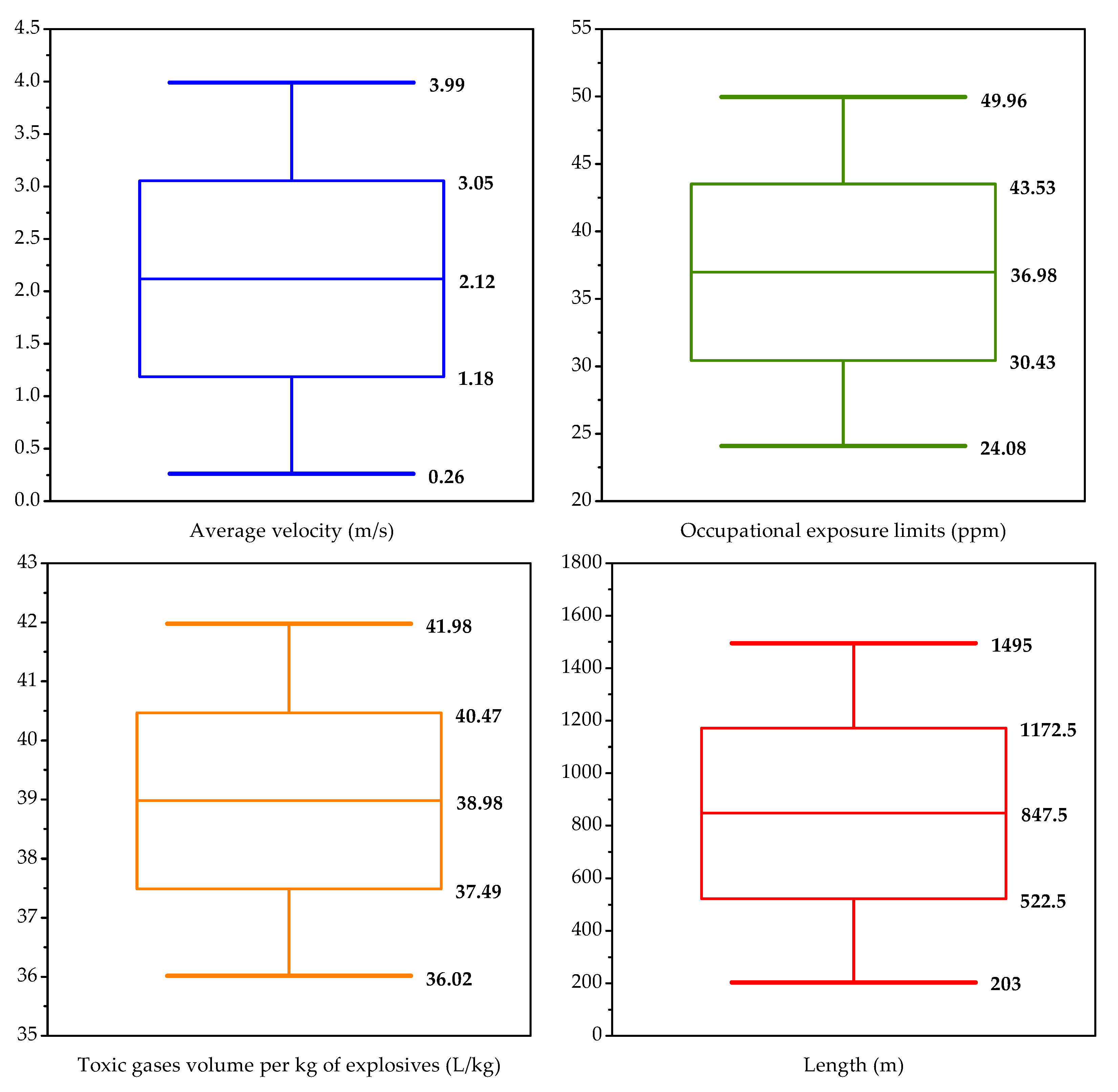
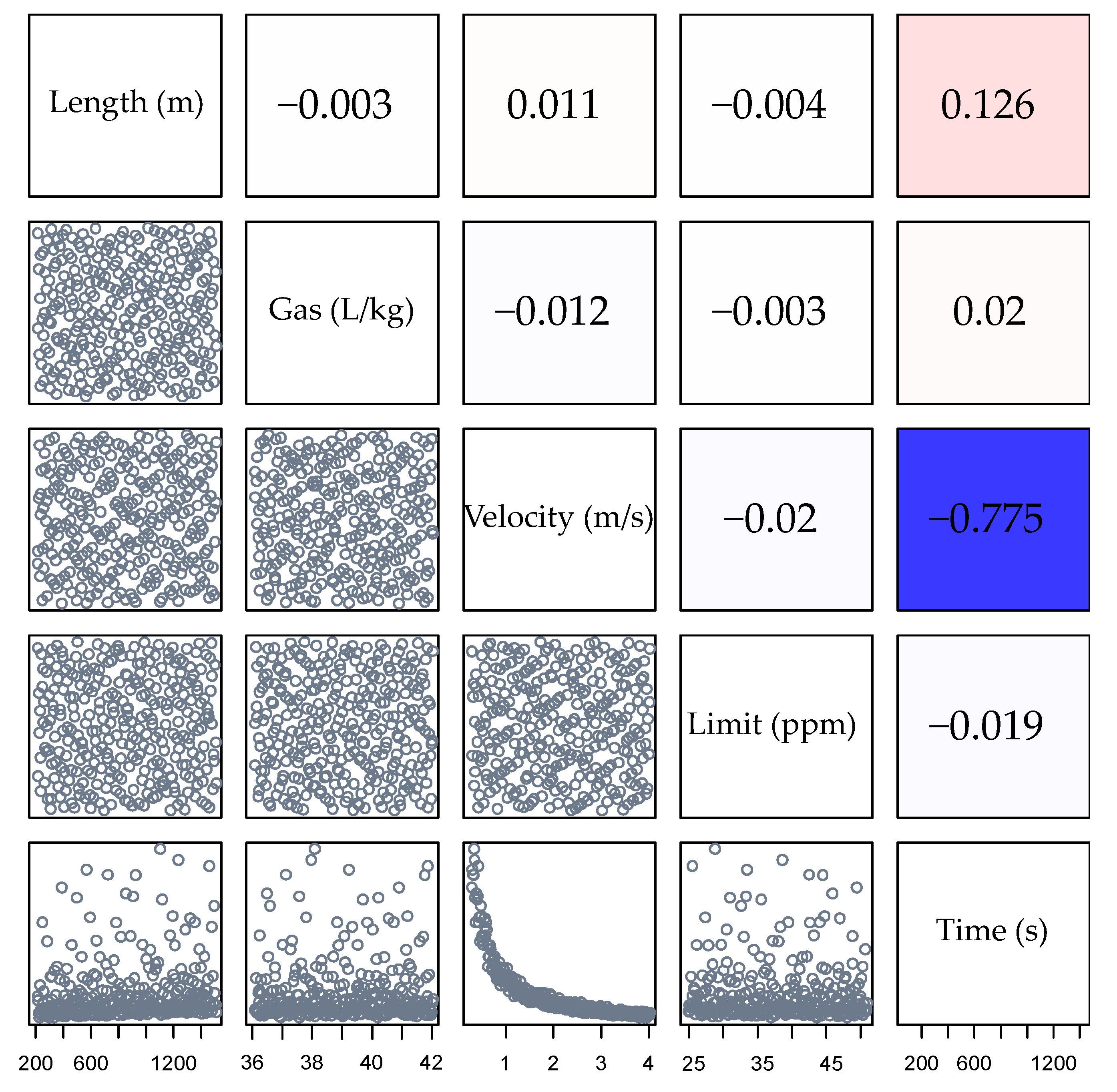
2.2. Database Generation
3. Methodology
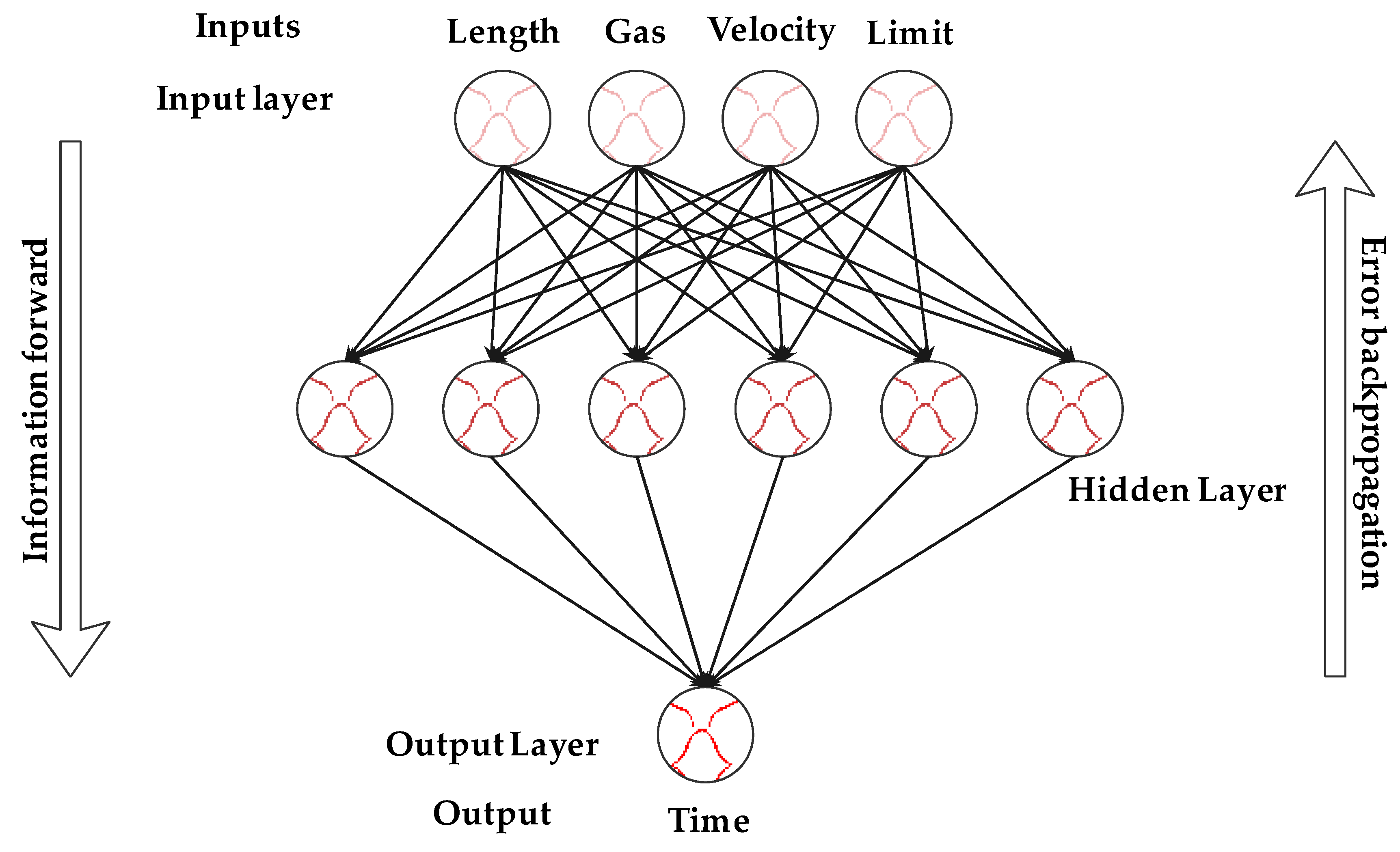
3.1. BPNN Algorithm
3.2. Calibrating Empirical Formula
3.3. Performance Indicators for the Assessment of Models
4. Results and Discussion
4.1. Building the Architecture of the BPNN
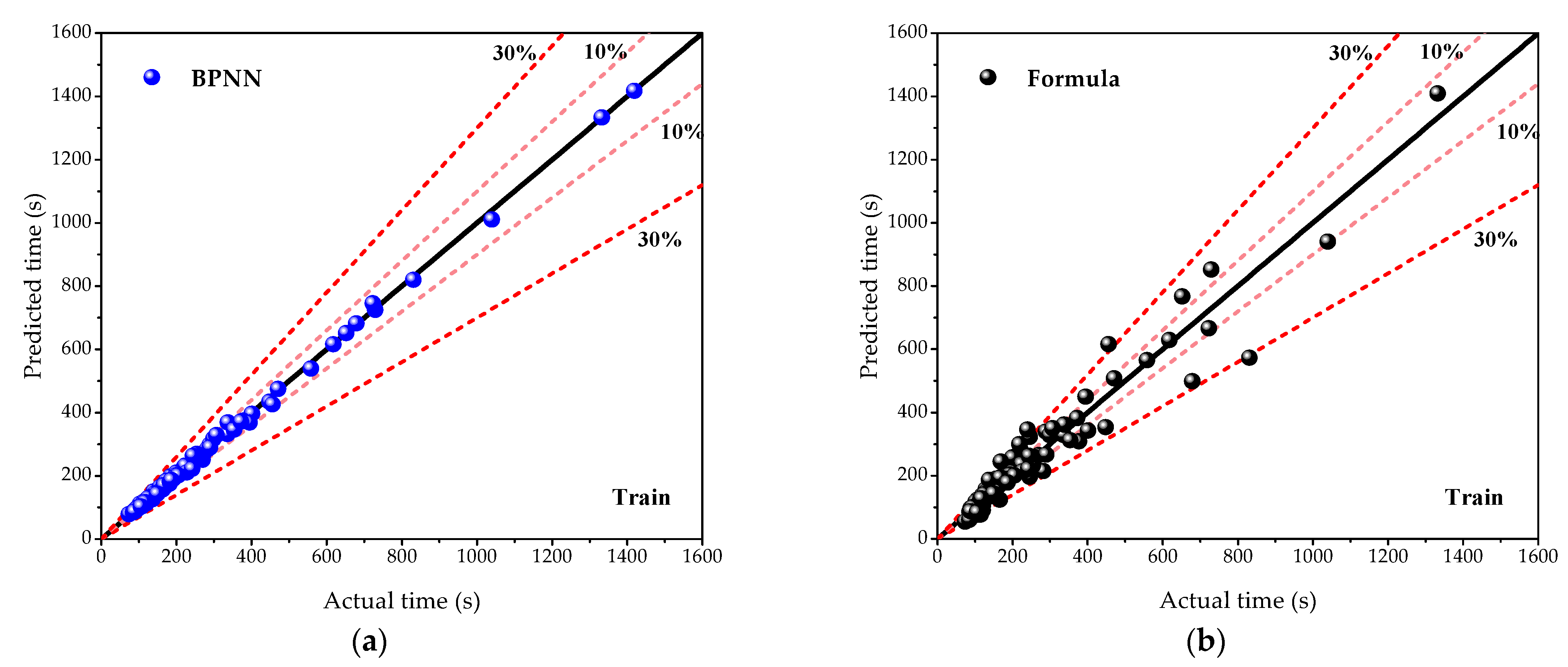
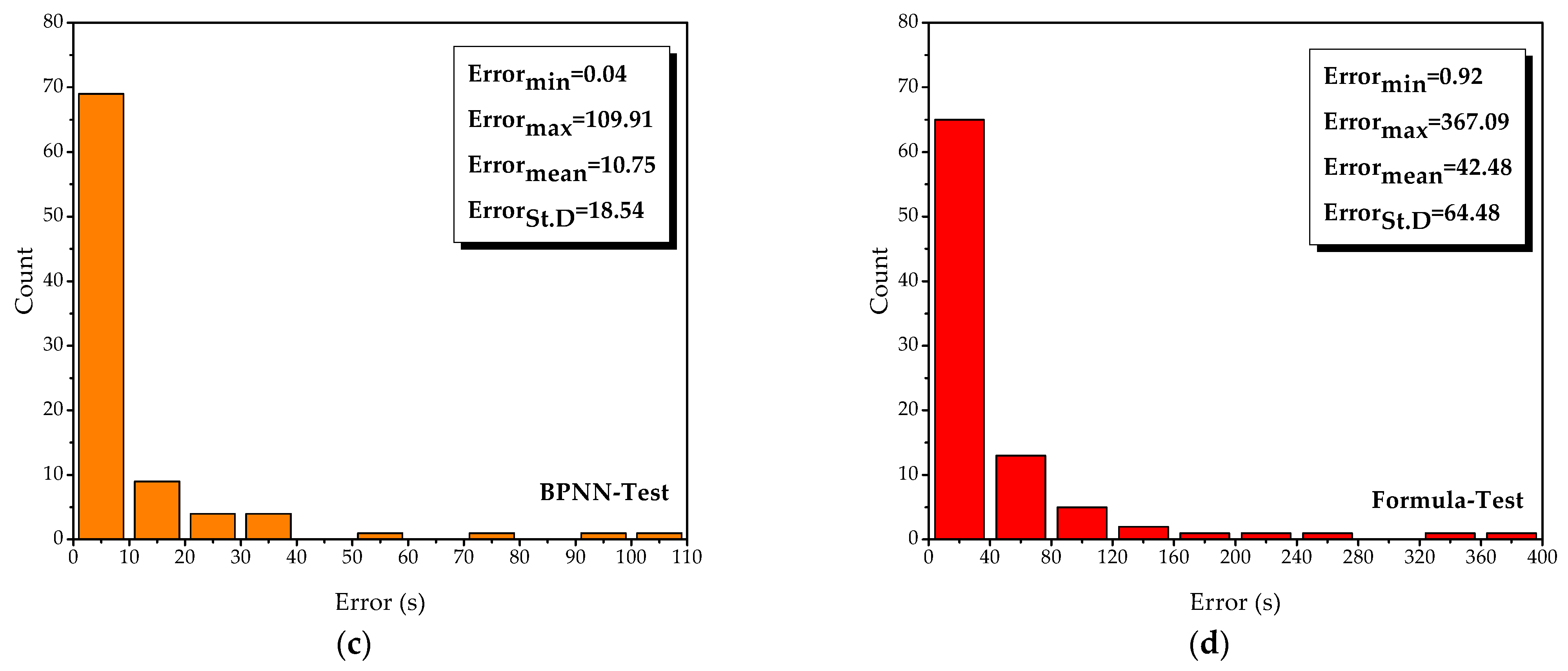
4.2. Performance Comparison between BPNN and Formula
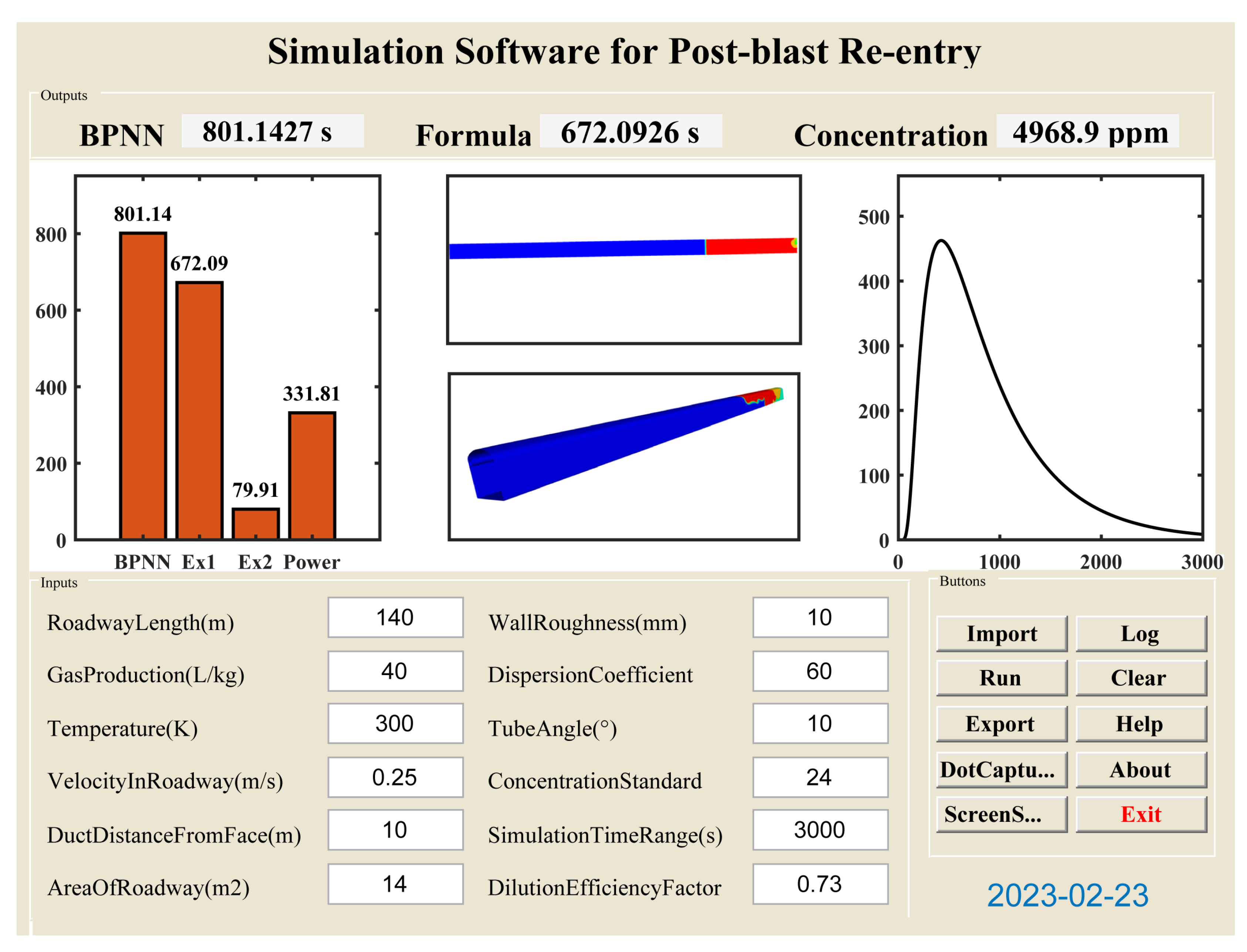
5. Algorithm Embedding
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| Length/(m) | Gas/(L/kg) | Velocity/(m/s) | Limit/(ppm) | Time/(s) | |
| 1 | 469 | 40.47 | 1.31 | 38.52 | 246 |
| 2 | 921 | 39.53 | 2.57 | 31.90 | 140 |
| 3 | 1475 | 40.77 | 2.33 | 32.69 | 185 |
| 4 | 893 | 37.50 | 0.38 | 32.40 | 1040 |
| 5 | 393 | 40.27 | 1.34 | 24.62 | 246 |
| 6 | 243 | 38.16 | 2.37 | 37.60 | 121 |
| 7 | 256 | 40.40 | 3.25 | 33.73 | 90 |
| 8 | 439 | 40.02 | 2.10 | 41.43 | 152 |
| 9 | 324 | 40.61 | 0.69 | 29.08 | 448 |
| 10 | 347 | 41.58 | 1.77 | 44.34 | 166 |
| 11 | 510 | 38.91 | 2.31 | 31.86 | 145 |
| 12 | 474 | 36.20 | 3.79 | 33.98 | 86 |
| 13 | 954 | 36.09 | 3.50 | 38.44 | 107 |
| 14 | 1145 | 37.83 | 1.59 | 30.45 | 246 |
| 15 | 1381 | 36.61 | 1.99 | 40.52 | 201 |
| 16 | 967 | 39.21 | 1.72 | 34.15 | 221 |
| 17 | 385 | 41.72 | 3.21 | 36.36 | 94 |
| 18 | 601 | 38.99 | 1.03 | 36.23 | 336 |
| 19 | 977 | 36.35 | 1.92 | 30.20 | 200 |
| 20 | 1028 | 38.84 | 2.40 | 38.10 | 169 |
| 21 | 957 | 40.69 | 2.92 | 41.64 | 129 |
| 22 | 733 | 37.23 | 3.53 | 25.00 | 101 |
| 23 | 1459 | 41.48 | 3.54 | 49.79 | 120 |
| 24 | 307 | 36.69 | 0.77 | 31.24 | 401 |
| 25 | 363 | 41.33 | 0.79 | 39.60 | 377 |
| 26 | 535 | 37.85 | 3.66 | 46.26 | 89 |
| 27 | 1358 | 37.93 | 1.17 | 42.51 | 337 |
| 28 | 1490 | 40.42 | 2.49 | 34.57 | 174 |
| 29 | 891 | 39.11 | 3.62 | 35.44 | 109 |
| 30 | 1388 | 36.72 | 3.89 | 36.69 | 104 |
| 31 | 1287 | 38.94 | 1.65 | 39.18 | 270 |
| 32 | 865 | 41.51 | 1.08 | 30.82 | 354 |
| 33 | 1089 | 38.02 | 0.30 | 27.91 | 1419 |
| 34 | 271 | 41.53 | 0.42 | 37.10 | 679 |
| 35 | 799 | 38.20 | 3.26 | 26.70 | 121 |
| 36 | 1056 | 40.83 | 0.92 | 35.32 | 456 |
| 37 | 1218 | 39.50 | 1.45 | 24.92 | 289 |
| 38 | 1261 | 41.46 | 2.26 | 41.85 | 193 |
| 39 | 540 | 39.51 | 3.22 | 41.22 | 102 |
| 40 | 1160 | 36.17 | 0.55 | 42.26 | 729 |
| 41 | 454 | 41.63 | 2.36 | 45.01 | 131 |
| 42 | 875 | 39.01 | 0.47 | 47.88 | 723 |
| 43 | 1343 | 36.12 | 1.73 | 26.25 | 270 |
| 44 | 1414 | 41.35 | 1.38 | 38.31 | 299 |
| 45 | 606 | 40.44 | 3.77 | 26.08 | 92 |
| 46 | 1002 | 41.98 | 1.80 | 48.54 | 219 |
| 47 | 1449 | 37.53 | 2.19 | 47.50 | 193 |
| 48 | 266 | 39.80 | 2.53 | 45.38 | 115 |
| 49 | 302 | 41.93 | 3.31 | 25.87 | 95 |
| 50 | 1383 | 41.23 | 0.85 | 45.80 | 471 |
| 51 | 1033 | 40.59 | 1.70 | 37.31 | 240 |
| 52 | 1134 | 38.15 | 2.47 | 40.43 | 157 |
| 53 | 530 | 41.75 | 0.88 | 28.33 | 395 |
| 54 | 1495 | 37.79 | 3.83 | 28.24 | 114 |
| 55 | 1302 | 38.35 | 2.76 | 29.16 | 163 |
| 56 | 779 | 36.96 | 2.51 | 29.41 | 152 |
| 57 | 931 | 36.44 | 1.63 | 43.76 | 224 |
| 58 | 487 | 39.94 | 1.22 | 44.68 | 257 |
| 59 | 246 | 36.57 | 1.04 | 40.81 | 282 |
| 60 | 322 | 36.89 | 3.92 | 42.72 | 74 |
| 61 | 1114 | 36.37 | 3.69 | 27.95 | 120 |
| 62 | 373 | 39.85 | 3.13 | 30.66 | 98 |
| 63 | 1322 | 40.91 | 3.38 | 37.06 | 136 |
| 64 | 591 | 41.14 | 3.61 | 29.78 | 94 |
| 65 | 1363 | 39.36 | 2.08 | 36.44 | 228 |
| 66 | 467 | 37.42 | 1.89 | 24.50 | 182 |
| 67 | 771 | 36.16 | 1.30 | 27.20 | 290 |
| 68 | 317 | 41.21 | 2.79 | 39.35 | 107 |
| 69 | 738 | 39.38 | 1.75 | 47.09 | 205 |
| 70 | 809 | 37.48 | 1.40 | 28.99 | 254 |
| 71 | 916 | 37.14 | 1.46 | 34.98 | 244 |
| 72 | 1048 | 41.88 | 3.02 | 40.39 | 138 |
| 73 | 952 | 39.93 | 2.24 | 46.67 | 167 |
| 74 | 236 | 38.77 | 0.34 | 43.09 | 831 |
| 75 | 520 | 36.46 | 0.61 | 34.48 | 558 |
| 76 | 566 | 36.22 | 0.94 | 30.24 | 372 |
| 77 | 1332 | 38.68 | 1.91 | 44.88 | 242 |
| 78 | 1221 | 37.90 | 0.32 | 37.69 | 1332 |
| 79 | 946 | 37.95 | 2.94 | 45.17 | 126 |
| 80 | 759 | 40.64 | 2.03 | 30.86 | 183 |
| 81 | 936 | 38.12 | 1.19 | 36.65 | 307 |
| 82 | 1279 | 38.09 | 2.96 | 43.64 | 149 |
| 83 | 406 | 36.83 | 3.60 | 45.72 | 85 |
| 84 | 642 | 36.32 | 3.86 | 44.55 | 88 |
| 85 | 352 | 37.98 | 2.87 | 27.74 | 110 |
| 86 | 449 | 39.46 | 0.50 | 25.21 | 652 |
| 87 | 1211 | 38.54 | 3.55 | 35.19 | 117 |
| 88 | 1373 | 37.21 | 0.64 | 49.75 | 618 |
| 89 | 489 | 37.68 | 1.69 | 49.96 | 187 |
| 90 | 855 | 37.75 | 3.56 | 39.77 | 106 |
| 91 | 1231 | 41.73 | 2.56 | 47.25 | 166 |
| 92 | 225 | 41.01 | 2.23 | 27.08 | 133 |
| 93 | 1292 | 40.32 | 1.18 | 26.87 | 379 |
| 94 | 446 | 40.91 | 1.84 | 30.32 | 177 |
| 95 | 804 | 41.65 | 0.49 | 32.07 | 717 |
| 96 | 1424 | 38.79 | 3.72 | 30.41 | 111 |
| 97 | 860 | 38.52 | 1.52 | 25.46 | 250 |
| 98 | 1246 | 40.86 | 3.64 | 25.66 | 118 |
| 99 | 495 | 38.49 | 2.67 | 35.65 | 120 |
| 100 | 708 | 38.59 | 3.85 | 32.11 | 89 |
| 101 | 1180 | 39.75 | 3.03 | 49.13 | 134 |
| 102 | 1038 | 37.36 | 1.00 | 26.04 | 409 |
| 103 | 576 | 40.05 | 3.05 | 38.77 | 107 |
| 104 | 1297 | 36.15 | 2.32 | 35.23 | 194 |
| 105 | 1063 | 41.38 | 2.82 | 26.29 | 150 |
| 106 | 1068 | 37.06 | 3.63 | 31.65 | 117 |
| 107 | 814 | 39.68 | 1.16 | 34.36 | 309 |
| 108 | 794 | 37.80 | 2.38 | 43.72 | 146 |
| 109 | 1119 | 38.47 | 3.45 | 33.32 | 111 |
| 110 | 413 | 37.38 | 0.68 | 43.97 | 463 |
| 111 | 203 | 41.79 | 1.15 | 49.04 | 242 |
| 112 | 210 | 40.52 | 2.59 | 42.10 | 109 |
| 113 | 220 | 39.48 | 0.86 | 39.39 | 331 |
| 114 | 1444 | 41.80 | 0.39 | 24.58 | 1284 |
| 115 | 748 | 36.07 | 2.97 | 40.02 | 123 |
| 116 | 1378 | 39.56 | 1.78 | 32.32 | 269 |
| 117 | 291 | 36.30 | 1.82 | 37.94 | 164 |
| 118 | 784 | 39.28 | 3.78 | 49.33 | 91 |
| 119 | 1368 | 41.60 | 2.95 | 29.82 | 161 |
| 120 | 850 | 40.00 | 2.39 | 44.80 | 157 |
| 121 | 677 | 39.98 | 3.95 | 38.14 | 91 |
| 122 | 1282 | 36.47 | 3.99 | 48.92 | 111 |
| 123 | 934 | 41.57 | 2.06 | 25.12 | 202 |
| 124 | 703 | 36.62 | 1.33 | 32.90 | 283 |
| 125 | 690 | 40.24 | 3.67 | 36.56 | 90 |
| 126 | 1348 | 39.19 | 2.90 | 48.34 | 135 |
| 127 | 1470 | 39.83 | 1.06 | 27.33 | 404 |
| 128 | 251 | 38.96 | 3.58 | 28.37 | 84 |
| 129 | 873 | 40.39 | 1.61 | 42.60 | 241 |
| 130 | 429 | 36.25 | 3.07 | 28.74 | 107 |
| 131 | 1226 | 38.05 | 1.98 | 33.57 | 214 |
| 132 | 261 | 37.70 | 2.09 | 33.15 | 145 |
| 133 | 545 | 40.81 | 1.93 | 44.59 | 173 |
| 134 | 698 | 41.19 | 0.75 | 27.54 | 496 |
| 135 | 1454 | 39.65 | 2.63 | 42.47 | 161 |
| 136 | 1129 | 37.65 | 2.25 | 37.27 | 172 |
| 137 | 332 | 40.72 | 1.21 | 31.49 | 251 |
| 138 | 568 | 41.50 | 2.52 | 42.80 | 128 |
| 139 | 1124 | 40.20 | 1.11 | 44.38 | 345 |
| 140 | 926 | 40.99 | 3.70 | 46.63 | 98 |
| 141 | 880 | 41.16 | 2.13 | 37.73 | 183 |
| 142 | 1251 | 36.02 | 3.17 | 31.03 | 136 |
| 143 | 718 | 37.60 | 0.81 | 35.02 | 430 |
| 144 | 1178 | 41.13 | 0.46 | 43.84 | 883 |
| 145 | 1241 | 39.14 | 0.93 | 40.18 | 461 |
| 146 | 444 | 37.78 | 3.23 | 36.48 | 100 |
| 147 | 1327 | 37.31 | 1.27 | 32.94 | 363 |
| 148 | 357 | 39.35 | 3.52 | 33.11 | 87 |
| 149 | 629 | 40.09 | 0.82 | 33.24 | 404 |
| 150 | 1256 | 38.44 | 1.09 | 46.88 | 397 |
| 151 | 1434 | 36.40 | 1.10 | 38.93 | 378 |
| 152 | 682 | 40.68 | 2.98 | 24.08 | 122 |
| 153 | 657 | 36.49 | 2.28 | 25.25 | 153 |
| 154 | 652 | 40.35 | 0.62 | 40.60 | 555 |
| 155 | 1340 | 38.24 | 0.99 | 31.36 | 468 |
| 156 | 1353 | 40.62 | 3.48 | 43.30 | 113 |
| 157 | 886 | 36.54 | 2.48 | 24.79 | 159 |
| 158 | 1155 | 40.74 | 3.28 | 47.30 | 121 |
| 159 | 434 | 38.86 | 0.96 | 46.46 | 326 |
| 160 | 548 | 38.39 | 3.75 | 25.96 | 90 |
| 161 | 789 | 40.37 | 1.02 | 48.75 | 340 |
| 162 | 1170 | 40.46 | 2.75 | 29.28 | 146 |
| 163 | 992 | 37.41 | 2.74 | 38.98 | 142 |
| 164 | 688 | 36.67 | 1.86 | 48.96 | 178 |
| 165 | 1312 | 37.43 | 1.79 | 41.01 | 254 |
| 166 | 1480 | 36.52 | 0.45 | 31.70 | 966 |
| 167 | 1150 | 39.43 | 1.26 | 48.29 | 314 |
| 168 | 378 | 40.84 | 0.26 | 48.50 | 1113 |
| 169 | 459 | 37.28 | 2.71 | 39.97 | 116 |
| 170 | 609 | 39.57 | 0.76 | 45.92 | 417 |
| 171 | 550 | 36.02 | 2.61 | 37.48 | 129 |
| 172 | 1139 | 41.68 | 3.84 | 39.56 | 102 |
| 173 | 812 | 41.28 | 2.29 | 47.80 | 155 |
| 174 | 555 | 39.16 | 0.27 | 32.53 | 1254 |
| 175 | 710 | 37.05 | 0.28 | 41.56 | 1213 |
| 176 | 337 | 36.10 | 2.02 | 46.21 | 147 |
| 177 | 743 | 41.06 | 0.95 | 42.05 | 381 |
| 178 | 835 | 40.17 | 2.69 | 25.62 | 137 |
| 179 | 1236 | 37.04 | 1.37 | 45.22 | 312 |
| 180 | 662 | 38.10 | 2.86 | 30.61 | 123 |
| 181 | 1216 | 40.22 | 3.08 | 40.64 | 136 |
| 182 | 1317 | 39.41 | 3.81 | 44.18 | 120 |
| 183 | 1195 | 38.81 | 0.63 | 26.91 | 649 |
| 184 | 723 | 39.88 | 1.94 | 28.95 | 180 |
| 185 | 627 | 37.26 | 0.48 | 36.27 | 687 |
| 186 | 284 | 37.57 | 3.14 | 41.76 | 92 |
| 187 | 368 | 37.09 | 1.96 | 38.73 | 154 |
| 188 | 941 | 40.30 | 3.97 | 32.74 | 93 |
| 189 | 479 | 38.32 | 3.32 | 47.67 | 93 |
| 190 | 987 | 40.10 | 0.72 | 35.81 | 539 |
| 191 | 1462 | 39.28 | 0.53 | 37.40 | 797 |
| 192 | 342 | 38.07 | 0.60 | 49.38 | 479 |
| 193 | 286 | 40.12 | 3.87 | 47.05 | 75 |
| 194 | 1175 | 37.33 | 3.46 | 29.20 | 116 |
| 195 | 1109 | 41.28 | 1.64 | 28.53 | 270 |
| 196 | 223 | 36.39 | 2.68 | 32.20 | 109 |
| 197 | 281 | 38.67 | 2.70 | 33.36 | 113 |
| 198 | 616 | 38.30 | 1.29 | 43.14 | 250 |
| 199 | 972 | 40.89 | 1.24 | 24.83 | 307 |
| 200 | 728 | 41.56 | 2.85 | 37.52 | 124 |
| 201 | 1404 | 37.58 | 2.84 | 33.94 | 143 |
| 202 | 1185 | 41.85 | 0.98 | 35.86 | 414 |
| 203 | 1307 | 40.49 | 0.52 | 46.05 | 865 |
| 204 | 241 | 41.11 | 1.47 | 45.84 | 191 |
| 205 | 754 | 38.25 | 0.70 | 39.14 | 527 |
| 206 | 528 | 37.13 | 2.22 | 33.44 | 157 |
| 207 | 621 | 41.95 | 1.87 | 34.77 | 192 |
| 208 | 693 | 39.09 | 2.80 | 43.93 | 119 |
| 209 | 1023 | 37.19 | 2.05 | 41.06 | 197 |
| 210 | 901 | 36.05 | 0.91 | 49.17 | 387 |
| 211 | 1015 | 36.24 | 1.53 | 46.96 | 262 |
| 212 | 1198 | 37.72 | 1.07 | 46.76 | 385 |
| 213 | 1190 | 36.84 | 2.15 | 27.70 | 190 |
| 214 | 312 | 39.60 | 1.88 | 40.22 | 155 |
| 215 | 1409 | 38.64 | 0.73 | 41.26 | 560 |
| 216 | 1165 | 39.31 | 2.34 | 24.17 | 171 |
| 217 | 418 | 39.73 | 1.49 | 36.85 | 214 |
| 218 | 505 | 36.74 | 1.14 | 26.50 | 290 |
| 219 | 830 | 38.74 | 2.21 | 36.90 | 166 |
| 220 | 647 | 38.89 | 3.39 | 45.63 | 101 |
| 221 | 1360 | 41.05 | 2.43 | 28.04 | 195 |
| 222 | 764 | 37.35 | 2.45 | 48.71 | 136 |
| 223 | 388 | 38.02 | 3.68 | 42.68 | 83 |
| 224 | 1073 | 39.04 | 0.83 | 29.62 | 513 |
| 225 | 464 | 39.26 | 1.55 | 41.47 | 205 |
| 226 | 304 | 39.05 | 1.35 | 48.84 | 217 |
| 227 | 1200 | 40.02 | 1.54 | 32.28 | 268 |
| 228 | 1393 | 39.06 | 3.09 | 25.41 | 157 |
| 229 | 825 | 36.77 | 3.40 | 37.89 | 107 |
| 230 | 1058 | 39.90 | 1.39 | 42.89 | 302 |
| 231 | 1485 | 38.17 | 1.62 | 46.42 | 268 |
| 232 | 649 | 37.94 | 1.76 | 39.48 | 195 |
| 233 | 769 | 39.78 | 0.40 | 41.68 | 830 |
| 234 | 1271 | 39.95 | 0.57 | 29.57 | 774 |
| 235 | 713 | 41.36 | 3.15 | 46.84 | 110 |
| 236 | 1421 | 40.16 | 3.44 | 48.00 | 120 |
| 237 | 327 | 39.23 | 2.99 | 35.40 | 100 |
| 238 | 962 | 36.94 | 0.58 | 28.78 | 653 |
| 239 | 853 | 39.79 | 3.29 | 38.64 | 115 |
| 240 | 383 | 36.59 | 2.78 | 47.71 | 108 |
| 241 | 1053 | 37.56 | 0.71 | 47.92 | 504 |
| 242 | 296 | 38.62 | 0.80 | 24.37 | 400 |
| 243 | 581 | 37.73 | 0.41 | 26.45 | 872 |
| 244 | 586 | 39.70 | 2.44 | 24.42 | 150 |
| 245 | 974 | 38.61 | 2.83 | 49.88 | 135 |
| 246 | 911 | 41.70 | 0.29 | 43.55 | 1209 |
| 247 | 820 | 41.83 | 3.74 | 40.85 | 96 |
| 248 | 525 | 38.00 | 1.32 | 34.40 | 261 |
| 249 | 870 | 36.81 | 3.01 | 34.19 | 128 |
| 250 | 1094 | 41.78 | 2.16 | 31.28 | 201 |
| 251 | 896 | 40.57 | 3.18 | 27.29 | 125 |
| 252 | 423 | 41.04 | 3.51 | 34.82 | 92 |
| 253 | 1007 | 36.68 | 0.84 | 43.51 | 472 |
| 254 | 365 | 39.13 | 2.60 | 26.16 | 121 |
| 255 | 398 | 37.88 | 0.87 | 29.99 | 363 |
| 256 | 1013 | 39.33 | 2.93 | 28.16 | 136 |
| 257 | 1104 | 39.63 | 0.37 | 34.61 | 1016 |
| 258 | 1137 | 37.28 | 3.37 | 27.00 | 135 |
| 259 | 632 | 38.69 | 1.85 | 28.12 | 198 |
| 260 | 1266 | 37.63 | 3.43 | 24.21 | 127 |
| 261 | 637 | 40.94 | 2.72 | 49.58 | 123 |
| 262 | 1299 | 41.94 | 3.90 | 34.28 | 115 |
| 263 | 611 | 37.46 | 3.33 | 31.45 | 105 |
| 264 | 774 | 40.79 | 1.57 | 35.61 | 241 |
| 265 | 1419 | 37.11 | 2.55 | 25.04 | 194 |
| 266 | 1035 | 39.72 | 2.14 | 31.16 | 191 |
| 267 | 1398 | 40.07 | 1.90 | 28.58 | 256 |
| 268 | 982 | 38.72 | 3.35 | 41.89 | 115 |
| 269 | 276 | 36.99 | 1.56 | 25.83 | 197 |
| 270 | 845 | 38.46 | 1.68 | 39.68 | 222 |
| 271 | 205 | 38.42 | 1.42 | 29.37 | 208 |
| 272 | 500 | 41.43 | 3.93 | 27.49 | 83 |
| 273 | 1338 | 40.67 | 0.56 | 38.56 | 834 |
| 274 | 731 | 38.83 | 3.06 | 30.12 | 116 |
| 275 | 561 | 40.54 | 1.41 | 45.59 | 225 |
| 276 | 667 | 41.41 | 1.67 | 33.78 | 212 |
| 277 | 1205 | 36.27 | 2.41 | 42.93 | 172 |
| 278 | 484 | 40.15 | 0.33 | 30.03 | 1030 |
| 279 | 906 | 38.40 | 2.17 | 44.13 | 162 |
| 280 | 215 | 37.51 | 3.76 | 36.02 | 71 |
| 281 | 1096 | 38.91 | 3.98 | 40.72 | 94 |
| 282 | 1079 | 40.25 | 2.00 | 49.54 | 184 |
| 283 | 840 | 36.42 | 0.35 | 44.97 | 1062 |
| 284 | 1018 | 41.09 | 0.65 | 33.53 | 614 |
| 285 | 515 | 41.31 | 3.41 | 43.34 | 91 |
| 286 | 1084 | 36.64 | 3.10 | 36.06 | 139 |
| 287 | 1099 | 36.79 | 2.64 | 46.01 | 142 |
| 288 | 1464 | 37.01 | 3.30 | 44.76 | 129 |
| 289 | 672 | 36.91 | 1.23 | 47.46 | 290 |
| 290 | 1277 | 41.26 | 2.62 | 31.07 | 168 |
| 291 | 403 | 38.22 | 2.01 | 27.12 | 160 |
| 292 | 1439 | 38.37 | 3.16 | 38.35 | 133 |
| 293 | 571 | 38.57 | 2.11 | 48.09 | 154 |
| 294 | 1259 | 36.91 | 2.91 | 35.52 | 150 |
| 295 | 408 | 41.90 | 2.46 | 32.49 | 125 |
| 296 | 230 | 37.16 | 3.20 | 48.13 | 89 |
| 297 | 997 | 39.58 | 3.91 | 26.66 | 100 |
| 298 | 1043 | 38.27 | 3.49 | 45.42 | 118 |
| 299 | 1429 | 40.96 | 1.44 | 39.81 | 288 |
| 300 | 596 | 36.86 | 1.50 | 42.30 | 228 |
References
- Cigla, M.; Yagiz, S.; Ozdemir, L. Application of tunnel boring machines in underground mine development. In Proceedings of the International Mining Congress and Exhibition, Turkey, Ankara, 19–22 June 2001. [Google Scholar]
- Zheng, Y.L.; Zhang, Q.B.; Zhao, J. Challenges and opportunities of using tunnel boring machines in mining. Tunn. Undergr. Space Technol. 2016, 57, 287–299. [Google Scholar] [CrossRef]
- Pu, Q.; Luo, Y.; Huang, J.; Zhu, Y.; Hu, S.; Pei, C.; Zhang, G.; Li, X. Simulation study on the effect of forced ventilation in tunnel under single-head drilling and blasting. Shock. Vib. 2020, 2020, 8857947. [Google Scholar] [CrossRef]
- Bahrami, D.; Yuan, L.; Rowland, J.H.; Zhou, L.; Thomas, R. Evaluation of post-blast re-entry times based on gas monitoring of return air. Min. Metall. Explor. 2019, 36, 513–521. [Google Scholar] [CrossRef]
- Menéndez, J.; Merlé, N.; Fernández-Oro, J.M.; Galdo, M.; de Prado, L.Á.; Loredo, J.; Bernardo-Sánchez, A. Concentration, propagation and dilution of toxic gases in underground excavations under different ventilation modes. Int. J. Environ. Res. Public Health 2022, 19, 7092. [Google Scholar] [CrossRef]
- Chen, J.; Qiu, W.; Rai, P.; Ai, X. Emission characteristics of CO and NOx from tunnel blast design models: A comparative study. Pol. J. Environ. Stud. 2021, 30, 5503–5517. [Google Scholar] [CrossRef]
- Gillies, A.D.S.; Wu, H.W.; Shires, D. Development of an assessment tool to minimize safe after blast re-entry time to improve the mining cycle. In Proceedings of the Tenth US/North American Mine Ventilation Symposium, Anchorage, AK, USA, 16–19 May 2004. [Google Scholar]
- De Souza, E. Procedures for mitigating safety risks associated with post-blast re-entry times. CIM J. 2023, 14, 2–10. [Google Scholar] [CrossRef]
- Torno, S.; Torano, J.; Ulecia, M.; Allende, C. Conventional and numerical models of blasting gas behaviour in auxiliary ventilation of mining headings. Tunn. Undergr. Space Technol. 2013, 34, 73–81. [Google Scholar] [CrossRef]
- Wang, X.L.; Liu, X.P.; Sun, Y.F.; An, J.; Zhang, J.; Chen, H.C. Construction schedule simulation of a diversion tunnel based on the optimized ventilation time. J. Hazard. Mater. 2009, 165, 933–943. [Google Scholar] [CrossRef]
- Souza, E.D.; Katsabanis, P.D. On the prediction of blasting toxic fumes and dilution ventilation. Eng. Geol. 1991, 13, 223–235. [Google Scholar] [CrossRef]
- Hebda-Sobkowicz, J.; Gola, S.; Zimroz, R.; Wylomanska, A. Identification and statistical analysis of impulse-like patterns of carbon monoxide variation in deep underground mines associated with the blasting procedure. Sensors 2019, 19, 2757. [Google Scholar] [CrossRef]
- Torno, S.; Toraño, J. On the prediction of toxic fumes from underground blasting operations and dilution ventilation. Conventional and numerical models. Tunn. Undergr. Space Technol. 2020, 96, 103194. [Google Scholar] [CrossRef]
- Zhou, Y.; Yang, Y.; Bu, R.W.; Ma, F.; Shen, Y.J. Effect of press-in ventilation technology on pollutant transport in a railway tunnel under construction. J. Clean. Prod. 2020, 243, 118590. [Google Scholar] [CrossRef]
- Stewart, C.M. Practical prediction of blast fume clearance and workplace re-entry times in development headings. In Proceedings of the 10th International Mine Ventilation Congress, Sun City, South Africa, 2–8 August 2014. [Google Scholar]
- Li, C.Q.; Zhou, J.; Armaghani, D.J.; Cao, W.Z.; Yagiz, S. Stochastic assessment of hard rock pillar stability based on the geological strength index system. Geomech. Geophys. Geo-Energy Geo-Resour. 2021, 7, 47. [Google Scholar] [CrossRef]
- Li, J.; Li, C.; Zhang, S. Application of six metaheuristic optimization algorithms and random forest in the uniaxial compressive strength of rock prediction. Appl. Soft Comput. 2022, 131, 109729. [Google Scholar] [CrossRef]
- Li, C.; Zhou, J.; Dias, D.; Gui, Y. A kernel extreme learning machine-grey wolf optimizer (KELM-GWO) model to predict uniaxial compressive strength of rock. Appl. Sci. 2022, 12, 8468. [Google Scholar] [CrossRef]
- Zhou, J.; Li, E.; Wei, H.; Li, C.; Qiao, Q.; Armaghani, D.J. Random forests and cubist algorithms for predicting shear strengths of rockfill materials. Appl. Sci. 2019, 9, 1621. [Google Scholar] [CrossRef]
- Li, C.; Zhou, J.; Khandelwal, M.; Zhang, X.; Monjezi, M.; Qiu, Y. Six novel hybrid extreme learning machine–swarm intelligence optimization (ELM–SIO) models for predicting backbreak in open-pit blasting. Nat. Resour. Res. 2022, 31, 3017–3039. [Google Scholar] [CrossRef]
- Eslami, E.; Choi, Y.; Lops, Y.; Sayeed, A. A real-time hourly ozone prediction system using deep convolutional neural network. Neural Comput. Appl. 2019, 32, 8783–8797. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, P.; Xu, C.; Peng, C.; Wu, J. A deep learning approach to real-time CO concentration prediction at signalized intersection. Atmos. Pollut. Res. 2020, 11, 1370–1378. [Google Scholar] [CrossRef]
- Li, C.Q.; Zhou, J.; Armaghani, D.J.; Li, X.B. Stability analysis of underground mine hard rock pillars via combination of finite difference methods, neural networks, and Monte Carlo simulation techniques. Undergr. Space 2021, 6, 379–395. [Google Scholar] [CrossRef]
- Huang, R.Y.; Shen, X.; Wang, B.; Liao, X. Migration characteristics of CO under forced ventilation after excavation roadway blasting: A case study in a plateau mine. J. Clean. Prod. 2020, 267, 122094. [Google Scholar] [CrossRef]
- Chang, P.; Xu, G.; Zhou, F.; Mullins, B.J.; Abishek, S.; Chalmers, D. Minimizing DPM pollution in an underground mine by optimizing auxiliary ventilation systems using CFD. Tunn. Undergr. Space Technol. 2019, 87, 112–121. [Google Scholar] [CrossRef]
- Toraño, J.; Torno, S.; Menéndez, M.; Gent, M.R.; Velasco, J. Models of methane behaviour in auxiliary ventilation of underground coal mining. Int. J. Coal Geol. 2009, 80, 35–43. [Google Scholar] [CrossRef]
- Wei, N.; Zhong-an, J.; Dong-mei, T. Numerical simulation of the factors influencing dust in drilling tunnels: Its application. Min. Sci. Technol. (China) 2011, 21, 11–15. [Google Scholar] [CrossRef]
- Zhang, H.; Sun, J.; Lin, F.; Chen, S.; Yang, J. Optimization scheme for construction ventilation in large-scale underground oil storage caverns. Appl. Sci. 2018, 8, 1952. [Google Scholar] [CrossRef]
- Bismark, A.; Opafunso, Z.O.; Oniyide, G.O. Predicting the re-entry time at Chirano Gold Mine limited southwestern Ghana using ventsim simulation software. Niger. J. Eng. 2022, 29, 102–112. [Google Scholar]
- GB 16423-2020Safety Regulation for Metal and Nonmetal Mines; Ministry of Emergency Management of the People’s Republic of China: Beijing, China; Emergency Management Press: Beijing, China, 2020.
- AQ 2031-2011Regulations for The Construction of Monitoring and Supervision System in Metal and Nonmetal Underground Mine; Ministry of Emergency Management of the People’s Republic of China: Beijing, China; China Coal Industry Publishing House: Beijing, China, 2011.
- Zawadzka-Małota, I. Testing of mining explosives with regard to the content of carbon oxides and nitrogen oxides in their detonation products. J. Sustain. Min. 2015, 14, 173–178. [Google Scholar] [CrossRef]
- Brake, D.J. A review of good practice standards and re-entry procedures after blasting and gas detection generally in underground hardrock mines. In Proceedings of the 15th North American Mine Ventilation Symposium, Blacksburg, VA, USA, 21–23 June 2015; pp. 20–25. [Google Scholar]
- Wang, Y.M. Mine Ventilation and Dust Control; Metallurgical Industry Press: Beijing, China, 1993; p. 198. [Google Scholar]
- Wang, X.G. Emulsion Explosives, 2nd ed.; Metallurgical Industry Press: Beijing, China, 2008; p. 575. [Google Scholar]
- Zhao, H.; Wang, Y.J.; Song, J.; Gao, G. The pollutant concentration prediction model of NNP-BPNN based on the INI algorithm, AW method and neighbor-PCA. J. Ambient. Intell. Hum. Comput. 2018, 10, 3059–3065. [Google Scholar] [CrossRef]
- Zhang, J.; Dias, D.; An, L.; Li, C. Applying a novel slime mould algorithm-based artificial neural network to predict the settlement of a single footing on a soft soil reinforced by rigid inclusions. Mech. Adv. Mater. Struct. 2022, 1–16. [Google Scholar] [CrossRef]
- Song, Y.; Zhong, D.H. Study on construction schedule management and control method for hydraulic & hydropower engineering based on visual simulation. Syst. Eng.-Theory Pract. 2006, 8, 55–62. [Google Scholar] [CrossRef]


| TWA/ppm | STEL/ppm | |
|---|---|---|
| ASM-2 | 50 | 100 |
| NIOSH REL | 35 | 200 |
| NOHSC | 30 | 200 |
| OSHA PEL | 35 | 200 |
| CHINA | 16 | 24 |
| Reference | Equation | Way |
|---|---|---|
| [4] | Calibration | |
| [7] | Calibration | |
| [7] | Calibration | |
| [9] | Fitting | |
| [9] | Fitting | |
| [10] | Fitting | |
| [11] | Derivation | |
| [11] | Derivation | |
| [15] | Calibration |
| Model | Neurons | RMSE | R2 | ||
|---|---|---|---|---|---|
| Training | Testing | Training | Testing | ||
| 1 | 2 | 16.0196 | 21.9249 | 0.9959 | 0.9922 |
| 2 | 3 | 55.9012 | 37.0202 | 0.9502 | 0.9776 |
| 3 | 4 | 72.4646 | 60.601 | 0.9163 | 0.9401 |
| 4 | 5 | 61.6996 | 50.5617 | 0.9393 | 0.9583 |
| 5 | 6 | 12.6171 | 21.3421 | 0.9975 | 0.9926 |
| 6 | 7 | 14.3551 | 21.026 | 0.9967 | 0.9928 |
| 7 | 8 | 14.7677 | 21.4577 | 0.9965 | 0.9925 |
| 8 | 9 | 14.2703 | 22.0516 | 0.9968 | 0.9921 |
| 9 | 10 | 13.1419 | 21.6439 | 0.9973 | 0.9924 |
| Indicators | Training | Testing | ||
|---|---|---|---|---|
| Empirical | BPNN | Empirical | BPNN | |
| RMSE | 61.81 | 12.61 | 76.89 | 21.34 |
| MAE | 38.34 | 7.66 | 42.06 | 10.78 |
| R2 | 0.94 | 0.99 | 0.90 | 0.99 |
| SSE | 798352 | 33429 | 526147 | 40934 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, J.; Li, C.; Zhang, T. Application of Back-Propagation Neural Network in the Post-Blast Re-Entry Time Prediction. Knowledge 2023, 3, 128-148. https://doi.org/10.3390/knowledge3020010
Zhang J, Li C, Zhang T. Application of Back-Propagation Neural Network in the Post-Blast Re-Entry Time Prediction. Knowledge. 2023; 3(2):128-148. https://doi.org/10.3390/knowledge3020010
Chicago/Turabian StyleZhang, Jinrui, Chuanqi Li, and Tingting Zhang. 2023. "Application of Back-Propagation Neural Network in the Post-Blast Re-Entry Time Prediction" Knowledge 3, no. 2: 128-148. https://doi.org/10.3390/knowledge3020010
APA StyleZhang, J., Li, C., & Zhang, T. (2023). Application of Back-Propagation Neural Network in the Post-Blast Re-Entry Time Prediction. Knowledge, 3(2), 128-148. https://doi.org/10.3390/knowledge3020010







