An Investigation of Various Controller Designs for Multi-Link Robotic System (Robogymnast)

Abstract

An approach to controlling the three-link Robogymnast robotic gymnast and assessing stability is proposed and examined. In the study, a conventionally configured linear quadratic regulator is applied and compared with a fuzzy logic linear quadratic regulator hybrid approach for stabilising the Robogymnast. The Robogymnast is designed to replicate the movement of a human as they hang with both hands holding the high bar and then work to wing up into a handstand, still gripping the bar. The system, therefore has a securely attached link between the hand element and the ‘high bar’, which is mounted on ball bearings and can rotate freely. Moreover, in the study, a mathematical model for the system is linearised, investigating the means of determining the state space in the system by applying Lagrange’s equation. The fuzzy logic linear quadratic regulator controller is used to identify how far the system responses stabilise when it is implemented. This paper investigates factors affecting the control of swing-up in the underactuated three-link Robogymnast. Moreover, a system simulation using MATLAB Simulink is conducted to show the impact of factors including overshoot, rising, and settling time. The principal objective of the study lies in investigating how a linear quadratic regulator or fuzzy logic controller with a linear quadratic regulator (FLQR) can be applied to the Robogymnast, and to assess system behaviour under five scenarios, namely the original value, this value plus or minus ±25%, and plus or minus ±50%. In order to further assess the performance of the controllers used, a comparison is made between the outcomes found here and findings in the recent literature with fuzzy linear quadratic regulator controllers.

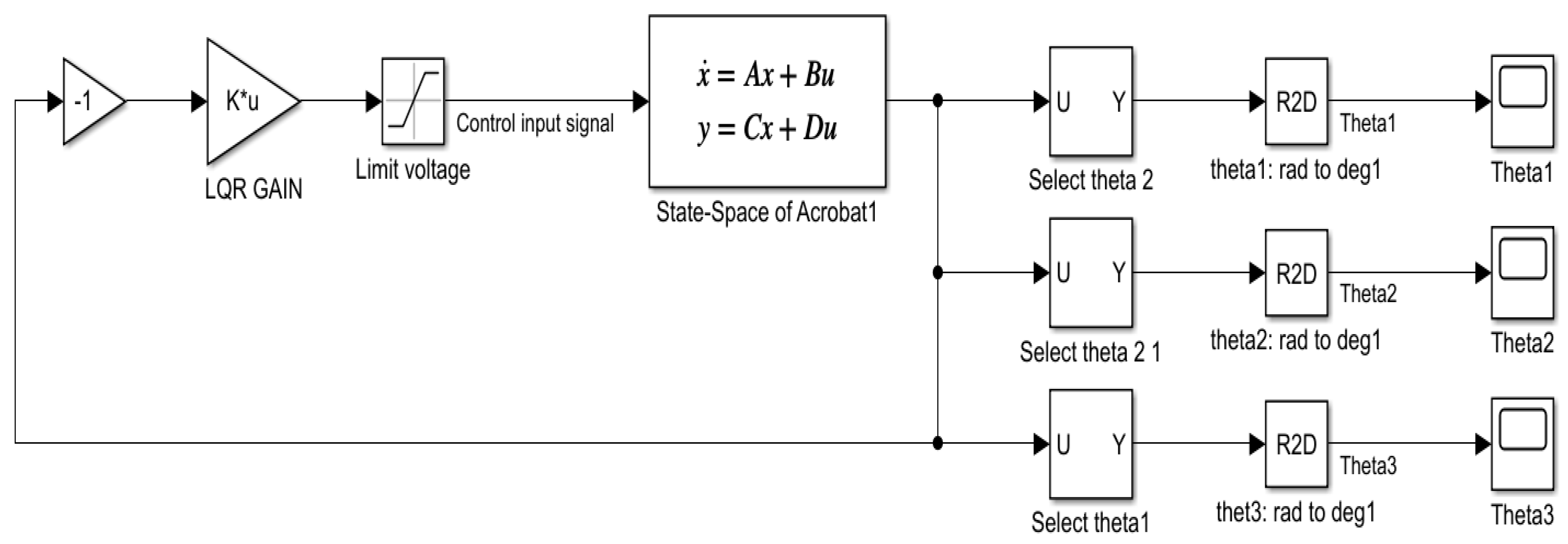
1. Introduction

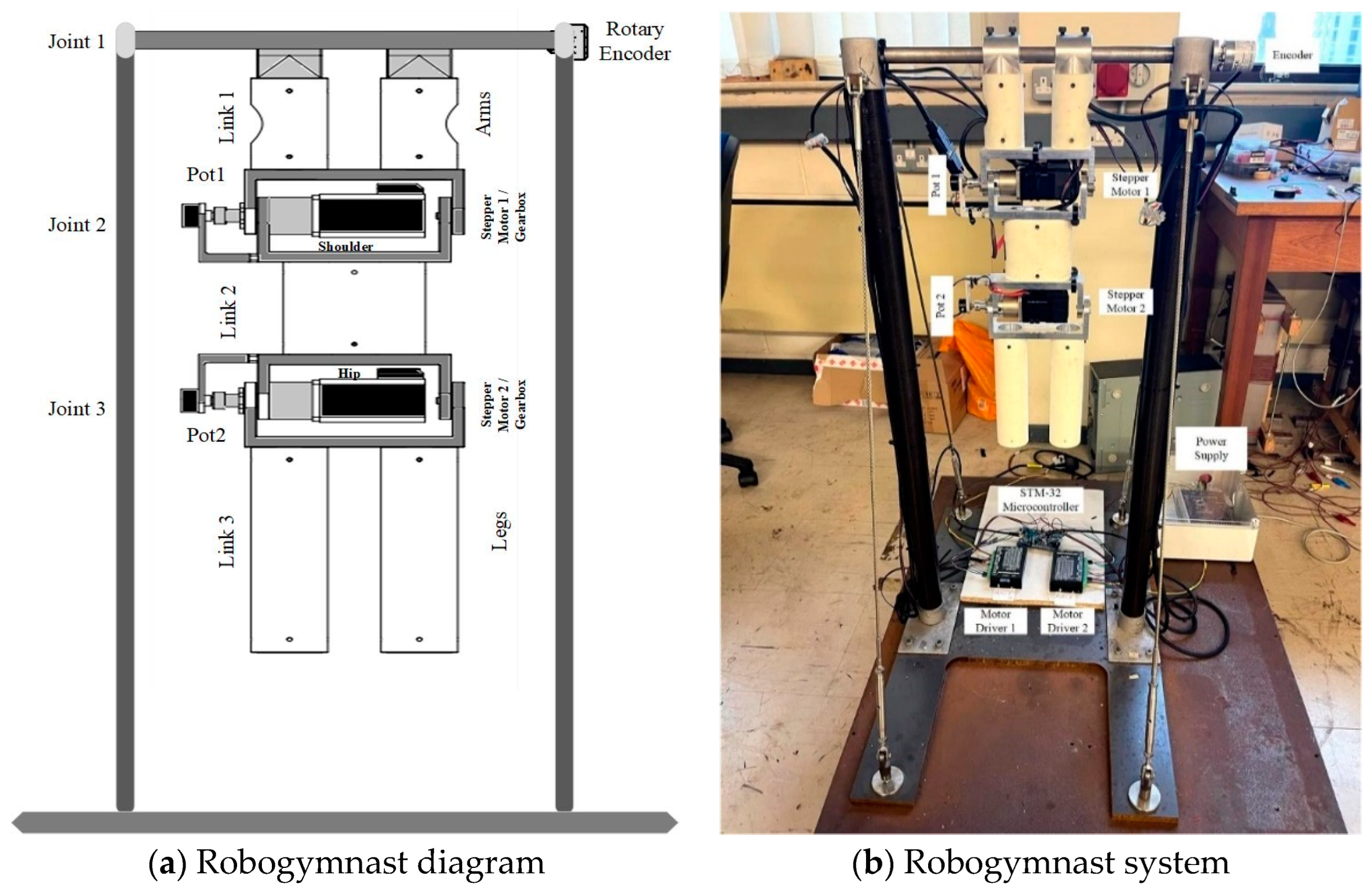
Non-linear control theory research frequently uses Inverted Pendulum Systems (IPSs) [1] as an example of unstable, underactuated systems [2]. Continuing work to develop novel control technology reflects advances made across a range of areas within the realm of science and technology. Effective measurement of a control system can be achieved through the design and application of a controller with a specific system, to monitor its activities. This paper presents an investigation of swing-up movement in the Robogymnast as a three-link, non-linear robotic system [3]. The Robogymnast exemplifies complex mechanical systems with more than one link and with underactuation and is therefore a suitable case study for evaluating and comparing different types of control system [4]. The underactuated system presents control challenges because of the lack of ability to linearise full-state feedback about a specific point of equilibrium in many of these systems, as well as potentially not being small-time local controllable (STLC) [5]. Various research has been conducted to address this issue in the control engineering and robotics literature [6]. An inverted pendulum-derived system is a frequent choice with which to demonstrate an underactuated mechanism. This type of system has a component attached to a set point from which it swings freely, and gravity acts upon this component. Motion control investigations frequently employ pendulum systems, which enable hybrid and chaotic systems to be demonstrated [7,8,9].

The triple-inverted pendulum mechanism is of interest to the robotics field because it is analogous to the way in which human bodies are structured and achieve balance. The Acrobat robotic system, named for its similarities to acrobatic movements, is an unstable and underactuated system based on an inverted pendulum, and is therefore an appropriate model for studies of non-linear controls in theory and in implementation [6,10]. The Acrobat was used with a designed intelligent control system to allow the robot to balance, with the design combining a conventional controller with fuzzy and adaptive-fuzzy controllers, to achieve swing and catch actions and to balance in inversion [9]. State variable feedback was utilised here, as well as LQR and proportional-integral-derivative.

In brief, the novelty of this work is to apply and compare a different controller on a multi-link robotic system, to analyse and review the stability and robustness of both proposed controllers’ performance, and then investigate the performance of the normal conventional LQR compared with the hybrid fuzzy LQR successfully implemented in various cases by adding and subtracting ±25% and ±50% to the system.

In this work, the paper is organised as follows. Section 2 describes the relative study and examination of previous research; Section 3 contains two parts, which are, firstly, an overview of the system, as well as the mathematical model of the Robogymnast analysed; fourthly, the control design of LQR and FLQR are presented. Moreover, Section 5 presents the robustness investigation for the proposed controller, followed by the results and comparison of all suggested cases. Lastly, we summarize the investigation and future outcomes of the system are mentioned.

2. Literature Review

Various studies [11,12,13,14,15,16] examine autonomous upswing for a three-link robot with a single non-actuated and two actuated joints. The current study’s contribution to this area involves assessing the use of an LQR controller and a fuzzy LQR controller when applied with the Robogymnast: a robot with multiple links and a pendulum action. The robotic system used is described in Section 2, and a discussion of the system’s mathematical model is also given. Section 3 considers the upswing control problem, while Section 4 describes the application of each controller to the Robogymnast and details the responses recorded. Then, Section 5 discusses the simulation and its findings, while Section 6 provides the study’s conclusions.

Earlier studies [17,18,19] demonstrate LQR as an active method for designing controllers for the performance of complex systems. In addition, state feedback control (SFC) operates based on where the system’s poles are located, which depends upon state variables and K as the gain matrix. Using SFC, the location of closed-loop system poles can be freely set, while, when using output feedback controls, poles are located at predefined points. The controller used combines LQR as an optimal control method with fuzzy approaches to control [20]. A fuzzy logic control system is rule-based, and depends centrally on a Fuzzy Control Rule (FCR) set connected through fuzzy implication as well as the compositional rule of inference [21]. FPD controllers use a combination of a PD and fuzzy logic controller [22], and the choice of this controller type to bring stability to the Robogymnast was made here because the system is non-linearly unstable, and FDP can address this issue and stabilise the robot [23]. The PD controller is a feedback controller whose output is a control variable, generally derived from error (e) when a comparison is made of a process variable’s (PV’s) reference value as set by the user against the measured value. The error is then used by the different elements within the controller to choose a particular action [18]. Employed-feedback proportional integral derivative (PID) controllers are widely used for co-ordinating industrial controls, as well as in any context where controls must be modulated on an ongoing basis. A PID controller works by analysing and measuring errors using the difference between the target set-point (SP) and the measured value of the PV, making real-time modifications based on integral (I), derivative (D) and proportional (P) terms. In practice, this results in automated, accurate responses in altering a control function. Through increasing system capabilities, the PID algorithm used by the controller brings the output measured into line with desired inputs while minimising deferral error [24]. Modelling and simulation of both PID and LQR controllers for use to control the Robogymnast took place in MATLAB/Simulink. Within this, a PID controller was developed and implemented with the robotic pendulum system and its performance compared to that of the conventional LQR controller [25]. The initial stage involved creating a mathematical model of the robotic system and then modelling a robotics manipulation drive with PI [19].

3. Materials and Methods

3.1. System Description

The basis of the design for the three-link robotic system used in this study comes from an established movement in gymnastics in which an individual hanging from a high bar uses free rotation to swing up and over the top. Figure 1a provides a block diagram representing the system (Figure 1b) in its principal components. The first link is analogous to the arms of the gymnast, with no wrist or elbow jointing; Link 2 combines the gymnast’s trunk, neck, and head into one unified part, and Link 3 connects the legs and feet, with no jointing for the knees and ankles. The non-actuated, passive joint (Joint 1) in the system is analogous to the athlete’s hands, and the active second and third joints relate to the shoulder and then the hip joints in a human [26,27]. As shown in Figure 1a,b’s representation, the system is operated using two stepper motors connected to a stepper driver, which allows the system to move smoothly. In addition, the STM32F Microcontroller (ST, Italy) is used for programming of the control system, using the language C++ for converting commands passed from the PC-based control system and the robotic system. A sensor is also assigned to each of the links, with Link 1 being connected to a rotary encoder, while potentiometers 2 and 3 were connected to Links 2 and 3, respectively, and the sensors monitored the absolute angles at each position [17].

3.2. Mathematical Model

This subsection provides the mathematical modelling of the designed controller, in relation to the Robogymnast as shown in Figure 1a,b. Lagrange equations were utilised to generate system motion equations [3].

Modelling of the robot while vertical used linear, continuous-time, state-space approaches, applied using multiple tools in MATLAB and additional researcher-generated M-files. In Table 1, names and values are provided for each parameter. Matrices to model state space are termed A, B, C and D. The anti-swing controller’s purpose is to stabilise pendulum links in vertical downward alignment with minimal vibration. Link state as representing the point of stable is as follows: θ₁ = θ₂ = θ₃ = 0. The equations’ state space for the robotic system is given by

ẋ = Ax + Bu

(1)

y = Cx

(2)

x is the state vector of the system, y is the output vector. The numerical model of the Robogymnast was calculated by MATLAB/Toolbox to obtain A, B and C, whereas

$$\mathrm{A}=\left[\begin{array}{cc}{0}_3& I_3\\ A_{22}& A_{22}\end{array}\right]$$

where

$$0_3=\left[\begin{array}{ccc}0& 0& 0\\ 0& 0& 0\\ 0& 0& 0\end{array}\right]I_3=\left[\begin{array}{ccc}1& 0& 0\\ 0& 1& 0\\ 0& 0& 1\end{array}\right]$$

$${\mathrm{A}}_{21}=\left[\begin{array}{ccc}0& 2.8625& -0.0657\\ 0& 29.2751& -15.8236\\ 0& -57.5286& 247.5924\end{array}\right]$$

$${\mathrm{A}}_{22}=\left[\begin{array}{ccc}-0.0286& -0.0083& 0.0284\\ -0.0391& -0.1957& 1.2358\\ 0.0589& 1.0485& -18.0527\end{array}\right]$$

State-space matrices for Robogymnast (A, B, C and D) are shown below:

$$\mathrm{A}=\left[\begin{array}{cccccc}0& 0& 0& 1& 0& 0\\ 0& 0& 0& 0& 1& 0\\ 0& 0& 0& 0& 0& 1\\ 0& 2.6825& -0.0657& -0.0286& -0.0083& 0.0284\\ 0& 29.2751& -15.8236& -0.0391& -0.1957& 1.2358\\ 0& -57.5286& 247.5924& 0.0589& 1.4085& -18.0527\end{array}\right]$$

$$\mathrm{B}=\left[\begin{array}{c}0\\ 0\\ 0\\ 1.0314\\ 1.6582\\ -2.4837\end{array}\right]\mathrm{C}=\left[\begin{array}{cccccc}1& 0& 0& 0& 0& 0\\ 0& 1& 0& 0& 0& 0\\ 0& 0& 1& 0& 0& 0\\ 0& 0& 0& 1& 0& 0\\ 0& 0& 0& 0& 1& 0\\ 0& 0& 0& 0& 0& 1\end{array}\right]$$

(3)

The Robogymnast’s discrete-time modelling was performed through discretisation of Equations (1) and (2), which were then applied in the MATLAB command window for the implementation of mathematical model matrices in the simulation to determine outcomes. This was carried out through the MATLAB commands described in which

sys = ss [A, B, C, D]
ss2tf: h = tf [sys]

Table 1. Robogymnast parameters [18].

Parameters	Symbol	Mean Values
Length of the first link	$L_1$	0.16 m
Length of the second link	$L_2$	0.18 m
Length of the third link	$L_3$	0.24 m
Weight of the first link	$m_1$	1.2 kg
Weight of the second link	$m_2$	1.2 kg
Weight of the third link	$m_3$	0.5 kg
Angles between poles 1, 2, and 3	$\theta$	${\theta }_1$,${\theta }_2$,${\theta }_3$ (rad)
Initial values of the angles	q1, q2, q3	0 (rad)
Gravity	g	$9.81 \mathrm{m}/{\mathrm{s}}^2$

Table 1. Robogymnast parameters [18].

Parameters	Symbol	Mean Values
Length of the first link	$L_1$	0.16 m
Length of the second link	$L_2$	0.18 m
Length of the third link	$L_3$	0.24 m
Weight of the first link	$m_1$	1.2 kg
Weight of the second link	$m_2$	1.2 kg
Weight of the third link	$m_3$	0.5 kg
Angles between poles 1, 2, and 3	$\theta$	${\theta }_1$,${\theta }_2$,${\theta }_3$ (rad)
Initial values of the angles	q1, q2, q3	0 (rad)
Gravity	g	$9.81 \mathrm{m}/{\mathrm{s}}^2$

4. Control Design

This section discusses the control methods applied within the study in detail. This begins with a discussion of the function of the LQR control system and how this was implemented for the parameters of the robotic system, with a similar discussion following for the FLQR control system.

4.1. LQR

LQR provides an active method for a controller when considering performance in a complex system [28]. In addition, SFC uses the system’s pole sites, as set using state variables and gain matrix K, permitting the free location of poles in closed-loop systems as required, while fixed locations are used in output feedback control methods [29]. In this approach, SFC is used for implementation of the state variables, which generate feedback. Each feedback component is then multiplied using the state feedback gain matrix and compared to reference input values [24]. Gain matrix calculations are the main application of state feedback control [30]. To achieve this, an LQR controller is commonly used, and for the greatest effectiveness with this type of controller, among the parameters of the K matrix parameters should be the cost function (J) for stat optimisation, x(t), and u(t) as the systems control signal [31]. Here, where Q is the constant symmetry positive, and matrix R is constant, optimal control is written as follows.

The algebraic Riccati equation is used to calculate K and P values.

u (t) = −K × (t)

(4)

$$\mathrm{J}=\frac{1}{2}{\displaystyle {\int }_0^{\infty }}(x^t Qx+u^t Ru) \mathrm{dt}$$

(5)

$$U=R^{-1} B^T PX=-KX$$

(6)

The algebraic Riccati equation is used to calculate K and P values.

$$A^T+PA-PB{R}^{-1}{B}^{T}P+Q=0$$

(7)

$$\mathrm{K}=R^{-1}{B}^{T}P=[K_1 K_2 K_3 \dots . K_6].$$

(8)

K = [0.2581 22.789 −507.886 0.940 −12.250 −19.480]

In this work, LQR is implemented by MATLAB/Simulink as shown in Figure 2.

4.2. FLQR

The resulting controller offers a combination of LQR optimised control and fuzzy logic-based control (FLC) [20]. FLC operates on a rule-based premise by applying an FCR set linked through fuzzy implication and the compositional rule of inference [21,32]. The design procedure followed to produce the FLC is given in this subsection. Structuring of the FLC is as illustrated in Figure 3, with the FLC functioning as complementary to the main controller in changing conditions [33]. There are varied tool and system applications for fuzzy logic in the manufacturing sector, with FLCs enabling more intelligent technologies [34]. The Mamdani approach was used to develop the fuzzy model, and this enabled modifications of closed-loop controller feedback gains. Transformation of the input control signal parameters error (E) and change of error (EC), and of the output U, generated variables based on language: NB = negative big; NM = negative medium; NM = negative small; Z = zero; PS = positive small; PM = positive medium; and PB = positive big. Graphic inference of input and output variables was performed via triangular membership functions. Figure 4 and Figure 5 show the inputs E and EC, and the output variable range is given in Figure 6 [18]. The fuzzy rules that apply to the controller are given in Table 2, Table 3 presents rules of the FL controller, and a sample Simulink implementation of the Robogymnast and FLQR controller is provided in Figure 6.

MATLAB Simulink was used as a simulation environment for determining system responses, with the findings being used in designing the control systems put forward here. A performance evaluation of closed-loop systems operation was performed, related to the step response with the controller. Both the linear LQR and non-linear FLQR controller were modelled and their use in stabilising the robotic system simulated in MATLAB Simulink [17]. Outcomes for output responses demonstrated enhanced overshoot and rise times as well as other benefits when the FLQR controller was applied, considering the system’s step response (see Figure 6).

Table 2. Fuzzy rules linguistic variables.

Symbol	Linguistic Variable
NB	Negative Big
Nm	Negative Medium
NS	Negative Small
Z	Zero
PS	Positive Small
PM	Positive Medium
PB	Positive Big

Table 2. Fuzzy rules linguistic variables.

Symbol	Linguistic Variable
NB	Negative Big
Nm	Negative Medium
NS	Negative Small
Z	Zero
PS	Positive Small
PM	Positive Medium
PB	Positive Big

Figure 3. Membership function of fuzzy input.

Figure 3. Membership function of fuzzy input.

Figure 4. Membership (error of change) function of fuzzy input (error).

Figure 4. Membership (error of change) function of fuzzy input (error).

Figure 5. Membership function of fuzzy output variable (u).

Figure 5. Membership function of fuzzy output variable (u).

Table 3. Rules of FL controller [18].

Error	Change in Error
	NB	NM	NS	Z	PS	PM	PB
NB	NB	NB	NB	NM	NM	NS	Z
NM	NB	NB	NB	NM	NS	Z	PS
NS	NB	NM	NM	NS	Z	PS	PM
Z	NM	NM	NS	Z	PS	PM	PB
PS	NM	NS	Z	PS	PM	PM	PB
PM	NS	Z	PS	PM	PM	PB	PB
PB	Z	PS	PM	PM	PB	PB	PB

Table 3. Rules of FL controller [18].

Error	Change in Error
	NB	NM	NS	Z	PS	PM	PB
NB	NB	NB	NB	NM	NM	NS	Z
NM	NB	NB	NB	NM	NS	Z	PS
NS	NB	NM	NM	NS	Z	PS	PM
Z	NM	NM	NS	Z	PS	PM	PB
PS	NM	NS	Z	PS	PM	PM	PB
PM	NS	Z	PS	PM	PM	PB	PB
PB	Z	PS	PM	PM	PB	PB	PB

Figure 6. FLQR Simulink.

Figure 6. FLQR Simulink.

4.3. Robustness Investigation for the Proposed Controller

In order to determine whether the proposed controller is robust, this section analyses parametric uncertainty within the three-link system and the impacts of this on stabilising the system, in a multi-scenario approach. Various possible parametric system conditions are explored, and these results are listed in Section 5. Primarily, the testbed parameters were each altered in isolation, before altering multiple parameters at one time, increasing, and then decreasing them by 25% and 50% from the baseline.

To evaluate both the LQR and the fuzzy LQR controller in terms of robust performance, variations were made to the testbed system as shown in Section 5, where the original values of both controllers were tested and compared as shown in Figure 7a–c, and

Table 4. LQR vs. FLQR performance [13].

Symbol	Controller	${\mathit{O}}_{\mathit{s}\mathit{h}}\mathbf{\left(}\mathbf{pu}\mathbf{\right)}$	${\mathit{U}}_{\mathit{s}\mathit{h}}\mathbf{\left(}\mathbf{pu}\mathbf{\right)}$	${\mathit{T}}_{\mathit{r}}\mathbf{\left(}\mathbf{s}\mathbf{\right)}$	${\mathit{T}}_{\mathit{s}}\mathbf{\left(}\mathbf{s}\mathbf{\right)}$
${\mathsf{\theta }}_{\mathbf{1}}$	LQR	8.02	−5.69	0.3557	15.5196
	Fuzzy LQR	2.88	−5.71	0.4074	11.1823
${\mathsf{\theta }}_{\mathbf{2}}$	LQR	1.03	−1.32	0.0758	4.9142
	Fuzzy LQR	0.42	−1.44	0.30	4.1694
${\mathsf{\theta }}_{\mathbf{3}}$	LQR	0.25	−0.41	0.0509	3.3310
	Fuzzy LQR	0.25	−0.40	0.0523	2.4428

. Figure 8 shows the controller in the original value where the Robogymnast parameters are constant. Then plus 25% of the original parameters were implemented in Section 5.2 for both LQR and FLQR which are signified in Figure 9a–c and the compared outcomes are displayed in Figure 10 and Table 5 to show the difference between cases 1 and 2. A third scenario is by adding 50% more of the original parameters to verify the stability as seen in Figure 11a–c and Figure 12 and Table 6. On the other hand, −25% and −50% were implemented respectfully to the robotic system to verify the response of the system as seen in Section 5.4 in which case 4 is compared in Table 7. Moreover, Figure 13a–c and Figure 14 insulate the outcomes of −25% of the system. In the last scenario, −50% less of the original value was applied to the initial values as it can be seen in Table 8, and the difference is presented in Figure 15a–c and Figure 16. Finally, Section 5.6 demonstrates the integral time of absolute error (ITAE) for each case 1−5, then Table 9. Figure 17 demonstrates the comparison between LQR and FLQR controllers in all scenarios respectively. As a result, parametric uncertainty conditions were formed that might frequently be encountered operationally within the testbed. Optimal gains were achieved in all cases; there are multiple variables within the testbed system that can change as operations are running and increases or decreases in any of this impact how stable the system is, where the parameters change mathematically.

5. Results

5.1. Case 1: Original Value [17]

As shown, Figure 8 displayed the controller in the original value where the Robogymnast parameters are constant.

Figure 8. Case 1 comparison.

Figure 8. Case 1 comparison.

5.2. Case 2: +(%25)

In Table 5, a full outcome of case2 comparison between LQR and FLQR controllers is presented.

Figure 9. (a) The system response for link-1 of Robogymnast in Case 2 (T1); (b) The system response for each middle link of Robogymnast in Case 2 (T2); (c) The system response for link-3 of Robogymnast in Case 2 (T3).

Figure 9. (a) The system response for link-1 of Robogymnast in Case 2 (T1); (b) The system response for each middle link of Robogymnast in Case 2 (T2); (c) The system response for link-3 of Robogymnast in Case 2 (T3).

Table 5. Comparison performance of LQR and FLQR controllers in Case 2.

Symbol	Controller	${\mathit{O}}_{\mathit{s}\mathit{h}}$ (pu)	${\mathit{U}}_{\mathit{s}\mathit{h}}$ (pu)	${\mathit{T}}_{\mathit{r}}$ (s)	${\mathit{T}}_{\mathit{s}}$ (s)
${\mathsf{\theta }}_{\mathbf{1}}$	LQR	8.026	−5.621	0.2844	12.4151
	Fuzzy LQR	3.122	−5.716	0.3249	8.9536
${\mathsf{\theta }}_{\mathbf{2}}$	LQR	1	−1.326	0.0605	3.9305
	Fuzzy LQR	1	−1.445	0.84	3.3397
${\mathsf{\theta }}_{\mathbf{3}}$	LQR	0.2537	−0.4	0.0406	2.6648
	Fuzzy LQR	0.2562	−0.4	0.0418	1.9637

Table 5. Comparison performance of LQR and FLQR controllers in Case 2.

Symbol	Controller	${\mathit{O}}_{\mathit{s}\mathit{h}}$ (pu)	${\mathit{U}}_{\mathit{s}\mathit{h}}$ (pu)	${\mathit{T}}_{\mathit{r}}$ (s)	${\mathit{T}}_{\mathit{s}}$ (s)
${\mathsf{\theta }}_{\mathbf{1}}$	LQR	8.026	−5.621	0.2844	12.4151
	Fuzzy LQR	3.122	−5.716	0.3249	8.9536
${\mathsf{\theta }}_{\mathbf{2}}$	LQR	1	−1.326	0.0605	3.9305
	Fuzzy LQR	1	−1.445	0.84	3.3397
${\mathsf{\theta }}_{\mathbf{3}}$	LQR	0.2537	−0.4	0.0406	2.6648
	Fuzzy LQR	0.2562	−0.4	0.0418	1.9637

Figure 10. Case 2 comparison.

Figure 10. Case 2 comparison.

5.3. Case 3: +(%50)

As shown, Table 6 presents the controller in the case 3 value where the Robogymnast parameters are add +(50) to LQR and FLQR to investigate the difference.

Table 6. Comparison performance of LQR and FLQR controllers in Case 3.

Symbol	Controller	${\mathit{O}}_{\mathit{s}\mathit{h}}$ (pu)	${\mathit{U}}_{\mathit{s}\mathit{h}}$ (pu)	${\mathit{T}}_{\mathit{r}}$ (s)	${\mathit{T}}_{\mathit{s}}$ (s)
${\mathsf{\theta }}_{\mathbf{1}}$	LQR	8.025	−5.679	0.2369	10.3460
	Fuzzy LQR	3.013	−5.711	0.2709	7.4641
${\mathsf{\theta }}_{\mathbf{2}}$	LQR	1	−1.326	0.0504	3.2747
	Fuzzy LQR	1	−1.433	0.0486	2.7863
${\mathsf{\theta }}_{\mathbf{3}}$	LQR	0.2542	−0.4	0.0337	2.2205
	Fuzzy LQR	0.2582	−0.4	0.48	1.6402

Table 6. Comparison performance of LQR and FLQR controllers in Case 3.

Symbol	Controller	${\mathit{O}}_{\mathit{s}\mathit{h}}$ (pu)	${\mathit{U}}_{\mathit{s}\mathit{h}}$ (pu)	${\mathit{T}}_{\mathit{r}}$ (s)	${\mathit{T}}_{\mathit{s}}$ (s)
${\mathsf{\theta }}_{\mathbf{1}}$	LQR	8.025	−5.679	0.2369	10.3460
	Fuzzy LQR	3.013	−5.711	0.2709	7.4641
${\mathsf{\theta }}_{\mathbf{2}}$	LQR	1	−1.326	0.0504	3.2747
	Fuzzy LQR	1	−1.433	0.0486	2.7863
${\mathsf{\theta }}_{\mathbf{3}}$	LQR	0.2542	−0.4	0.0337	2.2205
	Fuzzy LQR	0.2582	−0.4	0.48	1.6402

Figure 11. (a) The system response for upper link of Robogymnast in Case 3 (T1); (b) The system response for second link of Robogymnast in Case 3 (T2); (c) The system response for 3rd link of Robogymnast in Case 3 (T3).

Figure 11. (a) The system response for upper link of Robogymnast in Case 3 (T1); (b) The system response for second link of Robogymnast in Case 3 (T2); (c) The system response for 3rd link of Robogymnast in Case 3 (T3).

Figure 12. Case 3 comparison.

Figure 12. Case 3 comparison.

5.4. Case 4: −(%25)

In Table 7, a full outcome of case 5 comparison between LQR and FLQR controllers is described to verify the system stability.

Figure 13. (a) The system response for 1st link of Robogymnast in Case 4 (T1); (b) The system response for central link of Robogymnast in Case 4 (T2); (c) The system response for link-3 of Robogymnast in Case 4 (T3).

Figure 13. (a) The system response for 1st link of Robogymnast in Case 4 (T1); (b) The system response for central link of Robogymnast in Case 4 (T2); (c) The system response for link-3 of Robogymnast in Case 4 (T3).

Table 7. Comparison performance of LQR and FLQR controllers in Case 4.

Symbol	Controller	${\mathit{O}}_{\mathit{s}\mathit{h}}\mathbf{\left(}\mathbf{pu}\mathbf{\right)}$	${\mathit{U}}_{\mathit{s}\mathit{h}}\mathbf{\left(}\mathbf{pu}\mathbf{\right)}$	${\mathit{T}}_{\mathit{r}}\mathbf{\left(}\mathbf{s}\mathbf{\right)}$	${\mathit{T}}_{\mathit{s}}\mathbf{\left(}\mathbf{s}\mathbf{\right)}$
${\mathsf{\theta }}_{\mathbf{1}}$	LQR	8.025	−5.679	0.4744	20.6922
	Fuzzy LQR	2.742	−5.712	0.5445	14.8923
${\mathsf{\theta }}_{\mathbf{2}}$	LQR	1	−1.326	0.1012	6.5537
	Fuzzy LQR	1	−1.437	0.0975	5.5485
${\mathsf{\theta }}_{\mathbf{3}}$	LQR	0.2546	−0.4	0.0681	4.4410
	Fuzzy LQR	0.2584	−0.4	0.0699	3.2399

Table 7. Comparison performance of LQR and FLQR controllers in Case 4.

Symbol	Controller	${\mathit{O}}_{\mathit{s}\mathit{h}}\mathbf{\left(}\mathbf{pu}\mathbf{\right)}$	${\mathit{U}}_{\mathit{s}\mathit{h}}\mathbf{\left(}\mathbf{pu}\mathbf{\right)}$	${\mathit{T}}_{\mathit{r}}\mathbf{\left(}\mathbf{s}\mathbf{\right)}$	${\mathit{T}}_{\mathit{s}}\mathbf{\left(}\mathbf{s}\mathbf{\right)}$
${\mathsf{\theta }}_{\mathbf{1}}$	LQR	8.025	−5.679	0.4744	20.6922
	Fuzzy LQR	2.742	−5.712	0.5445	14.8923
${\mathsf{\theta }}_{\mathbf{2}}$	LQR	1	−1.326	0.1012	6.5537
	Fuzzy LQR	1	−1.437	0.0975	5.5485
${\mathsf{\theta }}_{\mathbf{3}}$	LQR	0.2546	−0.4	0.0681	4.4410
	Fuzzy LQR	0.2584	−0.4	0.0699	3.2399

Figure 14. Case 4 comparison.

Figure 14. Case 4 comparison.

5.5. Case 5: −(%50)

Finally, in Table 8 a full result of case5, the LQR and FLQR controllers’ comparison is illustrated to validate the system stability.

Figure 15. (a) The system response for the first link of Robogymnast in Case 5 (T1); (b) The system response for the 2nd link of Robogymnast in Case 5 (T2); (c) The system response for the lower link of Robogymnast in Case 5 (T3).

Figure 15. (a) The system response for the first link of Robogymnast in Case 5 (T1); (b) The system response for the 2nd link of Robogymnast in Case 5 (T2); (c) The system response for the lower link of Robogymnast in Case 5 (T3).

Table 8. Comparison performance of LQR and FLQR controllers in Case 5.

Symbol	Controller	${\mathit{O}}_{\mathit{s}\mathit{h}}\mathbf{\left(}\mathbf{pu}\mathbf{\right)}$	${\mathit{U}}_{\mathit{s}\mathit{h}}\mathbf{\left(}\mathbf{pu}\mathbf{\right)}$	${\mathit{T}}_{\mathit{r}}\mathbf{\left(}\mathbf{s}\mathbf{\right)}$	${\mathit{T}}_{\mathit{s}}\mathbf{\left(}\mathbf{s}\mathbf{\right)}$
${\mathsf{\theta }}_{\mathbf{1}}$	LQR	8.025	−5.679	0.711	31.0403
	Fuzzy LQR	3.146	−5.706	0.7952	21.3793
${\mathsf{\theta }}_{\mathbf{2}}$	LQR	1	−1.3626	0.1520	9.8323
	Fuzzy LQR	1	−1.421	0.1483	7.8387
${\mathsf{\theta }}_{\mathbf{3}}$	LQR	0.2548	−0.4	0.1024	6.6633
	Fuzzy LQR	0.2604	−0.4	0.1060	4.8405

Table 8. Comparison performance of LQR and FLQR controllers in Case 5.

Symbol	Controller	${\mathit{O}}_{\mathit{s}\mathit{h}}\mathbf{\left(}\mathbf{pu}\mathbf{\right)}$	${\mathit{U}}_{\mathit{s}\mathit{h}}\mathbf{\left(}\mathbf{pu}\mathbf{\right)}$	${\mathit{T}}_{\mathit{r}}\mathbf{\left(}\mathbf{s}\mathbf{\right)}$	${\mathit{T}}_{\mathit{s}}\mathbf{\left(}\mathbf{s}\mathbf{\right)}$
${\mathsf{\theta }}_{\mathbf{1}}$	LQR	8.025	−5.679	0.711	31.0403
	Fuzzy LQR	3.146	−5.706	0.7952	21.3793
${\mathsf{\theta }}_{\mathbf{2}}$	LQR	1	−1.3626	0.1520	9.8323
	Fuzzy LQR	1	−1.421	0.1483	7.8387
${\mathsf{\theta }}_{\mathbf{3}}$	LQR	0.2548	−0.4	0.1024	6.6633
	Fuzzy LQR	0.2604	−0.4	0.1060	4.8405

Figure 16. Case 5 comparison.

Figure 16. Case 5 comparison.

5.6. Compression of ITAE

This section shows the integral time of absolute error for every case investigated, which are original, (±25%), and (±50) values, respectively, in both the LQR and FLQR controllers in all cases examined as mentioned above (Table 9).

Figure 17. ITAE comparison.

Figure 17. ITAE comparison.

Table 9. ITAE values.

	Case 1	Case 2	Case 3	Case 4	Case 5
LQR1	159.7	283.9	102.20	31.0403	70.98
FLQR1	21.29	38.16	26.72	87.19	8.971
LQR2	0.322	0.5741	0.2136	1.29	0.148
FLQR2	0.313	0.5309	0.2066	1.257	0.143
LQR3	0.022	0.0395	0.0138	0.088	0.009
FLQR3	0.021	0.0385	0.0142	0.086	0.009

Table 9. ITAE values.

	Case 1	Case 2	Case 3	Case 4	Case 5
LQR1	159.7	283.9	102.20	31.0403	70.98
FLQR1	21.29	38.16	26.72	87.19	8.971
LQR2	0.322	0.5741	0.2136	1.29	0.148
FLQR2	0.313	0.5309	0.2066	1.257	0.143
LQR3	0.022	0.0395	0.0138	0.088	0.009
FLQR3	0.021	0.0385	0.0142	0.086	0.009

5.7. Comparison of LQR and FLQR in All Cases

Table 10 shows a full comparision between LQR and FLQR in all cases implemented where (±25%) and (±50%) added to the system to test their stabilty and robostance. As well as Figure 18 illustrates the comparions between the system outcomes for 5 different cases in terms of Over and undershoot, rising and settling time in both controllers examined.

Table 10. Comparison of LQR and FLQR in all cases.

Case	Symbol	Controller	${\mathit{O}}_{\mathit{s}\mathit{h}}\mathbf{\left(}\mathbf{pu}\mathbf{\right)}$	${\mathit{U}}_{\mathit{s}\mathit{h}}\mathbf{\left(}\mathbf{pu}\mathbf{\right)}$	${\mathit{T}}_{\mathit{r}}\mathbf{\left(}\mathbf{s}\mathbf{\right)}$	${\mathit{T}}_{\mathit{s}}\mathbf{\left(}\mathbf{s}\mathbf{\right)}$
Original value	${\mathsf{\theta }}_{\mathbf{1}}$	LQR	8.02	−5.69	0.3557	15.5196
		Fuzzy LQR	2.88	−5.71	0.4074	11.1823
	${\mathsf{\theta }}_{\mathbf{2}}$	LQR	1.03	−1.32	0.0758	4.9142
		Fuzzy LQR	0.42	−1.44	0.0730	4.1694
	${\mathsf{\theta }}_{\mathbf{3}}$	LQR	0.25	−0.41	0.0509	3.3310
		Fuzzy LQR	0.25	−0.40	0.0523	2.4428
Case 2	${\mathsf{\theta }}_{\mathbf{1}}$	LQR	8.026	−5.677	0.2844	12.4151
		Fuzzy LQR	3.122	−5.716	0.3249	8.9536
	${\mathsf{\theta }}_{\mathbf{2}}$	LQR	1	−1.326	0.0605	3.9305
		Fuzzy LQR	1	−1.445	0.0584	3.3397
	${\mathsf{\theta }}_{\mathbf{3}}$	LQR	0.2537	−0.4	0.0406	2.6648
		Fuzzy-LQR	0.2562	−0.4	0.0418	1.9637
Case 3	${\mathsf{\theta }}_{\mathbf{1}}$	LQR	8.025	−5.679	0.2369	10.3460
		Fuzzy LQR	3.013	−5.711	0.2709	7.4641
	${\mathsf{\theta }}_{\mathbf{2}}$	LQR	1	−1.326	0.0504	3.2747
		Fuzzy LQR	1	−1.433	0.0486	2.7863
	${\mathsf{\theta }}_{\mathbf{3}}$	LQR	0.2542	−0.4	0.0337	2.2205
		Fuzzy LQR	0.2582	−0.4	0.0348	1.6402
Case 4	${\mathsf{\theta }}_{\mathbf{1}}$	LQR	8.025	−5.679	0.4744	20.6922
		Fuzzy LQR	2.742	−5.712	0.5445	14.8923
	${\mathsf{\theta }}_{\mathbf{2}}$	LQR	1	−1.326	0.1012	6.5537
		Fuzzy LQR	1	−1.437	0.0975	5.5485
	${\mathsf{\theta }}_{\mathbf{3}}$	LQR	0.2546	−0.4	0.0681	4.4410
		Fuzzy LQR	0.2584	−0.4	0.0699	3.2399
Case 5	${\mathsf{\theta }}_{\mathbf{1}}$	LQR	8.025	−5.679	0.711	31.0403
		Fuzzy LQR	3.146	−5.706	0.7952	21.3793
	${\mathsf{\theta }}_{\mathbf{2}}$	LQR	1	−1.3626	0.1520	9.8323
		Fuzzy LQR	1	−1.421	0.1483	7.8387
	${\mathsf{\theta }}_{\mathbf{3}}$	LQR	0.2548	−0.4	0.1024	6.6633
		Fuzzy LQR	0.2604	−0.4	0.1060	4.8405

Table 10. Comparison of LQR and FLQR in all cases.

Case	Symbol	Controller	${\mathit{O}}_{\mathit{s}\mathit{h}}\mathbf{\left(}\mathbf{pu}\mathbf{\right)}$	${\mathit{U}}_{\mathit{s}\mathit{h}}\mathbf{\left(}\mathbf{pu}\mathbf{\right)}$	${\mathit{T}}_{\mathit{r}}\mathbf{\left(}\mathbf{s}\mathbf{\right)}$	${\mathit{T}}_{\mathit{s}}\mathbf{\left(}\mathbf{s}\mathbf{\right)}$
Original value	${\mathsf{\theta }}_{\mathbf{1}}$	LQR	8.02	−5.69	0.3557	15.5196
		Fuzzy LQR	2.88	−5.71	0.4074	11.1823
	${\mathsf{\theta }}_{\mathbf{2}}$	LQR	1.03	−1.32	0.0758	4.9142
		Fuzzy LQR	0.42	−1.44	0.0730	4.1694
	${\mathsf{\theta }}_{\mathbf{3}}$	LQR	0.25	−0.41	0.0509	3.3310
		Fuzzy LQR	0.25	−0.40	0.0523	2.4428
Case 2	${\mathsf{\theta }}_{\mathbf{1}}$	LQR	8.026	−5.677	0.2844	12.4151
		Fuzzy LQR	3.122	−5.716	0.3249	8.9536
	${\mathsf{\theta }}_{\mathbf{2}}$	LQR	1	−1.326	0.0605	3.9305
		Fuzzy LQR	1	−1.445	0.0584	3.3397
	${\mathsf{\theta }}_{\mathbf{3}}$	LQR	0.2537	−0.4	0.0406	2.6648
		Fuzzy-LQR	0.2562	−0.4	0.0418	1.9637
Case 3	${\mathsf{\theta }}_{\mathbf{1}}$	LQR	8.025	−5.679	0.2369	10.3460
		Fuzzy LQR	3.013	−5.711	0.2709	7.4641
	${\mathsf{\theta }}_{\mathbf{2}}$	LQR	1	−1.326	0.0504	3.2747
		Fuzzy LQR	1	−1.433	0.0486	2.7863
	${\mathsf{\theta }}_{\mathbf{3}}$	LQR	0.2542	−0.4	0.0337	2.2205
		Fuzzy LQR	0.2582	−0.4	0.0348	1.6402
Case 4	${\mathsf{\theta }}_{\mathbf{1}}$	LQR	8.025	−5.679	0.4744	20.6922
		Fuzzy LQR	2.742	−5.712	0.5445	14.8923
	${\mathsf{\theta }}_{\mathbf{2}}$	LQR	1	−1.326	0.1012	6.5537
		Fuzzy LQR	1	−1.437	0.0975	5.5485
	${\mathsf{\theta }}_{\mathbf{3}}$	LQR	0.2546	−0.4	0.0681	4.4410
		Fuzzy LQR	0.2584	−0.4	0.0699	3.2399
Case 5	${\mathsf{\theta }}_{\mathbf{1}}$	LQR	8.025	−5.679	0.711	31.0403
		Fuzzy LQR	3.146	−5.706	0.7952	21.3793
	${\mathsf{\theta }}_{\mathbf{2}}$	LQR	1	−1.3626	0.1520	9.8323
		Fuzzy LQR	1	−1.421	0.1483	7.8387
	${\mathsf{\theta }}_{\mathbf{3}}$	LQR	0.2548	−0.4	0.1024	6.6633
		Fuzzy LQR	0.2604	−0.4	0.1060	4.8405

Figure 18. LQR and FLQR comparison.

Figure 18. LQR and FLQR comparison.

6. Discussion

The proposed FLQR controller, as a combined LQR and fuzzy logic control method, performed well for the three-link Robogymnast robotics system, with the examination of the system’s robustness showing that it outperformed the conventional controller across all variables, including time to settle and under- and over-shoot. A more detailed summary of the findings for robustness is provided here.

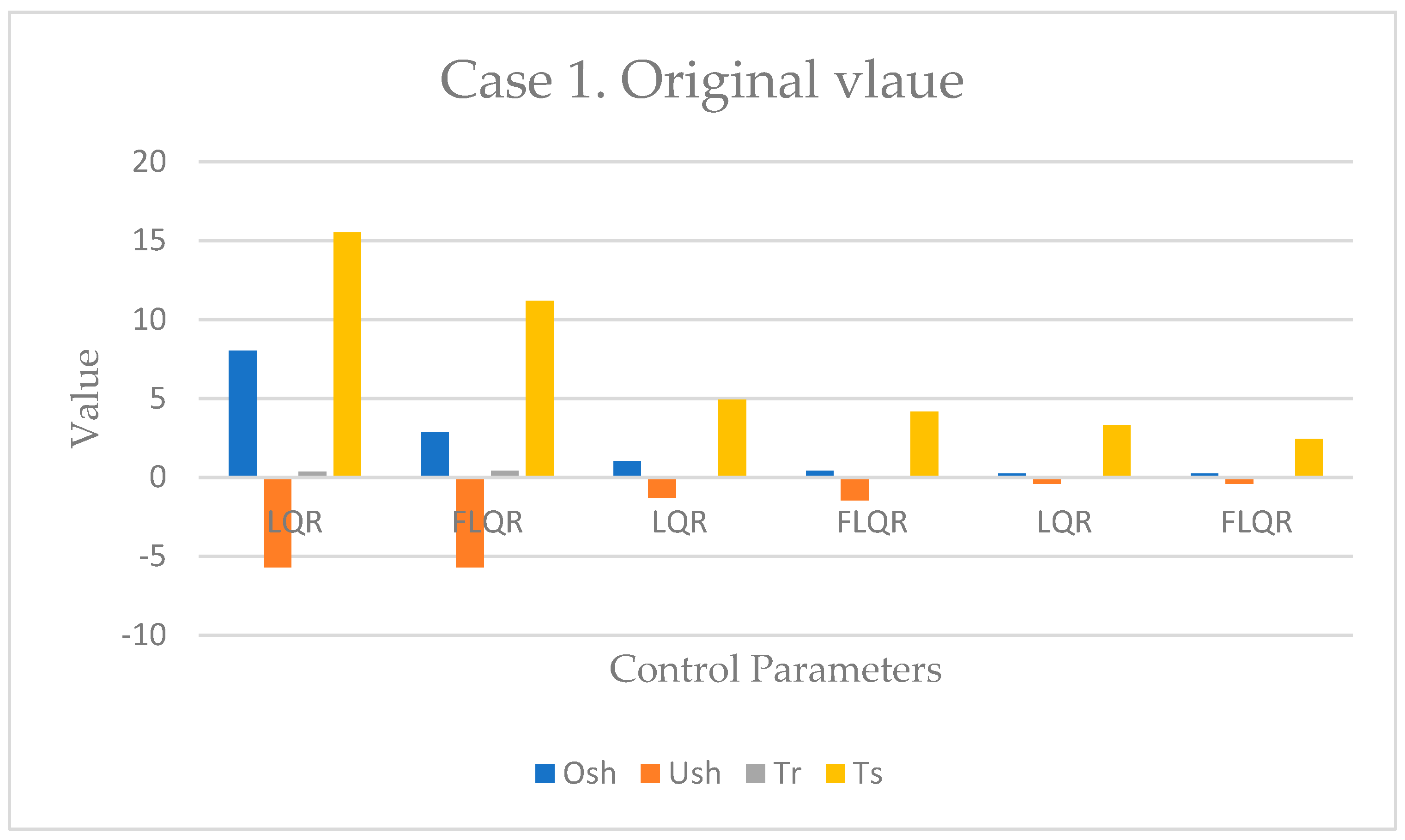
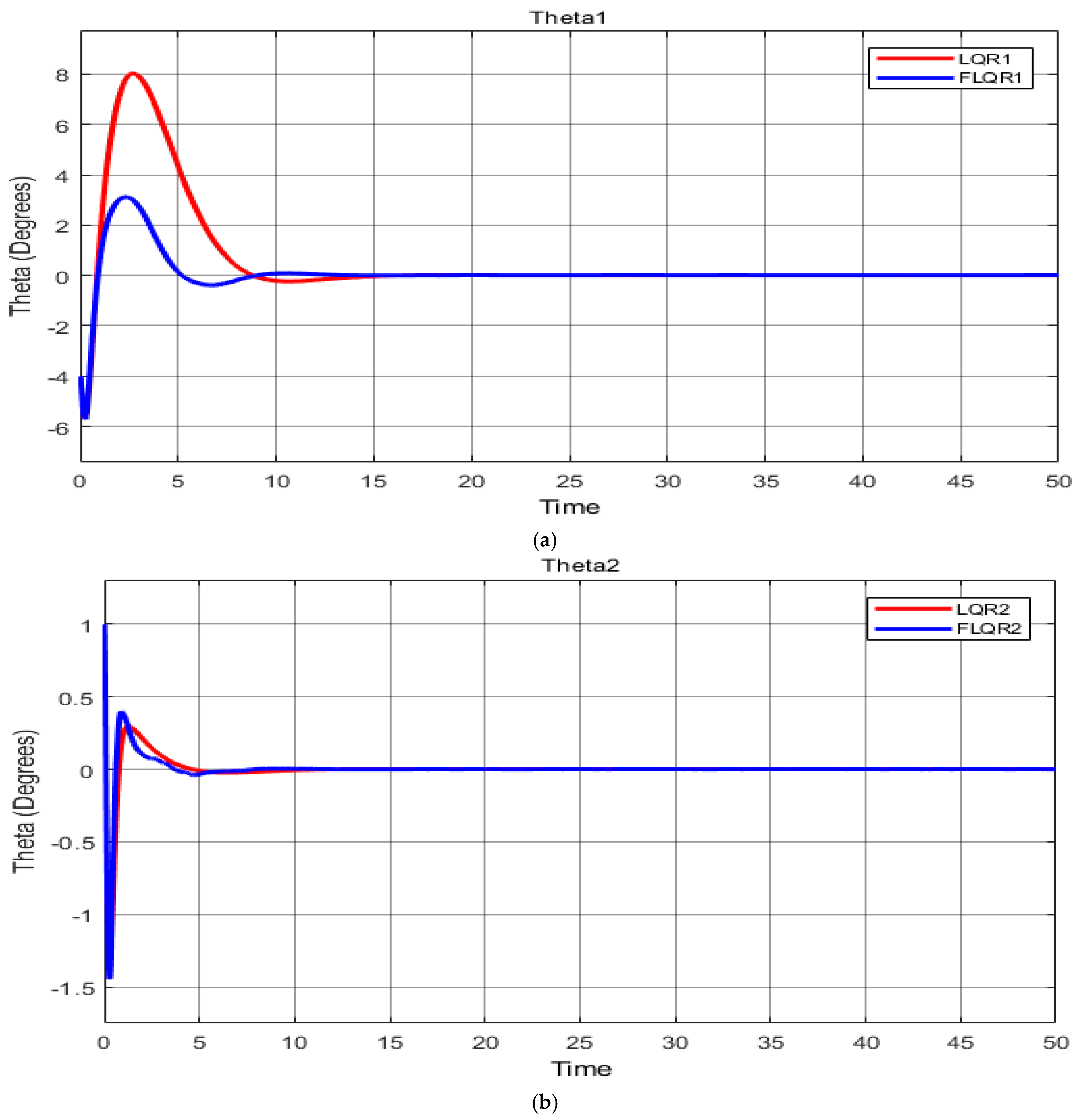
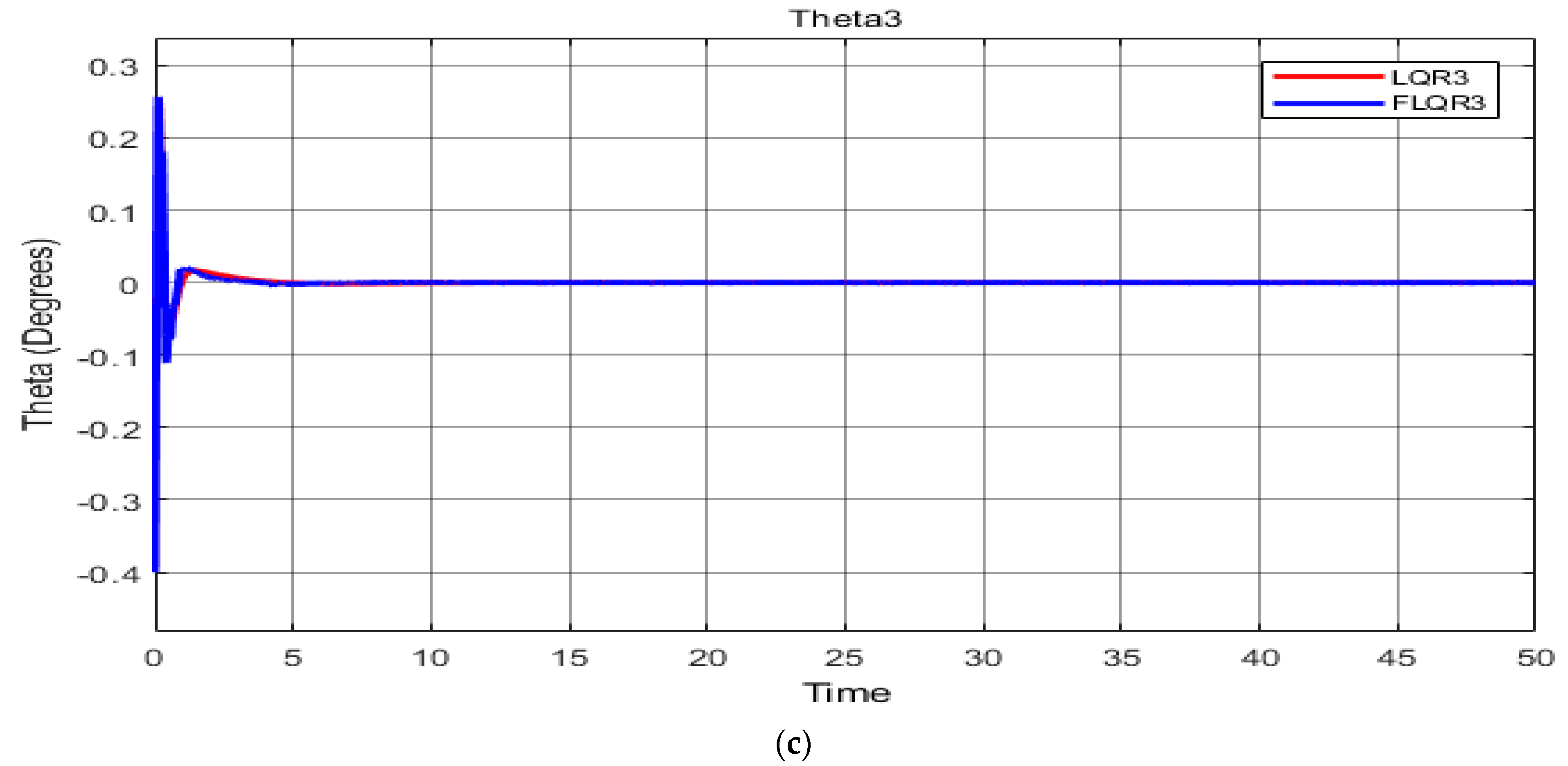
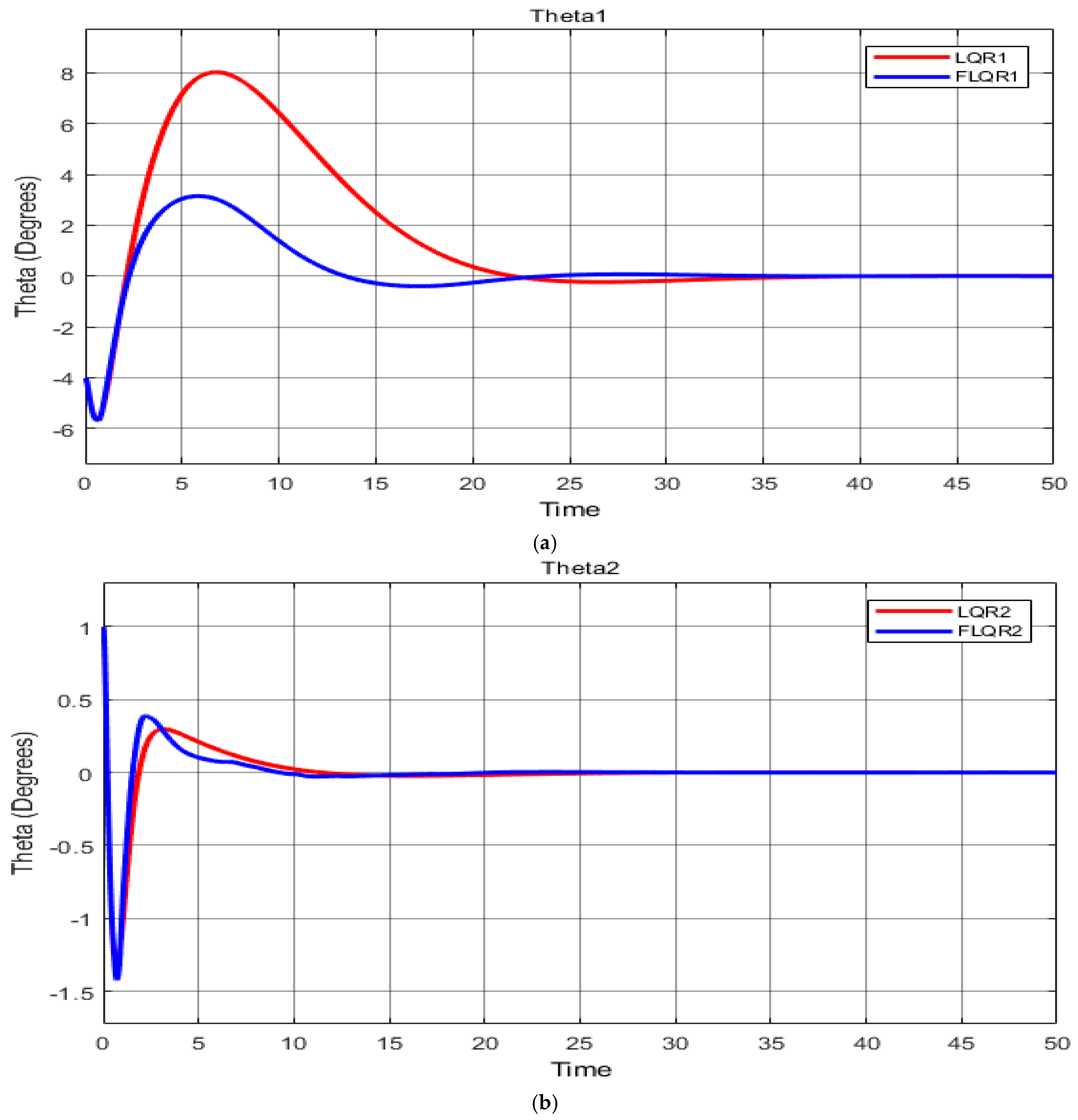
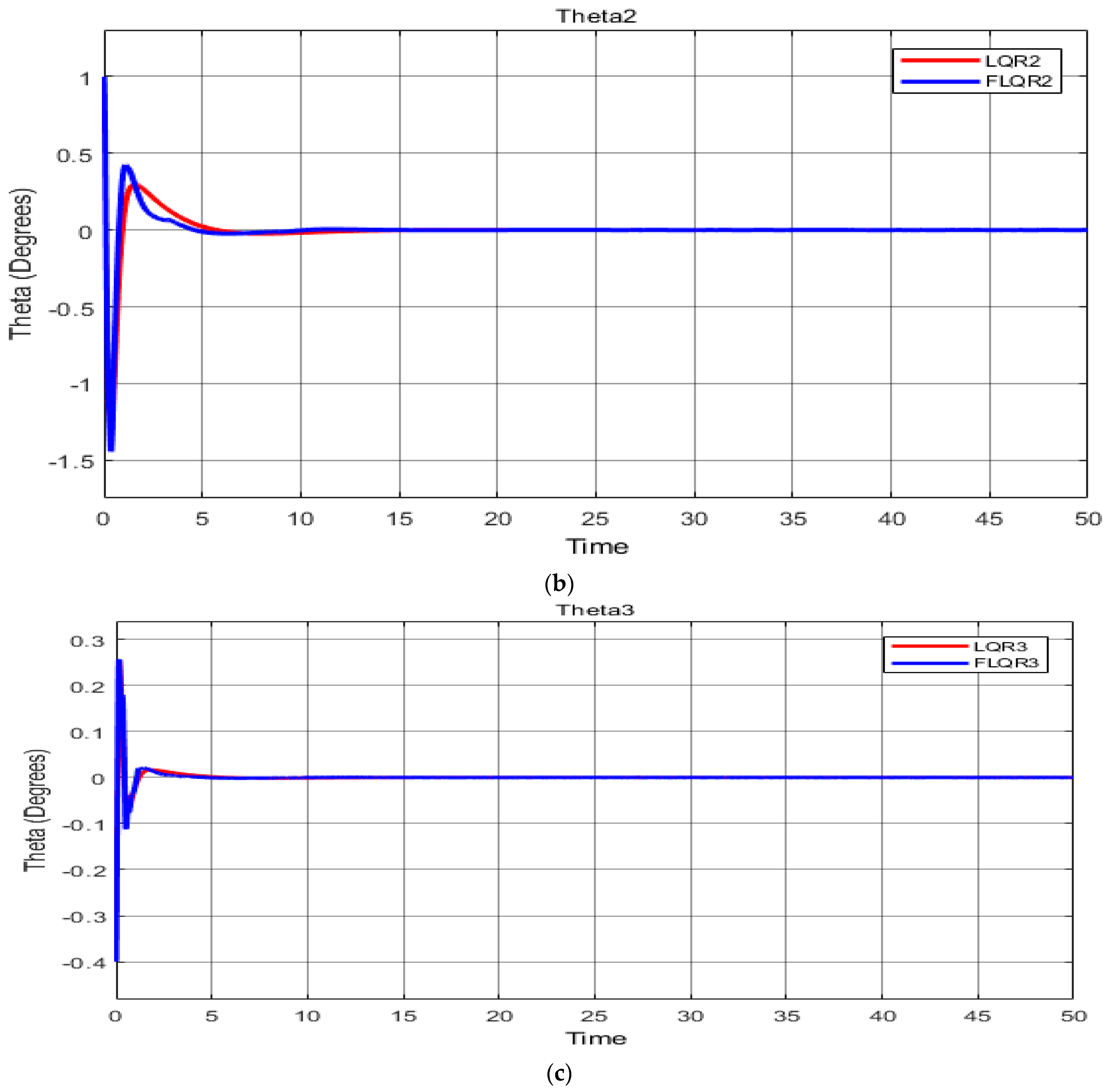
For the first scenario, the measured system response is shown in Figure 7a–c and Table 8, giving baseline systems values with no alterations. Comparing the LQR with the FLQR controller, the latter shows decreased overshoot (Osh) and undershoot (Ush), with respective overshoot values of 8.02 and 2.88. In addition, while the LQR controller’s rise time was faster (c. 0.35 s), the FLQR showed a faster settling time (11.18 s).

For the second case, in which the mathematical model values are increased by 25%, Table 5 shows the performance comparison between the two controllers examined for robustness. For the LQR controller, undershoot and overshoot did not differ significantly, but there was a difference of 0.07 s in rise time, and the settling time dropped to 12.41 s from 15.51 s. In contrast, the findings for FLQR demonstrate an increase in overshoot of approximately 0.242 pu, with no alteration in undershoot, and reductions in settling and rising times for the controllers. In addition, for LQR, there was a slight decrease in second angle ${\mathsf{\theta }}_2$ overshoot, while undershoot did not change significantly and the times were reduced for each parameter. For FLQR, decreases were found across each parameter. Finally, for ${\mathsf{\theta }}_3$, no change was seen in under- or overshoot for the LQR controller, although reductions occurred in the rising and settling times. For FLQR, time decreases were also found, while the values of the remaining parameters were unchanged from the initial scenario.

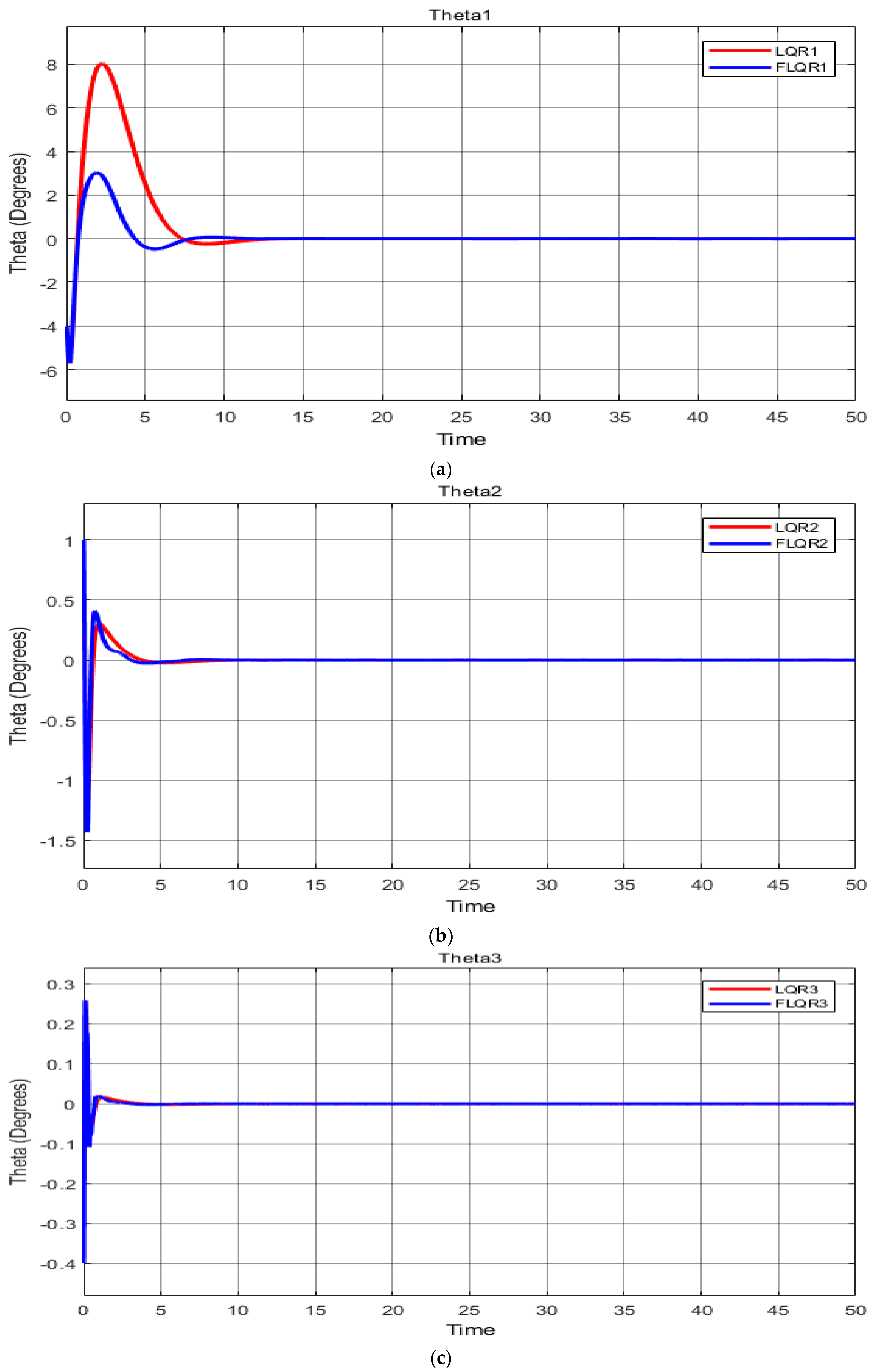
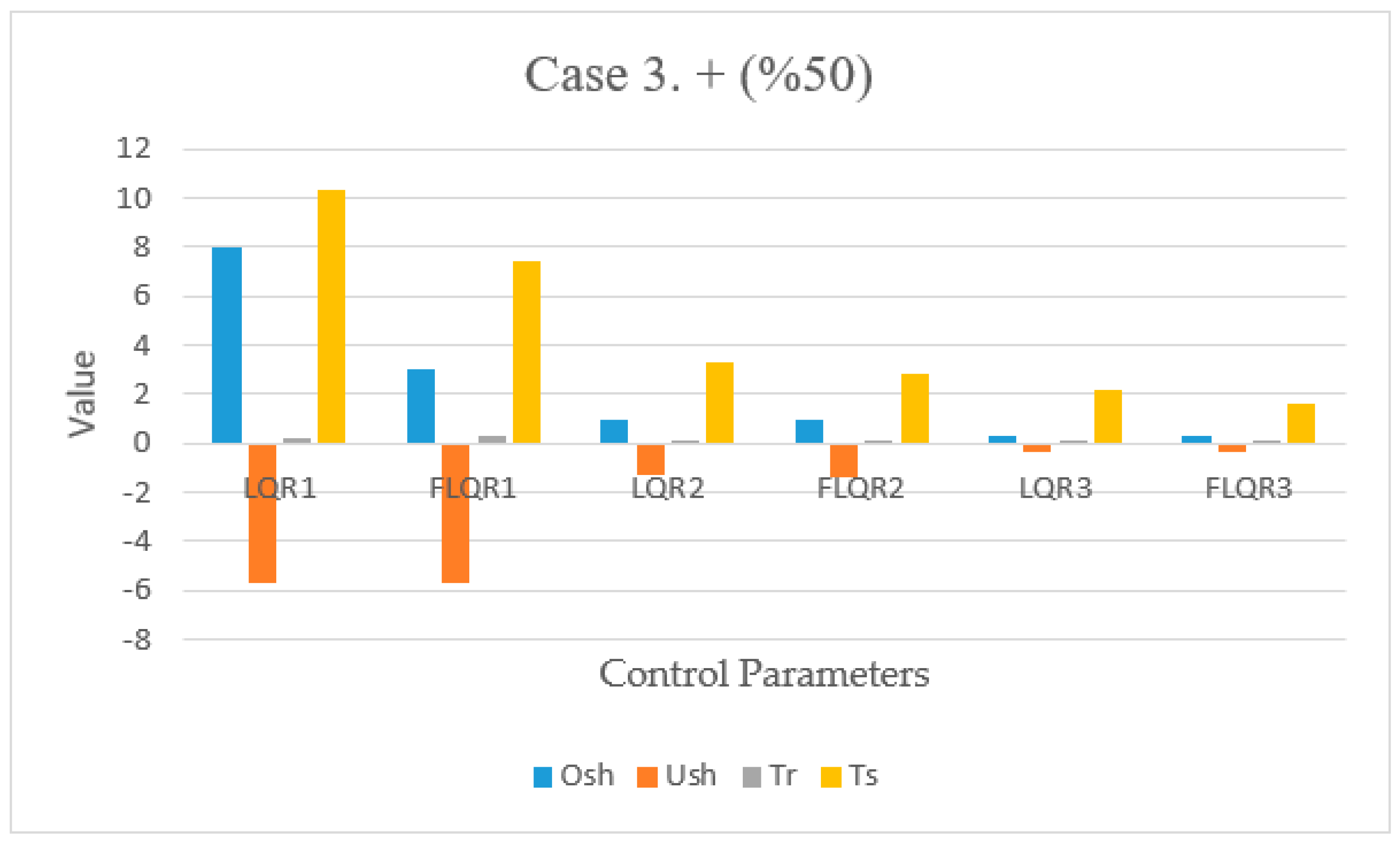
In the third scenario, values were increased by 50% over the system’s baseline. While overshoot remained unchanged for the LQR, undershoot altered only slightly, from −5.69 at baseline to −5.67, but both the rising and settling times were quicker, altering from 0.35 to 0.24 s for rising and a slightly change of 5 s for the settling time. For link ${\mathsf{\theta }}_2$ with the LQR controller, there was no change in under- or overshoot, but a reduction in the two time variables. Meanwhile, for the FLQR controller, times were also reduced, while no change was seen for under- and overshoot. For the third link ${\mathsf{\theta }}_3$, again, under- and overshoot remained the same, while smaller values were found for the time variables.

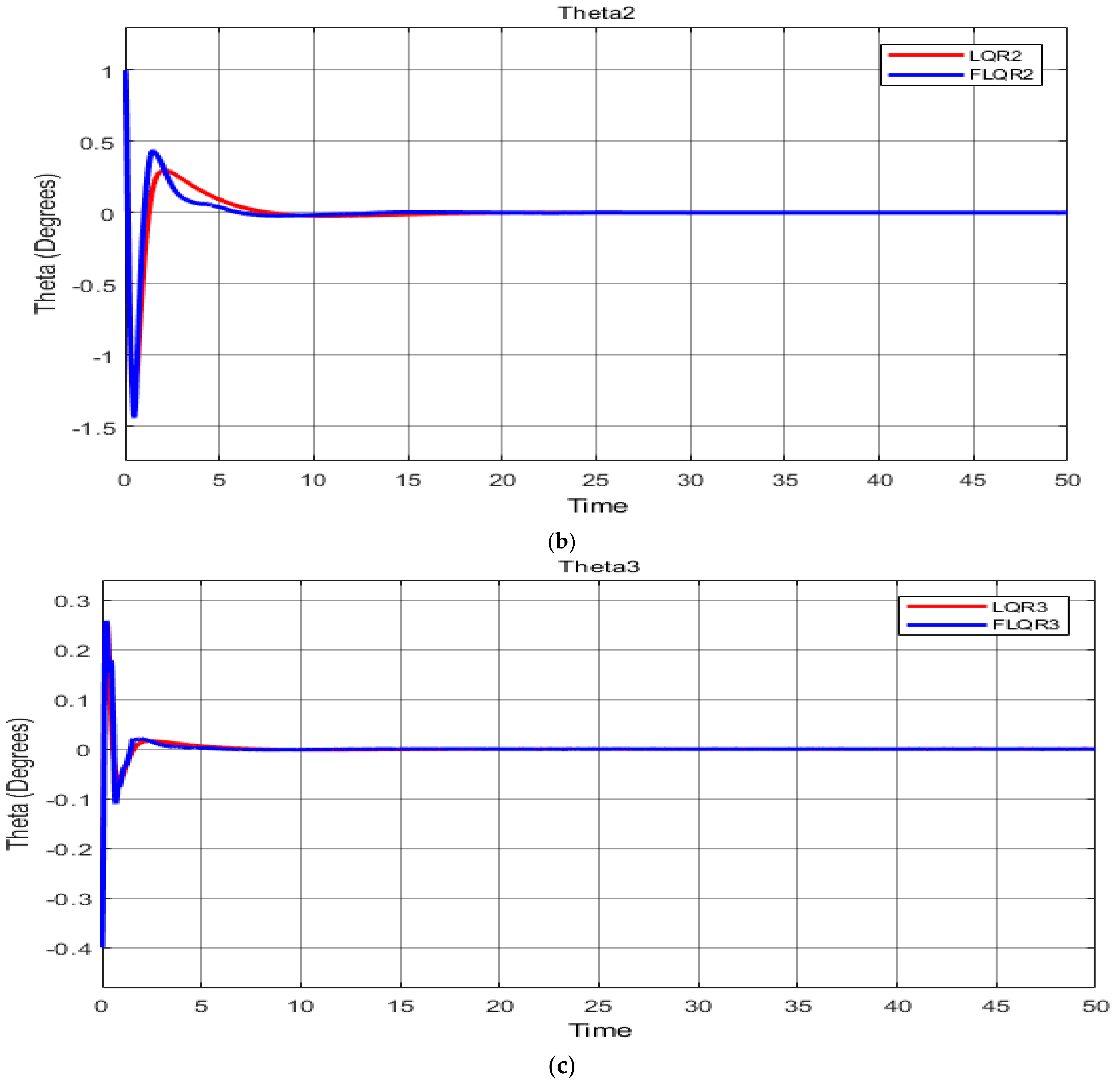
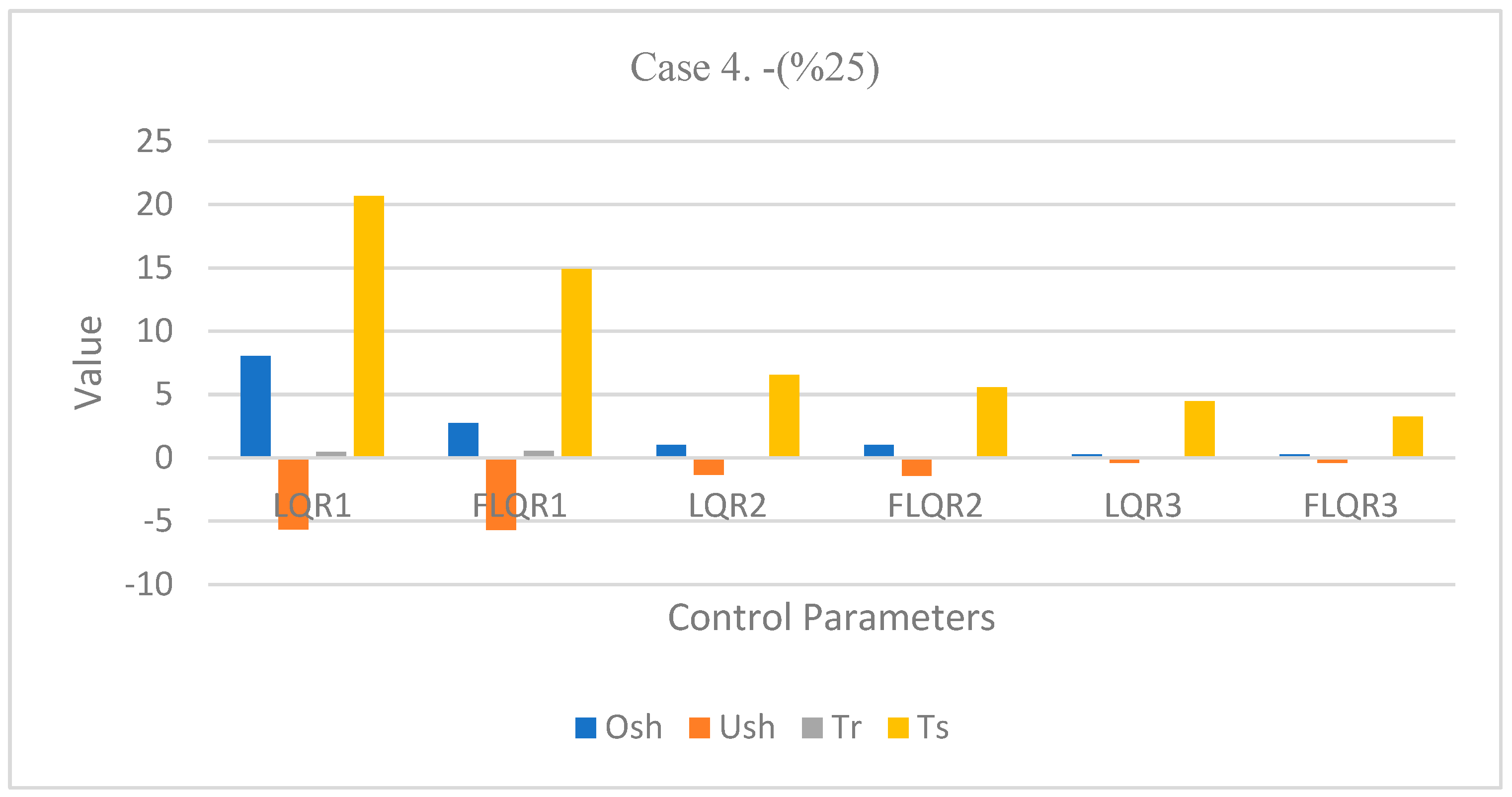
For the fourth scenario, system variables were reduced by 25%, as shown in Table 7. In the first link, for the LQR, a one-second increase in rising time was recorded for the LQR, and settling time was observed to change by roughly 5 s against the original case, from 15.51 to 20.69 s. By contrast, the FLQR controller produced lower values for each time parameter, and only very small differences for the remaining variables. Moreover, for ${\mathsf{\theta }}_2$, there was little change in under- or overshoot, with reductions in rising and settling times. Finally, for ${\mathsf{\theta }}_3$, a small increase in rising time was seen compared with the original scenario, from 0.052 to 0.0699 s. Settling time was altered by approximately 1 s, with no changes in under- or overshoot.

The final scenario reduced the system parameters by 50% and, again, stability and response were tested to indicate robustness. It is notable here that for the LQR controller, each of the links displayed small increases in rising and settling time differences, with major alterations in overshoot and undershoot. In contrast, FLQR performed markedly better here than the conventional controller. Settling times across each link were 21.37 s, 7.83 s and 4.83 s, with higher rising times for each of the links. Under- and overshoot were also greater across each link. Table 10 offers a comparison of all the findings in all cases and scenarios between each link.

7. Conclusions and Future Work

This paper has presented modelling and simulation for the application of an LQR/fuzzy logic controller to stabilise a robotic gymnast system in MATLAB/Simulink. In this study, an FLQR was developed and then compared against an established LQR control approach for the Robogymnast. Mathematical modelling was performed for the starting values of variables within the pendulum-based system, and then a comprehensive model for the simulation of a robotic manipulation drive with the FLQR controller was developed. The primary variables were established, with calculations for overshoot as well as settle and rise times. An assessment was performed for the dynamic performance of the system. Calculations for stability and robustness were performed for each of the FLQR and LQR controllers, with comparisons across each scenario, in which variables were increased or decreased by several values. The results of the comparison show that the proposed FLQR controller performs better with the Robogymnast than does the established LQR controller.

To conclude, it is possible to declare that this work involved the investigation of the modulation of a triple-link robotics mechanism for the swing-up position, and the selected controller can be further extended to implement optimized algorithms for additional studies. In conclusion, this study examining the control of swing-up in three-link robotic systems suggests that the controller proposed here could be studied further and implemented in different optimised algorithms.