A Rule-Based Method to Locate the Bounds of Neural Networks
Abstract
:1. Introduction
2. Method Description
2.1. Locating the Best Rules
- Apply to S, yielding .
- Apply to , yielding .
2.1.1. Initialization Step
- SetK as the number of rules.
- Set as the initial bounding box for the parameters of the neural network. D is considered as a positive number with .
- Set as the total number of chromosomes.
- Set as the number of samples in the fitness evaluation.
- Set as the selection rate, where .
- Set as the mutation rate, where .
- Set as the current generation number.
- Set as the maximum number of generations allowed.
- Initialize randomly the chromosomes , as sets of Equation (10).
2.1.2. Termination Check Step
- Set.
- If, terminate.
2.1.3. Genetic Operations Step
- For every chromosome , calculate the corresponding fitness value using the algorithm in Section 2.2.
- Apply the selection operator. Initially, the chromosomes are sorted according to their fitness values. The sorting utilizes the function of Equation (11) to compare fitness values. The best are copied to the next generation while the rest of them are substituted by offspring created through the crossover procedure. The mating parents for the crossover procedure are selected using the well-known technique of tournament selection.
- Apply the crossover operator: For every pair of selected parents two children are produced using the uniform crossover procedure described in Section 2.3.
- Apply the mutation operator using the algorithm in Section 2.4.
- Goto Termination Check Step.
2.2. Fitness Evaluation for the Rule Genetic Algorithm
- Set.
- Set.
- Apply the rule set g to the original bounding box S. The outcome of this application is the new bounding box .
- Fordo
- (a)
- Produce a random sample .
- (b)
- Calculate the training error using Equation (1).
- (c)
- If then .
- (d)
- If then .
- EndFor
- Return the interval as the fitness of chromosome
2.3. Crossover for the Rule Genetic Algorithm
- Fordo
- (a)
- Let be the i-th item of the chromosome z.
- (b)
- Let be the i-th item of the chromosome w.
- (c)
- Produce a random number .
- (d)
- Ifthen
- Set.
- Set.
- (e)
- Else
- Set.
- Set.
- (f)
- Endif
- EndFor
2.4. Mutation for the Rule Genetic Algorithm
- Fordo
- (a)
- Let be the i-th chromosome of the population.
- (b)
- Fordo
- Let.
- Take1 a random number.
- Ifthen alter randomly with probability 50% the or the part of .
- (c)
- EndFor
- EndFor
2.5. Second Phase
2.5.1. Initialization Step
- Set as the total number of chromosomes.
- Set as the selection rate, where .
- Set as the mutation rate, where .
- Set as the current generation number.
- Set as the maximum number of generations allowed.
- Initialize randomly the chromosomes , inside the bounding box .
2.5.2. Termination Check Step
- Set.
- Ifgoto Local Search Step.
2.5.3. Genetic Operations Step
- Calculate the fitness value of every chromosome.
- (a)
- ForDo
- Set using Equation (1).
- (b)
- EndFor
- Apply the crossover operator. In this phase, the best chromosomes are transferred intact to the next generation. The rest of the chromosomes are substituted by offspring created through crossover. The selection of two parents and for crossover is performed using tournament selection. Having selected the parents, the offspring and are formed using the following:where are random numbers in [43].
- Apply the mutation operator. The mutation scheme is the same as in the work of Kaelo and Ali [50]:
- (a)
- Fordo
- Fordo
- Let be a random number.
- If alter the element using the following:where t is a random number that takes either the value 0 or 1 and is calculated as:where is a random number and z is a user-defined parameter.
- EndFor
- (b)
- EndFor
- Goto Termination check step.
2.5.4. Local Search Step
- Set as the best chromosome of the population.
- Apply a local search procedure . The local search procedure used here is a BFGS method of Powell [51].
3. Experiments
- UCI dataset repository, https://archive.ics.uci.edu/ml/index.php (accessed on 23 May 2022.)
- Keel repository, https://sci2s.ugr.es/keel/datasets.php (accessed on 23 May 2022) [52].
3.1. Experimental Datasets
- Appendicitis, a medical dataset, proposed in [53].
- Australian dataset [54], which is related to credit card applications.
- Balance dataset [55], which is used to predict psychological states.
- Bands dataset, a printing problem used to identify cylinder bands.
- Dermatology dataset [58], which is used for the differential diagnosis of erythemato-squamous diseases.
- Hayes Roth dataset. This dataset [59] contains 5 numeric-valued attributes and 132 patterns.
- Heart dataset [60], used to detect heart disease.
- HouseVotes dataset [61], which is about votes for U.S. House of Representatives Congressmen.
- Liverdisorder dataset [64], used for detecting liver disorders in people using blood analysis.
- Mammographic dataset [65]. This dataset be used to identify the severity (benign or malignant) of a mammographic mass lesion from BI-RADS attributes and the patient’s age. It contains 830 patterns of 5 features each.
- PageBlocks dataset [66], used to detect the page layout of a document.
- Parkinsons dataset. This dataset is composed of a range of biomedical voice measurements from 31 people, 23 with Parkinson’s disease (PD) [67].
- Pima dataset [68], used to detect the presence of diabetes.
- Popfailures dataset [69], which is related to climate model simulation crashes of simulation crashes.
- Regions2 dataset. It is created from liver biopsy images of patients with hepatitis C [70]. From each region in the acquired images, 18 shape-based and color-based features were extracted, while it was also annotated by medical experts. The resulting dataset includes 600 samples belonging to 6 classes.
- Saheart dataset [71], used to detect heart disease.
- Segment dataset [72]. This database contains patterns from a database of 7 outdoor images (classes).
- Wdbc dataset [73], which contains data for breast tumors.
- Eeg datasets. As a real-world example, consider an EEG dataset described in [9] is used here. The dataset consists of five sets (denoted as Z, O, N, F and S) each containing 100 single-channel EEG segments each having 23.6 sec duration. With different combinations of these sets, the produced datasets are Z_F_S, ZO_NF_S and ZONF_S.
- ZOO dataset [76], where the task is to classify animals in seven predefined classes.
- ABALONE dataset [77]. This dataset can be used to obtain a model to predict the age of abalone from physical measurements.
- AIRFOIL dataset, which is used by NASA for a series of aerodynamic and acoustic tests [78].
- BASEBALL dataset, a dataset to predict the salary of baseball players.
- BK dataset. This dataset comes from smoothing methods in statistics [79] and is used to estimate the points scored per minute in a basketball game.
- BL dataset: This dataset can be downloaded from StatLib. It contains data from an experiment on the effects of machine adjustments on the time to count bolts.
- CONCRETE dataset. This dataset is taken from civil engineering [80].
- DEE dataset, used to predict the daily average price of electricity energy in Spain.
- DIABETES dataset, a medical dataset.
- HOUSING dataset. This dataset was taken from the StatLib library which is maintained at Carnegie Mellon University and it is described in [81].
- FA dataset, which contains percentage of body fat and ten body circumference measurements. The goal is to fit body fat to the other measurements.
- MB dataset. This dataset is available from smoothing methods in statistics [79] and it includes 61 patterns.
- MORTGAGE dataset, which contains the economic data information of the U.S.
- PY dataset (pyrimidines problem). The source of this dataset is the URL https://www.dcc.fc.up.pt/~ltorgo/Regression/DataSets.html (accessed on 23 May 2022) and it is a problem of 27 attributes and 74 patterns. The task consists of learning quantitative structure activity relationships (QSARs) and is provided by [82].
- QUAKE dataset. The objective here is to approximate the strength of an earthquake.
- TREASURY dataset, which contains economic data information of the U.S. from 1 April 1980 to 2 April 2000 on a weekly basis.
- WANKARA dataset, which contains weather information.
3.2. Experimental Results
- A genetic algorithm with the same parameters that are shown in Table 1. In addition, after the termination of the genetic algorithm, the local search procedure of BFGS was applied to the best chromosome of the population, in order to enhance the quality of the solution. The column GENETIC in the experimental tables denotes the results from the application of this method.
- The Adam stochastic optimization method [83] as implemented in OptimLib, freely available from https://github.com/kthohr/optim (accessed on 23 May 2022). The results for this method are listed in the column ADAM in the relevant tables.
- The NEAT method (neuroevolution of augmenting topologies) [85] as implemented in the EvolutionNet package which is freely available from https://github.com/BiagioFesta/EvolutionNet (accessed on 23 May 2022). The maximum number of generations was the same as in the case of the genetic algorithm.
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Bishop, C. Neural Networks for Pattern Recognition; Oxford University Press: Oxford, UK, 1995. [Google Scholar]
- Cybenko, G. Approximation by superpositions of a sigmoidal function. Math. Control Signals Syst. 1989, 2, 303–314. [Google Scholar] [CrossRef]
- Baldi, P.; Cranmer, K.; Faucett, T.; Sadowski, P.; Whiteson, D. Parameterized neural networks for high-energy physics. Eur. Phys. J. C 2016, 76, 235. [Google Scholar] [CrossRef]
- Valdas, J.J.; Bonham-Carter, G. Time dependent neural network models for detecting changes of state in complex processes: Applications in earth sciences and astronomy. Neural Netw. 2006, 19, 196–207. [Google Scholar] [CrossRef]
- Carleo, G.; Troyer, M. Solving the quantum many-body problem with artificial neural networks. Science 2017, 355, 602–606. [Google Scholar] [CrossRef]
- Shirvany, Y.; Hayati, M.; Moradian, R. Multilayer perceptron neural networks with novel unsupervised training method for numerical solution of the partial differential equations. Appl. Soft Comput. 2009, 9, 20–29. [Google Scholar] [CrossRef]
- Malek, A.; Beidokhti, R.S. Numerical solution for high order differential equations using a hybrid neural network—Optimization method. Appl. Math. Comput. 2006, 183, 260–271. [Google Scholar] [CrossRef]
- Topuz, A. Predicting moisture content of agricultural products using artificial neural networks. Adv. Eng. 2010, 41, 464–470. [Google Scholar] [CrossRef]
- Escamilla-García, A.; Soto-Zarazúa, G.M.; Toledano-Ayala, M.; Rivas-Araiza, E.; Gastélum-Barrios, A. Applications of Artificial Neural Networks in Greenhouse Technology and Overview for Smart Agriculture Development. Appl. Sci. 2020, 10, 3835. [Google Scholar] [CrossRef]
- Shen, L.; Wu, J.; Yang, W. Multiscale Quantum Mechanics/Molecular Mechanics Simulations with Neural Networks. J. Chem. Theory Comput. 2016, 12, 4934–4946. [Google Scholar] [CrossRef]
- Manzhos, S.; Dawes, R.; Carrington, T. Neural network-based approaches for building high dimensional and quantum dynamics-friendly potential energy surfaces. Int. J. Quantum Chem. 2015, 115, 1012–1020. [Google Scholar] [CrossRef]
- Wei, J.N.; Duvenaud, D.; Aspuru-Guzik, A. Neural Networks for the Prediction of Organic Chemistry Reactions. ACS Cent. Sci. 2016, 2, 725–732. [Google Scholar] [CrossRef]
- Falat, L.; Pancikova, L. Quantitative Modelling in Economics with Advanced Artificial Neural Networks. Procedia Econ. Financ. 2015, 34, 194–201. [Google Scholar] [CrossRef]
- Namazi, M.; Shokrolahi, A.; Maharluie, M.S. Detecting and ranking cash flow risk factors via artificial neural networks technique. J. Bus. Res. 2016, 69, 1801–1806. [Google Scholar] [CrossRef]
- Tkacz, G. Neural network forecasting of Canadian GDP growth. Int. J. Forecast. 2001, 17, 57–69. [Google Scholar] [CrossRef]
- Baskin, I.I.; Winkler, D.; Tetko, I.V. A renaissance of neural networks in drug discovery. Expert Opin. Drug Discov. 2016, 11, 785–795. [Google Scholar] [CrossRef]
- Bartzatt, R. Prediction of Novel Anti-Ebola Virus Compounds Utilizing Artificial Neural Network (ANN). Chem. Fac. 2018, 49, 16–34. [Google Scholar]
- Tsoulos, I.G.; Gavrilis, D.; Glavas, E. Neural network construction and training using grammatical evolution. Neurocomputing 2008, 72, 269–277. [Google Scholar] [CrossRef]
- Rumelhart, D.E.; Hinton, G.E.; Williams, R.J. Learning representations by back-propagating errors. Nature 1986, 323, 533–536. [Google Scholar] [CrossRef]
- Chen, T.; Zhong, S. Privacy-Preserving Backpropagation Neural Network Learning. IEEE Trans. Neural Netw. 2009, 20, 1554–1564. [Google Scholar] [CrossRef]
- Riedmiller, M.; Braun, H. A Direct Adaptive Method for Faster Backpropagation Learning: The RPROP algorithm. In Proceedings of the IEEE International Conference on Neural Networks, San Francisco, CA, USA, 28 March–1 April 1993; pp. 586–591. [Google Scholar]
- Pajchrowski, T.; Zawirski, K.; Nowopolski, K. Neural Speed Controller Trained Online by Means of Modified RPROP Algorithm. IEEE Trans. Ind. Inform. 2015, 11, 560–568. [Google Scholar] [CrossRef]
- Hermanto, R.P.; Nugroho, A. Waiting-Time Estimation in Bank Customer Queues using RPROP Neural Networks. Procedia Comput. Sci. 2018, 135, 35–42. [Google Scholar] [CrossRef]
- Robitaille, B.; Marcos, B.; Veillette, M.; Payre, G. Modified quasi-Newton methods for training neural networks. Comput. Chem. Eng. 1996, 20, 1133–1140. [Google Scholar] [CrossRef]
- Liu, Q.; Liu, J.; Sang, R.; Li, J.; Zhang, T.; Zhang, Q. Fast Neural Network Training on FPGA Using Quasi-Newton Optimization Method. IEEE Trans. Very Large Scale Integr. (VLSI) Syst. 2018, 26, 1575–1579. [Google Scholar] [CrossRef]
- Yamazaki, A.; de Souto, M.C.P.; Ludermir, T.B. Optimization of neural network weights and architectures for odor recognition using simulated annealing. In Proceedings of the 2002 International Joint Conference on Neural Networks (IJCNN’02), Honolulu, HI, USA, 12–17 May 2002; Volume 1, pp. 547–552. [Google Scholar]
- Da, Y.; Xiurun, G. An improved PSO-based ANN with simulated annealing technique. Neurocomputing 2005, 63, 527–533. [Google Scholar] [CrossRef]
- Leung, F.H.F.; Lam, H.K.; Ling, S.H.; Tam, P.K. Tuning of the structure and parameters of a neural network using an improved genetic algorithm. IEEE Trans. Neural Netw. 2003, 14, 79–88. [Google Scholar] [CrossRef]
- Yao, X. Evolving artificial neural networks. Proc. IEEE 1999, 87, 1423–1447. [Google Scholar]
- Zhang, C.; Shao, H.; Li, Y. Particle swarm optimisation for evolving artificial neural network. In Proceedings of the IEEE International Conference on Systems, Man, and Cybernetics, Nashville, TN, USA, 8–11 October 2000; pp. 2487–2490. [Google Scholar]
- Yu, J.; Wang, S.; Xi, L. Evolving artificial neural networks using an improved PSO and DPSO. Neurocomputing 2008, 71, 1054–1060. [Google Scholar] [CrossRef]
- Ivanova, I.; Kubat, M. Initialization of neural networks by means of decision trees. Knowl.-Based Syst. 1995, 8, 333–344. [Google Scholar] [CrossRef]
- Yam, J.Y.F.; Chow, T.W.S. A weight initialization method for improving training speed in feedforward neural network. Neurocomputing 2000, 30, 219–232. [Google Scholar] [CrossRef]
- Chumachenko, K.; Iosifidis, A.; Gabbouj, M. Feedforward neural networks initialization based on discriminant learning. Neural Netw. 2022, 146, 220–229. [Google Scholar] [CrossRef]
- Shahjahan, M.D.; Kazuyuki, M. Neural network training algorithm with possitive correlation. IEEE Trans. Inf. Syst. 2005, 88, 2399–2409. [Google Scholar] [CrossRef]
- Treadgold, N.K.; Gedeon, T.D. Simulated annealing and weight decay in adaptive learning: The SARPROP algorithm. IEEE Trans. Neural Netw. 1998, 9, 662–668. [Google Scholar] [CrossRef] [PubMed]
- Leung, C.S.; Wong, K.W.; Sum, P.F.; Chan, L.W. A pruning method for the recursive least squared algorithm. Neural Netw. 2001, 14, 147–174. [Google Scholar] [CrossRef]
- Lonen, J.; Kamarainen, J.K.; Lampinen, J. Differential Evolution Training Algorithm for Feed-Forward Neural Networks. Neural Processing Lett. 2003, 17, 93–105. [Google Scholar]
- Baioletti, M.; Bari, G.D.; Milani, A.; Poggioni, V. Differential Evolution for Neural Networks Optimization. Mathematics 2020, 8, 69. [Google Scholar] [CrossRef]
- Salama, K.M.; Abdelbar, A.M. Learning neural network structures with ant colony algorithms. Swarm Intell. 2015, 9, 229–265. [Google Scholar] [CrossRef]
- Tsoulos, I.G.; Gavrilis, D.; Glavas, E. Solving differential equations with constructed neural networks. Neurocomputing 2009, 72, 2385–2391. [Google Scholar] [CrossRef]
- Martínez-Zarzuela, M.; Díaz Pernas, F.J.; Díez Higuera, J.F.; Rodríguez, M.A. Fuzzy ART Neural Network Parallel Computing on the GPU. In Computational and Ambient Intelligence; Sandoval, F., Prieto, A., Cabestany, J., Graña, M., Eds.; IWANN 2007; Lecture Notes in Computer Science; Springer: Berlin/Heidelberg, Germany, 2007; Volume 4507. [Google Scholar]
- Huqqani, A.A.; Schikuta, E.; Chen, S.Y.P. Multicore and GPU Parallelization of Neural Networks for Face Recognition. Procedia Comput. Sci. 2013, 18, 349–358. [Google Scholar] [CrossRef]
- Hansen, E.; Walster, G.W. Global Optimization Using Interval Analysis; Marcel Dekker Inc.: New York, NY, USA, 2004. [Google Scholar]
- Markót, M.C.; Fernández, J.; Casado, L.G.; Csendes, T. New interval methods for constrained global optimization. Mathematics 2006, 106, 287–318. [Google Scholar] [CrossRef]
- Žilinskas, A.; Žilinskas, J. Interval Arithmetic Based Optimization in Nonlinear Regression. Informatica 2010, 21, 149–158. [Google Scholar] [CrossRef]
- Rodriguez, P.; Wiles, J.; Elman, J.L. A Recurrent Neural Network that Learns to Count. Connect. Sci. 1999, 11, 5–40. [Google Scholar] [CrossRef]
- Chandra, R.; Zhang, M. Cooperative coevolution of Elman recurrent neural networks for chaotic time series prediction. Neurocomputing 2012, 86, 116–123. [Google Scholar] [CrossRef]
- Dagum, L.; Menon, R. OpenMP: An industry standard API for shared-memory programming. IEEE Comput. Sci. Eng. 1998, 5, 46–55. [Google Scholar] [CrossRef]
- Kaelo, P.; Ali, M.M. Integrated crossover rules in real coded genetic algorithms. Eur. J. Oper. Res. 2007, 176, 60–76. [Google Scholar] [CrossRef]
- Powell, M.J.D. A Tolerant Algorithm for Linearly Constrained Optimization Calculations. Math. Program. 1989, 45, 547–566. [Google Scholar] [CrossRef]
- Alcalá-Fdez, J.; Fernández, A.; Luengo, J.; Derrac, J.; García, S.; Sánchez, L.; Herrera, F. KEEL Data-Mining Software Tool: Data Set Repository, Integration of Algorithms and Experimental Analysis Framework. J. -Mult.-Valued Log. Soft Comput. 2011, 17, 255–287. [Google Scholar]
- Weiss, S.M.; Kulikowski, C.A. Computer Systems That Learn: Classification and Prediction Methods from Statistics, Neural Nets, Machine Learning, and Expert Systems; Morgan Kaufmann Publishers Inc.: Burlington, MA, USA, 1991. [Google Scholar]
- Quinlan, J.R. Simplifying Decision Trees. Int. Man Mach. Stud. 1987, 27, 221–234. [Google Scholar] [CrossRef]
- Shultz, T.; Mareschal, D.; Schmidt, W. Modeling Cognitive Development on Balance Scale Phenomena. Mach. Learn. 1994, 16, 59–88. [Google Scholar] [CrossRef]
- Zhou, Z.H.; Jiang, Y. NeC4.5: Neural ensemble based C4.5. IEEE Trans. Knowl. Data Eng. 2004, 16, 770–773. [Google Scholar] [CrossRef]
- Setiono, R.; Leow, W.K. FERNN: An Algorithm for Fast Extraction of Rules from Neural Networks. Appl. Intell. 2000, 12, 15–25. [Google Scholar] [CrossRef]
- Demiroz, G.; Govenir, H.A.; Ilter, N. Learning Differential Diagnosis of Eryhemato-Squamous Diseases using Voting Feature Intervals. Artif. Intell. Med. 1998, 13, 147–165. [Google Scholar]
- Hayes-Roth, B.; Hayes-Roth, B.F. Concept learning and the recognition and classification of exemplars. J. Verbal Learning Verbal Behav. 1977, 16, 321–338. [Google Scholar] [CrossRef]
- Kononenko, I.; Šimec, E.; Robnik-Šikonja, M. Overcoming the Myopia of Inductive Learning Algorithms with RELIEFF. Appl. Intell. 1997, 7, 39–55. [Google Scholar] [CrossRef]
- French, R.M.; Chater, N. Using noise to compute error surfaces in connectionist networks: A novel means of reducing catastrophic forgetting. Neural Comput. 2002, 14, 1755–1769. [Google Scholar] [CrossRef] [PubMed]
- Dy, J.G.; Brodley, C.E. Feature Selection for Unsupervised Learning. J. Mach. Learn. Res. 2004, 5, 845–889. [Google Scholar]
- Perantonis, S.J.; Virvilis, V. Input Feature Extraction for Multilayered Perceptrons Using Supervised Principal Component Analysis. Neural Process. Lett. 1999, 10, 243–252. [Google Scholar] [CrossRef]
- Garcke, J.; Griebel, M. Classification with sparse grids using simplicial basis functions. Intell. Data Anal. 2002, 6, 483–502. [Google Scholar] [CrossRef]
- Elter, M.; Schulz-Wendtland, R.; Wittenberg, T. The prediction of breast cancer biopsy outcomes using two CAD approaches that both emphasize an intelligible decision process. Med. Phys. 2007, 34, 4164–4172. [Google Scholar] [CrossRef]
- Malerba, F.E.F.D.; Semeraro, G. Multistrategy Learning for Document Recognition. Appl. Artif. Intell. 1994, 8, 33–84. [Google Scholar]
- Little, M.A.; McSharry, P.E.; Hunter, E.J.; Spielman, J.; Ramig, L.O. Suitability of dysphonia measurements for telemonitoring of Parkinson’s disease. IEEE Trans. Biomed. Eng. 2009, 56, 1015–1022. [Google Scholar] [CrossRef]
- Smith, J.W.; Everhart, J.E.; Dickson, W.C.; Knowler, W.C.; Johannes, R.S. Using the ADAP learning algorithm to forecast the onset of diabetes mellitus. In Proceedings of the Symposium on Computer Applications and Medical Care, Minneapolis, MN, USA, 8–10 June 1988; pp. 261–265. [Google Scholar]
- Lucas, D.D.; Klein, R.; Tannahill, J.; Ivanova, D.; Brandon, S.; Domyancic, D.; Zhang, Y. Failure analysis of parameter-induced simulation crashes in climate models. Geosci. Model Dev. 2013, 6, 1157–1171. [Google Scholar] [CrossRef]
- Giannakeas, N.; Tsipouras, M.G.; Tzallas, A.T.; Kyriakidi, K.; Tsianou, Z.E.; Manousou, P.; Hall, A.; Karvounis, E.C.; Tsianos, V.; Tsianos, E. A clustering based method for collagen proportional area extraction in liver biopsy images. In Proceedings of the Annual International Conference of the IEEE Engineering in Medicine and Biology Society, EMBS, Milan, Italy, 25–29 August 2015; pp. 3097–3100. [Google Scholar]
- Hastie, T.; Tibshirani, R. Non-parametric logistic and proportional odds regression. JRSS-C Appl. Stat. 1987, 36, 260–276. [Google Scholar] [CrossRef]
- Dash, M.; Liu, H.; Scheuermann, P.; Tan, K.L. Fast hierarchical clustering and its validation. Data Knowl. Eng. 2003, 44, 109–138. [Google Scholar] [CrossRef]
- Wolberg, W.H.; Mangasarian, O.L. Multisurface method of pattern separation for medical diagnosis applied to breast cytology. Proc. Natl. Acad. Sci. USA 1990, 87, 9193–9196. [Google Scholar] [CrossRef]
- Raymer, M.; Doom, T.E.; Kuhn, L.A.; Punch, W.F. Knowledge discovery in medical and biological datasets using a hybrid Bayes classifier/evolutionary algorithm. IEEE Trans. Syst. Man Cybern. Part B Cybern. 2003, 33, 802–813. [Google Scholar] [CrossRef]
- Zhong, P.; Fukushima, M. Regularized nonsmooth Newton method for multi-class support vector machines. Optim. Methods Softw. 2007, 22, 225–236. [Google Scholar] [CrossRef]
- Koivisto, M.; Sood, K. Exact Bayesian Structure Discovery in Bayesian Networks. J. Mach. Learn. Res. 2004, 5, 549–573. [Google Scholar]
- Nash, W.J.; Sellers, T.L.; Talbot, S.R.; Cawthor, A.J.; Ford, W.B. The Population Biology of Abalone (_Haliotis_ Species) in Tasmania. I. Blacklip Abalone (_H. rubra_) from the North Coast and Islands of Bass Strait; Report No. 48; Sea Fisheries Division, Department of Primary Industry and Fisheries: Taroona, Australia, 1994. [Google Scholar]
- Brooks, T.F.; Pope, D.S.; Marcolini, A.M. Airfoil Self-Noise and Prediction; Technical Report, NASA RP-1218; National Aeronautics and Space Administration: Washington, DC, USA, 1989.
- Simonoff, J.S. Smooting Methods in Statistics; Springer: Berlin/Heidelberg, Germany, 1996. [Google Scholar]
- Yeh, I.C. Modeling of strength of high performance concrete using artificial neural networks. Cem. Concr. Res. 1998, 28, 1797–1808. [Google Scholar] [CrossRef]
- Harrison, D.; Rubinfeld, D.L. Hedonic prices and the demand for clean ai. J. Environ. Econ. Manag. 1978, 5, 81–102. [Google Scholar] [CrossRef]
- King, R.D.; Muggleton, S.; Lewis, R.; Sternberg, M.J.E. Drug design by machine learning: The use of inductive logic programming to model the structure-activity relationships of trimethoprim analogues binding to dihydrofolate reductase. Proc. Nat. Acad. Sci. USA 1992, 89, 11322–11326. [Google Scholar] [CrossRef]
- Kingma, D.P.; Ba, J.L. ADAM: A method for stochastic optimization. In Proceedings of the 3rd International Conference on Learning Representations (ICLR 2015), San Diego, CA, USA, 7–9 May 2015; pp. 1–15. [Google Scholar]
- Klima, G. Fast Compressed Neural Networks. Available online: https://rdrr.io/cran/FCNN4R/ (accessed on 23 May 2022).
- Stanley, K.O.; Miikkulainen, R. Evolving Neural Networks through Augmenting Topologies. Evol. Comput. 2002, 10, 99–127. [Google Scholar] [CrossRef] [PubMed]
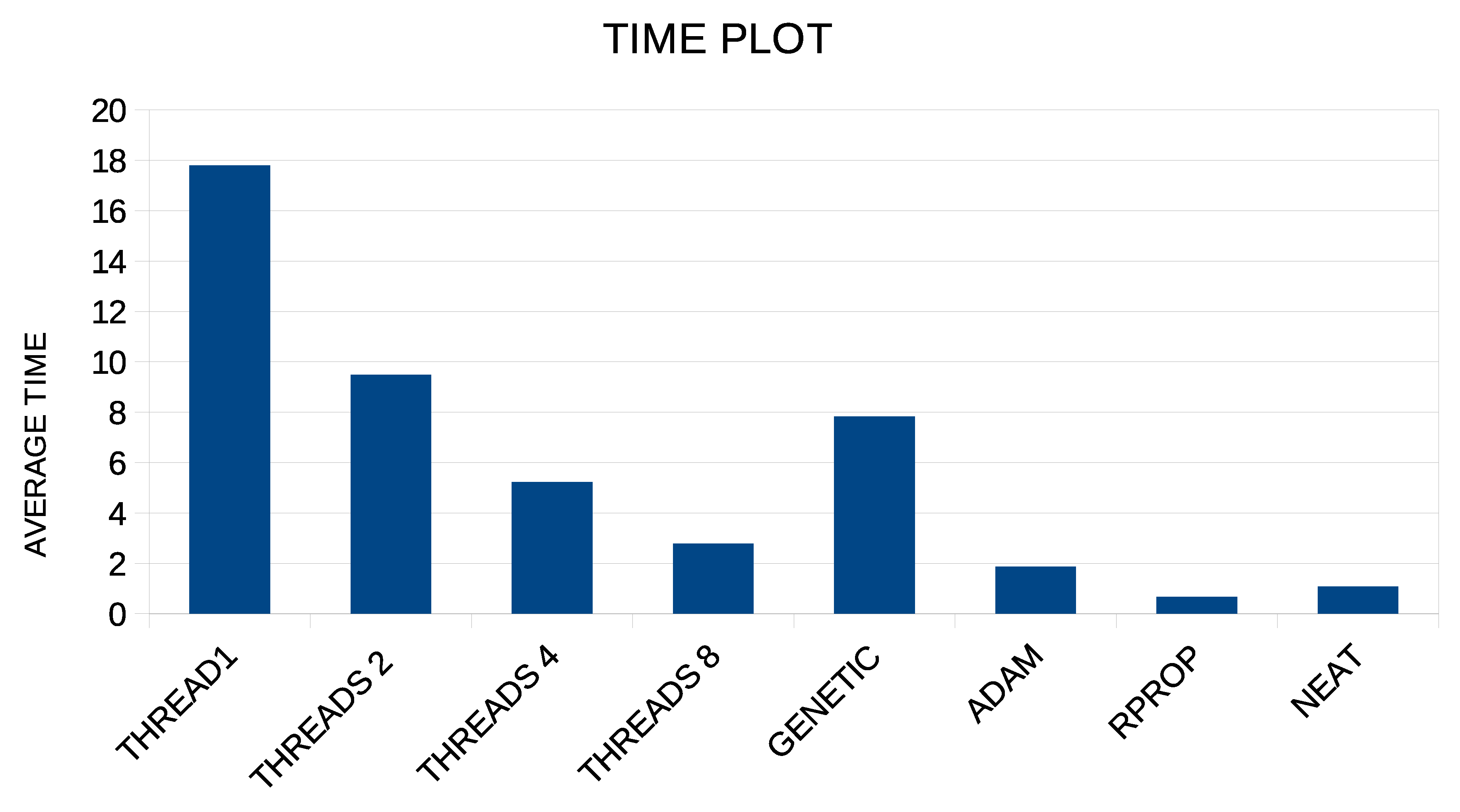
| PARAMETER | VALUE |
|---|---|
| K | 20 |
| H | 10 |
| 200 | |
| 50 | |
| 200 | |
| 0.10 | |
| 0.01 |
| DATASET | GENETIC | ADAM | RPROP | NEAT | |||
|---|---|---|---|---|---|---|---|
| Appendicitis | 18.10% | 16.50% | 16.30% | 17.20% | 15.00% | 14.00% | 16.07% |
| Australian | 32.21% | 35.65% | 36.12% | 31.98% | 24.85% | 30.20% | 28.52% |
| Balance | 8.97% | 7.87% | 8.81% | 23.14% | 7.42% | 7.42% | 7.67% |
| Bands | 35.75% | 36.25% | 36.32% | 34.30% | 32.00% | 32.25% | 33.06% |
| Cleveland | 51.60% | 67.55% | 61.41% | 53.44% | 41.64% | 44.66% | 44.39% |
| Dermatology | 30.58% | 26.14% | 15.12% | 32.43% | 15.49% | 11.00% | 10.80% |
| Hayes Roth | 56.18% | 59.70% | 37.46% | 50.15% | 28.72% | 28.84% | 32.05% |
| Heart | 28.34% | 38.53% | 30.51% | 39.27% | 15.58% | 17.07% | 16.22% |
| HouseVotes | 6.62% | 7.48% | 6.04% | 10.89% | 3.92% | 3.78% | 3.26% |
| Ionosphere | 15.14% | 16.64% | 13.65% | 19.67% | 12.25% | 9.71% | 7.12% |
| Liverdisorder | 31.11% | 41.53% | 40.26% | 30.67% | 30.90% | 29.54% | 30.70% |
| Lymography | 23.26% | 29.26% | 24.67% | 33.70% | 18.98% | 17.52% | 17.67% |
| Mammographic | 19.88% | 46.25% | 18.46% | 22.85% | 17.01% | 17.60% | 15.97% |
| PageBlocks | 8.06% | 7.93% | 7.82% | 10.22% | 7.73% | 7.01% | 6.71% |
| Parkinsons | 18.05% | 24.06% | 22.28% | 18.56% | 14.81% | 13.86% | 12.53% |
| Pima | 32.19% | 34.85% | 34.27% | 34.51% | 23.51% | 25.31% | 27.49% |
| Popfailures | 5.94% | 5.18% | 4.81% | 7.05% | 6.13% | 5.93% | 5.30% |
| Regions2 | 29.39% | 29.85% | 27.53% | 33.23% | 24.01% | 23.14% | 23.62% |
| Saheart | 34.86% | 34.04% | 34.90% | 34.51% | 28.94% | 29.04% | 29.93% |
| Segment | 57.72% | 49.75% | 52.14% | 66.72% | 47.38% | 49.49% | 40.61% |
| Wdbc | 8.56% | 35.35% | 21.57% | 12.88% | 6.23% | 5.28% | 5.49% |
| Wine | 19.20% | 29.40% | 30.73% | 25.43% | 5.51% | 6.55% | 6.22% |
| Z_F_S | 10.73% | 47.81% | 29.28% | 38.41% | 4.70% | 5.61% | 6.01% |
| ZO_NF_S | 8.41% | 47.43% | 6.43% | 43.75% | 5.39% | 4.67% | 5.81% |
| ZONF_S | 2.60% | 11.99% | 27.27% | 5.44% | 1.85% | 2.07% | 2.24% |
| ZOO | 16.67% | 14.13% | 15.47% | 20.27% | 14.83% | 11.40% | 8.50% |
| AVERAGE | 23.47% | 30.81% | 25.37% | 28.87% | 17.49% | 17.42% | 17.08% |
| DATASET | GENETIC | ADAM | RPROP | NEAT | |||
|---|---|---|---|---|---|---|---|
| ABALONE | 7.17 | 4.30 | 4.55 | 9.88 | 4.22 | 4.18 | 3.89 |
| AIRFOIL | 0.003 | 0.005 | 0.002 | 0.067 | 0.003 | 0.003 | 0.003 |
| BASEBALL | 103.60 | 77.90 | 92.05 | 100.39 | 49.47 | 51.07 | 53.57 |
| BK | 0.027 | 0.03 | 1.599 | 0.15 | 0.017 | 0.017 | 0.019 |
| BL | 5.74 | 0.28 | 4.38 | 0.05 | 0.0019 | 0.0016 | 0.0016 |
| CONCRETE | 0.0099 | 0.078 | 0.0086 | 0.081 | 0.0053 | 0.0044 | 0.0042 |
| DEE | 1.013 | 0.63 | 0.608 | 1.512 | 0.187 | 0.205 | 0.203 |
| DIABETES | 19.86 | 3.03 | 1.11 | 4.25 | 0.31 | 0.31 | 0.29 |
| HOUSING | 43.26 | 80.20 | 74.38 | 56.49 | 19.28 | 18.50 | 17.75 |
| FA | 1.95 | 0.11 | 0.14 | 0.19 | 0.011 | 0.012 | 0.012 |
| MB | 3.39 | 0.06 | 0.055 | 0.061 | 0.048 | 0.047 | 0.047 |
| MORTGAGE | 2.41 | 9.24 | 9.19 | 14.11 | 0.57 | 0.70 | 0.53 |
| PY | 105.41 | 0.09 | 0.039 | 0.075 | 0.016 | 0.014 | 0.014 |
| QUAKE | 0.040 | 0.06 | 0.041 | 0.298 | 0.036 | 0.036 | 0.036 |
| TREASURY | 2.929 | 11.16 | 10.88 | 15.52 | 0.473 | 0.677 | 0.622 |
| WANKARA | 0.012 | 0.02 | 0.0003 | 0.005 | 0.0003 | 0.0002 | 0.0002 |
| AVERAGE | 18.55 | 11.70 | 12.44 | 12.70 | 4.67 | 4.74 | 4.81 |
| DATASET | |||
|---|---|---|---|
| Appendicitis | 15.23% | 15.37% | 15.77% |
| Australian | 32.85% | 33.15% | 30.18% |
| Balance | 11.92% | 7.61% | 8.71% |
| Bands | 35.61% | 33.86% | 32.96% |
| Cleveland | 43.91% | 43.35% | 41.29% |
| Dermatology | 28.41% | 21.28% | 14.33% |
| Hayes Roth | 50.33% | 38.56% | 36.80% |
| Heart | 20.61% | 21.16% | 19.99% |
| HouseVotes | 4.07% | 4.31% | 3.58% |
| Ionosphere | 12.14% | 11.19% | 9.23% |
| Liverdisorder | 31.47% | 33.01% | 31.24% |
| Lymography | 22.24% | 22.57% | 20.74% |
| Mammographic | 18.66% | 17.37% | 15.71% |
| PageBlocks | 7.95% | 7.68% | 6.81% |
| Parkinsons | 17.28% | 17.44% | 13.86% |
| Pima | 33.19% | 31.94% | 30.71% |
| Popfailures | 6.65% | 5.81% | 5.24% |
| Regions2 | 26.33% | 26.03% | 22.25% |
| Saheart | 36.11% | 32.96% | 34.45% |
| Segment | 66.37% | 58.33% | 49.85% |
| Wdbc | 7.38% | 6.95% | 7.68% |
| Wine | 13.49% | 11.55% | 8.39% |
| Z_F_S | 7.77% | 7.59% | 8.38% |
| ZO_NF_S | 8.21% | 7.52% | 7.28% |
| ZONF_S | 2.26% | 1.87% | 1.99% |
| ZOO | 14.70% | 12.30% | 13.50% |
| AVERAGE | 22.12% | 20.41% | 18.88% |
| DATASET | |||
|---|---|---|---|
| ABALONE | 4.88 | 4.77 | 4.63 |
| AIRFOIL | 0.004 | 0.004 | 0.004 |
| BASEBALL | 69.83 | 65.37 | 69.72 |
| BK | 0.02 | 0.02 | 0.02 |
| BL | 0.006 | 0.005 | 0.007 |
| CONCRETE | 0.008 | 0.006 | 0.005 |
| DEE | 0.224 | 0.225 | 0.199 |
| DIABETES | 0.357 | 0.343 | 0.321 |
| HOUSING | 26.43 | 25.88 | 20.65 |
| FA | 0.019 | 0.019 | 0.017 |
| MB | 0.05 | 0.05 | 0.05 |
| MORTGAGE | 2.11 | 1.76 | 1.44 |
| PY | 0.02 | 0.018 | 0.022 |
| QUAKE | 0.042 | 0.037 | 0.037 |
| TREASURY | 2.37 | 2.12 | 1.48 |
| WANKARA | 0.0004 | 0.0003 | 0.0003 |
| AVERAGE | 6.65 | 6.29 | 6.16 |
| DATASET | ||||
|---|---|---|---|---|
| Appendicitis | 17.70% | 18.10% | 18.87% | 18.97% |
| Australian | 33.00% | 33.21% | 33.16% | 33.03% |
| Balance | 9.09% | 8.97% | 9.43% | 9.36% |
| Bands | 34.87% | 35.75% | 33.92% | 33.88% |
| Cleveland | 54.91% | 51.60% | 57.25% | 55.83% |
| Dermatology | 33.59% | 30.58% | 24.83% | 20.07% |
| Hayes Roth | 58.44% | 56.18% | 57.21% | 55.51% |
| Heart | 30.20% | 28.34% | 29.65% | 29.43% |
| HouseVotes | 7.45% | 6.62% | 8.22% | 8.02% |
| Ionosphere | 14.69% | 15.14% | 10.02% | 9.84% |
| Liverdisorder | 33.30% | 31.11% | 33.24% | 33.19% |
| Lymography | 23.48% | 23.26% | 23.95% | 25.45% |
| Mammographic | 20.83% | 19.88% | 21.19% | 21.13% |
| PageBlocks | 8.28% | 8.06% | 8.04% | 7.42% |
| Parkinsons | 19.55% | 18.05% | 18.81% | 19.14% |
| Pima | 34.64% | 32.19% | 33.54% | 33.62% |
| Popfailures | 5.37% | 5.94% | 5.30% | 5.38% |
| Regions2 | 29.11% | 29.39% | 28.54% | 28.47% |
| Saheart | 35.25% | 34.86% | 34.60% | 34.93% |
| Segment | 56.07% | 57.72% | 52.43% | 51.00% |
| Wdbc | 9.08% | 8.56% | 9.02% | 9.19% |
| Wine | 30.43% | 19.20% | 25.35% | 21.55% |
| Z_F_S | 18.23% | 10.73% | 11.94% | 11.49% |
| ZO_NF_S | 16.61% | 8.41% | 10.85% | 10.09% |
| ZONF_S | 2.70% | 2.60% | 2.75% | 2.10% |
| ZOO | 16.37% | 16.67% | 13.47% | 13.33% |
| AVERAGE | 25.12% | 23.47% | 23.68% | 23.13% |
| DATASET | ||||
|---|---|---|---|---|
| ABALONE | 6.88 | 7.17 | 6.28 | 6.49 |
| AIRFOIL | 0.008 | 0.003 | 0.04 | 0.01 |
| BASEBALL | 106.47 | 103.60 | 107.04 | 107.30 |
| BK | 0.65 | 0.027 | 0.038 | 0.097 |
| BL | 9.80 | 5.74 | 1.38 | 2.85 |
| CONCRETE | 0.017 | 0.01 | 0.29 | 0.42 |
| DEE | 0.36 | 1.01 | 0.48 | 0.25 |
| DIABETES | 38.04 | 19.86 | 13.70 | 13.50 |
| HOUSING | 38.44 | 43.26 | 36.51 | 35.81 |
| FA | 1.55 | 1.95 | 0.74 | 2.06 |
| MB | 0.61 | 3.39 | 1.13 | 0.62 |
| MORTGAGE | 2.12 | 2.41 | 1.94 | 1.84 |
| PY | 151.49 | 105.41 | 96.79 | 90.59 |
| QUAKE | 0.22 | 0.04 | 0.05 | 0.04 |
| TREASURY | 2.72 | 2.93 | 2.28 | 2.19 |
| WANKARA | 0.065 | 0.012 | 0.001 | 0.003 |
| AVERAGE | 22.47 | 18.55 | 16.74 | 16.51 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tsoulos, I.G.; Tzallas, A.; Karvounis, E. A Rule-Based Method to Locate the Bounds of Neural Networks. Knowledge 2022, 2, 412-428. https://doi.org/10.3390/knowledge2030024
Tsoulos IG, Tzallas A, Karvounis E. A Rule-Based Method to Locate the Bounds of Neural Networks. Knowledge. 2022; 2(3):412-428. https://doi.org/10.3390/knowledge2030024
Chicago/Turabian StyleTsoulos, Ioannis G., Alexandros Tzallas, and Evangelos Karvounis. 2022. "A Rule-Based Method to Locate the Bounds of Neural Networks" Knowledge 2, no. 3: 412-428. https://doi.org/10.3390/knowledge2030024
APA StyleTsoulos, I. G., Tzallas, A., & Karvounis, E. (2022). A Rule-Based Method to Locate the Bounds of Neural Networks. Knowledge, 2(3), 412-428. https://doi.org/10.3390/knowledge2030024








