Physical and Logical Synchronization of Clocks: The Ramsey Approach

Abstract

Ramsey analysis is applied to the problem of the relativistic and quantum synchronization of clocks. Various protocols of synchronization are addressed. Einstein and Eddington special relativity synchronization procedures are considered, and quantum synchronization is discussed. Clocks are seen as the vertices of the graph. Clocks may be synchronized or unsynchronized. Thus, introducing complete, bi-colored, Ramsey graphs emerging from the lattices of clocks becomes possible. The transitivity of synchronization plays a key role in the coloring of the Ramsey graph. Einstein synchronization is transitive, while general relativity and quantum synchronization procedures are not. This fact influences the value of the Ramsey number established for the synchronization graph arising from the lattice of clocks. Any lattice built of six clocks, synchronized with quantum entanglement, will inevitably contain the mono-chromatic triangle. The transitive synchronization of logical clocks is discussed. Interrelation between the symmetry of the clock lattice and the structure of the synchronization graph is addressed. Ramsey analysis of synchronization is important for the synchronization of computers in networks, LIGO, and Virgo instruments intended for the registration of gravitational waves and GPS tame-based synchronization.

1. Introduction

The synchronization of clocks is a cornerstone of special and general relativity [1,2,3,4]. In Newtonian mechanics, the synchronization of clocks is a trivial, straightforward procedure because time is considered absolute, meaning it flows the same for all observers, regardless of their state of motion or location [5,6,7]. In contrast, in Einstein relativity, the situation is more complicated: synchronized clocks cannot be transported from one point to another without an intervention regarding their functioning. Two solutions were suggested for the synchronization of clocks in special relativity: (i) the Einstein lattice of synchronized clocks [1,2,3,4] and (ii) Eddington slow-clock transport [8,9]. Einstein synchronization is described as follows [3]: John records an arbitrary time on his clock, denoted $t_J$, and simultaneously sends a light pulse to Peter, who records the time, $t_P$, on his clock when he received the pulse (see Figure 1). He reflects the pulse back to John, who records the time on his clock when he receives it as $t_J^{\prime }$. John then sends Peter the time ${\displaystyle \frac{t_J^{\prime }+t_J}{2}}$, instructing him that it is the time his clock should have been reading at time $t_P$ (see Figure 1). Thus, Peter obtains an estimate of ${\tau }_{PJ}$, the time difference between their clocks. This procedure is repeated many times and the results are averaged to obtain an accurate estimate of the interval ${\tau }_{PJ}.$ A modern experimental technique using Einstein synchronization is known as Time Transfer by Laser Link, developed by OCA (Observatoire de la Cote d’Azur) and tested with the Russian space station Mir, which predicted that ground stations communicating their light pulses to a common satellite can synchronize within 100 ps [10].

Within the Eddington scheme, the two clocks, A and B, are first synchronized locally, and then they are transported adiabatically (infinitesimally slowly) to their final separate locations [8]. These schemes of synchronization, adopted in special relativity, are very different, as will be discussed in detail below. The Einstein synchronization procedure is transitive. This means that if clock “A” is synchronized with clock “B” and clock “B” is synchronized with clock “C”, this necessarily means that clock “A” is synchronized with clock “C”, and the transitivity does not hold for the Eddington synchronization procedure.

The synchronization of clocks becomes much more complicated in general relativity [1,11]. The aforementioned Einstein synchronization does not hold in general relativity. It is noteworthy that the procedure of synchronization in general relativity is not defined unambiguously [12]. We adopt the synchronization procedure adopted in the classical textbook by Landau and Lifshitz [1] and also by Zheng and Chen [11]. We consider that the observers, named John and Peter, are located at different points of the curved space. In general relativity, the time difference between their coordinate clocks is given by [1,11]:

$${\Delta t=t}_J-t_P=-\left({\displaystyle \frac{g_{0i}}{g_{00}}}\right)d{x}_i,$$

(1)

where $g_{ik},i,k=0,\dots ,3$ is the metric tensor. The time span $\Delta t$ in general relativity is not an exact differential:

$$\oint \Delta t\cong 0.$$

(2)

The synchronization of clocks placed along a closed path becomes possible, when Equation (3) is true, namely [11]:

$$g_{0i}=0$$

(3)

which may be re-written as follows:

$$\oint \Delta t=0$$

(4)

Thus, synchronization is generally not transitive, and simultaneously, it is transitive if and only if space–time is time-orthogonal [1,11]. In particular, Eddington’s slow-clock-transport method involves physically moving a clock. If the clock moves through different gravitational potentials, this inevitably leads to the non-transitivity of synchronization, if space–time is not time-orthogonal. This synchronization procedure is approximately transitive only in weakly time-orthogonal gravitational fields.

Quantum synchronization has been intensively discussed in recent decades [13,14,15,16,17,18]. Quantum synchronization is not necessarily transitive [13,14,15,16,17,18]. If two clocks are entangled for synchronization, their relationship does not necessarily extend transitively to a third clock [13,14,15,16,17,18]. The relation of transitivity of clock synchronization is crucial for our approach. We apply the Ramsey theory to the problem of the synchronization of clocks, whether relativistic or quantum. The Ramsey theory is in the field of the general graph theory [19,20]. The fundamental idea, resulting from the Ramsey graph theory, is that in any sufficiently large graph (seen as a set of vertices connected by edges), patterns or structures must emerge [21,22,23,24]. More specifically, no matter how one colors the edges of a sufficiently large complete graph (where every pair of vertices is connected), one is guaranteed to find a monochromatic subgraph of a particular type (for example, represented by monochromatic triangles). The philosophical meaning of the Ramsey theory may be understood as follows: complete chaos does not exist, and ordered structures are necessarily present in sufficiently large structures [21,22,23,24]. We apply the Ramsey graph to the analysis of the synchronization of lattices of clocks. The paper is structured as follows: (i) Ramsey analysis of relativistic synchronization is addressed first; (ii) then, quantum synchronization is considered; (iii) synchronization of the logical clocks is then treated; and finally, (iv) generalization of our suggested approach for pairs of synchronized clocks is discussed.

2. Results

2.1. Einstein Relativistic Synchronization of Clocks: The Ramsey Approach

Consider the pair of clocks depicted in Figure 2. We see the clocks as the vertices of the graph. If the clocks/vertices are synchronized with the Einstein synchronization procedure [3,4,25], they are connected via the red link/edge (see Figure 2A). If the clocks are not synchronized/unsynchronized, they are connected via the violet link/edge (see Figure 2B).

This convention gives rise to a complete, bi-colored graph, which may be introduced for any lattice of clocks. We call this graph the synchronization graph. The structure and properties of synchronization graphs will be addressed below in detail.

Now consider a triad of clocks, represented by the vertices of the graphs depicted in Figure 3. Let us start from inset A. The synchronization of clocks with the Einstein protocol is transitive. Thus, if clock “1” is synchronized with clock “2” and clock “2” is synchronized with clock “3” via the Einstein procedure, clock “1” is necessarily synchronized with clock “3”, as shown in inset A of Figure 3. Thus, all of the clocks appearing in inset A are connected via red links, and consequently, a monochromatic red triangle emerges. In contrast, the relation “to be not synchronized” is not transitive for Einstein synchronization, as shown in inset B. Pairs of clocks “1” and “3” and “1” and “2” are not synchronized, and they are connected via violet links. In contrast, clocks “2” and “3” may be synchronized under the Einstein protocol, as illustrated in inset B.

Thus, the relation between vertices/clocks to “be synchronized with the Einstein protocol” is transitive, while the relation “the clocks are not synchronized” is not transitive. Thus, a semi-transitive, complete, bi-colored graph emerges from any lattice of clocks synchronized with the Einstein procedure. The properties of semi-transitive graphs were studied and reported recently [26]. Consider the bi-colored, complete graph representing four clocks, some of which are synchronized under Einstein protocol and some of which are not, depicted in Figure 4. This graph is regarded as the synchronization graph for a given lattice of four clocks.

The coloring procedure is prescribed in Figure 2. No monochromatic triangle is present in the graph.

Now consider a lattice built of five clocks synchronized with the Einstein protocol, as depicted in Figure 5. The coloring is, again, prescribed in Figure 2. We recognize four monochromatic red triangles in the synchronization graph shown in Figure 5; namely, triangles “245”, “235” “234”, and “345”. In other words, triangles “245”, “235” “234”, and “345” are built from synchronized clocks only.

This observation follows from the fact that the Ramsey semi-transitive number was established as $R_{trans}\left(\mathrm{3,3}\right)=5$. Thus, any semi-transitive, complete graph built of five vertices will necessarily contain at least one monochromatic triangle [26]. Recall that for the non-transitive, complete, bi-colored graph, $R_{trans}\left(\mathrm{3,3}\right)=6$. This means that in any bi-colored, complete graph built of six vertices, a monochromatic triangle will inevitably appear.

2.2. Synchronization of Clocks in General Relativity: The Ramsey Approach

Consider the synchronization of clocks in general relativity, when space–time is not time-orthogonal. We first address a lattice built of five clocks, as depicted in Figure 6. The coloring procedure is prescribed in Figure 2. Now, the synchronization is non-transitive [1,11].

Now, we address a lattice built of six clocks, as depicted in Figure 7. The procedure of synchronization is supposed to be non-transitive. This lattice contains two monochromatic triangles; namely, we recognize from Figure 7 that triangle “456” is monochromatic red and represents a triad of synchronized clocks. Triangle “135” is, in turn, monochromatic violet and, in turn, represents a triad of non-synchronized clocks. Moreover, any lattice built of six clocks will contain at least one monochromatic triangle. This immediately follows from the Ramsey theorem and the fact that the Ramsey number is $R\left(\mathrm{3,3}\right)=6$.

Thus, we have demonstrated the following Theorem 1.

Theorem 1.

Consider a lattice built of six clocks embedded into relativistic curved space–time. Some pairs of the clocks are synchronized and some of them are not synchronized. The procedure of synchronization is supposed to be non-transitive. The lattice will inevitably contain a triad of synchronized, or alternatively non-synchronized, clocks.

It should be emphasized that the Ramsey theory does not predict the exact color of the monochromatic triangle present in the lattice built of synchronized/non-synchronized clocks [21,22,23,24].

2.3. Ramsey Approach to Quantum Synchronization of Clocks

Various procedures of quantum synchronization have been suggested [13,14,15,16,17,18]. We consider a synchronization protocol exploiting quantum entanglement [14,15,16,17,18]. The synchronization of clocks based on quantum entanglement is not transitive [13,14,15,16,17,18]. Thus, we consider a lattice of six clocks, as depicted in Figure 7. Some of the clocks are synchronized with quantum entanglement and some of them are not. Any lattice built of six clocks, represented by the synchronization graph, will inevitably contain a mono-chromatic triangle, as follows from the Theorem, demonstrated in the previous section.

2.4. Ramsey Approach to Synchronization of Logical Clocks

Logical clocks were introduced to order events in distributed databases. Logical clocks order events without relying on physical time. Logical clocks were introduced by Lamport in 1978 [27]. Lamport clocks lead to a situation where all events in a distributed system are completely ordered. That is, if $\to b$, then we define that a logically happened before b [28]. The synchronization of logical clocks (such as Lamport timestamps) is transitive, but only in the sense of causality propagation [27,28]. The relation “to be not synchronized” is not transitive for the synchronization of logical clocks. Thus, we return to semi-transitive graphs, such as those depicted in Figure 4 and Figure 5. Thus, any lattice built of five synchronized/non-synchronized clocks will contain at least one monochromatic triangle.

2.5. Synchronization of Clocks and Symmetry

Symmetry considerations are one of the most fundamental concepts in physics [29,30]. Let us introduce symmetry considerations in our analysis. Consider a four-fold symmetrical lattice of clocks, synchronized with the Einstein transitive relativistic protocol, as depicted in inset A of Figure 8. The synchronization graph, reflecting the symmetry of the lattice shown in inset A, does not contain monochromatic triangles. A five-fold symmetrical lattice of five clocks synchronized with the Einstein transitive relativistic protocol that does not contain monochromatic triangles is impossible.

A f-fold symmetrical lattice of clocks synchronized/non-synchronized with the non-transitive protocol that does not contain monochromatic triangles is possible, and its synchronization graph is depicted in inset B of Figure 8.

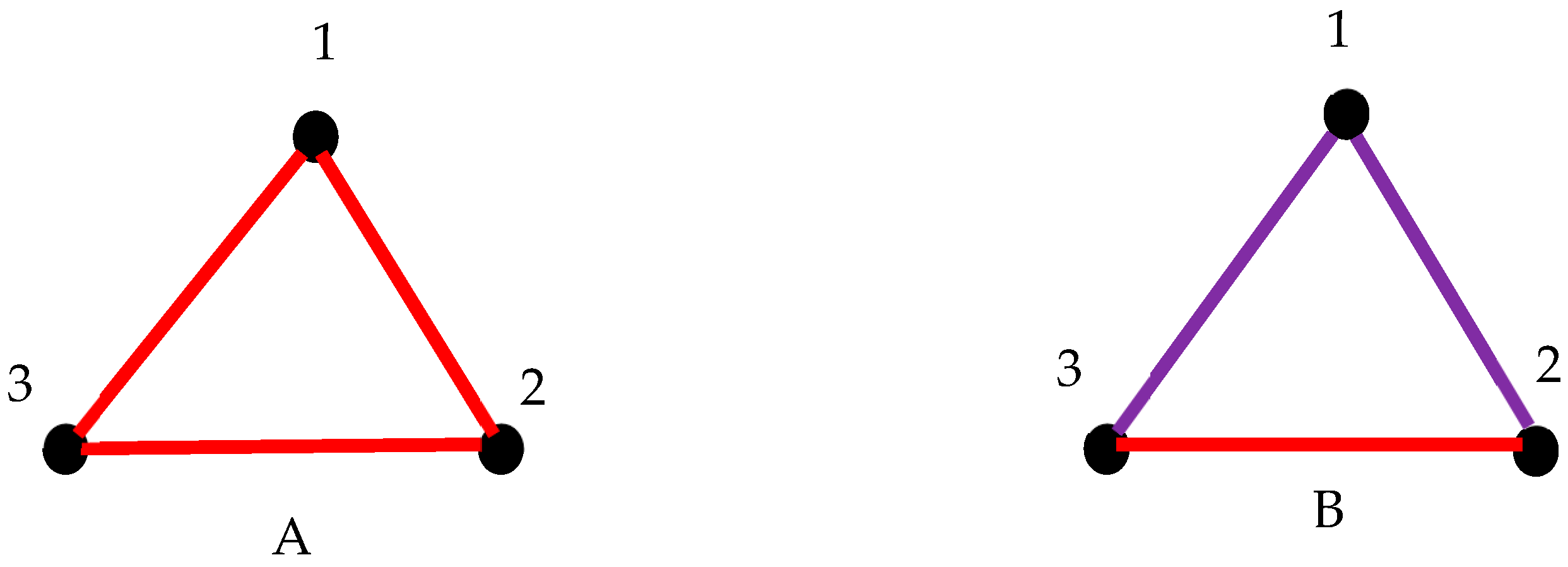
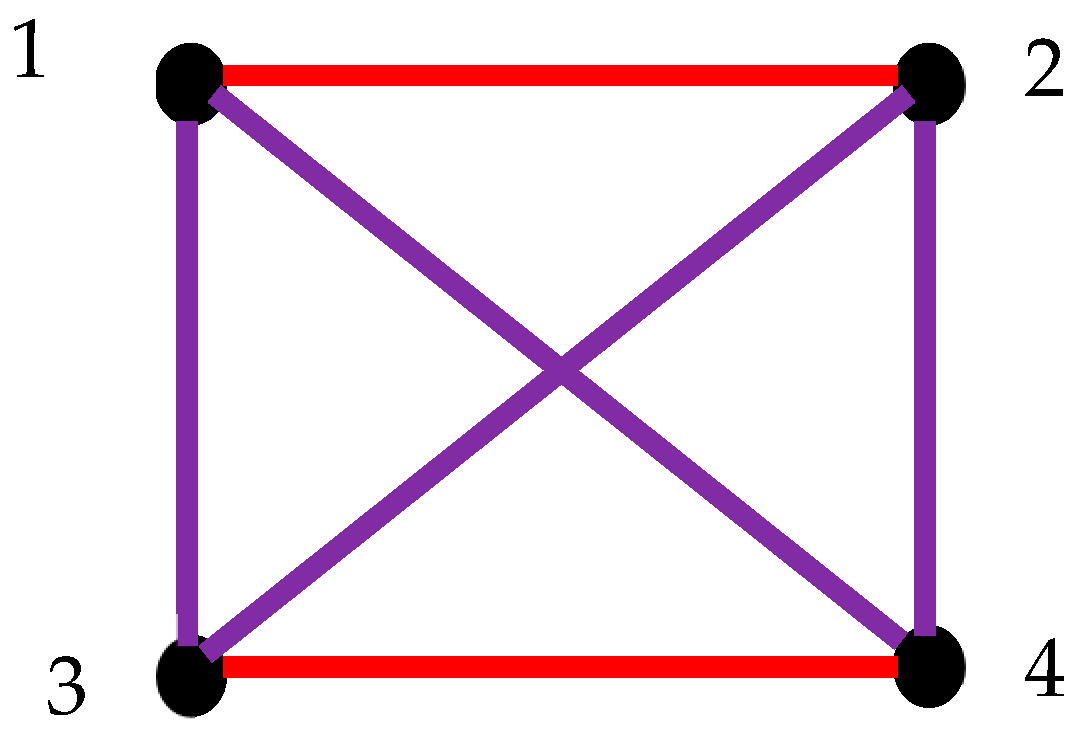
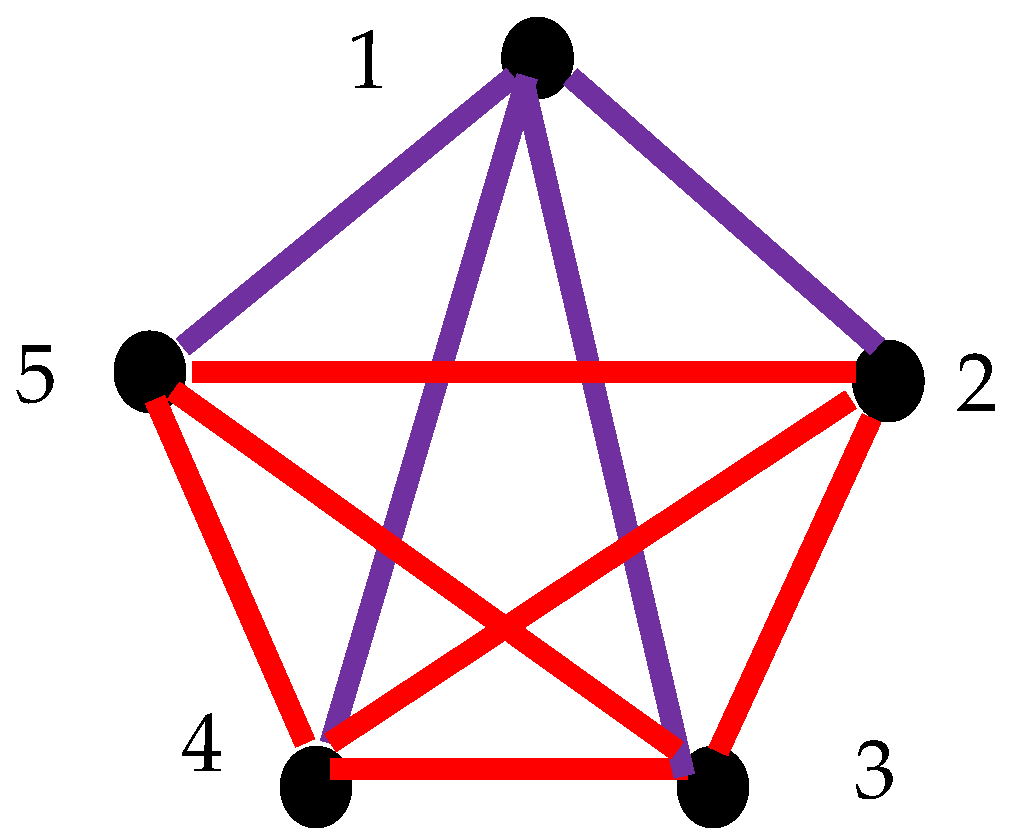
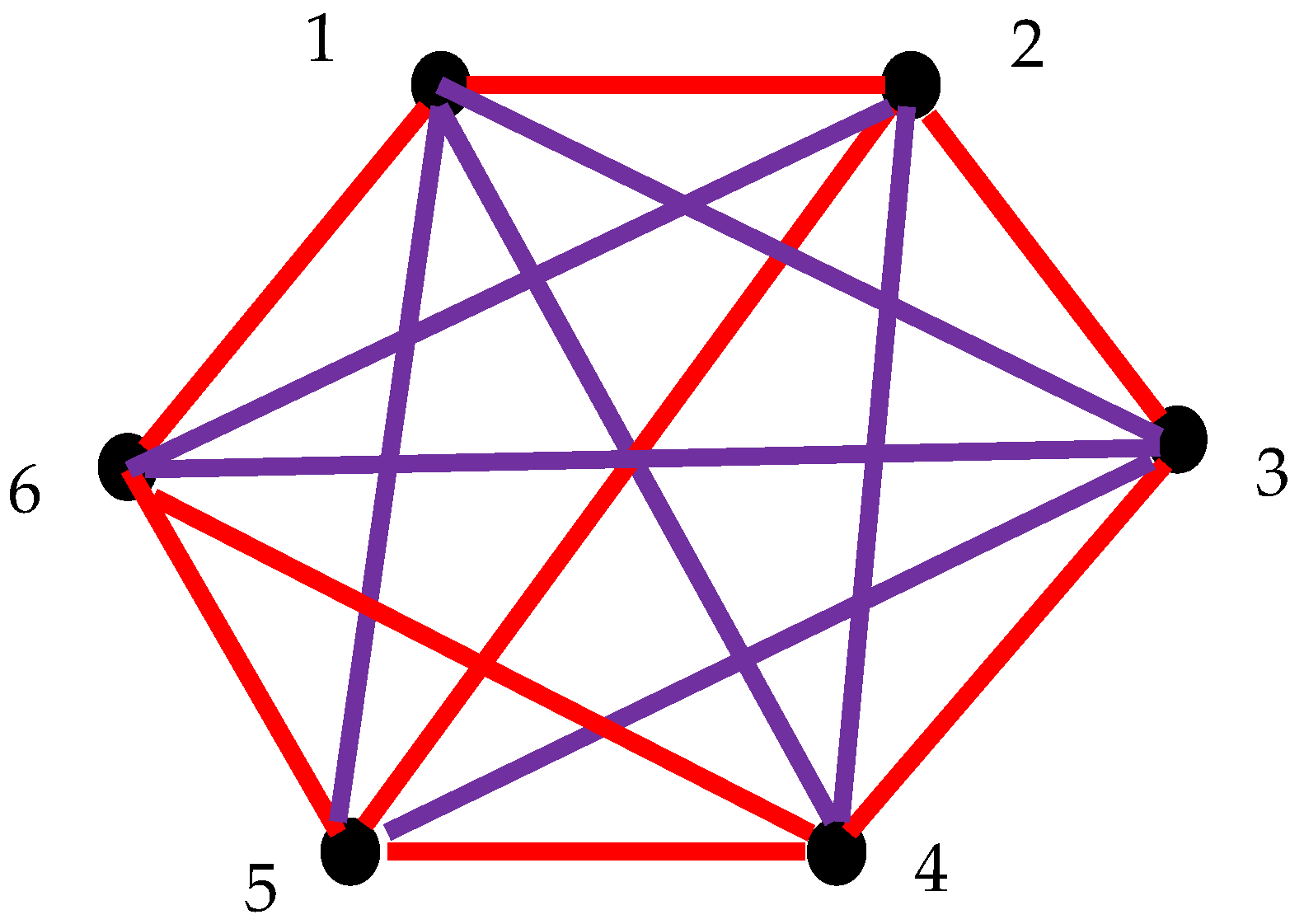
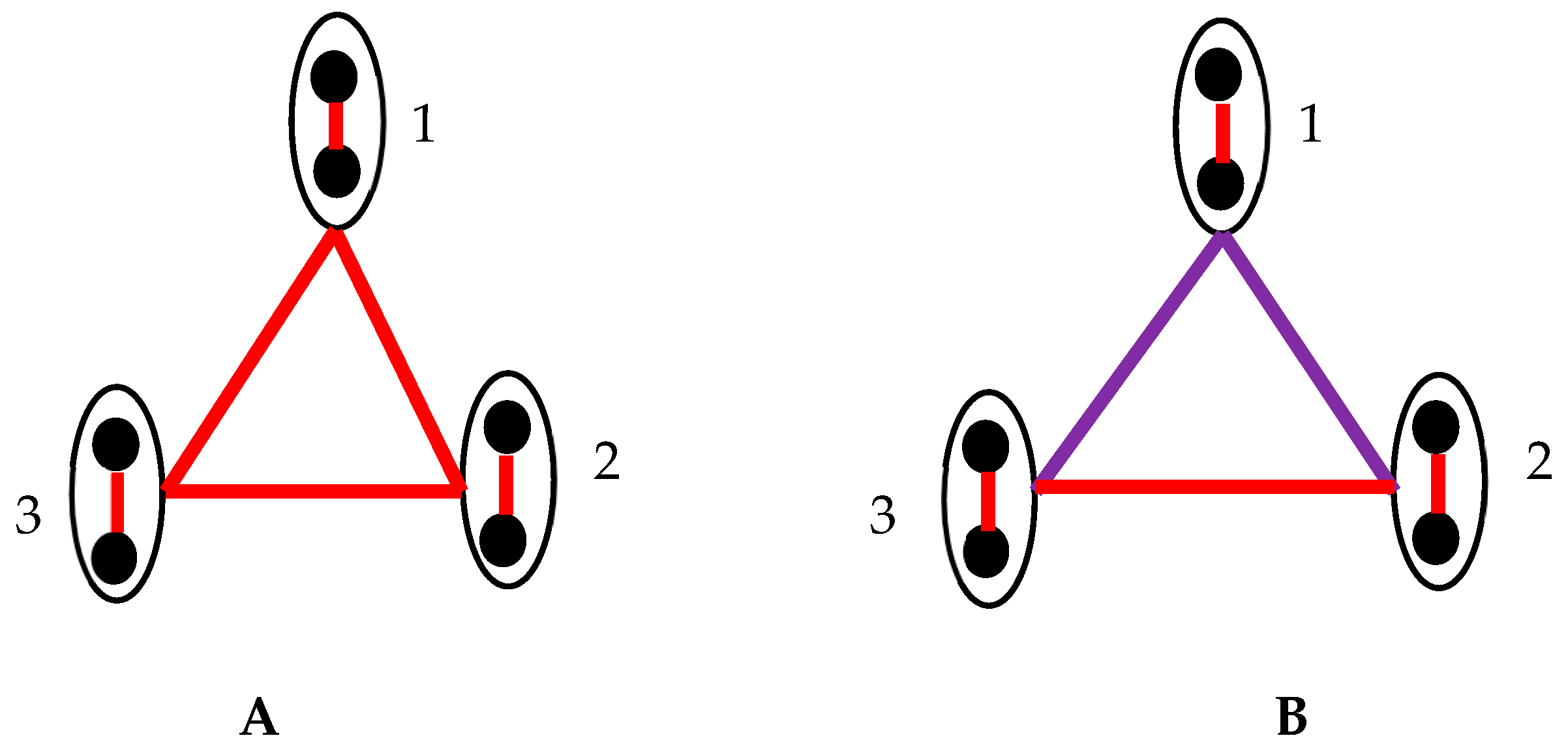
2.6. Generalization of Suggested Approach: Pairs of Synchronized Clocks Seen as the Vertices of Bi-Colored, Complete Graph

Generalization of the suggested approach for pairs of synchronized clocks, seen as the vertices of a bi-colored, complete graph, is possible. An even number of N clocks may be separated into ${\displaystyle \frac{\mathit{N}}{2}}$ pairs of clocks. These pairs may be synchronized within one of the aforementioned synchronization protocols. Now, we consider these pairs of clocks as the vertices of the graph. The pairs are not necessarily synchronized. At the next stage, the pairs may be synchronized with one of the aforementioned procedures. Synchronization with the Einstein protocol is shown in Figure 9. The transitivity of Einstein synchronization is illustrated in Figure 9A. Further analysis is straightforward, and general relativity and quantum synchronization of the pairs of clocks are performed in similar ways. The suggested procedure is easily extended to the logical clocks.

3. Discussion

Ramsey theory is applicable to any set of physical objects related to each other with different kinds of physical relations. These relations may, for example, represent interactions between physical bodies, seen as the vertices of the graph [31]. The interactions, classified as attractions and repulsions, may be seen as the differently colored links of the graph [31]. Thus, a bi-colored, complete Ramsey graph emerges. The transitivity of the interactions plays a crucial role in the analysis of the graph [31]. Thus, it seems that the Ramsey theory demonstrates enormous potential in physics. However, the application of the Ramsey theory to physical problems is still infrequent [31,32,33,34,35,36].

Bi-colored graphs emerging from the time evolution of mechanical systems were introduced [35]. Vectors of momenta of the particles serve as the vertices of the graph [36]. The coloring procedure we introduced is invariant relative to the rotations/translations of frames; thus, the graph representing the system contains at least one monochromatic triangle in any of the frames emerging from the rotation/translation of the original frame [36]. The Ramsey approach supplied a novel kind of mechanical invariant [36].

Ramsey theory has been applied to modeling the vibrational modes of cyclic molecules by representing them as complete graphs [36]. In this framework, atoms are depicted as vertices connected by edges (springs) of different types, corresponding to various chemical bonds [37]. This theory predicts that certain vibrational modes (eigenfrequencies) must necessarily exist due to the inherent structure of these graphs. This approach provides insights into the selection rules governing molecular vibrations [37].

It should be emphasized that the calculation of large Ramsey numbers remains a challenging and unsolved problem. An algorithm based on adiabatic quantum evolution that calculates the two-color Ramsey numbers R(m, n) was reported [38,39]. Lower bounds for Ramsey numbers calculated with the method of statistical physics were reported [35].

The application of the Ramsey graph theory to the analysis of physical systems built of electrical charges and electric and magnetic dipoles was reported [31]. Physical interactions may be very generally classified as attractive and repulsive. Thus, bi-colored, complete graphs emerge and the Ramsey approach becomes applicable [31]. This approach allows for the prediction of properties of crystalline structures [31].

We have proposed the application of the Ramsey approach to the synchronization of lattices of clocks, in which the clocks serve as the vertices of the synchronization graph and the relations between the clicks considering their synchronization define the color links connecting the vertices/clocks. The synchronized clocks are connected via the red link. Thus, the synchronized clocks are considered “friends” in terms of the Ramsey theory. In contrast, the vertices/clocks that are not synchronized are considered “strangers” [21,22,23,24]. Thus, a complete, bi-colored, Ramsey graph describing the synchronization within a given lattice of clocks emerges. Clock synchronization is one of the critical factors for time-based localization, particularly in GPS-based time synchronization [40,41]. GPS relies on a constellation of satellites with synchronized atomic clocks. Precise synchronization ensures compensation for relativistic effects (both gravitational and due to the satellite’s velocity). If synchronization fails, GPS accuracy collapses. The problem is also crucial for the synchronization of computers in networks [42]. Instruments like LIGO (Laser Interferometer Gravitational-Wave Observatory) and the Virgo interferometer rely on the extremely precise timing of laser beams traveling over long distances [43]. The synchronization of the interferometers at different locations is crucial for detecting the minute time differences caused by passing gravitational waves [43]. Thus, our proposed approach demonstrates obvious applicative potential.

In our future investigations, we plan to extend the suggested Ramsey approach to the synchronization of clocks in the realm of quantum gravity [44,45]. In canonical loop quantum gravity, space–time is quantized and there is no global time parameter. One approach is to choose a physical degree of freedom as a clock (such as a scalar field). Synchronization is then achieved by checking the evolution of other variables with respect to this chosen clock variable. In this way, a pair of clocks may be considered “synchronized” and “non-synchronized”. Thus, the aforementioned bi-coloring procedure is possible, and the Ramsey approach becomes applicable [46].

4. Conclusions

The synchronization of clocks plays a key role in special and general relativity and also in quantum theory. Various protocols providing such synchronization have been suggested. We propose the Ramsey approach to the synchronization of the lattices of clocks. The clocks may be synchronized and unsynchronized. The clocks serve as the vertices of the graph and the synchronization defines the color of the link connecting the vertices/clocks. Synchronized clocks are connected via the red link and are seen as “friends” in terms of the famous “party problem” of the Ramsey theory. Unsynchronized clocks are seen, in turn, as “strangers”. They are connected, in turn, via the violet link. Thus, a complete, bi-colored, Ramsey synchronization graph emerges in any given lattice of physical clocks. The coloring of the graph depends on the transitivity of the applied method of synchronization of the clocks. For example, the Einstein protocol of synchronization of clocks in special relativity is transitive, whereas the synchronization of clocks in general relativity is not necessarily transitive. The relation “to be unsynchronized” is not transitive for any kind of accepted protocols of synchronization. If the synchronization is transitive, the semi-transitive Ramsey graph emerges. The Ramsey number for semi-transitive graphs was established as $R_{trans}\left(\mathrm{3,3}\right)=5$. This means that in any semi-transitive lattice built of five clocks, at least one monochromatic triangle will necessarily appear. If the synchronization is non-transitive, the usual, bi-colored, complete Ramsey graph arises. The Ramsey numbers for these graphs are $R\left(\mathrm{3,3}\right)=6.$ This means that in any non-transitive graph reflecting a lattice built of six clocks, at least one monochromatic triangle will necessarily appear. The Ramsey theory does not predict the exact color of the monochromatic triangle present in a bi-colored, complete graph built of six vertices. Thus, the triangle comprising synchronized or, alternatively, the triangle comprising non-synchronized clocks, will necessarily appear within a set of six clocks synchronized with a non-transitive procedure.

This approach is easily extended to the quantum synchronization protocol exploiting quantum entanglement. The synchronization of clocks based on quantum entanglement is not transitive. Any lattice built of six clocks synchronized with quantum entanglement will inevitably contain a mono-chromatic triangle built of synchronized/non-synchronized clocks. Thus, “ordering” spontaneously emerges in the lattices of clocks.

The Ramsey analysis we introduced, which revealed loops of synchronized and non-synchronized clocks, is important for GPS-based time synchronization and synchronization of the LIGO (Laser Interferometer Gravitational-Wave Observatory) and Virgo interferometers intended for the registration of gravitational waves.

We also considered logical clocks, which were introduced to order events in distributed databases. Logical (Lamport) clocks order events, are disconnected from physical time, and keep logical causality. The synchronization of logical clocks is transitive. Any lattice built of five synchronized/non-synchronized clocks will contain at least one monochromatic triangle.

The relationship between the symmetry of the lattices of clocks and their coloring was addressed. A four-fold symmetrical lattice of clocks synchronized with the Einstein transitive relativistic protocol is possible, while a five-fold symmetrical lattice of clocks synchronized with the Einstein protocol that does not contain monochromatic triangles is impossible. A five-fold symmetrical lattice of clocks synchronized/unsynchronized with the non-transitive protocol that does not contain a monochromatic triangle is possible. The applications of the developed approach were addressed. We conclude that logical transitivity deeply influences synchronization within the given lattices of clocks. In other words, logical transitivity could not be separated from the properties of space–time.