Generalizing the Classical Remainder Theorem: A Reflection-Based Methodological Strategy
Abstract
1. Introduction
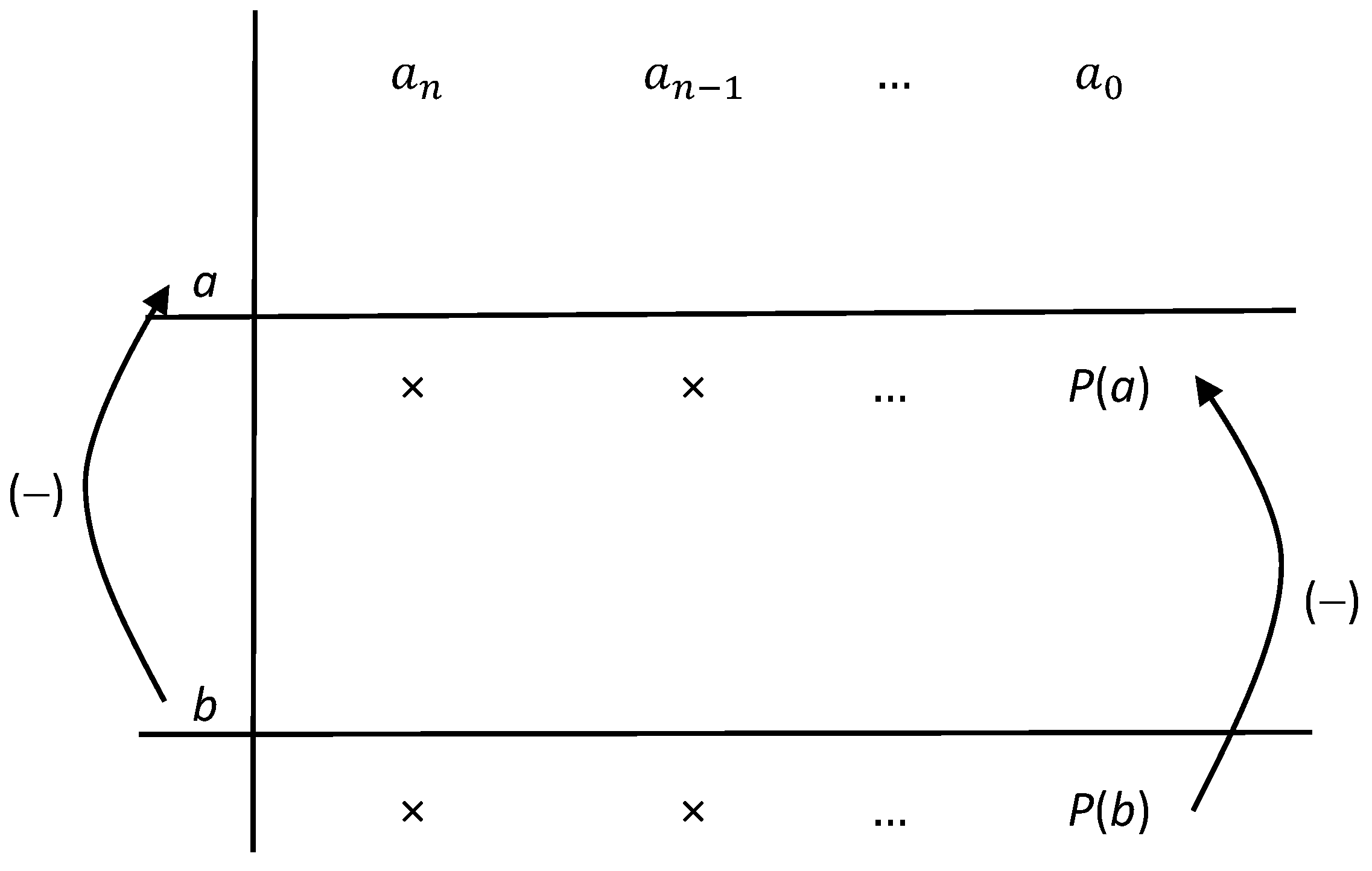
2. Generalizing the Classical Remainder Theorem
2.1. Case of a Quadratic Divisor
- .
- .
- .
- 1.
- By considering Formula (14),
- 2.
- By considering Formula (15),
2.2. Particular Case
- .
- .
- .
- .
2.3. Case of a Cubic Divisor
- .
- .
- .
2.4. Particular Case
- .
- .
- .
- .
2.5. General Case
3. Conclusions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Winger, R.M. Generalization as a method in teaching mathematics. Math. Teach. 1936, 29, 241–250. [Google Scholar] [CrossRef]
- Ellis, A.B. Generalizing-promoting actions: How classroom collaborations can support students’ mathematical generalizations. J. Res. Math. Educ. 2011, 42, 308–345. [Google Scholar] [CrossRef]
- Kinach, B.M. Generalizing: The core of algebraic thinking. Math. Teach. 2014, 107, 432–439. [Google Scholar] [CrossRef]
- Dumitrascu, G. Understanding the process of generalization in mathematics through activity theory. Int. J. Learn. Teach. Educ. Res. 2017, 16, 46–69. [Google Scholar] [CrossRef]
- Ellis, A.B. A taxonomy for categorizing generalizations: Generalizing actions and reflection generalizations. J. Learn. Sci. 2007, 16, 221–262. [Google Scholar] [CrossRef]
- Harel, G.; Martin, G. A pedagogical approach to forming generalizations. Int. J. Math. Educ. Sci. Technol. 1988, 19, 101–107. [Google Scholar] [CrossRef]
- Hashemi, N.; Abu, M.S.; Kashefi, H.; Rahimi, K. Generalization in the learning of mathematics. In Proceedings of the 2nd International Seminar on Quality and Affordable Education (ISQAE 2013), Johor, Malaysia, 7–10 October 2013; pp. 208–215. [Google Scholar]
- Burgos, M.; Tizón-Escamilla, N.; Chaverri, J. A model for problem creation: Implications for teacher training. Math. Educ. Res. J. 2024, 1–30. [Google Scholar] [CrossRef]
- Biza, I.; Hewitt, D.; Watson, A.; Mason, J. Generalization strategies in finding the nth term rule for simple quadratic sequences. Int. J. Sci. Math. Educ. 2020, 18, 1105–1126. [Google Scholar] [CrossRef]
- Laudano, F. A generalization of the remainder theorem and factor theorem. Int. J. Math. Educ. Sci. Technol. 2019, 50, 960–967. [Google Scholar] [CrossRef]
- Cuida, A.; Laudano, F.; Martinez-Moro, E. General remainder theorem and factor theorem for polynomials over non-commutative coefficient rings. Int. J. Math. Educ. Sci. Technol. 2020, 51, 775–785. [Google Scholar] [CrossRef]
- Wanicharpichat, W. A Hermite’s interpolation formula with generalized quotient and remainders theorems. Sci. Math. Jpn. Online 2010, e-2010, 183–192. [Google Scholar]
- Idarraga, I.R.A.; Salas, A.H. A generalized factor theorem. Int. J. Algebra 2011, 5, 809–816. [Google Scholar]
- Hidalgo Rosas, M.A.; Laudano, F. A vectorial approach to generalize the remainder theorem. Ann. Univ. Craiova Math. Comput. Sci. Ser. 2022, 49, 52–61. [Google Scholar] [CrossRef]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cruz Rambaud, S. Generalizing the Classical Remainder Theorem: A Reflection-Based Methodological Strategy. Foundations 2024, 4, 704-712. https://doi.org/10.3390/foundations4040044
Cruz Rambaud S. Generalizing the Classical Remainder Theorem: A Reflection-Based Methodological Strategy. Foundations. 2024; 4(4):704-712. https://doi.org/10.3390/foundations4040044
Chicago/Turabian StyleCruz Rambaud, Salvador. 2024. "Generalizing the Classical Remainder Theorem: A Reflection-Based Methodological Strategy" Foundations 4, no. 4: 704-712. https://doi.org/10.3390/foundations4040044
APA StyleCruz Rambaud, S. (2024). Generalizing the Classical Remainder Theorem: A Reflection-Based Methodological Strategy. Foundations, 4(4), 704-712. https://doi.org/10.3390/foundations4040044





