Do Pores Exist?—Foundational Issues in Pore Structural Characterisation
Abstract
1. Introduction
- Is the conceptualisation of a ‘pore’ a necessity?
- If so, how does one define a ‘pore’?
- How isomorphic with the real material does the abstract model need to be in order to be successful in the above aim?
2. Are Pores Real?
2.1. Can Pores Be Observed?
2.2. Manipulation of Pores
2.3. Structural Reality of Pores
3. The Problem of the Definition of a ‘Pore’
3.1. The Identification of Pores
3.2. Scattering Methods
3.3. Imaging Methods
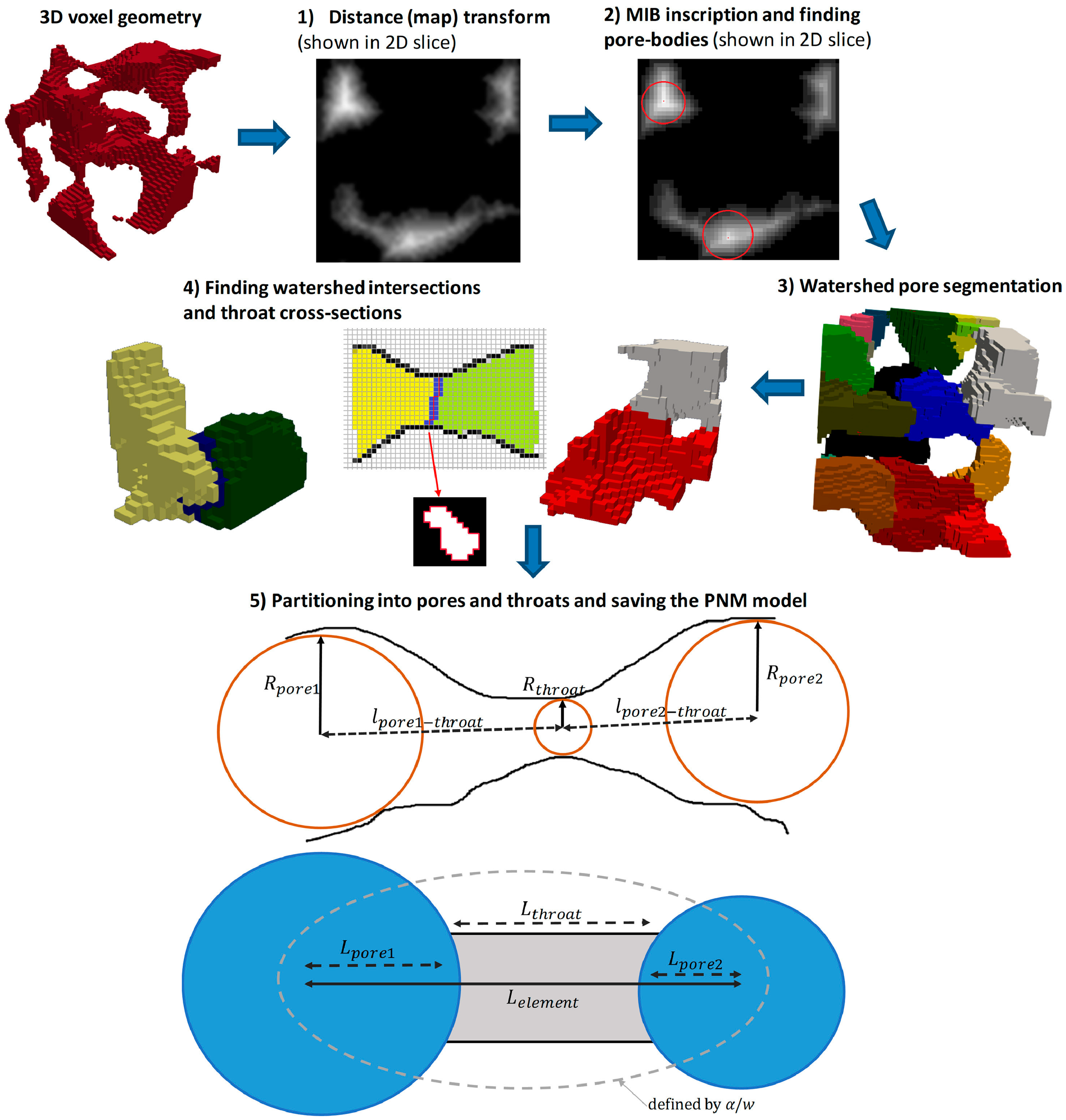
3.4. Extraction of Simplified Models
3.5. The Pore Size Distribution
4. Virtual Pores
5. Conclusions
Funding
Conflicts of Interest
References
- Rigby, S.P. Structural Characterisation of Natural and Industrial Porous Materials: A Manual; Springer International Publishing: Cham, Switzerland, 2020. [Google Scholar]
- Gregg, S.J.; Sing, K.S.W. Adsorption, Surface Area and Porosity, 2nd ed.; Academic Press: London, UK, 1982. [Google Scholar]
- Lowell, S.; Shields, J.E. Powder Surface Area and Porosity; Springer: Dordrecht, The Netherlands, 2011. [Google Scholar]
- Rouquerol, F.; Rouquerol, J.; Sing, K. Adsorption by Powders and Porous Solids: Principles, Methodology and Applications; Academic Press: London, UK, 1999. [Google Scholar]
- Dullien, F.A.L. Porous Media: Fluid Transport and Pore Structure, 2nd ed.; Academic Press: San Diego, CA, USA, 1992. [Google Scholar]
- Monton, B.; Mohler, C. Constructive Empiricism. Available online: https://plato.stanford.edu/entries/constructive-empiricism/ (accessed on 19 January 2024).
- Maxwell, G. The Ontological Status of Theoretical Entities. In Scientific Explanation, Space, and Time; Feigl, H., Maxwell, G., Eds.; Minnesota Studies in the Philosophy of Science 3; University of Minnesota Press: Minneapolis, MN, USA, 1962; pp. 181–192. [Google Scholar]
- Churchland, P. The Ontological Status of Observables: In Praise of the Superempirical Virtues. In Images of Science: Essays on Realism and Empiricism (with a reply from Bas C. van Fraassen); Churchland, P., Hooker, C., Eds.; University of Chicago Press: Chicago, IL, USA, 1985; pp. 35–47. [Google Scholar]
- Rigby, S.P.; Hasan, M.; Hitchcock, I.; Fletcher, R.S. Detection of the delayed condensation effect and determination of its impact on the accuracy of gas adsorption pore size distributions. Colloids Surf. A 2017, 517, 33–44. [Google Scholar] [CrossRef]
- Nepryahin, A.; Fletcher, R.; Holt, E.M.; Rigby, S.P. Techniques for direct experimental evaluation of structure–transport relationships in disordered porous solids. Adsorption 2016, 22, 993–1000. [Google Scholar] [CrossRef] [PubMed]
- van Fraassen, B. The Scientific Image; Oxford University Press: Oxford, UK, 1980. [Google Scholar]
- Raeini, A.Q.; Bijeljic, B.; Blunt, M.J. Generalized network modeling: Network extraction as a coarse-scale discretization of the void space of porous media. Phys. Rev. E 2017, 96, 013312. [Google Scholar] [CrossRef] [PubMed]
- Kresge, C.T.; Leonowicz, M.E.; Roth, W.J.; Vartuli, W.C.; Beck, J.S. Ordered mesoporous molecular sieves synthesised by a liquid-crystal template mechanism. Nature 1992, 359, 710–712. [Google Scholar] [CrossRef]
- Zhao, D.; Huo, Q.; Feng, J.; Chmelka, B.F.; Stucky, C.D. Nonionic triblock and star diblock copolymer and oligomeric surfactant syntheses of highly ordered, hydrothermally stable, mesoporous silica structures. J. Am. Chem. Soc. 1998, 120, 6024–6036. [Google Scholar] [CrossRef]
- Velev, O.D.; Jede, T.A.; Lobo, R.F.; Lenhoff, A.M. Porous silica via colloidal crystallization. Nature 1997, 389, 447–448. [Google Scholar] [CrossRef]
- Hacking, I. Experimentation and Scientific Realism. Philos. Top. 1982, 13, 71–87. [Google Scholar] [CrossRef]
- Neimark, A.V.; Ravikovitch, P.I. Capillary Condensation in MMS and Pore Structure Characterization. Micropor Mesopor Mater. 2001, 44, 697–707. [Google Scholar] [CrossRef]
- Ravikovitch, P.I.; O’Domhnaill, S.C.; Neimark, A.V.; Schuth, F.; Unger, K.K. Capillary Hysteresis in Nanopores: Theoretical and Experimental Studies of Nitrogen Adsorption on MCM-41. Langmuir 1995, 11, 4765–4772. [Google Scholar] [CrossRef]
- Impéror-Clerc, M.; Davidson, P.; Davidson, A. Existence of a microporous corona around the mesopores of silica-based SBA-15 materials templated by triblock copolymers. J. Am. Chem. Soc. 2000, 122, 11925–11933. [Google Scholar] [CrossRef]
- Ladyman, J. Structural Realism, Stanford Encyclopedia of Philosophy. Available online: https://plato.stanford.edu/entries/structural-realism/ (accessed on 19 January 2024).
- Porion, P.; Faugère; Levitz, P.; Van Damme, H.; Raoof, A.; Guilbaud, J.P.; Chevoir, F. A NMR investigation of adsorption/desorption hysteresis in porous silica gels. Magn. Reson. Imaging 1998, 16, 679–682. [Google Scholar] [CrossRef] [PubMed]
- Brownstein, K.R.; Tarr, C.E. Spin-lattice relaxation in a system governed by diffusion. J. Magn. Reson. 1977, 26, 17–25. [Google Scholar] [CrossRef]
- de Boer, J.H. The shapes of capillaries. In The Structure and Properties of Porous Solids; Everett, D.H., Stone, F.S., Eds.; Butterworths Scientific Publications: London, UK, 1958; p. 68. [Google Scholar]
- Hitchcock, I.; Chudek, J.A.; Holt, E.M.; Lowe, J.P.; Rigby, S.P. NMR Studies of Cooperative Effects in Adsorption. Langmuir 2010, 26, 18061–18070. [Google Scholar] [CrossRef]
- Page, J.H.; Liu, J.; Abeles, B.; Deckman, H.W.; Weitz, D.A. Pore-space correlations in capillary condensation in Vycor. Phys. Rev. Lett. 1993, 71, 1216. [Google Scholar] [CrossRef] [PubMed]
- Page, J.H.; Liu, J.; Abeles, B.; Herbolzheimer, E.; Deckman, H.W.; Weitz, D.A. Adsorption and desorption of a wetting fluid in Vycor studied by acoustic and optical techniques. Phys. Rev. E 1995, 52, 2763. [Google Scholar] [CrossRef] [PubMed]
- Liabastre, A.A.; Orr, C. Evaluation of pore structure by mercury penetration. J. Colloid. Interface Sci. 1978, 64, 1–18. [Google Scholar] [CrossRef]
- Wardlaw, N.C.; McKellar, M. Mercury porosimetry and the interpretation of pore geometry in sedimentary rocks and artificial models. Powder Technol. 1981, 29, 127–143. [Google Scholar] [CrossRef]
- Rigby, S.P.; Chigada, P.I.; Perkins, E.L.; Watt-Smith, M.J.; Lowe, J.P.; Edler, K.J. Fundamental studies of gas sorption within mesopores situated amidst an inter-connected, irregular network. Adsorption 2008, 14, 289–307. [Google Scholar] [CrossRef]
- Mousa, S.; Baron, K.; Fletcher, R.S.; Rigby, S.P. Triangulation of pore structural characterisation of disordered mesoporous silica using novel hybrid methods involving dual-probe porosimetries. Colloids Surf. A 2022, 653, 130026. [Google Scholar] [CrossRef]
- Pellenq, R.J.M.; Rousseau, B.; Levitz, P. A Grand Canonical Monte Carlo study of argon adsorption/condensation in mesoporous silica glasses. Phys. Chem. Chem. Phys. 2001, 3, 1207–1212. [Google Scholar] [CrossRef]
- Manwart, C.; Torquato, S.; Hilfer, R. Stochastic reconstruction of sandstones. Phys. Rev. E 2000, 62, 893–899. [Google Scholar] [CrossRef] [PubMed]
- Štěpánek, F.; Šoóš, M.; Rajniak, P. Characterisation of porous media by the virtual capillary condensation method. Colloids Surf. A 2007, 300, 11–20. [Google Scholar] [CrossRef]
- Yamada, H.; Tagawa, T.; Nagao, S.; Kato, S. Investigation of gas diffusion phenomena in porous catalyst support pellets based on microstructure. Catal. Today 2021, 375, 30–35. [Google Scholar] [CrossRef]
- Jivkov, A.P.; Xiong, Q. A network model for diffusion in media with partially resolvable pore space characteristics. Trans. Porous Media 2014, 105, 83–104. [Google Scholar] [CrossRef]
- Arif, M.; Mahmoud, Y.; Zhang, S.; Iglauer, S. X-ray tomography imaging of shale microstructures: A review in the context of multiscale correlative imaging. Int. J. Coal Geol. 2020, 233, 103641. [Google Scholar] [CrossRef]
- Khirevich, S.; Ginzburg, I.; Tallarek, U. Coarse-and fine-grid numerical behavior of MRT/TRT lattice-Boltzmann schemes in regular and random sphere packings. J. Comput. Phys. 2015, 281, 708–742. [Google Scholar] [CrossRef]
- Dashtian, H.; Bakhshian, S.; Hajirezaie, S.; Nicot, J.P.; Hosseini, S.A. Convection-diffusion-reaction of CO2-enriched brine in porous media: A pore-scale study. Comput. Geosci. 2019, 125, 19–29. [Google Scholar] [CrossRef]
- Bakhshian, S.; Hosseini, S.A.; Shokri, H. Pore-scale characteristics of multiphase flow in heterogeneous porous media using the lattice Boltzmann method. Sci. Rep. 2019, 9, 3377. [Google Scholar] [CrossRef]
- Hao, L.; Cheng, P. Pore-scale simulations on relative permeabilities of porous media by lattice Boltzmann method. Int. J. Heat. Mass. Transf. 2010, 53, 1908–1913. [Google Scholar] [CrossRef]
- Zhang, M.Z.; Xu, K.M.; He, Y.J.; Jivkov, A.P. Pore-scale modelling of 3D moisture distribution and critical saturation in cementitious materials. Constr. Build. Mater. 2014, 64, 222–230. [Google Scholar] [CrossRef]
- Raeini, A.Q.; Blunt, M.J.; Bijeljic, B. Modelling two-phase flow in porous media at the pore scale using the volume-of-fluid method. J. Comput. Phys. 2012, 231, 5653–5668. [Google Scholar] [CrossRef]
- Bilger, C.; Aboukhedr, M.; Vogiatzaki, K.; Cant, R.S. Evaluation of two-phase flow solvers using level set and volume of fluid methods. J. Comput. Phys. 2017, 345, 665–686. [Google Scholar] [CrossRef]
- Holmes, D.W.; Williams, J.R.; Tilke, P.; Leonardi, C.R. Characterizing flow in oil reservoir rock using SPH: Absolute permeability. Comput. Particle Mech. 2016, 3, 141–154. [Google Scholar] [CrossRef]
- Tartakovsky, A.M.; Meakin, P.; Scheibe, T.D.; West, R.M.E. Simulations of reactive transport and precipitation with smoothed particle hydrodynamics. J. Comput. Phys. 2007, 222, 654–672. [Google Scholar] [CrossRef]
- Tartakovsky, A.M.; Meakin, P. Pore scale modeling of immiscible and miscible fluid flows using smoothed particle hydrodynamics. Adv. Water Resour. 2006, 29, 1464–1478. [Google Scholar] [CrossRef]
- Shabro, V.; Torres-Verdín, C.; Javadpour, F.; Sepehrnoori, K. Finite-difference approximation for fluid-flow simulation and calculation of permeability in porous media. Transp. Porous Media 2012, 94, 775–793. [Google Scholar] [CrossRef]
- Oren, P.E.; Bakke, S.; Held, R. Direct pore-scale computation of material and transport properties for North Sea reservoir rocks. Water Resour. Res. 2007, 43, W12S04. [Google Scholar] [CrossRef]
- Verma, R.; Icardi, M.; Prodanović, M. Effect of wettability on two-phase quasi-static displacement: Validation of two pore scale modeling approaches. J. Contam. Hydrol. 2018, 212, 115–133. [Google Scholar] [CrossRef] [PubMed]
- Demianov, A.; Dinariev, O.; Evseev, N. Density functional modelling in multiphase compositional hydrodynamics. Can. J. Chem. Eng. 2011, 89, 206–226. [Google Scholar] [CrossRef]
- Rokhforouz, M.R.; Akhlaghi Amiri, H.A. Phase-field simulation of counter-current spontaneous imbibition in a fractured heterogeneous porous medium. Phys. Fluids 2017, 29, 062104. [Google Scholar] [CrossRef]
- Gerke, K.M.; Sizonenko, T.O.; Karsanina, M.V.; Lavrukhin, E.V.; Abashkin, V.V.; Korost, D.V. Improving watershed-based pore-network extraction method using maximum inscribed ball pore-body positioning. Adv. Water Resour. 2020, 140, 103576. [Google Scholar] [CrossRef]
- Nepryahin, A.; Fletcher, R.; Holt, E.M.; Rigby, S.P. Structure-transport relationships in disordered solids using integrated rate of gas sorption and mercury porosimetry. Chem. Eng. Sci. 2016, 152, 663–673. [Google Scholar] [CrossRef]
- Weisberg, M. Simulation and Similarity: Using Models to Understand the World; Oxford University Press: Oxford, UK, 2013. [Google Scholar]
- Xiong, Q.; Baychev, T.G.; Jivkov, A.P. Review of pore network modelling of porous media: Experimental characterisations, network constructions and applications to reactive transport. J. Contam. Hydrol. 2016, 192, 101–117. [Google Scholar] [CrossRef] [PubMed]
- Houston, A.N.; Otten, W.; Falconer, R.; Monga, O.; Baveye, P.C.; Hapca, S.M. Quantification of the pore size distribution of soils: Assessment of existing software using tomographic and synthetic 3D images. Geoderma 2017, 299, 73–82. [Google Scholar] [CrossRef]
- Baychev, T.G.; Jivkov, A.P.; Rabbani, A.; Raeini, A.Q.; Xiong, Q.; Lowe, T.; Withers, P.J. Reliability of Algorithms Interpreting Topological and Geometric Properties of Porous Media for Pore Network Modelling. Transp. Porous Med. 2019, 128, 271–301. [Google Scholar] [CrossRef]
- Miao, X.; Gerke, K.M.; Sizonenko, T.O. A new way to parameterize hydraulic conductances of pore elements: A step forward to create pore-networks without pore shape simplifications. Adv. Water Resour. 2017, 105, 162–172. [Google Scholar] [CrossRef]
- Rabbani, A.; Babaei, M. Hybrid pore-network and lattice-Boltzmann permeability modelling accelerated by machine learning. Adv. Water Resour. 2019, 126, 116–128. [Google Scholar] [CrossRef]
- Baldwin, C.A.; Sederman, A.J.; Mantle, M.D.; Alexander, P.; Gladden, L.F. Determination and characterization of the structure of a pore space from 3D volume images. J. Colloid. Interface Sci. 1996, 181, 79–92. [Google Scholar] [CrossRef]
- Lindquist, W.B.; Venkatarangan, A.; Dunsmuir, J.; Wong, T.F. Pore and throat size distributions measured from synchrotron X-ray tomographic images of Fontainebleau sandstones. J. Geophys. Res. Solid. Earth 2000, 105, 21509–21527. [Google Scholar] [CrossRef]
- Prodanović, M.; Lindquist, W.B.; Seright, R.S. 3D image-based characterization of fluid displacement in a Berea core. Adv. Water Resour. 2007, 30, 214–226. [Google Scholar] [CrossRef]
- Jiang, Z.; Wu, K.; Couples, G.; Van Dijke, M.; Sorbie, K.; Ma, J. Efficient extraction of networks from three-dimensional porous media. Water Resour. Res. 2007, 43, W12S03. [Google Scholar] [CrossRef]
- Silin, D.; Patzek, T. Pore space morphology analysis using maximal inscribed spheres. Physica A Stat. Mech. Appl. 2006, 371, 336–360. [Google Scholar] [CrossRef]
- Dong, H.; Blunt, M.J. Pore-network extraction from micro-computerized-tomography images. Phys. Rev. E 2009, 80, 036307. [Google Scholar]
- Arand, F.; Hesser, J. Accurate and efficient maximal ball algorithm for pore network extraction. Comput. Geosci. 2017, 101, 28–37. [Google Scholar] [CrossRef]
- Sheppard, A.P.; Sok, R.M.; Averdunk, H. Improved pore network extraction methods. In Proceedings of the International Symposium of the Society of Core Analysts, Toronto, ON, Canada, 21–25 August 2005; p. 2125. [Google Scholar]
- Rabbani, A.; Jamshidi, S.; Salehi, S. An automated simple algorithm for realistic pore network extraction from micro-tomography images. J. Petrol. Sci. Eng. 2014, 123, 164–171. [Google Scholar] [CrossRef]
- Gostick, J.T. Versatile and efficient pore network extraction method using marker-based watershed segmentation. Phys. Rev. E 2017, 96, 023307. [Google Scholar] [CrossRef] [PubMed]
- Bakhshian, S.; Hosseini, S. Pore–scale analysis of supercritical CO2–brine immiscible displacement under fractional–wettability conditions. Adv. Water Resour. 2019, 126, 96–107. [Google Scholar] [CrossRef]
- Yi, Z.; Lin, M.; Jiang, W.; Zhang, Z.; Li, H.; Gao, J. Pore network extraction from pore space images of various porous media systems. Water Resour. Res. 2017, 53, 3424–3445. [Google Scholar] [CrossRef]
- Bondino, I.; Hamon, G.; Kallel, W.; Kac, D. Relative permeabilities from simulation in 3D rock models and equivalent pore networks: Critical review and way forward. Petrophysics 2013, 54, 538–546. [Google Scholar]
- Ams, C.H.; Knackstedt, M.A.; Val Pinczewski, W.; Martys, N.S. Virtual permeametry on microtomographic images. J. Pet. Sci. Eng. 2004, 45, 41–46. [Google Scholar]
- Diamond, S. Mercury porosimetry—An inappropriate method for the measurement of pore size distributions in cement-based materials. Cem. Concr. Res. 2000, 30, 1517–1525. [Google Scholar] [CrossRef]
- Münch, B.; Holzer, L. Contradicting geometrical concepts in pore size analysis attained with electron microscopy and mercury intrusion. J. Am. Ceram. Soc. 2008, 91, 4059–4067. [Google Scholar] [CrossRef]
- Androutsopoulos, G.P.; Mann, R. Evaluation of mercury porosimeter experiments using a network pore structure model. Chem. Eng. Sci. 1979, 34, 1203–1212. [Google Scholar] [CrossRef]
- Portsmouth, R.L.; Gladden, L.F. Determination of pore connectivity by mercury porosimetry. Chem. Eng. Sci. 1991, 46, 3023–3036. [Google Scholar] [CrossRef]
- Malek, K.; Coppens, M.-O. Knudsen self- and Fickian diffusion in rough nanoporous media. J. Chem. Phys. 2003, 119, 2801–2811. [Google Scholar] [CrossRef]
- Mann, R.; Allamy, A.; Holt, A. Visualised porosimetery for pore structure characterisation of nickel/alumina reforming catalysts. Chem. Eng. Res. Des. 1995, 73, 147–153. [Google Scholar]
- Ruffino, L.; Mann, R.; Oldham, R.J.; Rigby, S.; Allen, S. Using low melting point alloy intrusion to quantify pore structure: Studies on an alumina catalyst support. Stud. Surf. Sci. Catal. 2001, 133, 155–162. [Google Scholar]
- Allamy, A.; Mann, R.; Holt, A. Modelling of catalyst particle skin effects using a 3-D pore network model and quantitative microscopy. Chem. Eng. Sci. 2003, 58, 1989–2000. [Google Scholar] [CrossRef]
- Ruffino, L.; Mann, R.; Oldman, R.; Stitt, E.H.; Boller, E.; Cloetens, P.; DiMichiel, M.; Merino, J. Using x-ray microtomography for characterisation of catalyst particle pore structure. Can. J. Chem. Eng. 2005, 83, 132–139. [Google Scholar] [CrossRef]
- Rieckmann, C.; Keil, F.J. Simulation and experiment of multicomponent diffusion and reaction in three-dimensional networks. Chem. Eng. Sci. 1999, 54, 3485–3493. [Google Scholar] [CrossRef]
- Seaton, N.A. Determination of the connectivity of porous solids from nitrogen sorption measurements. Chem. Eng. Sci. 1991, 46, 1895–1909. [Google Scholar] [CrossRef]
- Mousa, S.; Novak, V.; Fletcher, R.S.; Garcia, M.; Mcleod, N.; Corfield, M.; Rigby, S.P. Integration of multi-scale porosimetry and multi-modal imaging in the study of structure-transport relationships in porous catalyst pellets. Chem. Eng. J. 2023, 452, 139122. [Google Scholar] [CrossRef]
- Rigby, S.P.; Watt-Smith, M.J.; Fletcher, R.S. Simultaneous determination of the pore-length distribution and pore connectivity for porous catalyst supports using integrated nitrogen sorption and mercury porosimetry. J. Catal. 2004, 227, 68–76. [Google Scholar] [CrossRef]
- Mousa, S.; Novak, V.; Fletcher, R.S.; Kelly, G.; Garcia, M.; Mcleod, N.; Parmenter, C.; Rigby, S.P. Evolution of the pore structure-transport relationship during catalyst reduction and sintering studied by integrated multi-scale porosimetry and multi-modal imaging. Chem. Eng. Sci. 2023, 277, 118880. [Google Scholar] [CrossRef]









| Pore Characterisation Method | Pore Size Range | Most Appropriate Porous Materials | Advantages | Disadvantages |
|---|---|---|---|---|
| Gas sorption (with overcondensation) | 0.3 nm–10 μm | Sol–gel silica, alumina, carbons, MOFs, zeolites, shales. | Wide pore size range within single experiment. | Indirect—requires model of interpretation. Sample needs pre-preparation (e.g., drying and evacuation) |
| Mercury porosimetry | 3.5 nm–100 μm | Sol–gel silica, alumina, monoliths, rocks. | Wide pore size range within single experiment. | Indirect—requires model of interpretation. Sample needs pre-preparation (e.g., drying and evacuation). High pressure may cause mechanical damage. |
| Thermoporometry | 2 nm–100 nm | Wet samples, e.g., gels. | Can run wet samples using pore fluid as probe. | The Gibbs–Thomson parameter limits pore size range for many probe fluids. |
| Small-angle X-ray scattering (SAXS) | 0.3 nm–200 nm | Samples with closed porosity, e.g., shales. | Can probe closed porosity. | Struggles with deconvolution of partially ordered systems. |
| NMR relaxometry | 1 nm–10 μm | Wet samples. | Can use on already wet samples using existing fluid as probe. Can be made fully 3D by coupling with MRI methods. | The presence of paramagnetic impurities can complicate interpretation. |
| FIB-SEM | 10 nm–1000 nm | Silicas, aluminas, carbons, rocks. | Direct characterisation. | Small sample size (microns). Slice thickness is finite. Beam can cause sample damage. Requires image analysis to remove noise and artefacts. |
| TEM | 0.1 nm–100 nm | Mesoporous solids. | Direct characterisation. Can be made tomographic. | Small sample size (few microns). Beam can cause sample damage. Requires image analysis to remove noise and artefacts. |
| Computerised X-ray Tomography (CXT) | 50 nm–100 μm | Rocks, monoliths. | Direct characterisation. Can add contrast agent to enhance image clarity. | Beam can cause sample damage. Can only obtain large sample volumes with low resolution. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rigby, S.P. Do Pores Exist?—Foundational Issues in Pore Structural Characterisation. Foundations 2024, 4, 225-248. https://doi.org/10.3390/foundations4020015
Rigby SP. Do Pores Exist?—Foundational Issues in Pore Structural Characterisation. Foundations. 2024; 4(2):225-248. https://doi.org/10.3390/foundations4020015
Chicago/Turabian StyleRigby, Sean P. 2024. "Do Pores Exist?—Foundational Issues in Pore Structural Characterisation" Foundations 4, no. 2: 225-248. https://doi.org/10.3390/foundations4020015
APA StyleRigby, S. P. (2024). Do Pores Exist?—Foundational Issues in Pore Structural Characterisation. Foundations, 4(2), 225-248. https://doi.org/10.3390/foundations4020015






