Towards a Social-Ecological-Entropy Perspective of Sustainable Exploitation of Natural Resources

Abstract

An innovative and integrative modeling strategy for assessing the sustainability and resilience of social-ecological systems (SES) is presented by introducing a social-ecological entropy production (SEEP) method. In analogy to the thermodynamic entropy production of irreversible processes, we discuss a theoretical model that relates energy and information flow with the cultural and epistemological peculiarities of different communities that exploit the same natural resource. One of the innovative aspects of our approach comes from the fact that sustainability is assessed by a single parameter (SEEP) incorporating the simulation outcomes of all the populations participating in the dynamics, and not only on the fate of the resource. This is significant as far as the non-linearities introduced by the coupling of the different dynamics considered may lead to high sensitivity to small perturbations. Specifically, by assuming two possible types of technical and environmental knowledge-transfer methods [direct (D) and phase-in (P)] within each one of the two communities that exploit and restore a resource, we generate four mathematical models to explore the long-term sustainability scenario due to the intervention, by a new epistemological community, of an initially sustainable resource-community SES. By exploring the space of four key parameters characterizing the degree of technical and environmental knowledge, as well as the rates of social inclusion and knowledge transfer, our simulations show that, from 400 scenarios studied in each case, the P-P model predicts 100% sustainable cases in the use of the resource after the intervention by the second community. The mixed scenarios P-D and D-P predict about 29%, and the D-D scenario only predicts 23% of sustainable cases. Catastrophic outcomes are predicted at about 71% in P-D and D-P scenarios, and about 77% of extinction of the system by exhaustion of the resource and community populations in the D-D scenario. In this form, our theoretical strategy and the knowledge-transfer scenarios studied may help policymakers to find a priori science-based criteria to solve possible controversies arising from social-ecological interventions.

1. Introduction

The coupling between humanity and the environment relies on bidirectional feedback [1,2,3,4,5,6]. On the one hand, society impacts the natural systems by exploiting, extracting, and (sometimes) restoring resources and polluting and leaving waste. However, conversely, the environment affects the social systems by providing or restricting the resources required for their survival or any other purpose [2,7,8].

If the relation between both systems implies that their impacts do not threaten their future existence, the association is sustainable [7,9]. However, overpopulation, overconsumption, and economic inequality have decreased the viability of social-ecological systems, leading them to possible unsustainable future scenarios, that is, risking the persistence of the actual roles and functions of both human and natural systems [1,4,5,6].

In practice, implementing sustainable strategies and policies that regulate social behavior to restructure socio-ecological relations ignores epistemological aspects and focuses above all on the ecological-economic part [10,11,12,13]. The resource management and intervention policies cannot be regarded as social-ecological experiments. The effects produced by some policies, similarly to the experiments, are a priori unknown and sometimes cause irreversible alterations in the life and activities of individuals and in environmental processes [5,12].

Unlike the experiments, the main objective of the policies is not to test hypotheses, and the justification is not to deduce some knowledge. Instead, their objective is the regulation of social behavior. They are based on political ideologies and economic interests. In the attempt to reduce risks in deciding policies, regulations establishing wide-view analyses on the viability and possible scope and effects of the intervention are welcome [4,5,14,15,16]. However, these requirements are fulfilled with isolated studies of economic, ecologic, and social impacts. Thus, in non-integrated studies, the complex processes of the coupled social and natural systems are not evident [1,7]. Furthermore, the policies usually do not consider the possibility of most actors’ perspectives, perspectives emerging from diverse interests and epistemological backgrounds [13,15]. This fact often raised the question about the advisability of an a priori assessment of the possible results of implementing a given policy that incorporates feedback information associated with social practices, such as the implementation of different information transfer methods for resource exploitation and management [7,12,14].

Historically, many civilizations have collapsed due to their poor resource-management policies and the lack of an ability to modify their cultural practices, creating unsustainable trajectories [6,17]. However, it has been pointed out that our society could be considered advantageous over those civilizations for having valuable tools to predict and anticipate some possible future events [6,18]. Mathematical models can be helpful for the forethought of our actions. Specifically, the use of dynamic models allows one to explore the complex relations between society and the environment as coupled systems [4,5,6,16], rather than to conduct unnecessary social experiments by implementing policies or strategies based only on ideological statements. Therefore, it is beneficial to implement them on quantitative models that can predict several possible scenarios of complex social-ecological phenomena. Implementing those models may reduce the uncertainty of proposed policies and interventions and lead to insights and highlights that may produce knowledge-based plans.

The modeling and understanding of the complexity of the social-ecological systems entail the contribution of many ingredients [19,20,21]. Therefore, any mathematical model of their dynamics should be performed via numerical calculations or simulations of deterministic or stochastic systems. In the realm of deterministic or mean-field models, for example, a considerable number of applicable dynamical models have been constructed in virology and in epidemiology to control outbreaks, invasions, and transmissions [22,23,24,25] and also for informing and analyzing health policies [26,27,28]. Mathematical models describe the dynamics of a complex system through a set of rules. These rules are assumptions and hypotheses about the properties and relations between the elements of the system. With the proper links, it is possible to describe the current and possible future states of the system [24,26]. Therefore, to formulate a model, we need to form explicit and compelling hypotheses, and abstract fundamental properties and relevant relations of the system. All these elements should be introduced as mathematical rules. Simulations of the model system then bring a spectrum of possible results and foresight that can guide actors in implementing social interventions.

The overwhelming quantity of factors and actors involved, and the multiple relations between a large number of variables that seem to play a relevant role in the social-ecological processes, raises the question of how to reduce the system’s complexity without oversimplifying it.

How can the abstraction of simple relations between relatively few variables give us adequate and relevant information about their influence in the studied situation and produce knowledge about complex social structures? These are indeed non-trivial questions, and the multiple answers are still incomplete today. However, certain principles help us to reduce complexity while avoiding oversimplification. First, a model should be consistent with the known general laws of physics, chemistry, and biology. This consistency allows us to make more realistic models without losing generality. The second is that a model should be flexible enough to incorporate local or particular characteristics of the social-ecological system it is trying to describe. Informative campaigns, surveys, and social or economic indexes are helpful when the policies concern a vast number of actors with common properties or when the characteristics of the population are almost homogeneous. However, the problem may become different when the cultural, social, and epistemological features of the communities are more heterogeneous.

In the present work, we focus our attention on the effect that cultural diversity and epistemological heterogeneity may have on a system’s sustainability because local communities can often initially exploit a natural resource with primitive technical knowledge before a more technological community attempts to exploit that resource. Since cultural diversity and epistemological heterogeneity determine different perceptions of the individuals and the communities on their own activities and on the activities of other communities with which they need to interact when they are interested in the exploitation of a natural resource, social and political controversies may arise. A possible consequence of these controversies is the accelerated degradation of the environment, as well as the degradation of inclusion of different population sectors on the dynamics of the whole SES, leading to poverty and social marginalization. We account for this heterogeneity by considering the different types of knowledge that a social group (sector) possesses and how this knowledge is transferred between several social groups in each community. Knowledge transfer becomes, therefore, of crucial importance when trying to foresee the consequences of adopting a policy that promotes or inhibits the interactions between different epistemological communities and among them and with the natural resource in question.

Hence, we propose that an adequate modeling and simulation strategy of a social-ecological system should be flexible and must consider the different types of knowledge and knowledge-transfer methods of a social group and should be general enough to deal with them with some general laws of physics that we will describe in detail later. This consistency provides a robust helpful parameter to provide an a priori assessment of the assumptions in the proposal of a policy, thereby yielding a less ideological decision-making strategy.

Based on the previous considerations, we develop the model formulation and search for quantitative results in the following sections. Accordingly, in Section 2 we start by defining terminology that will be used in subsequent sections with specific meanings. It defines an SES and its relation with knowledge and knowledge transfer, which are two key ingredients of the theoretical model. We also provide the main hypothesis of this work, and arguments in favor of considering information (knowledge exchange between individuals and communities) as a form of energy exchange. After this and, in comparison with the thermodynamics of irreversible processes, we postulate the SEEP as a single integrative helpful parameter to quantify the sustainability degree of social-ecological interventions in exploiting a natural resource. In Section 3, we proceed to fix ideas presenting an in abstracto formulation of the model developed and mapped to mathematical equations through the section. Section 4 is devoted to simulating one resource and two community cases. Large simulations of the dynamical system are presented and characterized in terms of parametric planes, in which the amount of technical and restoring knowledge serves to evaluate the following three possible outcomes of the model: sustainable, catastrophic, and extinction scenarios, with all of them properly defined in the same section. Final comments and conclusions are presented in Section 5.

2. What We Mean by Social-Ecological System?

Social-ecological systems are mostly composed by several social groups interacting in and with their ecological surroundings. Hence, the elements of these systems are social subsystems and ecological resources.

We conceive three kinds of interactions between these elements:

• A social subsystem interacts with its environment through extraction or restoration of ecological resources.
• A social subsystem interacts with another social subsystem by cooperation or competition processes.
• The members of a social subsystem interact with each other by sharing, transmitting, or transferring knowledge.

The consequences of the interactions between a social group and the environment imply an energy exchange. On the other hand, the interaction inside a social group consists of communication and exchanging information. Consequently, the interaction between social groups can be understood as a combination of energy and information exchanges [7]. Here, it is important to stress that only part of this information can be considered knowledge [15].

When talking about energy exchange, one must keep in mind that the laws of thermodynamics dictate how energy and entropy are exchanged and produced. This fact suggests that it should be possible to treat the energy and information exchanges and their inner transformations by employing the laws of thermodynamics, at least in analogy. The concept of energy quantifies the capacity of a system to conduct physical or chemical work, which is a way to change the state of a system. The concept of entropy quantifies the different ways the energy exchanges take place and how they influence the global state of a thermodynamic system. In other words, the entropy measures the more probable possibilities for energy distribution in a thermodynamic system.

In the case of a social-ecological system, one can conceptualize and quantify the exchange of energy and entropy in terms of the modifications of the states of the different social subsystems and ecological resources that make up it. These states can be characterized by different types of indexes such as populations, representing a social system (for instance, the number of healthy citizens and citizens having a specific kind of disease; or the wealth distribution across different regions of a country) or intensities (for instance, the energy consumption per citizen per squared meter in a country or an area). The dynamics of these populations are dictated mainly by some inherent properties of the social groups and cultures involved (such as growth–death dynamics) and in part by their interaction with an environment that provides them resources (exploitation–restoration dynamics) [7,9,12,15].

In the case of social systems, it is possible to conceptualize these interactions among the members of a social group (system) and the interactions among two or more social groups (systems) as information-knowledge exchanges [15]. This is because part of the interaction takes place by exchanging material products or energy; however, if these products are not ecological resources, the interaction can be interpreted as an information-knowledge exchange. This conclusion follows from the fact that every product produced by man has been previously known.

An important example of this is money. The value of money is not the energy of the coin. Instead, it depends on the constructed social meaning assigned to it. Therefore, in money exchange, what is really exchanged is the information-knowledge content. As we have previously explained, this information content may change the state of the social subsystem and, therefore, its energy and entropy.

Given the previous considerations, here, we attempt to use some principles of irreversible thermodynamics [29] as general criteria for studying the dynamics of social-ecological systems and benefit our comprehension of their time and spatial development.

2.1. Irreversibility in a SES

The energy exchange among several physicochemical subsystems is irreversible when it involves increasing the number of states accessible to the whole system due to the dissipation of the energy in, precisely, the creation or exploration of these new states. The entropy, therefore, characterizes this creation of new states [29].

Similarly to energy and entropy in physicochemical systems, exchanging information can also be considered an irreversible process. The point is that one may understand, in terms of irreversibility associated with an exchange of information, that the total number of epistemological states available for a given social subsystem tends to increase after every interaction. The acquisition of new information, such as one new concept, raises the whole set of possible relations between it and all the previous concepts. The enlargement in possible connections increases the entropy of the social-ecological system. This reasoning applies to all types of information; that is, those comprising efficient and valid knowledge and the remaining, which can be rationalized as irrelevant or misunderstood information or even false knowledge. In all cases, the number of available information states increases as it can be related to the previous accessible states of information.

Therefore, we further consider that the energy and information exchanges are, in general, irreversible; in agreement with the second law of thermodynamics, all irreversible processes imply the production entropy, that is, the creation of new possible accessible states in the whole system [29].

However, this might raise questions about the possibility of balanced exchanges of energy and information that do not entail an increase in the total number of states. In such a case, the relation between the social subsystem and the corresponding ecological resource does not produce entropy. This situation seems similar to what is recognized as a reversible process in thermodynamics. There are two possible interpretations for these situations. Consider, for instance, the exploitation of a resource by a given community. The first interpretation is that it could happen that the environment immediately replaces the exploitation of the resource (for example, harvesting). However, the opposite possibility may also happen. That is, the environment immediately rejects the restoration of the resource (for example, sowing). The second interpretation, a more realistic one, is that the relation between them does not exist.

A similar situation may be considered if the inner interactions of a social subsystem do not produce entropy. No entropy production will imply that nobody is learning anything and every new death is immediately replaced by a newborn or, in a more realistic interpretation, those interactions do not exist. Thus, in the framework we are proposing, the system produces social entropy in every existing interaction, including energy and information exchanges.

In summary, one may extend the application of the second law of thermodynamics by introducing the concept of a social-ecological entropy (SEE) that measures how the interactions among different elements of the social-ecological systems take place and how they change the state of the whole system. More formally, by introducing the social-ecological entropy, we assume that the energy distribution of a social-ecological system is modified and perturbed by the information exchanges in such a way that the entropy must be a function of the energy and the energy a function of the information; that is,

$$S_{se}=S_{se}\left[E\left(I\right)\right],$$

(1)

$S_{se}$ stands for the social-ecological entropy, E for the energy and I for the information.

Irreversible thermodynamics uses the entropy production law as the criterium that dictates the direction of the temporal and natural evolution of systems exchanging energy [29]. Accordingly, we propose that the time evolution of a social-ecological system is determined by the social-ecological entropy production per unit of time in such a way that the time change of the entropy can be used as a single global parameter, which is helpful in assessing both the state and the dynamics of a social-ecological system. One of the key points of this work is as follows: The time evolution of social-ecological entropy, which collects all the energetic and informative interactions among the relevant actors of a given social-ecological system in a single concept, allows us to evaluate: (i) the state of the system as a function of time, (j) the state of the dynamics and, as a consequence, (k) the sustainability of these dynamics.

2.2. The Analogy with Chemical Kinetics

The chemical kinetics of elementary step reaction mechanisms is consistent with the laws of irreversible thermodynamics [29]. Chemical kinetics establishes the time evolution equations of the number of molecules per unit volume (that is, concentrations) during a non-equilibrated chemical reaction. The chemical kinetics of complex reactions are mathematically accounted for by systems of ordinary differential equations that constitute non-linear dynamical systems and therefore are at the heart of complex systems theories. Therefore, all the corresponding analyses and mathematical results of the theory of non-linear dynamical systems (for instance, stability and bifurcation analysis, chaos) can be used to understand the formal results emerging from the presented systems of equations.

Using chemical kinetics analogously, we will assume that the social-ecological dynamics depend on the energetic and entropic considerations already described. Thus, to model the time evolution of a social-ecological system, we proceed by establishing an analogy with the chemical kinetics of reactant and product concentrations, that is, by using the same mathematical tools of non-linear dynamical systems.

2.3. Bio-Mathematical Models and SEE Novelty

A chemical reactant’s concentration represents the molecules’ population per unit volume. Therefore, at the thermodynamic level of description, different molecules are described in terms of their molecule populations and the formation of intermediary or final products as transitory or final populations.

Historically, the extrapolation of the chemical kinetics principles to describe the behavior of other kinds of populations has been helpful, especially in the mathematical modeling of biological systems. For instance, in disciplines such as fishery [10,11,30], ecology [12,19,31] or epidemiology [19,24,25,28,31,32], mathematical models have become helpful in understanding and “predicting” risks on the population’s dynamics and their possible fates. From these examples, epidemiology provides good insight into how human dynamics can be introduced in mathematical modeling, since the usual epidemiological models treat the spread of diseases by classifying sectors of the total population and analyzing how each sector reacts when interaction with another sector occurs, leading to a certain outcome. This is the case of the classical SIR model (susceptible, infected, and recovered individuals) [19] and other models adapted to specific outbreaks such as COVID-19 [24,25,32]. On the other hand, ecological models focus on the interactions among different species [31], such as the logistic model for population growth and the mathematical representation of resource competition.

In our approach to the dynamics and thermodynamics of social-ecological systems, we incorporate the energetic and entropic assumptions previously discussed, the representation of chemical kinetics by non-linear dynamical systems, and some functional forms of bio-mathematical models.

The novelty of our approach lies in the fact that we introduce a coupling between social and ecological systems through the use of a two-level description: the internal and external dynamics of the social subsystems characterized through the information-knowledge exchange and their exploitation of a natural resource, that is, the interaction with a given ecological environment [5,12,15,30]. Finally, all the information is integrated and analyzed according to social-ecological entropy production that provides one with a general criterium to evaluate the time evolution of the sustainability and the dynamics of the system.

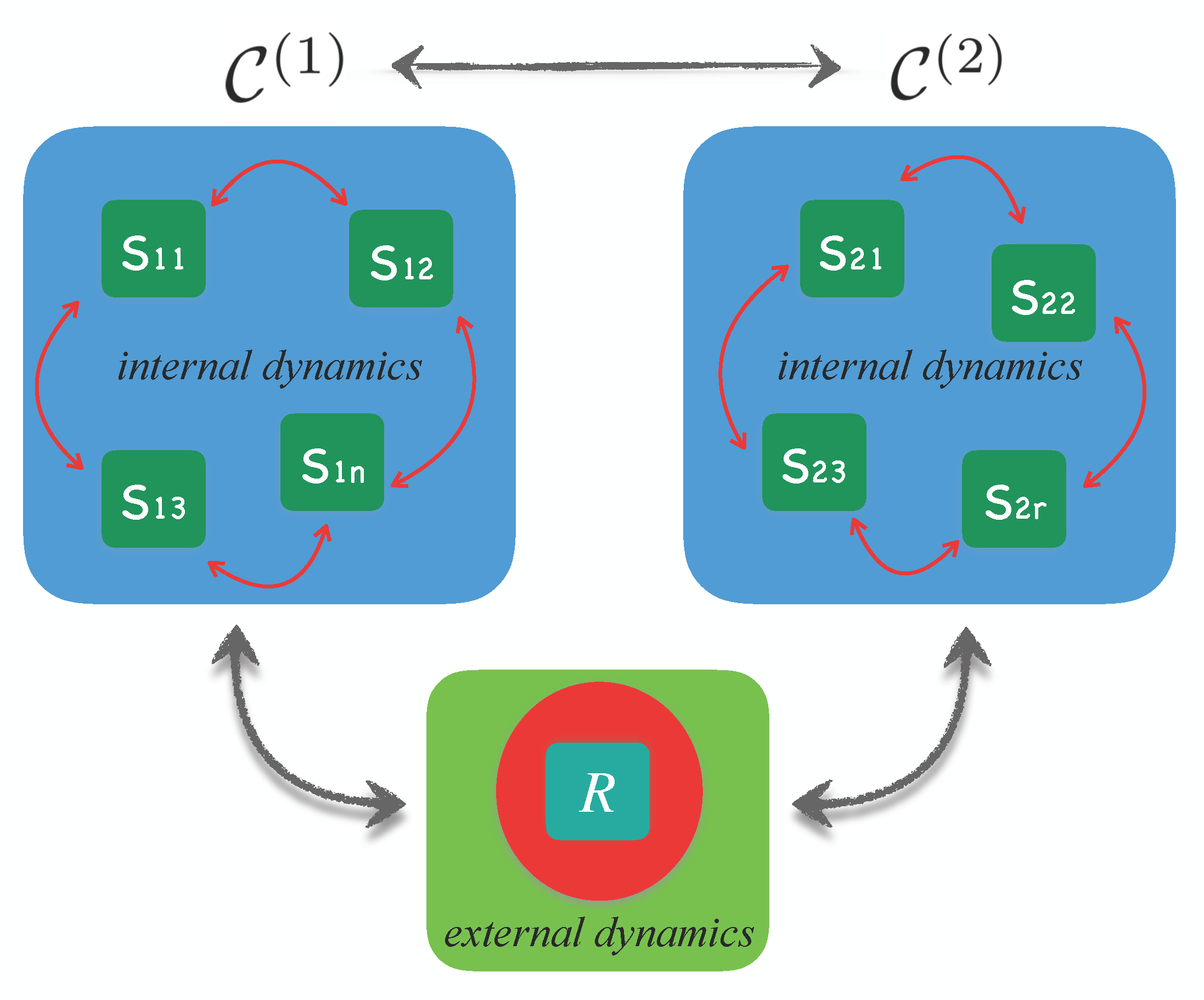
3. The Modeling Strategy

Before considering an explicit case, it is worth formulating the general modeling strategy we have in mind. This in abstracto formulation may help emphasize the type of insights that can be inferred and how they serve to suggest modifications that are consistent with a sustainability criterion prior to the real intervention. In this general model, this sustainability criterion will be defined quantitatively.

It is necessary to make explicit assumptions and hypotheses about the configuration of the whole social-ecological system before formulating a reliable mathematical model. Since the solutions depend on the initial assumptions, the presence or absence of acceptable solutions can be interpreted as the falsification or validation of the initial postulates.

The general hypotheses used in the formulation of our model are:

• The relations between social subsystems and their ecological surroundings can be treated as energetic transformations;
• The dynamics of these relations respond to irreversible processes;
• The social subsystems can exploit and restore their environment;
• Each social subsystem has an internal structure that modifies the interaction with its environment;
• The internal structure consists of differentiated sectors and there exists a population flux between them;
• The population flux is regulated by some rates that are inherent to the system;
• External agents can modify some rates and others are controlled internally.

Using these ideas, we formulate the mathematical model using ordinary differential equations.

3.1. Model in Abstracto

The model has the following two kinds of variables: ecological resources and social subsystems. The variable $\mathcal{R}$ is the resource population and reflects the availability of a resource that provides enough energy to maintain the social-ecological system. The variables $C^{\left(i\right)}$ represent the populations of different epistemological communities that exploit and restore the resource for survival.

Following the points 4 and 5, each social subsystem is described with an internal structure that depends on how different types of knowledge are shared, transmitted, and transferred among various sectors. Since their relation provides the population with knowledge, we call each social subsystem an epistemological community.

The sectors of each epistemological community are a partition of the total population into some associated learning stages required to acquire the necessary knowledge (the know-how) for resource exploitation and restoration. The direction in which the population flows through sectors is given by the knowledge-transfer method.

The previous considerations suggest that the model has to consist of two levels of description: one accounting for the internal structure of the communities, that is, the knowledge sectors $S_{lm}$ and the other one for their relation with the resource $\mathcal{R}$.

The dynamics of the whole social-ecological system will be determined by how epistemological communities interact with the ecological resources and among them, but their interactions are always dependent on their internal structure. Figure 1 shows a scheme of the arrangement of the interactions that may be generated. The dynamics of the resource will depend on how those levels of interaction are structured. A perturbation of the dynamics of any knowledge sector of an epistemological community will have a consequence, in principle, on all the other knowledge sectors. The following question emerges: Will the internal structure’s nature drastically influence a given system’s faith when it is subjected to an intervention?

The general purpose of making a model is to test possible policies. In order to achieve this objective, we identify the following two kinds of parameters in the model: (i) the characterization parameters and (ii) the control parameters. The first ones define the specific properties of an epistemological community and cannot be modified by external agents. On the other hand, the control parameters can be modified by external regulations or influences. Thus, the complete internal structure of an epistemological community is given by:

• Knowledge sectors: answer the question of who knows what?
• Knowledge transfer-method: answer the question of who learns from who?
• Characterization parameters: describe which type of and how much knowledge the epistemological community has.
• Control parameters represent when an epistemological community considers that someone already knows the necessary information and can change sector.

Once the characterization parameters are fixed for all the epistemological communities, we can simulate the system’s response to intervention policies or, equivalently, to changes in the control parameters. Accordingly, the term tests a policy by predicting the behavior of the epistemological communities and the ecological resources through time for some fixed characterization parameters and some varying values of the control parameters.

The result of these theoretical experiments is that we may compare and classify the solutions for each value (or interval of values) of the control parameters for which the system’s destiny is sustainable. An answer to whether the assessment of the time evolution is sustainable or not is provided by a unique criterium based on the time-dependent behavior of the social-ecological entropy production of the whole social-ecological system.

3.2. Social-Ecological Entropy Production as Sustainability Criterion

The points (1,2) assume that the energy and information exchanges in a social-ecological system are considered irreversible processes, which implies that the social-ecological system is constantly producing entropy. The previous statement means, in turn, that the temporal behavior of the populations must be non-stationary. In a social subsystem, every birth, death, interaction, and transfer of knowledge sector causes a variation in the populations. In the case of the ecological resource, natural growth and death, and other physicochemical conditions and their exploitation and restoration cause variations in the corresponding populations.

These variations are, in mathematical terms, oscillations of the populations that can be described by the following two main parameters: amplitude and frequency. The amplitude reveals how much the population changes, while the frequency describes how often it changes. Other variations of the populations can originate from some stochastic changes in the physicochemical conditions, for instance. The dynamics induced by stochastic perturbations require their work and reach beyond the goal of the present study. It should be emphasized, however, that the general modeling strategy and the analysis of their consequences do not change in the case when stochastic perturbations are included [33].

If the behavior of an ecological resource presents fluctuations at a high frequency, it is exploited or restored very often, for example, because the communities gather food daily. On the other hand, if the fluctuations are of low frequency, the resource interacts across a longer period, for instance, trees growing.

Fluctuations with high amplitude in a population imply that the size of the population changes drastically. For example, the accelerated migration of one community may lead to a high amplitude. Instead, with low amplitude, the population varies just from a few people, for example, a new birth.

When the system does not produce entropy, the populations are stationary. Their fluctuations have zero amplitude; therefore nobody is being born, dying, or learning. In parallel, the resource is not growing but also being exploited or restored, so we can interpret that there is an absence of interactions in that system. Therefore, one may consider that the cases leading to stationary solutions can be valid only for very short periods when stationarity is not reached. Additionally, these cases could be further studied by adding stochastic perturbations to the equations. Those perturbations will continually reset the initial conditions of the equations, preventing the system from reaching a stationary state.

We know the expected entropy production in a living, interacting social-ecological system is more significant than zero. However, we do not know by how much. Cancer cells indicate that the excessive entropy production of a system accelerates its degradation, leading the whole system to a stationary state solution, i.e., the death of the organism. Because of these considerations, we propose that an entropy production threshold should exist and that it can be used accordingly to classify the set of scenarios that will be simulated with the model.

Since our objective is to assess the sustainability of a specific resource management policy that acts as a guideline of an intervention over a pre-existing social-ecological system, we have selected the entropy production threshold as the entropy production peak of the system at the precise moment when the intervention takes place. This threshold will dictate when a system loses sustainable dynamics. We will return to this point when analyzing a particular case in the next section.

3.3. Types of Intervention

According to the previous discussion, we can identify three types of interventions:

• Natural intervention: the change of environmental conditions. For example, the change of temperature or humidity or a natural disaster that occurs across the natural ecosystem affects the resource or the social subsystems.
• Addition intervention: the increase, decrease, or substitution of elements in the system. For example, the arrival of a new community into a pre-existing system.
• Behavior intervention: the change of control parameters to regulate the behavior of the communities. For example, a change in the number of years of elementary school.

When an intervention occurs in a social-ecological system, the population dynamics will oscillate differently; therefore, the entropy production dynamics will also change. If the changes induced by the intervention in the amplitude and frequency at which a population oscillates produce more entropy that the intervention itself, we consider the intervention risky. If the entropy production of the population is lower than the threshold, then the intervention seems plausible.

Therefore, if the entropy production of a social-ecological system fluctuates with an amplitude and frequency that induce an entropy production of between zero and the selected threshold, we can consider that its dynamics are sustainable. For example, an epistemological community adapted to its environment in a sustainable way and interacting with a single resource will lead to time oscillations of its population and of the amount of resources at its disposal. These oscillations will take place with a fixed amplitude and frequency. As both populations are not stationary and are not threatened in their existence by any type of intervention, we consider that they are in a dynamic balance in such a way that the corresponding social-ecological system they form with its ecological niche, can be qualified as sustainable. Notice here that even chaotic oscillations that never exceed the threshold value for entropy production can be considered as sustainable.

Then, using the unique criterium of the production of the proposed social-ecological entropy, we can compare, classify and predict the possible sustainability of the social-ecological system and, therefore, conclude in which cases of a simulated intervention the control parameters appear to mitigate the damage.

3.4. The Model

Differentiated knowledge about a given natural resource leads to an internal structure of a community. This happens, for instance, because only a fraction of the total population knows how to exploit and preserve the resource. That is, within the community one sector of producers ($P_i\subset C_i$) able to extract the resource exists since it has the necessary knowledge. However, other community sectors may also have partial knowledge about how to exploit the resource and acquire it and learn how to be a producer.

More accurately, the two types of relevant knowledge for exploiting and managing a resource within each community can be distinguished as follows: the technical knowledge ($\omega$) and the environmental knowledge ($\lambda$). Technical knowledge is assumed to be related to pragmatic and systematized exploiting practices. Environmental knowledge may have intuitive (and/or scientific) insights from experience and interaction with the environment and is oriented to its preservation. It is worth noting here that it is plausible to assume a learning process exists for each type of knowledge. This learning process will be carefully analyzed in the following paragraph. The total population $C_i$ of the community i is expressed by the sum of all the sectors’ populations, and the differential equation can write its change with time

$$\frac{d}{dt}{C}_i=\frac{d}{dt}\left(N_i+A_i+E_i+P_i\right).$$

(2)

Here, $N_i$ stands for new individuals in the i-th community, $A_i$ for the number of individuals acquiring technical knowledge, $E_i$ for individuals experimenting with the technical knowledge and, finally, $P_i$ for individuals able to exploit a resource. For more details on the relation between the previous sectors and their learning processes (technical and environmental), please see

Table 1. Definitions of the sectors in which a community is structured. Own creation.

N	Sector of new individuals in the community or that does not have any relevant knowledge in order to exploit the resource.
A	Sector of individuals acquiring technical knowledge or learning how to manipulate a resource.
E	Sector of individuals experimenting with the technical knowledge, that is, acquiring environmental knowledge by interacting with the surroundings or ecosystem.
P	Sector of individuals able to produce, extract or exploit a resource.

.

3.5. Knowledge Transfer Methods

The learning process establishes the nature of the interactions among different sectors of a given community. In this form, how a community is structured depends on how knowledge is transferred among sectors. Thus, an analysis of possible transfer methods is necessary for a better understanding of the structure of a community.

Different knowledge-transfer methods can represent the structure of the learning processes. To characterize epistemological communities, we distinguish two methods: the direct knowledge-transfer method and the phase-in knowledge-transfer method. The direct-transfer mode schematized in the left panel of Figure 2 assumes that only producers (P) can teach the other sectors how to produce. The phase-in transfer mode indicates that knowledge is transferred by the immediate superior sector, as indicated in the right scheme of the same figure.

Both schemes indicate the parameters that regulate the knowledge flux, ${ϵ}_{\omega }$ for the technical knowledge and ${ϵ}_{\lambda }$ for the environmental knowledge.

Hereafter, we describe the model by using $X_i$ ($i=1,2\dots$) to denote the sectors that change according to the knowledge-transfer method that the community possesses. For example, the learning process of the sector A could depend on the interactions with other sectors. In the direct-transfer mode, the interaction takes place with the producer P (see Figure 2a) and will be denoted as $A·P$. In the phase-in mode, the interaction takes place with the experimental sector E (see Figure 2b); therefore, it is denoted as $A·E$. Thus, in abstracto, both possibilities will be represented in the following form: $A·X$.

3.6. Mobility through Sectors: The Mathematical Model

As a starting point, we assume that the sector N of new individuals in the community grows logistically. The upper bound of the possible growth has to be proportional to the extracting capacity provided by the technical knowledge ($\omega$) of the community, in such a form that we may represent this fact as $\omega R$, with R as the amount of resources at disposal. The population of this sector decreases when the individuals begin their learning process, that is, when they interact with a member of a teaching sector $X_1$, where subindex 1 indicates the level of the teaching hierarchy. The incorporation of new members into the learning process is mediated by the quality-of-inclusion rate, denoted by $\gamma$. Finally, the desertion, migration, and death rates will be regulated by the same parameter $\mu$. Therefore, the total change in time of the sector N is governed by the evolution equation

$$\frac{d}{dt}N=\rho N\left(1-\frac{N}{\omega R}\right)-\gamma N·X_1-\mu N,$$

(3)

where $\rho$ is the population growth rate of the community, N is the population of new individuals, R is the amount of resource and $X_1$ is the population of the first level teaching sector. For the direct knowledge-transfer method (D) (see Figure 2a), $X_1$ corresponds to the producer population P, whereas for the phase-in knowledge-transfer method, $X_1$ corresponds to the population of individuals acquiring technical knowledge A. Note that if $N\to \omega R$, the growth approaches zero, but if $\omega R\gg N$ the growth accelerates.

The sector of individuals acquiring technical knowledge A increases when some members of N begin their learning process. On the other hand, the sector’s population decreases when someone develops sufficient technical knowledge and moves to the following sector in the hierarchy of knowledge of the community. In addition, this sector reduces by the factors regulated by $\mu$, the rate accounting for desertion, migration, and death. Thus we have

$$\frac{d}{dt}A=\gamma N·X_1-{ϵ}_{\omega }\omega A·X_2-\mu A,$$

(4)

where $X_2$ now stands for the population of members of the second-level teaching sector. For the direct knowledge-transfer method (D) (see Figure 2a), $X_2$ again corresponds to the producer population P, whereas for the phase-in knowledge-transfer method $X_2$ corresponds to the population of individuals experimenting with the technical knowledge A. Here, it is important to emphasize that, unlike the quality-of-inclusion rate $\gamma$, the technical knowledge $\omega$ does not represent an interaction. It symbolizes the quantity or amount of technical knowledge that a community has. Thus, we have included the parameter ${ϵ}_{\omega }$ representing the technical-knowledge transfer rate.

In the next step of the hierarchy, the sector E of individuals with technical knowledge $\omega$ and acquiring environmental knowledge $\lambda$, increases with the knowledge transferred from the members of the second-level teaching sector $X_2$, and decreases when they learn from the members of the third level teaching sector, denoted by $X_3$, the sufficient environmental knowledge $\lambda$ needing to be produced. Furthermore, the sector reduces with the multiple causes represented by $\mu$. Thus, temporal evolution is dictated by the following equation:

$$\frac{d}{dt}E={ϵ}_{\omega }\omega A·X_2-{ϵ}_{\lambda }\lambda E·X_3-\mu E,$$

(5)

where we have introduced ${ϵ}_{\lambda }$ to represent the environmental-knowledge transfer rate. Additionally, the members of the third-level teaching sector, $X_3$, are the producer population P for both the direct-transfer and the phase-in knowledge methods, (see Figure 2).

Finally, the productive sector P comprises the population capable of extracting and exploiting a natural resource. The increase in P is due to individuals of the sector E that acquired both types of knowledge. This population decreases due to the desertion, migration, and death rate $\mu$, and its time evolution equation is given by

$$\frac{d}{dt}P={ϵ}_{\lambda }\lambda E·X_3-\mu P.$$

(6)

Equations (3)–(6) define the dynamical structure of different epistemic communities in terms of their different knowledge-transfer methods. As already explained, the explicit learning process is modeled by substituting $X_i$ ($i=1,2,3$) by the proper sectors of each knowledge-transfer method, (see Figure 2). Particular cases will be studied below.

The parameters that regulate the knowledge-transfer process are the quality of inclusion rate of one sector to another one ($\gamma$), the knowledge-transfer rates of each knowledge type (${ϵ}_{\alpha }$ with $\alpha =\omega ,\lambda$), the technical knowledge for extraction ($\omega$) and the environmental knowledge necessary for restoring the resources ($\lambda$). They are listed in

Table 2. Definitions of the parameters in Equations (3)–(6). The table is the authors’ own creation.

$\mathit{\gamma }$	Quality-of-inclusion rate of one sector into another one.
$\omega$	Amount of technical knowledge for extraction.
$\lambda$	Amount of environmental knowledge for restoration of the resources.
${ϵ}_{\alpha }$	Knowledge-transfer rate of knowledge type $\alpha =\omega ,\lambda$.

.

3.7. Relation with Resource

Since at a given time, each community interacts with the environment, their state, that is, the set of values of the sector populations N, A, E, and P, will depend on the state of the environment. The corresponding interactions among the communities and the environment should involve the amount of resource at disposal $R\left(t\right)$ and the state of the productive sectors $P_i$. This dependence constitutes a type of environmentally mediated feedback process that has to be weighted by the amount of technical and environmental knowledge $\omega$ and $\lambda$. Additionally, for consistency we have to consider the rate constants measuring the intensity of interaction—the load—between the productive sectors $P_i$ and the environment. We will denote these constants by ${\kappa }_i$, with $i=i,2,\dots$. In this form, as a first approximation, we may assume that the resource grows logistically and, meanwhile, that it is perturbed by the extraction and restoration activities of the communities $C_i$ with $i=i,2,\dots$. In terms of sectors populations of the different communities, the simpler model that can be formulated is

$$\begin{array}{c}\frac{d}{dt}R=rR\left(1-\frac{R}{k}\right)-{\kappa }_i\left(\frac{{\omega }_i}{{\lambda }_i+R}\right)P_i·R\hfill \\ \hspace{1em}-{\kappa }_j\left(\frac{{\omega }_j}{{\lambda }_j+R}\right)P_j·R+\delta ({\lambda }_i+{\lambda }_j)({\gamma }_i+{\gamma }_j)P_i·P_j,\hfill \end{array}$$

(7)

where repeated indexes imply a sum over the number of communities participating in the exploitation of the natural resource. In this equation, the first term on the right-hand side represents a logistic growth of the resource, at rate r, in the absence of perturbations or human interventions. The parameter k stands for the maximal amount of resources in the unperturbed ecosystem. Adopting a logistic growth dynamic for the unperturbed ecosystem is a drastic hypothesis. However, it is regularly performed and can be considered valid for relatively short time periods, as it does not consider the variability of physicochemical, biological, or natural perturbations that may induce time variations in the number of resources [10,11,30]. The second and third terms account for the resource exploitation by each community, $P_i·R$ and $P_j·R$. The exploitation depends on the resource amount so that, in abundance, a community extracts all the possible resources. However, when the resource is limited the extraction is regulated by environmental knowledge. These conditions are accounted for in Equation (7) by the corresponding factors that have the following limiting behaviors

$$\begin{gathered} {lim}_{R\to \infty }\left(\frac{\omega }{\lambda +R}\right)P_i·R\approx \frac{\omega }{\frac{\lambda }{R}+1}P\approx \omega P, \\ {lim}_{R\to 0}\left(\frac{\omega }{\lambda +R}\right)P_i·R\approx \frac{\omega }{\lambda }{P}_i·R. \end{gathered}$$

(8)

The last term of Equation (7) accounts for the interaction between the productive sectors of both communities, $P_i·P_j$. This contribution is multiplied by a constant $\delta$ that may be synergetic ($\delta >0$) or not ($\delta <0$), depending on the quality of the relations established between both communities. In the synergetic case, this constant is accompanied by a measure of resource restoration. Restoration is quantified according to the quality of the inclusion rate $\gamma$ and the environmental knowledge $\lambda$ of each community. A synergetic interaction between producers ($P_i·P_j$) can lead to resource restoration for mutual benefits.

Complete Model

The complete model consists of Equations (1)–(6) which are a set of non-linear ordinary differential equations. The mathematical model represents the set of epistemic communities $C_i$ ($i=1,2,\dots$) interacting with a resource R. Each community has an internal structure in which the sectors $X_{ni}$ ($n=1,2,3$) need to be defined according to their particular knowledge-transfer method. Thus, the sets of equations for the i-th community can be summarized in the following form:

$$\frac{d}{dt}{C}_i=\frac{d}{dt}\left(N_i+A_i+E_i+P_i\right)$$

(9)

$$\frac{d}{dt}{N}_i=\rho N_i\left(1-\frac{N_i}{\omega R}\right)-\gamma N_i·X_{1i}-\mu N_i$$

(10)

$$\frac{d}{dt}{A}_i=\gamma N_i·X_{1i}-{ϵ}_{\omega }\omega A_i·X_{2i}-\mu A_i$$

(11)

$$\frac{d}{dt}{E}_i={ϵ}_{\omega }\omega A_i·X_{2i}-{ϵ}_{\lambda }\lambda E_i·X_{3i}-\mu E_i$$

(12)

$$\frac{d}{dt}{P}_i={ϵ}_{\lambda }\lambda E_i·X_{3i}-\mu P_i$$

(13)

$$cc\frac{d}{dt}R=rR\left(1-\frac{R}{k}\right)+{\sum }_{i,j}{\lambda }_i{\gamma }_j{P}_1·P_2-{\sum }_i{\kappa }_i\left(\frac{{\omega }_i}{{\lambda }_i+R}\right)P_i·R$$

(14)

For practical purposes, it is convenient to rewrite the model in a non-dimensional form. Generally, the adequate characteristic of time $\tau$ should depend on the resource growth rate $\tau =rt$. In a similar form, all the populations can be normalized with respect to the initial resource $C\left(\tau \right)=C\left(t\right)/R_0$. In this way, the time evolution of the system of differential equations depends on the time necessary for a new resource generation and its corresponding amount.

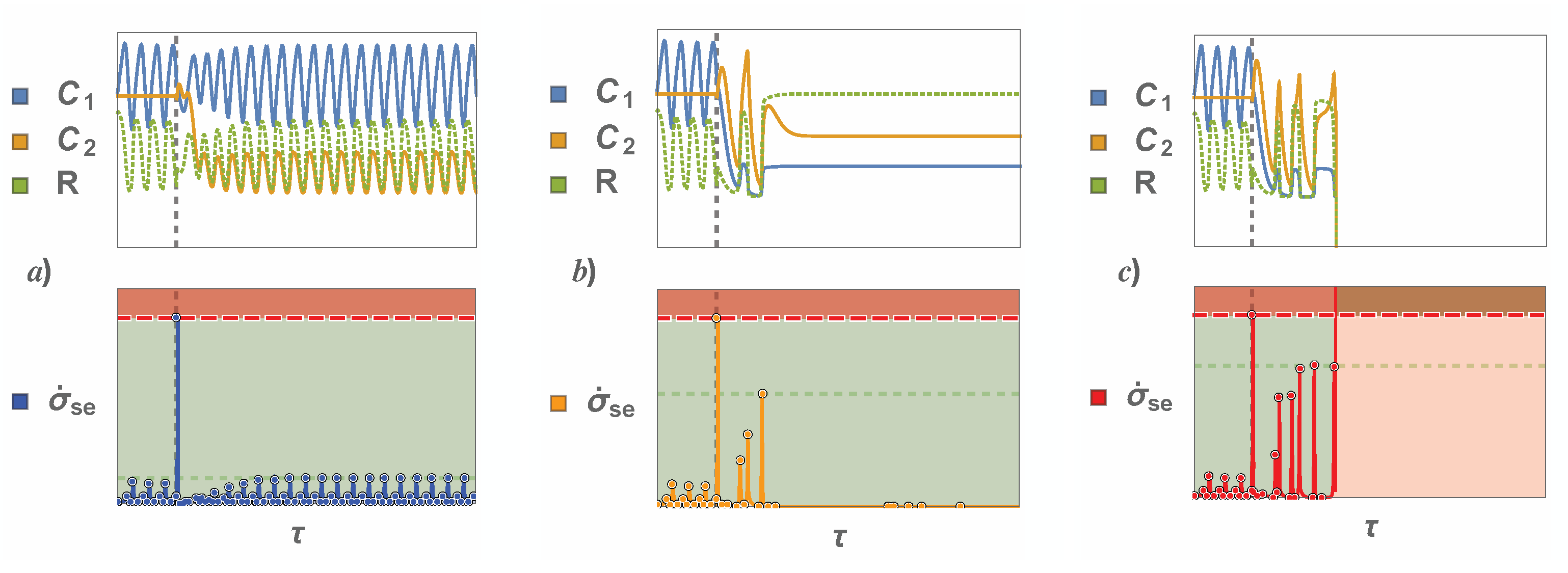
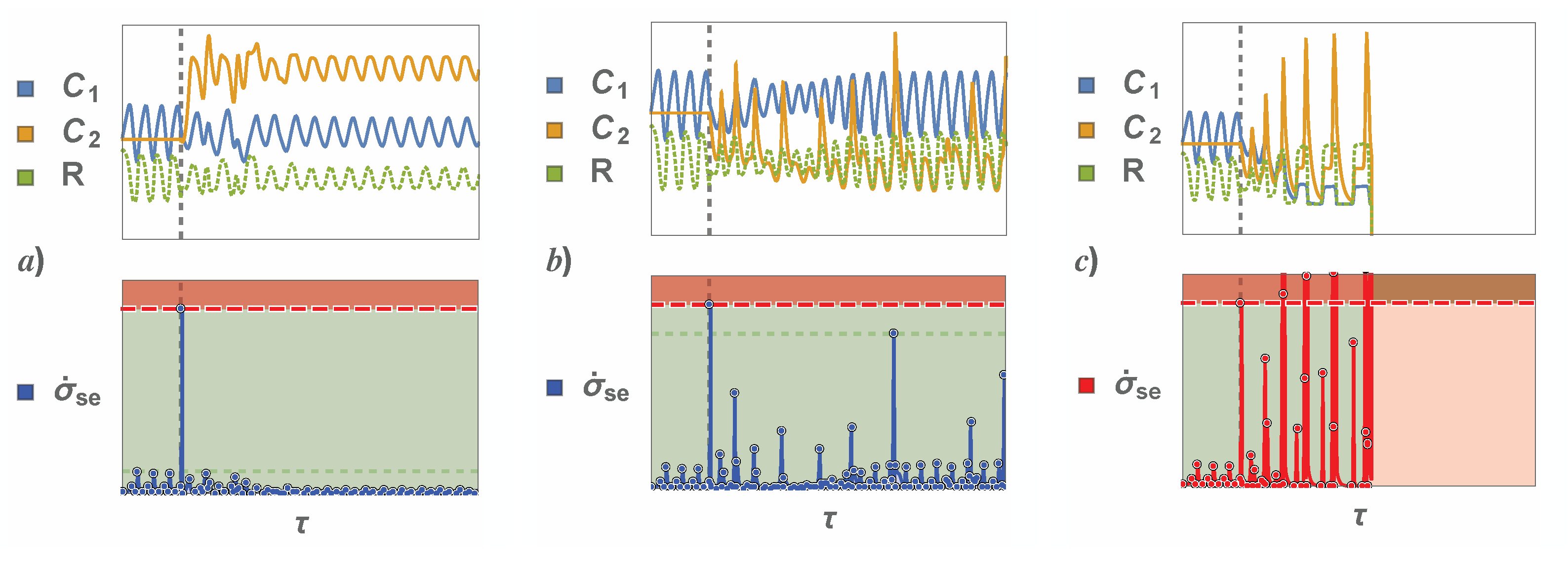
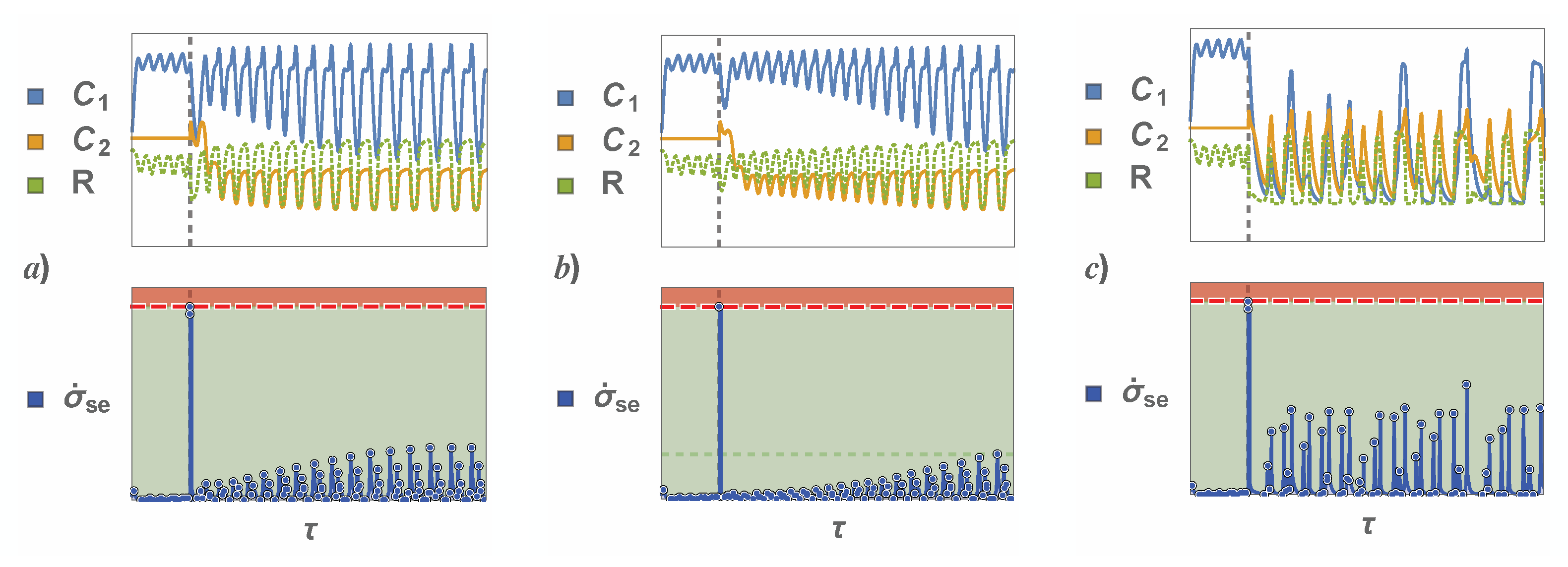
4. Results and Discussion: The Two Community Case

To analyze the implications of the model, we define a scenario with two epistemic communities, $C_1$ and $C_2$. In this scenario, the community $C_1$ is sustainably adapted to their environment and, suddenly, the community $C_2$ perturbs the dynamics by exploiting the resource at a given time. Both communities have the same quality of inclusion rate (${\gamma }_1={\gamma }_2$). However, because of their adaptation to the ecosystem, community $C_1$ has a high environmental knowledge and low technical knowledge, while community $C_2$ has more technical than environmental knowledge (${\omega }_1<{\omega }_2$ and ${\lambda }_1>{\lambda }_2$). The quality of inclusion rate ($\gamma$) and the quantity of both knowledge types (${\omega }_i$, ${\lambda }_i$) of each community can be modified only internally; thus, they are characterization parameters. On the other hand, the knowledge-transfer rates, i.e., the rates at which each community considers the acquired type of knowledge sufficient in order to move to the next sector (${ϵ}_{\omega 1}$, ${ϵ}_{\omega 2}$, ${ϵ}_{\lambda 1}$ and ${ϵ}_{\lambda 2}$), are considered as control parameters.

Hence, our simulations will construct a political strategy that measures the amount of resources exploited by varying the control parameters of the perturbing community $C_2$, that is, by varying ${ϵ}_{\omega 2}$ and ${ϵ}_{\lambda 2}$.

Table 3. Parameters used in simulations to create different scenarios.

C1	C2
Characterization
${\rho }_1\to 0.45$	${\rho }_2\to 0.5$
${\gamma }_1\to 0.4$	${\gamma }_2\to 0.4$
${\omega }_1\to 0.3$	${\omega }_2\to 0.6$
${\lambda }_1\to 0.6$	${\lambda }_2\to 0.3$
${\mu }_1\to 0.01$	${\mu }_2\to 0.01$
${\kappa }_1\to 0.8$	${\kappa }_2\to 0.8$
Control
${ϵ}_{\omega 1}\to 0.3$	${ϵ}_{\omega 2}\to \alpha$
${ϵ}_{\lambda 1}\to 0.3$	${ϵ}_{\lambda 2}\to \beta$

shows the values used for the characterization and control parameters. As we are exploring the effects of varying the control parameters of $C_2$, we show them as variables $\alpha$ and $\beta$, where $\alpha ,\beta \in \mathbb{R}\mid \alpha ,\beta \in (0,1]$; in contrast, the control parameters of $C_1$ were fixed. The resource R parameters were set as $r\to 0.39$ and $k\to 1$. We establish that the intervention of $C_2$ occurred at time $t=500$. To summarize, we defined the number of epistemic communities involved in the social-ecological system. Then, we fixed numeric values for the characterization parameters and chose the control parameters that act as a variable factor.

4.1. Methodology of Simulations

Once the model is characterized, we proceed to simulate scenarios from distinct control parameters values. Then, we compare and classify the solutions in order to obtain insights and conclusions. We implemented the following steps:

• Select a knowledge-transfer method for $C_1$ and $C_2$ substituting in the system (14) the corresponding populations $X_{ni}$.
• Obtain the model solutions by fixing the characterization parameters and varying the control parameters of $C_2$.
• Calculate the entropy production of each solution and classify it.
• Compare the obtained results with steps (1–3) for different knowledge-transfer methods.

4.2. Entropic Threshold

As our hypothesis, we assumed that the social-ecological processes are ultimately energetic transformations. To compare and evaluate the model solutions, we calculated the SEEP of the complete social-ecological system, that is, communities and resource. A higher entropy production implies drastic energetic transformation, i.e., abrupt changes in the populations and the resource. On the contrary, lower entropy production reflects gradual changes and synchronic dynamics among communities and resource.

In this way, the social-ecological entropy production per unit time of the whole social-ecological system, ${\dot{\sigma }}_{se}$, can be postulated by the following relation:

$${\dot{\sigma }}_{se}\equiv \sum _{\alpha ,i}{\left(\frac{d{C}_i^{\alpha }}{dt}\right)}^2,$$

(15)

where the subindex i accounts for the i-th sector of the community $\alpha$, with a population $C_i^{\alpha }$. Equation (15) means that the SEEP can be calculated as the sum of the square fluxes of the different populations that characterize the model. The total social-ecological entropy $S_{se}\left(\tau \right)$ produced during a given time period $\tau$ can therefore be calculated by a time integration

$$S_{se}\left(\tau \right)=\frac{1}{\tau }{\int }_0^{\tau }{\dot{\sigma }}_{se}dt.$$

(16)

Due to the intervention of $C_2$, the dynamics of $C_1$ and R become considerably disturbed and the whole system shows a peak in the entropy production per unit time. The sustainable situation is that, after a transient time, the communities can accomplish their mutual adaptation and survive with a sustainable exploitation of the resource. To identify these solutions, we define the threshold of the rate of entropy production at the moment of the intervention as the maximum value the system would have in a sustainable process. We call this value the entropic threshold, and we classified the solutions based on it as follows:

Sustainable: Solutions in which the SEEP of the system after the intervention maintains bellow the entropic threshold, see Figure 3a.

Exhaust: The SEEP is null, implying that there are no energy fluctuations. Since we have assumed that social-ecological processes are irreversible, the absence of energy fluctuations implies the exhaustion of the interaction, even when the level of populations is not null, see Figure 3b.

Catastrophic: The SEEP crosses the entropic threshold. These results imply that the system does not adapt, and the energy fluctuations do not allow the social-ecological system to survive, (see Figure 3c).

Once we conclude steps (1) and (2), SEEP, as indicated above, the entropic threshold enables us to execute step (3) and obtain the whole analysis of a specific scenario.

4.3. Comparison of Knowledge Transfer Methods

The foresight of the possible scenarios simulated follows from the execution of step (4), and by making a comparison of the results in each combination of the knowledge-transfer methods simulated. In each case, we obtain:

Parametric plane: A plane (${ϵ}_{\lambda }\times {ϵ}_{\omega }\in [0,1]\times [0,1]$) of all the possible values of the control parameters. Each point of this plane represents one solution to the model, fixing the control parameters with the coordinates values. The point’s color indicates the class of solutions according to the entropic threshold.

Solutions: In every solution, we obtain the time series of the variables ($C_1$, $C_2$ and R) and, by using Equation (15), we obtain the corresponding time series of the entropy production. The color of the entropy production plot shows the entropic threshold classification.

Given the parametric plane and the solutions, we compared different knowledge-transfer methods, identifying the regions in the parametric plane that lead to sustainable, catastrophic, or exhaust solutions.

We denote the direct and the phase-in method as D and P, respectively. The letters in the next description refer to the $C_1$ and $C_2$ methods, respectively:

4.4. D-D

In this case, 73% of the area predicts an exhaustion destiny of the SES (yellow points). Only 23% of the combination of the control parameters leads to a sustainable fate (blue points). Additionally, 4% is predicted to be a catastrophic result (red points) (see Figure 4a).

4.5. D-P

The area of sustainable solutions (blue points) reaches 29%, whereas the catastrophic area (red points) is 71% in the cases studied. The sustainable area is wider than the D-D case. There are no exhaustion solutions between the sustainable and catastrophic regions, see Figure 4b and Figure 5.

4.6. P-P

In total. 100% of the parametric plane shows sustainable solutions, but the time series behavior indicates the possible presence of chaotic behavior (see Figure 5). In such a case, it could be interesting to calculate the predictive horizon (see Figure 4c and Figure 6).

4.7. P-D

The area corresponding to sustainable foresights is also about 29%, but in this case the time series behaviors are more regular behavior than in the P-D case (see Figure 4d and Figure 7).

The parametric planes in Figure 4 show the values of the control parameters used to explore sustainable strategies in terms of the knowledge-transfer methods adopted by the two epistemological communities. Each point represents a case simulation characterized by its particular SEEP and has its time series, see Figure 5. Thus, each figure represents 400 cases studied. Blue points correspond to sustainable combinations of parameters, whereas yellow and red points correspond to unsustainable cases. In this form, Figure 4 plays the role of phase diagrams, indicating that when approaching from blue regions to yellow or red areas, a qualitative change of the dynamics may occur, making the system less resilient. Crossing from blue to yellow or red areas implies passing from a sustainable interaction to an unsustainable one. Furthermore, Figure 4 provides an overall assessment of the sustainability of the SES when a given strategy for knowledge-transfer methods is adopted (D-D, D-P, P-D, P-P). If we compare the area covered by the different scenarios obtained (blue, yellow, and red points) with the total of cases simulated for Figure 4a, we find that only 23% of the combinations of the knowledge-transfer methods lead to a sustainable outcome. This situation changes if the knowledge-transfer method implemented by the intervening community corresponds to the phase-in method (P). In this case, Figure 4b indicates that the D-P case has a higher sustainability percentage (29%) and, therefore, may be more successful than the D-D case. For the examples studied form Figure 4, it follows that if the pre-existent community has a phase-in knowledge-transfer method for the formation of new producers in the community, then the best scenario corresponds to the case when the second community also adopts a phase-in strategy, (Figure 4) since the 100% of the cases studied can be sustainable in this case.

Each point in Figure 4 has a population and entropy production time series counterpart similar to those shown in Figure 3 and Figure 5. For instance, a blue point in Figure 4a for the D-D knowledge-transfer method corresponds to the populations and entropy productions of Figure 5a, in which the long time post-intervention behavior of the system has the same level of entropy production as the original system. A point in the yellow zone leads to an extinction behavior by exhaustion, as shown in Figure 3b.

It is important to stress that not all blue points in the different sustainability spaces are equivalent. For instance, the case of the D-P knowledge-transfer method shows a strongly sustainable situation in which synergetic interaction with community 2 leads to an overall decrease in the entropy production rate (see Figure 5a). This corresponds to a blue point with high environmental knowledge and low technical knowledge rates, ${ϵ}_{\lambda }$ and ${ϵ}_{\omega }$, respectively. In contrast, having a blue point with high technical knowledge and low environmental knowledge rates may lead to a weakly sustainable situation such as that illustrated in Figure 5b. A non-sustainable catastrophic situation is illustrated in Figure 5c by taking a red point with large values of both environmental and technical rates. In particular, for this knowledge-transfer method, the weak sustainable state shows a possible emergence of chaotic behavior of the populations as well as for the entropy production rate.

The P-D mode of the knowledge-transfer method is the most adequate for sustainable intervention since the whole parametric plane is blue. Clearly, for larger values of the technical knowledge rate ${ϵ}_{\omega }$ and low values of the environmental knowledge rates ${ϵ}_{\lambda }$, the solutions are less resilient than those with the opposite relations of magnitudes (see Figure 6a,b). Once again, high technical and environmental knowledge values yield unstable solutions suggesting the appearance of chaotic time series.

The P-P mode shows (Figure 7a) that for larger values of the technical knowledge rate ${ϵ}_{\omega }$ and low values of the environmental knowledge rates ${ϵ}_{\lambda }$ the solutions tend to be weakly sustainable since their entropy production shows peaks near the threshold value of the entropy rate. This mode is expected to be less resilient because a new small intervention will induce a sustainability transition from sustainable to non-sustainable regions of the parametric plane. In contrast, high environmental and low technical knowledge rates yield stronger sustainability, as shown in Figure 7b. As in the D-P case, a red region of the parametric plane indicates the presence of a catastrophic situation at high levels of ${ϵ}_{\lambda }$ and ${ϵ}_{\omega }$.

We understand that care has to be taken when evaluating the parametric plane because some solutions appear to lead to sustainable situations at shorter time periods, while for longer time periods they become unsustainable. This situation is illustrated in Figure 8a,b. For longer time periods, some blue points for low environmental and high technical knowledge pass from blue to red, as expected.

The comparison among distinct scenarios based on the SEEP showed that an SES is more resilient when both communities have a phase-in knowledge-transfer method because of the more extensive sustainable solutions region in the parametric plane. Another interesting case predicting sustainable but chaotic behavior of the populations is observed when the original community follows a phase-in knowledge-transfer strategy, but the intervening community does not. Even though all the predicted scenarios are sustainable, the apparent chaotic behavior in both sectors’ populations makes it, in principle, difficult to assess a predictive evaluation for times larger than the predictive horizon. Nevertheless, the possible predictive uncertainty already mentioned supports the necessity and convenience of theoretically testing possible social interventions before their implementation in practice.

Before moving to the Conclusions section, it is necessary to discuss the results obtained here alongside previous works in the literature. The study of coupled human and natural systems is currently a strongly developing discipline [7,12,30] to which several disciplines, including computer science, biology, ecology, economy, and even philosophy may contribute [15]. On the one hand, it is a well-known fact that mathematical models (statistical, dynamic, stochastic, agent-based) have been used for investigating cause–effect relationships in a wide variety of complex natural-human systems. However, many models that analyze or forecast specific phenomena related to, for instance, fishery [10,11] or epidemiology [25,28,31,32], may lead to diverging causal claims [30]. The reason seems to be a lack of a wider scope that not only takes into account the specific characteristics of the phenomena studied but a larger spectrum of couplings and feedback [7,15].

Let us consider the case of the cod fishery, which was extensively modeled and whose mathematical models were summarized and discussed in the excellent review provided in Ref. [30]. It is apparent that most of the models used are based on assumptions regarding the physicochemical and biological conditions of the environment, and their goal is to obtain predictions about the possible future of the population of cod and other species in the Baltic sea [11]. Models can be found that also introduce, as a factor influencing the cod’s population dynamics, interaction with fishers. In the case of dynamic models, such as the one used in our work, the obtained results are presented as a time series of the fish populations. Those dynamics are similar to the ones obtained here [11] in terms of sustainable or catastrophic fates.

From those analyses, it is not clear how the different ways of fishing or the internal dynamics of the fishers community may influence, by the human practices adopted, the dynamics of the resource [12,13,14]. However, we have shown in this section that the epistemic condition [5,15] of the human communities (amount of environmental and technical knowledge) as well as their strategies for forming new agents (knowledge-transfer methods) able to exploit and restore the environmental conditions of the resource, have considerable influence on the possible sustainability of the exploitation practices.

Clearly, the two-community model studied here, as an illustrative case, can be improved by considering more precise aspects of the dynamics of the different communities considered, such as those of the already cited literature. For instance, instead of using a simple logistic model for the population dynamics of the resource, more precise models can be introduced that better account for the resource’s interaction with its natural environment. However, the novelty of our approach is to incorporate the influence of human activities on the dynamics not only in terms of the number of fishers, but in terms of the whole epistemological and technical context in which human communities live.

5. Conclusions

In this work, we have presented a theoretical framework appropriate to analyze the sustainability of human practices during the exploitation of natural resources by different epistemological communities. The theoretical framework includes the following two general aspects: (a) The formulation of a theoretical model justifying the use of an entropic measure in social-ecological systems. (b) The formulation of specific mathematical models based on an analysis of knowledge types and knowledge-transfer methods within different epistemological communities, and their mutual interaction. This second aspect allowed us to exemplify the implications of the practical use of the theoretical model to provide a quantitative measure of the sustainability perspective of exploiting a natural resource by competing–collaborating communities.

The novelty of our work lies, precisely, in the establishment of a direct correlation between knowledge types and knowledge-transfer methods in social dynamics, with its influence on ecosystem dynamics. Common modeling tools devote their attention to the interrelation of the resource dynamics with the ecosystem variables and the load of human exploitation [12,13,14]. However, although these approaches are, of course, very valuable, their descriptions lack the fact that human exploitation practices are determined by the above-mentioned knowledge types and knowledge-transfer methods in the different societies whose survival or standard of living relies on ecosystem resources (for instance, water or soil uses). That is, there is a lack of a quantitative correlation between the ecosystems dynamics and the highly complex dynamics of human societies, particularly those in which epistemological diversity is strong. Our work tries to substantiate this correlation in terms of a global integrative parameter called social-ecological entropy production (SEEP), Equations (15) and (16), which translate the theoretical (conceptual) model to a practical mathematical tool able to assess the sustainability of social-ecological practices before and after a human intervention affects the dynamics of an ecosystem.

We have exemplified the previous statements through the two-community one-resource dynamic model. Therefore, the problem that needs to be solved can be stated as follows: Determining the sustainability of human practices in the intervention of a pre-existent sustainable SES (one community plus one natural resource) by a second community that aims to exploit the same resource. The mathematical analysis was developed by considering the perturbation of the dynamics of the pre-existent sustainable SES, by the sudden introduction of the second community, and given that both communities have different amounts of technical and environmental knowledge, as well as two different strategies for knowledge transfer among the sectors in which each community is divided. As an aside, these considerations reflect the internal social and epistemological structure of the communities that are coupled with the dynamics of the resource, determined by inherent ecosystem interactions. Proceeding in this way establishes feedback correlations among the resource and the populations of the communities in terms of technical and environmental knowledge.

Under the variation of appropriate control parameters associated with the type and transfer rate of knowledge of the second community (controllable, for instance, by establishing exploitation policies), the simulation of the model provided insights about the sustainability of the intervention in terms of the calculated SEEP for different values of the control parameters. The outcomes, provided in terms of the time dependence of the rate of SEEP (${\dot{\sigma }}_{se}$), were classified as sustainable, catastrophic, and extinction by exhaustion. The outcomes were presented through colored points in a parametric space determined by the control parameters used, that is, environmental (${ϵ}_{\lambda }$) and technical (${ϵ}_{\omega }$) knowledge-transfer rates. In this way, we present the combinations of values of ${ϵ}_{\lambda }$ and ${ϵ}_{\omega }$ for which the simulation predicts a sustainable solution (blue points in Figure 4), a catastrophic one (red points in Figure 4), and extinction by exhaustion (yellow points in Figure 4).

The a priori knowledge of the values of these parameters that predict a sustainable situation should bring attention to and make more precise the legal and economic considerations before adopting a policy on exploiting and managing a given resource and its associated ecosystem. In this way, the decisions will incorporate the specific epistemological characteristics of the involved communities and provide an objective base that may reduce or even avoid social controversies.