Abstract
Considering that a fair coin has two sides and a cylindrical edge, the probability that it would fall on its edge is calculated, yielding the probability of heads or tails of less than 50%. In this first part, the theoretical models for a static case and for five dynamic cases, without rebounds, show that there is a small probability that the coin does not fall on its head or tail, depending on the initial toss conditions, the coin geometry and conditions of the coin and landing surfaces. It is found that the probability that a 50 Eurocent coin thrown from a normal height with common initial velocity conditions and appropriate surface conditions will end up on its edge is in the order of one against several thousand. In the second part of the paper, the dynamic model with rebounds is investigated.
1. Introduction
To toss a coin is the simplest of experiments in probability and statistics. Students usually learn that there is a 50–50% chance that it falls on either side. Repeat this simple experiment with a fair coin a sufficient number of times and the result should show that, on average, half of the tosses yield heads and half yield tails. However, is it really so, even with a fair coin? A coin is a flat cylinder made of some metallic alloy. It has, of course, two sides, but it also has a small cylindrical surface, the edge.
In the first part of this paper, we calculate the probability that a coin would fall on its edge, yielding the probability of heads or tails of less than 50%. Several models are considered: a simple static model and five dynamic models, without rebounds. Depending on the initial toss conditions, the coin geometry and conditions of the coin and landing surfaces, there is a small probability that the coin does not fall on its head or tail.
The mechanical model equations are derived from classical textbooks [1,2].
In the second part of the paper [3], the dynamic model with rebounds is investigated, yielding a more realistic model.
2. Static Model
Let us consider a flat cylindrical coin, perfectly circular and homogeneous with a basis diameter much larger than its height . From the center of mass at the coin mid-height, the height is seen under an angle . The coin is placed on a perfectly smooth horizontal surface, with the coin edge making an angle with the horizontal surface (see Figure 1).
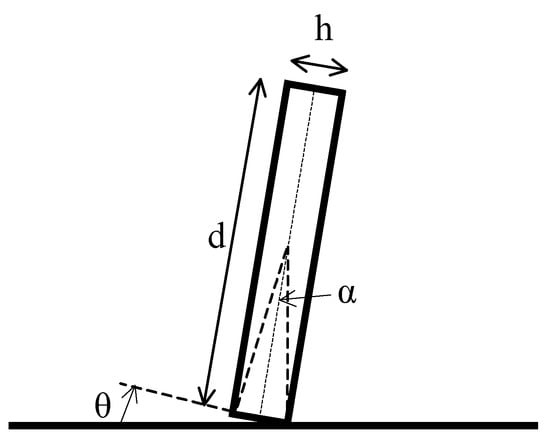
Figure 1.
Static model of a coin on its edge.
Clearly, the coin will fall on the right side if
Note that the position is an unstable equilibrium position. Theoretically, the coin will fall if there is even the slightest perturbation to the right, but as we consider a static model here, i.e., without any dynamics or perturbations, the coin should theoretically stay in equilibrium for this position .
As , and if , , one has
Therefore, the probability that the coin will fall on a side can be estimated as
and the probability that it will stay on its edge is
Another way to see it is to calculate the probability as the ratio of all values of , yielding the coin to stay on its edge in the range to to all possible values of in the range to , yielding
For a 50 Eurocent coin, mm, mm, yielding , which gives a probability in the order of 5%. This means that approximately one out of twenty tosses should end with the coin on its edge, which is clearly too many.
This static model is obviously not adequate to describe a real situation and must be refined. It shows, however, that the probability of a coin falling on its edge is not nil.
3. Dynamic Model
3.1. General Model and Equations
In addition to the hypothesis of a fair coin, i.e., a homogeneous flat circular cylinder of mass , one considers the following hypotheses (with bold characters denoting vectors):
- -
- the coin is thrown manually from an initial height with a velocity under an angle on a horizontal surface, and an initial angular velocity ; for a manual throw, the minimum and maximum possible values are considered to be
- -
- the coin rotation axis is horizontal and passes through the coin center of mass at all times during the fall until impacting the landing surface;
- -
- the coin angular velocity after impact is along a (yet) undefined instantaneous axis of rotation that stays horizontal at all times;
- -
- the atmosphere is windless, without any disturbance, and the air friction is negligible;
- -
- the landing surface is a perfectly horizontal, plane, solid and immovable surface;
- -
- in the first approach, one considers that there is no rebound of the coin; the rebound case is addressed in the second part of the paper [3].
One considers further a referential frame with its origin at the impact point on the landing surface, its axis perpendicular to the landing surface and directed downward, its and axes in the horizontal plane of the landing surface, with pointing in the direction of the throw (see Figure 2).
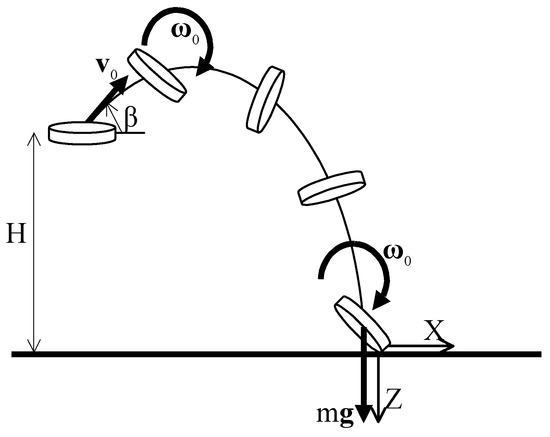
Figure 2.
Dynamic model of a coin throw with a clockwise initial rotation.
The velocity vectors of the coin center of mass before and after impact are noted as, respectively, and , and the coin angular velocity vectors before and after impact are noted as, respectively, and . Since the landing surface is immovable and with denoting the vector product, the equations of impact are [1]
where is the impulse of the impact, having components and respectively, normal to and along the surface at the point of contact; and are the moments of inertia of at the coin center of mass with respect to the instantaneous axis of rotation immediately after and before impact; and is the distance vector from the impact point to the coin center of mass.
The components of the coin velocities before impact are obviously
since the initial rotation can be in either direction. The coin moment of inertia before impact is
with respect to the instantaneous horizontal axis of rotation passing through the coin center of mass.
The components of the distance vector are (see Figure 3)
with and where, from here onward, is the angle from the downward vertical to the mid-plane parallel to the coin sides counted positively in the counterclockwise direction.
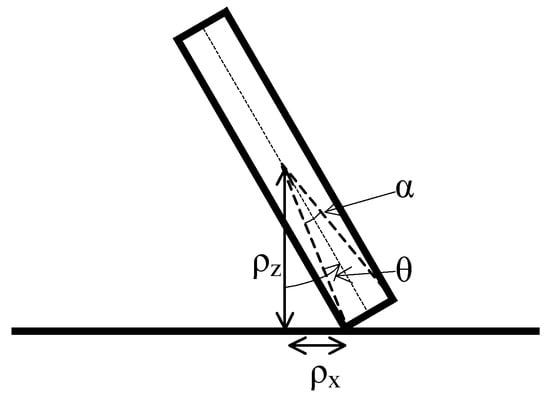
Figure 3.
Angles and distances at the moment of impact.
Note that to be exact, the height from which the coin falls should be less, as the coin’s center of mass never touches the landing surface. The height should be replaced by , but as is much smaller than for any value of at impact, one can simplify the problem by considering only.
With the hypothesis that the angular velocity after impact is along a horizontal instantaneous axis of rotation, one also has
Equations (7) and (8) reduce then to
An additional condition is given by the nature of the impacting bodies and their surfaces. Four cases can be classically considered:
- (1)
- both bodies are inelastic and perfectly rough,
- (2)
- both bodies are inelastic and perfectly smooth,
- (3)
- both bodies are elastic and perfectly smooth,
- (4)
- both bodies are elastic and partially rough.
3.2. Inelastic and Perfectly Rough Bodies
In the first case, if the bodies are inelastic and perfectly rough, the particles of the coin and of the landing surface do not separate after collision, and their relative velocity is nil, giving the condition
yielding
which, with Equations (14) and (16), allow us to find the tangential and normal components of the impulse at impact
The replacement in (15) yields the angular velocity after impact
where
For the coin to stay on its edge, the angular velocity after impact must become nil, while . Solving Equation (22) for the variable and using the formulae for the half-angle yield
with the resolution condition
The condition yields successively
meaning that the argument of the arctan function in relations (24) or (25) must be positive and smaller than .
For the positive condition, the numerator and the denominator must be of the same sign. Considering the negative sign in front of the second root in the numerator of (24):
- -
- for both numerator and denominator to be positive, the first root must be greater than the second, yielding
- -
- for both numerator and denominator to be negative, the first root must be smaller than the second, yielding
Considering the positive sign in front of the second root in the numerator of (24), the denominator must be positive, which is true either for a positive sign in front of , i.e., an initial coin counterclockwise rotation, or for a negative sign in front of , i.e., an initial coin clockwise rotation, in addition to
However, the solution, in this case, yields too large a value of , as the right-hand part of the double inequality of condition (28) is not fulfilled.
In conclusion, for this first case, the only possible solution is given by an initial coin counterclockwise rotation with the condition (29), which coupled with condition (26), yields
For the right part of the condition (28), considering a positive sign in front of , it yields
where vertical bars denote the absolute value. These two conditions constrain the vertical velocity of the falling coin.
Within the above conditions, the maximum and minimum values of are
The probability that the coin will end on its edge is thus
The maximum value of this probability will occur for the largest value of and the smallest value of . Considering that is bound by and (27), and , which would yield the same value of the maximum probability as for the static case (5). However, one still has to verify that the values of and can be achieved within the ranges (6) of the four initial parameters , , and .
For to occur, the argument of the arctan function in Equation (38) must be nil, i.e., for the limiting case where and either and , or and taking any value, with taking any value.
For , the arctan function in Equation (39) must be equal to or larger than , which in most cases is not possible within the conditions (36) and (37). In fact, the argument of the arctan function in (39) is maximum for , and , with taking any value between and , yielding
yielding for the ranges of values (6) with and ,
The maximum probability that the falling coin stays on its edge at impact then becomes slightly less than in the static case, namely
For the values given in Equation (6) for a 50 Eurocent coin, relation (43) yields a probability = 0.04366 or nearly 1 throw every 23 that ends with the coin on its edge.
For more common and practical values, let us consider a series of vertical throws up or down (i.e., ) from a height 1.5 m with the initial coin velocities ranging from 1 to 5 m/s and initial rotation ranging from 0.5 to 5 turns/s. The probability that the coin will end on its edge is then 4.96 × 10−3 or approximately 1 throw every 202. For another series of throws with , 1.5 m and the initial coin velocities ranging from 0.01 to 0.1 m/s and initial rotation ranging from 0.5 to 5 turns/s, 1.17 × 10−3 or approximately 1 throw every 856.
3.3. Inelastic and Perfectly Smooth Bodies
In the second case, if the bodies are inelastic and perfectly smooth, at the moment of impact, the and components of the relative velocity of the coin contact point with respect to the landing surface are unaltered, while the component is reduced to zero [1], giving the condition (with • denoting the scalar product):
where is the unit vector following the axis, , yielding
Replacing these last two relations in Equations (14) and (16) yield
indicating that the impulse lies only in the normal direction to the surface. The replacement in Equation (15) yields
For the coin to stay on its edge, the angular velocity after impact must become nil, while . Solving Equation (50) for the variable yields
under the condition that the denominator in Equation (50) is different from zero, which is always the case, as all terms are positive. For the condition to hold, the argument of the arcsin function in Equation (51) must be, first, positive, which is the case only for a positive sign in front of , i.e., an initial coin counterclockwise rotation, and second, smaller than , yielding for a positive sign in front of
If this condition holds, the probability that the coin will end on its edge is then
The maximum probability will occur for for the limiting case where = 0 and , and taking any value ), and for the argument of the arcsin function in being maximum, i.e., for , and either and , or and taking any value, yielding
which, for the values given in Equation (6) for a 50 Eurocent coin, yields a probability = 0.04366 or nearly 1 throw every 23 that ends with the coin on its edge, like in the previous case.
Throwing the coin vertically, upward or downward, i.e., , from an initial height = 1.5 m with the initial coin velocities ranging from 1 to 5 m/s and initial rotation ranging from 0.5 to 5 turns/s yields the same result as in the first case above. For a series of throws with initial conditions , = 1.5 m and ranging from 0.1 to 5 m/s and varying between 0.5 and 5 turn/s, = 4.99 × 10−3 or approximately 1 throw every 200 will deliver the coin on its edge.
3.4. Elastic and Perfectly Smooth Bodies
In the third case, if the bodies are elastic and perfectly smooth, at the moment of greatest compression at impact, the component of the relative velocity of the coin contact point with respect to the landing surface is reduced to zero, while the and components are unaltered. The magnitude of the normal impulse can be computed as in the second case, multiplying it by where is the coefficient of restitution.
This yields, from Equation (49),
with still being nil. The replacement in Equation (15) yields
As above, for the coin to stay on its edge, the angular velocity after impact must become nil, while . Solving Equation (56) = 0 for the variable yields
where the positive sign in front of , i.e., an initial coin counterclockwise rotation, was chosen to guarantee that the first part of the condition holds, while the second part yields
Under this condition, the probability that the coin will end on its edge is then
As in the previous case, the maximum probability will occur for and for the maximum value of the argument of the arcsin function in , yielding
The coefficient of restitution obviously depends on the nature of the surface of both bodies and can take values [2] from 0.2 for lead on lead to 0.95 for glass on glass, with approximately 0.55 for steel on steel, yielding values of ranging approximately from 1.2 to slightly less than 2.
Assuming a coefficient of restitution = 0.5, i.e., both the coin and the landing surface being made of steel alloy, for a 50 Eurocent coin and the values given in (6), Equation (60) yields a probability = 0.02905 or nearly 1 throw every 34 that ends with the coin on its edge.
Throwing the coin vertically, upward or downward, i.e., , from an initial height = 1.5 m with the initial coin velocities ranging from 1 to 5 m/s and initial rotation ranging from 0.5 to 5 turns/s yields = 3.304 × 10−3 or approximately 1 throw every 303 will end with the coin on its edge, i.e., less than in the first two cases.
For a series of throws of a 50 Eurocent coin with initial conditions , = 1.5 m and ranging from 0.1 to 5 m/s and varying between 0.5 and 5 turns/s, = 3.33 × 10−3 or approximately 1 throw every 300 will deliver the coin on its edge.
3.5. Elastic and Partially Rough Bodies
Contrary to the first three idealized cases, this fourth case depicts reality more closely because the partially rough character of both surfaces in contact will cause slippage to occur. For simplicity, the following two assumptions are made:
- -
- the slip is always in the same direction;
- -
- the frictional impulse has a magnitude μN, where μ is the coefficient of friction and a direction opposite to the relative motion of the point of contact on the landing surface.
The normal impulse is still calculated as in the third case.
This yields, from Equation (55),
The replacement in Equation (15) yields
As above, for the coin to stay on its edge, the angular velocity after impact must be nil, while . Solving Equation (63) = 0 for the variable yields
under the condition that the denominator of Equation (63) is different from zero, i.e., for
To verify condition (65), one must evaluate in (23) the coin moment of inertia after impact, which depends on the position of the instantaneous rotation axis after impact. Under the hypothesis that the coin rotation axis after impact stays horizontal along the direction, its position can be assumed between two extreme cases. The first corresponds to the coin rotation axis after impact being identical to the one before impact, namely along the horizontal axis passing through the coin center of mass, i.e., and . The second case corresponds to the coin rotation horizontal axis after impact passing through the coin contact point with the landing surface, yielding
These two extreme cases can be extended to other positions of the instantaneous axis of rotation, e.g., outside the coin at a distance from the coin center several times the diameter of the coin, which would increase the values of parameters and . For the sake of argument, we limit ourselves to the two positions indicated.
Condition (65) then yields
where and take the values, respectively, = 1/3 and = 1/4 in the first case () and = 4/3 and = 5/4 in the second case (66).
For to be real in Equation (64), the condition for the radical in the numerator reads
For the condition to hold, the argument of the arctan function in Equation (64) must be positive and smaller than . For the positive condition, the numerator and the denominator must be of the same sign. Considering the negative sign in front of the root in the numerator of Equation (64):
- -
- both the numerator and denominator are positive if
- -
- both the numerator and denominator are negative if
For the positive sign in front of the root in the numerator of Equation (64), the denominator must be positive, which is true if condition (69) holds, meaning that the positive sign in front of must be chosen, i.e., an initial coin counterclockwise rotation. However, the solution, in this case, yields too large a value of .
The other part of the condition, i.e., the argument of the arctan in Equation (64) smaller than , as in condition (28), yields
These three conditions include condition (68), as the right part of (68) is always greater than the right parts of conditions (72) to (74).
Summarizing the conditions for this case:
- -
- if , then condition (72) includes condition (70) and must be positive, i.e., an initial coin counterclockwise rotation;
- -
- if , then condition (73) is the limiting case of conditions (70) and (71), and is positive, i.e., an initial coin counterclockwise rotation;
- -
- if , then condition (74) includes condition (71) and is positive, i.e., an initial coin counterclockwise rotation;
- -
- if , then condition (74) includes Equation (71) and can be either positive or negative, i.e., an initial coin counterclockwise rotation or clockwise rotation.
Discussing the probabilities as in the first case and depending on the above conditions, the probability that the coin will end on its edge is
The maximum probability will occur first, for for the limiting case where
with the approximate equal sign taken to recall that the exact equality is not allowed by conditions (69) or (71), and second, for the argument of the arctan function in being maximum, i.e., for , and either and , or and taking any value, yielding
The coefficient of friction depends on the nature of the surface of both bodies and can take values from 0.05 to 0.2 for steel on steel depending on whether the surfaces are wet or dry, or up to 0.6 for steel on wood.
Assuming, for a 50 Eurocent coin, coefficients of restitution = 0.5 and of friction = 0.05, i.e., both the coin and the landing surface being made of a steel alloy with wet surfaces, the case applies and with the values Equation (6), Equation (77) yields a probability = 0.04492 or nearly 1 throw every 22 that ends with the coin on its edge.
For more common values, condition (72) restricts drastically the choice of values of the coin’s initial rotation velocities with respect to the coin’s vertical velocity at impact. For the above values of coefficients and , condition (72) yields
with = 2.955 × 10−3 m, which leaves a relatively limited range of values for the four initial parameters. This shows that a coin ending on its edge is a very rare event in reality.
Nevertheless, if one extends the ranges (6) of the allowed initial conditions, throwing the coin either horizontally () with any initial velocity or vertically () with a nil initial velocity, from initial heights between 5 and 10 cm and with initial rotation velocities between 6 and 12 turns/s yields a probability = 9.916 × 10−3 or 1 throw approximately every 100 that would end with the coin on its edge.
From a normal initial height = 1.5 m, tossing the coin upward at 45° () with an initial rotation of 33 turns/s with initial velocities ranging from 0.1 to 1 m/s leads to a probability = 1.993 × 10−4 or 1 throw every 5017 ending with the coin on its edge.
For larger values of the friction coefficient, i.e., , the friction quickly becomes too important, and the coin cannot come to a vertical position after impact; it falls immediately on one of its sides.
For all the above values, the term under the root sign in condition (67) is negative, yielding imaginary values for the argument of the arctan function, which shows that condition (67) is fulfilled for all practical values of .
4. Conclusions
The five theoretical models developed in this paper show that there is a non-nil probability that a falling coin will not end up on one of its sides but on its edge, with decreasing probabilities for models describing reality from closer up. It is interesting to note that the probabilities calculated in all the above case models are independent of the coin mass but strongly depend on several other factors, mainly the coin vertical velocity before impact, which depends on the initial height and the initial angle of the throw. It appears that increasing the initial height decreases the probability that the coin will end on its edge, while increasing the initial rotation will increase this probability. Depending on the characteristics of the surface, throwing the coin vertically seems to decrease the probability of the coin ending on its edge. The role of friction is obviously important; if the surface conditions are such as to increase the friction coefficient above a certain value depending on the models, the coin can no longer stop on its edge and will inevitably fall on one side. For a series of throws from an average height with common velocity values and appropriate surface conditions, the probability that a 50 Eurocent coin ends up on its edge is calculated to be in the order of one against several thousand.
Coin geometry is also an important factor. A 25 US Dollar cent coin has a thinner edge (approximately ≈ 1.5 mm), which would decrease all the above-calculated probabilities, although these would stay in the same order of magnitude.
However, these theoretical models are just what they are: theoretical models. To verify these different theoretical models, real experiments would be needed with a coin-throwing machine that could be designed and built in a way to deliver coin throws with exactly similar initial conditions. This could be envisaged as a continuation of this theoretical work.
Furthermore, all effects cannot be taken completely into account, e.g., the coin may spin around its symmetry axis, the coin may not be exactly “fair” (i.e., with a perfectly homogeneous mass distribution), surface conditions of the coin and the landing surface may not be optimal, as assumed above, etc. In addition, not all dynamic effects have been taken into account. Among these, a dynamic instability due to vibration inside the body of the coin is caused by the impact of the coin edge side with the landing surface. This instability might be sufficient to destabilize a configuration that was found sufficiently stable in the theoretical models above and consequently decreases even further the probability of a coin landing on its edge. The destabilizing effect of this instability will be investigated further in a subsequent paper.
Therefore, to throw a coin in the air and let it fall will usually end up with the coin on one of its sides. Nevertheless, the probability that the coin ends on its edge is not nil, even in reality.
In the second part of the paper, the case of rebounds is investigated, and it shows that the probability of a coin landing on its edge is even smaller than in the case without rebounds.
Funding
This research did not receive any specific grant from funding agencies in the public, commercial or not-for-profit sectors.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Conflicts of Interest
The authors declare no conflict of interest.
References
- MacMillan, W.D. Dynamics of Rigid Bodies; Dover Publ.: New York, NY, USA, 1960; pp. 301–303. [Google Scholar]
- Grant, D.F. Chambers Science and Technology Dictionary; Walker, P.M.B., Ed.; Chambers Ltd.: Edinburgh, UK, 1991; p. 455. [Google Scholar]
- Pletser, V. Is the probability of tossing a coin really 50–50%? Part 2: Dynamic Model with rebounds. Preprints, 2022; submitted. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).