Abstract
We analyze Molecular Hydrogen Ions (MHIs) formed by collisions of low-energy protons with the Second Flavor of Hydrogen Atoms SFHA, whose existence was previously proven by two kinds of atomic experiments and also evidenced by two kinds of astrophysical observations. We find that the resulting MHIs would lack a significant number of terms compared to the MHIs formed by collisions of low-energy protons with the usual hydrogen atoms. We show that, in this situation, the radiative transition between the terms of such MHIs of the lowest quantum numbers would be between the terms 5fσ and 4dσ. We calculate the position of the edge of the corresponding molecular band and find it to be at the frequency 14,700 cm−1 or equivalently at the wavelength of 680 nm, which belongs to the visible range. It should be easier to observe this band compared to the spectral bands that are completely beyond the visible range. We emphasize that these results open up another avenue for finding an additional experimental proof of the existence of the SFHA. Namely, if the SFHA is present in gas (in addition to the usual hydrogen atoms), on which a beam of low-energy protons is incident, then the relative intensity of the band, corresponding to the radiative transitions between the terms 5fσ and 4dσ of the MHIs, would be enhanced compared to the absence of the SFHA.
1. Introduction
The Second Flavor of Hydrogen Atoms (SFHA) has been discovered theoretically and proven experimentally to exist (by analyzing atomic experiments related to the distribution of the linear momentum in the ground state of hydrogen atoms) first in 2001 [1]. The gist of the theoretical discovery was that, for the states of zero angular momentum, the so-called “singular” solution of the Dirac equation outside the atomic proton, which was usually disregarded, can be tailored without any problem with the regular solution inside the proton. Therefore, for this second solution, the wave function did not have a singularity at the origin and thus there was no reason to disregard this solution. Since then, there was also found evidence of the existence of the SFHA from atomic experiments: this time from the experiments on the charge exchange of hydrogen atoms with incoming protons [2].
There are also two kinds of astrophysical evidence for the existence of the SFHA. The first one is related to the puzzling observation of the redshifted 21 cm spectral line from the early universe by Bowman et al. [3]. They found that the absorption in this spectral line was about two times stronger than predicted by standard cosmology. This meant that the primordial hydrogen gas was significantly cooler than predicted by standard cosmology. In paper [4], it was shown that this big discrepancy between the observations by Bowman et al. [3] and standard cosmology can be eliminated—qualitatively and quantitatively—in the case where the additional cooling was due to collisions with the SFHA. These results made the SFHA a candidate for dark matter.
The second astrophysical evidence of the existence of the SFHA is the following. Jeffrey et al. [5] recently found through observations that the distribution of dark matter in the universe is smoother than predicted by Einstein’s gravitation, which prompted calls for a non-Einsteinian gravity, i.e., for new physical laws. However, in paper [6] it was demonstrated that this perplexing observation can be also explained—qualitatively and quantitatively—by using the SFHA.
The SFHA-based explanations of the puzzling astrophysical observations by Bowman et al. [3] and by Jeffrey et al. [5] did not require any change of physical laws (and thus were favored by the Occam razor principle). The theoretical discovery of the SFHA in paper [1] was based on the standard Dirac equation of quantum mechanics.
In the present paper, we offer an experimental possibility for an additional proof of the existence of the SFHA; it is about collisions of low-energy protons with the SFHA. One of the possible outcomes of such collisions is charge exchange: for the SFHA it has a slightly larger cross-section than for the usual hydrogen atoms—as shown in paper [2] where the comparison with experiments confirmed this theoretical result. In the present paper, we focus on another outcome of such collisions: the capture of the incoming proton and the formation of the Molecular Hydrogen Ions (MHIs). We reveal the peculiar features of the MHIs formed in this way. This opens up another avenue for finding an additional experimental proof of the existence of the SFHA.
2. Allowed Molecular Terms and Radiative Transitions
There have been lots of theoretical studies of the MHI—see, e.g., reviews [7,8,9] and references therein, as well as papers [10,11] and references therein. There are several reasons for this. From the theoretical point of view, the MHI is the simplest stable molecule and thus represents the test-bench for molecular quantum mechanics. From the applied point of view, the MHI is important in astrophysics because it is involved in reaction chains leading to the formation of polyatomic molecules.
From the theoretical point of view, at fixed nuclei (which in this situation are protons), the MHI is a particular case of the two-Coulomb center system, the latter consisting of two fixed nuclei of charges Z1 and Z2 separated by a distance R and one electron. The two-Coulomb center system allows the complete separation of variables (in elliptical coordinates)—see, e.g., the textbook [12]. This is the consequence of the higher than geometric symmetry of this system, manifested by the existence of an additional conserved quantity: the projection of the super-generalized Runge–Lenz vector on the internuclear axis [13].
As a result of the complete separation of variables, the states of the system are described by sets of elliptical quantum numbers {k, q, m}. Here, k is the radial quantum number, q is the angular quantum number, and m is the azimuthal quantum number. They are equal to the number of nodes of the corresponding parts of the wave function. In particular, the azimuthal quantum number m is the projection of the orbital momentum (in atomic units) on the internuclear axis.
Usually, instead of (k, q, m), there are introduced the following linear combinations—i.e., the orbital quantum number,
and the principal quantum number,
l = q + m
N = k + q + m + 1 = k + l +1.
Then the states are described by the sets (N, l, m). Finally, the numerical values l = 0, 1, 2, 3,… are substituted by letters s, p, d, f,…, respectively, and the numerical values of m = 0, 1, 2,… are substituted by Greek letters σ, π, δ,…. For example, the state (1, 0, 0) becomes denoted as 1sσ, the state (3, 2, 1) becomes denoted as 3dπ, and so on.
When the incoming slow proton is relatively far from the hydrogen atom, i.e., for a relatively large internuclear separation R, the states are described by the sets of the parabolic quantum numbers [n1, n2, m]—see, e.g., the textbook [12]. For the purpose of our paper, the most important is the correspondence between these parabolic quantum numbers (relevant for relatively large R) and the elliptical quantum numbers (relevant for relatively small R). According to book [14], the correspondence is the following.
For any Z1 and Z2:
k = n1.
As for the correspondence between the other quantum numbers, for Z1 = Z2 (i.e., for the situation we are interested in), there are two subcases. For even q, one has,
while for odd q, one has,
q = 2n2,
q = 2n2 + 1.
Here we come to the central point. The primary distinctive feature of the SFHA is that it only has states of the zero-orbital momentum [1,4,15]: the S-states, which are spherically symmetric. Only for S-states, the highest probability of the location of the atomic electron is at or near the origin, so that only the S-states are sensitive to the finite size of the atomic proton and to the behavior of the solution of the Dirac equation in and around the proton. In terms of the parabolic quantum numbers, the spherically symmetric states can correspond only to the situation where,
n1 = n2, m = 0.
Therefore, in this situation, Equation (1) becomes,
and Equation (3) becomes,
so that Equation (2) becomes,
l = q
k = n2,
N = l + n2 + 1.
On substituting q = l (according to Equation (7)) in Equations (4) and (5), we arrive to the following results (taking into account also Equation (9)). For even n2, the possible states have the quantum numbers,
l = 2n2, N = 3n2 + 1.
For odd n2, the possible states have the quantum numbers,
(We remind that n2 = 0, 1, 2,…)
l = 2n2 + 1, N = 3n2 + 2.
In other words, the MHI formed by collisions with low-energy protons with the SFHA would have a significantly smaller number of energy terms compared to the usual MHI. Namely, the even terms are,
1sσ, 4dσ, 7fσ,…
The odd terms are,
2pσ, 5fσ, 8gσ,…
Now, let us consider the consequences of these peculiar features of the energy terms (of this kind of the MHI) in the radiation spectrum. All allowed radiative transitions are between the terms of m = 0, so that the radiation would have the π-polarization only (Δm = 0). Further, taking into account the selection rule |Δl| = 1, we find the following.
The radiative transitions between the terms of the lowest quantum numbers might have been between the terms 2pσ and 1sσ. The term 1sσ corresponds to the stable state of the molecule, the term 2pσ does not.
During the collisions of low-energy protons with hydrogen atoms, the stable theoretical terms of the MHI indicate the possibility of capturing the proton and forming a stable state for the NHI. As for the unstable theoretical terms of the MHI, they should correspond to the formation of transient, quasi-molecular states. Radiative transitions between the meta-stable and stable molecular states in principle should be possible to observe.
However, for the radiative transition between the terms 2pσ and 1sσ there is a problem, as follows. Figure 1 shows the frequency F (in units of 105 cm−1) of the radiative transitions between these two terms versus the internuclear distance R (in atomic units). It would seem that the corresponding spectral band does not have an edge (theoretically it occupies the entire continuous spectrum of frequencies). Therefore, for this band, its intensity per unit frequency range would be very low, thus making it virtually impossible to observe.
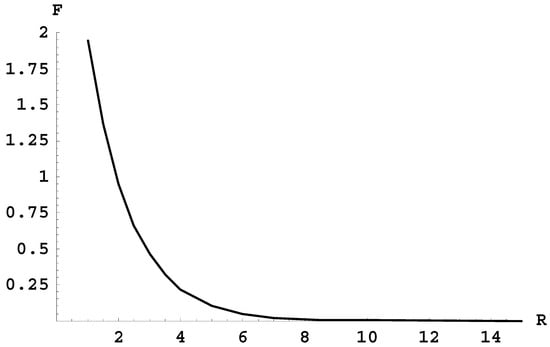
Figure 1.
The frequency F (in units of 105 cm−1) of the radiative transitions between the terms 2pσ and 1sσ versus the internuclear distance R (in atomic units).
As we proceed to the terms of higher quantum numbers, the next possibility is the radiative transition between the terms 5fσ and 4dσ. The term 4dσ corresponds to the stable state of the molecule, the term 5fσ does not. Fortunately, the corresponding spectral band has an edge.
Figure 2, which we created using the tables from the Madsen and Peek paper [16], shows the frequency F (in units of 105 cm−1) of the radiative transitions between these two terms versus the internuclear distance R (in atomic units). At the maximum (located at R = 5), the frequency is F = 14,700 cm−1. This means that this spectral band indeed has an edge, and it is in the vicinity of which the intensity per unit frequency range should be heightened. Moreover, the edge of this spectral band is at a wavelength of 680 nm. Thus, it should be easier to observe compared to the spectral bands that are completely beyond the visible range.
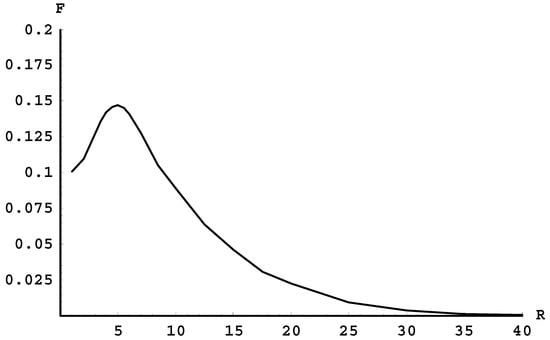
Figure 2.
The frequency F (in units of 105 cm−1) of the radiative transitions between the terms 5fσ and 4dσ versus the internuclear distance R (in atomic units).
These results open up another avenue for finding an additional experimental proof of the existence of the SFHA. Indeed, let us consider an experiment where a beam of low-energy protons is incident on a gas of hydrogen atoms. If the SFHA is present in the gas (in addition to the usual hydrogen atoms), then the relative intensity of the band, corresponding to the radiative transitions between the terms 5fσ and 4dσ, would be enhanced compared to the absence of the SFHA. This is because the SFHA would not contribute to the usually observed bands, corresponding to the radiative transitions between the terms of lower quantum numbers.
In closing this section, we make the following comments. First, some terms of the MHI, formed by collisions of the usual hydrogen atoms with low-energy protons, can exhibit an additional (typically shallow) potential well caused by the van der Waals interaction. Generally, it corresponds to the dipole–dipole interaction (see, e.g., the textbook [12]). It has the form,
where n is the unit vector along the internuclear direction. Since generally the non-diagonal matrix elements of the dipole moment operators are non-zero, then in the second order of the perturbation theory one obtains a non-zero result proportional to 1/R6 (because the result is quadratic with respect to V). In particular, for the ground state, the second order correction is always negative so that the corresponding interaction energy U(R) = −const/R6 < 0 (where const > 0). This corresponds to the attraction and might manifest in molecular terms as a shallow potential well located at relatively large R. The above is true for the usual hydrogen atoms. However, the SFHA has only the S-states, so that, due to the selection rules, all matrix elements of the dipole moment operator are zeros. Therefore, the dipole–dipole interaction vanishes, as well as the charge–dipole interaction. Thus, in the case of the SFHA, there is no van der Waals interaction.
V = [−d1d2 + 3(d1n)(d2n)]/R3
Second, in paper [15] we discussed the consequences of the fact that the ground state of hydrogen atoms turns out to be double-degenerate (due to the SFHA) despite these two states having the same values of all the known conserved quantities. Actually, this additional double-degeneracy is related to all S-states of hydrogen atoms. According to the fundamentals of quantum mechanics, this means that there should be an additional, new conserved quantity by eigenvalues of which any S-state of the SFHA differs from the corresponding S-state of the usual hydrogen atoms. Consequently, hydrogen atoms have two flavors, differing by the eigenvalue of an additional, new conserved quantity that we called isohydrogen spin (abbreviated as isohyspin)—by analogy with the isotopic spin (isospin) distinguishing two flavors of quarks (the up-quark and down-quark). We also emphasized in paper [15] that, since the isospin does not couple to the electromagnetic force/interaction, there seems to be no reason for the isohyspin to couple to the electromagnetic force/interaction either. A hypothetical (though actually impossible) transition from a state of the SFHA (the state being the S-state) would require the “flip” of the isohyspin, thus transforming the state into the S-state (of the same energy) of the usual hydrogen atom. Obviously, this would not be a radiative transition because it would be the transition between states of the same energy. Finally, in paper [15] we emphasized that the idea of the isohyspin is not necessary for considering the second kind of hydrogen atoms as the candidate for dark matter or for a part of dark matter. The idea of the isohyspin is also not necessary for the analysis of different types of atomic and molecular experiments involving the SFHA, such as the experiments analyzed in paper [1,2] and the experiments suggested in the present paper.
3. Conclusions
We considered the MHIs formed by collisions of low-energy protons with the SFHA. We found that the resulting MHIs would lack a significant number of terms compared to the MHIs formed by collisions of low-energy protons with the usual hydrogen atoms.
We showed that, in this situation, the radiative transition between the terms of such MHIs of the lowest quantum numbers would be between the terms 5fσ and 4dσ. We calculated the position of the edge of the corresponding molecular band and found it to be at the frequency 14,700 cm−1 or equivalently at the wavelength of 680 nm, which belongs to the visible range. So, it should be easier to observe this band compared to the spectral bands that are completely beyond the visible range.
We emphasized that these results open up another avenue for finding an additional experimental proof of the existence of the SFHA. Namely, if the SFHA is present in the gas (in addition to the usual hydrogen atoms) on which a beam of low-energy protons is incident, then the relative intensity of the band, corresponding to the radiative transitions between the terms 5fσ and 4dσ of the MHIs, would be enhanced compared to the absence of the SFHA.
Funding
This research received no external funding.
Institutional Review Board Statement
Not applicable.
Informed Consent Statement
Not applicable.
Data Availability Statement
All data is included in the manuscript.
Conflicts of Interest
The author declares no conflict of interest.
References
- Oks, E. High-Energy Tail of the Linear Momentum Distribution in the Ground State of Hydrogen Atoms or Hydrogen-like Ions. J. Phys. B At. Mol. Opt. Phys. 2001, 34, 2235–2243. [Google Scholar] [CrossRef]
- Oks, E. Analysis of Experimental Cross-Sections of Charge Exchange between Hydrogen Atoms and Protons Yields another Evidence of the Existence of the Second Flavor of Hydrogen Atoms. Foundations 2021, 1, 265–270. [Google Scholar] [CrossRef]
- Bowman, J.D.; Rogers, A.E.E.; Monsalve, R.A.; Mozdzen, T.J.; Mahesh, N. An Absorption Profile Centred at 78 Megahertz in the Sky-Averaged Spectrum. Nature 2018, 555, 67–70. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Oks, E. Alternative Kind of Hydrogen Atoms as a Possible Explanation of the Latest Puzzling Observation of the 21 cm Radio Line from the Early Universe. Res. Astron. Astrophys. 2020, 20, 109. [Google Scholar] [CrossRef]
- Jeffrey, N.; Gatti, M.; Chang, C.; Whiteway, L.; Demirbozan, U.; Kovacs, A.; Pollina, G.; Bacon, D.; Hamaus, N.; Kacprzak, T. Dark Energy Survey Year 3 results: Curved-Sky Weak Lensing Mass Map Reconstruction. Mon. Not. R. Astron. Soc. 2021, 505, 4626–4645. [Google Scholar] [CrossRef]
- Oks, E. DES Map Shows a Smoother Distribution of Matter than Expected: A Possible Explanation. Res. Astron. Astrophys. 2021, 21, 241–245. [Google Scholar] [CrossRef]
- Roth, B.; Koelemeij, J.; Schiller, S.; Hilico, L.; Karr, J.-P.; Korobov, V.; Bakalov, D. Precision Spectroscopy of Molecular Hydrogen Ions: Towards Frequency Metrology of Particle Masses. In Precision Physics of Simple Atoms and Molecules; Karshenboim, S.G., Ed.; Lecture Notes in Physics; Springer: Berlin/Heidelberg, Germany, 2008; Volume 745. [Google Scholar]
- Leach, C.A.; Moss, R.E. Spectroscopy and Quantum Mechanics of the Hydrogen Molecular Cation: A Test of Molecular Quantum Mechanics. Annu. Rev. Phys. Chem. 1995, 46, 46–82. [Google Scholar] [CrossRef] [PubMed]
- Carrington, A.; McNab, I.R.; Montgomerie, C.A. Spectroscopy of the Hydrogen Molecular Ion. J. Phys. B At. Mol. Opt. Phys. 1989, 22, 3551–3586. [Google Scholar] [CrossRef]
- Scott, T.C.; Aubert-Frecon, M.; Grotendorst, J. New Approach for the Electronic Energies of the Hydrogen Molecular Ion. Chem. Phys. 2006, 324, 323–338. [Google Scholar] [CrossRef] [Green Version]
- Carrington, A.; McNab, I.R. Spectroscopy of the H…H+ and D…D+ Charge/Induced-Dipole Complexes. J. Chem. Soc. Faraday Trans. 1990, 86, 1957–1962. [Google Scholar] [CrossRef]
- Landau, L.D.; Lifshitz, E.M. Quantum Mechanics; Pergamon: Oxford, UK, 1965. [Google Scholar]
- Kryukov, N.; Oks, E. Super-generalized Runge-Lenz Vector in the Problem of Two Coulomb or Newton Centers. Phys. Rev. A 2012, 85, 054503. [Google Scholar] [CrossRef]
- Komarov, I.V.; Ponomarev, L.I.; Slavjanov, S.Y. Spheroidal and Coulomb Spheroidal Functions; Nauka: Moscow, Russia, 1976; Section II.3. (In Russian) [Google Scholar]
- Oks, E. Two Flavors of Hydrogen Atoms: A Possible Explanation of Dark Matter. Atoms 2020, 8, 33. [Google Scholar] [CrossRef]
- Madsen, M.M.; Peek, J.M. Eigenparameters for the Lowest Twenty Electronic States of the Hydrogen Molecule Ion. At. Data 1971, 2, 171–204. [Google Scholar] [CrossRef]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).