On Fractional Lyapunov Functions of Nonlinear Dynamic Systems and Mittag-Leffler Stability Thereof
Abstract
1. Introduction
2. Basic Preliminary
3. Model Description
4. Mittag-Leffler Stability
- (i)
- is Lipschitz in regard to y.
- (ii)
- ∃ satisfying and if then
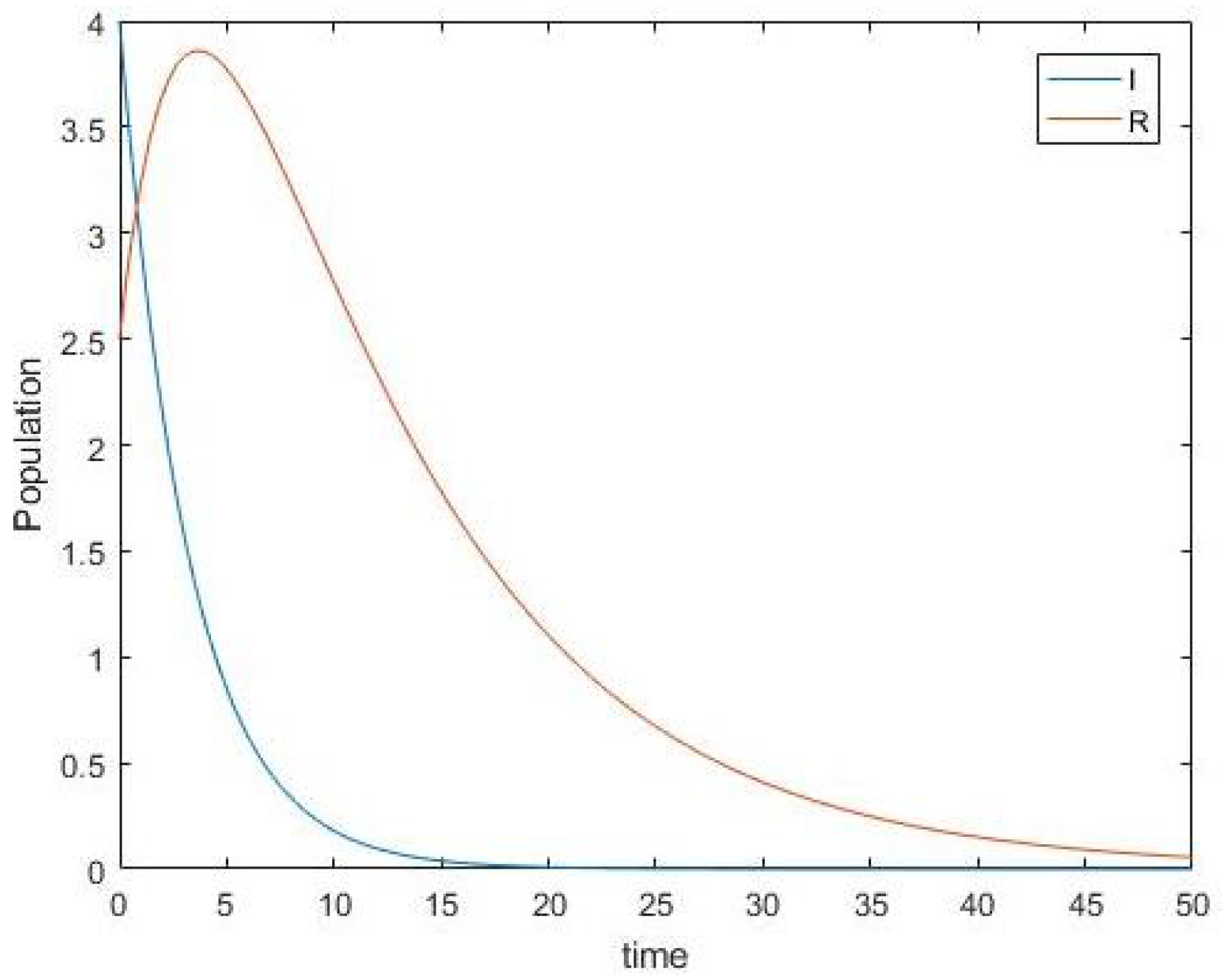
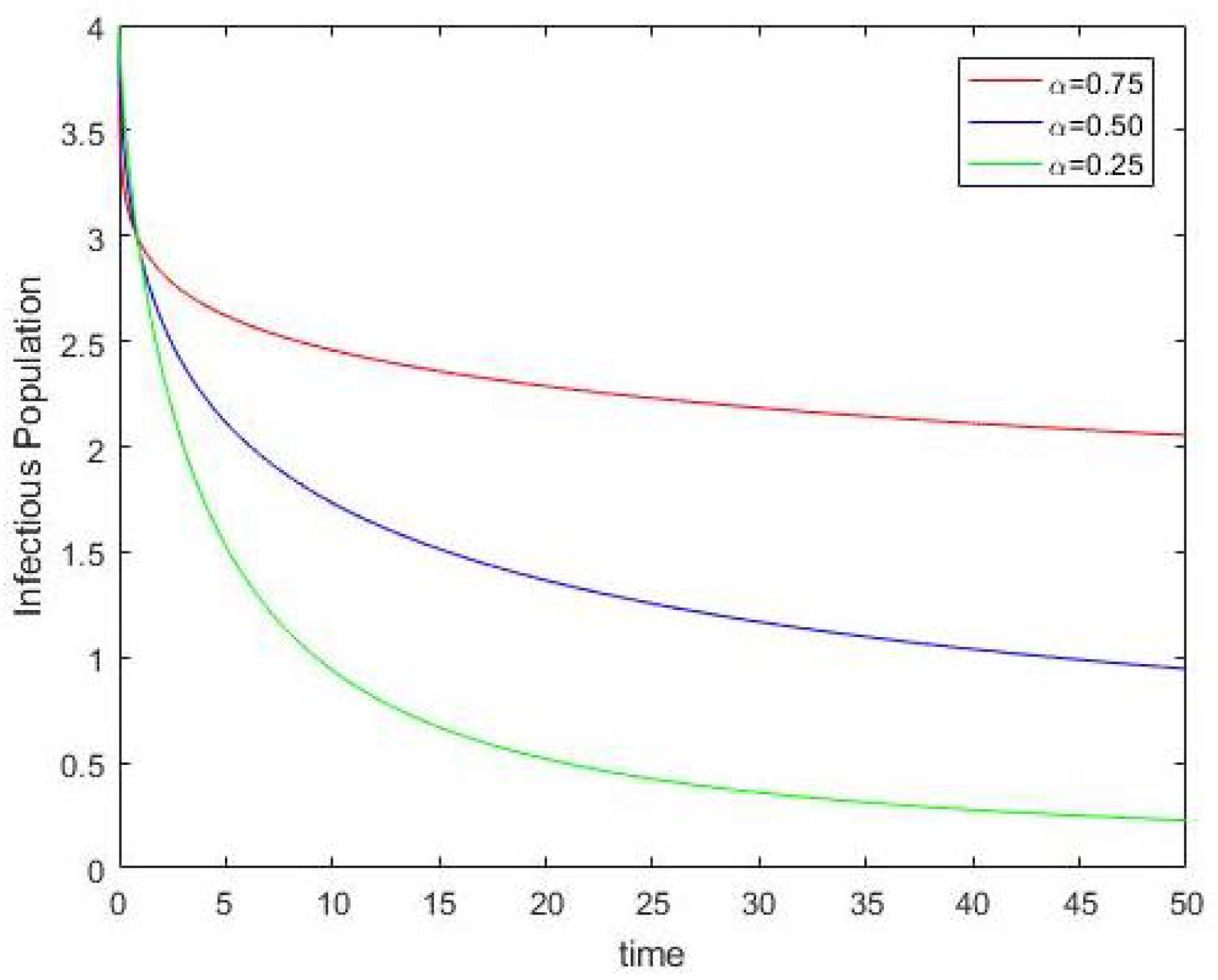
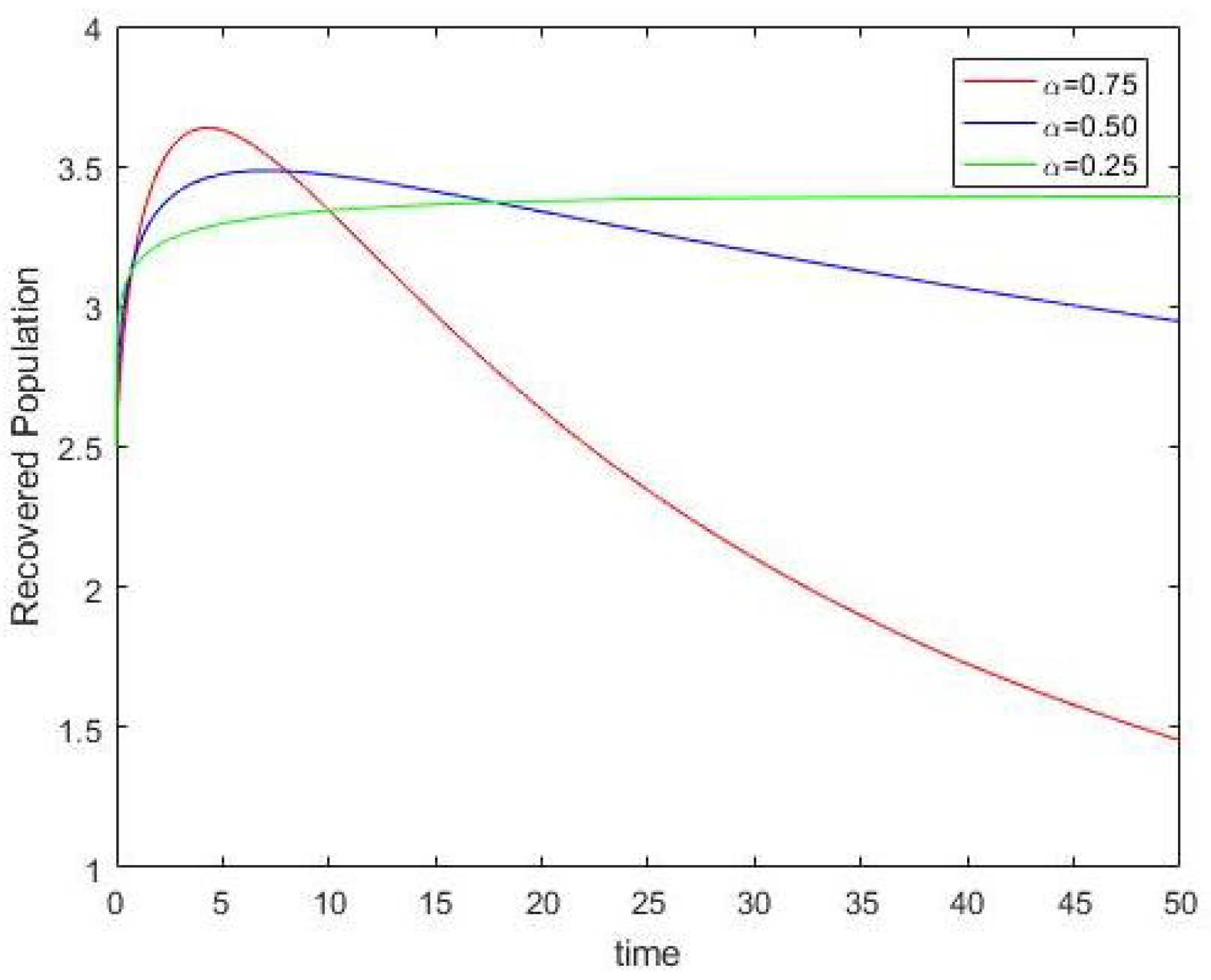
5. Numerical Simulations
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| SIR | Susceptible–infected–recovered |
| SIRS | Susceptible–infected–recovered–susceptible |
| RL | Riemann–Liouville |
| C | Caputo |
References
- Li, Y.; Chen, Y.; Podlubny, I. Mittag-Leffler stability of fractional-order nonlinear dynamic systems. Automatica 2009, 45, 1965–1969. [Google Scholar] [CrossRef]
- Sena, N. Cascade of fractional differential equations and generalized Mittag-Leffler stability. Int. J. Math. Model. Comput. 2020, 10, 25–35. [Google Scholar]
- Aleksandrov, A. On the existence of a common lyapunov function for a family of nonlinear positive systems. Syst. Control Lett. 2021, 147, 1–4. [Google Scholar] [CrossRef]
- Owoyemi, A.E.; Sulaiman, I.M.; Mamat, M.; Olowo, S.E. Stability and bifurcation analysis in a fractional-order epidemic model with sub-optimal immunity, nonlinear incidence and saturated recovery rate. Int. J. Appl. Math. 2021, 51, 515–525. [Google Scholar]
- Goh, B.S. Management and Analysis of Biological Populations; Elsevier Science: Amsterdam, The Netherlands, 1980. [Google Scholar]
- Agarwal, P.; Singh, R.; Rehman, A.U. Numerical solution of a hybrid mathematical model of dengue transmission with relapse and memory via Adam-Bashforth-Moulton predictor-corrector. Chaos Solit. Fractals 2021, 143, 1–20. [Google Scholar] [CrossRef]
- Sharma, N.; Pathak, R.; Singh, R. Modeling of media impact with stability analysis and optimal solution of SEIRS epidemic model. J. Interdiscip. Math. 2019, 22, 1123–1156. [Google Scholar] [CrossRef]
- Korobeinikov, A.; Wake, G.C. Lyapunov functions and global stability for SIR, SIRS, and SIS epidemiological models. Appl. Math. Lett. 2002, 15, 955–960. [Google Scholar] [CrossRef]
- Korobeinikov, A.; Maini, P.K. A Lyapunov function and global properties for SIR and SEIR epidemiological models with nonlinear incidence. Math. Biosci. Eng. 2004, 1, 57–60. [Google Scholar] [PubMed]
- Korobeinikov, A. Lyapunov functions and global stability for SIR and SIRS epidemiological models with the non-linear transmission. Bull. Math. Biol. 2006, 68, 615–626. [Google Scholar] [CrossRef] [PubMed]
- Okuonghae, D.; Korobeinikov, A. Dynamics of tuberculosis: The effect of direct observation therapy strategy (DOTS) in Nigeria. Math. Model. Nat. Phenom. 2007, 2, 113–128. [Google Scholar] [CrossRef][Green Version]
- Georgescu, P.; Hsieh, Y.H. Global stability for a virus dynamics model with nonlinear incidence of infection and removal. SIAM J. Appl. Math. 2006, 67, 337–353. [Google Scholar] [CrossRef]
- Arshad, S.; Sohail, A.; Javed, S. Dynamical Study of Fractional Order Tumor Model. Int. J. Comput. Methods 2015, 12, 1–12. [Google Scholar] [CrossRef]
- Altaf, K.M.; Wahid, A.; Islam, S.; Khan, I.; Shafie, S.; Gul, T. Stability analysis of an SEIR epidemic model with non-linear saturated incidence and temporary immunity. Int. J. Adv. Appl. Math. Mech. 2015, 2, 1–14. [Google Scholar]
- O′Regan, S.M.; Kelly, T.C.; Korobeinikov, A.; O’Callaghan, M.J.A.; Pokrovskii, A.V. Lyapunov functions for SIR and SIRS epidemic models. Appl. Math. Lett. 2010, 23, 446–448. [Google Scholar]
- Miller, K.S.; Ross, B. An Introduction to the Fractional Calculus and Fractional Differential Equations; Wiley: New York, NY, USA, 1993. [Google Scholar]
- Kilbas, A.A.; Srivastava, H.M.; Trujillo, J.J. Theory and Application of Fractional Differential Equations; Elsevier: Amsterdam, The Netherlands, 2006. [Google Scholar]
- Busenberg, S.; Cooke, K. Vertically Transmitted Diseases: Models and Dynamics; Springer: Berlin, Germany, 1993. [Google Scholar]
- Jumarie, G. Table of some basic fractional calculus formulae derived from a modified Riemann-Liouville derivative for non-differentiable functions. Appl. Math. Lett. 2009, 22, 378–385. [Google Scholar] [CrossRef]
- Bohner, M.; Tunç, O.; Tunç, C. Qualitative analysis of caputo fractional integro–differential equations with constant delays. Comput. Appl. Math. 2021, 40, 1–17. [Google Scholar] [CrossRef]
- Li, Y.; Chen, Y.; Podlubny, I. Stability of fractional-order nonlinear dynamic systems: Lyapunov direct method and generalized Mittag-Leffler stability. Comput. Math. Appl. 2010, 59, 1810–1821. [Google Scholar] [CrossRef]
- Camacho, N.A.; Mermoud, M.A.D.; Gallegos, J.A. Lyapunov functions for fractional order systems. Commun. Nonlinear Sci. Numer. Simulat. 2014, 19, 2951–2957. [Google Scholar] [CrossRef]
- Narendra, K.S.; Annaswamy, A.M. Stable Adaptive Systems; Dover Publications: New York, NY, USA, 2005. [Google Scholar]
- Korobeinikov, A. Global asymptotic properties of virus dynamics models with dose-dependent parasite reproduction and virulence and non-linear incidence rate. Math. Med. Biol. 2009, 26, 225–239. [Google Scholar] [CrossRef] [PubMed]
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Rehman, A.u.; Singh, R.; Agarwal, P. On Fractional Lyapunov Functions of Nonlinear Dynamic Systems and Mittag-Leffler Stability Thereof. Foundations 2022, 2, 209-217. https://doi.org/10.3390/foundations2010013
Rehman Au, Singh R, Agarwal P. On Fractional Lyapunov Functions of Nonlinear Dynamic Systems and Mittag-Leffler Stability Thereof. Foundations. 2022; 2(1):209-217. https://doi.org/10.3390/foundations2010013
Chicago/Turabian StyleRehman, Attiq ul, Ram Singh, and Praveen Agarwal. 2022. "On Fractional Lyapunov Functions of Nonlinear Dynamic Systems and Mittag-Leffler Stability Thereof" Foundations 2, no. 1: 209-217. https://doi.org/10.3390/foundations2010013
APA StyleRehman, A. u., Singh, R., & Agarwal, P. (2022). On Fractional Lyapunov Functions of Nonlinear Dynamic Systems and Mittag-Leffler Stability Thereof. Foundations, 2(1), 209-217. https://doi.org/10.3390/foundations2010013






