Figure 1.
Adjusted global plastic production (1950–2019) and projection (2020–2060).
Figure 1.
Adjusted global plastic production (1950–2019) and projection (2020–2060).
Figure 2.
Diagrammatic presentation of the flow chart of the methodological procedure.
Figure 2.
Diagrammatic presentation of the flow chart of the methodological procedure.
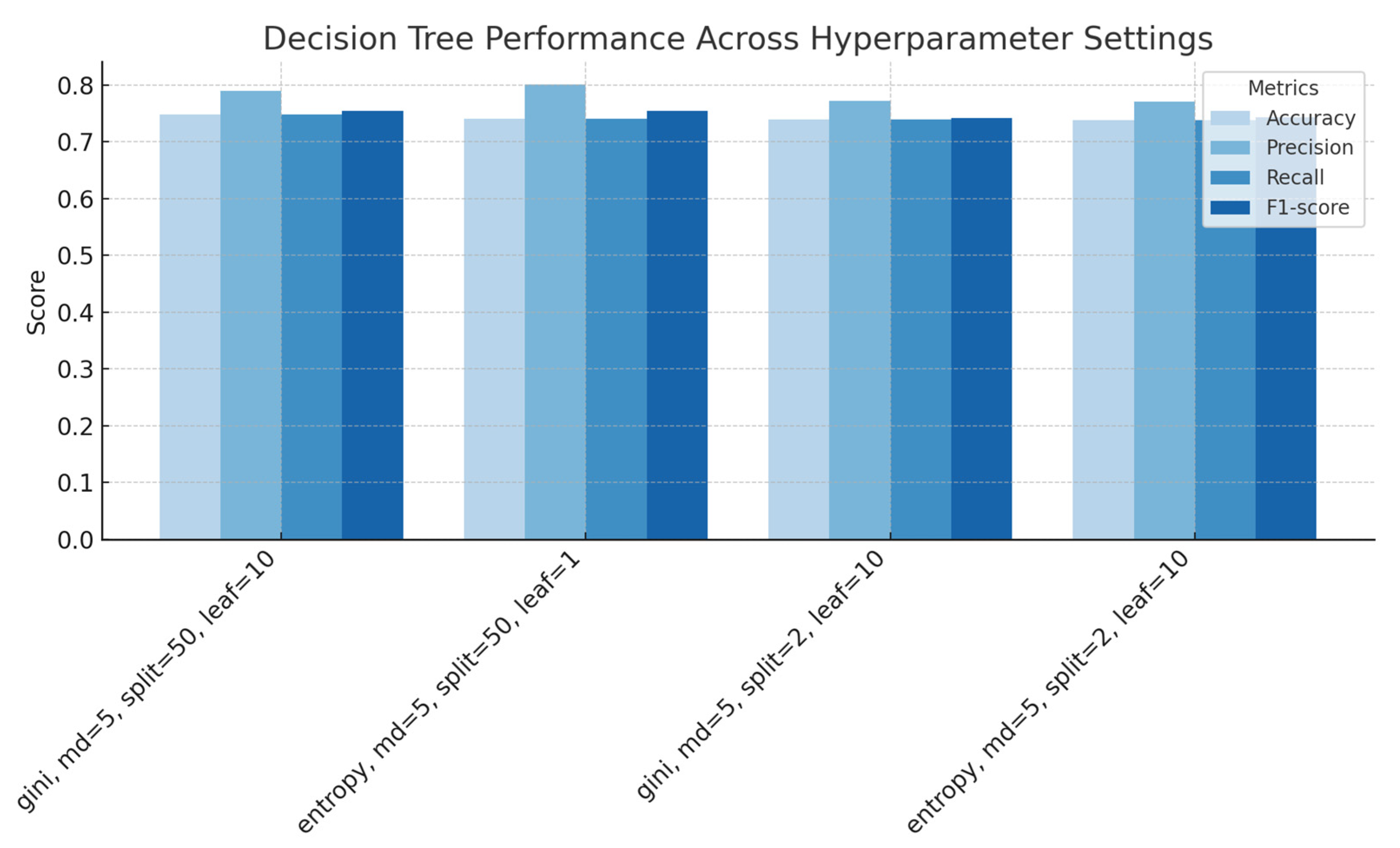
Figure 3.
Decision Trees performance across splitting criteria and sample parameters, showing accuracy, precision, recall and F1-score for each configuration.
Figure 3.
Decision Trees performance across splitting criteria and sample parameters, showing accuracy, precision, recall and F1-score for each configuration.
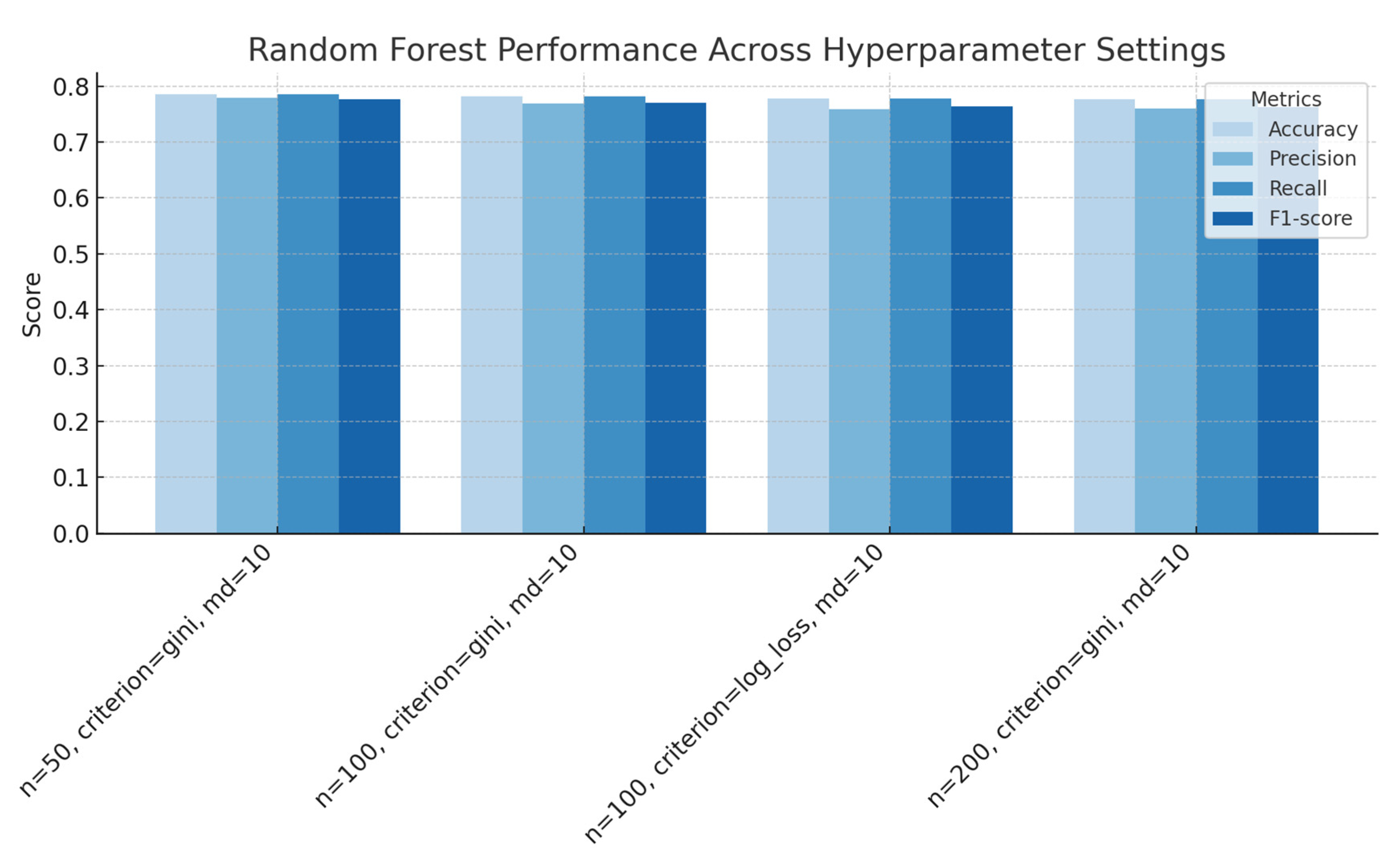
Figure 4.
Random Forest performance across different numbers of estimators and splitting criteria (Gini versus log-loss), with a fixed maximum depth of 10, showing accuracy, precision, recall and F1-score for each configuration.
Figure 4.
Random Forest performance across different numbers of estimators and splitting criteria (Gini versus log-loss), with a fixed maximum depth of 10, showing accuracy, precision, recall and F1-score for each configuration.
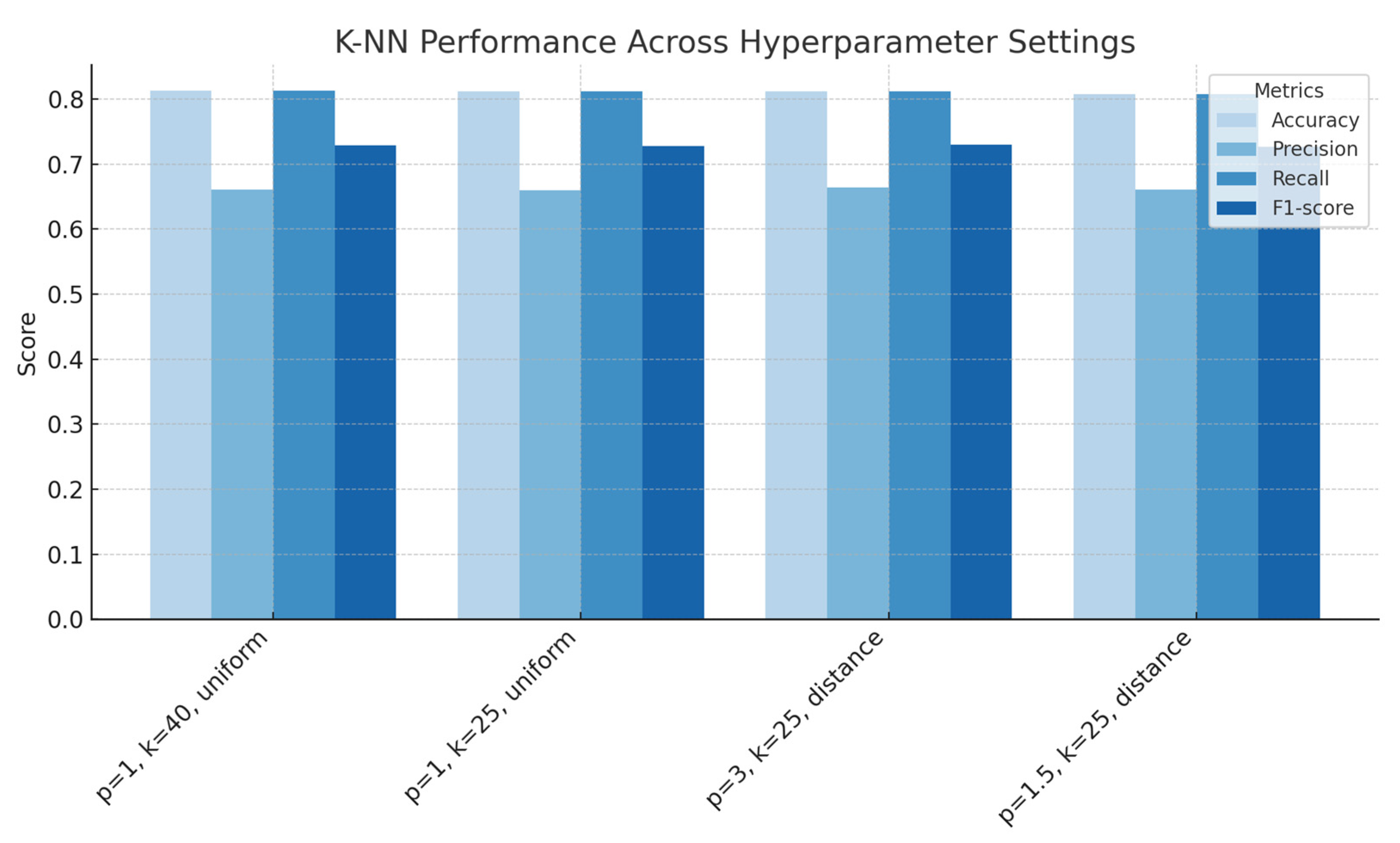
Figure 5.
k-Nearest Neighbours performance across with a variety of hyperparameters (number of neighbours, distance norms, weighing schemes), showing accuracy, precision, recall and F1-score for each configuration.
Figure 5.
k-Nearest Neighbours performance across with a variety of hyperparameters (number of neighbours, distance norms, weighing schemes), showing accuracy, precision, recall and F1-score for each configuration.
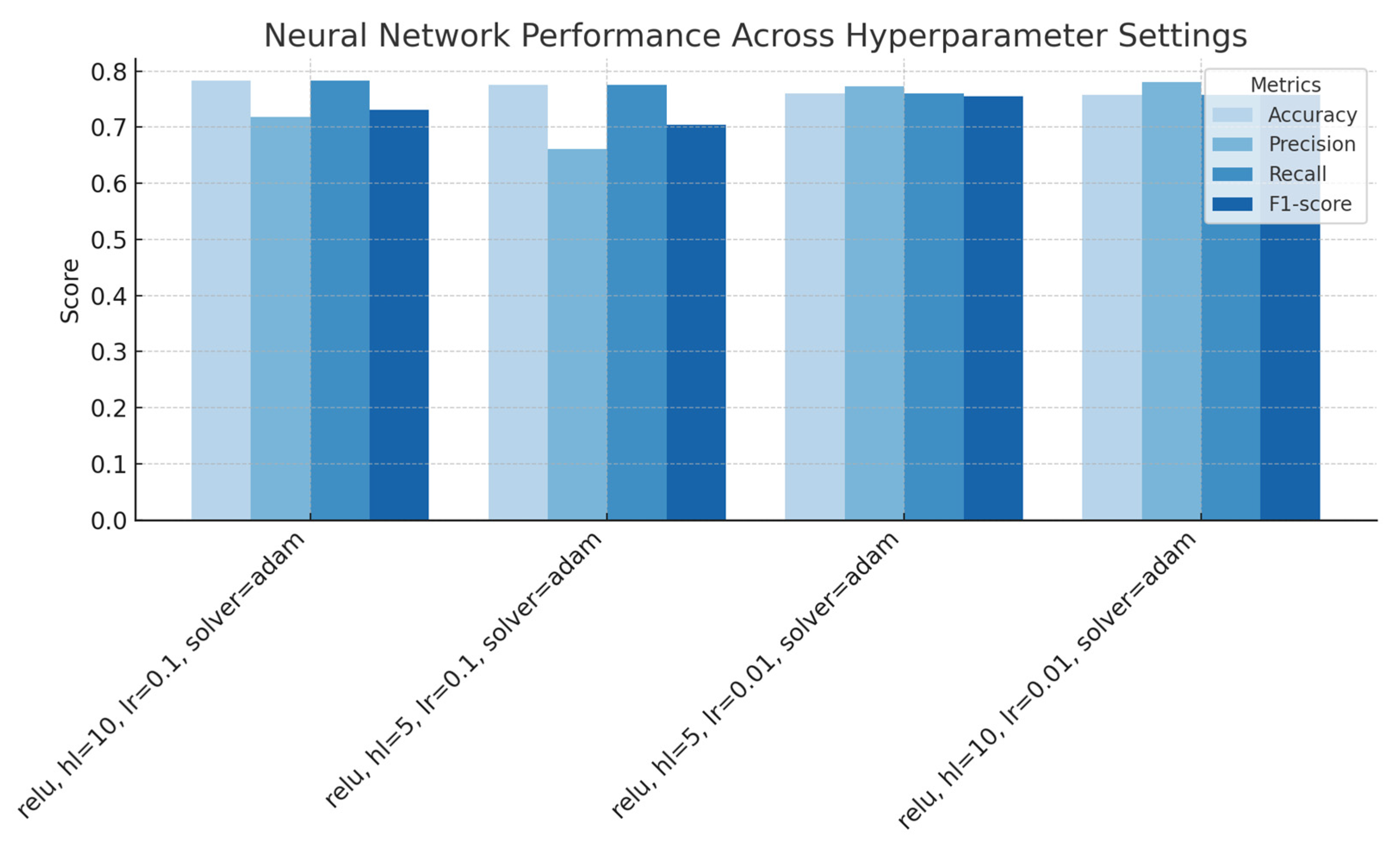
Figure 6.
Neural Networks performance across with a variety of hyperparameters (activation = relu, varying hidden layer size, initial learning rate, and solver), showing accuracy, precision, recall, and F1-score for each configuration.
Figure 6.
Neural Networks performance across with a variety of hyperparameters (activation = relu, varying hidden layer size, initial learning rate, and solver), showing accuracy, precision, recall, and F1-score for each configuration.
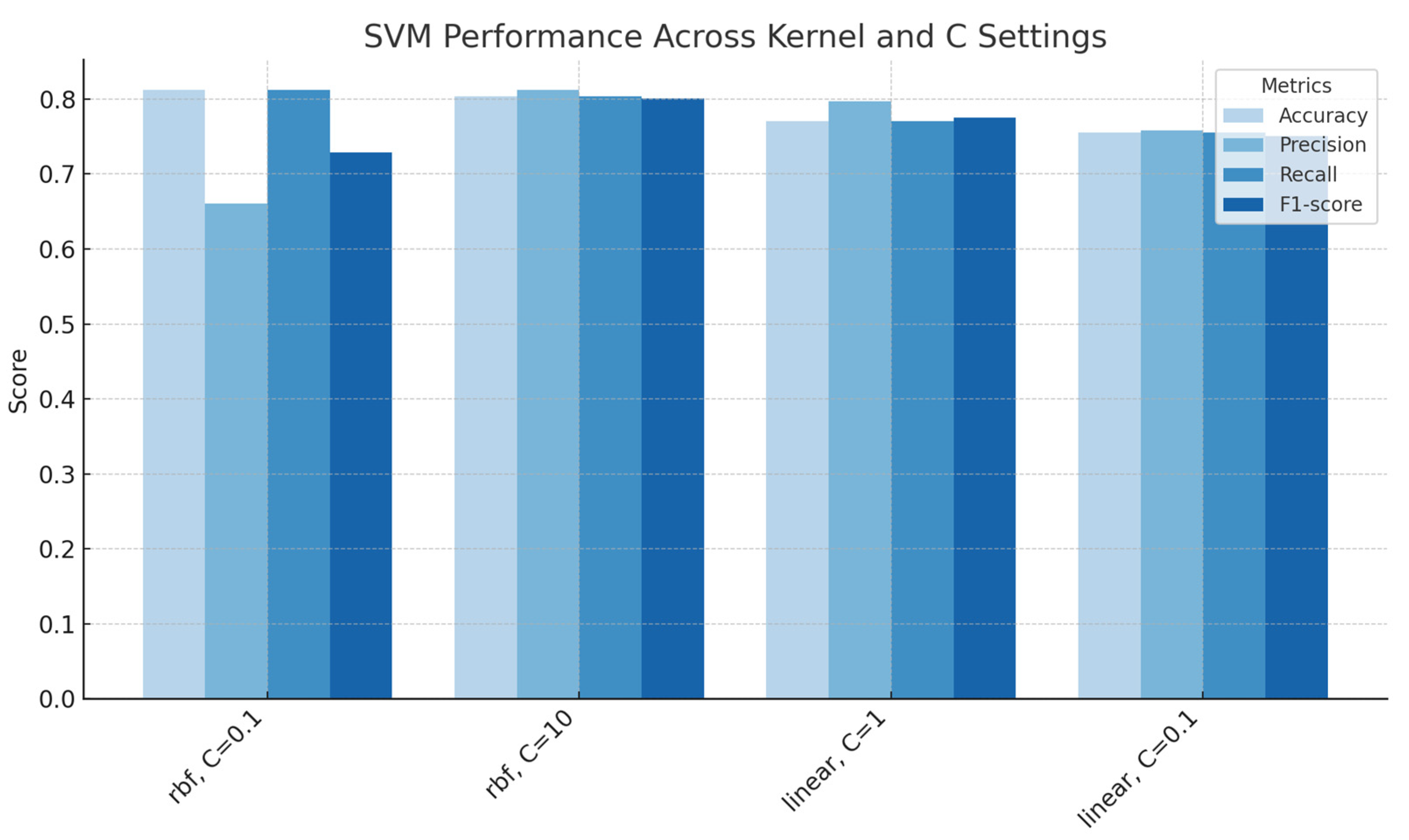
Figure 7.
Support Vector Machines performance across kernel types and regularization parameters, showing accuracy, precision, recall and F1-score for each configuration.
Figure 7.
Support Vector Machines performance across kernel types and regularization parameters, showing accuracy, precision, recall and F1-score for each configuration.
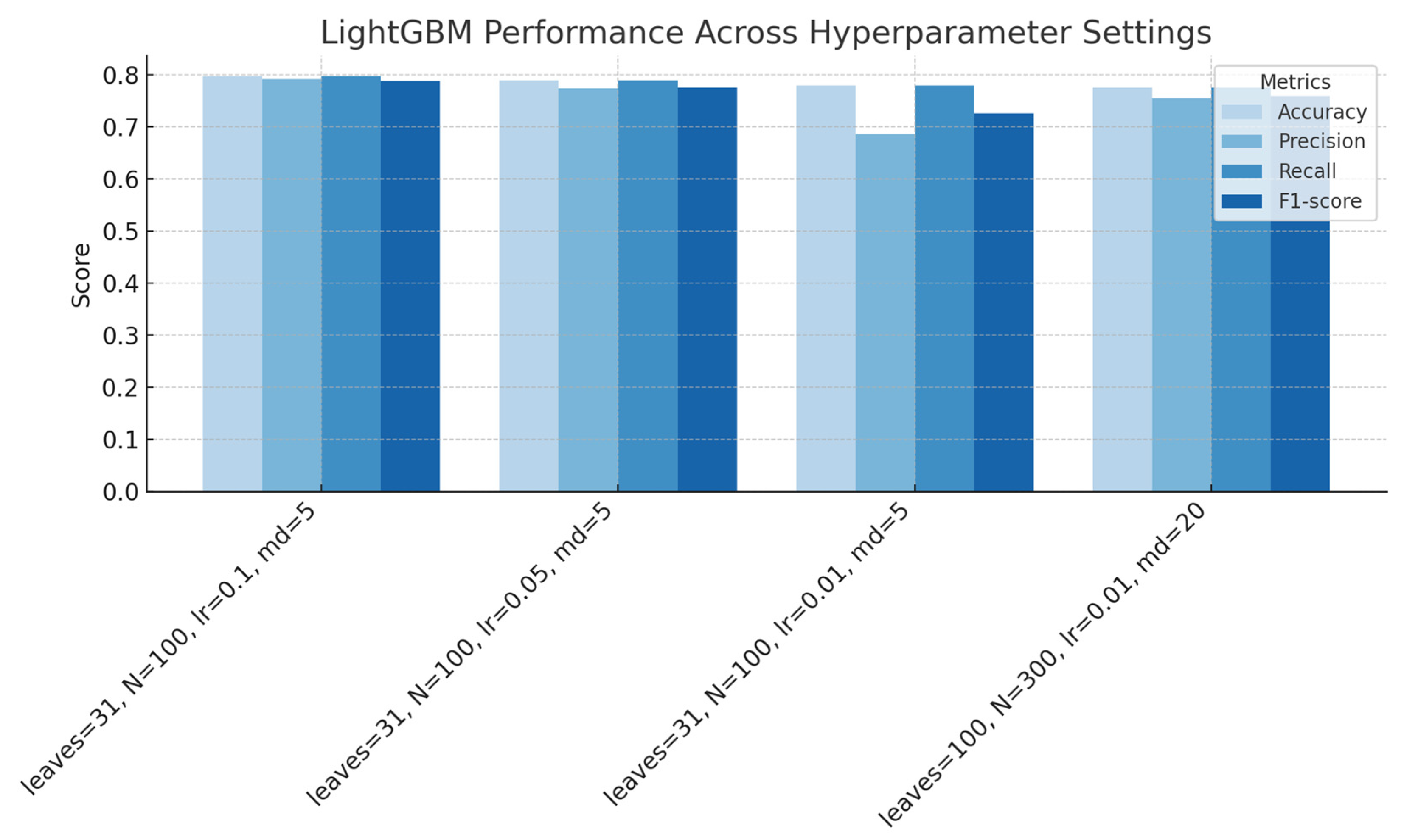
Figure 8.
LightGBM performance across hyperparameter settings (regularization, number of estimators, learning rate, and maximum depth), showing accuracy, precision, recall, and F1-score for each configuration.
Figure 8.
LightGBM performance across hyperparameter settings (regularization, number of estimators, learning rate, and maximum depth), showing accuracy, precision, recall, and F1-score for each configuration.
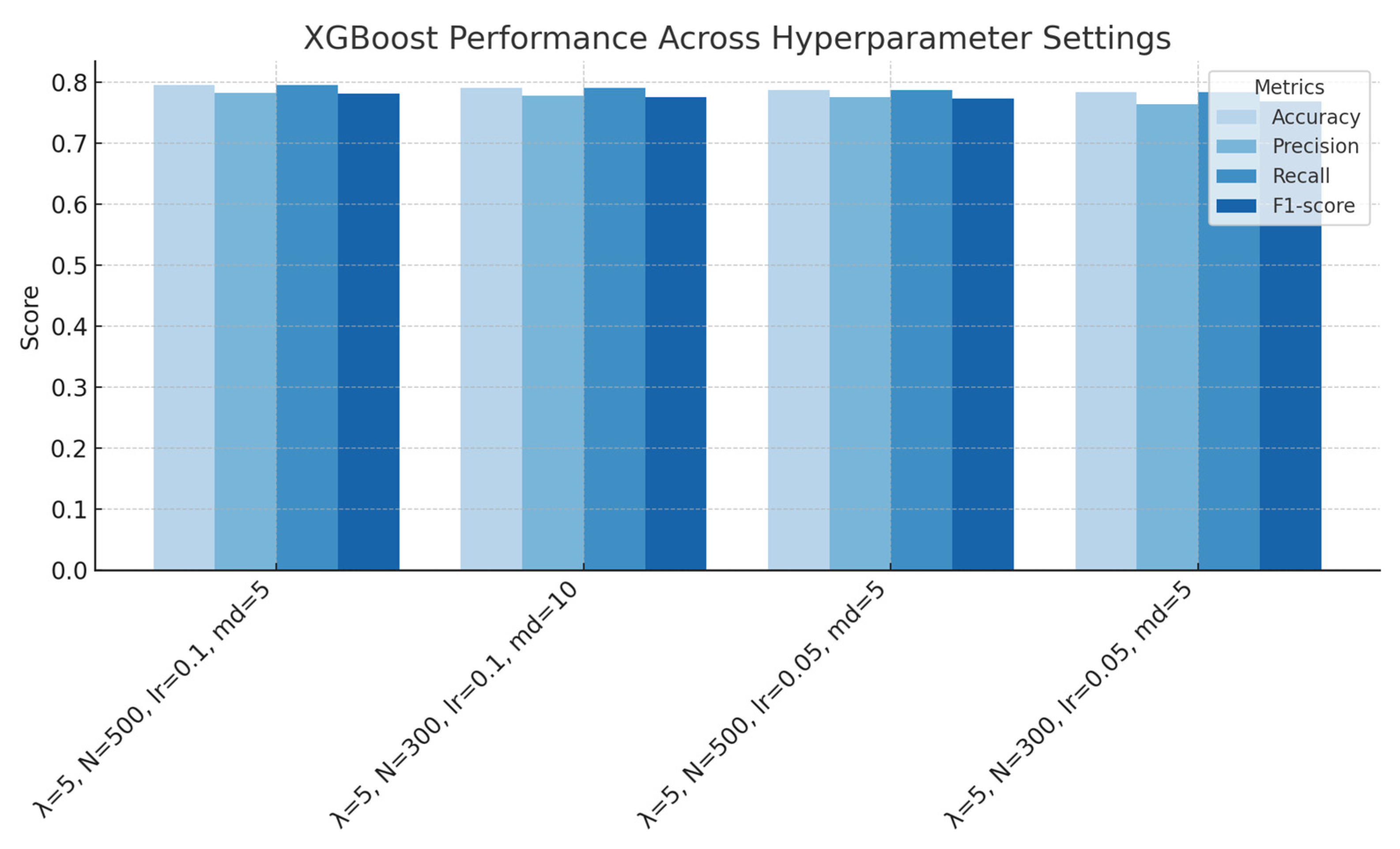
Figure 9.
XGBoost performance across hyperparameter settings (regularization, number of estimators, learning rate, and maximum depth), showing accuracy, precision, recall and F1-score for each configuration.
Figure 9.
XGBoost performance across hyperparameter settings (regularization, number of estimators, learning rate, and maximum depth), showing accuracy, precision, recall and F1-score for each configuration.
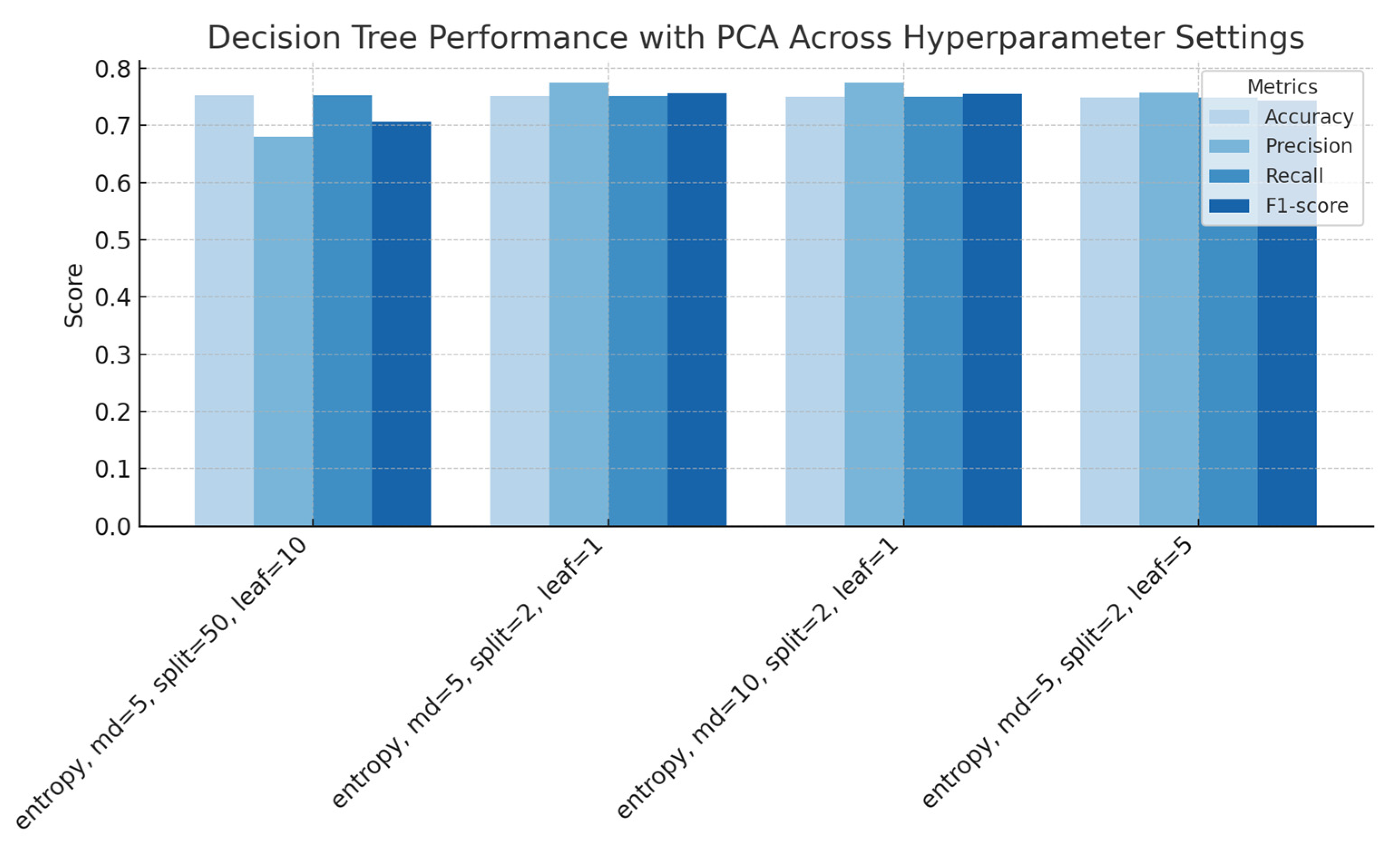
Figure 10.
Decision Trees performance with application of PCA across hyperparameter settings (splitting criterion, maximum depth, minimum samples split, and minimum samples leaf), showing accuracy, precision, recall, and F1-score for each configuration.
Figure 10.
Decision Trees performance with application of PCA across hyperparameter settings (splitting criterion, maximum depth, minimum samples split, and minimum samples leaf), showing accuracy, precision, recall, and F1-score for each configuration.
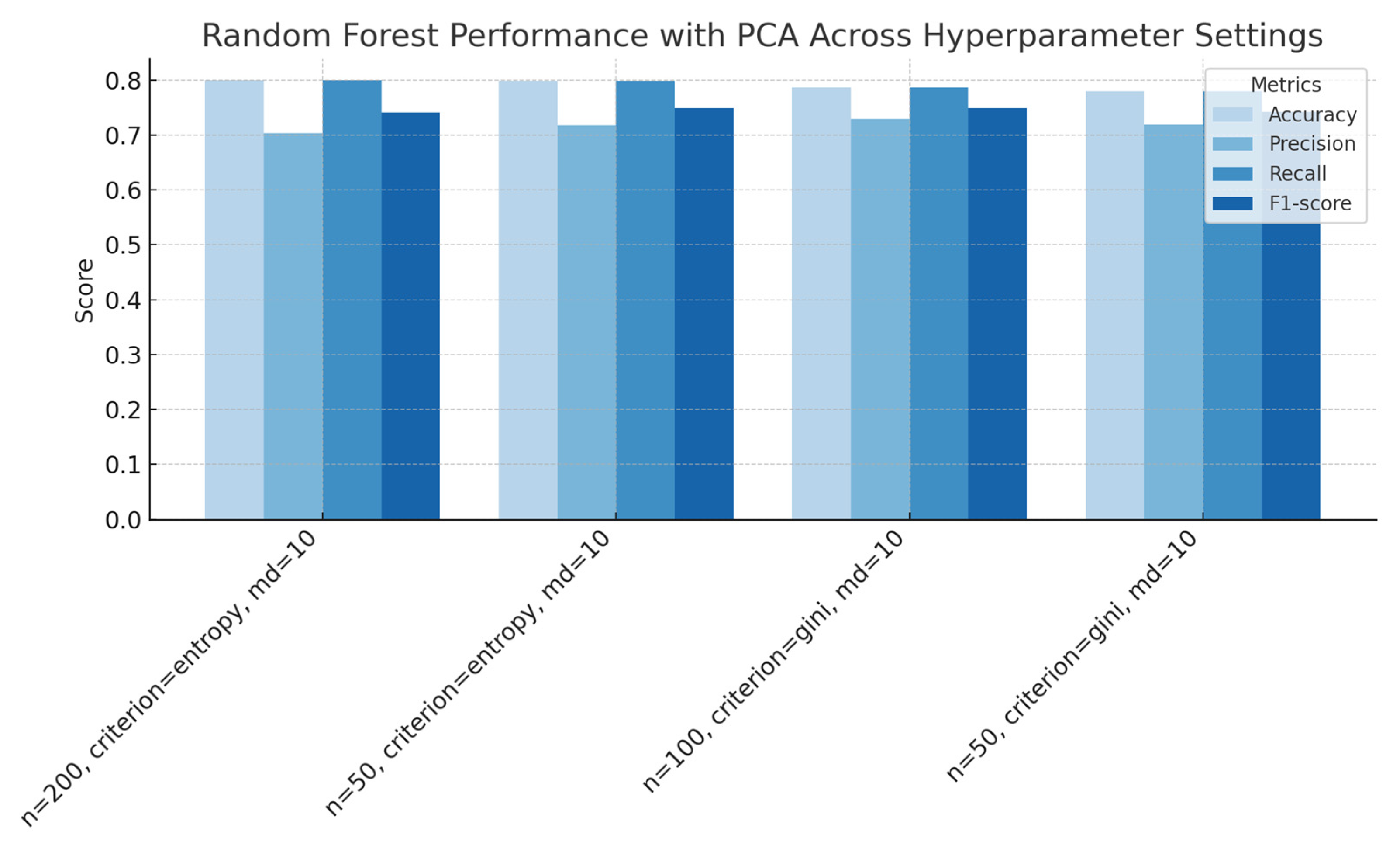
Figure 11.
Random Forest performance with PCA across hyperparameter settings (number of estimators, splitting criterion, and maximum depth), showing accuracy, precision, recall, and F1-score for each configuration.
Figure 11.
Random Forest performance with PCA across hyperparameter settings (number of estimators, splitting criterion, and maximum depth), showing accuracy, precision, recall, and F1-score for each configuration.
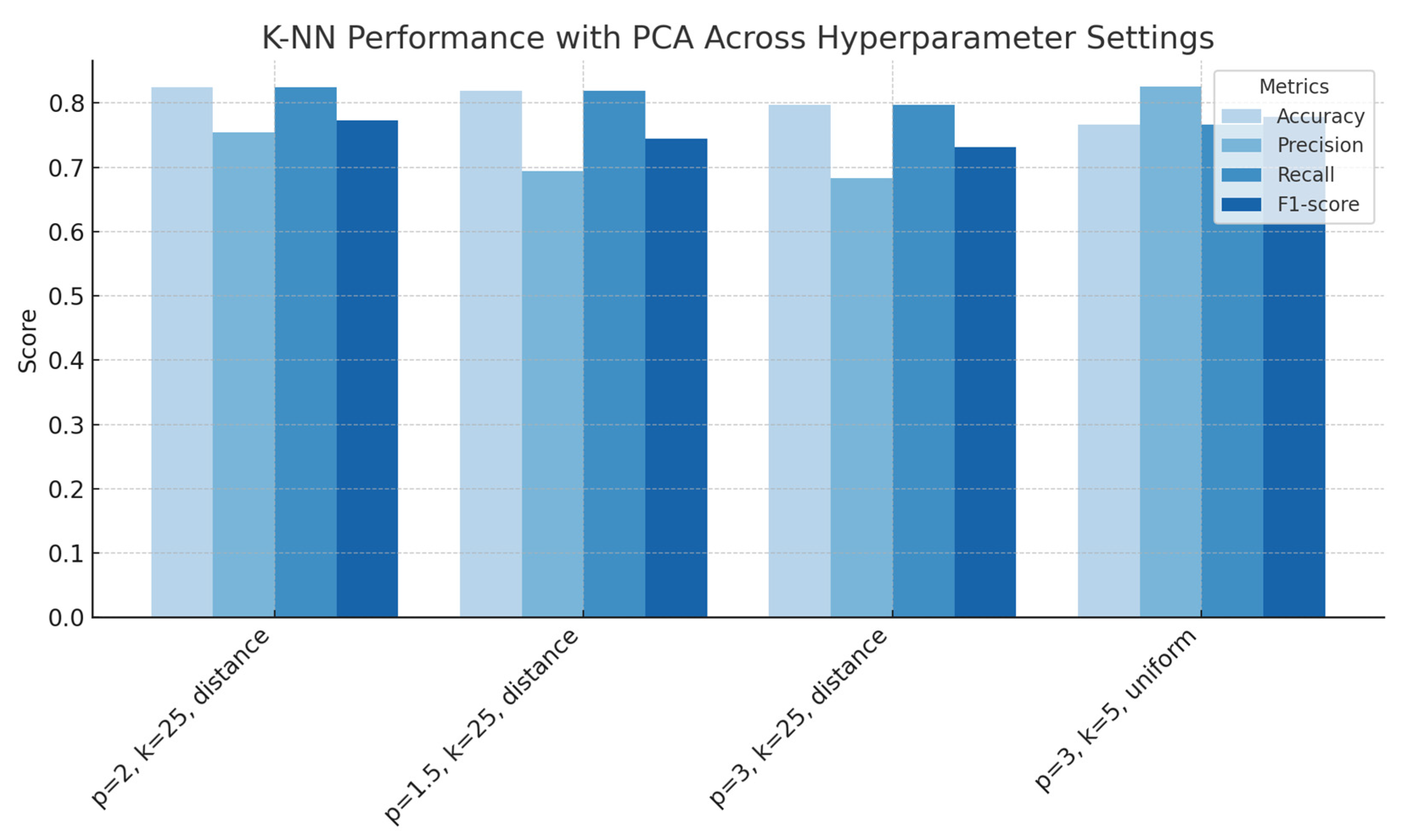
Figure 12.
k-Nearest Neighbours performance with PCA across hyperparameter settings (number of neighbours, distance norms, weighing schemes), showing accuracy, precision, recall and F1-score for each configuration.
Figure 12.
k-Nearest Neighbours performance with PCA across hyperparameter settings (number of neighbours, distance norms, weighing schemes), showing accuracy, precision, recall and F1-score for each configuration.
Figure 13.
Neural Networks performance with PCA across with a variety of hyperparameters (activation = relu, varying hidden layer size, initial learning rate, and solver), showing accuracy, precision, recall, and F1-score for each configuration.
Figure 13.
Neural Networks performance with PCA across with a variety of hyperparameters (activation = relu, varying hidden layer size, initial learning rate, and solver), showing accuracy, precision, recall, and F1-score for each configuration.
Figure 14.
Support Vector Machines performance with PCA across kernel types and regularization parameters, showing accuracy, precision, recall, and F1-score for each configuration.
Figure 14.
Support Vector Machines performance with PCA across kernel types and regularization parameters, showing accuracy, precision, recall, and F1-score for each configuration.
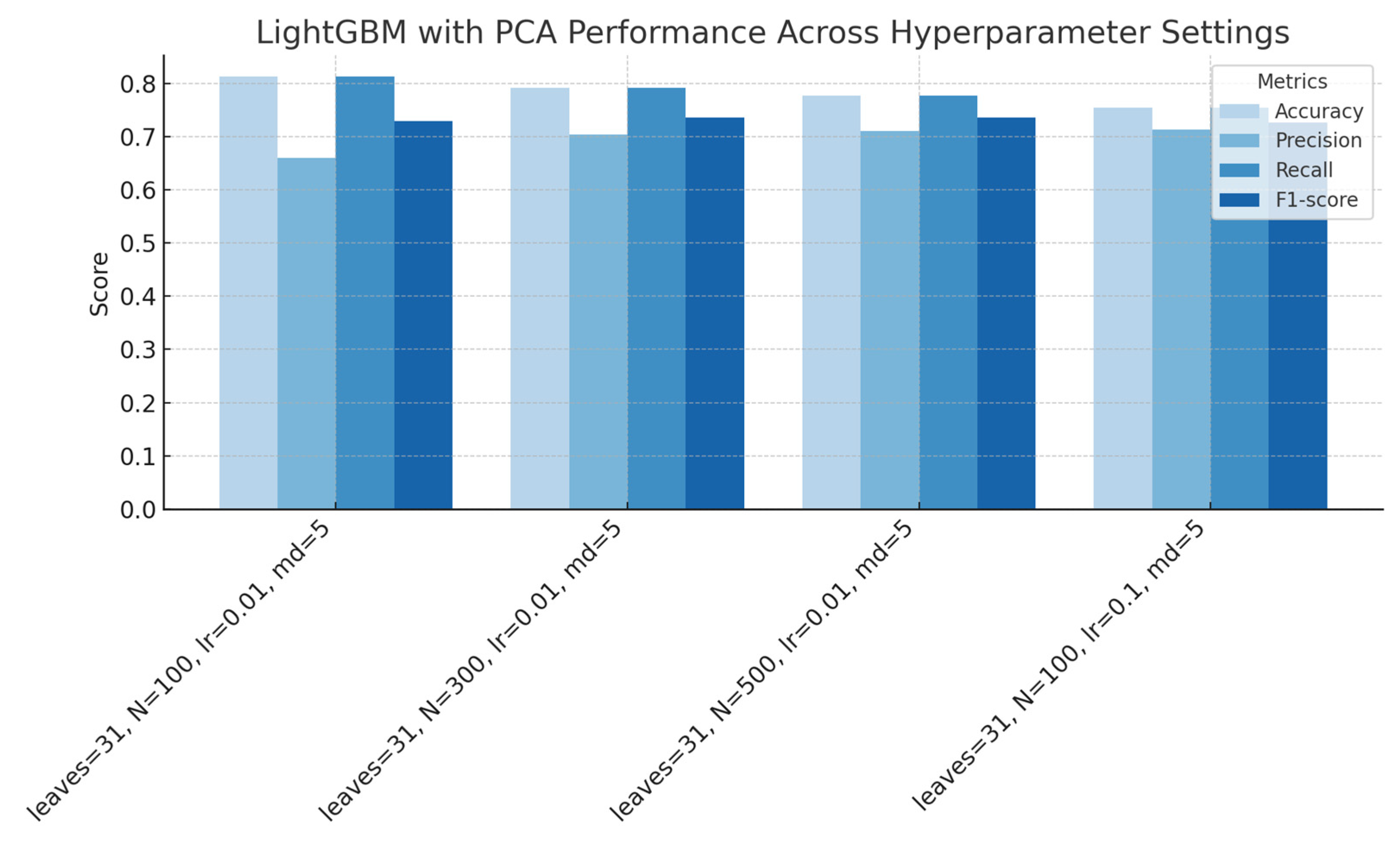
Figure 15.
LightGBM performance with PCA across hyperparameter settings (regularization, number of estimators, learning rate, and maximum depth), showing accuracy, precision, recall, and F1-score for each configuration.
Figure 15.
LightGBM performance with PCA across hyperparameter settings (regularization, number of estimators, learning rate, and maximum depth), showing accuracy, precision, recall, and F1-score for each configuration.
Figure 16.
XGBoost performance with PCA across hyperparameter settings (regularization, number of estimators, learning rate and maximum depth), showing accuracy, precision, recall and F1-score for each configuration.
Figure 16.
XGBoost performance with PCA across hyperparameter settings (regularization, number of estimators, learning rate and maximum depth), showing accuracy, precision, recall and F1-score for each configuration.
Figure 17.
Model Comparison based on Accuracy and F1-Score without PCA and with PCA.
Figure 17.
Model Comparison based on Accuracy and F1-Score without PCA and with PCA.
Figure 18.
The heatmap of mean absolute SHAP values across all wavenumbers for SVM without PCA, for both classes, plastic and biological.
Figure 18.
The heatmap of mean absolute SHAP values across all wavenumbers for SVM without PCA, for both classes, plastic and biological.
Figure 19.
The heatmap of mean absolute SHAP values across all wavenumbers for LightGBM without PCA, for both classes, plastic and biological.
Figure 19.
The heatmap of mean absolute SHAP values across all wavenumbers for LightGBM without PCA, for both classes, plastic and biological.
Figure 20.
The barplot mean SHAP values across all wavenumbers for SVM without PCA, for both classes, plastic and biological.
Figure 20.
The barplot mean SHAP values across all wavenumbers for SVM without PCA, for both classes, plastic and biological.
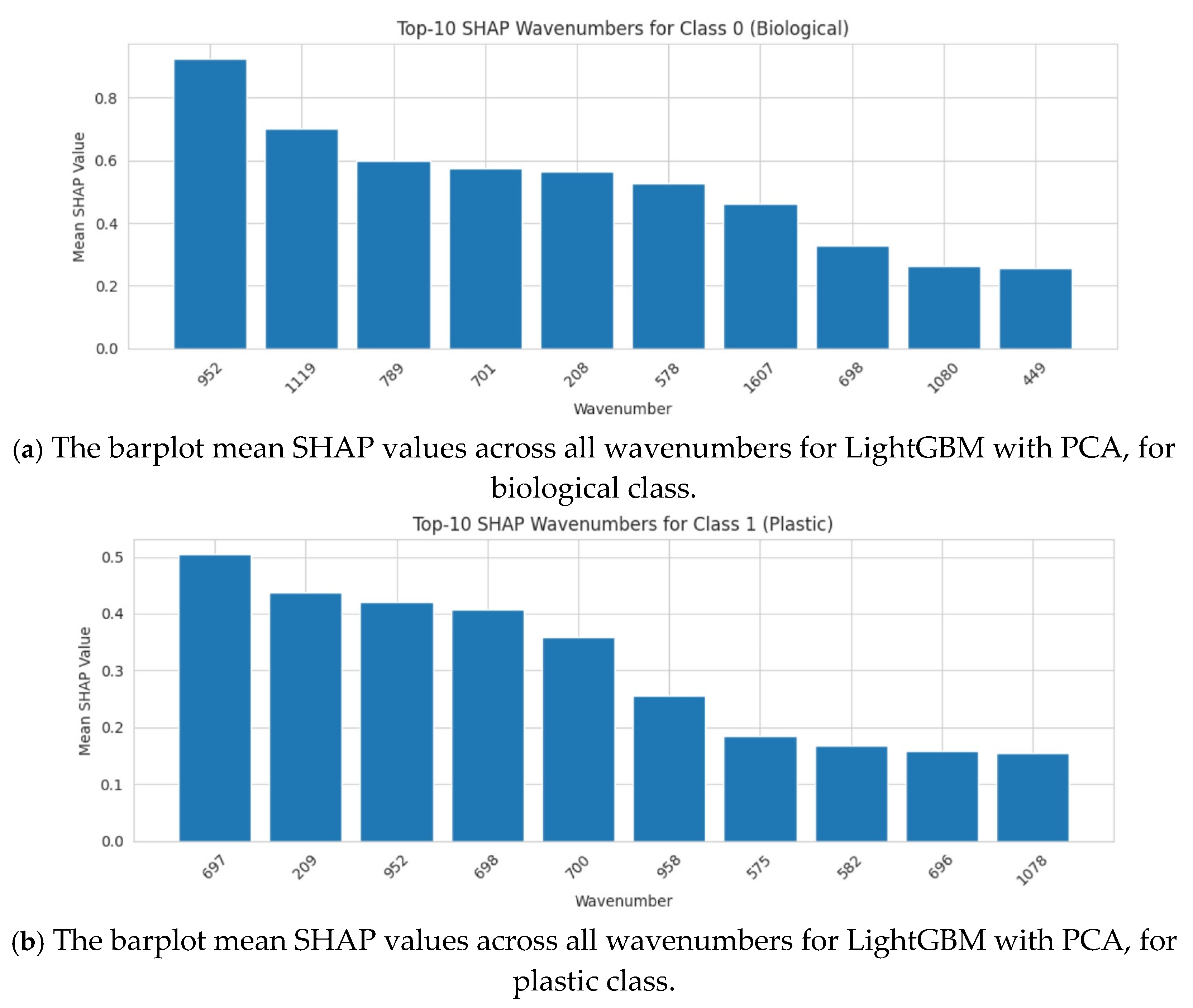
Figure 21.
The barplot mean SHAP values across all wavenumbers for LightGBM with PCA, for both classes, plastic and biological.
Figure 21.
The barplot mean SHAP values across all wavenumbers for LightGBM with PCA, for both classes, plastic and biological.
Table 1.
Machine learning tools and relevant hyperparameters employed in the study.
Table 1.
Machine learning tools and relevant hyperparameters employed in the study.
| Machine Learning Tool | Hyperparameters |
|---|
| Decision Tree | Criterion: gini, entropy | Maximum depth: 5, 10 |
| Minimum samples split: 2, 50 | Minimum samples leaf: 1, 10 |
| Random Forest | Number of trees: 50, 100, 200 | Criterion: gini, entropy |
| Maximum depth: 10 | |
| k-Nearest Neighbours | Number of neighbours (k): 5, 25, 40 | Distance metric (p): 1, 1.5, 2, 3 |
| Weighing: uniform, distance | |
| Neural Networks | Hidden layer size: 5, 10, 20 | Learning rate: 0.01, 0.1 |
| Activation: ReLU | |
| Support Vector Machines | Kernel: linear, RBF | Regularization (C): 0.1, 1, 10 |
| LightGBM | Number of leaves: 31, 100 | Number of estimators: 100, 300, 500 |
| Learning rate: 0.01, 0.1 | Maximum depth: 5, 20 |
| XGBoost | Regularization (C): 1, 5 | Number of estimators: 300, 500 |
| Learning rate: 0.05, 0.1 | Maximum depth: 5, 10 |
Table 2.
Performance metrics for Decision Trees with Gini Criterion.
Table 2.
Performance metrics for Decision Trees with Gini Criterion.
| Metric | Mean | Standard Deviation | 95% Lower Confidence Interval | 95% Upper Confidence Interval |
|---|
| Accuracy | 0.749 | 0.107 | 0.719 | 0.778 |
| Precision | 0.790 | 0.105 | 0.761 | 0.819 |
| Recall | 0.749 | 0.107 | 0.719 | 0.778 |
| F1-score | 0.755 | 0.099 | 0.728 | 0.782 |
Table 3.
Performance metrics for Random Forest with Gini Criterion.
Table 3.
Performance metrics for Random Forest with Gini Criterion.
| Metric | Mean | Standard Deviation | 95% Lower Confidence Interval | 95% Upper Confidence Interval |
|---|
| Accuracy | 0.785 | 0.093 | 0.756 | 0.807 |
| Precision | 0.779 | 0.108 | 0.739 | 0.799 |
| Recall | 0.785 | 0.093 | 0.756 | 0.807 |
| F1-score | 0.776 | 0.094 | 0.744 | 0.796 |
Table 4.
Performance metrics for k-Nearest Neighbours.
Table 4.
Performance metrics for k-Nearest Neighbours.
| Metric | Mean | Standard Deviation | 95% Lower Confidence Interval | 95% Upper Confidence Interval |
|---|
| Accuracy | 0.813 | <0.001 | 0.813 | 0.813 |
| Precision | 0.660 | <0.001 | 0.660 | 0.660 |
| Recall | 0.813 | <0.001 | 0.813 | 0.813 |
| F1-score | 0.728 | <0.001 | 0.728 | 0.728 |
Table 5.
Performance metrics for Neural Networks.
Table 5.
Performance metrics for Neural Networks.
| Metric | Mean | Standard Deviation | 95% Lower Confidence Interval | 95% Upper Confidence Interval |
|---|
| Accuracy | 0.784 | 0.107 | 0.754 | 0.814 |
| Precision | 0.718 | 0.095 | 0.692 | 0.744 |
| Recall | 0.784 | 0.107 | 0.754 | 0.814 |
| F1-score | 0.731 | 0.096 | 0.704 | 0.757 |
Table 6.
Performance metrics for Support Vector Machines with RBF Kernel (C = 0.1).
Table 6.
Performance metrics for Support Vector Machines with RBF Kernel (C = 0.1).
| Metric | Mean | Standard Deviation | 95% Lower Confidence Interval | 95% Upper Confidence Interval |
|---|
| Accuracy | 0.812 | 0.000 | 0.813 | 0.813 |
| Precision | 0.812 | 0.000 | 0.660 | 0.660 |
| Recall | 0.804 | 0.000 | 0.813 | 0.813 |
| F1-score | 0.801 | <0.001 | 0.728 | 0.728 |
Table 7.
Performance metrics for LightGBM configuration.
Table 7.
Performance metrics for LightGBM configuration.
| Metric | Mean | Standard Deviation | 95% Lower Confidence Interval | 95% Upper Confidence Interval |
|---|
| Accuracy | 0.798 | 0.091 | 0.772 | 0.823 |
| Precision | 0.792 | 0.110 | 0.761 | 0.822 |
| Recall | 0.798 | 0.091 | 0.772 | 0.823 |
| F1-score | 0.788 | 0.094 | 0.762 | 0.814 |
Table 8.
Performance metrics for XGBoost Configuration.
Table 8.
Performance metrics for XGBoost Configuration.
| Metric | Mean | Standard Deviation | 95% Lower Confidence Interval | 95% Upper Confidence Interval |
|---|
| Accuracy | 0.795 | 0.096 | 0.763 | 0.817 |
| Precision | 0.782 | 0.112 | 0.747 | 0.809 |
| Recall | 0.790 | 0.096 | 0.763 | 0.817 |
| F1-score | 0.781 | 0.095 | 0.749 | 0.802 |
Table 9.
Comparison of performance metrics for seven machine learning tools without PCA.
Table 9.
Comparison of performance metrics for seven machine learning tools without PCA.
| Metric | Accuracy | Precision | Recall | F1-Score |
|---|
| Decision Tree | 0.749 | 0.790 | 0.749 | 0.755 |
| Random Forest | 0.785 | 0.779 | 0.785 | 0.776 |
| k-Nearest Neighbours | 0.813 | 0.660 | 0.813 | 0.728 |
| Neural Networks | 0.784 | 0.718 | 0.784 | 0.731 |
| Support Vector Machines | 0.812 | 0.812 | 0.804 | 0.801 |
| LightGBM | 0.798 | 0.792 | 0.798 | 0.788 |
| XGBoost | 0.795 | 0.782 | 0.790 | 0.781 |
Table 10.
Performance metrics for Decision Trees with PCA.
Table 10.
Performance metrics for Decision Trees with PCA.
| Metric | Mean | Standard Deviation | 95% Lower Confidence Interval | 95% Upper Confidence Interval |
|---|
| Accuracy | 0.753 | 0.091 | 0.727 | 0.778 |
| Precision | 0.681 | 0.051 | 0.667 | 0.695 |
| Recall | 0.753 | 0.091 | 0.727 | 0.778 |
| F1-score | 0.706 | 0.051 | 0.692 | 0.720 |
Table 11.
Performance metrics for Random Forest with PCA.
Table 11.
Performance metrics for Random Forest with PCA.
| Metric | Mean | Standard Deviation | 95% Lower Confidence Interval | 95% Upper Confidence Interval |
|---|
| Accuracy | 0.800 | 0.071 | 0.760 | 0.800 |
| Precision | 0.703 | 0.096 | 0.6931 | 0.746 |
| Recall | 0.800 | 0.071 | 0.7604 | 0.800 |
| F1-score | 0.743 | 0.072 | 0.723 | 0.763 |
Table 12.
Performance metrics for k-Nearest Neighbours with PCA.
Table 12.
Performance metrics for k-Nearest Neighbours with PCA.
| Metric | Mean | Standard Deviation | 95% Lower Confidence Interval | 95% Upper Confidence Interval |
|---|
| Accuracy | 0.825 | 0.047 | 0.812 | 0.838 |
| Precision | 0.754 | 0.111 | 0.724 | 0.785 |
| Recall | 0.825 | 0.047 | 0.812 | 0.838 |
| F1-score | 0.773 | 0.062 | 0.756 | 0.790 |
Table 13.
Performance metrics for Neural Networks with PCA.
Table 13.
Performance metrics for Neural Networks with PCA.
| Metric | Mean | Standard Deviation | 95% Lower Confidence Interval | 95% Upper Confidence Interval |
|---|
| Accuracy | 0.784 | 0.047 | 0.732 | 0.808 |
| Precision | 0.754 | 0.111 | 0.724 | 0.785 |
| Recall | 0.784 | 0.047 | 0.732 | 0.808 |
| F1-score | 0.773 | 0.062 | 0.756 | 0.790 |
Table 14.
Performance metrics for SVM with PCA.
Table 14.
Performance metrics for SVM with PCA.
| Metric | Mean | Standard Deviation | 95% Lower Confidence Interval | 95% Upper Confidence Interval |
|---|
| Accuracy | 0.813 | 0.001 | 0.812 | 0.814 |
| Precision | 0.660 | 0.001 | 0.659 | 0.661. |
| Recall | 0.813 | 0.001 | 0.812 | 0.814 |
| F1-score | 0.728 | 0.001 | 0.727 | 0.729 |
Table 15.
Performance metrics for LightGBM with PCA.
Table 15.
Performance metrics for LightGBM with PCA.
| Metric | Mean | Standard Deviation | 95% Lower Confidence Interval | 95% Upper Confidence Interval |
|---|
| Accuracy | 0.813 | 0.001 | 0.812 | 0.814 |
| Precision | 0.660 | 0.001 | 0.659 | 0.661. |
| Recall | 0.813 | 0.001 | 0.812 | 0.814 |
| F1-score | 0.728 | 0.001 | 0.727 | 0.729 |
Table 16.
Performance metrics for XGBoost with PCA.
Table 16.
Performance metrics for XGBoost with PCA.
| Metric | Mean | Standard Deviation | 95% Lower Confidence Interval | 95% Upper Confidence Interval |
|---|
| Accuracy | 0.795 | 0.096 | 0.763 | 0.817 |
| Precision | 0.782 | 0.112 | 0.747 | 0.809. |
| Recall | 0.790 | 0.096 | 0.763 | 0.817 |
| F1-score | 0.781 | 0.095 | 0.749 | 0.802 |
Table 17.
Comparison of performance metrics for seven machine learning tools with PCA.
Table 17.
Comparison of performance metrics for seven machine learning tools with PCA.
| Metric | Accuracy | Precision | Recall | F1-Score |
|---|
| Decision Tree | 0.7761 | 0.790 | 0.749 | 0.755 |
| Random Forest | 0.813 | 0.779 | 0.785 | 0.776 |
| k-Nearest Neighbours | 0.825 | 0.754 | 0.825 | 0.773 |
| Neural Networks | 0.784 | 0.814 | 0.784 | 0.791 |
| Support Vector Machines | 0.813 | 0.660 | 0.813 | 0.728 |
| LightGBM | 0.813 | 0.660 | 0.813 | 0.728 |
| XGBoost | 0.761 | 0.725 | 0.761 | 0.737 |
Table 18.
Raman peaks of polyethylene (PE) and polyvinyl chloride (PVC). Adapted from Jung et al., 2024 [
34].
Table 18.
Raman peaks of polyethylene (PE) and polyvinyl chloride (PVC). Adapted from Jung et al., 2024 [
34].
| Polymer | Dominant Raman Peaks (cm−1) |
|---|
| Polyethylene (PE) | 1062, 1129, 1295, 1416, 1440, 1460, 2727, 2856, 2892 |
| Polyvinyl chloride (PVC) | 363, 637, 694, 1119, 1334, 1430, 2935 |