Quantification of Very Low Concentrations of Colloids with Light Scattering Applied to Micro(Nano)Plastics in Seawater
Abstract
1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Light Scattering
3. Results
3.1. Model Particles
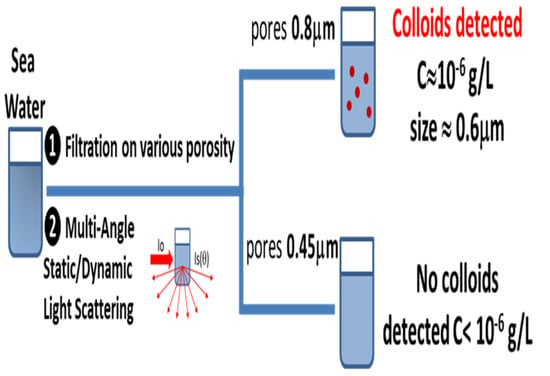
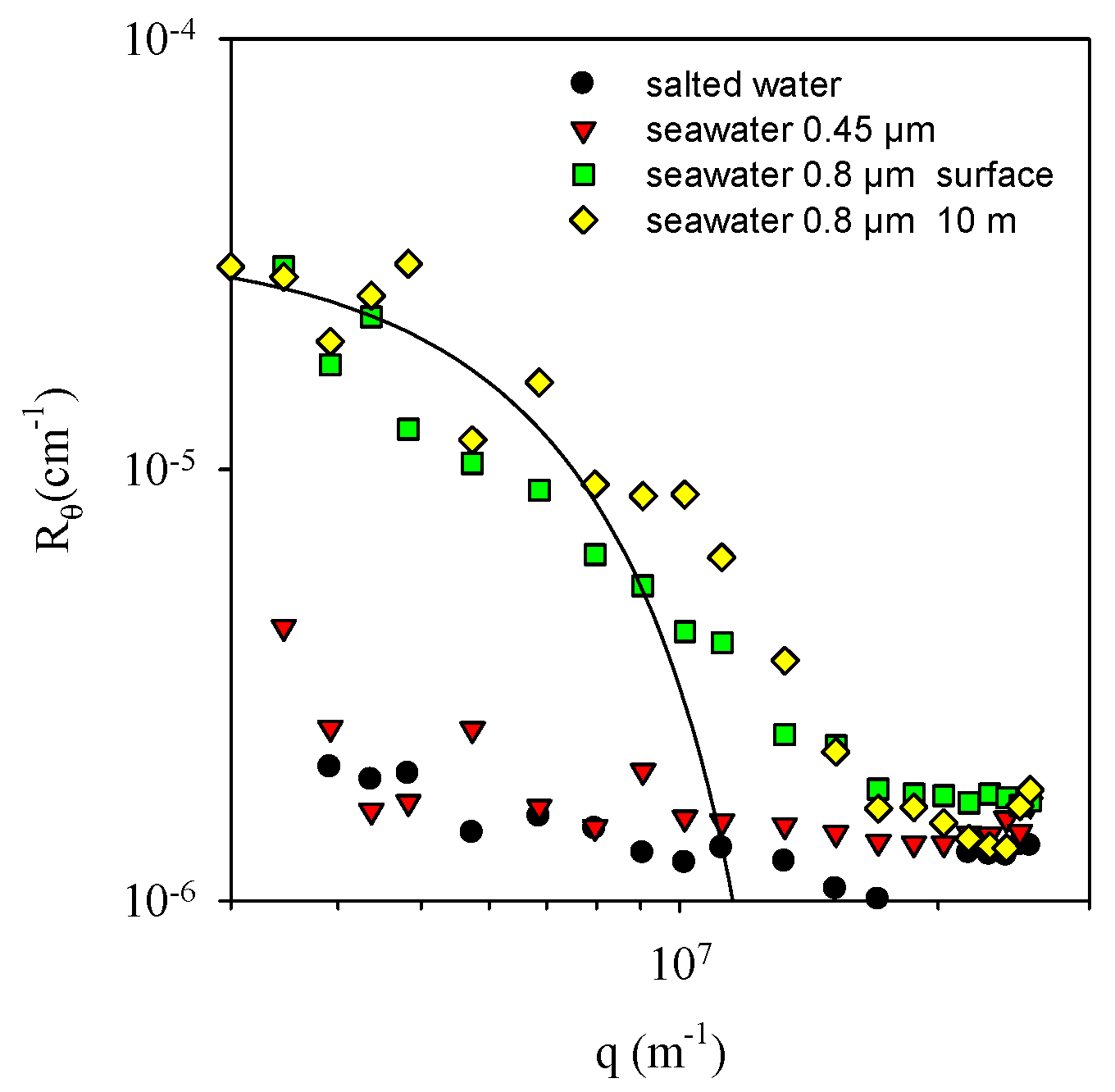
3.2. Colloidal Particles in Seawater
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Da Costa, J.P.; Santos, P.S.M.; Duarte, A.C.; Rocha-Santos, T. (Nano)plastics in the environmental sources, fates and effects. Sci. Total Environ. 2016, 566, 15–26. [Google Scholar] [CrossRef] [PubMed]
- Andrady, A.L. The plastic in microplastics: A review. Mar. Pollut. Bull. 2017, 119, 12–22. [Google Scholar] [CrossRef]
- Barnes, D.K.A.; Galgani, F.; Thompson, R.C.; Barlaz, M. Accumulation and fragmentation of plastic debris in global environments. Philos. Trans. R. Soc. Lond. B Biol. Sci. 2009, 364, 1985–1998. [Google Scholar] [CrossRef] [PubMed]
- Koelmans, A.A.; Besseling, E.; Shim, W.J. Nanoplastics in the Aquatic Environment. Critical Review. In Marine Anthropogenic Litter; Springer: Cham, Switzerland, 2015; pp. 325–340. [Google Scholar]
- Eriksen, M.; Lebreton, L.C.; Carson, H.S.; Thiel, M.; Moore, C.J.; Borerro, J.C.; Galgani, F.; Ryan, P.G.; Reisser, J. Plastic pollution in the world’s oceans: More than 5 trillion plastic pieces weighing over 250,000 tons afloat at sea. PLoS ONE 2014, 9, e111913. [Google Scholar] [CrossRef]
- Moore, C.J. Synthetic polymers in the marine environment: A rapidly increasing, long-term threat. Environ. Res. 2008, 108, 131–139. [Google Scholar] [CrossRef]
- Arthur, C.; Baker, J.E.; Bamford, H.A. Proceedings of the International Research Workshop on the Occurrence, Effects, and Fate of Microplastic Marine Debris, 9–11 September 2008; University of Washington Tacoma: Tacoma, WA, USA, 2009. [Google Scholar]
- Gigault, J.; Pedrono, B.; Maxit, B.; Ter Halle, A. Marine plastic litter: The unanalyzed nano-fraction. Environ. Sci. Nano 2016, 3, 346–350. [Google Scholar] [CrossRef]
- Gigault, J.; Ter Halle, A.; Baudrimont, M.; Pascal, P.-Y.; Gauffre, F.; Phi, T.-L.; El Hadri, H.; Grassl, B.; Reynaud, S.P. Current opinion: What is a nanoplastic? Environ. Pollut. 2018, 235, 1030–1034. [Google Scholar] [CrossRef]
- Browne, M.A.; Galloway, T.; Thompson, R. Microplastic—An emerging contaminant of potential concern? Integr. Environ. Assess. Manag. 2007, 3, 559–561. [Google Scholar] [CrossRef] [PubMed]
- Hammer, J.; Kraak, M.H.S.; Parsons, J.R. Plastics in the Marine Environment: The Dark Side of a Modern Gift. In Reviews of Environmental Contamination and Toxicology; Whitacre, D.M., Ed.; Springer: New York, NY, USA, 2012; pp. 1–44. [Google Scholar] [CrossRef]
- Qu, M.; Miao, L.; Liu, X.; Lai, H.; Hao, D.; Zhang, X.; Chen, H.; Li, H. Organismal response to micro(nano)plastics at environmentally relevant concentrations: Toxicity and the underlying mechanisms. Ecotoxicol. Environ. Saf. 2023, 254, 114745. [Google Scholar] [CrossRef]
- Ter Halle, A.; Jeanneau, L.; Martignac, M.; Jardeé, E.; Pedrono, B.; Brach, L.; Gigault, J. Nanoplastic in the North Atlantic subtropical gyre. Environ. Sci. Technol. 2017, 51, 13689–13697. [Google Scholar] [CrossRef] [PubMed]
- Koelmans, A.A.; Kooi, M.; Law, K.L.; Van Sebille, E. All is not lost: Deriving a top-down mass budget of plastic at sea. Environ. Res. Lett. 2017, 12, 114028. [Google Scholar] [CrossRef]
- Thompson, R.C.; Olsen, Y.; Mitchell, R.P.; Davis, A.; Rowland, S.J.; John, A.W.; McGonigle, D.; Russell, A.E. Lost at sea: Where is all the plastic? Science 2004, 304, 838. [Google Scholar] [CrossRef]
- Ivleva, N.P. Chemical analysis of microplastics and nanoplastics: Challenges, advanced methods, and perspectives. Chem. Rev. 2021, 121, 11886–11936. [Google Scholar] [CrossRef] [PubMed]
- Erni-Cassola, G.; Gibson, M.I.; Thompson, R.C.; Christie-Oleza, J.A. Lost, but found with Nile red: A novel method for detecting and quantifying small microplastics (1 mm to 20 μm) in environmental samples. Environ. Sci. Technol. 2017, 51, 13641–13648. [Google Scholar] [CrossRef] [PubMed]
- Gagné, F. Detection of polystyrene nanoplastics in biological tissues with a fluorescent molecular rotor probe. J. Xenobiotics 2019, 9, 8147. [Google Scholar] [CrossRef] [PubMed]
- Catarino, A.I.; Frutos, A.; Henry, T.B. Use of fluorescent-labelled nanoplastics (NPs) to demonstrate NP absorption is inconclusive without adequate controls. Sci. Total Environ. 2019, 670, 915–920. [Google Scholar] [CrossRef]
- Cole, M. A novel method for preparing microplastic fibers. Sci. Rep. 2016, 6, 34519. [Google Scholar] [CrossRef]
- Fabbri, D. Use of pyrolysis-gas chromatography/mass spectrometry to study environmental pollution caused by synthetic polymers: A case study: The Ravenna Lagoon. J. Anal. Appl. Pyrolysis 2001, 58, 361–370. [Google Scholar] [CrossRef]
- Correia, M.; Loeschner, K. Detection of nanoplastics in food by asymmetric flow field-flow fractionation coupled to multi-angle light scattering: Possibilities, challenges and analytical limitations. Anal. Bioanal. Chem. 2018, 410, 5603–5615. [Google Scholar] [CrossRef]
- Gillibert, R.; Balakrishnan, G.; Deshoules, Q.; Tardivel, M.; Magazzù, A.; Donato, M.G.; Maragò, O.M.; Lamy de La Chapelle, M.; Colas, F.; Lagarde, F.; et al. Raman Tweezers for Small Microplastics and Nanoplastics Identification in Seawater. Environ. Sci. Technol. 2019, 53, 9003–9013. [Google Scholar] [CrossRef]
- Schurtenberger, P.; Newman, M.E. Characterization of biological and environmental particles using static and dynamic light scattering. In IUPAC Series on Analytical and Physical Chemistry of Environmental Systems; Buffle, J., van Leeuwen, H.P., Eds.; Lewis: Boca Raton, FL, USA, 1993; Volume 2, pp. 37–115. [Google Scholar]
- Filella, M.; Zhang, J.; Newman, M.E.; Buffle, J. Analytical applications of photon correlation spectroscopy for size distribution measurements of natural colloidal suspensions: Capabilities and limitations. Colloids Surf. A Physicochem. Eng. Asp. 1997, 120, 27–46. [Google Scholar] [CrossRef]
- Van de Hulst, H.C. Light Scattering by Small Particles; Academic Press: New York, NY, USA, 1981. [Google Scholar]
- Brown, W. (Ed.) Dynamic Light Scattering. In The Method and Some Applications; Clarendon Press: Oxford, UK, 1993. [Google Scholar]
- Berne, B.; Pecora, R. Dynamic Light Scattering with Applications to Chemistry, Biology, and Physics; Dover Publications: New York, NY, USA, 2000. [Google Scholar]
- Jonasz, M.; Fournier, G. Light Scattering by Particles in Water: Theoretical and Experimental Foundations; Elsevier: London, UK, 2010. [Google Scholar]
- Morel, A. Optical properties of pure water and pure sea water. In Optical Aspects of Oceanography; Jerov, N.E., Nielson, E.S., Eds.; Academic: London, UK, 1974; pp. 1–24. [Google Scholar]
- Cozar, A.; Sanz-Martin, M.; Marti, E.; Gonzalez-Gordillo, J.I.; Ubeda, B.; Galvez, J.A.; Irigoien, X.; Duarte, C.M. Plastic accumulation in the Mediterranean Sea. PLoS ONE 2015, 10, e0121762. [Google Scholar] [CrossRef] [PubMed]
- Singh, N.; Tiwari, E.; Khandelwal, N.; Darbha, G.K. Understanding the stability of nanoplastics in aqueous environments: Effect of ionic strength, temperature, dissolved organic matter, clay, and heavy metals. Environ. Sci. Nano 2019, 6, 2968–2976. [Google Scholar] [CrossRef]
- Tallec, K.; Blard, O.; González-Fernández, C.; Brotons, G.; Berchel, M.; Soudant, P.; Huvet, A.; Paul-Pont, I. Surface functionalization determines behavior of nanoplastic solutions in model aquatic environments. Chemosphere 2019, 225, 639–646. [Google Scholar] [CrossRef]
- Li, X.; Ji, S.; He, E.; Peijnenburg, W.J.G.M.; Cao, X.; Zhao, L.; Xu, X.; Zhang, P.; Qiu, H. UV/ozone induced physicochemical transformations of polystyrene nanoparticles and their aggregation tendency and kinetics with natural organic matter in aqueous systems. J. Hazard. Mater. 2022, 433, 128790. [Google Scholar] [CrossRef]
- Liu, Y.; Hu, Y.; Yang, C.; Chen, C.; Huang, W.; Dang, Z. Aggregation kinetics of UV irradiated nanoplastics in aquatic environments. Water Res. 2019, 163, 114870. [Google Scholar] [CrossRef]
- Wilkinson, K.J.; Lead, J.R. (Eds.) Environmental Colloids and Particles: Behaviour, Separation and Characterisation; John Wiley & Sons: Chichester, UK, 2007; Volume 10, pp. 1–687. [Google Scholar]
- Delay, M.; Frimmel, F.H. Nanoparticles in aquatic systems. Anal. Bioanal. Chem. 2012, 402, 583–592. [Google Scholar] [CrossRef]
- Linders, T.; Infantes, E.; Joyce, A.; Karlsson, T.; Ploug, H.; Hassellov, M.; Skold, M.; Zetsche, E.-M. Particle sources and transport in stratified Nordic coastal seas in the Anthropocene. Elem Sci Anth 2018, 6, 29. [Google Scholar] [CrossRef]
- Koike, I.; Hara, S.; Terauchi, K.; Kogure, K. Correction: Role of sub-micrometre particles in the ocean. Nature 1990, 345, 556. [Google Scholar] [CrossRef]
- Chin, W.-C.; Orellana, M.V.; Verdugo, P. Spontaneous assembly of marine dissolved organic matter into polymer gels. Nature 1998, 391, 568. [Google Scholar] [CrossRef]
- Wu, C.-Y.; Martel, J.; Wong, T.-Y.; Young, D.; Liu, C.-C.; Lin, C.-W.; Young, J.D. Formation and characteristics of biomimetic mineralo-organic particles in natural surface water. Sci. Rep. 2018, 6, 28817. [Google Scholar] [CrossRef] [PubMed]
- Babin, M.; Morel, A.; Fournier-Sicre, V.; Fell, F.; Stramski, D. Light scattering properties of marine particles in coastal and open ocean waters as related to the particle mass concentration. Limnol. Oceanogr. 2003, 48, 843–859. [Google Scholar] [CrossRef]





Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Balakrishnan, G.; Lagarde, F.; Chassenieux, C.; Nicolai, T. Quantification of Very Low Concentrations of Colloids with Light Scattering Applied to Micro(Nano)Plastics in Seawater. Microplastics 2023, 2, 202-214. https://doi.org/10.3390/microplastics2020016
Balakrishnan G, Lagarde F, Chassenieux C, Nicolai T. Quantification of Very Low Concentrations of Colloids with Light Scattering Applied to Micro(Nano)Plastics in Seawater. Microplastics. 2023; 2(2):202-214. https://doi.org/10.3390/microplastics2020016
Chicago/Turabian StyleBalakrishnan, Gireeshkumar, Fabienne Lagarde, Christophe Chassenieux, and Taco Nicolai. 2023. "Quantification of Very Low Concentrations of Colloids with Light Scattering Applied to Micro(Nano)Plastics in Seawater" Microplastics 2, no. 2: 202-214. https://doi.org/10.3390/microplastics2020016
APA StyleBalakrishnan, G., Lagarde, F., Chassenieux, C., & Nicolai, T. (2023). Quantification of Very Low Concentrations of Colloids with Light Scattering Applied to Micro(Nano)Plastics in Seawater. Microplastics, 2(2), 202-214. https://doi.org/10.3390/microplastics2020016