Integrating Reinforcement Learning and LLM with Self-Optimization Network System
Abstract
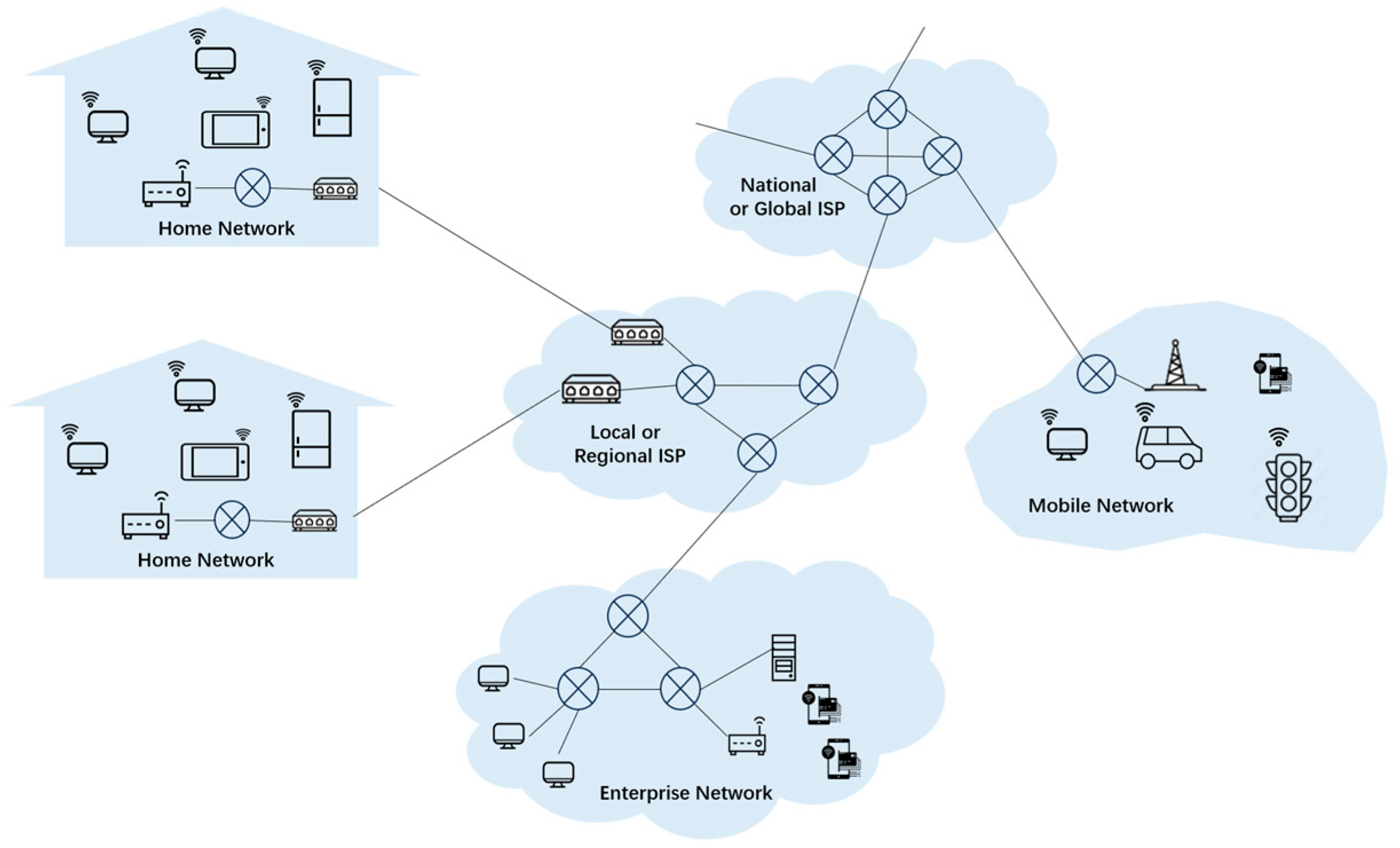
1. Introduction
- We propose a collaborative network optimization structure of LLM and RL, which integrates LLM’s predictive abilities with RL’s decision-making. LLMs forecast future traffic patterns using historical and contextual data, enabling proactive, informed optimization beyond relying solely on current network states.
- To manage network resources effectively, we model each communication link as an autonomous intelligent agent. These agents function in a cooperative multi-agent environment, where the Multi-Agent Deep Deterministic Policy Gradient (MADDPG) algorithm facilitates continuous action control and policy learning.
- We validate the framework through extensive experiments on the Mininet simulation platform. Results demonstrate the superiority of LLM-enhanced RL decision-making over conventional RL baselines and further confirm our approach’s practicality and scalability for future communication and real-world-like scenarios.
2. Related Works
2.1. Deep Reinforcement Learning for Bandwidth Allocation and Network Slicing Resource Management
2.2. LLM-Based Traffic Prediction for Network Optimization
3. Materials and Methods
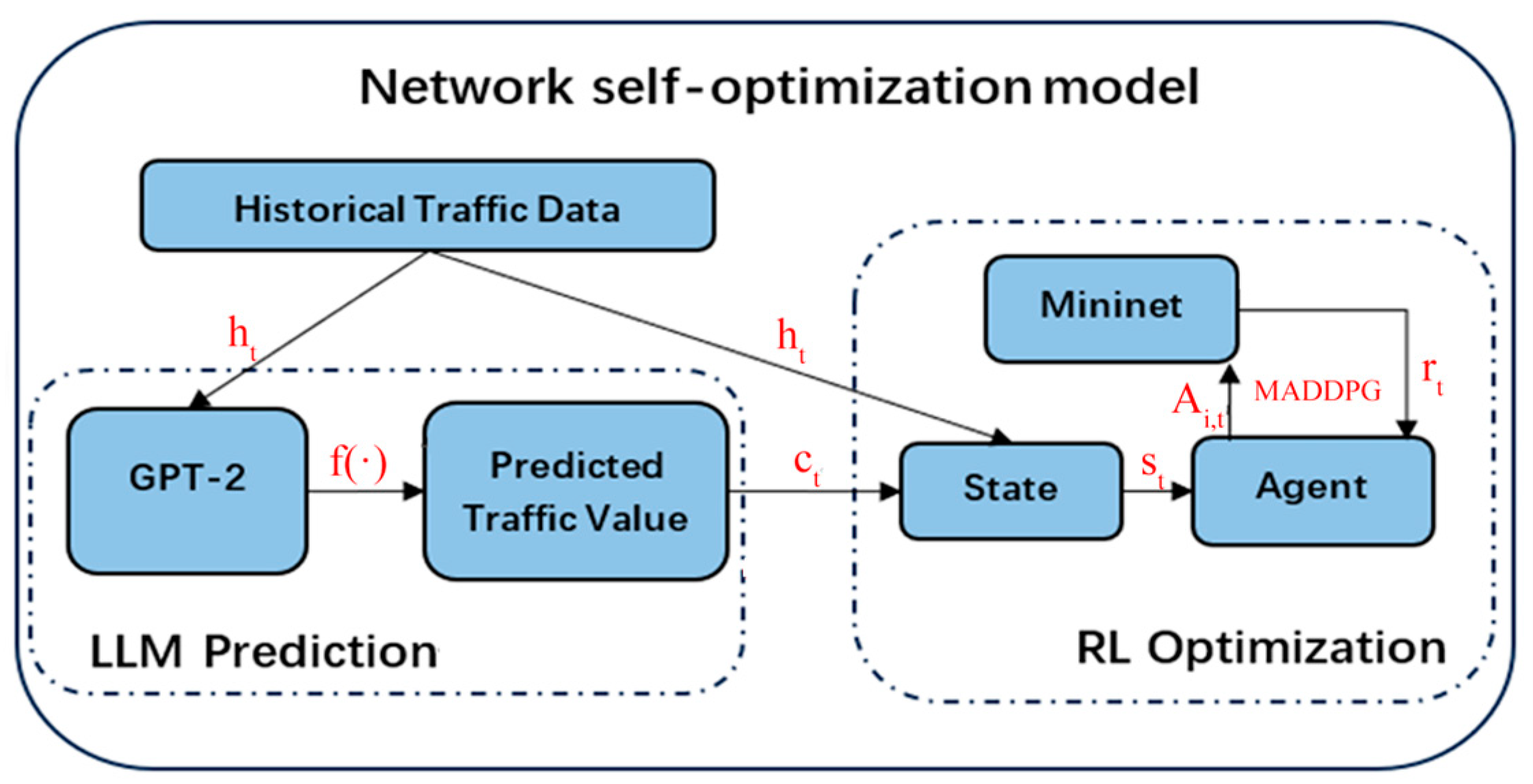
3.1. Overall Algorithm Structure
3.2. LLM-Based Network Traffic Prediction
3.3. Implementation of Self-Optimization Strategy Based on Reinforcement Learning
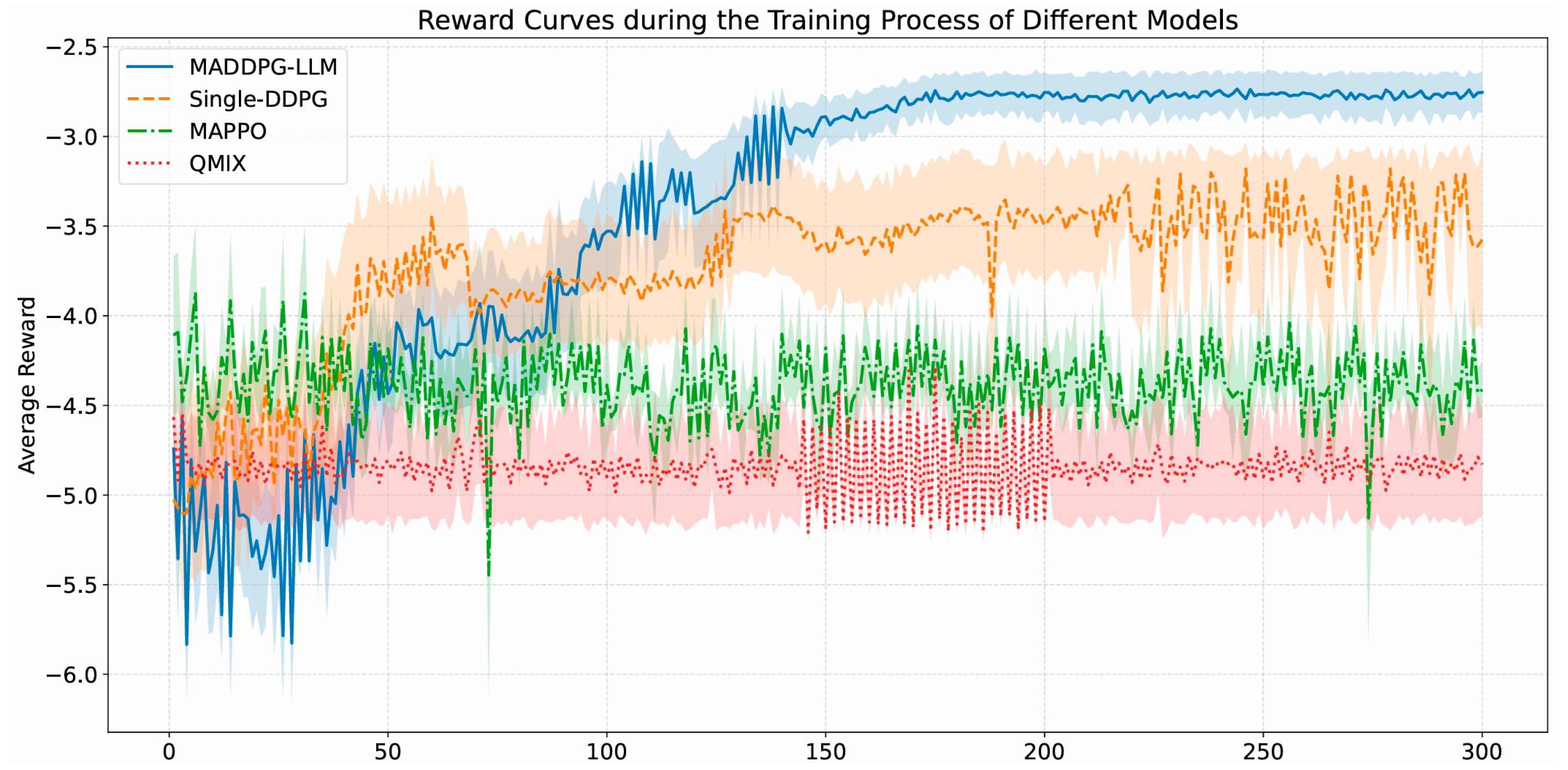
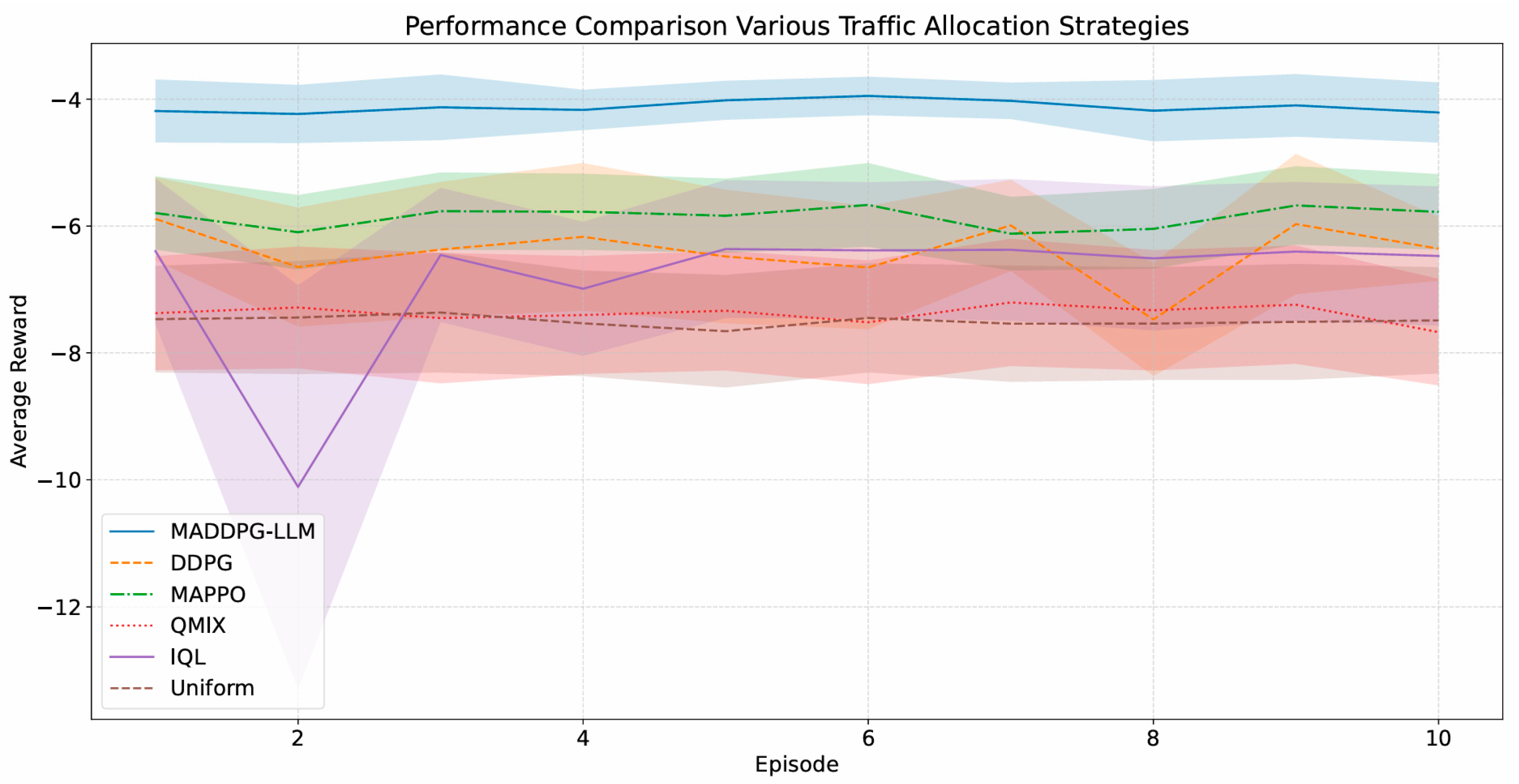
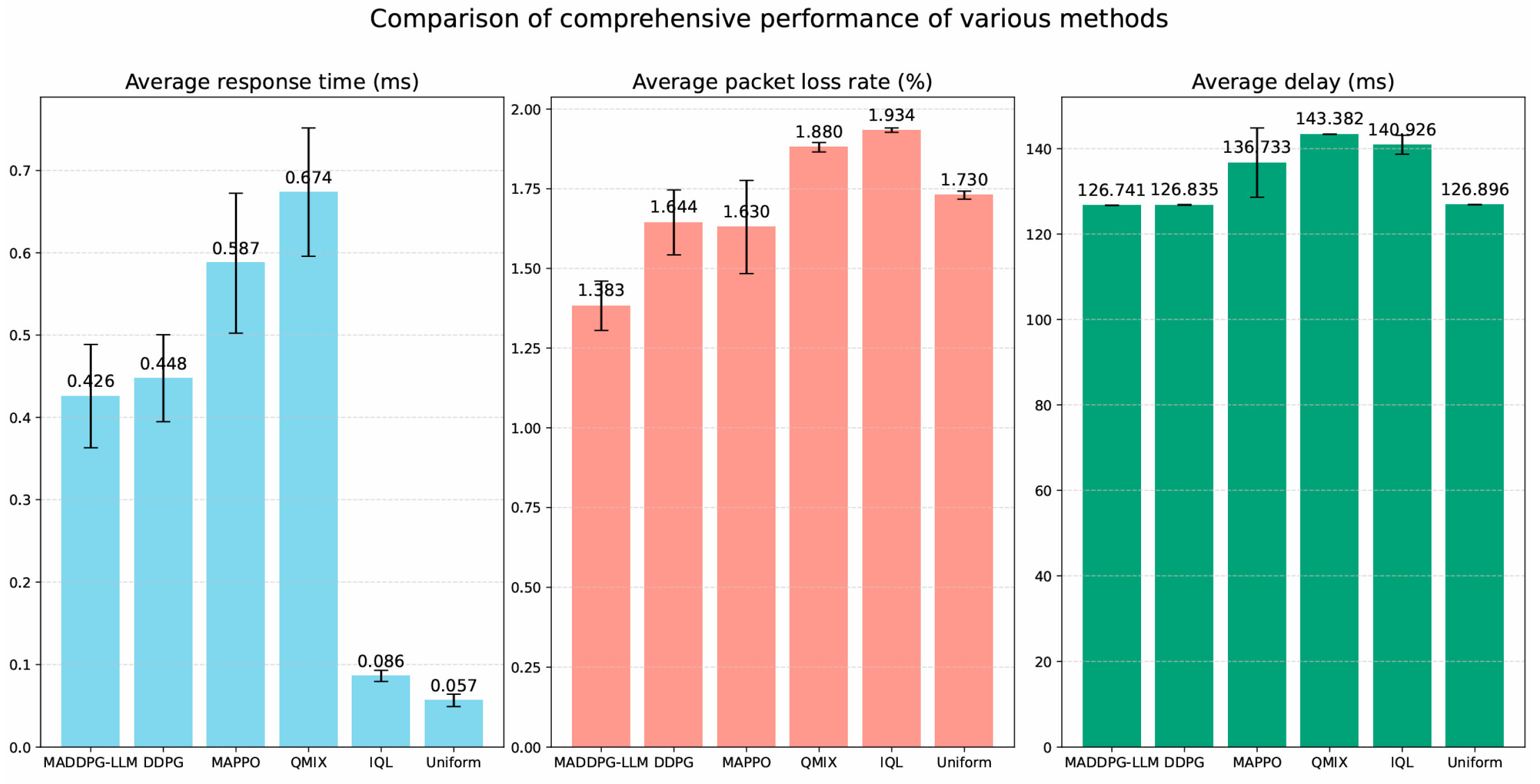
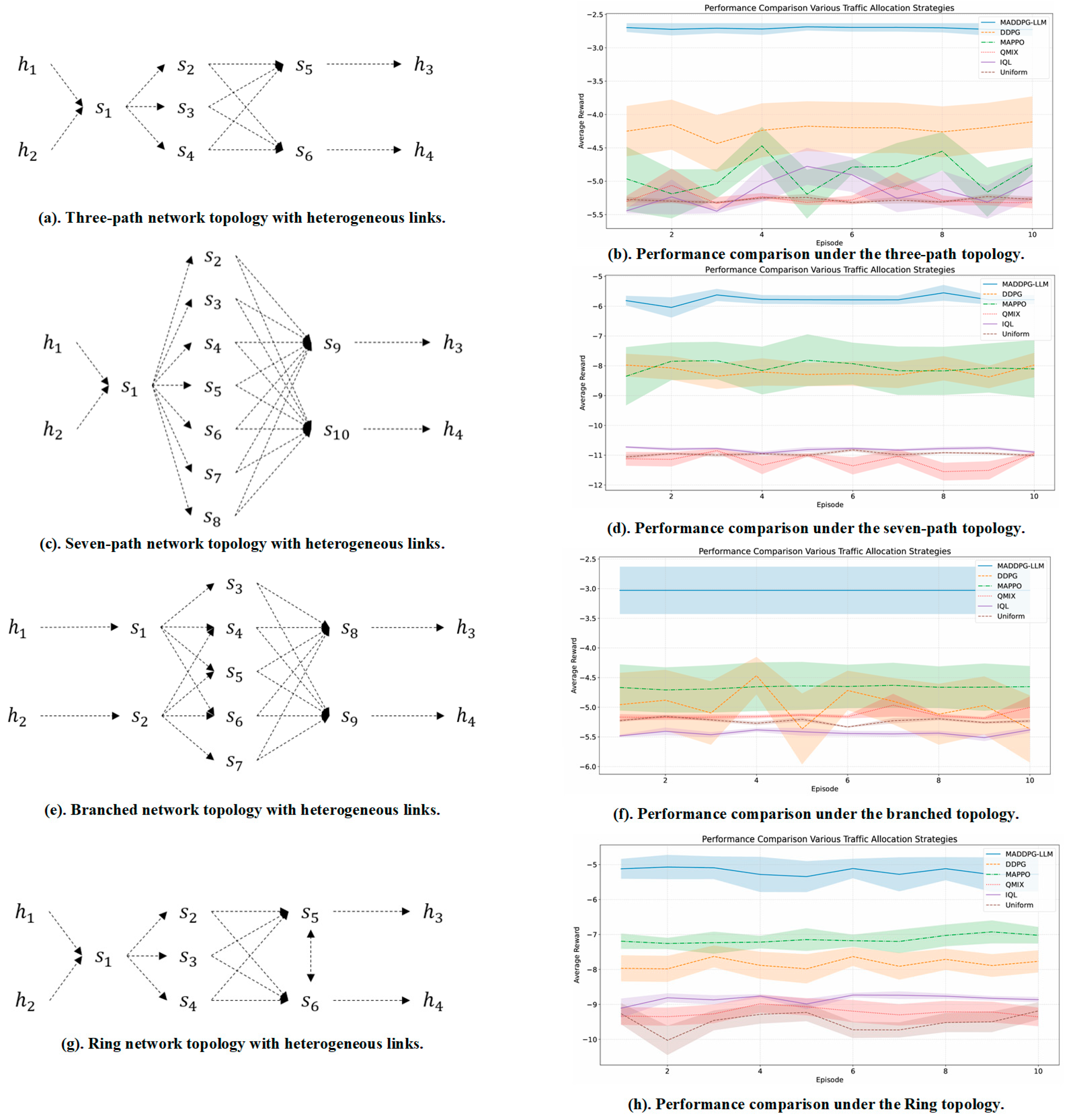
4. Results
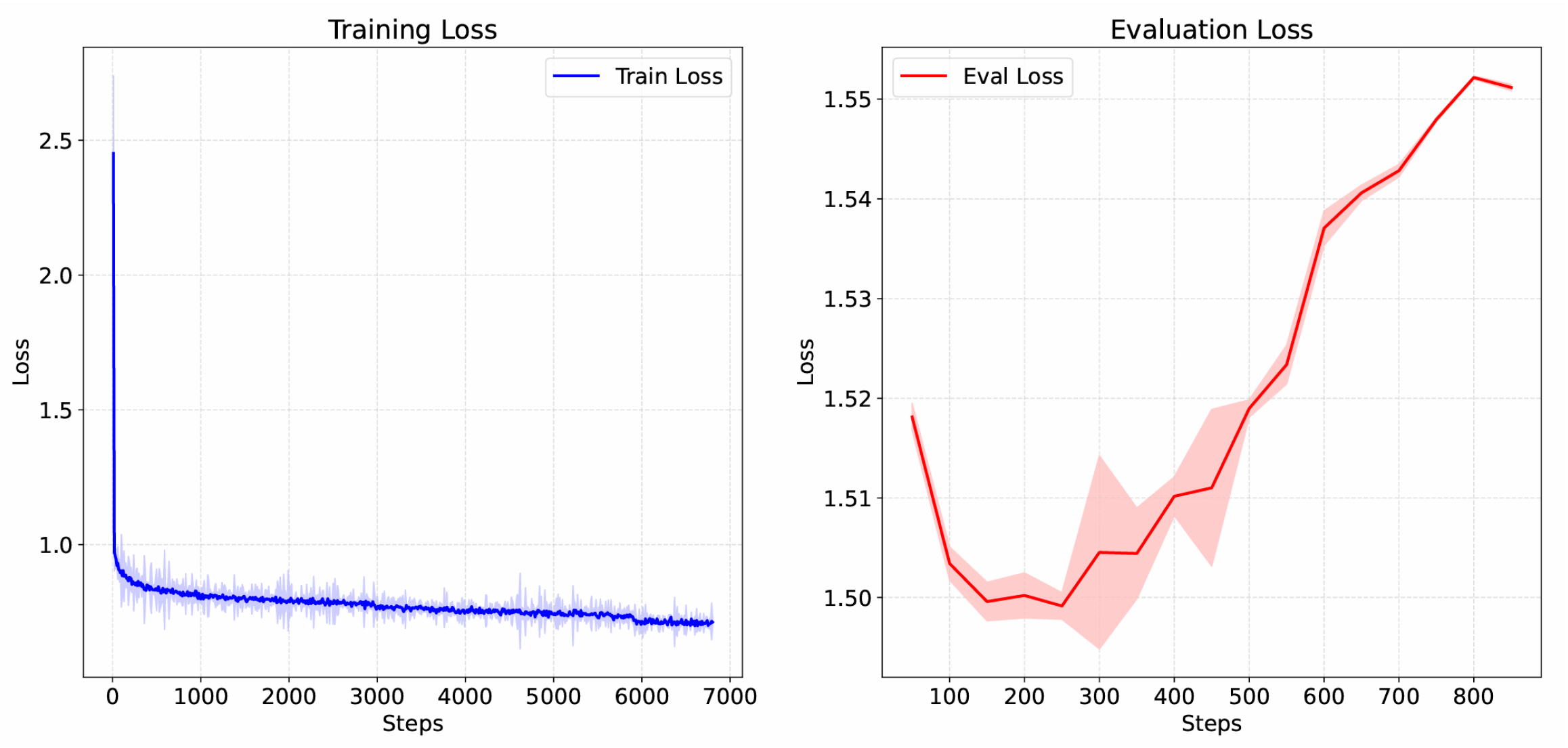
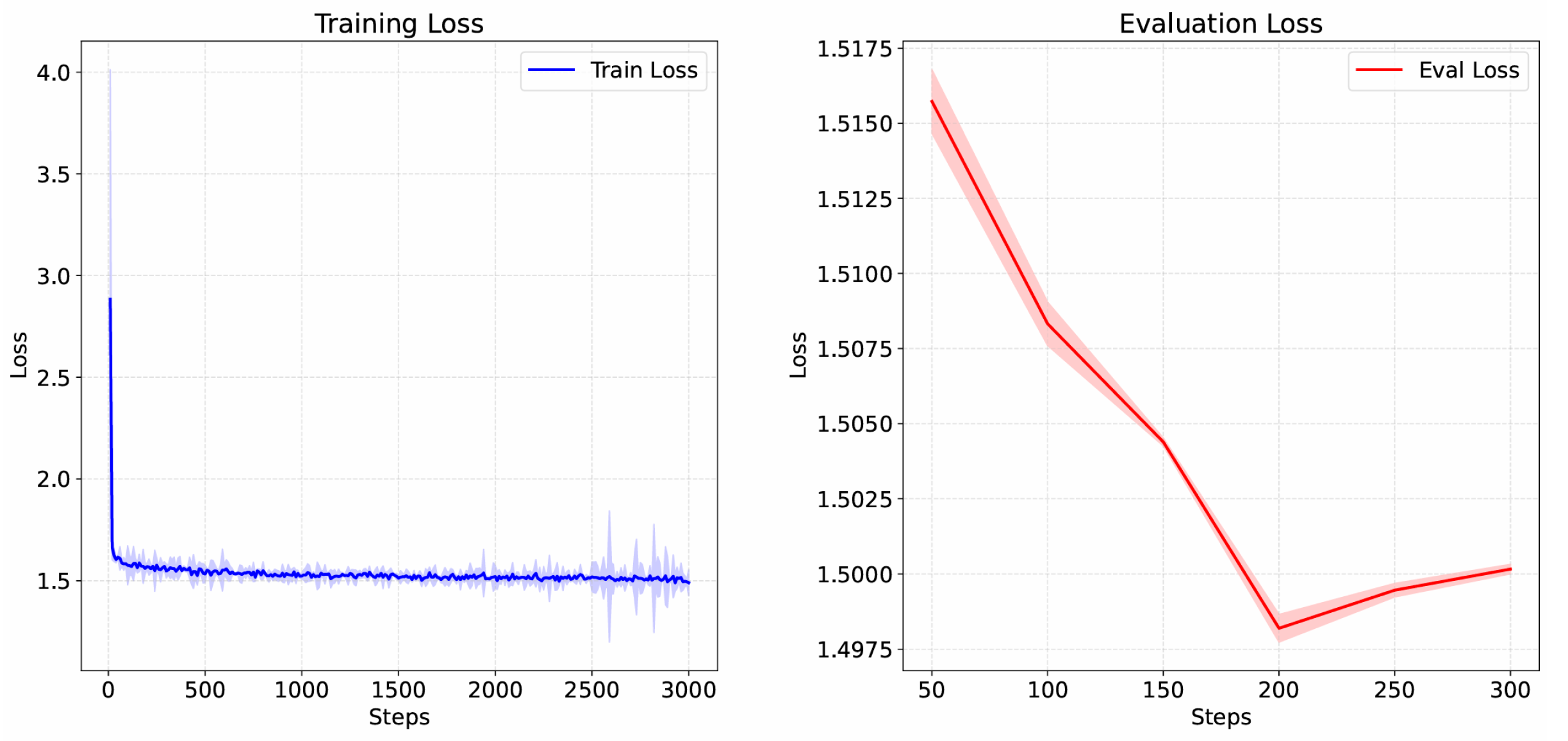
4.1. Network Traffic Forecasting
4.2. Network Self-Optimization Model Designing
4.3. Network Self-Optimization Model Testing
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Dandy, G.; Simpson, A.; Murphy, L. An improved genetic algorithm for pipe network optimization. Water Resour. Res. 1996, 32, 449–458. [Google Scholar] [CrossRef]
- Ephremides, A.; Verdú, S. Control and optimization methods in communication network problems. IEEE Trans. Autom. Control 1989, 34, 930–942. [Google Scholar] [CrossRef]
- Mammeri, Z. Reinforcement learning based routing in networks: Review and classification of approaches. IEEE Access 2019, 7, 55916–55950. [Google Scholar] [CrossRef]
- Pan, Z.; Yang, J. Deep reinforcement learning-based optimization method for D2D communication energy efficiency in heterogeneous cellular networks. IEEE Access 2024, 12, 140439–140455. [Google Scholar] [CrossRef]
- O’Shea, T.; Hoydis, J. An introduction to deep learning for the physical layer. IEEE Trans. Cogn. Commun. Netw. 2017, 3, 563–575. [Google Scholar] [CrossRef]
- Luong, N.C.; Hoang, D.T.; Gong, S.; Niyato, D.; Wang, P.; Liang, Y.C.; Kim, D.I. Applications of deep reinforcement learning in communications and networking: A survey. IEEE Commun. Surv. Tutor. 2019, 21, 3133–3174. [Google Scholar] [CrossRef]
- Chen, Y.; Guo, Y. Network link weight optimization based on antisymmetric deep graph networks and reinforcement learning. In Proceedings of the 2024 Sixth International Conference on Next Generation Data-Driven Networks (NGDN), Shenyang, China, 26–28 April 2024. [Google Scholar]
- Gómez-delaHiz, J.; Galán-Jiménez, J. Improving the traffic engineering of SDN networks by using local multi-agent deep reinforcement learning. In Proceedings of the NOMS 2024 IEEE Network Operations and Management Symposium, Seoul, Republic of Korea, 6–10 May 2024. [Google Scholar]
- Wu, D.; Wang, X.; Qiao, Y.; Lu, J.; Zhang, M.; Wang, K. NetLLM: Adapting large language models for networking. In Proceedings of the ACM SIGCOMM 2024 Conference, Sydney, Australia, 4–8 August 2024. [Google Scholar]
- Liu, B.; Liu, X.; Gao, S.; Cheng, X.; Yang, L. LLM4CP: Adapting large language models for channel prediction. J. Commun. Inf. Netw. 2024, 9, 113–125. [Google Scholar] [CrossRef]
- Nascimento, N.; Alencar, P.; Cowan, D. Self-adaptive large language model (LLM)-based multiagent systems. In Proceedings of the 2023 IEEE International Conference on Autonomic Computing and Self-Organizing Systems Companion, Toronto, ON, Canada, 25–29 September 2023. [Google Scholar]
- Mondal, A.; Mishra, D.; Prasad, G.; Hossain, A. Joint Optimization Framework for Minimization of Device Energy Consumption in Transmission Rate Constrained UAV-Assisted IoT Network. IEEE Internet Things J. 2022, 9, 9591–9607. [Google Scholar] [CrossRef]
- Oliehoek, F.A.; Amato, C. A Concise Introduction to Decentralized POMDPs; Springer: Berlin, Germany, 2016; Volume 1. [Google Scholar]
- Li, Z.; Wang, X.; Pan, L.; Zhu, L.; Wang, Z.; Feng, J.; Deng, C.; Huang, L. Network topology optimization via deep reinforcement learning. IEEE Trans. Commun. 2022, 71, 2847–2859. [Google Scholar] [CrossRef]
- Do, Q.V.; Koo, I. Dynamic bandwidth allocation scheme for wireless networks with energy harvesting using actor-critic deep reinforcement learning. In Proceedings of the 2019 International Conference on Artificial Intelligence in Information and Communication, Okinawa, Japan, 10–16 August 2019. [Google Scholar]
- Attiah, K.; Ammar, M.; Alnuweiri, H.; Shaban, K. Load balancing in cellular networks: A reinforcement learning approach. In Proceedings of the 2020 IEEE 17th Annual Consumer Communications & Networking Conference, Las Vegas, NV, USA, 10–13 January 2020. [Google Scholar]
- Abu-Ein, A.; Abuain, W.; Alhafnawi, M.; Al-Hazaimeh, O. Security enhanced dynamic bandwidth allocation-based reinforcement learning. WSEAS Trans. Inf. Sci. Appl. 2024, 22, 21–27. [Google Scholar] [CrossRef]
- Li, R.; Zhao, Z.; Sun, Q. Deep reinforcement learning for resource management in network slicing. IEEE Access 2018, 6, 74429–74441. [Google Scholar] [CrossRef]
- Liu, Y.; Ding, J.; Liu, X. A constrained reinforcement learning based approach for network slicing. In Proceedings of the 2020 IEEE 28th International Conference on Network Protocols, Madrid, Spain, 13–16 October 2020. [Google Scholar]
- Wang, H.; Wu, Y.; Min, G.; Xu, J.; Tang, P. Data-driven dynamic resource scheduling for network slicing: A deep reinforcement learning approach. Inf. Sci. 2019, 498, 106–116. [Google Scholar] [CrossRef]
- Shokouhi, M.H.; Wong, V.W.S. Large language models for wireless cellular traffic prediction: A multi-timespan approach. In Proceedings of the GLOBECOM 2024 IEEE Global Communications Conference, Cape Town, South Africa, 8–12 December 2024. [Google Scholar]
- Yang, S.; Wang, D.; Zheng, H.; Jin, R. TimeRAG: Boosting LLM time series forecasting via retrieval-augmented generation. In Proceedings of the ICASSP 2025 IEEE International Conference on Acoustics, Speech and Signal Processing, Hyderabad, India, 6–11 April 2025. [Google Scholar]
- Guo, X.; Zhang, Q.; Jiang, J.; Peng, M.; Zhu, M.; Yang, H. Towards explainable traffic flow prediction with large language models. Commun. Transp. Res. 2024, 4, 100150. [Google Scholar] [CrossRef]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, Ł.; Polosukhin, I. Attention is all you need. Adv. Neural Inf. Process. Syst. 2017, 30, 6000–6010. [Google Scholar]
- Raiaan, M.A.K.; Mukit, M.S.H.; Fatema, K.; Nahid, A.A.; Islam, M.; Uddin, M.S.; Podder, P.; Alsaikhan, F.; Alqahtani, A. A review on large language models: Architectures, applications, taxonomies, open issues and challenges. IEEE Access 2024, 12, 26839–26874. [Google Scholar] [CrossRef]
- de Oliveira, R.L.S.; Schweitzer, C.M.; Shinoda, A.A.; Prete, L.R. Using Mininet for emulation and prototyping software-defined networks. In Proceedings of the 2014 IEEE Colombian Conference on Communications and Computing, Bogota, Colombia, 4–6 June 2014. [Google Scholar]
- Li, T.; Zhu, K.; Luong, N.C.; Niyato, D.; Wu, Q.; Zhang, Y.; Chen, B. Applications of multi-agent reinforcement learning in future internet: A comprehensive survey. IEEE Commun. Surv. Tutor. 2022, 24, 1240–1279. [Google Scholar] [CrossRef]
- Sutton, R.S.; Barto, A.G. Reinforcement learning: An introduction. IEEE Trans. Neural Netw. 1998, 9, 1054. [Google Scholar] [CrossRef]
- Radford, A.; Wu, J.; Child, R.; Luan, D.; Amodei, D.; Sutskever, I. Language models are unsupervised multitask learners. OpenAI Blog 2019, 1, 9. [Google Scholar]
- Hochreiter, S.; Schmidhuber, J. Long Short-Term Memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Lea, C.; Vidal, R.; Reiter, A.; Hager, G.D. Temporal Convolutional Networks: A Unified Approach to Action Segmentation. In Proceedings of the European Conference on Computer Vision (ECCV), Amsterdam, The Netherlands, 11–14 October 2016; Springer: Cham, Switzerland, 2016; pp. 47–54. [Google Scholar]
- Lowe, R.; Wu, Y.I.; Tamar, A.; Harb, J.; Abbeel, P.; Mordatch, I. Multi-agent actor-critic for mixed cooperative-competitive environments. In Proceedings of the 31st International Conference on Neural Information Processing Systems (NIPS’17), Red Hook, NY, USA, 4–9 December 2017. [Google Scholar]
- Li, B.; Chen, L.; Yang, Z.; Xiang, H. preDQN-Based TAS Traffic Scheduling in Intelligence Endogenous Networks. IEEE Syst. J. 2024, 18, 997–1008. [Google Scholar] [CrossRef]
- Teerapittayanon, S.; McDanel, B.; Kung, H.T. Branchynet: Fast inference via early exiting from deep neural networks. In Proceedings of the 2016 23rd International Conference on Pattern Recognition, Cancun, Mexico, 4–8 December 2016. [Google Scholar]
- Louppe, G. Understanding Random Forests: From Theory to Practice. Ph.D. Thesis, Université de Liège, Liège, Belgium, 2014. [Google Scholar]
- Lillicrap, T.P.; Hunt, J.J.; Pritzel, A.; Heess, N.; Erez, T.; Tassa, Y.; Silver, D.; Wierstra, D. Continuous control with deep reinforcement learning. arXiv 2019, arXiv:1509.02971. [Google Scholar] [PubMed]
- Kostrikov, I.; Nair, A.; Levine, S. Offline reinforcement learning with implicit Q-learning. arXiv 2021, arXiv:2110.06169. [Google Scholar] [CrossRef]
- Rashid, T.; Samvelyan, M.; De Witt, C.S.; Farquhar, G.; Foerster, J.; Whiteson, S. Monotonic value function factorisation for deep multi-agent reinforcement learning. J. Mach. Learn. Res. 2020, 21, 7234–7284. [Google Scholar]
- Yu, C.; Velu, A.; Vinitsky, E.; Gao, J.; Wang, Y.; Bayen, A.; Wu, J. The surprising effectiveness of PPO in cooperative multi-agent games. Adv. Neural Inf. Process. Syst. 2022, 35, 24611–24624. [Google Scholar]


| Name | Principle | Effects | Parameter Value |
|---|---|---|---|
| Time offset | Shift the entire sequence of traffic forward or backward by several time steps | Improve the time adaptability of the model | {−5, −3, −1, +1, +3, +5} step |
| Noise disturbances | Add Gaussian noise to the raw data | Improve model robustness and prevent overfitting | 0.1 |
| Extreme event synthesis | Artificially synthesize abnormal traffic events, such as Distributed Denial of Service attacks | Enhance the ability of the model to identify and respond to burst traffic | Training: one event per 1700 data points; Testing: one event at a random position |
| Item | Value |
|---|---|
| Maximum input length | 128 |
| Learning rate | |
| Batch size | 8 |
| Weight decay | 0.01 |
| Optimizer | Adam |
| Loss function | MAE, MSE |
| Component | Configuration |
|---|---|
| Actor network | [64, 64] with ReLU and tanh |
| Critic network | [64, 64] with ReLU and tanh |
| Target update parameter | 0.001 |
| Noise process | |
| Replay memory | |
| ) Optimizer learning rate | 0.95 Adam (actor), (critic) |
| Number | Bandwidth | Latency (ms) | Description |
|---|---|---|---|
| 1 | 20 | 5 | High bandwidth and low latency |
| 2 | 10 | 10 | Medium bandwidth and latency |
| 3 | 5 | 15 | Low bandwidth and high latency |
| 4 | 20 | 15 | High bandwidth and high latency |
| 5 | 5 | 5 | Low bandwidth and high latency |
| Topology | Three-Path | Five-Path | Seven-Path | Branched | Ring |
|---|---|---|---|---|---|
| Inference time (ms) | 0.358 | 0.586 | 1.002 | 0.436 | 0.753 |
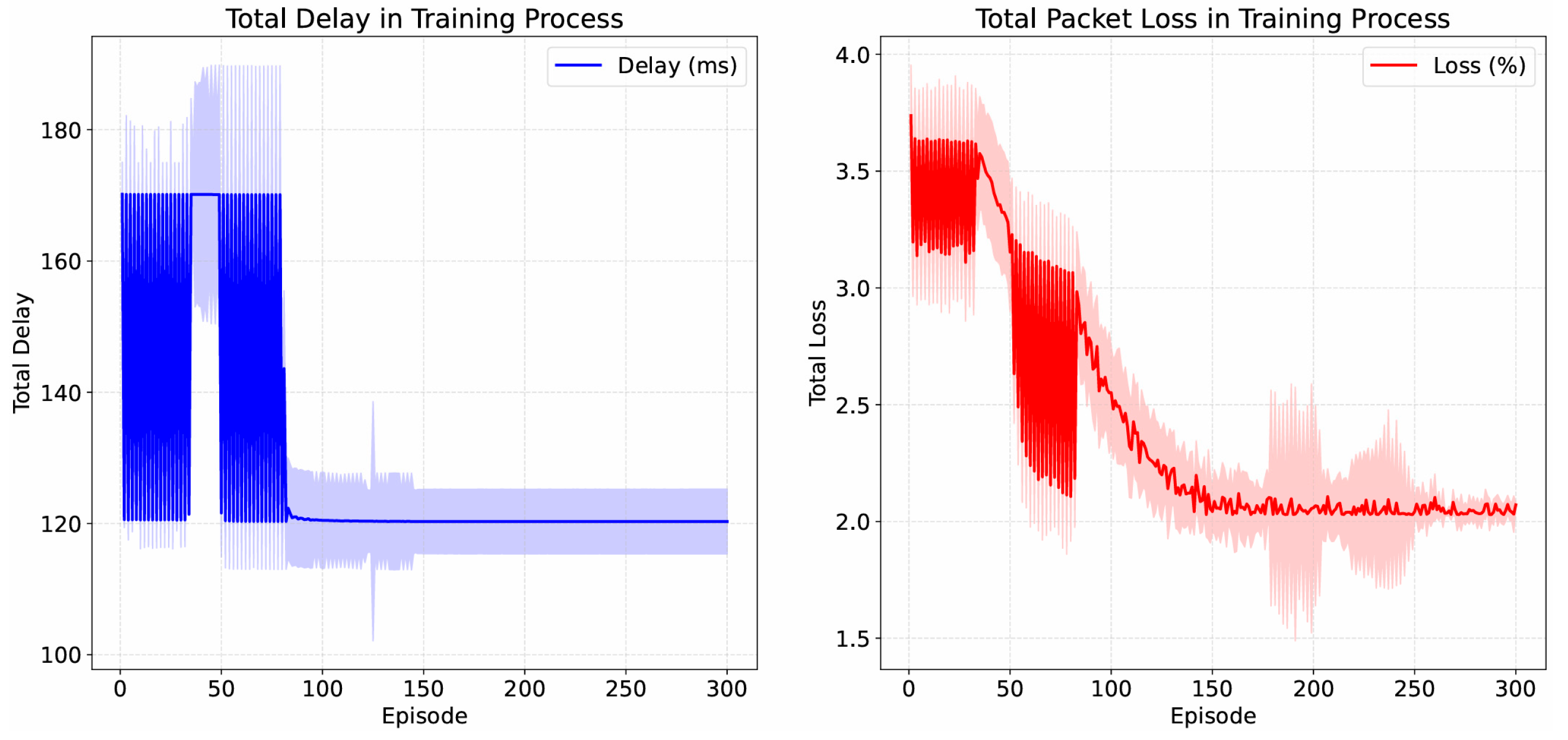
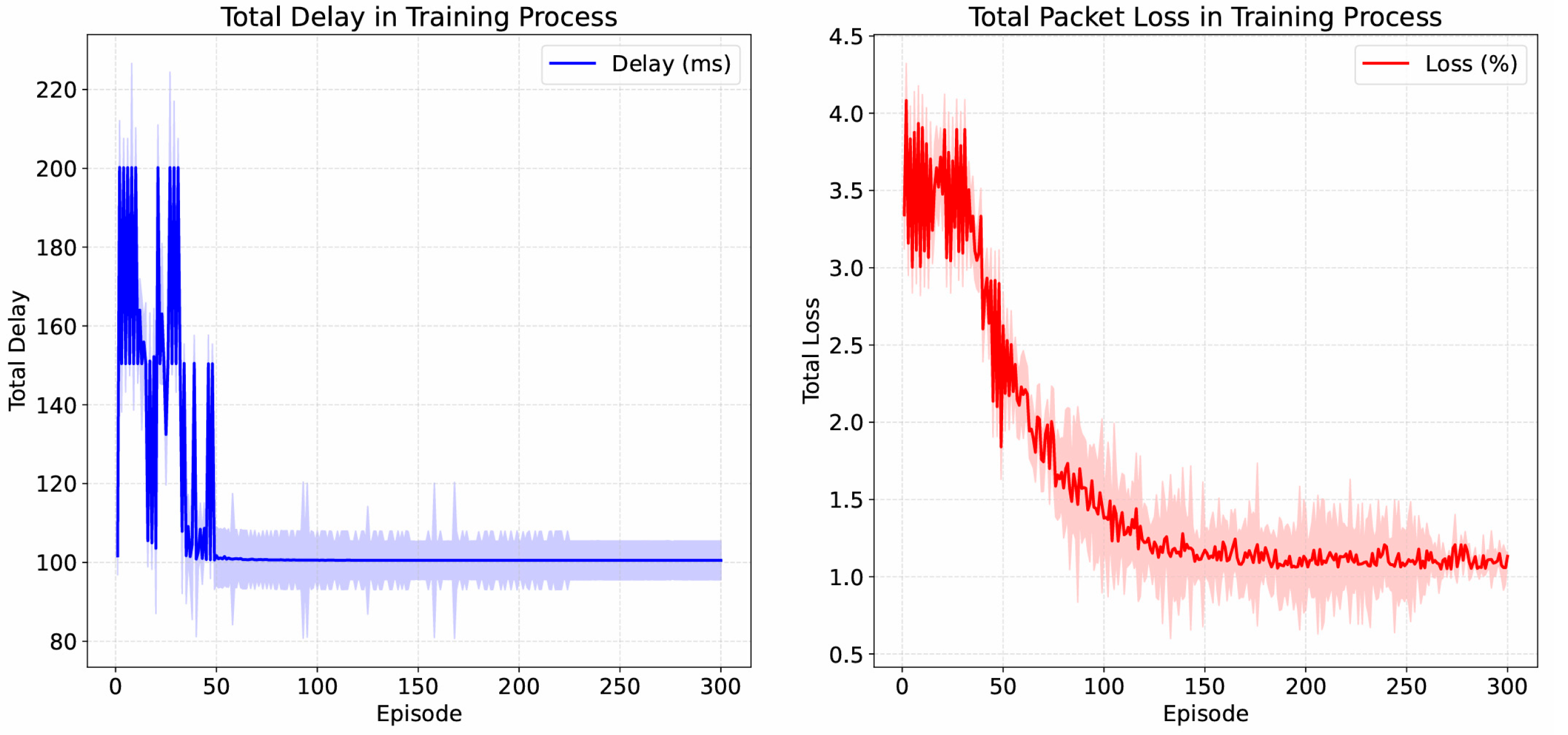
| Topology | Latency (ms) | Loss | Reward | Rel. Improv. (Reward) | |
|---|---|---|---|---|---|
| Three-path | 133.84 | 1.72 | −2.64 | +42.77% | |
| Five-path | 159.36 | 2.17 | −5.17 | +8.19% | |
| Seven-path | 82.87 | 1.69 | −4.69 | +51.89% | |
| Ring | 133.81 | 2.21 | −2.93 | +36.33% | |
| Branched | 129.65 | 2.19 | −5.74 | +22.16% | |
| Inference time of our method (ms) | |||||
| Three-path | 0.358 | ||||
| Five-path | 0.586 | ||||
| Seven-path | 1.002 | ||||
| Ring | 0.753 | ||||
| Branched | 0.436 | ||||
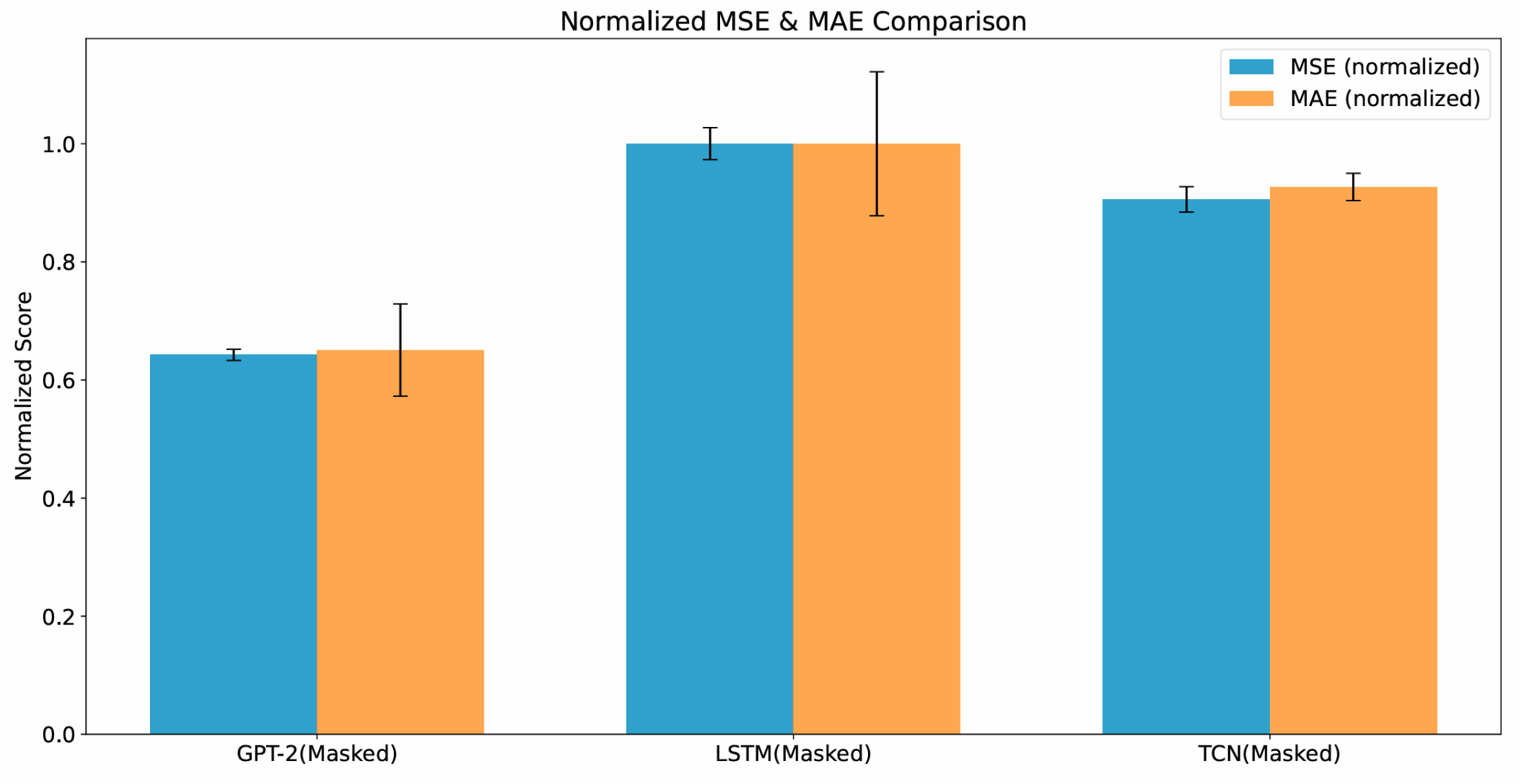
| Prediction error (perturbed) | |||||
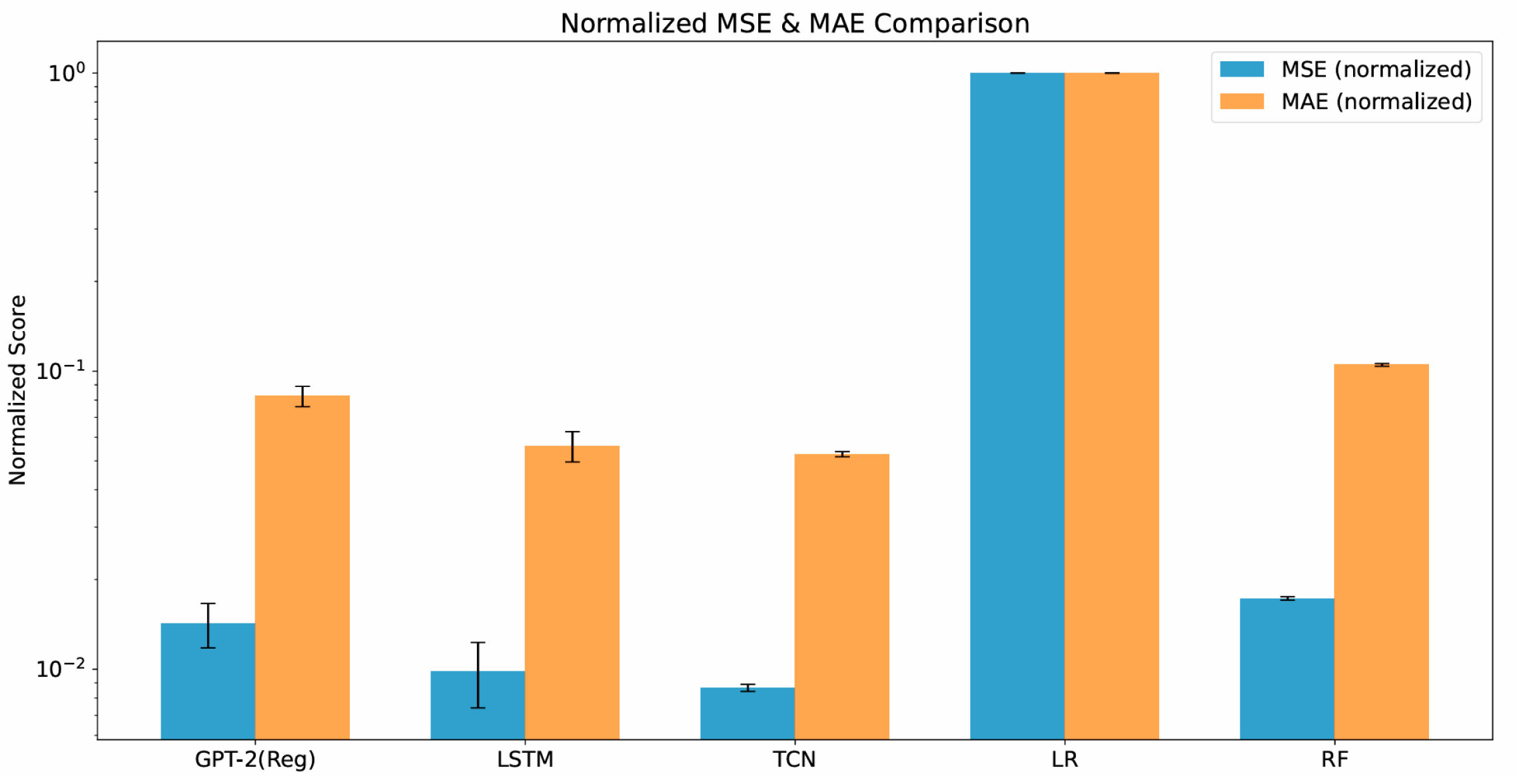
| Model | MSE (normalized) | MAE (normalized) | |||
| LSTM | 1.000 ± 0.027 | 1.000 ± 0.122 | |||
| TCN | 0.906 ± 0.022 | 0.927 ± 0.023 | |||
| GPT-2 | 0.643 ± 0.010 | 0.651 ± 0.078 | |||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, X.; Zhao, J.; Zhang, Y.; Li, R. Integrating Reinforcement Learning and LLM with Self-Optimization Network System. Network 2025, 5, 39. https://doi.org/10.3390/network5030039
Xu X, Zhao J, Zhang Y, Li R. Integrating Reinforcement Learning and LLM with Self-Optimization Network System. Network. 2025; 5(3):39. https://doi.org/10.3390/network5030039
Chicago/Turabian StyleXu, Xing, Jianbin Zhao, Yu Zhang, and Rongpeng Li. 2025. "Integrating Reinforcement Learning and LLM with Self-Optimization Network System" Network 5, no. 3: 39. https://doi.org/10.3390/network5030039
APA StyleXu, X., Zhao, J., Zhang, Y., & Li, R. (2025). Integrating Reinforcement Learning and LLM with Self-Optimization Network System. Network, 5(3), 39. https://doi.org/10.3390/network5030039






