When Robust Isn’t Resilient: Quantifying Budget-Driven Trade-Offs in Connectivity Cascades with Concurrent Self-Healing

Abstract

Cascading link failures continue to imperil power grids, transport networks, and cyber-physical systems, yet the relationship between a network’s robustness at the moment of attack and its subsequent resiliency remains poorly understood. We introduce a dynamic framework in which connectivity-based cascades and distributed self-healing act concurrently within each time-step. Failure is triggered when a node’s active-neighbor ratio falls below a threshold $\phi$; healing activates once the global fraction of inactive nodes exceeds trigger $T$ and is limited by budget $B$. Two real data sets—a 332-node U.S. airport graph and a 1133-node university e-mail graph—serve as testbeds. For each graph we sweep the parameter quartet ($\phi ,\hspace{0.17em}B,\hspace{0.17em}T,attackmode$) and record (i) immediate robustness $R$, (ii) 90% recovery time T₉₀, and (iii) cumulative average damage. Results show that targeted hub removal is up to three times more damaging than random failure, but that prompt healing with $B\ge 0.12$ can halve T₉₀. Scatter-plot analysis reveals a non-monotonic correlation: high-$R$ states recover quickly only when $B$ and $T$ are favorable, whereas low-$R$ states can rebound rapidly under ample budgets. A multiplicative fit $T_{90}\propto B^{-\beta }g\left(T\right)h\left(R\right)$ (with $\beta \approx 1$) captures these interactions. The findings demonstrate that structural hardening alone cannot guarantee fast recovery; resource-aware, early-triggered self-healing is the decisive factor. The proposed model and data-driven insights provide a quantitative basis for designing infrastructure that is both robust to failure and resilient in restoration.

1. Introduction

Modern infrastructure, from transportation and power grids to digital communication and finance, is increasingly organized as interacting networks. When a local fault occurs, the disturbance can propagate through the web of inter-node dependencies, potentially disabling a large fraction of the system. Two complementary performance concepts are therefore central to design:

• Robustness is the ability of the system to withstand the initial disturbance; it is often quantified by the fraction of components that remain functional immediately after the shock [1].
• Resiliency (or recovery) is the ability to return to acceptable performance after the disturbance. It combines the depth of degradation with the speed and extent of restoration [2].

Because many critical sectors now demand guarantees on both attributes [3,4], understanding how robustness and resiliency interact has become an urgent research topic.

Many real-world systems have been widely modeled as networked complex systems such as communication networks [5], power grids [6,7], command and control systems [8,9], and financial transaction systems [10]. Therefore, a better understanding of both terminologies and the interplay among them is essential in prolonging the performance sustainability of modern society infrastructures.

1.1. State of the Art: Cascading Failures and Recovery

Cascading-failure models fall into two broad classes. Connectivity-based models—pioneered by Watts [11]—assume a node becomes inactive when the fraction of its active neighbors drops below a threshold. They have been used to study opinion shifts, information diffusion, virus spreading and community effects [12]. Load-based models, exemplified by Motter & Lai [13], track the redistribution of traffic or flow after a node failure and disable any node whose new load exceeds its capacity. Each paradigm has generated a large body of robustness studies, including targeted attacks on interdependent networks [14], the influence of clustering [15], degree-distribution breadth [16], and optimal interlinking strategies [17].

By contrast, few studies incorporate explicit recovery processes. Early work on network “self-healing’’ proposed instantaneous re-wiring or capacity boosts [18,19,20,21], but did not model the temporal competition between failure propagation and repair. Liu et al. [22] introduced a concurrent self-healing rule for overload cascades, yet the literature still lacks a systematic analysis of how recovery parameters modify the robustness–resiliency trade-off. Metrics for post-disaster performance—resilience triangles [23], disruption cost [24], agent-based restoration times [25]—have been proposed, but none link those metrics back to the pre-failure robustness of the same network. Surveys of network repair strategies [26] and comparisons of connectivity-versus-load-based cascade mechanisms [27] highlight this research gap.

Recent work moves restoration from stylized to operations-aware formulations. Co-optimization models now jointly schedule repair crews and dynamic network reconfiguration, often with mobile resources (e.g., MESS/MPS) and road constraints, to maximize critical-load pickup and shorten outages [28,29], with related logistics and pre-positioning results extending to transportation–power couplings [28,30].

At the same time, learning-augmented restoration has matured from proofs-of-concept to strong baselines: graph-based RL controllers and multi-agent RL (MARL) policies learn switching and load-shedding actions that achieve near-real-time restoration on IEEE feeders while respecting topology and operational limits [31,32,33].

On the theory and synthesis side, new results sharpen our understanding of critical behavior in overload-induced cascades (universality, mixed-vs.-first-order transitions) [34], while recent reviews organize failure dependence and real-world interdependence evidence and lay out open problems for infrastructure resilience [35,36]. These complement existing interdependence and self-healing references and motivate our multiplex, budget-constrained self-healing model.

In this study we use a connectivity-based cascade rule: a node fails when its degree drops below threshold $\phi$. This family of models is a standard baseline for large empirical graphs and has been extensively used to study error/attack tolerance and percolation-driven fragility [26,27]. We deliberately favor this class because (i) it does not require domain-specific flow or capacity data and thus applies uniformly across our networks, and (ii) repeatedly solving flow re-dispatch problems at every time step, as required by load/flow-based cascade models, can dwarf the compute budget and confound the budget–trigger signal we wish to quantify [13,37,38]. Our implementation is modular: the same budget–trigger pipeline can be paired with alternative failure modules (e.g., overload-based), which we outline as a natural extension.

1.2. Objectives and Contributions of This Work

This paper focuses exclusively on the connectivity-based (link-breaking) cascade and augments it with a dynamic self-healing mechanism that operates concurrently with failure propagation. Building on that framework we make four contributions:

• Concurrent cascade + self-healing model. We formulate two algorithms—one for link-breaking failure and one for distributed healing—that act within the same simulation step, controlled by a budget parameter $B$ and a triggering threshold $T$.
• Quantitative evaluation on real data. Using a U.S. airport network (332 nodes) [39] and a university e-mail network (1133 nodes) we measure robustness $R$ and two resiliency metrics: 90% recovery time T₉₀ and cumulative average damage.
• Systematic exploration of parameter space. We vary the degree-loss threshold $\phi$, the attack mode (random vs. targeted), the healing budget and the trigger time, producing a comprehensive map of robustness and resiliency responses.
• First empirical correlation study. Scatter-plot analysis reveals that robustness and resiliency are only weakly correlated unless the trigger is early and the budget adequate; high robustness can coexist with slow or costly recovery and vice versa. We summarize the relationship with a simple multiplicative fit and discuss design implications.

1.3. Paper Organization

Section 2 introduces the connectivity-based model, the self-healing algorithm, and the data sets. Section 3 presents robustness results, resiliency results, and their correlation. Section 4 concludes and outlines directions for recovery-aware network design.

2. Description of Models and Methods

In this section we outline the mechanism used to model the cascading-failure (CF) phenomenon that often arises in networked systems subjected to disruptions.

2.1. Connectivity-Based Failure and Healing

A connectivity-based (link-breaking) cascade proceeds as described in Algorithm 1. In the original graph G, a set of nodes is initially attacked. Those attacked nodes, together with all incident links, are removed and become inactive. The initial set can be chosen randomly or by targeting high-degree hubs.

After the attack, the algorithm scans each remaining active node and computes the ratio

$$\phi ={\displaystyle \frac{current degree}{original degree}}$$

(1)

If $\phi$ falls below critical threshold $\phi c$, the node is scheduled to fail in the next step. The failure–check cycle repeats until the graph reaches a steady state in which some (or all) of the original nodes are inactive.

To restore functionality, we employ a self-healing (SH) scheme controlled by two parameters: Budget B is defined as the maximum number of inactive nodes that can be reactivated in a single time step and Triggering level T is defined as the fraction of nodes that must be inactive (with respect to the original network size) before healing begins.

In the baseline implementation we use global trigger $T$: repairs begin when the system-wide inactive fraction first exceeds $T$. Operationally, interventions are often regional. Our code admits this directly by keeping local inactive fractions $I_r\left(t\right)$ for regions/sectors r (e.g., geographic districts, asset clusters) and using per-region thresholds $T_r$ (or rolling triggers) so that repairs in region r start when $I_r\left(t\right)\ge T_r$. This generalization changes only the decision module; the failure/repair dynamics and budget accounting remain as in the global-T case. The monotonic properties driving our findings (earlier triggers and larger budgets cannot degrade recovery) hold region-wise as well. See also restoration discussions in [40,41].

The healing stage comprises two sub-algorithms (Algorithms 2 and 3):

• Step 1—Decision (Algorithm 2).
  All inactive nodes that still have at least one active neighbor are identified. Each candidate node is assigned
  • A primary impact: the number of active neighbors that would be saved if the node were reactivated (i.e., neighbors whose ratio $\phi$ would rise from $\phi$ <$\phi$_c to ${\phi }^{\prime }$).
  • A secondary impact: the average increase ${\phi }^{\prime }- \phi$ of those neighbors. Nodes are ranked first by primary impact and then, to break ties, by secondary impact.
• Step 2—Implementation (Algorithm 3).
  Up to B highest-ranked inactive nodes are reactivated, and their original edges to currently active neighbors are restored, all within the current step.

The combined procedure iteratively applies failure propagation (Algorithm 1) and, once the trigger T is reached—healing (Algorithms 2 and 3) until no further changes occur.

Interpreting the degree-loss threshold $\phi c$. In our model a node becomes inactive when the fraction of its incident functional connections falls below $\phi c$; degree is used as an operational proxy for available service capacity. Two domain-based anchors motivate the values we study. (i) Airport/transport analogy. Ground operations and schedule feasibility depend on active gates/runways and staffing. Once an airport loses a majority of its usable connections, it behaves as a spoke rather than a hub—schedules cannot be maintained, and the airport is effectively “inactive’’ for the purpose of maintaining the giant component. This places $\phi c$ in the 0.4–0.6 range. (ii) E-mail/communication analogy. In enterprise e-mail systems (or departmental communication graphs), the ability of a server/site to relay messages and route around outages degrades sharply when about half of its peering links or trusted relays are down; delivery latencies explode and the node ceases to keep the organization connected. This motivates the same 0.4–0.6 range as a coarse, degree-based surrogate for service loss. In Results we also vary $\phi c \in \left\{\mathrm{0.3,0.5,0.6,0.7,0.8}\right\}$ and observe the same qualitative budget–trigger trade-off; thus, our conclusions are robust to the exact threshold choice.

Rationale for a local repair rule. In the baseline implementation we select repair targets using a local, one-hop heuristic (neighbors of failed/high-impact nodes). We deliberately favor this class of rules because (i) during the early stage of disruptive events, operators typically act under limited global situational awareness, and (ii) repeatedly evaluating global centrality metrics at each time step is computationally intensive. For example, even the standard fast algorithm for exact betweenness centrality runs in O(nm) time for unweighted graphs (with n nodes and m edges), and would need to be recomputed as the topology evolves [42]; while dynamic/approximate methods exist, maintaining betweenness on fully dynamic networks remains non-trivial [43]. As our objective is to study budget–trigger timing trade-offs under cascading dynamics, rather than to optimize the decision rule itself, we adopt a lightweight heuristic that is implementable with the information and time budgets available in practice.

Modularity. The framework is model-agnostic with respect to the repair policy. The code exposes a single function: target = chooseRepair (G, state, budget, t), so that any scoring function (e.g., betweenness-, closeness-, or community-aware rules) can replace the default. Thus, the trade-off curves reported in this work reflect the interaction between resource timing and cascading dynamics; a different policy may shift absolute recovery speed but does not alter the definition of the trade-offs we quantify.

Algorithm 1. Connectivity-Based CF

Input:   G, attack, mode, ${\mathit{\phi }}_{\mathit{c}}$  // network, attack size, mode, threshold Output:  G_dmg   // damaged graph after cascading failure  1  N  ← all functional nodes in G  2  E  ← all edges in G  3  active ← degree(G)       // original degrees of every node  4  idx ← sort(active, descend)     // high-degree first  5  IF mode = 0  THEN        // random attack  6          rmodes ⊂ N ← randomsample(N, attack)  7  ELSEIF mode = 1  THEN // targeted (highest-degree) attack  8          rmodes ⊂ N ← idx(1: attack)  9  ENDIF 10  FOR each v ∈ rmodes  DO       // initial removals 11          remove v and all incident edges from G 12  ENDFOR // -------- cascading failures until no new node violates $\mathit{\phi }$ < $\mathit{\phi }\mathit{c}$ 13  REPEAT 14         fail  ← degree(G)       // current degrees 15         $\phi$  ← fail ./ active    // element-wise ratio (0 ≤ $\phi$ ≤ 1) 16         needrmv ← ($\phi$ < $\phi c$)    // Boolean vector 17         cand   ← nodes( needrmv = true ) 18         FOR each u ∈ cand DO  // remove newly failed nodes 19              remove u and all incident edges from G 20         ENDFOR 21  UNTIL cand = ∅   // stop when no additional failures 22  G_dmg ← G 23  RETURN G_dmg

Algorithm 2. Connectivity-Based SH-Decision

Input:   G_dmg,   // current damaged graph               G_orig,   // original graph (before any failure)                        ${\mathit{\phi }}_{\mathit{c}}$        // degree–loss threshold Output:  inAtv_ranked    // inactive nodes ordered by healing impact  1  inAtv ← all INACTIVE nodes in G_dmg  2  impact ← zeros(|inAtv|)   // primary-impact score for each inactive node     // ---------- Step 1: compute primary impact ------------  3  FOR k = 1 to |inAtv| DO  4           ii   ← inAtv[k]  5           nbx  ← active neighbors of ii in G_dmg  6           FOR each nb ∈ nbx DO  7                 d_orig ← degree of nb in G_orig  8                 d_dmg  ← degree of nb in G_dmg   9                 $\phi$      ← d_dmg / d_orig 10                 IF $\phi$ ≤ ${\phi }_{\mathit{c}}$ THEN                   // nb is currently endangered 11                      drst ← d_dmg + 1    // edge (ii, nb) would be restored 12                      ${\phi }^{\prime }$    ← drst / d_orig       // nb’s ratio *after* healing ii 13                      IF ${\phi }^{\prime }$ > ${\phi }_c$ THEN 14                           impact[k] ← impact[k] + 1 // nb would be rescued 15                      ENDIF 16                 ENDIF 17           ENDFOR 18  ENDFOR  19 idx  ← argsort(impact, ‘descend’)      // indices in decreasing impact  20 inAtv1 ← inAtv[idx]           // reordered list after primary sort         // ---------- Step 2: tie-break with average ${\mathit{\phi }}^{\mathit{\prime }}-\mathit{\phi }$ improvement ---------  21 d ← −∞ · ones(|inAtv|)       // secondary score (only for ties)  22 FOR m = 1 to |inAtv1| DO  23       ii ← inAtv1[m]  24       if impact[m] = impact[1] THEN  // compute only for nodes sharing max  25                      nbx ← active neighbors of ii in G_dmg  26                      Δ$\phi$_list ← ∅  27                      FOR each nb ∈ nbx DO  28                               d_orig ← degree of nb in G_orig  29                               d_dmg  ← degree of nb in G_dmg  30                               $\phi$      ← d_dmg / d_orig  31                               drst   ← d_dmg + 1  32                               ${\phi }^{\prime }$     ← drst / d_orig  33                            $\Delta \phi \_list$ ← $\Delta \phi \_list$ ∪ { ${\phi }^{\prime } - \phi$ }  34                      ENDFOR  35                      IF |$\Delta \phi \_list$| > 0 THEN  36                               d[m] ← mean($\Delta \phi \_list$) // average improvement  37                      ENDIF  38           ENDIF  39 ENDFOR  40 idx2 ← lexicographic-sort(impact(desc), d(desc))  41 inAtv_ranked ← inAtv[ idx2 ]    // final ranking (impact, then $\Delta \phi$)  42 RETURN  inAtv_ranked

Algorithm 3. Connectivity-Based SH-Implement

Input:   G_dmg,         // current damaged graph              G_orig,         // original graph              inAtv,          // inactive nodes ranked by Algorithm 2              B              // healing budget (number of nodes to reactivate) Output:  G_rec         // graph after applying self-healing  1  healed ← 0         // number of nodes already reactivated  2  FOR k = 1 to |inAtv| DO  3        IF healed = B THEN  4             BREAK            // budget exhausted  5        ENDIF  6        ii   ← inAtv[k]       // next candidate to heal  7        IF ii is ACTIVE in G_dmg THEN  8             CONTINUE         // node already healed by earlier iteration  9        ENDIF 10        nbx  ← active neighbors of ii in G_dmg 11        IF nbx ≠ ∅ THEN 12             FOR each nb ∈ nbx DO 13                   IF edge (ii, nb) ∈ E(G_orig) AND edge (ii, nb) ∉ E(G_dmg) THEN 14                        add edge (ii, nb) to G_dmg 15                   ENDIF 16             ENDFOR 17             mark ii as ACTIVE in G_dmg 18             healed ← healed + 1 19        ENDIF    // if nbx = ∅, skip without spending budget 20  ENDFOR 21  G_rec ← G_dmg                22  RETURN G_rec

We simulate the system in discrete global time-steps t = 0,1,2,… Each step contains two phases that are executed within the same step: (i) failure propagation (applying the degree-loss rule and inter-layer dependencies to obtain the inactive set at time t), and (ii) self-healing (applying the repair policy subject to the available budget B(t) and the trigger condition). We refer to this as concurrent self-healing at the step level: both failure and repair are completed before the clock advances from t to t + 1, and the resulting state is then committed as x(t + 1). Internally the order is fail → heal, but because both occur within the same global step, repair decisions respond to the failures of that step. If finer temporal inter-leaving is desired, the step can be subdivided into k ≥ 1 micro-iterations (we use k = 1 in all reported results), which emulates tighter fail/heal alternation without changing the modeling framework.

2.2. Robustness and Resiliency Metrics

For graphs with |G| > 0, robustness is quantified by the metric R defined as

$$R={\displaystyle \frac{number of active nodes immediately after the damage}{number of nodes in the original network G}}$$

(2)

During the damage step, all nodes scheduled to fail in the current iteration are removed simultaneously; subsequent propagation then follows the failure–heal cycle described in Algorithms 1–3. Because every node is active at $t=0$, the denominator equals $\left|G\right|$; thus $R ϵ \left[\mathrm{0,1}\right]$.

Resiliency is evaluated with two complementary metrics:

• Average Damage $\overline{D}$ over a predefined time window $t = 1, \dots , t_{max}$:

  $$\overline{D}={\displaystyle \frac{1}{t_{max}}} \sum _{t=1}^{t_{max}}(1-a(t\left)\right)$$

  (3)

  where $a\left(t\right)$ is the fraction of nodes that are active at time $t$.
• 90% Recovery time, $T_{90}$.

$T_{90}$ is the earliest time step at which at least 90% of the original nodes are active again. If the fraction of inactive nodes never falls below 10% within the simulation horizon, we set $T_{90}=\infty$; this indicates that the system is unable to recover to the 90% level.

These two metrics together capture both the depth of disruption $\overline{D}$ and the speed of recovery $T_{90}$.

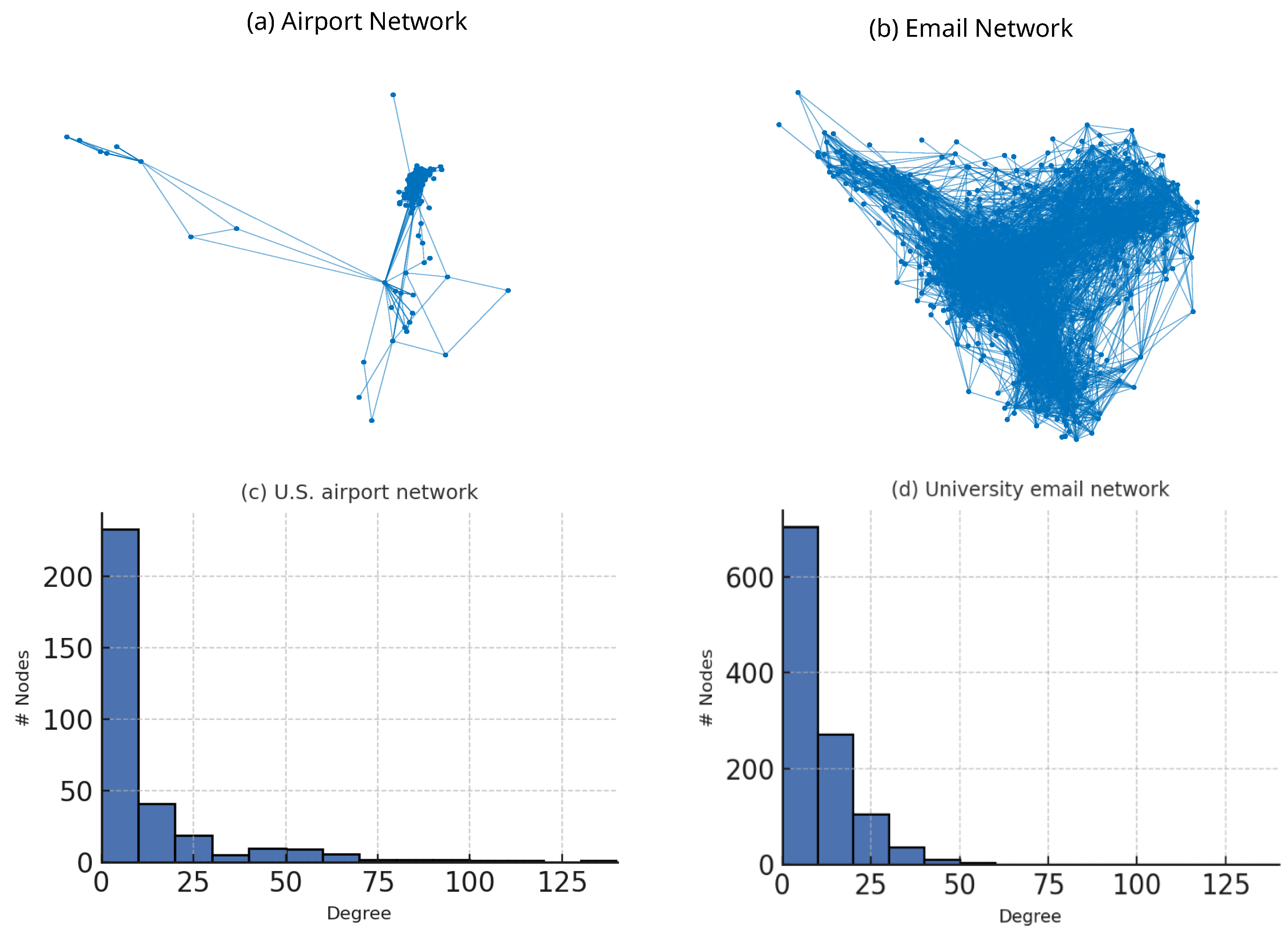
2.3. Description of Data

Two real-world networks [28] are studied in this work. Figure 1 shows both datasets. The first is a U.S. airport network with 332 nodes, where each node represents an airport and each link indicates at least one direct flight between the corresponding airports. The second is a university email network with 1133 nodes; the nodes represent email accounts and the links indicate that at least one message was exchanged between the accounts. Figure 1a uses randomly assigned node coordinates for visual clarity and therefore does not reflect true airport locations. Figure 1c,d depict the degree histograms of the airport and email networks, respectively.

We intentionally select the airport and e-mail graphs because they span two ends of the density/heterogeneity spectrum. The airport network is a spatially embedded transportation system with modest average degree and limited redundancy—sparse in link density. By contrast, the university e-mail graph is an ICT network with heavy-tailed degree distribution and hub nodes, remaining very sparse overall. This contrast is visible in the degree histograms in Figure 1c,d. The pair therefore exercises our framework in two qualitatively different regimes: (i) a low-redundancy, geographically constrained network in which removing a few high-impact nodes can detach large regions (airport), and (ii) a hub-dominated network that is a canonical test-bed for degree-targeted failures (e-mail), consistent with the targeted-attack vulnerability of heterogeneous graphs. (As in common practice, node coordinates in Figure 1a are schematic and do not represent physical airport locations).

Applicability of the failure rule to both domains. Although our failure model is connectivity-based, it is intended as an operational proxy: a node becomes inactive when it loses a large fraction of its incident connections. In transportation systems, once an airport loses many usable connections, flight schedules can no longer be maintained; in departmental communication systems, the loss of peering links or trusted relays severely limits message routing. Our degree-loss threshold ${\phi }_c$ therefore captures a common service-loss condition in both domains.

3. Results and Discussion

To probe the connectivity-based (CB) cascade model, we evaluate nine initial-attack fractions $\alpha =0.10, 0.20,\dots , 0.90$. For each $\alpha$ we run 500 Monte-Carlo trials of Algorithms 1–3 under random attack, where the attacked nodes are selected uniformly at random. In the targeted-attack setting we also conduct 500 trials per $\alpha$, but in each trial the attacked set is chosen as the highest-degree hubs.

The remainder of this section is organized as follows: Section 3.1 presents robustness patterns $R(\alpha ,\phi )$ for the two real-world networks (U.S. airports, university e-mail), Section 3.2 analyses their resiliency metrics—average damage D and 90% recovery time $T_{90}$, and Section 3.4 examines the correlation between robustness and resiliency and discusses topological drivers of the observed trends.

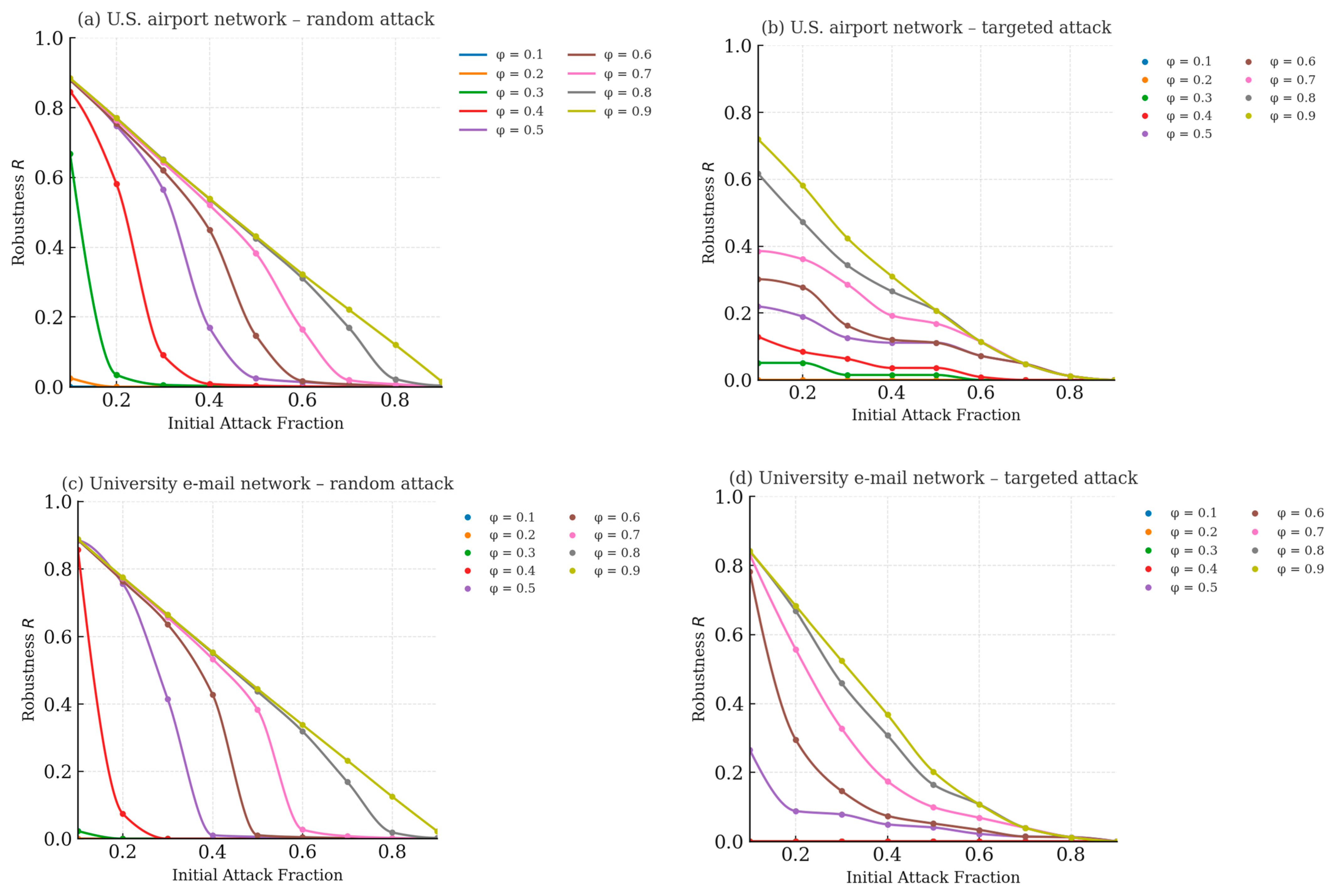
3.1. Robustness Patterns

We quantify robustness with the metric R (Section 2) and examine how it varies with the degree-loss threshold $\phi$. Figure 2 displays R for the U.S. airport network ((a) random, (b) targeted) and for the university e-mail network ((c) random, (d) targeted). Each curve is the mean of 500 Monte-Carlo runs. The x-axis lists the initial-attack fraction $\alpha \in \{0.1,\dots ,0.9\}$; nine threshold values $\phi$ = 0.1,…,0.9 are plotted.

The four panels in Figure 2 reveal three consistent trends.

• First, targeted removal of high-degree hubs produces a markedly steeper drop in robustness R than an equivalent random failure, as can be seen by comparing panels (b) and (d) with panels (a) and (c).
• Second, increasing the degree-loss threshold $\phi$ invariably postpones secondary cascades: larger $\phi$ values preserve a greater fraction of nodes for every initial-attack fraction α, whereas low thresholds allow the network to collapse rapidly.
• Third, even under identical $\alpha -\phi$ settings the U.S. airport graph retains a higher R than the university e-mail graph; this difference aligns with simple topological descriptors—most notably the airport network’s higher mean degree (12.8 versus 9.6) and its richer redundancy among hubs.
• Taken together, these results confirm that the connectivity-based model reproduces intuitive robustness dynamics and underscore the need for mitigation strategies that are tailored to a network’s specific connectivity profile.

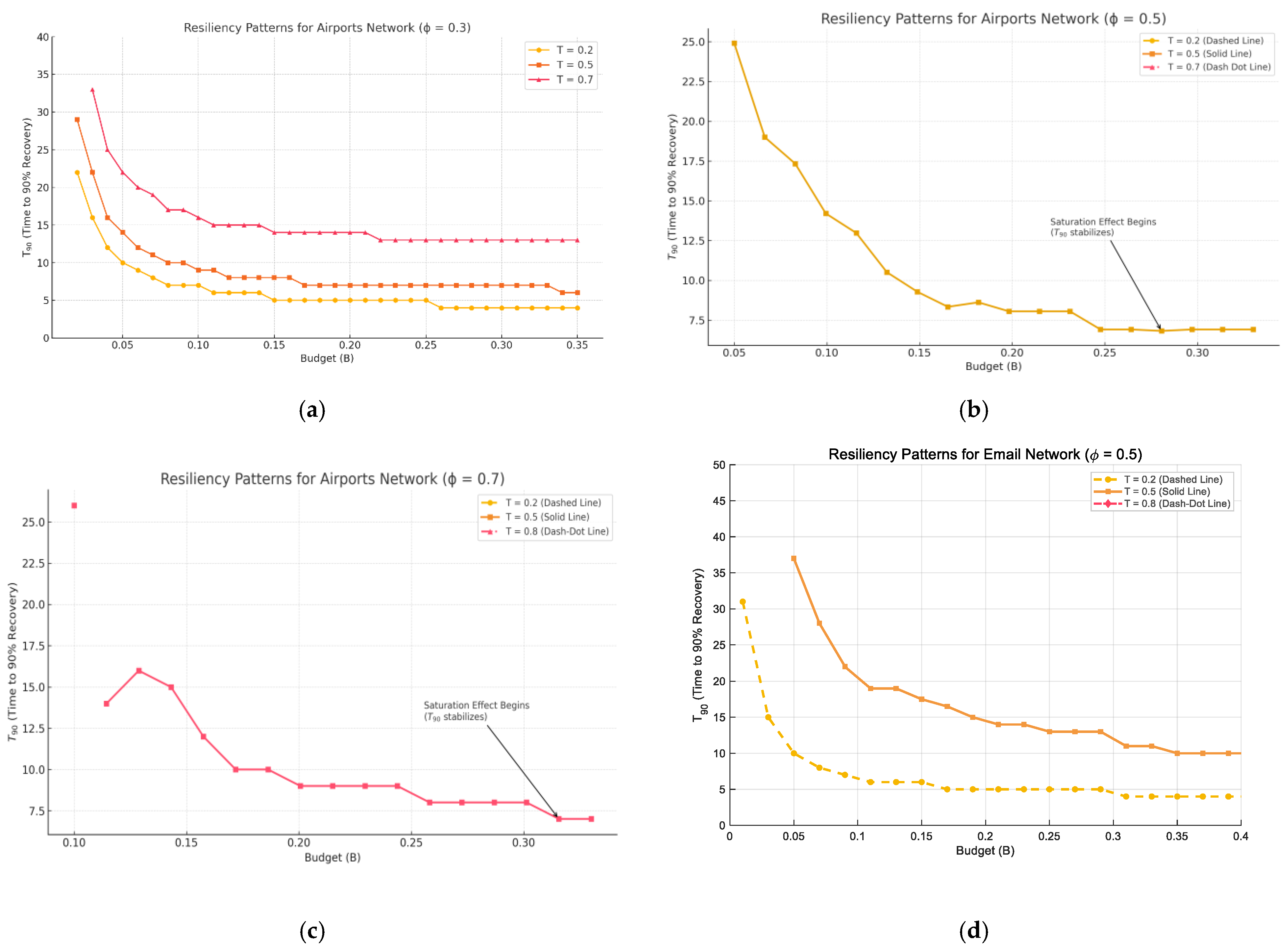
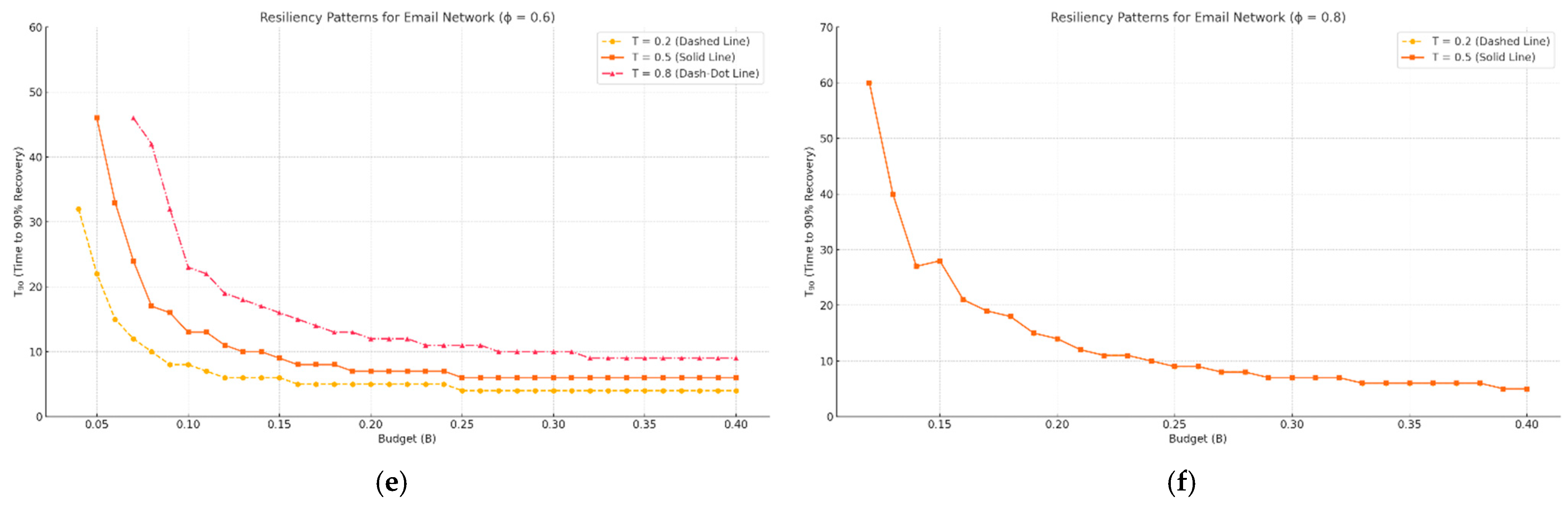
3.2. Resiliency Patterns

The resiliency study focuses on the worst-case, targeted-attack scenario and uses the recovery-time metric T₉₀—the number of simulation steps required for the network to return to at least 90% active nodes. To provide an intuitive, easy-to-interpret benchmark, we adopt 90% as the recovery target and define $T_{90}$ as the first time step at which at least 90% of nodes are active again. This level is commonly used in practice-oriented studies because it (i) indicates the system is largely functional from the user’s perspective while (ii) still leaving head-room to discriminate between faster and slower recovery trajectories. Figure 3 collects six panels that plot T₉₀ against the healing budget B for three degree-loss thresholds $\phi$ and three triggering levels (T). In every panel the same qualitative tendencies appear but their quantitative expression differs between the two real-world graphs. While absolute recovery speed can depend on the specific repair policy, the shape and location of the budget–trigger trade-off are governed by when resources are deployed relative to the cascade’s growth. This monotonic timing effect is not specific to targeted removal and is expected under random failures as well; targeted attacks simply start from a more damaged state [26,44].

For the airport network the low-threshold case $\phi =0.3$ (Figure 3a) is highly sensitive to the triggering level. When self-healing is postponed to $T=0.7$ the network may need more than 30 steps to regain 90% functionality, whereas an early start at $T=0.2$ roughly halves the recovery time. As $\phi$ rises to 0.5 and 0.7 (Figure 3b,c) the curves for the three triggering levels converge; once the threshold is high enough the cascade dies out quickly and T₉₀ becomes almost independent of when healing begins. In every panel an initial increase in the budget yields marked reductions in T₉₀, but beyond a critical budget the curves flatten, and additional resources no longer accelerate recovery.

The e-mail network displays a different landscape. When the degree-loss threshold is low ($\phi =0.3$, not shown) the network never reaches the 90% mark and T₉₀ is infinite for all $T$ and B. At $\phi =0.5$ (Figure 3d) recovery becomes possible, yet the outcome remains extremely sensitive to $T$: an early trigger restores the graph in fewer than ten steps for moderate budgets, whereas a late trigger can still leave T₉₀ infinite at the same budget. Increasing $\phi$ to 0.6 (Figure 3e) widens the range of budgets that guarantee finite recovery times, but the curves retain a pronounced separation by $T$. A further increase to $\phi =0.8$ (Figure 3f) paradoxically brings the system back to fragility—delayed healing never succeeds and even the earliest trigger needs large budgets to pull T₉₀ below ten steps. Thus the e-mail graph shows a non-monotonic relation between robustness (as measured by $\phi$) and resiliency: intermediate thresholds perform best, whereas very low or very high thresholds lead to unrecoverable states.

Across all panels, increasing the budget always shortens recovery time until a saturation point is reached. For the airport graph that threshold is about $B=0.12$ at $\phi =0.7$; below it the system can oscillate between finite and infinite T₉₀, while one incremental budget step above removes the bottleneck and halves T₉₀. The same saturation effect appears in the e-mail graph, but it emerges at a lower budget fraction because that network is sparser—its nodes have fewer neighbors on average—so fewer reactivations are required to reconnect the giant component even though the graph contains more nodes overall.

These observations confirm that the timely activation of self-healing and sufficient—but not excessive—budget allocation are the dominant levers of resiliency. The airport network profits from its denser, more redundant topology; once $\phi$ exceeds 0.5 its recovery speed is largely budget-limited and almost independent of the trigger. By contrast, the sparser e-mail network remains vulnerable to both late triggers and undersized budgets even at intermediate thresholds, while extreme thresholds ($\phi =0.3 or 0.8$) push it into regimes where recovery is impossible.

3.2.1. Budget Thresholds and Non-Linear Effects

A closer look at the airport data for $\phi =0.7$ illustrates how delicately recovery hinges on budget near a critical point. At $B=0.10$ the system still manages to heal, but slowly (T₉₀ = 26). Reducing the budget by a single percentage point to $B=0.11$ drops the available resources below the minimum needed to reactivate key hubs; cascading failures therefore persist indefinitely and T₉₀ diverges. Raising the budget again to $B=0.12$ supplies just enough edges to halt the cascade and T₉₀ falls abruptly to 14. Such sharp transitions emphasize that resource planning must account for non-linear gains: small increments around the critical budget yield disproportionate improvements in resiliency.

3.2.2. Interplay Between Robustness and Resiliency

Because $\phi$ evolves during a cascade, robustness and resiliency are intertwined in a non-linear fashion. In the airport graph intermediate thresholds ($\phi =0.5-0.6$) strike an effective balance: the network can withstand initial damage and still recover under realistic budgets. Thresholds that are too low ($\phi =0.3$) or too high ($\phi =0.8$) push the system into failure modes that are hard to reverse, producing the same qualitative outcome—unbounded T₉₀—for opposite structural reasons. The e-mail graph exhibits the same pattern but with much narrower safe intervals; it remains acutely sensitive to trigger times and budget sizes even at $\phi =0.6$.

3.2.3. Implications

Our work uses two real-world graphs (airport and e-mail) to isolate the budget–trigger mechanism. Our conclusions are mechanism-level: recovery time behaves as backlog at trigger divided by repair capacity. Earlier triggers accumulate less backlog; larger budgets increase capacity; both effects show diminishing returns once the giant component is re-established. These properties are not domain-specific and are consistent with observations across transport, power, and communication systems reported in the cascading-failure/restoration literature. Nevertheless, the numerical thresholds depend on topology and operational constraints; testing additional domains is an important avenue for future work. We release code and scripts to facilitate replication on other networks.

We analyze budget–timing trade-offs using a single global trigger to expose the underlying mechanism cleanly. In practice, operators often rely on regional or priority-based activation. Our framework supports this by replacing $T$ with per-region thresholds $T_r$ (or rolling triggers) that monitor local inactive fractions; this affects only when/where repairs start, not the dynamics. Exploring policy design for $T_r$ informed by operational constraints is a valuable direction for future work; see the restoration surveys in [40].

The combined analysis of robustness and resiliency shows that network topology dictates the feasible operating window. Dense, hub-rich infrastructures such as the airport network can tolerate delayed healing once $\phi$ is moderate, whereas sparse peer-to-peer structures such as the e-mail network demand both early intervention and carefully calibrated budgets. Beyond a network-specific saturation point additional resources bring diminishing returns, so precise allocation at or just above the critical budget is more effective than indiscriminate over-provisioning.

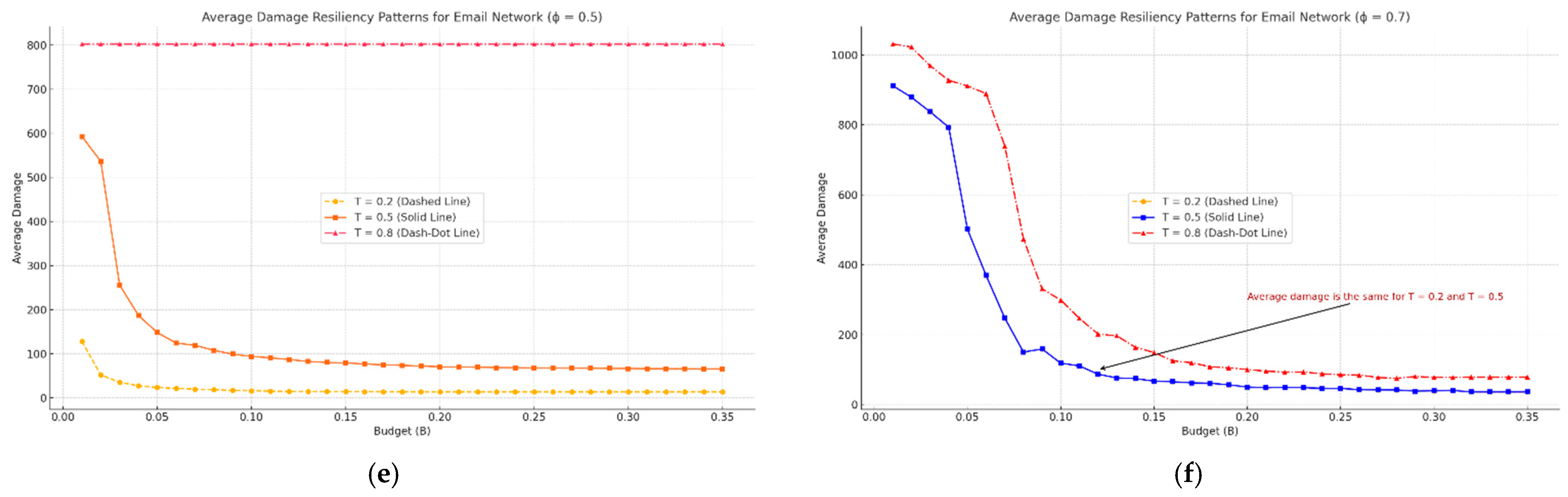
3.2.4. Average Damage as an Alternative Resiliency Metric

Because T₉₀ cannot distinguish between partial-recovery and no-recovery trajectories that both end with an “infinite’’ time, we complement it with the average-damage measure, defined as the cumulative number of inactive nodes averaged over the observation window. Whereas T₉₀ is a timing metric, average damage reflects the severity and persistence of cascade effects. Figure 4 plots this quantity for the two real-world graphs under the same targeted-attack setting used in Section 3.2; each panel pairs a degree-loss threshold $\phi$ with three triggering levels $T=0.2, 0.5, 0.8$ and sweeps the healing budget $B$.

For the airport network the behavior changes markedly with $\phi$. When $\phi =0.3$ average damage falls rapidly as soon as the budget rises above a few percent of the node count, but the final plateau depends on when recovery begins: early triggering ($T=0.2$) stabilizes below ten inactive nodes, an intermediate trigger ($T=0.5$) settles near a dozen, and a late trigger ($T=0.8$) remains much higher. At the intermediate threshold $\phi =0.5$ those three curves collapse onto one another; any trigger time is adequate, provided the budget exceeds about five percent, emphasizing that resource availability rather than response time controls performance in this regime. Raising the threshold to $\phi =0.7$ eliminates temporal sensitivity: the three triggering levels collapse onto a single curve, so recovery performance depends almost exclusively on whether the budget exceeds the critical value of about twelve percent. A further increase to $\phi =0.8$ pushes the system beyond its tipping point; the cumulative damage stays above two hundred inactive nodes for all budgets and trigger times, revealing a paradox in which extreme structural robustness offers no practical resiliency because the initial loss is already too large.

The e-mail network exhibits the same qualitative pattern but at different budget scales and with steeper transitions. At $\phi =0.3$ the curves are flat: average damage hovers around 191 for every B and T, confirming that the graph never recovers. Moving to $\phi =0.5$ introduces strong dependence on both control parameters. An early trigger combined with a budget above ten percent drives the average damage into double digits, but postponing recovery by only three time-steps causes the cumulative loss to exceed six hundred nodes unless the budget is very high. The threshold $\phi =0.7$ widens the window of successful operation; early and intermediate triggers converge once B passes fifteen percent, yet a late trigger remains ineffective. At $\phi =0.8$ the network again collapses irrespective of budget: the proportion of failures is simply too large to be reversed.

Across both graphs two conclusions emerge. First, average damage confirms the non-monotonic link between robustness and resiliency inferred from T₉₀: thresholds that are either too low or too high leave the system in unrecoverable states, whereas an intermediate range ($\phi \approx 0.5-0.7$) minimizes cumulative loss. Second, budget and trigger time trade off against each other only within that favorable range; outside it no realistic allocation can compensate for an untimely response or overwhelming initial damage. These findings suggest that effective recovery policy must identify the internal threshold regime where additional resources still translate into tangible resiliency gains and must prioritize rapid activation when the network operates near its tipping points.

3.3. Limitations and Alternative Heuristics

Operational scope of the local rule. Our baseline repair policy is deliberately local and one-hop to reflect the information and time constraints faced by operators during fast-moving disruptions. Global-metric strategies (e.g., prioritizing nodes with high current betweenness or community bridges) can reconnect large detached components faster when reliable system-wide situational awareness and compute are available. We therefore position the local rule as a baseline under operational constraints, not as uniquely optimal.

Modeling choice (connectivity vs. load) and attack model. Our degree-based failure rule treats $\phi c$ as a local service-loss proxy; flow-aware stress rules (capacity, queueing, or line-loading) are compatible with the same simulation shell and are a natural extension for future work. We stress-test timing and budget using adversarial (degree-targeted) attacks, which are known to be more damaging than random failures in heterogeneous networks [26,44]; the latter primarily shift recovery curves downward but do not change our ordering of trigger-versus-budget in the scenarios we study. Comparisons with load-based cascade models—and guidance on when each is appropriate—are reviewed in [45]. The pipeline is modular, so a load-aware failure module can be substituted without changing the analysis.

3.4. Correlation Between Robustness and Resiliency (Airport Network, 10% Initial Attack)

Figure 5 brings together six scatter plots obtained from the airport network after a fixed 10% targeted attack. Each marker represents one of the seven degree-loss thresholds $\phi =0.3,\dots ,0.7$ and is colored by the healing-budget fraction $B$ (blue 0.02, orange 0.05, gray 0.10, yellow 0.20). Robustness $R$ measured immediately after the attack is shown on the horizontal axis, while the vertical axis carries one of two resiliency indicators. Panels a, b, c plot the recovery time T₉₀; and panels d, e, f plot the cumulative average damage. All panels correspond to the three triggering thresholds $T=0.2, 0.5, 0.8$.

3.4.1. Robustness Versus T₉₀ (Panels a–c)

Early triggering ($T=0.2$, panel a) produces an oblique cloud; high robustness combined with a tiny budget ($B=0.02$) still needs roughly thirty steps to reach 90% activity, whereas ample funding ($B=0.20$) lets even fragile states ($R\approx 0.10$) recover in fewer than ten steps. Panel b ($T=0.5$) shifts every point upward by two–three time-steps but preserves the same diagonal ordering, confirming that budget can compensate for limited robustness when the trigger is not too late. In contrast, panel c ($T=0.8$) shows nearly horizontal bands: after a long delay the cascade has spent itself and T₉₀ depends almost solely on budget, with robustness contributing little additional leverage.

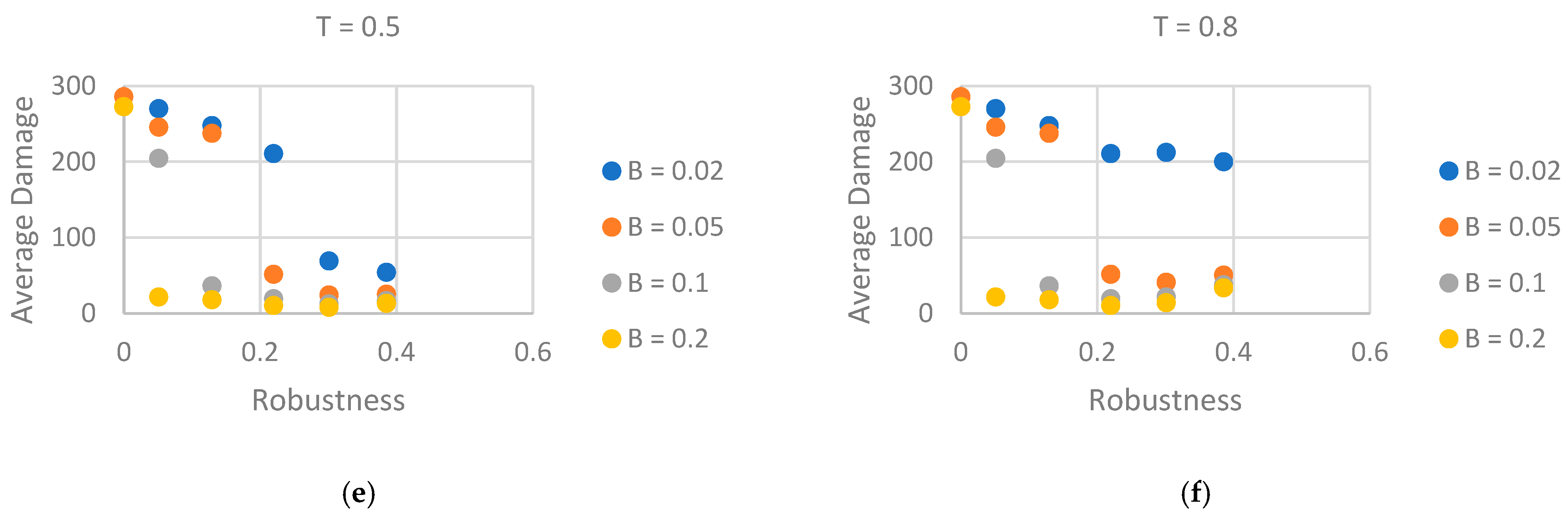
3.4.2. Robustness Versus Average Damage (Panels d–f)

The average-damage panels trace the same interplay in terms of damage magnitude. With a prompt trigger (panel d) cumulative loss stays below fifty nodes whenever either robustness or budget is high, but exceeds 250 nodes when both are low. A moderate delay (panel e) widens the damage gap between low and high budgets, especially for fragile states. Under the late trigger $T=0.8$ (panel f) damage stratifies almost perfectly by budget: blue markers ($B=0.02$) cluster near 200 inactive nodes regardless of robustness, while yellow markers ($B=0.20$) cluster below fifty nodes, indicating that once intervention is late, budget dominates and robustness ceases to influence cumulative loss.

3.4.3. Interpretation and Design Implications

Taken together, the six panels show that robustness and resiliency are related but distinct. A configuration that survives the initial attack well can still recover slowly or sustain heavy loss if resources are tight, whereas a fragile configuration can rebound rapidly given timely and ample funding. Budget and trigger time trade off only when intervention is early; once healing is substantially delayed, increasing robustness adds little benefit. Empirically, the relationship can be approximated by a multiplicative form $T_{90}\propto B^{-\beta }g\left(T\right)h\left(R\right)$ with β ≈ 1 and a weak robustness factor $h\left(R\right)$ when $T$ is large—underscoring that prompt, well-funded self-healing is more effective than structural hardening alone.

Validation of the multiplicative fit. The multiplicative ansatz $T_{90}\propto B^{-\beta }g\left(T\right)h\left(R\right)$ is supported by the collapse of the curves in Figure 5 after a two–step rescaling. First, plotting $T_{90}$ against budget on log–log axes reveals a nearly constant slope of −1 across all trigger levels, indicating $\beta \approx 1$. Second, dividing each curve by $B^{-1}$ aligns the data for different budgets; the remaining vertical offsets depend only on the trigger threshold and the pre-attack robustness, consistent with separable factors $g\left(T\right)$ and $h\left(R\right)$. Within each trigger group, the residual spread is of the same order as the symbol size, and no systematic pattern persists after normalization, implying that higher-order interactions are negligible at the resolution of the study. Taken together, these observations confirm that the proposed product form captures the dominant joint influence of budget, trigger timing, and robustness on the 90%-recovery time.

4. Conclusions

This paper developed and analyzed a concurrent failure-and-healing framework for connectivity-based cascades on real-world networks. The model couples a link-breaking failure rule—activated when a node’s active-neighbor ratio drops below a threshold—with a distributed self-healing rule that is governed by a triggering level $T$ and a budget $B$. By sweeping the four-dimensional parameter space ($\phi ,\hspace{0.17em}B,\hspace{0.17em}T, attackmode$) on a U.S. airport graph and a university e-mail graph we obtained three main results.

• Distinct robustness regimes. Robustness $R$ declines smoothly under random attack but collapses abruptly under targeted hub removal; increasing $\phi$ mitigates both effects, although the airport network remains consistently more robust owing to its higher mean degree and redundant hub set.
• Budget-trigger trade-off in resiliency. Early activation with a modest budget outperforms late activation with a larger budget. A critical “saturation” budget exists—about 12% of nodes for the airport graph and 10% for the e-mail graph—beyond which additional resources yield only marginal gains in T₉₀ and average damage.
• Weak correlation between robustness and resiliency. Scatter-plot analysis showed that configurations with high robustness can still recover slowly when under-funded, while low-robustness configurations can rebound rapidly if healing is timely and well resourced. A simple multiplicative fit $T_{90}\propto B^{-\beta }g\left(T\right)h\left(R\right)$ (with $\beta \approx 1$) summarizes this interaction.

4.1. Design Implications

Structural hardening alone is insufficient. Ensuring prompt, adequately funded self-healing is equally, and sometimes more effective than raising the robustness threshold. Resource allocation policies should therefore target the critical budget that precedes saturation, and detection systems should minimize trigger delays.

4.2. Limitations and Future Work

We studied static budgets and single-layer networks. Extending the framework to adaptive budgets, multi-layer interdependencies and spatially constrained repair crews would bring the analysis closer to operational practice. Incorporating load-based dynamics in the same concurrent setting is another important step, as is validating the model on time-stamped failure-and-repair data from real infrastructures.

By quantifying both robustness and resiliency, and their subtle interplay, this work provides a foundation for the recovery-aware design of complex networked systems.