Age of Information Minimization in Vehicular Edge Computing Networks: A Mask-Assisted Hybrid PPO-Based Method

Abstract

With the widespread deployment of various emerging intelligent applications, information timeliness is crucial for intelligent decision-making in vehicular networks, where vehicular edge computing (VEC) has become an important paradigm to enhance computing capabilities by offloading tasks to edge nodes. To promote the information timeliness in VEC, an optimization problem is formulated to minimize the age of information (AoI) by jointly optimizing task offloading and subcarrier allocation. Due to the time-varying channel and the coupling of the continuous and discrete optimization variables, the problem exhibits non-convexity, which is difficult to solve using traditional mathematical optimization methods. To efficiently tackle this challenge, we employ a hybrid proximal policy optimization (HPPO)-based deep reinforcement learning (DRL) method by designing the mixed action space involving both continuous and discrete variables. Moreover, an action masking mechanism is designed to filter out invalid actions in the action space caused by limitations in the effective communication distance between vehicles. As a result, a mask-assisted HPPO (MHPPO) method is proposed by integrating the action masking mechanism into the HPPO. Simulation results show that the proposed MHPPO method achieves an approximately 28.9% reduction in AoI compared with the HPPO method and about a 23% reduction compared with the mask-assisted deep deterministic policy gradient (MDDPG).

1. Introduction

In 2025, there are already 400 million connected vehicles on the road globally, with applications in the Internet of Vehicles (IoV), such as intelligent traffic control and autonomous driving, that are experiencing exponential growth [1,2,3]. With the widespread deployment of these applications, the data generated by connected vehicles each month have exceeded 10 exabytes. These data-intensive applications will substantially increase the demand for computational resources and low latency, which cannot be fully met by the limited computational capacity of vehicles, thereby intensifying the need for advanced network architectures. Vehicular edge computing (VEC), as an emerging computing architecture, has been presented as an effective solution [4]. By offloading the tasks to road-side units (RSUs) equipped with mobile edge computing (MEC) servers or to neighboring vehicles which have idle computational resources [5], VEC is able to reduce computation latency and alleviate local computational burdens, which makes it an indispensable component of future IoV systems.

The joint optimization of computation offloading and resource allocation in VEC has made significant progress. Some existing studies primarily focus on optimizing latency [6,7], energy consumption [8,9], the trade-off between latency and energy consumption [10,11], or utility functions [12,13]. In VEC networks, latency is a crucial metric for evaluating the efficiency of task processing, which directly impacts the timeliness of real-time applications. Many existing latency-related studies on VEC networks mainly study vehicle-to-infrastructure (V2I) offloading strategies [14,15,16,17,18,19]. That is, in the aforementioned studies, the tasks were only allowed to be offloaded to the RSUs over V2I links for computing, where vehicle-to-vehicle (V2V) links were not involved for offloading tasks to vehicles with idle resources. Motivated by this, [20,21,22,23,24,25] integrated V2I offloading with V2V offloading to improve the network performance further. Haibo et al. [20] proposed a tabu search-based matching method to minimize the delays and energy consumption by jointly optimizing offloading ratios, target selection, channel allocation, mode selection, and computation resource allocation coefficients. Wenhao et al. [21] proposed an algorithm based on generalized Benders decomposition to minimize the total task processing delays by jointly optimizing the task offloading, allocation of wireless channels, and distribution of computing resources. Huang et al. [22] proposed a distributed algorithm based on coalition formation games to minimize the total task completion delay in VEC networks by jointly optimizing sub-channel allocation, power control, and bandwidth allocation policies. Chenhao et al. [23] proposed a Deep Q-Network-based method to maximize the delay and energy consumption utility by optimizing the offloading decision. Song et al. [24] proposed a novel RSU-assisted learning-based method to minimize the task execution delay by jointly optimizing offloading ratio and offloading decision. Jianbin et al. [25] proposed deep reinforcement learning (DRL)-based method for the ISAC-assisted VEC network to minimize the delay and energy consumption by jointly optimizing offloading ratio and proportion of bandwidth. The aforementioned studies have made progress in delay optimization, but this metric is not able to fully satisfy the need for freshness and timeliness of information as it primarily focuses on the end-to-end transmission latency and computing latency while neglecting other critical factors that determine information utility in time-sensitive applications. Specifically, conventional delay metrics do not adequately capture the complete lifecycle of tasks, as they overlook the critical time interval between task generation and the commencement of processing, during which tasks may remain queued in the system.

Age of information (AoI), an effective metric of information freshness, has been presented to describe the time interval between the reception of the latest packet by the information receiver and the generation of the packet [26]. The larger the AoI, the less fresh the information becomes. Owing to its critical role in evaluating real-time system performance, AoI has gained increasing research attention and spurred a wealth of research [27,28,29,30,31,32,33,34,35,36]. Refs. [29,30,31,32,33,34,35,36] are studies on AoI in the field of edge computing, most of them following conventional paradigms, primarily focusing on assessing the freshness of raw task data or state information while overlooking the timeliness of task computation processes in edge computing environments [29,30,31,32,33]. Some studies extend the scope of AoI to the domain of computational timeliness [34,35,36]. In [34], Yingying et al. proposed an AoI-based optimization strategy for computation offloading and transmission scheduling, aiming to optimize AoI in both the transmission and execution phases under latency and energy constraints in Internet of Things (IoT) networks. In [35], Long et al. investigated a multi-device MEC system, where status updates were achieved through task computation, and the timeliness of these updates was evaluated using AoI. And they proposed an online algorithm to minimize AoI by jointly optimizing task generation, computation offloading, and resource allocation. In [36], Liqin et al. investigated a VEC scenario that supports only vehicle-to-infrastructure (V2I) communication, using AoI as a key metric for evaluating task timeliness. And they formulated an optimization model aimed at maximizing the utility function of AoI and computational energy efficiency (CEE).

Therefore, to meet the timeliness requirements of vehicles, this paper focuses on minimizing the AoI in a VEC network that integrates both V2I and V2V offloading. To the best of our knowledge, this paper is the first work to use AoI as a metric for task timeliness in a VEC network that combines the V2I and V2V offloading. The main contributions of this paper are summarized as follows.

• To fully utilize vehicular computing resources, we consider a VEC network in which vehicles can offload computational tasks to the RSU as well as vehicles with idle computational resources. To effectively optimize the characteristic of information timeliness, an optimization problem that aims to minimize the Aol by jointly optimizing task offloading ratios, service node selection strategies, and subcarrier resource allocation schemes is formulated.
• Due to the time-varying channel and the coupling of continuous and discrete optimization variables, a mask-assisted hybrid proximal policy optimization (MHPPO)-based DRL method is proposed, which the mixed action space is designed to handle the challenge coupling of the continuous and discrete optimization variables. Moreover, within the MHPPO method, an action masking mechanism is employed to filter the invalid actions.
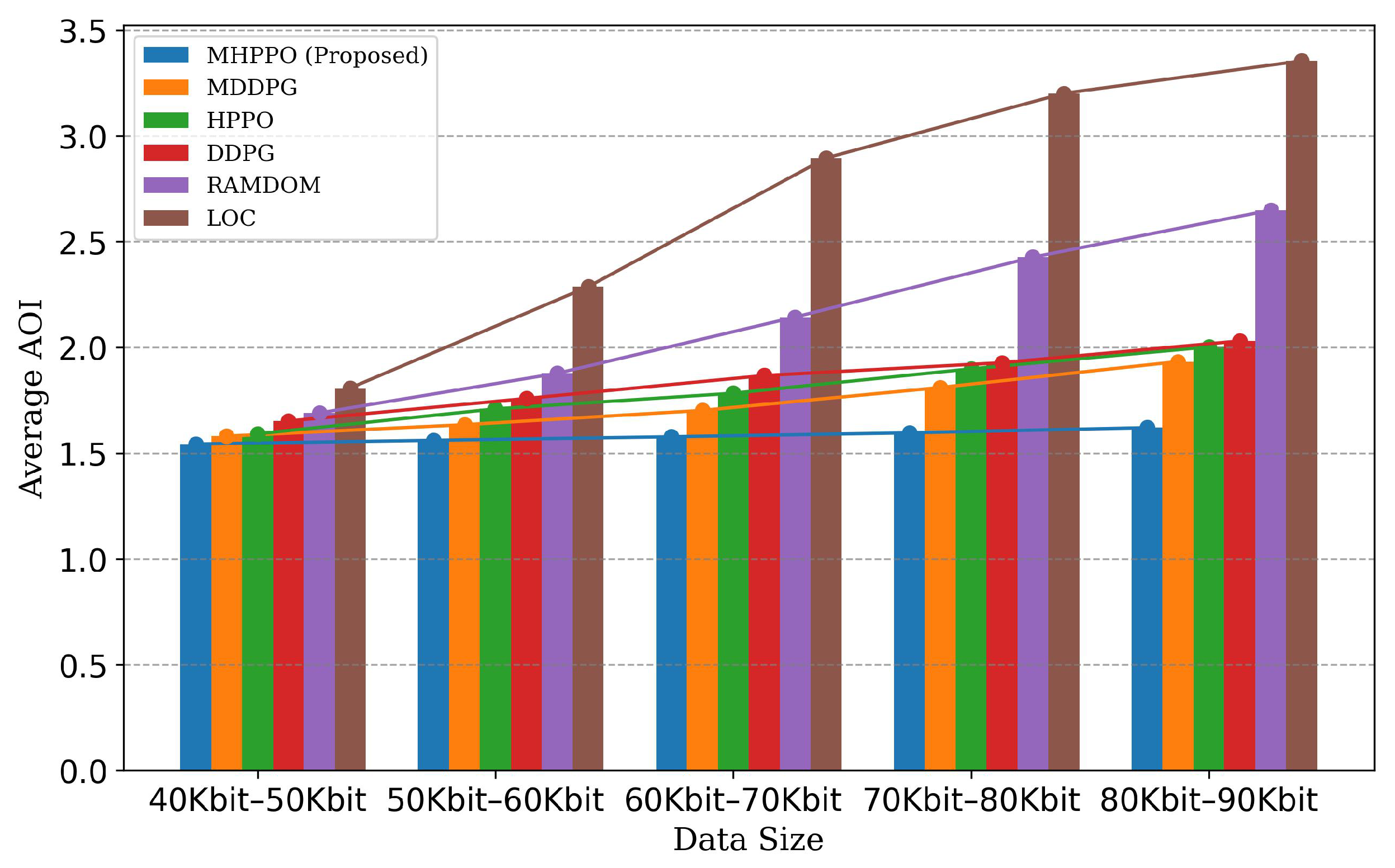
• Simulation results show that the proposed MHPPO method can achieve much lower average AoI and outperforms other benchmark methods. Specifically, the proposed MHPPO method reduces AoI by approximately 28.9% compared with the HPPO method, and by about 23% and 38.2% compared with the mask-assisted deep deterministic policy gradient (MDDPG) and the conventional DDPG method.

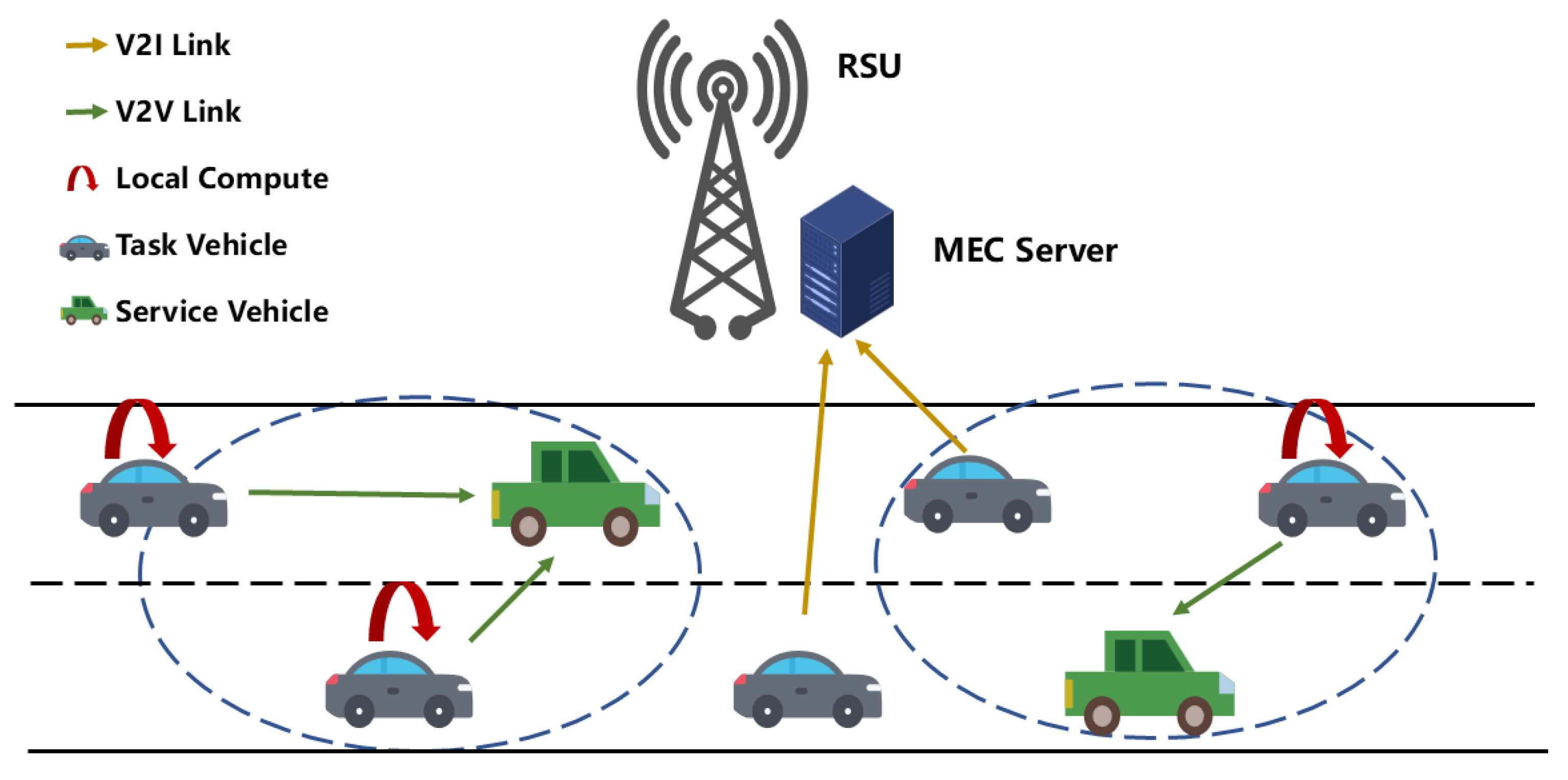
2. System Model

As depicted in Figure 1, a typical VEC network is considered, which consists of an RSU, multiple task vehicles, and multiple service vehicles moving at constant speeds in the same direction. Computational offloading services for the vehicles are provided by the MEC server deployed on the RSU and the service vehicles that have idle computing resources. Denote $\mathcal{TV}=\{1,2,\dots ,V\}$ as the sets of the task vehicles and $\mathcal{SV}=\{1,2,\dots ,S\}$ as the sets of the service vehicles.

The system is executed in a time-slotted manner, the time is split into many time slots of equal length, and $\tau$ represents the length of each such time slot. At the beginning of each time slot, a task with a data amount of $D_i$ is randomly generated by the i-th task vehicle, $\forall i\in \mathcal{TV}$, with a probability $\lambda$, where $\lambda \in [0,1]$. Each task vehicle manages a task queue. When a new task is generated, it is appended to the end of the queue. And tasks are processed in a first-in-first-out (FIFO) manner, starting from the head of the queue. Once a task is completed, it is immediately removed from the queue. The partial offloading model is considered, where the task is capable of being partitioned into two parts: one part is processed locally, and the other part is offloaded either to the RSU via a V2I link or to the neighboring service vehicles via a V2V link for processing [37]. So, we define $\mathcal{N}=\{0,1,2,\dots ,j,\dots ,S\}$ as the set of service nodes that consists of the MEC server and service vehicles, where 0 is the MEC server and j is the j-th service node. At the start of every time slot, the task vehicles process the task at the head of the queue based on the offloading ratio ${\xi }_i$.

We employ orthogonal frequency-division multiple access (OFDMA) technology to allocate K subcarrier resources among multiple task vehicles, which the set denotes as $\mathcal{K}=\{1,2,\dots ,K\}$ with each subcarrier having a bandwidth of B. The subcarrier allocation matrix is denoted as $\mathit{W}=\left\{w_{s,i,j}\mid w_{s,i,j}\in \{0,1\},s\in \mathcal{K},i\in \mathcal{TV},j\in \mathcal{N}\right\}$, where $w_{s,i,0}=1$ means that the subcarrier s is allocated to the i-th task vehicle for the purpose of offloading its task to the RSU, otherwise $w_{s,i,0}=0$. Similarly, $w_{s,i,j}=1$ means that the subcarrier s is allocated to the i-th task vehicle to enable the offloading of its task offload the task to the j-th service node, otherwise $w_{s,i,j}=0$.

2.1. Communication Model

For the communication model, we adopt the Vehicle-to-Everything (V2X) standard based on the 5G New Radio (NR) air interface for data transmission [38]. Given the OFDMA mechanism, interference is ignored due to exclusive subcarrier allocation. Therefore, for all $j\in \mathcal{N}$, the transmission rate between the i-th task vehicle and the j-th service node for task offloading in time slot t is expressed by

$$r_{i,j}\left(t\right)=B{\sum }_{s\in \mathcal{K},j\in \mathcal{N}}{w}_{s,i,j}{log}_2\left(1+{\displaystyle \frac{p_i^{\max }{h}_{i,j}\left(t\right)}{{\sigma }^2}}\right),$$

(1)

where $h_{i,j}\left(t\right)$ is the channel quality between the i-th task vehicle and the j-th service node in time slot t, ${\sigma }^2$ is the noise power, and $p_i^{\max }$ is the upper limit of the transmission power of the i-th task vehicle.

2.2. Computation Model

(1) Local Computing: The maximum data volume that the i-th task vehicle can process locally in time slot t is

$$D_{i,\mathrm{loc}}^{\max }\left(t\right)={\displaystyle \frac{f_i\tau }{C}},$$

(2)

where $f_i$ is the CPU frequency for the i-th task vehicle and C is the the task’s computational intensity, representing the CPU cycles needed per bit of data processing. Denote $D_i^{\mathrm{rem}}\left(t\right)$ as the remaining data amount of the task at the head of the task queue for the i-th task vehicle in time slot t. If $D_{i,\mathrm{loc}}^{\max }\left(t\right)\ge {\xi }_i{D}_i^{\mathrm{rem}}\left(t\right)$, the part of the task processed locally can be completed in time slot t, otherwise it cannot be completed. Therefore, the amount of local computation data $D_i^{\mathrm{loc}}\left(t\right)$ of the i-th task vehicle in time slot t is

$$D_i^{\mathrm{loc}}\left(t\right)=min\left\{D_{i,\mathrm{loc}}^{\max }\left(t\right),{\xi }_i{D}_i^{\mathrm{rem}}\left(t\right)\right\}.$$

(3)

(2) Edge Computing: When offloading the task to the service nodes, we can choose the RSU or other service vehicles to assist in the computation. Let the binary variable ${\beta }_{ij}$ denote the offloading selection factor. ${\beta }_{ij}=1$ indicates that the i-th task vehicle offloads the task to the j-th service node; ${\beta }_{ij}=0$ indicates that the i-th task vehicle does not offload the task to the j-th service node. Denote $D_{i,j}^{\mathrm{trans}}$ as the amount of data offloaded by the i-th task vehicle to the j-th service node in time slot t, which is given by

$$D_{i,j}^{\mathrm{trans}}\left(t\right)=min\left\{{\beta }_{i,j}\tau r_{i,j}\left(t\right),{\beta }_{i,j}(1-{\xi }_i)D_i^{\mathrm{rem}}\left(t\right)\right\}.$$

(4)

The MEC server and each service vehicle maintain their own independent task queues. When tasks are offloaded from a task vehicle to the service nodes, they are directly added to the tail of the corresponding queue and processed on a first-come, first-served (FCFS) basis. Specifically, if $D_{i,j}^{\mathrm{trans}}\left(t\right)=0$, it means that no task is offloaded; otherwise, the task volume $D_{i,j}^{\mathrm{trans}}\left(t\right)$ is added to the task queue of the j-th service node. So, the task queue of the MEC server $Q_{\mathrm{MEC}}\left(t\right)$ consists of the offloaded tasks from all task vehicles, which is given by

$$Q_{\mathrm{MEC}}\left(t\right)=\{(N_k^{\mathrm{MEC}},R_k^{\mathrm{MEC}}\left(t\right))\mid k\in \{1,2,...,K^{\mathrm{MEC}}\left(t\right)\}\},$$

(5)

where $N_k^{\mathrm{MEC}}$ is the ID of the task vehicle that offloaded the task k in the queue of MEC server, $R_k^{\mathrm{MEC}}\left(t\right)$ is the remaining unprocessed data volume of the task k in time slot t, and $K^{\mathrm{MEC}}\left(t\right)$ is the total number of tasks in the MEC server queue in time slot t.

Similarly, for all $n\in \mathcal{SV}$, the task queue of the n-th service vehicle $Q_n\left(t\right)$ is given by

$$Q_n\left(t\right)=\{(N_k^n,R_k^n\left(t\right))\mid k\in \{1,2,...,K_n\left(t\right)\}\},$$

(6)

where $N_k^n$ is the ID of the task vehicle that offloaded the k-th task in the queue of n-th service vehicle, $R_k^n\left(t\right)$ is the remaining unprocessed data volume of task k in time slot t, and $K_n\left(t\right)$ is the total number of tasks in the queue of the n-th service vehicle in time slot t.

For the MEC server, it sequentially processes tasks from the head of the queue at the beginning of each time slot. $C_{\mathrm{rem}}^{\mathrm{MEC}}\left(t\right)$ is defined as the remaining computational capacity of the MEC server during time slot t. At the beginning of the time slot, it is initialized to the maximum data volume that the MEC server can process within that time slot, denoted as

$$C_{\max }^{\mathrm{MEC}}={\displaystyle \frac{f^{\mathrm{MEC}}\tau }{C}},$$

(7)

where $f^{\mathrm{MEC}}$ is the CPU frequency for the MEC server. The change in $C_{\mathrm{rem}}^{\mathrm{MEC}}\left(t\right)$ during time slot t is expressed by

$$C_{\mathrm{rem}}^{\mathrm{MEC}}\left(t\right)=\left\{\begin{array}{cc}{C}_{\mathrm{rem}}^{\mathrm{MEC}}\left(t\right)-R_k^{\mathrm{MEC}}\left(t\right),\hfill & C_{\mathrm{rem}}^{\mathrm{MEC}}\left(t\right)\ge R_k^{\mathrm{MEC}}\left(t\right),\hfill \\ 0,\hfill & C_{\mathrm{rem}}^{\mathrm{MEC}}\left(t\right)<R_k^{\mathrm{MEC}}\left(t\right).\hfill \end{array}\right.$$

(8)

In time slot t, at each task completion, $C_{\mathrm{rem}}^{\mathrm{MEC}}\left(t\right)$ decreases by the corresponding data volume. This process continues until either all tasks in the queue are completed or $C_{\mathrm{rem}}^{\mathrm{MEC}}\left(t\right)$ is fully exhausted. If the total data volume of the task queue is less than or equal to $C_{\max }^{\mathrm{MEC}}$, it indicates that the MEC server can process all tasks within the time slot t, resulting in the task queue being cleared. Conversely, if the total data volume of the task queue exceeds $C_{\max }^{\mathrm{MEC}}$, it means that the MEC server cannot process all tasks within the time slot t, leading to only a subset of tasks being processed, with the remaining tasks deferred to the next time slot. Therefore, for task k with remaining data volume $R_k^{\mathrm{MEC}}\left(t\right)$, the amount of data processed by the k-th task in the MEC server in time slot t is

$$P_k^{\mathrm{MEC}}\left(t\right)=min\{R_k^{\mathrm{MEC}}\left(t\right),C_{\mathrm{rem}}^{\mathrm{MEC}}\left(t\right)\}.$$

(9)

Let $N_{\mathrm{MEC}}\left(t\right)$ denote the number of tasks that can be processed by the MEC in time slot t. So, the total task data of the i-th task vehicle processed by the MEC server in time slot t is

$$D_i^{\mathrm{MEC}}\left(t\right)={\sum }_{k\in {\mathcal{I}}_i^{\mathrm{MEC}}\left(t\right)}{P}_k^{\mathrm{MEC}}\left(t\right),$$

(10)

where ${\mathcal{I}}_i^{\mathrm{MEC}}\left(t\right)=\{k\mid N_k^{\mathrm{MEC}}=i,k\in [1,N_{\mathrm{MEC}}\left(t\right)]\}$ denotes the set of tasks that belong to the i-th task vehicle and are processed by the MEC server in time slot t.

The service vehicles are the same as the MEC server, so the total task data of the i-th task vehicle processed by the n-th service vehicle in time slot t is

$$D_{i,n}\left(t\right)={\sum }_{k\in {\mathcal{I}}_{i,n}\left(t\right)}{P}_{k,n}\left(t\right),$$

(11)

where ${\mathcal{I}}_{i,n}\left(t\right)=\{k\mid N_{k,n}=i,k\in [1,N_n\left(t\right)]\}$ represents the set of tasks that belong to the i-th task vehicle and are processed by the the n-th service vehicle in time slot t, $N_n\left(t\right)$ is the number of tasks that can be processed by the n-th service vehicle in time slot t, and $P_{k,n}\left(t\right)$ is the amount of data processed by task k in the the n-th service vehicle in time slot t.

So, the amount of data that belong to the i-th task vehicle’s task computed by the service nodes in time slot t is given by

$$D_i^{\mathrm{off}}\left(t\right)=D_i^{\mathrm{MEC}}\left(t\right)+{\sum }_{n=1}^S{D}_{i,n}\left(t\right).$$

(12)

As mentioned above, $D_i^{\mathrm{rem}}\left(t\right)$ is the remaining data amount of the task at the head of the task queue for the i-th task vehicle in time slot t. If $D_i^{\mathrm{rem}}\left(t\right)=0$, the task at the head of the queue is completed and is removed from the task queue. Then, the remaining data amount of the task at the head of the task queue for the i-th task vehicle in time slot $(t+1)$ is

$$D_i^{\mathrm{rem}}(t+1)=min\{0,D_i^{\mathrm{rem}}\left(t\right)-D_i^{\mathrm{loc}}\left(t\right)-D_i^{\mathrm{off}}\left(t\right)\}.$$

(13)

2.3. AoI Model

In this scenario, the task vehicles obtain decision information derived through a series of processing steps. We use AoI to evaluate the timeliness of this decision information. $Ao{I}_i\left(t\right)$ denotes the time elapsed since the last time the i-th task vehicle completed computing the task at the head of queue. Denote $t_i^{\mathrm{next}}$ as the generation time of the second task in the queue of the i-th task vehicle and $Len\left(Q_i\right)$ represents the length of task queue in the i-th task vehicle. If the i-th task vehicle is able to finish the task at the head of the queue in time slot t and there are other tasks in the queue, $Ao{I}_i\left(t\right)$ is updated to the time elapsed since the generation of the second computational task; if the i-th task vehicle is not able to finish the task at the head of the queue in time slot t, $Ao{I}_i\left(t\right)$ increases linearly, otherwise $Ao{I}_i\left(t\right)$ is set to 1. Therefore, the evolution of AoI for the i-th task vehicle in time slot $(t+1)$ is expressed by

$$Ao{I}_i(t+1)=\left\{\begin{array}{cc}t-t_i^{\mathrm{next}},\hfill & D_i^{\mathrm{rem}}\left(t\right)\le D_i^{\mathrm{loc}}\left(t\right)+D_i^{\mathrm{off}}\left(t\right),Len\left(Q_i\right)>0,\hfill \\ Ao{I}_i\left(t\right)+\tau ,\hfill & D_i^{\mathrm{rem}}\left(t\right)>D_i^{\mathrm{local}}\left(t\right)+D_i^{\mathrm{off}}\left(t\right),\hfill \\ 1,\hfill & \mathrm{otherwise}.\hfill \end{array}\right.$$

(14)

3. Problem Formulation

For the considered VEC network, we aim to minimize the average AoI under given resource constraints. This is achieved by jointly optimizing the variables associated with the offloading ratio $\mathsf{\xi }$, offloading object $\mathit{B}$, and subcarrier allocation $\mathit{W}$. Mathematically, the task offloading and subcarrier allocation problem for the considered VEC network is expressed by

$$\begin{array}{cc}{\mathbf{P}}_{\mathbf{1}}\hfill & :\underset{\mathsf{\xi },\mathit{B},\mathit{W}}{min}\underset{T\to \infty }{lim}{\displaystyle \frac{{\sum }_{t=1}^T{\sum }_{i=1}^{V}Ao{I}_i\left(t\right)}{VT}}\hfill \\ \mathrm{s}.\mathrm{t}.\hfill & C1:0\le {\xi }_i\le 1\hfill \\ \hfill & C2:{\beta }_{ij}\in \{0,1\},i\in \mathcal{TV},j\in \mathcal{N}\hfill \\ \hfill & C3:{\sum }_{j\in \mathcal{N}}{\beta }_{ij}=1\hfill \\ \hfill & C4:\mathcal{N}\in \{0,1,2,\dots ,S\}\hfill \\ \hfill & C5:w_{s,i,j}\in \{0,1\}\hfill \\ \hfill & C6:{\sum }_{i\in \mathcal{TV},j\in \mathcal{N}}{w}_{s,i,j}=1,s\in \mathcal{K}\hfill \end{array}$$

(15)

where $C1$ is the range of values for the offloading ratio; $C2$ and $C3$ denote that only one offloading object can be selected, i.e., either to the RSU or to the service vehicles; $C4$ denotes the set of nodes that can be served; and $C5$ and $C6$ denote that each subcarrier is assigned to at most one task vehicle.

It is noted that problem ${\mathbf{P}}_{\mathbf{1}}$ is an NP-hard mixed-integer nonlinear programming problem (MINLP) because of its non-convex objective function and constraints, high coupling, and the involvement of both continuous and discrete variables. Therefore, the formulated optimization problem (${\mathbf{P}}_{\mathbf{1}}$) is highly complex and challenging to solve using conventional mathematical approaches [39,40]. Due to the limitations of traditional methods, DRL has gained increasing attention for its ability to adapt to dynamic environments. To address this challenge, Section 4 introduces an effective DRL-based method designed to tackle this problem efficiently.

4. Proposed PPO-Based Method

To solve ${\mathbf{P}}_{\mathbf{1}}$, we firstly transform it into a Markov Decision Process (MDP) and then solve it based on the HPPO method [41].

4.1. MDP Formulation

In this section, the RSU acts as the decision-making agent, collecting state information from task vehicles and generating optimized decisions based on these states. These decisions are transmitted to the task vehicles, which then interact with the environment and receive corresponding rewards, completing the MDP process. The design of the state space, the action space, and the reward function are described in detail below.

(1) State space: The state $\mathit{S}\left(\mathit{t}\right)$ in time slot t consists of the data sizes, the channel gains, and the AoI of each task vehicle, as described by

$$\mathit{S}\left(\mathit{t}\right)=\{{\mathit{D}}^{\mathrm{rem}}\left(\mathit{t}\right),\mathit{D}\left(\mathit{t}\right),{\mathit{D}}^{\mathrm{mec}}\left(\mathit{t}\right),{\mathit{D}}^{\mathrm{sv}}\left(\mathit{t}\right),\mathit{H}\left(\mathit{t}\right),\mathit{AoI}\left(\mathit{t}\right)\},$$

(16)

where ${\mathit{D}}^{\mathrm{rem}}\left(\mathit{t}\right)$ is the set of the remaining data amount of the head task in the task queue of each task vehicle in time slot t, $\mathit{D}\left(\mathit{t}\right)$ is the set of the total data size of tasks in the task queue of each task vehicle, ${\mathit{D}}^{\mathrm{mec}}\left(\mathit{t}\right)$ is the set of the sum of the task data to be computed by MEC, ${\mathit{D}}^{\mathrm{sv}}\left(\mathit{t}\right)$ is the set of the total sum of task data to be processed by service vehicles in time slot t, $\mathit{H}\left(\mathit{t}\right)$ gives the channel gains, and $\mathit{AoI}\left(\mathit{t}\right)$ is the set of AoI for task vehicles in time slot t.

(2) Action space: The action space includes the offloading ratio ${\xi }_i$, offloading object ${\beta }_{ij}$, and subcarrier allocation $w_{s,i}$, which is expressed by

$$\mathit{A}\left(t\right)=\left\{\mathsf{\xi }\right(t),\mathit{B}(t),\mathit{W}(t\left)\right\},$$

(17)

where $\mathsf{\xi }\left(t\right)=\{{\xi }_1,{\xi }_2,\cdots ,{\xi }_n\}$, ${\xi }_i$ is between 0 and 1; when ${\xi }_i=0$, the head task belongs to the i-th task vehicle is only processed locally; when ${\xi }_i=1$, the head task belongs to the i-th task vehicle is all offloaded to the service node for computation. $\mathit{B}\left(t\right)=\left\{{\beta }_{ij}\mid {\beta }_{ij}\in \{0,1\},i\in \mathcal{TV},j\in \mathcal{N}\right\}$ and $\mathit{W}\left(t\right)$ is the subcarrier allocation matrix. $\mathsf{\xi }\left(t\right)$ is continuous vector, and $\mathit{B}\left(t\right)$ and $\mathit{W}\left(t\right)$ are discrete vectors.

(3) Reward function: The goal of the offloading and subcarrier allocation policy is to minimize the AoI. Therefore, the reward function is

$$R\left(t\right)=-{\sum }_{i=1}^{V}Ao{I}_i\left(t\right).$$

(18)

4.2. MHPPO-Based Solution Strategy

Figure 2 illustrates the overall architecture of the proposed MHPPO method. The method consists of two main networks: the actor network and the critic network. The actor network generates both continuous and discrete action strategies. The continuous actor network, parameterized by ${\theta }_{\mathrm{c}}$, outputs the mean and variance which are used to construct a Gaussian distribution over the continuous action space. The discrete actor network, parameterized by ${\theta }_{\mathrm{d}}$, outputs a probability distribution over the discrete action space. The critic network, parameterized by $\varphi$, evaluates the value of the state. The agent interacts with the environment in the following way: the actor network outputs the probability distribution for discrete actions and the mean and variance for continuous actions to construct a Gaussian distribution based on the input state $s_t$ and generates specific actions $a_t$ by sampling. After interacting with the environment, a reward $r_t$ will received by the agent, followed by a transition to the next state $s_{t+1}$. So, the data $\{s_t,a_t,r_t,s_{t+1}\}$ are obtained and stored in the replay buffer.

In the process of action selection, due to the distance limitation of inter-vehicle communication, the action space of unloading objects may contain some targets that cannot be unloaded. To address the problem, an action masking mechanism is introduced. The specific realization idea is to set the sampling probability of invalid actions to zero in the action selection stage. Specifically, if the distance between the task vehicle and the n-th service vehicle exceeds the predefined communication range, the sampling probability of selecting this service vehicle in the action space for offloading decisions is set to 0. With the action masking mechanism applied, the discrete action probability distribution is transformed into a mask categorical distribution, where invalid actions are masked out by assigning them zero probability.

In the update phase, a random mini-batch of Msamples is extracted from the experience replay buffer and the actor and critic networks perform parameter updates by minimizing their respective objective functions. After several iterations, the optimized policy is applied to the environment interaction and new data are continuously collected to further improve performance. In order to continuously optimize the actor networks, their parameters ${\theta }_c$ and ${\theta }_d$ need to be updated by continuous training. In this paper, we adopt the PPO-Clip approach, which relies on specialized tailoring of the objective function to reduce the differences between the old and new policies. The strategies are updated by multi-step stochastic gradient descent to maximize the objective function. The continuous actor network’s objective function is

$$L_{\mathrm{c}}^{\mathrm{clip}}\left({\theta }_{\mathrm{c}}\right)={\mathbb{E}}_t\left[min\left(r_t^{\mathrm{c}}\left({\theta }_{\mathrm{c}}\right)\widehat{A_t},\mathrm{clip}(r_t^{\mathrm{c}}\left({\theta }_{\mathrm{c}}\right),1-ϵ,1+ϵ)\widehat{A_t}\right)\right],$$

(19)

where $\widehat{A_t}$ is the advantage function and $r_t^{\mathrm{c}}\left({\theta }_{\mathrm{c}}\right)$ is the ratio coefficient between the new continuous strategy and the old continuous strategy, which is represented as

$$r_t^{\mathrm{c}}\left({\theta }_{\mathrm{c}}\right)={\displaystyle \frac{{\pi }_{{\theta }_{\mathrm{c}}}\left(a_t^{\mathrm{c}}\right|s_t)}{{\pi }_{{\theta }_{\mathrm{c}}\left(\mathrm{old}\right)}\left(a_t^{\mathrm{c}}\right|s_t)}}.$$

(20)

Similarly, the objective function of the discrete actor network is

$$L_{\mathrm{d}}^{\mathrm{clip}}\left({\theta }_{\mathrm{d}}\right)={\mathbb{E}}_t\left[min\left(r_t^{\mathrm{d}}\left({\theta }_{\mathrm{d}}\right)\widehat{A_t},\mathrm{clip}(r_t^{\mathrm{d}}\left({\theta }_{\mathrm{d}}\right),1-ϵ,1+ϵ)\widehat{A_t}\right)\right],$$

(21)

where $r_t^{\mathrm{d}}\left({\theta }_{\mathrm{d}}\right)$ is the ratio coefficient between the new discrete strategy and the old discrete strategy.

The critic network continuously updates the parameters $\varphi$ by minimizing the loss function $L_{critic}\left(\varphi \right)$, expressed as

$$L_{\mathrm{critic}}\left(\varphi \right)={\displaystyle \frac{1}{M}}{\sum }_{i=1}^M{(V_{\varphi }\left(s_t\right)-V_{\mathrm{target}})}^2,$$

(22)

where $V_{\varphi }\left(s_t\right)$ is value function and $V_{\mathrm{target}}$ is given by

$$V_{\mathrm{target}}={\sum }_{t^{\prime }=t}^T{\gamma }^{t^{\prime }-t}{r}_{t^{\prime }}.$$

(23)

5. Results and Discussion

In this section, a typical VEC system model is simulated, the detailed parameter settings of the simulation are presented, and the performance of the proposed method is discussed.

5.1. Simulation Settings

We performed simulation experiments in Python 3.7 using pytorch. In our simulation, we set up one MEC server, and 10 task vehicles and 5 service vehicles were randomly distributed along a single-directional road stretching 1 km. The speed of each vehicle ranged between 40 and 50 km/h. Each task vehicle generates a task of a certain data size at each time slot with a probability of 0.4, and the time slot length is 10 ms. The size of the data size of each task is limited to [40, 50] kB, and its computational intensity is all 1000 cycles/byte. In addition, the bandwidth of each subcarrier is 180 KHz. The transmit power and CPU cycle frequency of each task vehicle were 0.2 W and [0.5, 1] GHz, the CPU frequency of the MEC server was selected at 30 GHz, and the CPU frequency of each SV was selected at [2, 4] GHz. Vehicles could communicate up to a maximum distance of 200 m. Regarding the proposed MHPPO method, two hidden layers were set up for both the actor network and the critic network. The first hidden layer comprises 256 units, followed by 128 units in the second layer. Additionally, the experience replay buffer maintains a capacity of 1000 transitions, with mini-batches of 128 samples randomly sampled during training. A discount factor of 0.99 is applied, while the Adam optimizer is employed to minimize the loss function throughout the training phase.

5.2. Simulation Results

To demonstrate the efficiency of the proposed MHPPO method, we compared its performance with the benchmark methods, as detailed below:

(1) HPPO: The method does not employ an action masking mechanism, allowing the agent to select from the full action space, which may result in the choice of invalid actions.

(2) MDDPG: Based on the DDPG method, an action masking mechanism is the same to the proposed method is incorporated to filter out invalid actions.

(3) DDPG: A traditional DDPG method is trained to learn the offloading and allocation policy.

(4) RAMDOM: Task vehicles randomly select actions.

(5) LOC: All tasks are computed locally.

The convergence performance of the proposed method under diverse learning rate combinations is illustrated in Figure 3. The results indicate that the proposed method achieves convergence within 150 iterations across most learning rate settings. And different learning rates exhibit varying effects on the convergence performance. Too large learning rates may lead to oscillations in the convergence curve, while too small learning rates may result in slower convergence speeds. Therefore, we set the learning rate to 0.001 for the actor network and 0.01 for the critic network in the simulation.

To validate the effectiveness and superiority of the proposed method, Figure 4 illustrates the curves of the average AoI versus the number of iterations for the proposed MHPPO and the other benchmark methods. The results indicate that the proposed method consistently outperforms the baseline methods, and compared with the LOC, it achieves about a 113% reduction in average AoI. These improvements are attributed to the edge-assisted computing scenario considered in this work, which makes full use of more computational resources for optimization, and at the same time introduces the action masking mechanism to effectively shield illegitimate actions.

To investigate how the quantity of task vehicles influences the average AoI, Figure 5 illustrates the average AoI performance of the six methods with varying numbers of task vehicles. The number of task vehicles ranges from 10 to 50, increasing by 10 each time. The results indicate that, apart from LOC, the average AoI of the other five methods rises as the number of task vehicles increases. This can be attributed to the fact that, under conditions of constrained edge computing and communication resources, an increase in the number of users leads to a higher task load, while the communication resources allocated to each task vehicles decrease, thereby leading to a rise in task latency. Specifically, the proposed MHPPO method demonstrates a noticeable increase in AoI, but it remains the best in terms of performance among all these six methods. And the performance degradation is more gradual compared to other baseline methods, indicating its robustness in handling a higher number of task vehicles. In contrast, the average AoI of the LOC is basically unaffected by the change in the number of task vehicles because it only relies on the computational capability of the local device itself, which is independent of the number of task vehicles. In conclusion, as the number of task vehicles grows, the proposed MHPPO consistently demonstrates better AoI performance compared to the other baseline methods.

To explore how task data volume influences the average AoI, Figure 6 compares the AoI performance of different methods under varying data size ranges. The experiment systematically evaluates the effect of task data volume on AoI by adjusting the data size from [40–50] Kbit to [80–90] Kbit. The number of task vehicles is 20. The results demonstrate that the average AoI gradually increases as the data size increases. Moreover, among all benchmark methods, the proposed MHPPO method achieves better performance, maintaining the lowest average AoI across all tested data sizes, and its AoI tends to change more gently with the increase of task data volume, which further validates its superiority.

To investigate how the quantity of service vehicles affects performance, Figure 7 shows the average AoI performance for both methods across varying numbers of service vehicles. The system configuration consists of 20 task vehicles with data sizes ranging from 100 to 110 Kbit. When increasing the number of service vehicles from 0 to 20 in increments of 5, experimental results demonstrate a decrease in average AoI. Notably, the scenario without any service vehicles exhibits about a 45.3% performance gap compared to the scenario equipped with 20 service vehicles. This is due to the fact that more computing resources are available to process the tasks more efficiently, thus reducing the information delay. Meanwhile, the proposed method has better performance.

To investigate the impact of two-way traffic on computation offloading performance and stability of the system, Figure 8 shows the rewards performance for both the one-way traffic scenario and two-way traffic scenario. The scenarios include two experimental settings with task vehicle counts of 10 (TV = 10) and 20 (TV = 20), respectively. The results show that there is no significant difference in system performance between them. This can be attributed to the fact that offloading efficiency is primarily constrained by computational and communication resources rather than vehicle movement patterns. The reward values converge to similar levels, indicating that the traffic direction has minimal impact on computational offloading efficiency. And system stability remains unaffected, as curves remain stable in both one-way and two-way conditions without significant fluctuations or performance degradation.

To investigate the impact of service nodes’ scheduling strategies on system performance, Figure 9 compares the reward function curves under three distinct task scheduling policies:

(1) FCFS: The scheduling strategy adopted by the service nodes in this paper.

(2) Shortest-Job-First (SJF): Task with the smallest data volume is processed first.

(3) Priority: Tasks are processed according to their predefined priority levels.

The results show that the FCFS scheduling policy achieves relatively better performance compared to the priority and SJF strategies. Specifically, the FCFS strategy stabilizes faster and maintains a higher reward compared to the other two policies. And the SJF policy has the lowest rewards; a potential explanation is that the system prioritizes scheduling smaller tasks, resulting in prolonged accumulation of larger tasks and consequently increasing the overall waiting time. In conclusion, the proposed MHPPO method maintains stable performance regardless of the FCFS, SJF, and priority scheduling policies, indicating its strong adaptability to diverse scheduling policies across service nodes.

To investigate the impact of task arrival models on system performance, Figure 10 compares the reward function curves under three distinct arrival models: task arrival model based a Bernoulli process, task arrival model based on Poisson, and Pareto-distributed bursty traffic model.

It is observed that all task arrival models eventually converge to the same reward value while the number of task vehicles is 10 (TV = 10). This suggests that when the system is lightly loaded, the arrival model has negligible impact on overall performance, as the system can handle tasks efficiently regardless of their distribution. However, when the number of task vehicles increases to 20 (TV = 20), the task arrival model based on the Bernoulli process and task arrival model based on Poisson achieve similar performance, both outperforming the Pareto-distributed bursty traffic model. This can be attributed to the fact that the bursty traffic model results in clustered task arrivals, causing momentary overload and intensified resource competition, which in turn results in delays and reduces overall rewards.

6. Conclusions

In this paper, we focused on the collaborative service mechanism between idle vehicles and an MEC server in an VEC network, and investigated the problem of jointly optimizing computation offloading and subcarrier allocation. Unlike existing works that primarily aim at latency minimization, we introduced AoI as the optimization objective to better characterize the timeliness of information. To address this optimization problem, a MHPPO method was proposed. Simulation results showed that the proposed MHPPO method outperforms other baseline methods in reducing the average AoI. The findings of this study may provide some reference value for improving the performance of VEC systems, particularly in applications where real-time data freshness is important, such as autonomous driving, traffic management, and emergency response systems. In the future, we will expand our research to address more complex scenarios, including bidirectional vehicle mobility and multi-RSU environments. Furthermore, we will investigate incentive mechanisms for service vehicles to promote active participation and optimize overall system performance.